
Searching problems come in many varieties. A compiler looks up a variable name to find its type and address. A spelling checker looks up a word in a dictionary to ensure that it is spelled correctly. A directory program looks up a subscriber name to find a telephone number. An Internet domain name server looks up a name to find an IP address. These applications, and thousands like them, all need to search a set of data to find the information associated with a particular item.
This column studies in detail one searching problem: how do we store a set of integers, with no other associated data? Though tiny, this problem raises many of the key issues that arise in implementing any data structure. We’ll start with the precise definition of the task, and use that to investigate the most common set representations.
We’ll continue with the problem of the last column: generating a sorted sequence of m random integers in the range [0, maxval), chosen without duplicates. Our job is to implement this pseudocode:
initialize set S to empty
size = 0
while size < m do
t = bigrand() % maxval
if t is not in S
insert t into S
size++
print the elements of S in sorted order
We’ll call our data structure an IntSet, for set of integers. We’ll define the interface to be a C++ class with these public members:
class IntSetImp {
public:
IntSetImp(int maxelements, int maxval);
void insert(int t);
int size();
void report(int *v);
};
The constructor IntSetImp initializes the set to be empty. The function has two arguments describing the maximum number of elements in the set and (one greater than) the maximum size of any element; a particular implementation may ignore one or both of those parameters. The insert function adds a new integer to the set, if it is not already present. The size function tells the current number of elements, and report writes the elements (in sorted order) into the vector v.
This little interface is clearly for instructional use only. It lacks many components critical for an industrial-strength class, such as error handling and a destructor. An expert C++ programmer would probably use an abstract class with virtual functions to specify this interface, and then write each implementation as a derived class. We will instead take the simpler (and sometimes more efficient) approach of using names such as IntSetArr for the array implementation, IntSetList for the list implementation, and so forth. We’ll use the name IntSetImp to represent an arbitrary implementation.
This C++ code uses such a data structure in this function to generate a sorted set of random integers:
void gensets(int m, int maxval)
{ int *v = new int[m];
IntSetImp S(m, maxval);
while (S.size() < m)
S.insert(bigrand() % maxval);
S.report(v);
for (int i = 0; i < m; i++)
cout << v[i] << "\n";
}
Because the insert function does not put duplicate elements into the set, we need not test whether the element is in the set before we insert it.
The easiest implementation of an IntSet uses the powerful and general set template from the C++ Standard Template Library:
class IntSetSTL {
private:
set<int> S;
public:
IntSetSTL(int maxelements, int maxval) { }
int size() { return S.size(); }
void insert(int t) { S.insert(t); }
void report(int *v)
{ int j = 0;
set<int>::iterator i;
for (i = S.begin(); i != S.end(); ++i)
v[j++] = *i;
}
};
The constructor ignores its two arguments. Our IntSet, size and insert functions correspond exactly to their STL counterparts. The report function uses the standard iterator to write the elements of the set into the array, in sorted order. This general-purpose structure is good but not perfect: we’ll soon see implementations that are a factor of five more efficient for this particular task in both time and space.
We’ll build our first set implementation with the simplest structure: an array of integers. Our class keeps the current number of elements in the integer n, and the integers themselves in the vector x:
private:
int n, *x;
(The complete implementation of all classes can be found in Appendix 5.) This pseudocode version of the C++ constructor allocates the array (with one extra element for a sentinel) and sets n to zero:
IntSetArray(maxelements, maxval)
x = new int[1 + maxelements]
n = 0
x [0] = maxval
Because we have to report the elements in sorted order, we’ll store them that way at all times. (Unsorted arrays are superior in some other applications.) We’ll also keep the sentinel element maxval at the end of the sorted elements; maxval is larger than any element in the set. This replaces the test for running off the end of the list with a test for finding a greater element (which we already need). That will make our insertion code simpler, and will incidentally make it faster:
void insert(t)
for (i = 0; x[i] < t; i++)
;
if x[i] == t
return
for (j = n; j >= i; j--)
x[j+1] = x[j]
x[i] = t
n++
The first loop scans over array elements that are less than the insertion value t. If the new element is equal to t, then it is already in the set so we return immediately. Otherwise, we slide the greater elements (including the sentinel) up by one, insert t into the resulting hole, and increment n. This takes O(n) time.
The size function is identical in all of our implementations:
int size()
return n
The report function copies all of the elements (except the sentinel) to the output array in O(n) time:
void report(v)
for i = [0, n)
v[i] = x[i]
Arrays are an excellent structure for sets when the size is known in advance. Because our arrays are sorted, we could use binary search to build a member function that runs in O(log n) time. We’ll see details on the run times of arrays at the end of this section.
If the size of a set is not known in advance, linked lists are a prime candidate for set representation; lists also remove the cost of sliding over elements in an insertion.

Our class IntSetList will use this private data:
private:
int n;
struct node {
int val;
node *next;
node(int v, node *p) { val = v; next = p; }
};
node *head, *sentinel;
Each node in a linked list has an integer value and a pointer to the next node in the list. The node constructor assigns its two parameters to the two fields.
For the same reasons that we used sorted arrays, we’ll keep our linked lists in sorted order. Just as in arrays, our lists will use a sentinel node with a value larger than any real value. The constructor builds such a node and sets head to point to it.
IntSetList(maxelements, maxval)
sentinel = head = new node(maxval, 0)
n = 0
The report function walks the list, putting the sorted elements into the output vector:
void report(int *v)
j = 0
for (p = head; p != sentinel; p = p->next)
v[j++] = p->val
To insert an item into a sorted linked list we walk along the list until we either find the element (and immediately return), or find a greater value, and insert it at that point. Unfortunately, the variety of cases usually leads to complicated code; see Solution 4. The simplest code I know for the task is a recursive function that is originally called as
void insert(t)
head = rinsert(head, t)
node *rinsert(p, t)
if p->val < t
p->next = rinsert(p->next, t)
else if p->val > t
p = new node(t, p)
n++
return p
When a programming problem is hidden under a pile of special cases, recursion often leads to code as straightforward as this.
When we use either structure to generate m random integers, each of the m searches runs in time proportional to m, on the average. Each structure will therefore take total time proportional to m2. I suspected that the list version would be slightly faster than the array version: it uses extra space (for the pointers) to avoid moving over the upper values in the array. Here are the run times with n held fixed at 1,000,000 and m varying from 10,000 to 40,000:
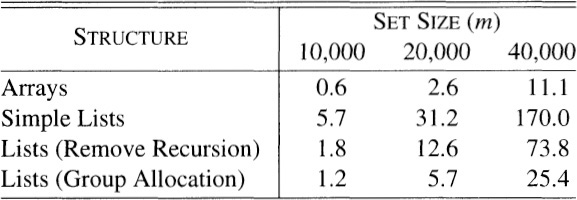
The run time of arrays grew quadratically, just as I expected, with very reasonable constants. My first implementation of lists, though, started out an order of magnitude slower than arrays, and grew faster than n2. Something was wrong.
My first response was to blame the recursion. In addition to the overhead of the recursive call, the recursion depth of the rinsert function is the position in which the element is found, which is O(n). And after recurring all the way down the list, the code assigns the original value back into almost every pointer. When I changed the recursive function to the iterative version described in Solution 4, the run time dropped by a factor of almost three.
My next response was to change the storage allocation to use the technique in Problem 5: rather than allocating a new node for every insertion, the constructor allocates a single block of m nodes, and insert passes them out as they are needed. This was an improvement in two distinct ways:
The cost model for run time in Appendix 3 shows that storage allocation is about two orders of magnitude more time-consuming than most simple operations. We have replaced m of those expensive operations with just one.
The cost model for space in Appendix 3 suggests that if we allocate nodes as a block, each node consumes just eight bytes (four for the integer and four for the pointer); 40,000 nodes consume 320 kilobytes and fit comfortably in my machine’s Level-2 cache. If we allocate the nodes individually, however, theneach consumes 48 bytes, and collectively their 1.92 megabytes overflows the Level-2 cache.
On a different system with a more efficient allocator, removing recursion gave a factor of five speedup, while changing to a single allocation gave just ten percent. Like most code-tuning techniques, caching and recursion removal sometimes yield great benefit, and other times have no effect.
The array insertion algorithm searches down the sequence to find the place to insert the target value, then pushes over the greater values. The list insertion algorithm does the first part, but not the second. So if lists do half the work, why do they take twice the time? Part of the reason is that they take twice as much memory: large lists must read 8-byte nodes into a cache to access the 4-byte integer. Another part of the reason is that arrays access data with perfect predictability, while access patterns for lists bounce all around memory.
We’ll turn now from linear structures to structures that support fast search and insertion. This picture shows a binary search tree after inserting the integers 31, 41, 59 and 26, in that order:
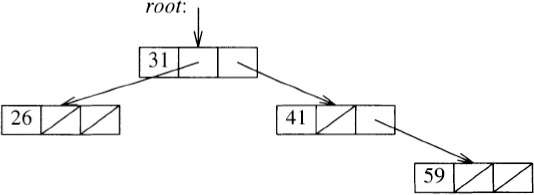
The IntSetBST class defines nodes and a root:
private:
int n, *v, vn;
struct node {
int val;
node *left, *right;
node(int i) { val = i; left = right = 0; }
};
node *root;
We initialize the tree by setting the root to be empty, and perform the other actions by calling recursive functions.
IntSetBST(int maxelements, int maxval) { root = 0; n = 0; }
void insert(int t) { root = rinsert(root, t); }
void report(int *x) { v = x; vn = 0; traverse(root); }
The insertion function walks down the tree until either the value is found (and the search terminates), or the search falls out of the tree (and the node is inserted):
node *rinsert(p, t)
if p == 0
p = new node(t)
n++
else if t < p->val
p->left = rinsert(p->left, t)
else if t > p->val
p->right = rinsert(p->right, t)
// do nothing i f p->val == t
return p
Because the elements in our application are inserted in a random order, we will not worry about sophisticated balancing schemes. (Problem 1 shows that other algorithms on random sets can lead to highly unbalanced trees.)
The inorder traversal† first processes the left subtree, then reports the node itself, and then processes the right subtree:
† My first version of this program led to a bizarre bug: the compiler reported an internal inconsistency and died. I turned off optimization, the “bug” went away, and I blamed the compiler writers. I later realized that the problem was that when I quickly wrote the traversal code, I forgot to include the if test for p being null. The optimizer tried to convert the tail recursion into a loop, and died when it could not find a test to terminate the loop.
void traverse(p)
if p == 0
return
traverse(p->left)
v[vn++] = p->val
traverse(p->right)
It uses the variable vn to index the next available element in the vector v.
This table gives the run time for the STL set structure that we saw in Section 13.1 (as it is implemented on my system), for binary search trees and for several structures that we’ll see in the next section. The maximum integer size is held fixed at n = 108, and m goes as high as possible until the system runs out of RAM and starts thrashing to disk.
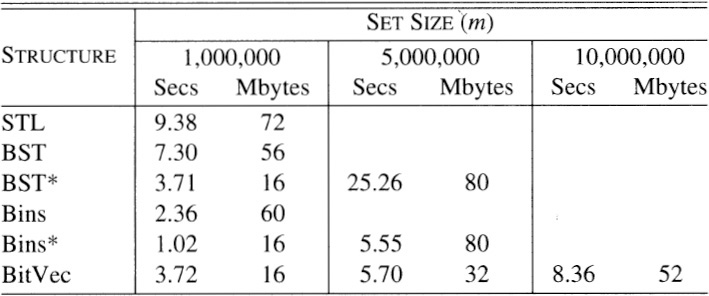
These times do not include the time required to print the output, which is slightly greater than the time of the STL implementation. Our simple binary search trees avoid the complex balancing scheme used by the STL (the STL specification guarantees good worst-case performance), and is therefore slightly faster and uses less space. The STL started thrashing at about m = 1,600,000, while our first BST thrashes at about m = 1,900,000. The row marked “BST*” describes a binary search tree incorporating several optimizations. The most important is that it allocates the nodes all at once (as in Problem 5). That greatly reduces the tree’s space requirements, which reduces the run time by about a third. The code also converts recursion to iteration (as in Problem 4) and uses the sentinel node described in Problem 7, for an additional speedup of about 25 percent.
We’ll turn now to two final structures that exploit the fact that our sets represent integers. Bit vectors are an old friend from Column 1. Here are their private data and functions:
enum { BITSPERWORD = 32, SHIFT = 5, MASK = 0x1F };
int n, hi, *x;
void set(int i) { x[i>>SHIFT] |= (1<<(i & MASK)); }
void clr(int i) { x[i>>SHIFT] &= ~(1<<(i & MASK)); }
int test(int i) { return x[i>>SHIFT] & (1<<(i & MASK)); }
The constructor allocates the arrays and turns off all bits:
IntSetBitVec(maxelements, maxval)
hi = maxval
x = new int[1 + hi/BITSPERWORD]
for i = [0, hi)
clr(i)
n = 0
Problem 8 suggests how we might speed this up by operating on a word of data at a time. Similar speedups apply to the report function:
void report(v)
j = 0
for i = [0, hi)
if test(i)
v[j++] = i
Finally, the insert function turns on the bit and increments n, but only if the bit was previously off:
void insert(t)
if test(t)
return
set(t)
n++
The table in the previous section shows that if the maximum value n is small enough so the bit vector fits in main memory, then the structure is remarkably efficient (and Problem 8 shows how to make it even more so). Unfortunately, if n is 232, a bit vector requires half a gigabyte of main memory.
Our final data structure combines the strengths of lists and bit vectors. It places the integers into a sequence of “buckets” or “bins”. If we have four integers in the range 0..99, we place them into four bins. Bin 0 contains integers in the range 0..24, bin 1 represents 25..49, bin 2 represents 50..74, and bin 3 represents 75..99:
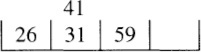
The m bins can be viewed as a kind of hashing. The integers in each bin are represented by a sorted linked list. Because the integers are uniformly distributed, each linked list has expected length one.
The structure has this private data:
private:
int n, bins, maxval;
struct node {
int val;
node *next;
node(int v, node *p) { val = v; next = p; }
};
node **bin, *sentinel;
The constructor allocates the array of bins and a sentinel element with a large value, and initializes each bin to point to the sentinel:
IntSetBins(maxelements, pmaxval)
bins = maxelements
maxval = pmaxval
bin = new node*[bins]
sentinel = new node(maxval, 0)
for i = [0, bins)
bin[i] = sentinel
n = 0
The insert function needs to place the integer t into its proper bin. The obvious mapping of t* bins/maxval can lead to numerical overflow (and some nasty debugging, as I can state from bitter personal experience). We will instead use the safer mapping in this code:
void insert(t)
i = t / (1 + maxval/bins)
bin[i] = rinsert(bin[i], t)
The rinsert is the same as for linked lists. Similarly, the report function is essentially the linked list code applied to every bin, in order:
void report(v)
j = 0
for i = [0, bins)
for (node *p = bin[i]; p != sentinel; p = p->next)
v[j++] = p->val
The table in the last section shows that bins are fast. The row marked “Bins*” describes the run time of bins that are modified to allocate all nodes during initialization (as in Problem 5); the modified structures use about one quarter the space and half the time of the original. Removing recursion dropped the run time by an additional ten percent.
We’ve skimmed five important data structures for representing sets. The average performance of those structures, when m is small compared to n, is described in this table (b denotes the number of bits per word):
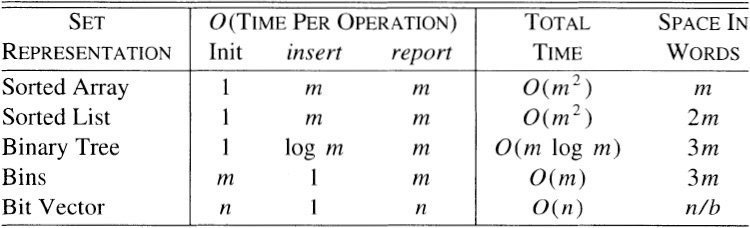
This table barely scratches the surface of set representations for problems like this; Solution 10 mentions other possibilities. Section 15.1 describes data structures for searching sets of words.
Although we’ve concentrated on data structures for set representations, we’ve learned several principles that apply to many programming tasks.
The Role of Libraries. The C++ Standard Template Library provided a general-purpose solution that was easy to implement and should prove simple to maintain and to extend. When you face a problem with data structures, your first inclination should be to search for a general tool that solves the problem. In this case, though, special-purpose code could exploit properties of the particular problem to be much faster.
The Importance of Space. In Section 13.2 we saw that finely tuned linked lists do half the work of arrays but take twice the time. Why? Arrays use half as much memory per element, and access memory sequentially. In Section 13.3 we saw that using custom memory allocation for binary search trees reduced space by a factor of three and time by a factor of two. Time increased substantially as we overflowed memory at magic boundaries (on my machine) at a half-megabyte (the Level-2 cache size) and near 80 megabytes (the amount of free RAM).
Code Tuning Techniques. The most substantial improvement we saw was replacing general-purpose memory allocation with a single allocation of a large block. This eliminated many expensive calls, and also used space more efficiently. Rewriting a recursive function to be iterative sped up linked lists by a whopping factor of three, but gave only a ten percent speedup for bins. Sentinels gave clean, simple code for most structures, and incidentally decreased the run time.
1. Solution 12.9 describes Bob Floyd’s algorithm for generating a sorted set of random integers. Can you implement his algorithm using the IntSets in this section? How do these structures perform on the nonrandom distributions generated by Floyd’s algorithm?
2. How would you change the toy IntSet interface to make it more robust?
3. Augment the set classes with a find function that tells whether a given element is in the set. Can you implement that function to be more efficient than insert?
4. Rewrite the recursive insertion functions for lists, bins and binary search trees to use iteration, and measure the difference in run times.
5. Section 9.1 and Solution 9.2 describe how Chris Van Wyk avoided many calls to a storage allocator by keeping a collection of available nodes in his own structure. Show how that same idea applies to IntSets implemented by lists, bins and binary search trees.
6. What can you learn by timing this fragment on the various implementations of IntSet?
IntSetImp S(m, n);
for (int i = 0; i < m; i++)
S.insert(i);
7. Our arrays, linked lists and bins all employ sentinels. Show how to apply the same technique to binary search trees.
8. Show how to speed up the initialization and reporting operations on bit vectors by using parallelism to operate on many bits at a time. Is it most efficient to operate on a char, short, int, long or some other unit?
9. Show how to speed up bins by replacing the expensive division operator with a cheaper logical shift.
10. What other data structures might be used to represent sets of integers in contexts similar to generating random numbers?
11. Build the fastest possible complete function to generate a sorted array of random integers without duplicates. (You need not feel constrained to use any prescribed interface for set representation.)
The excellent algorithms texts by Knuth and Sedgewick are described in Section 11.6. Searching is the topic of Chapter 6 (the second half) of Knuth’s Sorting and Searching, and is Part 4 (the final quarter) of Sedgewick’s Algorithms.
The toy structures in the body of this column have laid the groundwork for us to study an industrial-strength data structure. This sidebar surveys the remarkable structure that Doug McIlroy used to represent a dictionary in the spell program that he wrote in 1978. When I wrote the original columns in this book in the 1980’s, I spell-checked them all with McIlroy’s program. I used spell once again for this edition, and found that it is still a useful tool. Details of McIlroy’s program can be found in his paper “Development of a spelling list” in IEEE Transactions on Communications COM-30, 1 (January 1982, pp. 91-99). My dictionary defines a pearl as something “very choice or precious”; this program qualifies.
The first problem McIlroy faced was assembling the word list. He started by intersecting an unabridged dictionary (for validity) with the million-word Brown University corpus (for currency). That was a reasonable beginning, but there was much work left to do.
McIlroy’s approach is illustrated in his quest for proper nouns, which are omitted from most dictionaries. First came people: the 1000 most common last names in a large telephone directory, a list of boys’ and girls’ names, famous names (like Dijkstra and Nixon), and mythological names from an index to Bulfinch. After observing “misspellings” like Xerox and Texaco, he added companies on the Fortune 500 list. Publishing companies are rampant in bibliographies, so they’re in. Next came geography: the nations and their capitals, the states and theirs, the hundred largest cities in the United States and in the world, and don’t forget oceans, planets and stars.
He also added common names of animals and plants, and terms from chemistry, anatomy and (for local consumption) computing. But he was careful not to add too much: he kept out valid words that tend to be real-life misspellings (like the geological term cwm) and included only one of several alternative spellings (hence traveling but not travelling).
McIlroy’s trick was to examine spell’s output from real runs; for some time, spell automatically mailed a copy of the output to him (tradeoffs between privacy and efficacy were viewed differently in bygone days). When he spotted a problem, he would apply the broadest possible solution. The result is a fine list of 75,000 words: it includes most of the words I use in my documents, yet still finds my spelling errors.
The program uses affix analysis to peel prefixes and suffixes off words; that is both necessary and convenient. It’s necessary because there is no such thing as a word list for English; a spelling checker must either guess at the derivation of words like misrepresented or report as errors a lot of valid English words. Affix analysis has the convenient side effect of reducing the size of the dictionary.
The goal of affix analysis is to reduce misrepresented down to sent, stripping off mis-, re-, pre-, and -ed. (Even though represent doesn’t mean “to present again” and present doesn’t mean “sent beforehand”, spell uses coincidences to reduce dictionary size.) The program’s tables contain 40 prefix rules and 30 suffix rules. A “stop list” of 1300 exceptions halts good but incorrect guesses like reducing entend (a misspelling of intend) to en- + tend. This analysis reduces the 75,000 word list to 30,000 words. McIlroy’s program loops on each word, stripping affixes and looking up the result until it either finds a match or no affixes remain (and the word is declared to be an error).
Back-of-the-envelope analysis showed the importance of keeping the dictionary in main memory. This was particularly hard for McIlroy, who originally wrote the program on a PDP-11 that had a 64-kilobyte address space. The abstract of his paper summarizes his space squeezing: “Stripping prefixes and suffixes reduces the list below one third of its original size, hashing discards 60 percent of the bits that remain, and data compression halves it once again.” Thus a list of 75,000 English words (and roughly as many inflected forms) was represented in 26,000 16-bit computer words.
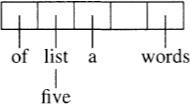
McIlroy used hashing to represent 30,000 English words in 27 bits each (we’ll see soon why 27 is a good choice). We’ll study a progression of schemes illustrated on the toy word list
a list of five words
The first hashing method uses an n-element hash table roughly the size of the list and a hash function that maps a string into an integer in the range [0, n). (We’ll see a hash function for strings in Section 15.1.) The ith entry of the table points to a linked list that contains all strings that hash to i. If null lists are represented by empty cells and the hash function yields h(a) = 2, h(list)= 1, etc., then a five-element table might look like
To look up the word w we perform a sequential search in the list pointed to by the h(w)th cell.
The next scheme uses a much larger table. Choosing n = 23 makes it likely that most hash cells contain just one element. In this example, h(a)= 13 and h(list) = 5.

The spell program uses n = 227 (roughly 134 million), and all but a few of the nonempty lists contain just a single element.
The next step is daring: instead of a linked list of words, McIlroy stores just a single bit in each table entry. This reduces space dramatically, but introduces errors. This picture uses the same hash function as the previous example, and represents zero bits by empty cells.

To look up word w, the program accesses the h(w)th bit in the table. If that bit is zero, then the program correctly reports that word w is not in the table. If the bit is one, then the program assumes that w is in the table. Sometimes a bad word happens to hash to a valid bit, but the probability of such an error is just 30,000/227, or roughly 1/4,000. On the average, therefore, one out of every 4000 bad words will sneak by as valid. McIlroy observed that typical rough drafts rarely contain more than 20 errors, so this defect hampers at most one run out of every hundred — that’s why he chose 27.
Representing the hash table by a string of n = 227 bits would consume over sixteen million bytes. The program therefore represents just the one bits; in the above example, it stores these hash values:
5 10 13 18 22
The word w is declared to be in the table if h(w) is present. The obvious representation of those values uses 30,000 27-bit words, but McIlroy’s machine had only 32,000 16-bit words in its address space. He therefore sorted the list and used a variable-length code to represent the differences between successive hash values. Assuming a fictitious starting value of zero, the above list is compressed to
5 5 3 5 4
McIlroy’s spell represents the differences in an average of 13.6 bits each. That left a few hundred extra words to point at useful starting points in the compressed list and thereby speed up the sequential search. The result is a 64-kilobyte dictionary that has fast access time and rarely makes mistakes.
We’ve already considered two aspects of spell’s performance: it produced useful output and it fit in a 64-kilobyte address space. It was also fast. Even on the ancient machines on which it was first built, it was able to spell-check a ten-page paper in half a minute, and a book the size of this one in about ten minutes (which seemed blazingly fast at the time). The spelling of a single word could be checked in a few seconds, because the small dictionary could be quickly read from disk.