CHAPTER I
THE PROPERTIES OF THE CIRCLE
INTRODUCTION
The long list of mathematical works written by Ibn al-Haytham includes several that are still missing. Among these are three that, in the mathematics of infinitesimals, speak for themselves: The Greatest Line that can be Drawn in a Segment of a Circle, a Treatise on Centres of Gravity and a Treatise on the Qarasṭūn. These treatises are all concerned with the geometry of measure. Their absence not only deprives historians of mathematics of facts that would have helped them to appreciate more clearly the range of Ibn al-Haytham’s oeuvre, but also, more seriously, it makes it absolutely impossible for them to understand the structures of this oeuvre and the network of meanings that they carry. If the first of the treatises cited above had been at our disposal, we should have a better understanding of the distance the author of a treatise on problems of figures with equal perimeters, on figures with equal areas and on the solid angle, travelled along the road of what was later to be called the calculus of variations.
This state of affairs is not peculiar to the geometry of measure; it is found also in the other type of geometry developed by Ibn al-Haytham and his predecessors: the geometry of position and forms. Among the books that until very recently were still missing we have one with the title On the Properties of Circles. A book with such a title is of course intriguing and surprising.1 We ask ourselves what Ibn al-Haytham might deal with in a book whose title appears so strikingly modern. His predecessors, his contemporaries and Ibn al-Haytham himself wrote books and papers on one or another aspect of a geometrical figure, for example triangles, but rarely on all its properties taken together as a whole. Furthermore, Ibn al-Haytham had written more than once on the circle, on finding its perimeter and finding its area. We may ask what reasons he might have had to return to the subject of the circle.
These were the kinds of questions that could have been asked, until I was able to produce a copy of the treatise, and establish a text of it, though a rather damaged one. Ibn al-Haytham’s short introduction could not fail to sharpen the reader’s curiosity and raise questions. The author indeed proposes to investigate the properties of the circle, or at least a certain number of them, since ‘the properties of circles are numerous, and their number is almost infinite’ (p. 87). He promises not to include in this treatise properties that have already been discovered. There is even a request to the reader that if, in the course of his reading, he happens to come upon a result that is already obtained elsewhere, he will see this as no more than a coincidence produced without the author’s knowledge. Thus, Ibn al-Haytham explicitly lays claim to novelty and originality.
Thus, the question becomes: where does Ibn al-Haytham see this novelty? A mathematician of his standing, of his universally inventive genius, could not describe as new a result that was secondary or partial: only an idea he considered fundamental could be called ‘new’. This last statement is not a petitio principi on our part, but the conclusion of a sufficiently long analysis of similar situations in the mathematical and optical works of Ibn al-Haytham. If it does sometimes happen that Ibn al-Haytham makes a mistake when proving a result, he always has a sharp eye in relation to the value of his programme of research.
And we shall in fact show that in this book Ibn al-Haytham did not confine himself to dealing with metrical properties of the circle, but also considered affine properties. It is as if he had intended to carry out a systematic exploration of the properties of the circle, and to classify them; which then has led him to investigate harmonic division and above all to devote about a third of the book to affine properties – similar ranges and, in particular, homothety. As far as I know, this is the first treatise in which this last form of geometrical transformation is studied in its own right.
The book sheds light on an important characteristic of Ibn al-Haytham’s research in geometry: his interest in geometrical transformations. As we have already pointed out, it is precisely this research that Ibn al-Haytham is pursuing in his book The Knowns. Four propositions from the treatise On the Properties of Circles reappear in The Knowns, and it is in any case very likely that the latter treatise was composed after the former one. The Knowns is closely connected2 with another of Ibn al-Haytham’s treatises, On Analysis and Synthesis, and his interest in transformations must have encouraged him to return to the concept of place – which is what Ibn al-Haytham worked on in a short paper that has survived – so it seems that On the Properties of Circles belongs to a substantial and homogeneous group of treatises.
The above statements are concerned with facts, titles and names, and are thus verifiable. It seems they might shed light on the novelty to which Ibn al-Haytham lays claim. But perhaps we should be wary of distorting the account of his thought by using the term homothety when he himself does not use such a word in his writings. We might be committing the cardinal sin of anachronism. The case would be further aggravated if we take into account that the term is not yet in use even at the end of the eighteenth century – it is indeed not to be found either in the Encyclopédie of d’Alembert and Diderot, or in the writings of mathematicians of the time – for example those of Euler and Clairaut. It is not until we come to Michel Chasles that the word ‘homothety (homothétie)’ appears, employed to designate a similarity of both form and position.3 All the same, it would hardly be reasonable to deny that mathematicians working earlier than the 1830s had any knowledge of homothety. In fact, in the history of mathematical concepts, such exclusive attitudes are often adopted at the cost of rather harsh simplifications; and, one might say, here as elsewhere, it does not greatly matter if we are taxed with anachronism, whatever judgment one wishes to convey by the term. On the other hand, it seems as important as it is difficult to discern what degree of rational awareness Ibn al-Haytham might have had of this concept, in work that followed on from that of Euclid, Pappus, the Banū Mūsā, Ibn Qurra, Ibn Sinān, al-Būzjānī, al-Qūhī, al-Sijzī and others, and preceded the work of Fermat and many later mathematicians. So the best approach is to examine the final group of propositions in his book, which deal with this concept, before setting about making comparisons with the works of his predecessors.
1. The concept of homothety
As we have already noted, in his book On the Properties of Circles, Ibn al-Haytham considers similar divisions, homothetic triangles and harmonic divisions and pencils, before again addressing homothety in his last ten propositions. A consecutive commentary on all the propositions, and in particular on the last ten, will be given below. Here we merely wish to point out the salient characteristics of this research on homothety, so as to get a better grasp of the idea Ibn al-Haytham may have had of this transformation.
So let us begin with Proposition 32. Ibn al-Haytham has two circles that touch one another – internally or externally (in the latter case equal or unequal circles) – and he intends to prove that certain elements are the transformed versions of others. In precise terms, let AC and CE be the two diameters from the point of contact C, and let CBD be a secant; we have
(1) the arcs BC and DC are similar,
(2) the arcs AB and DE are similar,
(3) 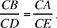
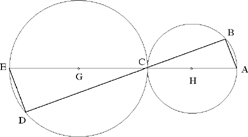
Fig. 1.1.1

Fig. 1.1.2
The reasoning emphasises that AB and ED are parallel, and the results in the statement follow immediately.
Ibn al-Haytham thus proves that to every secant straight line passing through C there correspond points B, D such that relation (3) holds. Now this ratio corresponds to the homothety with centre C and ratio 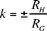
(where RH et RG are the radii of the two circles).
What we should note here is that Ibn al-Haytham’s procedure does not simply involve using homothetic triangles. He starts with two tangent circles, both given, and is seeking to prove that one is the transform of the other in a homothety, in order to deduce from this some correspondences between arcs. This procedure is different from that of his predecessor, al-Sijzī, who seems to make no deductions about the circles and the arcs.4 But it is also obviously different from the approach that starts from a single figure and finds another as its transform. In this last case, the homothety can be used heuristically, which is not so in the previous case.
The novelty of Ibn al-Haytham’s procedure consists, at least partly, in his identifying the elements of the homothety, its centre and its ratio. Thus, in Proposition 35, he again starts with two circles, but they are unequal and tangent externally. He draws the common exterior tangent and forms two homothetic triangles. He then characterises the position of the point of intersection of that tangent and the line of centres by means of a ratio. This gives the centre and the ratio of the homothety. He then deduces that the homologous radii are parallel and the homologous arcs are similar. Ibn al-Haytham does not stop there: once he has defined these concepts, he applies them to the other cases of the figure, taking as his starting point the point that divides the line segment joining the centres in the ratio of the radii, externally or internally; a point and a ratio that are none other than the centre and the ratio of one or other of the two homotheties in which one of the circles appears as the transform of the other.
Let us briefly return to Ibn al-Haytham’s method of proceeding; we run the risk of repeating ourselves, but our purpose is to understand his approach better. In Proposition 35, as later in Propositions 39 and 40, he continues to start with two circles C1 and C2, tangent externally or separate and unequal, as in Proposition 39. Let us consider – Proposition 35 – EE′ as a common tangent to the two circles; it cuts the line of centres HI in a point K beyond H. Ibn al-Haytham’s first concern is to determine the property of the point K.
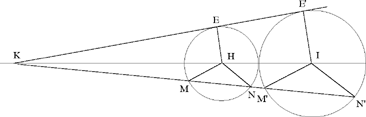
Fig. 1.2
From the property of the tangent EE′, he deduces that EH ‖ E′I, from which he deduces that the two triangles KEH and KE′I are homothetic; hence
(1) 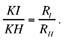
Ibn al-Haytham then proves that any secant passing through K to cut C2 in M and N and that cuts C1 in M′ and N′, the points homologous to them, defines similar arcs MN and M′N′. His reasoning proceeds as follows:
for a point K, centre of the positive homothety 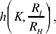 the following two properties are equivalent.
the following two properties are equivalent.
(1) Kis the point of intersection of the line of centres with the external common tangent;
(2) Klies on the straight line HI such that 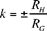
Ibn al-Haytham’s reasoning is the same in Propositions 39 and 40, where the circles are separate; the point K on the extended part of HI is defined by (1). In Proposition 39, Ibn al-Haytham proves that if KE is a tangent to C2, then it is a tangent to C1; that is E′ ∈ C1 and KE′ is a tangent to C1 at E′. Here, as in the following proposition, he proves that to any element of C2 (a point, an arc, a radius, a tangent, an angle and so on) there corresponds a homologous element of C1.
We may note that Ibn al-Haytham deals only with circles that touch one another, externally or internally, and separate circles, but never circles that intersect. This might have been a restriction designed to make the procedure easy. But it is not. The study of the homothety 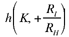 carried out in Propositions 35 and 39 would apply in an identical manner in the case where the circles cut one another; this application could not pass unnoticed by the mathematician.
carried out in Propositions 35 and 39 would apply in an identical manner in the case where the circles cut one another; this application could not pass unnoticed by the mathematician.
Ibn al-Haytham also considers cases in which, in today’s language, the homothety is negative. That is exactly what happens in Propositions 36 and 37. Here too he starts with two circles C1 and C2, one separate from the other, equal or unequal, and a point K on the segment IH such that
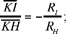
he proves that if KE touches C2 at E, then it touches C1 at E′ such that h(E) = E′. He proves that any secant passing through K cuts off two similar arcs on C2 and C1. In short, the two homotheties of ratio 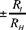 are studied for circles that touch externally and for circles that are separate from each other. As for circles that touch internally, in Proposition 32 Ibn al-Haytham studies the positive homothety. He returns to this study for circles touching internally in Proposition 43, but does not refer to the negative homothety for these last cases.
are studied for circles that touch externally and for circles that are separate from each other. As for circles that touch internally, in Proposition 32 Ibn al-Haytham studies the positive homothety. He returns to this study for circles touching internally in Proposition 43, but does not refer to the negative homothety for these last cases.
More generally, in all the research work incorporated into On the Properties of Circles, Ibn al-Haytham is much concerned with the properties of common tangents and proves that such tangents pass though one of the centres of homothety; he also emphasises the fact that homologous radii are parallel, the fact that angles at the centre are equal and repeatedly refers to homologous angles, whose homologous arcs he deduces are similar. That is, he emphasises the properties of the homothety, which itself now becomes the object of study. He was no doubt able to deduce from this that the two chords of the arcs were parallel and to find the ratio between them, one chord being that joining two arbitrary points on one of the circles, the other chord being that joining the homologous points of the second circle. Noticing that such chords were parallel would have simplified the investigation of the fact that certain straight lines are at right angles to one another, which plays a part in Propositions 35, 38, 41 and 42.
2. Euclid, Pappus and Ibn al-Haytham: on homothety
Ibn al-Haytham’s contribution to formulating the concept of a homothety is not confined to what can be found in his book On the Properties of Circles. But, before examining the corrections and generalisation he later introduced, we should take a brief look at the work of Euclid and of Pappus, to try to find possible relationships with the concepts they employ. Such investigation is required because it has been suggested that the same concept is indeed to be found in the work of these mathematicians. For Euclid, the reference is to Propositions 2, 5 and 6 of the sixth book of the Elements. These propositions consider two straight lines cut by two parallel straight lines.
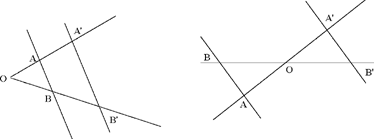
Fig. 1.3
In Proposition VI.2 we have

and in Propositions VI.5 and VI.6 we have
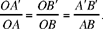
Similar triangles such as OAB and OA′B′ are what we call homothetic triangles. All the same, it is clear that Proposition VI.2 – which, moreover, serves as a basis for other propositions – is a special case of what is known as Thales’ theorem for two parallel straight lines. So we cannot identify this case with the one that appeals to homothetic triangles, with the centre and the ratio of a homothety, as in Propositions 11 and 26 of the treatise by Ibn al-Haytham. And it is precisely when we have the idea of the latter that we recognise the former; it is once we have an idea of that transformation, or at least of the correspondence between the two figures, that we identify Euclid’s results as an application of the transformation, but surely not conversely. Moreover, a knowledge of the property of homothetic triangles allowed Ibn al-Haytham to deduce the property of similar divisions on parallel straight lines, which are indeed called homothetic divisions. This is to say that the new property is fertile, and it is the property Ibn al-Haytham uses in Propositions 4 and 6. In short, Euclid’s work does not anticipate homothety, but rather is included in homothety.
One might ask whether the situation is different in regard to Pappus’ Mathematical Collection. It has been said this is so, at least for Propositions 102, 106 and 118 of the seventh book.
In the first two of these propositions, Pappus reasons in the same way. So it is enough to take Proposition 102. This is how the proposition is presented in the wording employed by the Alexandrian mathematician:
Let there be two circles ABΓ, ΔEB touching one another at the point B; let us draw through the point B straight lines ΓBΔ, ABE and let us draw the straight lines that join AΓ, ΔE; I say that the straight lines AΓ, ΔE are parallel.5

Fig. 1.4
To prove this proposition, Pappus begins from Elements III.32; if HBZ is the common tangent at the point B, he obtains
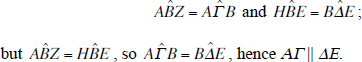
We have seen that Ibn al-Haytham established a proposition close to this one – but not identical with it – employing a different approach. Unlike Pappus, he immediately turns his attention to the homothetic triangles BAL and BEK. Better still, he determines the centre and the ratio of homothety.
Proposition 118 of Book VII is the one most often cited in connection with the question of homothety. The statement is:
Let there be two circles AB, ΓΔ; let us extend the straight line AΔ and let us make it such that the straight line EH is to the straight line HZ as the radius of the circle AB is to the radius of the circle ΓΔ; I say that, if a straight line drawn from the point H, to cut the circle ΓΔ, is extended, it also cuts the circle AB.6
It has already been pointed out that the statement is not perfectly precise.7 Pappus in fact begins his proof by saying:
[…] let us draw from the point H the straight line HΘ tangent to the circle ΓΔ; let us draw the straight line joining ZΘ, and let us draw the straight line EK parallel <to the straight line ZΘ>. Then, since the straight line EK is to the straight line ZΘ as the straight line EH is to the straight line ZH, the line passing through the points H, Θ, K is straight.8
Let us return to the proposition and try to make the most of Pappus’ text.
What we are given is two circles (E, RE) and (Z, RZ) and a point H on the straight line EZ such that 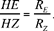
a) If HΘ is a tangent to (Z, RZ), it is a tangent to (E, RE). To prove this statement, Pappus draws EK ‖ ZΘ, where K lies on the circle (E, RE). So we have  it follows that H, Θ, K are collinear, and that the angle K is a right angle.
it follows that H, Θ, K are collinear, and that the angle K is a right angle.
b) A secant drawn to the circle (Z, RZ) cuts it between Δ and Θ; if we extend it, it passes between B and K; now HK is a tangent to (E, RE), so the secant also cuts the circle (E, RE).

Fig. 1.5
So we see that Pappus starts with two parallel radii, and from the equality of two ratios, given as equal by hypothesis, and that he draws his conclusion without appealing to the homothetic triangles. In contrast, in a closely similar case (see Propositions 39 and 40) Ibn al-Haytham draws attention to these triangles and uses the property of the homothety.
3. Ibn al-Haytham and homothety as a point by point transformation
All in all, it is very difficult to read Pappus’ texts as an application of homothety. So it seems Ibn al-Haytham might have been the first to have used homothety, before then going on to study it in its own right. This too turns out to be far from the truth. If we confine our attention simply to Ibn al-Haytham’s predecessors from the ninth century onwards, notably those who worked on geometrical transformations, we find they did indeed genuinely make use of homothety in their writings on infinitesimal mathematics as well as in those on geometrical analysis. For example, in the ninth century the Banū Mūsā made use of homothety in their study of concentric circles and regular polygons.9 Similarly, Thābit ibn Qurra used homothety for concentric circles and ellipses in his work on plane sections of the cylinder.10 Similarly, others in the tenth century, such as Ibn Sinān, al-Qūhī and al-Sijzī,11 in considering problems of geometrical analysis, used homothety before Ibn al-Haytham did. In this respect, we can again cite al-Qūhī and al-Sijzī, to look no further. Here, as elsewhere, Ibn al-Haytham’s work appears as the final stage in a tradition of research that is already a century and a half old. So, at least in historical terms, it is understandable why Ibn al-Haytham included this transformation and its applications in his treatise On the Properties of Circles. In this book, we see homothety being put to use as a technique for studying the correspondences between two figures; but it is much more significant that we are also witnessing the first known investigation into certain properties of the transformation: under homothety an arc becomes an arc, a radius becomes a radius, an angle between two straight lines becomes an angle between the two homologous straight lines; for two arcs related by homothety the tangents at homologous points are parallel, and so on.
This, it seems, is where the novelty of Ibn al-Haytham’s work is to be found. It would, however, be a mistake to ignore a limitation that is intrinsic to his conception that as yet – in this book on The Properties of Circles – prevents him from seeing homothety as a true point by point transformation. We have already noted that Ibn al-Haytham starts with two circles in order to prove that one is the transform of the other. Moreover, there is no proposition in his book in which he starts with the centre of homothety, the ratio of the homothety and a circle in order to then find another circle as the image of the first one. But if we do not look beyond this limitation, we are forgetting the place this book by Ibn al-Haytham occupies among his other works, and underestimating the intrinsic dynamics of on-going research in mathematics. Ibn al-Haytham’s treatise, as we now know, forms part of a group of writings in which he concerns himself with the geometry of transformations. Composing these works seems to be a necessary response to needs arising from various changes that affected the internal relationships between mathematical disciplines, and from the new outlook in some disciplines. We may note here, without elaborating further, that there was an increasingly close interpenetration between an Archimedean tradition of geometry and a tradition of the geometry of position and form. We may also take note that there was an awareness of algebra, direct or indirect but always huge. Even Ibn al-Haytham, a geometer par excellence, wrote on algebra.12 It is as these researches unfold that geometrical transformations appear more and more as being a new field of geometry; and it is at the end of this development that Ibn al-Haytham writes this group of books, to which his treatise The Knowns also belongs.
To attempt to illustrate this conceptual relationship, simply in regard to homothety, we shall return to a work by Ibn al-Haytham in which this affine transformation plays a part, not only in plane geometry but also in geometry in three dimensions; we shall then conclude with his study of this transformation in The Knowns.
In his work on figures with equal perimeters and equal surfaces (isoperimetric and isepiphanic figures), in which he presents the first account of a solid angle, Ibn al-Haytham employs homothety to obtain a sphere from another sphere. This is not the place to return to Ibn al-Haytham’s proof, of which we have already given an analysis.13 Here we shall confine ourselves to looking at some elements relating to the way homothety works.
Ibn al-Haytham starts from a sphere wih centre A, and in this sphere two pyramids with vertex A, whose bases are similar regular polygons. We can take the planes of these polygons to be parallel; in this case the centres of their circumcircles, B and E, lie on a straight line through A. In these circles we can also take the radii corresponding to the vertices of the polygons as parallel two by two; this we have BC ‖ EG and BD ‖ EH. In this case triangles CBD and GEH are similar. So if BF ⊥ CD and EM ⊥ GH, we have


Fig. 1.6
Ibn al-Haytham proves that the point K, the point of intersection of FM and AE, is the centre of the homothety with ratio 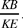 This homothety is then used throughout the proposition. He proves that this homothety transforms B, C, D into E, G, H respectively; that the planes (BCD) and (EGH) are homologous, as are the chords CD and GH. He then proves that the two angles CAD and GOH are equal if O is the transform of A. These angles are angles at the centre in two different spheres (A, AC) and (O, OG); so the planes (CAD) and (GOH) cut these spheres in similar arcs CLD and GUH. To show this, he proves that the two spheres and the two planes are homologous in this same homothety,
This homothety is then used throughout the proposition. He proves that this homothety transforms B, C, D into E, G, H respectively; that the planes (BCD) and (EGH) are homologous, as are the chords CD and GH. He then proves that the two angles CAD and GOH are equal if O is the transform of A. These angles are angles at the centre in two different spheres (A, AC) and (O, OG); so the planes (CAD) and (GOH) cut these spheres in similar arcs CLD and GUH. To show this, he proves that the two spheres and the two planes are homologous in this same homothety, 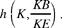
In fact, Ibn al-Haytham starts from the sphere (A, AC) using the previous homothety, and obtains the sphere (O, OG), then he proves that the plane (ACD) is homologous to the plane (OGH) and that the arc CLD is homologous to the arc GUH.
Thanks to widening its application to include plane figures as well as three-dimensional ones and its explicit use as a geometrical transformation, the status of homothety as a point by point transformation seems to be unambiguous. This is precisely what is confirmed by the study that Ibn al-Haytham carries out in The Knowns.
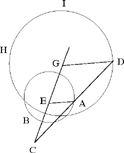
Fig. 1.7.1
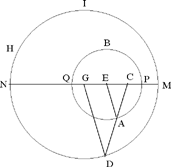
Fig. 1.7.2
The book followed naturally from this new research in geometry, and to some extent serves to complete it. In this book, Ibn al-Haytham studies the variability of elements of the figures and their transformations. It is lines that provide the basis for the theoretical treatment he puts forward in his work. In this connection, he returns to homothety in at least seven propositions in the first chapter of the book, as well as in the second chapter. So let us consider a single example, the first one, to illustrate his ideas. In Proposition 3 of the first chapter, he starts with a circle C (E, R), an arbitrary point C distinct from E, and a point A on the circumference of the circle. With the point A he associates a point D on the extended part of CA and such that 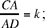 he then proves that D lies on another known circle. Thus, he proves that D is the image of A in the homothety
he then proves that D lies on another known circle. Thus, he proves that D is the image of A in the homothety 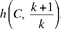 That is to say that D lies on the circle with centre G = h(E),
That is to say that D lies on the circle with centre G = h(E), 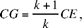 and radius
and radius 
It is hardly necessary to repeat that here, as in the preceding example, homothety appears as a point by point transformation. Indeed Ibn al-Haytham seems to want to confirm this idea, by proving what is more or less the converse in the following proposition – the fourth: if a straight line from the centre of the homothety, C, cuts the first circle in a point A, it will cut the second circle in D, and we shall have 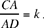
This is, moreover, the form in which the concept of a homothety appears after Ibn al-Haytham, for example in the work of Fermat. In the first proposition of his book The Reconstruction of the Two Books on Plane Loci by Apollonius of Perga (Apollonii Pergaei libri duo de locis planis restituti), Fermat proves that the homothetic image of a straight line is a parallel straight line and that the homothetic image of a circle is a circle.14
The history of the concept of a homothety from Euclid to Ibn al-Haytham and then to Fermat cannot be written as that of the prefiguration of a concept; it is rather the history of a double transition, a matter of gradual progression on the technical level, but somewhat abrupt on the theoretical one: from a correspondence between figures to the transformation of a figure, from technical use in the course of a proof to the study of the properties of the transformation. But, if we want to understand this double development, we must widen our scope beyond the narrow frame of the history of a concept. While not allowing ourselves to be led astray by the romantic notion of a complete history, we need, in this case, to situate homothety within the geometry of transformations, of which certain traces can be seen in the work of Archimedes and Apollonius, before it becomes a defined area of geometry from the mid ninth century onwards, and develops further in far distant climes in the seventeenth century. We need to remember that for Ibn al-Haytham homothety appears at the same time as other affine and projective transformations; and that later, in the book by Fermat that we have just cited, homothety is connected with similarity – notably with inversion. To the educated eye, the character of this intellectual landscape is not at all Hellenistic.
To this conclusion we may add another: although establishing the textual tradition was a necessary condition for tracing the evolution of the concept of homothety in Ibn al-Haytham’s works in the eleventh century, it is nevertheless the conceptual relationship that provided answers to the questions that arose in investigating the history of the text: it is highly likely that the text On the Properties of Circles preceded The Knowns.
4. History of the text
Ibn al-Haytham’s treatise On the Properties of Circles (Fī khawāṣṣ al-dawā’ir) appears in the list of his writings established by Ibn Abī Uṣaybi‘a.15 This important treatise was thought to be lost until the recent discovery of the manuscript in the V.I. Lenin Library in Kuibychev. Along with some writings by al-Bīrūnī, by Kamāl al-Dīn al-Fārisī, by al-Khafrī and by al-Kāshī, this manuscript includes several treatises by Ibn al-Haytham, one of them being the one that interests us here. This valuable collection has been transferred to St Petersburg and is now in the National Library with pressmark no. 600, Arabic new series.
The whole collection was copied on thin and transparent paper, slightly grey in colour. Because of the transparency of the paper, it often happens that the words of the text on the verso of the page show through on the recto, and vice versa, which sometimes makes reading awkward. Damp, decay of part of the folios and a tear in the lower left corner of a certain number of folios – notably in the text On the Properties of Circles – make reading very difficult, sometimes impossible.
The collection is not written in a single hand; we can in fact recognise at least two. Nevertheless the numerous treatises by Ibn al-Haytham are all in a single hand, the script is nasta‘līq, not very neat, the same script as in the copy of the treatise by the astronomer al-Khafrī, Zubdat al-mabsūṭāt, in the month of Rajab 1066, that is in May 1656. So the treatises by Ibn al-Haytham were copied at about this date, probably in some part of the Iranian world.
The text itself has been transcribed in black ink and the geometrical figures drawn in red ink. It has neither glosses nor additions in its margins and there seems to be nothing to indicate it has been compared with its original after the transcription was complete. Each folio measures 42.5 × 28 cm. We also observe that there are several series of numbering for the folios – evidence that the collection has been put together from several parts that have later been regrouped. In fact, in addition to the traces of a former numbering system, there are several others. Thus, the collection begins with a text by al-Kāshī in which we can recognise this old numbering, in Arabic numerals at the top of the page, a system which continues. A recent numbering in Indian numerals, at the bottom of the page, continues up to folio 493v. When we examined the manuscript, we were able to make the following list, adopting the recent numbering:
1v–10v: al-Kāshī, al-Risāla al-kamāliyya
11r: blank page
11v–31v: Muḥammad ibn Aḥmad al-Khafrī, Zubdat al-mabsūṭāt
32r: blank page
32v–270v: al-Fārisī, Tanqīḥ al-manāẓir
271r: title page
271r–301v: al-Fārisī, Zayl tanqīḥ al-manāẓir
301v–307v: al-Fārisī, Taḥrīr maqāla fī ṣūrat al-kusūf
308r–309v: Fihrist muṣannafāt Ibn al-Haytham
309v–310v: Ibn al-Haytham, Fī ḥall shakk fī al-shakl 4 min al-maqāla 12 li-Uqlīdis
310v–311r: Ibn al-Haytham, Fī qismat al-miqdarayn al-mukhtalifayn
311v: blank page
312r–326v: Ibn al-Haytham, Fī ḍaw’ al-qamar
326v–339v: Ibn al-Haytham, Fī aḍwā’ al-kawākib
339v–334v: Ibn al-Haytham, Fī kayfiyyat al-aẓlāl
335r–347v: Ibn al-Haytham, Fī al-ma‘lūmāt
348r–368r: Ibn al-Haytham, Fī al-taḥlīl wa-al-tarkīb
368v–420v: Ibn al-Haytham, Fī hay’at ḥarakāt kull wāḥid min al-kawākib
421r–431r: Ibn al-Haytham, Fī khawāṣṣ al-dawā’ir
431v: blank page
432r–432v: Ibn al-Haytham, Istikhrāj ḍil‘ al-muka‘‘ab
433r–489v: part of Tafhīm d’al-Bīrūnī, in another hand, with marginal glosses
490r–491v: part of Fī khawāṣṣ al-dawā’ir
492r–493v: treatise on algebra, anonymous and incomplete (late).
We note that the text On the Properties of Circles is made up of two parts (421r–431r and 490r–491v). But, whereas the first part (421r–431r) includes the title of the treatise as well as the colophon, the second part (490r–491v) is anonymous. It is for this reason that everyone who had examined the manuscript had thought that the complete text was to be found in the first part and had taken the second part as belonging to an anonymous mathematical treatise that appears at the end of the collection.16 It is identifying this last part that has allowed me to assemble a complete text of Ibn al-Haytham’s work, to put it in order and finally establish it as a text. The treatise appears in the following order:
421r–421v, 490r–490v, 422r–428v, 491v, 491r, 429r–431r.
We may also note that folio 491 is back to front. This kind of mistake is not rare; it reappears several times in other treatises. These mistakes have, in all probability, occurred when the collection was bound.
The bad state of the text On the Properties of Circles that we have described above made it extremely difficult to reconstruct. Sometimes we had no more than a few words to start from when reconstructing a whole paragraph. In reconstructing we called upon every means at our disposal: palaeography, philology and mathematics, as well as our familiarity with the writings of Ibn al-Haytham. Further, our long and numerous interventions require us to indicate explicitly what has been done, not only for the reader of Ibn al-Haytham’s Arabic text, as one has to do when establishing critical editions of texts, but also for the reader of the French and English translations. In the English translation (as in the French one) each of our interventions is isolated in the style <…>. Text between square brackets […] is an addition to the French text that is necessary for understanding the English text.
_______________
1 Another book by Ibn al-Haytham on conic sections, unfortunately missing, has an analogous title: Fī khawāṣṣ al-quṭū‘ (On the Properties of Conic Sections).
3 M. Chasles, Aperçu historique sur l’origine et le développement des méthodes en géométrie, Paris, 1889, p. 597, note. This is his memoir on the two general principles of geometry: duality and homography.
5 Pappus d’Alexandrie, La Collection mathématique, French trans. P. Ver Eecke, Paris/Bruges, 1933, p. 638.
6 Pappus, La Collection mathématique, p. 657.
7 Ibid., p. 657, note 3 by Ver Eecke.
8 Pappus, La Collection mathématique, pp. 657–8.
9 R. Rashed, Les Mathématiques infinitésimales du IXe au XIe siècle, vol. I: Fondateurs et commentateurs: Banū Mūsā, Thābit ibn Qurra, Ibn Sinān, al-Khāzin, al-Qūhī, Ibn al-Samḥ, Ibn Hūd, London, 1996, Chapter I, p. 37; English translation: Founding Figures and Commentators in Arabic Mathematics, A History of Arabic Sciences and Mathematics, vol. 1, Culture and Civilization in the Middle East, London, 2012, p. 43.
10 Ibid., for example Chapter II, pp. 475–6; English trans. p. 352.
11 We have mentioned several times that Ibn Sinān frequently employs geometrical transformations, both in his works on infinitesimal mathematics and in his research on conics. Among these numerous transformations, we also find homothety. See R. Rashed and H. Bellosta, Ibrāhīm ibn Sinān: Logique et géométrie au Xe siècle, Leiden, 2000, for example pp. 486–7, 551–2, 719–20. Ibn Sinān makes use of homothety, but without really investigating its properties as Ibn al-Haytham was to do. Ibn Sinān’s successor al-Qūhī, who took research on projections much further than his predecessors, also concerned himself with transformations and with homothety. Thus, in the first three propositions of his paper called Two Geometrical Problems, he gives the result stated and proved by Ibn al-Haytham in Proposition 3 of The Knowns (al-Mas’alatayn al-handasiyyatayn, ms. Istanbul, Aya Sofya 4832, fols 123v–124v; see the note on Proposition 3, p. 310). Al-Qūhī’s younger contemporary, Aḥmad ibn ‘Abd al-Jalīl al-Sijzī, in turn continues the use of transformations. Better still, he isolates the concept of transformation in its own right as an auxiliary method in analysis and in synthesis (see Appendix, Text 2). In various places he employs homothety, similarity, and even a primitive form of inversion (for homothety, see below, Proposition 32, note 22).
12 Les Mathématiques infinitésimales du IXe au XIe siècle, vol. II: Ibn al-Haytham, London, 1993, Tableau récapitulatif, no. 90, p. 532; English trans. Ibn al-Haytham and Analytical Mathematics. A History of Arabic Sciences and Mathematics, vol. 2, Culture and Civilization in the Middle East, London, 2012, List of Ibn al-Haytham’s works, p. 420.
13 Les Mathématiques infinitésimales du IXe au XIe siècle, vol. II, pp. 374–6 and vol. III; English trans. Ibn al-Haytham and Analytical Mathematics, pp. 289–95. The proof is long and complicated: five large pages. The figure has seventeen distinct points, eighteen solids, eight curves and thirty-five different straight lines.
14 Œuvres de Fermat, publiées par les soins de MM. Paul Tannery et Charles Henry, Paris, 1896, vol. III, pp. 3–5.
15 See vol. II, p. 522.
16 See Catalogue of the library of St Petersburg, no. 1588 and B. A. Rosenfeld in Nauka, Moscow, 1974, p. 124, no. 16.