1. L’assurda idea del giovanissimo
Werner Heisenberg: «gli osservabili»
«Erano più o meno le tre del mattino quando il risultato finale dei miei conti fu davanti a me. Mi sentivo profondamente scosso. Ero così agitato che non potevo pensare di dormire. Lasciai la casa e mi misi a camminare lentamente nell’oscurità. Mi arrampicai su una roccia a picco sul mare, sulla punta dell’isola, e attesi il sorgere del sole…».1
Mi sono chiesto spesso quali fossero i pensieri e le emozioni del giovane Heisenberg arrampicato sulla roccia a picco sul mare, nella spoglia e ventosa isola di Helgoland, nel Mare del Nord, mentre guardava la vastità delle onde, aspettando il sorgere del sole, dopo avere gettato per primo lo sguardo su uno dei più vertiginosi segreti della Natura che l’umanità abbia mai intravisto. Heisenberg aveva 23 anni.
Era lì per alleviare l’allergia di cui soffriva. Helgoland – il nome significa «isola sacra» – non ha praticamente alberi, c’è pochissimo polline. «Helgoland con il suo solo albero» la chiama Joyce nell’Ulisse. Era lì soprattutto per immergersi nel problema che lo ossessionava. La patata rovente che gli aveva messo fra le mani Niels Bohr. Dormiva pochissimo, passava il tempo in solitudine, tentando di calcolare qualcosa che giustificasse le incomprensibili regole di Bohr. Si interrompeva di tanto in tanto per arrampicarsi sulle rocce dell’isola. Nei brevi momenti di pausa imparava a memoria poesie del Divano occidentale-orientale di Goethe: la raccolta dove il massimo poeta tedesco canta il suo amore per l’Islam.
Niels Bohr era già scienziato rinomato. Aveva scritto formule semplici ma strane, che prevedevano le proprietà degli elementi chimici, prima ancora di misurarle. Prevedevano per esempio la frequenza della luce che emettono gli elementi scaldati: il colore che prendono. Un notevole successo. Le formule però erano incomplete: non permettevano di calcolare l’intensità della luce emessa.
Ma, soprattutto, queste formule avevano qualcosa di davvero assurdo: assumevano, senza motivo, che gli elettroni negli atomi orbitassero attorno al nucleo solo su certe precise orbite, a certe precise distanze dal nucleo, con certe precise energie; e poi «saltassero» magicamente da un’orbita all’altra. I primi «salti quantici». Perché solo quelle orbite? Che cosa sono questi incongrui «salti» da un’orbita all’altra? Quale forza sconosciuta può guidare un elettrone a seguire un comportamento così bizzarro?
L’atomo è il mattoncino elementare di tutto. Come funziona? Come si muovono gli elettroni al suo interno? Erano più di dieci anni che Bohr e i suoi colleghi giravano intorno a queste domande. A vuoto.
A Copenaghen Bohr aveva raccolto attorno a sé i più brillanti giovani fisici che era riuscito a trovare, per lavorare con loro, come nella bottega di un pittore del Rinascimento, sui misteri dell’atomo. Fra questi c’era Wolfgang Pauli, bravissimo, intelligentissimo, arrogante, spavaldo, amico e compagno di scuola di Heisenberg. Nonostante la sua arroganza, Pauli aveva raccomandato il suo amico Heisenberg al grande Bohr, dicendo che se si voleva andare avanti si doveva chiamare lui. Bohr gli aveva dato retta e nell’autunno del 1924 aveva invitato a Copenaghen anche Heisenberg, che era assistente del fisico Max Born a Göttingen. Heisenberg era rimasto a Copenaghen alcuni mesi, discutendo con Bohr davanti a lavagne piene di formule. Il ragazzo e il maestro avevano fatto insieme lunghe passeggiate in montagna parlando dei misteri dell’atomo, di fisica e di filosofia.2
Heisenberg si era immerso nel problema. Ne aveva fatto la sua ossessione. Aveva provato di tutto, anche lui, come gli altri. Niente funzionava. Nessuna forza ragionevole sembrava poter guidare gli elettroni sulle strane orbite e negli strani salti di Bohr. Eppure quelle orbite e quei salti portavano a predire bene i fenomeni atomici. Confusione.
Lo scoramento spinge a cercare rimedi estremi. Sull’isola del Mare del Nord, in solitudine, Heisenberg si era risolto a esplorare idee radicali.
In fondo erano idee radicali quelle con cui vent’anni prima Einstein aveva stupito il mondo. Il radicalismo di Einstein si era rivelato efficace. Pauli e Heisenberg erano innamorati della sua fisica. Einstein era il mito. Era forse arrivato il momento, si chiedevano, di azzardare un passo altrettanto radicale per uscire dall’impasse degli elettroni negli atomi? Se fossero riusciti loro a fare questo passo? A vent’anni si fanno sogni sfrenati.
Einstein aveva mostrato che le convinzioni più radicate possono essere sbagliate. Quello che sembra ovvio può non essere corretto. Abbandonare assunzioni che sembrano ovvie può portare a capire meglio. Aveva insegnato a basarsi solo su quanto vediamo, non su quanto pensiamo debba esistere.
Pauli ripeteva spesso queste idee a Heisenberg. I due ragazzi si erano abbeverati a questo miele velenoso. Avevano seguito le discussioni sulla relazione fra realtà e esperienza che attraversavano la filosofia austriaca e tedesca dell’inizio del secolo. Ernst Mach, che aveva avuto un’influenza determinante su Einstein, predicava la necessità di basare la conoscenza sulle sole osservazioni, liberandosi da ogni implicita assunzione «metafisica». Questi sono gli ingredienti disparati che si mescolano nei pensieri del giovanissimo Heisenberg, come componenti chimici di un esplosivo, quando si rifugia sull’isola di Helgoland, nell’estate del 1925.
E lì ha l’idea. Un’idea che si può avere solo nel radicalismo senza limiti dei vent’anni. L’idea destinata a sconvolgere l’intera fisica, l’intera scienza, la nostra intera concezione del mondo. L’idea che l’umanità, credo, non ha ancora digerito.
Il salto di Heisenberg è spericolato quanto semplice. Nessuno riusciva a trovare la forza capace di guidare gli elettroni nel loro bizzarro comportamento? Bene, allora lasciamo perdere una nuova forza. Usiamo piuttosto quella che già conosciamo: la forza elettrica che attira l’elettrone al nucleo. Non troviamo nuove leggi del moto che giustifichino le orbite e i salti di Bohr? Bene, teniamo le leggi del moto che già conosciamo, senza cambiarle.
Cambiamo invece il modo di pensare l’elettrone. Rinunciamo all’idea che un elettrone sia un oggetto che si muove lungo una traiettoria. Rinunciamo a descrivere il moto dell’elettrone. Descriviamo solo ciò che osserviamo dall’esterno: intensità e frequenza della luce emessa dall’elettrone. Basiamo tutto solo su quantità che siano osservabili. Questa è l’idea.
Heisenberg prova a ricalcolare il comportamento dell’elettrone usando unicamente le quantità che osserviamo: la frequenza e l’ampiezza della luce emessa. Cerca di ricalcolare l’energia dell’elettrone partendo da lì.
Noi osserviamo gli effetti di salti dell’elettrone da un’orbita di Bohr all’altra. Heisenberg rimpiazza le variabili fisiche con tabelle che hanno l’orbita di partenza sulle righe e l’orbita di arrivo sulle colonne. Ogni casella della tabella, che sta su una riga e su una colonna, descrive il salto da una particolare orbita a un’altra. Passa il tempo sull’isola cercando di usare queste tabelle per calcolare qualcosa che giustifichi le regole di Bohr. Dorme pochissimo. Non riesce a fare i conti per l’elettrone nell’atomo, sono troppo difficili. Prova a farli per un sistema più semplice: un pendolo. Cerca le regole di Bohr in questo caso semplificato.
Il 7 giugno qualcosa comincia a tornare:
«Quando il primo termine sembrò tornare giusto [ritrovare le regole di Bohr], cominciai ad agitarmi, a fare un errore di aritmetica dopo l’altro. Erano più o meno le tre del mattino quando il risultato finale dei miei conti fu davanti a me. Era giusto a tutti i termini.
«D’un tratto non ho più avuto dubbi sulla coerenza della nuova meccanica ‘quantistica’ che il mio calcolo indicava.
«Ero profondamente allarmato. Avevo la sensazione che attraverso la superficie dei fenomeni stavo guardando verso un interno di strana bellezza; mi sentivo stordito al pensiero che ora dovevo investigare questa nuova ricchezza di struttura matematica che la Natura così generosamente dispiegava davanti a me».
Parole che danno brividi. Attraverso la superficie dei fenomeni, «un interno di strana bellezza». Risuonano con le parole scritte da Galileo quando vede apparire una regolarità matematica nelle sue misure sulla caduta di oggetti lungo il piano inclinato, la prima legge matematica scoperta dall’umanità che descrive il moto di oggetti sulla Terra: «Non c’è emozione come intravedere la legge matematica dietro il disordine delle apparenze».
Il 9 giugno Heisenberg torna dall’isola di Helgoland alla sua università: Göttingen. Manda una copia dei risultati all’amico Pauli, commentando: «È tutto ancora molto vago e non mi è chiaro, ma sembra che gli elettroni non si muoveranno più su orbite».
Il 9 luglio consegna una copia del lavoro a Max Born, il professore di cui è assistente (non confondetelo con Niels Bohr, di Copenaghen), con una nota che dice: «Ho scritto un lavoro folle e non ho il coraggio di mandarlo a una rivista per pubblicazione». Gli chiede di leggerlo e consigliarlo.
Il 25 luglio Max Born manda lui stesso il lavoro di Heisenberg a «Zeitschrift für Physik».3
Ha intuito l’importanza del passo compiuto dal suo giovane assistente. Cerca di chiarire le cose. Coinvolge il suo studente Pascual Jordan per tentare di mettere ordine nei bizzarri risultati di Heisenberg.4 Heisenberg a sua volta prova a coinvolgere Pauli, ma Pauli è poco convinto: gli sembra un gioco matematico troppo astratto e astruso. All’inizio sono quindi solo in tre a lavorare sulla teoria: Heisenberg, Born e Jordan.
Lavorano febbrilmente e nel giro di pochi mesi riescono a mettere a punto l’intera struttura formale di una nuova meccanica. È semplicissima: le forze sono le stesse della fisica classica; le equazioni sono le stesse della fisica classica (più unaa di cui parlo più avanti); ma si sostituiscono variabili con tabelle di numeri, o «matrici».
Perché tabelle di numeri? Quello che osserviamo di un elettrone in un atomo è la luce emessa quando, secondo l’ipotesi di Bohr, l’elettrone salta da un’orbita all’altra. Un salto coinvolge due orbite: quella di partenza e quella di arrivo. Ciascuna osservazione si può quindi disporre, come ho accennato, nella casella di una tabella, dove l’orbita di partenza fissa la riga e quella di arrivo la colonna.
L’idea di Heisenberg è di scrivere tutte le quantità che descrivono il moto dell’elettrone non più come numeri, ma come tabelle di numeri. Invece di avere una sola posizione x per l’elettrone, si ha un’intera tabella X di possibili posizioni: una per ogni possibile salto. L’idea della nuova teoria è continuare a usare le equazioni della fisica di sempre, semplicemente rimpiazzando le quantità usuali (posizione, velocità, energia e frequenza dell’orbita…) con queste tabelle. Intensità e frequenza della luce emessa in un salto, per esempio, saranno determinate dalla corrispondente casella della tabella. La tabella che corrisponde all’energia ha numeri solo sulla diagonale, e questi saranno le energie delle orbite di Bohr.

Una matrice di Heisenberg: la tabella di numeri che «rappresenta» la posizione dell’elettrone. Il numero X23 per esempio si riferisce al salto dalla seconda alla terza orbita.
Chiaro? Per nulla. Oscuro come la pece.
Eppure, questa assurda ricetta di sostituire variabili con tabelle porta a calcolare i risultati giusti: prevede esattamente quello che osserviamo negli esperimenti.
Con grande stupore dei tre moschettieri di Göttingen, prima della fine dell’anno Born riceve per posta un breve articolo da uno sconosciuto giovane inglese. Nell’articolo è costruita essenzialmente la stessa teoria, in un linguaggio matematico ancora più astratto delle matrici di Göttingen.5 Il giovane è Paul Dirac. Heisenberg in giugno aveva tenuto in Inghilterra una conferenza, alla fine della quale aveva accennato alle sue idee; Dirac era nel pubblico, ma era stanco e non aveva capito nulla. Più tardi aveva avuto il lavoro di Heisenberg dal suo professore, che lo aveva ricevuto per posta e non ci aveva capito nulla neppure lui. Dirac lo legge, decide che non ha senso, lo mette via. Ma un paio di settimane dopo, rimuginandoci durante una passeggiata nella natura, si rende conto che le tabelle di Heisenberg somigliano a cose che aveva studiato in un corso, non si ricorda bene e deve aspettare lunedì l’apertura della biblioteca per andare a rinfrescarsi le idee su un libro…6 Da lì, in breve costruisce anche lui, indipendentemente, la stessa teoria completa dei tre maghi di Göttingen.
Non resta che applicare la nuova teoria all’elettrone nell’atomo e vedere se funziona davvero. Permette veramente di calcolare tutte le orbite di Bohr?
Il calcolo si rivela difficile e i tre non riescono a completarlo. Chiedono aiuto a Pauli,7 di tutti sempre il più brillante (e strafottente). Pauli risponde: «Effettivamente questo è un calcolo troppo difficile… per voi». Lo completa, con tecnicismi acrobatici, nel giro di poche settimane.8
Il risultato è perfetto: i valori dell’energia calcolati con la teoria delle matrici di Heisenberg, Born e Jordan sono esattamente quelli ipotizzati da Bohr. Le strane regole di Bohr per gli atomi seguono dal nuovo schema. Non solo. La teoria permette di calcolare anche l’intensità della luce emessa, le regole di Bohr non ci riuscivano. Anche questa viene giusta con gli esperimenti!
È un trionfo.
Einstein scrive in una lettera a Hedi, la moglie di Born: «Le idee di Heisenberg e Born tengono tutti con il fiato sospeso e occupano la mente di chiunque abbia interessi teorici».9 E in una lettera al caro amico di sempre, Michele Besso: «La teorizzazione più interessante degli ultimi tempi è quella di Heisenberg-Born-Jordan sugli stati quantistici: un vero e proprio calcolo di stregoneria».10
Bohr, il maestro, ricorderà anni dopo: «Si aveva allora soltanto una vaga speranza di [poter arrivare a] una riformulazione della teoria dove ogni uso non appropriato delle idee classiche fosse via via eliminato. Impressionati dalla difficoltà di un simile programma, sentimmo tutti la più grande ammirazione per Heisenberg quando, appena ventitreenne, raggiunse lo scopo in un solo colpo».11
A parte Born che è quarantenne, Heisenberg, Jordan, Dirac e Pauli sono tutti ventenni. A Göttingen chiamano la loro fisica «Knabenphysik»: la fisica dei ragazzi.
Sedici anni dopo. L’Europa è sconvolta dalla guerra mondiale. Heisenberg è diventato scienziato famoso. Hitler gli ha assegnato il compito di usare il sapere sull’atomo per costruire una bomba che gli faccia vincere la guerra. Heisenberg prende il treno, raggiunge Copenaghen, nella Danimarca occupata dall’esercito tedesco, e visita il vecchio maestro. Il vecchio e il giovane si parlano. Si lasciano senza capirsi. Heisenberg dirà che era andato da Bohr per parlare del problema morale sollevato dalla prospettiva di una bomba spaventosa. Non tutti gli crederanno. Poco dopo un commando inglese rapisce Bohr con il suo consenso e lo porta fuori dalla Danimarca occupata. Bohr viene trasferito in Inghilterra, lo riceve personalmente Churchill, poi negli Stati Uniti, dove il suo sapere è messo all’opera, con la generazione dei giovani fisici che hanno imparato a usare la meccanica dei quanti per maneggiare gli atomi. Hiroshima e Nagasaki sono annientate e duecentomila esseri umani, uomini donne e bambini, uccisi in una frazione di secondo. Oggi viviamo con decine di migliaia di testate nucleari puntate sulle nostre città. Se qualcuno perde la testa, può distruggere la vita sulla Terra. La potenza micidiale della «fisica dei ragazzi» è sotto gli occhi di tutti.
Non c’è solo la bomba, grazie al cielo. La teoria dei quanti è stata applicata a atomi, nuclei atomici, particelle elementari, alla fisica dei legami chimici, alla fisica dei materiali solidi, a quelli liquidi e ai gas, ai semiconduttori, ai laser, alla fisica delle stelle come il Sole, alla fisica delle stelle di neutroni, all’universo primordiale, alla fisica della formazione delle galassie… e via e via, potrei continuare per pagine. Ha portato a comprendere interi pezzi di Natura, per esempio la tavola periodica degli elementi, ad applicazioni mediche che hanno salvato milioni di vite umane, a nuove apparecchiature, nuove tecnologie, ai computer. La teoria ha predetto fenomeni nuovi mai osservati né sospettati prima: correlazioni quantistiche a chilometri di distanza, computer quantistici, teletrasporto… tutte predizioni che si sono rivelate corrette. La serie dei trionfi dura ininterrotta da un secolo, e continua.
Lo schema di calcolo di Heisenberg, Born, Jordan e Dirac, la strana idea di «limitarsi solo a quanto è osservabile», e sostituire variabili fisiche con matrici,12 non ha mai sbagliato. È la sola teoria fondamentale del mondo che finora non ha mai sbagliato e della quale non conosciamo i limiti.
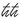
Ma perché non possiamo descrivere dove sia e cosa faccia l’elettrone quando non lo guardiamo? Perché dobbiamo parlare solo dei suoi «osservabili»? Perché possiamo parlare solo del suo effetto quando salta da un’orbita all’altra, e non possiamo semplicemente dire dove sia in ogni momento? Cosa significa sostituire numeri con tabelle di numeri?
Cosa significa: «È tutto ancora molto vago e non mi è chiaro, ma sembra che gli elettroni non si muoveranno più su orbite»? L’amico Pauli scriverà di Heisenberg: «Ragionava in modo terribile, era tutto intuizione, non prestava alcuna attenzione a elaborare chiaramente gli assunti fondamentali e la loro relazione con le teorie esistenti…».
Il magico articolo di Werner Heisenberg che ha dato origine a tutto, concepito sull’Isola Sacra del Mare del Nord, si apriva con questa frase: «L’obiettivo di questo lavoro è gettare le basi per una teoria di meccanica quantistica basata esclusivamente su relazioni fra quantità che siano in linea di principio osservabili».
Osservabili? Cosa ne sa la Natura se ci sia qualcuno a osservare?
La teoria non dice come si muova l’elettrone durante un salto. Dice solo cosa vediamo quando salta. Perché?
2. La fuorviante ψ di Erwin Schrödinger:
«la probabilità»
L’anno successivo, il 1926, tutto sembra chiarirsi. Il fisico austriaco Erwin Schrödinger riesce a ottenere lo stesso risultato di Pauli, calcola cioè le energie di Bohr dell’atomo, ma in modo completamente diverso.
Anche questo risultato non nasce in un dipartimento universitario: Schrödinger lo trova durante una fuga con un’amante segreta in uno chalet nelle Alpi svizzere. Cresciuto nell’atmosfera libera e permissiva della Vienna di inizio secolo, brillante e affascinante, Erwin Schrödinger ha sempre avuto diverse compagne contemporaneamente, e non ha nascosto una fascinazione per le preadolescenti. Anni dopo, nonostante il Premio Nobel, la sua posizione a Oxford salta a causa di uno stile di vita troppo poco conformista anche per il preteso anticonformismo inglese: vive con la moglie Anny e l’amante Hilde, che aspetta un figlio da lui ed è moglie del suo assistente. Negli Stati Uniti non va meglio: a Princeton, Erwin, Anny e Hilde vogliono convivere prendendosi cura insieme della piccola Ruth, nata nel frattempo; Princeton non digerisce. Andranno a vivere a Dublino, più liberale. Ma anche lì Schrödinger finirà per suscitare scandalo, dopo aver avuto due figli da due diverse studentesse… Commento di sua moglie Anny: «È più facile vivere con un canarino che con un puledro, io preferisco un puledro».13
Il nome della compagna con cui Schrödinger si rifugia in montagna nei primi giorni del 1926 è rimasto misterioso. Sappiamo solo che è una vecchia amica viennese. La leggenda vuole che sia partito portandosi solo lei, due perle da mettersi nelle orecchie per potersi isolare quando vuole pensare alla fisica, e la tesi di un giovane scienziato francese, Louis de Broglie, che Einstein gli aveva consigliato di leggere.
La tesi di de Broglie studia l’idea che le particelle come gli elettroni possano essere in realtà delle onde. Come le onde del mare o le onde elettromagnetiche. Sulla base di alcune analogie teoriche piuttosto vaghe, de Broglie suggerisce che possiamo immaginare un elettrone come un’ondina che corre.
Che relazione ci può essere fra un’onda, che si sparge ovunque, e una particella, che resta compatta seguendo una traiettoria fissa? Pensate al raggio di luce di un laser: sembra seguire una traiettoria netta. Ma è fatto di luce, che è un’onda, un’oscillazione del campo elettromagnetico. A lungo andare infatti il raggio laser si disperde nello spazio. La linea precisa disegnata dalla traiettoria di un raggio di luce è solo un’approssimazione che trascura questa dispersione.
Schrödinger è catturato dall’idea che le traiettorie delle particelle elementari siano anch’esse solo approssimazioni del comportamento di un’onda soggiacente.14 Aveva parlato di quest’idea in un seminario a Zurigo, e uno studente gli aveva domandato se queste onde obbedissero a un’equazione. In montagna, con le perle nelle orecchie e nelle pause fra i dolci momenti condivisi con l’amica viennese, Schrödinger fa abilmente a ritroso il percorso che porta dall’equazione di un’onda alla traiettoria di un raggio di luce,15 e in questo modo acrobatico indovina l’equazione che l’onda-elettrone deve soddisfare quando è in un atomo. Studia soluzioni di questa equazione, e… ne estrae esattamente le energie di Bohr.16 Wow!
Poi, venuto a conoscenza della teoria di Heisenberg, Born e Jordan, riesce a mostrare che dal punto di vista matematico le due teorie sono sostanzialmente equivalenti: predicono gli stessi valori.17
L’idea delle onde è talmente semplice che spiazza il gruppetto di Göttingen e le sue esoteriche speculazioni sulle quantità osservabili. Sembra l’uovo di Colombo: Heisenberg, Born, Jordan e Dirac hanno costruito una teoria intricata e oscura solo perché hanno preso una strada contorta e fuorviante. Le cose sono molto più semplici: l’elettrone è un’onda, tutto qui. Le «osservazioni» non c’entrano niente.
Anche Schrödinger è prodotto del vivace mondo filosofico e intellettuale viennese di inizio secolo: amico del filosofo Hans Reichenbach, è affascinato dal pensiero orientale, in particolare dal Vedānta induista, e appassionato della filosofia di Schopenhauer (come lo è Einstein), che interpreta il mondo come «rappresentazione». Di certo non frenato dal conformismo né preoccupato di «quello che penserà la gente», l’idea di sostituire un mondo di materia con un mondo di onde non lo spaventa.
La lettera che Schrödinger usa per designare le sue onde è la lettera ψ, la «Psi». La quantità ψ è spesso chiamata la «funzione d’onda».18 Lo splendido calcolo di Schrödinger sembra mostrare che il mondo microscopico non è fatto di particelle: è fatto di onde ψ. Intorno ai nuclei degli atomi non orbitano puntini di materia: ci sono ondulazioni continue delle onde di Schrödinger, come le onde che scuotono un piccolo lago sempre agitato dal vento.
Questa «meccanica ondulatoria» appare di colpo molto più convincente che la «meccanica delle matrici» di Göttingen, anche se dà le stesse predizioni. Il conto di Schrödinger è più semplice di quello di Pauli. I fisici della prima metà del XX secolo avevano familiarità con le equazioni delle onde, non avevano alcuna familiarità con le matrici. «La teoria di Schrödinger è arrivata come un sollievo: non dovevamo più imparare la strana matematica delle matrici» ricorda un noto fisico del tempo.19
E soprattutto: le onde di Schrödinger sono facili da immaginare e visualizzare. Ci mostrano chiaramente cosa ne è della «traiettoria dell’elettrone» che Heisenberg voleva far sparire: l’elettrone è un’onda che si può spargere, tutto qui.
Schrödinger sembra trionfare su tutta la linea.
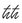
Ma è un’illusione.
Heisenberg si rende subito conto che la chiarezza concettuale delle onde di Schrödinger è fumo negli occhi. Un’onda prima o poi si diffonde nello spazio, un elettrone no: quando arriva da qualche parte, arriva sempre e solo tutt’intero in un singolo punto. Se un elettrone viene espulso da un nucleo atomico, l’equazione di Schrödinger prevede che l’onda ψ si sparga uniformemente ovunque nello spazio. Ma quando l’elettrone è rilevato, per esempio da un contatore Geiger, o da uno schermo televisivo, arriva in un punto solo, non è diffuso nello spazio.
La discussione sulla meccanica ondulatoria di Schrödinger si accende rapidamente e diventa subito virulenta. Heisenberg, che sente messa in dubbio l’importanza della sua scoperta, è tagliente: «Quanto più penso agli aspetti fisici della teoria di Schrödinger, tanto più repellenti li trovo. Quel che Schrödinger scrive della “visualizzabilità” della sua teoria “non è probabilmente del tutto esatto”, in altri termini: sono cretinate».20 Schrödinger cerca di ribattere con ironia: «Non posso immaginare che un elettrone salti qua e là come una pulce».21
Ma Heisenberg ha ragione. Risulta pian piano evidente che la meccanica ondulatoria non è più chiara della meccanica delle matrici di Göttingen. È un altro strumento di calcolo che produce numeri giusti, magari più semplice da usare, ma di per sé non ci dà l’immagine chiara e immediata di quello che succede, che Schrödinger sperava. La meccanica ondulatoria è oscura quanto le matrici di Heisenberg. Se ogni volta che vediamo un elettrone lo vediamo in un solo punto, come può l’elettrone essere un’onda diffusa nello spazio?
Anni dopo Schrödinger, che diventerà comunque uno dei più acuti pensatori sulle questioni suscitate dai quanti, riconoscerà la disfatta: «Ci fu un momento» scrive «in cui i creatori della meccanica ondulatoria [cioè lui] si cullarono nell’illusione di avere eliminato le discontinuità dalla teoria dei quanti. Ma le discontinuità eliminate dalle equazioni della teoria riappaiono nel momento di confrontare la teoria con quanto osserviamo».22
Di nuovo appare «quanto osserviamo». Ma – una volta di più – cosa ne sa la Natura se noi la osserviamo o no?
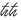
È Max Born, ancora lui, che aggiunge un tassello alla questione, comprendendo per primo23 il significato della ψ di Schrödinger. Born, con la sua aria da ingegnere serio e un po’ dimesso, è il meno flamboyant e il meno noto fra i creatori della teoria dei quanti, ma ne è forse il vero artefice, oltre a essere stato, come dicono gli americani, il «solo adulto nella stanza», in senso tanto figurato quanto letterale. Era lui, nel 1925, ad avere ben chiaro che i fenomeni quantistici rendevano necessaria una meccanica radicalmente nuova, è stato lui a instillare quest’idea nei giovani, è stato lui a riconoscere al volo l’idea giusta nel primo confuso calcolo di Heisenberg e a tradurla in una vera teoria.
Born capisce che il valore dell’onda ψ di Schrödinger in un punto nello spazio determina la probabilità di osservare l’elettrone in quel punto.24 Se un atomo emette un elettrone ed è circondato da contatori Geiger, il valore della ψ là dove c’è un contatore determina la probabilità che sia quel contatore, e non un altro, a rivelare l’elettrone.
La ψ di Schrödinger non è quindi la rappresentazione di un’entità reale: è uno strumento di calcolo che ci dice la probabilità che qualcosa di reale avvenga. È come le previsioni del tempo, che ci dicono cosa potrebbe succedere.
Lo stesso – si capisce subito dopo – vale per la meccanica delle matrici di Göttingen: la matematica ci dà predizioni probabilistiche, non predizioni esatte. La teoria dei quanti, tanto nella versione di Heisenberg che nella versione di Schrödinger, predice probabilità, non certezze.
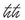
Perché probabilità? Di solito parliamo di probabilità quando non abbiamo tutti i dati del problema. La probabilità che esca il 5 sulla roulette è una su 37. Se conoscessimo esattamente lo stato iniziale della pallina al lancio e le forze che agiscono su di essa, potremmo predire il numero che uscirà. (Negli anni Ottanta un gruppo di giovani brillanti ha vinto molti dollari, nei casinò di Las Vegas, usando un computerino nascosto in una scarpa…).25 È quando non abbiamo tutti i dati del problema che non sappiamo con certezza cosa succederà, e parliamo di probabilità.
La meccanica quantistica di Heisenberg e Schrödinger predice probabilità: è una teoria che non tiene conto di tutti i dati rilevanti del problema? Per questo ci dà solo probabilità? Oppure la natura salta qui e là davvero a caso?
L’ateo Einstein ha formulato la domanda in un linguaggio colorito: «Davvero Dio gioca a dadi?».
Einstein amava il linguaggio figurato, e gli piaceva usare «Dio» per le sue metafore nonostante il dichiarato ateismo. Ma in questo caso la sua frase può essere letta in senso letterale: Einstein amava Spinoza per il quale «Dio» è sinonimo di «Natura». Quindi «Davvero Dio gioca a dadi?» significa letteralmente «Davvero le leggi della Natura non sono deterministiche?». A cent’anni di distanza dalle polemiche fra Heisenberg e Schrödinger, su questa domanda, come vedremo, si discute ancora.

In ogni caso l’onda ψ di Schrödinger non basta a chiarire le oscurità dei quanti. Non basta pensare che l’elettrone sia una semplice onda. L’onda ψ è qualcosa di poco chiaro, che determina la probabilità che l’elettrone, una particella che si mostra sempre concentrata in un punto solo, sia osservato in un luogo piuttosto che in un altro. L’onda ψ evolve nel tempo seguendo l’equazione scritta da Schrödinger, solo fintanto che non la guardiamo. Quando la guardiamo, puff!, si concentra in un punto, e lì vediamo la particella.26
Come se il solo fatto di osservare fosse sufficiente a modificare la realtà.
All’oscura idea di Heisenberg che la teoria descriva solo osservazioni, e non quello che succede tra una osservazione e l’altra, si aggiunge l’idea che la teoria predica solo la probabilità di osservare una cosa o un’altra. Il mistero si infittisce.
3. La granularità del mondo: «i quanti»
Ho raccontato la nascita della meccanica quantistica avvenuta nel 1925 e 1926, e ho introdotto due idee chiave della teoria: la strana idea di descrivere solo osservabili, trovata da Heisenberg, e il fatto che la teoria predica solo probabilità, compreso da Born.
C’è una terza idea chiave. Per illustrarla è meglio fare un salto indietro, ai due decenni che precedono il fatidico viaggio di Heisenberg sull’Isola Sacra. Il bizzarro comportamento degli elettroni negli atomi non era il solo fenomeno strano e incompreso, all’inizio del XX secolo. Ne erano stati osservati altri. Avevano una cosa in comune: mettevano in luce una curiosa granularità dell’energia e altre quantità fisiche. Prima dei quanti, nessuno sospettava che l’energia potesse essere granulare. L’energia in un sasso lanciato, per esempio, dipende dalla velocità del sasso: la velocità del sasso può essere qualunque, e l’energia può quindi essere qualunque. Ma bizzarri comportamenti dell’energia erano apparsi negli esperimenti a cavallo del secolo.
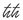
Dentro un forno, per esempio, le onde elettromagnetiche si comportano in maniera curiosa. Il calore (che è energia) non si distribuisce fra le onde di tutte le frequenze come sarebbe naturale aspettarsi: non arriva mai alle onde di alta frequenza. Nell’anno tondo 1900, venticinque anni prima del viaggio di Heisenberg a Helgoland, il fisico tedesco Max Planck aveva indovinato una formula27 che riproduceva bene il modo, misurato in laboratorio, in cui l’energia del calore si distribuisce fra le onde di diverse frequenze.28 Planck era riuscito a derivare questa formula dalle leggi generali, al prezzo però di aggiungere un’ipotesi bizzarra: che l’energia di ciascuna onda potesse essere solo un multiplo intero di una energia elementare.
Come se l’energia si concentrasse in pacchetti. La dimensione di questi pacchetti, per fare funzionare il conto di Planck, deve essere diversa per onde di diversa frequenza: deve essere proporzionale alla frequenza dell’onda.29 Cioè le onde di alta frequenza sono composte da pacchetti più energetici. L’energia non arriva alle frequenze altissime perché non ce n’è abbastanza per fare pacchetti abbastanza grossi.
Planck aveva calcolato la costante di proporzionalità fra l’energia di un pacchetto e la frequenza della sua onda, usando le osservazioni sperimentali. Aveva chiamato questa costante «h». Senza sapere bene cosa significasse. Di solito oggi invece di usare h si usa il simbolo ℏ, che sta per h divisa per 2π. È stato Heisenberg a prendere l’abitudine di mettere una lineetta sulla h perché nei calcoli h è spesso divisa per 2π e lui si stufava di scrivere «h/2π» ogni volta. Il simbolo ℏ in inglese si dice «h bar», in italiano «acca tagliata». Viene chiamato anch’esso «costante di Planck», come h senza il taglio, generando un po’ di confusione. Oggi è diventato il simbolo più caratteristico della teoria dei quanti. (Io ho una maglietta con una piccola ℏ ricamata, di cui vado molto fiero).
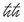
Cinque anni più tardi, Einstein suggerisce che la luce e tutte le altre onde elettromagnetiche siano proprio costituite di «grani» elementari, ciascuno con una energia fissa, che dipende dalla frequenza.30 I primi «quanti». Oggi li chiamiamo fotoni, i quanti di luce. La costante di Planck h misura la loro dimensione: ogni fotone ha un’energia h volte la frequenza della luce di cui fa parte.
Assumendo che questi «grani elementari di energia» esistano davvero, Einstein riesce a spiegare un fenomeno allora non compreso, chiamato effetto fotoelettrico,31 e prevederne caratteristiche prima che siano misurate.
Einstein è il primo, già dal 1905, a rendersi conto che i problemi sollevati da questi fenomeni sono così seri da richiedere una revisione dell’intera meccanica. Questo fa di lui il padre spirituale della teoria dei quanti. La sua idea che la luce sia un’onda ma anche una nuvola di fotoni è confusa, ma è l’idea che ispira de Broglie a pensare che tutte le particelle elementari siano onde, e poi Schrödinger a introdurre l’onda ψ. Einstein è quindi l’ispiratore della meccanica quantistica per più vie: Born impara da lui che la meccanica va interamente rivista; Heisenberg si ispira a lui nel restringere l’attenzione alle sole quantità misurabili; Schrödinger parte dall’idea di de Broglie ispirata dai fotoni di Einstein. C’è di più: Einstein è anche il primo a studiare fenomeni atomici usando la probabilità, mettendo così Born sulla strada per comprendere che il significato dell’onda ψ è una probabilità. La costruzione della teoria dei quanti è stata un gioco di squadra.
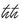
La costante di Planck appare di nuovo nel 1913 nelle regole di Bohr.32 Anche qui, la stessa logica: le orbite dell’elettrone nell’atomo possono avere solo certe energie, come se l’energia fosse in pacchetti, granulare. Quando un elettrone salta da un’orbita di Bohr all’altra, libera un pacchetto di energia che diventa un quanto di luce. E poi ancora nel 1922, in un esperimento concepito da Otto Stern e realizzato a Francoforte da Walther Gerlach, che mostra che anche la velocità di rotazione degli atomi non è continua, ma prende solo certi valori discreti.
Questi fenomeni – fotoni, effetto fotoelettrico, distribuzione dell’energia fra le onde elettromagnetiche, orbite di Bohr, la misura di Stern e Gerlach… – sono tutti regolati dalla costante di Planck ℏ.
Nel 1925, quando finalmente appare, la teoria di Heisenberg e compagni permette in un colpo solo di rendere conto di tutti questi fenomeni: prevederli, calcolarne le caratteristiche. Permette di derivare la formula di Planck per la distribuzione del calore tra le frequenze in un forno caldo, l’esistenza dei fotoni, l’effetto fotoelettrico, i risultati della misura di Stern e Gerlach e tutti gli altri strani fenomeni «quantistici».
Il nome della teoria quantistica viene proprio da «quanti», cioè «grani». I fenomeni quantistici rivelano un aspetto granulare del mondo, a piccolissima scala. La granularità non riguarda solo l’energia: è estremamente generale. Nel mio campo di studio, la gravità quantistica, si mostra che lo spazio fisico in cui viviamo è granulare a piccolissima scala. Anche in questo caso, la costante di Planck determina la scala (piccolissima) dei «quanti elementari di spazio».
La granularità è il terzo ingrediente concettuale chiave della teoria dei quanti, accanto alla probabilità e alle osservazioni. Righe e colonne delle matrici di Heisenberg corrispondono direttamente ai singoli valori granulari o, come si dice, discreti, che prende l’energia.
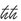
Stiamo avvicinandoci alla conclusione della prima parte del libro, che racconta la nascita della teoria e la confusione che ha generato. Nella seconda parte descrivo le strade per uscire dalla confusione. Prima di concludere questa parte, tuttavia, voglio dire qualche parola sulla singola equazione che, come ho accennato, la teoria dei quanti aggiunge alla fisica classica.
È una equazione buffa. Dice che moltiplicare la posizione per la velocità è diverso che moltiplicare la velocità per la posizione. Se posizione e velocità fossero numeri, non ci sarebbe differenza, perché 7 per 9 è lo stesso che 9 per 7. Ma posizione e velocità sono ora tabelle di numeri, e quando si moltiplicano due tabelle l’ordine conta. La nuova equazione ci dà la differenza fra moltiplicare due quantità in un ordine oppure nell’ordine inverso.
È compatta, semplicissima. Incomprensibile.
Non cercate di decifrarla: ci si accapigliano ancora scienziati e filosofi. Più avanti tornerò a discutere un po’ il contenuto di questa equazione. Ma qui la scrivo lo stesso, perché è il cuore della teoria dei quanti, e non si può concludere la presentazione della teoria senza di essa. Eccola:
XP – PX = iℏ
È tutto. La lettera X indica la posizione di una particella, la lettera P indica la sua velocità moltiplicata per la sua massa (in gergo si chiama «impulso»). La lettera i è il simbolo matematico per la radice quadrata di −1, e come abbiamo visto ℏ è la costante di Planck divisa per 2π.
In un certo senso, Heisenberg e amici hanno aggiunto alla fisica solo questa semplice equazione: il resto ne segue. Ne seguono i computer quantistici e la bomba atomica.
Il prezzo di questa estrema semplicità nella forma è l’estrema oscurità nel significato. La teoria dei quanti prevede granularità, salti, fotoni, e tutto il resto, sulla base di una sola equazione di otto caratteri aggiunta alla fisica classica. Un’equazione che dice che moltiplicare posizione per velocità è diverso che moltiplicare velocità per posizione. L’oscurità è totale. Forse non è un caso che Murnau abbia girato scene di Nosferatu a Helgoland.
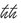
Nel 1927 Niels Bohr tiene una conferenza in Italia, sul lago di Como, dove riassume tutto quello che si è capito (o non si è capito) della nuova teoria dei quanti, e spiega come usarla.33 Nel 1930 Dirac scrive un libro in cui la struttura formale della nuova teoria è delucidata splendidamente.34 È tutt’ora il miglior libro per impararla. Due anni dopo il più grande matematico del tempo, John von Neumann, mette a posto le questioni formali in uno splendido testo di fisica matematica.35
La costruzione della teoria è premiata da una pioggia di premi Nobel senza eguale nella storia. Einstein riceve il Nobel nel 1921 per aver chiarito l’effetto fotoelettrico introducendo i quanti di luce. Bohr nel 1922 per le regole sulla struttura dell’atomo. De Broglie nel 1929 per l’idea delle onde di materia. Heisenberg nel 1932 «per la creazione della meccanica quantistica». Schrödinger e Dirac nel 1933 per «nuove scoperte» nella teoria atomica. Pauli nel 1945 per i contributi tecnici alla teoria. Born nel 1954 per aver compreso il ruolo della probabilità (ha fatto ben più di questo). L’unico che resta fuori è Pascual Jordan, nonostante Einstein avesse (correttamente) proposto Heisenberg, Born e lui come i veri autori della teoria. Ma Jordan aveva mostrato troppa lealtà alla Germania nazista, e gli uomini non riconoscono meriti ai vinti.36
Nonostante questi riconoscimenti, nonostante lo strepitoso successo, nonostante la tecnologia che ne è nata, la teoria resta un pozzo nero di oscurità. Niels Bohr scrive: «Non c’è un mondo quantistico. C’è solo un’astratta descrizione quantistica. È sbagliato pensare che il compito della fisica sia descrivere come la Natura è. La fisica si occupa solo di quanto possiamo dire della Natura».
Fedele all’intuizione originaria di Werner Heisenberg a Helgoland, la teoria non ci dice dove si trovi una qualunque particella di materia quando non la guardiamo. Ci dice solo quale sia la probabilità di trovarla in un punto se la osserviamo.
Ma cosa ne sa una particella di materia se la osserviamo o no? La più efficace e potente teoria scientifica che l’umanità abbia mai prodotto è un mistero.