© The Author(s) 2020
S.-J. Ran et al.Tensor Network ContractionsLecture Notes in Physics964https://doi.org/10.1007/978-3-030-34489-4_4

4. Tensor Network Approaches for Higher-Dimensional Quantum Lattice Models

Shi-Ju Ran1 , Emanuele Tirrito2, Cheng Peng3, Xi Chen4, Luca Tagliacozzo5, Gang Su6 and Maciej Lewenstein2
(1)
Department of Physics, Capital Normal University, Beijing, China
(2)
Quantum Optics Theory, Institute of Photonic Sciences, Castelldefels, Spain
(3)
Stanford Institute for Materials and Energy Sciences, SLAC and Stanford University, Menlo Park, CA, USA
(4)
School of Physical Sciences, University of Chinese Academy of Science, Beijing, China
(5)
Department of Quantum Physics and Astrophysics, University of Barcelona, Barcelona, Spain
(6)
Kavli Institute for Theoretical Sciences, University of Chinese Academy of Science, Beijing, China
 

Abstract

In this section, we will show several representative TN approaches for simulating the quantum lattice models in (d > 1) dimensions. We will mainly use the language of TN contractions. One may refer to several existing reviews (Schollwöck, Ann Phys 326:96–192, 2011; Verstraete et al., Adv Phys 57:143–224, 2008; Cirac and Verstraete, J Phys A Math Theor 42:504004, 2009; Orús, Ann Phys 349:117, 2014; Haegeman and Verstraete, Ann Rev Condens Matter Phys 8(1):355–406, 2017) for more exhaustive understanding on the TN simulations for quantum problems. We will focus on the algorithms based on PEPS , and show the key roles that the 2D TN contraction algorithms presented in Sect. 3 play in the higher-dimensional cases.

4.1 Variational Approaches of Projected-Entangled Pair State

Without losing generality, we consider a 2D quantum system with nearest-neighbor coupling on an infinite square lattice as an example. The ground state can be represented by an iPEPS (see Sect. 2.​2.​4). Similar to MPS (Sect. 3.​1.​3), the central task is to minimize the energy
$$\displaystyle \begin{aligned} \begin{array}{rcl} E= \frac{\langle \psi | \hat{H} | \psi \rangle}{ \langle \psi | \psi \rangle}. {} \end{array} \end{aligned} $$
(4.1)
There are in general two ways to do the minimization. One way proposed firstly by Verstraete and Cirac [1] is considering the elements in the tensors as variational parameters. The tensors in the TN are updated one by one. In a similar spirit as the boundary-state methods (see Sect. 3.​4), the key of this approach is to transform the global minimization to local ones, where one tensor (say P [i], see the PEPS form in Eq. (2.​23), Sect. 2.​2.​4) is updated by a local minimization problem
$$\displaystyle \begin{aligned} \begin{array}{rcl} E = \frac{P^{[i]\dagger} \hat{H}^{eff} P^{[i]}}{P^{[i]\dagger} \hat{N}^{eff} P^{[i]}}. {} \end{array} \end{aligned} $$
(4.2)
$$\hat {H}^{eff}$$ is an “effective” Hamiltonian by computing $$\langle \psi | \hat {H} | \psi \rangle $$ but after taking P [i]† in 〈ψ| and P [i] in |ψ〉 out. Figure 4.1 depicts $$\hat {H}^{eff}$$ where $$\hat {H}$$ is written as an infinite PEPO (iPEPO , also see Sect. 2.​2.​6 for PEPO) for a better illustration. Similarly, $$\hat {N}^{eff}$$ is defined by computing 〈ψ|ψ〉 but after taking P [i]† and P [i] out.
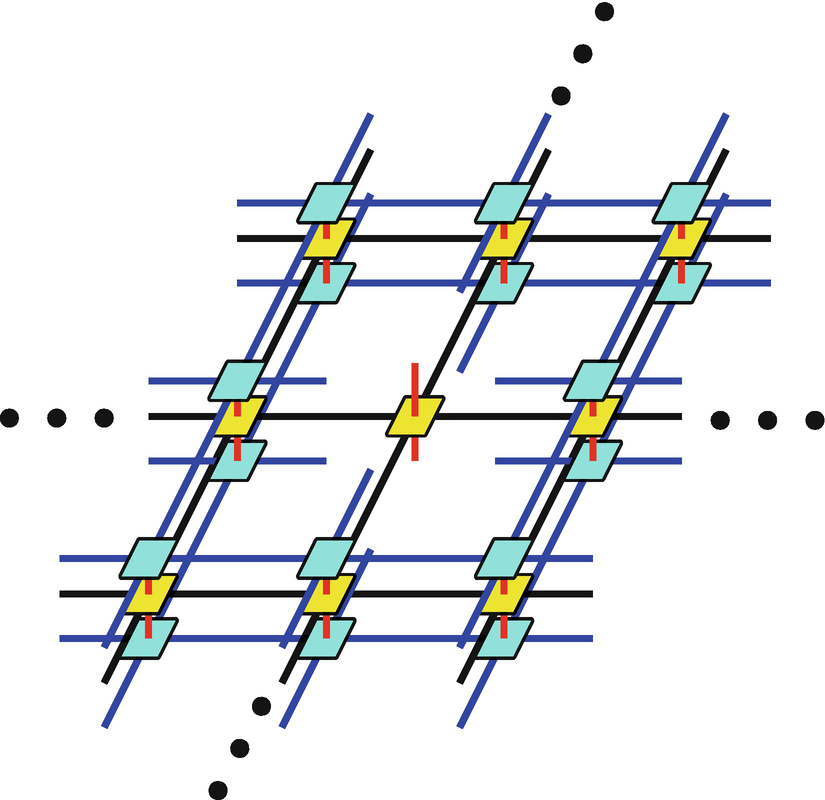
../images/489509_1_En_4_Chapter/489509_1_En_4_Fig1_HTML.png
Fig. 4.1

The illustration of $$\hat {H}^{eff}$$ in Eq. (4.2)

Obviously, the computations of both $$\hat {H}^{eff}$$ and $$\hat {N}^{eff}$$ are in fact to contract the corresponding 2D TN’s where the 2D TN contraction algorithms are needed. In [2], Corboz used CTMRG (see [3] or Sect. 3.​3) to compute the contractions. In [4], Vanderstraeten et al. further developed this idea to a gradient method, where the gradient is calculated by implementing similar 2D TN contractions. The gradient is given as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial E}{\partial P^{[i]\dag}} = \frac{\partial \langle \psi | \hat{H} | \psi \rangle / \langle \psi | \psi \rangle}{\partial P^{[i]\dag}} = 2 \frac{\partial_{P^{[i]\dag}} \langle \psi | \hat{H} | \psi \rangle}{\langle \psi | \psi \rangle} - 2 \frac{\langle \psi | \hat{H} | \psi \rangle}{\langle \psi | \psi \rangle^2} \partial_{P^{[i]\dag}} \langle \psi | \psi \rangle. {} \end{array} \end{aligned} $$
By imposing the normalization condition 〈ψ|ψ〉 = 1 and shifting the ground-state energy to zero by $$\hat {H} \leftarrow \hat {H} - \langle \psi | \hat {H} | \psi \rangle $$ , the gradient is simplified as
$$\displaystyle \begin{aligned} \frac{\partial E}{\partial P^{[i]\dag}} = 2 \partial_{P^{[i]\dag}} \langle \psi | \hat{H} | \psi \rangle. {} \end{aligned} $$
(4.3)
Thus the gradient is computed by contracting the TN of $$\langle \psi | \hat {H} | \psi \rangle $$ after taking P [i]† out.

The gradient method is consistent with the effective Hamiltonian schemes. In fact, one has $$\frac {\partial E}{\partial P^{[i]\dag }} = 2\hat {H}^{eff} P^{[i]}$$ . At the minimal point, the gradient should vanish $$\frac {\partial E}{\partial P^{[i]\dag }} = 0$$ . It means $$2\hat {H}^{eff} P^{[i]} = 0$$ , i.e., P [i] is the dominant eigenstate of $$\hat {H}^{eff}$$ with a zero eigenvalue. Considering the ground-state energy is shifted to zero, P [i] is the ground state of the effective Hamiltonian $$\hat {H}^{eff}$$ .

Note that the infinite PEPO (iPEPO) representation is not enforced to define $$\hat {H}^{eff}$$ . In fact, it is not easy to obtain the iPEPO of an arbitrary 2D (or 3D) Hamiltonian. The usual way is to start from the summation form of the Hamiltonian $$\hat {H} = \sum \hat {H}_{ij}$$ , and compute the contribution to $$\hat {H}^{eff}$$ from each $$\hat {H}_{ij}$$ separately [2]. Each term is computed by contracting a 2D TN, where one can reuse the results to improve the efficiency.

Following the same clue (minimizing E), algorithms were proposed to combine TN with the QMC methods [5–9]. Still let us focus on those based on PEPS . One may transform Eq. (4.1) as
$$\displaystyle \begin{aligned} \begin{array}{rcl} E = \frac{\sum_{S,S'} W(S') \langle S'|\hat{H}| S\rangle W(S)}{\sum_{S} W(S)^2}, \end{array} \end{aligned} $$
(4.4)
where S = (s 1, s 2, ⋯ ) goes through all spin configurations and W(S) = 〈s 1s 2⋯|ψ〉 is the coefficient of the iPEPS for the given configuration. QMC sampling can be implemented by defining the weight function as W(S)2 and the estimator E(S) as
$$\displaystyle \begin{aligned} \begin{array}{rcl} E(S) = \sum_{S'} \frac{W(S')}{W(S)} \langle S'|\hat{H}| S\rangle, \end{array} \end{aligned} $$
(4.5)
so that the energy becomes
$$\displaystyle \begin{aligned} E = \langle E(S) \rangle = \sum_{S} W(S)^2 E(S). \end{aligned} $$
(4.6)
It is easy to see that the normalization condition of the weights ∑ SW(S)2 = 1 is satisfied.
The task becomes to compute W(S) and $$\langle S'|\hat {H}| S\rangle $$ with different configurations. The computation of $$\langle S'|\hat {H}| S\rangle $$ is relatively easy since |S〉 and |S′〉 are just two product states. The computation of W(S) is more tricky. When |ψ〉 is a PEPS on a square lattice, W(S) is a 2D scalar TN by fixing all the physical indexes of the PEPS as
$$\displaystyle \begin{aligned} \begin{array}{rcl} W(S) = \text{tTr} \prod_{n} P^{[n]}_{s_n}, {} \end{array} \end{aligned} $$
(4.7)
where $$P^{[n]}_{s_n}$$ is a fourth-order tensor that only has the geometrical index.1 The n-th physical index is taken as s n. Considering that most of the configurations are not translationally invariant, such QMC-TN methods are usually applied to finite-size models. One may use the finite TN version of the algorithms reviewed in Sect. 3.

4.2 Imaginary-Time Evolution Methods

Another way to compute the ground-state iPEPS is to do imaginary-time evolution, analog to the MPS methods presented in Sect. 3.​1.​3. For a d-dimensional quantum model, its ground-state simulation can be considered as computing the contraction of a (d + 1)-dimensional TN.

Firstly, let us show how the evolution operator for an infinitesimal imaginary-time step τ can be written as an iPEPO, which is in fact one layer of the 3D TN (Fig. 4.2). The evolution of the iPEPS is to put the iPEPS at the bottom and to contract the TN layer by layer to it.
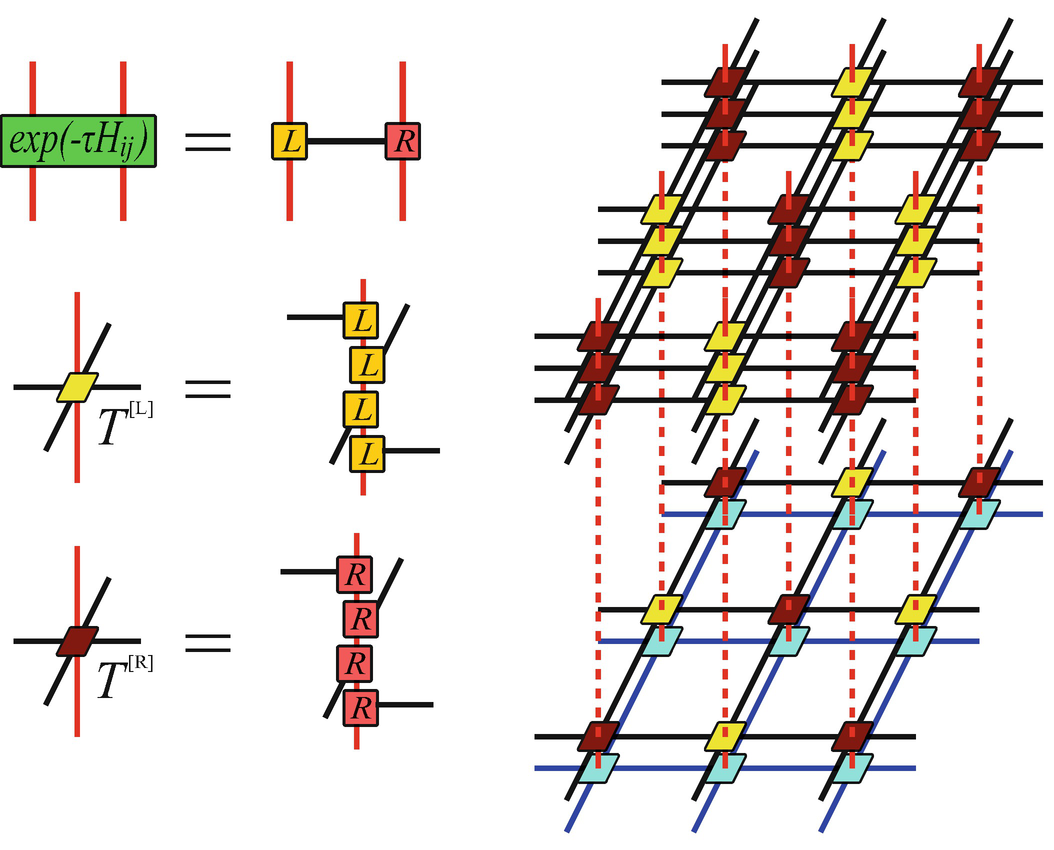
../images/489509_1_En_4_Chapter/489509_1_En_4_Fig2_HTML.png
Fig. 4.2

The evolution of a PEPS can be mapped to the contraction of a 3D TN

To proceed, we divide the local Hamiltonians on the square lattice into four group: $$\hat {H}_{e,e} = \sum _{\text{even i,j}} \hat {H}^{[i,j;i,j+1]} + \hat {H}^{[i.j;i+1,j]}$$ , $$\hat {H}_{o,o} = \sum _{\text{odd i,j}} \hat {H}^{[i,j;i,j+1]} + \hat {H}^{[i.j;i+1,j]}$$ , $$\hat {H}_{e,o} = \sum _{\text{even i, odd j}} \hat {H}^{[i,j;i,j+1]} + \hat {H}^{[i.j;i+1,j]}$$ , and $$H_{o,e} = \sum _{\text{odd i, even j}} \hat {H}^{[i,j;i,j+1]} + \hat {H}^{[i.j;i+1,j]}$$ . One can see that each two terms in one group commute to each other. The evolution operator for an infinitesimal imaginary-time step (τ → 0) then can be written as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{U} &\displaystyle =&\displaystyle \exp(-\tau \hat{H}) \\ &\displaystyle =&\displaystyle \exp\left(-\tau \hat{H}^{[e,e]}\right) \exp\left(-\tau \hat{H}^{[o,o]}\right) \exp\left(-\tau \hat{H}^{[e,o]}\right) \exp\left(-\tau \hat{H}^{[o,e]}\right) + O\left(\tau^2\right). {} \end{array} \end{aligned} $$
(4.8)
Let us assume translational invariance to the Hamiltonian, i.e., $$\hat {H}^{[i,j]} = \hat {H}^{[two]}$$ . The element of two-body evolution operator is a fourth-order tensor $$U_{s_is_js_i^{\prime }s_j^{\prime }} = \langle s_i^{\prime }s_j^{\prime }| \exp (-\tau \hat {H}^{[two]}) |s_is_j \rangle $$ . Implement SVD or QR decomposition on U (4.2) as
$$\displaystyle \begin{aligned} \begin{array}{rcl} U_{s_is_js_i^{\prime}s_j^{\prime}} = \sum_{\alpha} L_{s_is_i^{\prime}, a} R_{s_js_j^{\prime},a}. \end{array} \end{aligned} $$
(4.9)
Then the two tensors T [L] and T [R] that form the iPEPO of $$\hat {U}$$ is obtained as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \begin{aligned} T^{[L]}_{ss', a_1a_2a_3a_4} = \sum_{s_1s_2s_3} L_{ss_1,a_1} L_{s_1s_2,a_2} L_{s_2s_3, a_3} L_{s_3s',a_4}, \\ T^{[R]}_{ss', a_1a_2a_3a_4} = \sum_{s_1s_2s_3} R_{ss_1,a_1} R_{s_1s_2,a_2} R_{s_2s_3, a_3} R_{s_3s',a_4}. {} \end{aligned} \end{array} \end{aligned} $$
(4.10)
The four Ls (or Rs) in T [L] (or T [R]) correspond to the evolution operators of the two-body terms in $$\hat {H}^{[e,e]}$$ , $$\hat {H}^{[o,o]}$$ , $$\hat {H}^{[e,o]}$$ , and $$\hat {H}^{[o,e]}$$ in Eq. (4.9), respectively (see the left part of Fig. 4.2).

While the TN for the imaginary-time evolution with the iPEPO is a cubic TN , one may directly use the tensor U, which also gives a 3D but not cubic TN. Without losing generality, we in the following will use the iPEPO to present the algorithms for contraction a cubic TN. The algorithm can be readily applied to deal with the statistic models on cubic lattice or other problems that can be written as the contraction of a cubic TN.

The evolution $$\hat {U} |\psi \rangle $$ is to contract the iPEPO (one layer of the tensors) to the iPEPS . In accordance to the translational invariance of the iPEPO, the iPEPS is also formed by two inequivalent tensors (denoted by P [L] and P [R]). Locally, the tensors in the evolved iPEPS are given as
$$\displaystyle \begin{aligned} \begin{array}{rcl} \tilde{P}^{[L]}_{s, \tilde{\alpha}_1\tilde{\alpha}_2\tilde{\alpha}_3\tilde{\alpha}_4} = \sum_{s'} T^{[L]}_{ss', a_1a_2a_3a_4} P^{[L]}_{s', \alpha_1\alpha_2\alpha_3\alpha_4}, \end{array} \end{aligned} $$
(4.11)
$$\displaystyle \begin{aligned} \begin{array}{rcl} \tilde{P}^{[R]}_{s, \tilde{\alpha}_1\tilde{\alpha}_2\tilde{\alpha}_3\tilde{\alpha}_4} = \sum_{s'} T^{[R]}_{ss', a_1a_2a_3a_4} P^{[R]}_{s', \alpha_1\alpha_2\alpha_3\alpha_4}, \end{array} \end{aligned} $$
(4.12)
with the composite indexes $$\tilde {\alpha }_x = (a_x, \alpha _x)$$ (x = 1, 2, 3, 4). Obviously, the bond dimensions of the new tensors are increased by $$\dim (a_x)$$ times. It is necessary to preset a dimension cut-off χ: when the bond dimensions become larger than χ, approximations will be introduced to reduce the dimensions back to χ. One then can iterate the evolution of the iPEPS with bounded computational cost. After the iPEPS converges, it is considered that the ground state is reached. Therefore, one key step in the imaginary-time schemes (as well as the similar contraction schemes of 3D TN’s ) is to find the optimal truncations of the enlarged bonds. In the following, we will concentrate on the truncation of bond dimensions, and present three kinds of scheme known as full, simple, and cluster updates according to which environment the truncations are optimized [10].2

4.3 Full, Simple, and Cluster Update Schemes

For truncating the dimensions of the geometrical bonds of an iPEPS , the task is to minimize the distance between the iPEPSs before and after the truncation, i.e.,
$$\displaystyle \begin{aligned} \varepsilon = || \tilde{\psi} \rangle - |\psi \rangle|. \end{aligned} $$
(4.13)
With the normalization condition of the iPEPSs, the problem can be reduced to the maximization of the fidelity
$$\displaystyle \begin{aligned} \mathscr{Z} = \langle \tilde{\psi} |\psi \rangle. {} \end{aligned} $$
(4.14)
As discussed in Sect. 3.​1.​2, $$\mathscr {Z}$$ is in fact a scalar TN .
Full Update
Among the three kinds of update schemes, full update seems to be the most natural and reasonable, in which the truncation is optimized referring to the whole iPEPS [10–16]. Let us consider a translationally invariant iPEPS. For square lattice, the iPEPS is formed by the infinite copies of two tensors P [L] and P [R] located on the two sub-lattices, respectively. Their evolution is given by Eq. (4.10). We use $$\tilde {P}^{[L]}$$ and $$\tilde {P}^{[R]}$$ to denote the tensors with enlarged bond dimensions. Below, we follow Ref. [13] to explain the truncation process. To truncate the fourth bond $$\tilde {\alpha }_4$$ of the tensor, for example, one firstly defines the tensor M by contracting a pair of $$\tilde {P}^{[L]}$$ and $$\tilde {P}^{[R]}$$ as
$$\displaystyle \begin{aligned} M_{s_1\tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, s_2 \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime}} = \sum_{\tilde{\alpha}_4} \tilde{P}^{[L]}_{s_1, \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3 \tilde{\alpha}_4} \tilde{P}^{[R]}_{s_2, \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime} \tilde{\alpha}_4}. \end{aligned} $$
(4.15)
Note that P [L] and P [R] share the bond $$\tilde {\alpha }_4$$ that is to be truncated. Compute the environment tensorM e by contracting the TN of $$\mathscr {Z}$$ after taking a pair of $$\tilde {P}^{[L]}$$ and $$\tilde {P}^{[R]}$$ out from the TN. $$\mathscr {M}$$ is in fact an eighth-order tensor of the same dimensions as M. Decompose M e by SVD as
$$\displaystyle \begin{aligned} M^e_{s_1\tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, s_2 \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime}} = \sum_{\alpha} V^{[L]}_{s_1 \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, \alpha} \varLambda_{\alpha} V^{[R]}_{s_2 \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime}, \alpha}. {} \end{aligned} $$
(4.16)
Define a new matrix as $$\tilde {M} = \varLambda ^{1/2} V^{[R]} M V^{[L]} \varLambda ^{1/2}$$ and decompose it by SVD as $$\tilde {M} \simeq \tilde {V}^{[L]} \tilde {\varLambda } \tilde {V}^{[R]}$$ by taking only the χ-largest singular values and singular vectors. Finally, two tensors are updated by $$P^{[L]} = \tilde {\varLambda }^{1/2} \tilde {V}^{[L]T} \varLambda ^{-1/2} V^{[R]T}$$ and $$P^{[R]} = \tilde {\varLambda }^{1/2} \tilde {V}^{[R]} \varLambda ^{-1/2} V^{[L]}$$ . One can check
$$\displaystyle \begin{aligned} M_{s_1\tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, s_2 \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime}} \simeq \sum_{\alpha_4} P^{[L]}_{s_1, \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3 \alpha_4} P^{[R]}_{s_2, \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime} \alpha_4}, {} \end{aligned} $$
(4.17)
with the dimension of the shared bond $$\dim (\alpha _4) = \chi $$ . We shall stress that Eq. (4.17) is not the SVD of M; the decomposition and truncation are optimized by the SVD of M e, hence is a non-local optimization.

With the formula given above, the task is to compute the environment tensor M e by the contraction algorithms of 2D TN’s . In Ref. [13], the authors developed the SRG , where M e is computed by a modified version of TRG algorithm [17]. Other options include iTEBD [15], CTMRG [12], etc. Note that how to define the environment as well as how to truncate by the environment may have subtle differences in different works. The spirit is the same, which is to minimize the fidelity in Eq. (4.14) referring to the whole iPEPS .

Simple Update

A much more efficient way known as the simple update was proposed by Jiang et al. [18]; it uses local environment to determine the truncations, providing an extremely efficient algorithm to simulate the 2D ground states. As shown in Fig. 2.​8c, the iPEPS used in the simple update is formed by the tensors on the site and the spectra on the bonds: two tensors P [L] and P [R] located on the two sub-lattices, and λ [1], λ [2], λ [3], and λ [4] on the four inequivalent geometrical bonds of each tensor. The evolution of the tensors in such an iPEPS is given by Eq. (4.10). λ [i] should be simultaneously evolved as $$\tilde {\lambda }^{[i]}_{(a_i, \alpha _i)} = I_{a_i} \lambda _{\alpha _i}$$ with $$I_{a_i} = 1$$ .

To truncate the fourth geometrical bond of P [L] (and P [R]), for example, we construct a new tensor by contracting P [L] and P [R] and the adjacent spectra as
$$\displaystyle \begin{aligned} M_{s_1\tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, s_2 \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime}} = \sum_{\tilde{\alpha}_4} \tilde{P}^{[L]}_{s_1, \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3 \tilde{\alpha}_4} \tilde{P}^{[R]}_{s_2, \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime} \tilde{\alpha}_4} \tilde{\lambda}^{[1]}_{\tilde{\alpha}_1} \tilde{\lambda}^{[2]}_{\tilde{\alpha}_2} \tilde{\lambda}^{[3]}_{\tilde{\alpha}_3} \tilde{\lambda}^{[1]\prime}_{\tilde{\alpha}_1^{\prime}} \tilde{\lambda}^{[2]\prime}_{\tilde{\alpha}_2} \tilde{\lambda}^{[3]\prime}_{\tilde{\alpha}_3} \tilde{\lambda}^{[4]}_{\tilde{\alpha}_4}. \end{aligned} $$
(4.18)
Then implement SVD on M as
$$\displaystyle \begin{aligned} M_{s_1\tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, s_2 \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime}} \simeq \sum_{\alpha=1}^{\chi} U^{[L]}_{s_1 \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, \alpha} \lambda_{\alpha} U^{[R]}_{s_2 \tilde{\alpha}_1^{\prime} \tilde{\alpha}_2^{\prime} \tilde{\alpha}_3^{\prime}, \alpha}, \end{aligned} $$
(4.19)
where one takes only the χ-largest singular values and the basis. P [L] and P [R] are updated as
$$\displaystyle \begin{aligned} \begin{aligned} P^{[L]}_{s_1, \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3 \alpha} = U^{[L]}_{s_1 \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, \alpha} \left(\tilde{\lambda}^{[1]}_{\tilde{\alpha}_1}\right)^{-1} \left(\tilde{\lambda}^{[2]}_{\tilde{\alpha}_2}\right)^{-1} \left(\tilde{\lambda}^{[3]}_{\tilde{\alpha}_3}\right)^{-1}, \\ P^{[R]}_{s_2, \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3 \alpha} = U^{[R]}_{s_2 \tilde{\alpha}_1 \tilde{\alpha}_2 \tilde{\alpha}_3, \alpha} \left(\tilde{\lambda}^{[1]}_{\tilde{\alpha}_1}\right)^{-1} \left(\tilde{\lambda}^{[2]}_{\tilde{\alpha}_2}\right)^{-1} \left(\tilde{\lambda}^{[3]}_{\tilde{\alpha}_3}\right)^{-1}. \end{aligned} \end{aligned} $$
(4.20)
The spectrum $$\tilde {\lambda }_4$$ is updated by λ in the SVD.

The above procedure truncates $$\dim (\tilde {\alpha }_4)$$ to the dimension cut-off χ, which can be readily applied to truncate any other bonds. According to the discussion about SVD in Sect. 2.​2.​1, the environment is the two tensors and the adjacent spectra λs in M, where the λs play the role of an “effective” environment that approximate the true environment (M e in the full update). From this viewpoint, the simple update uses local environment. Later by borrowing from the idea of the orthogonal form of the iPEPS on Bethe lattices [19–26], it was realized that the environment of the simple update is the iPEPS on the infinite trees [27–29], not just several tensors. We will talk about this in detail in the next chapter from the perspective of the multi-linear algebra.

Cluster Update

By keeping the same dimension cut-off, the simple update is much more efficient than the full update. On the other hand, obviously, the full update possesses higher accuracy than the simple update by considering better the environment. The cluster update is between the simple and full updates, which is more flexible to balance between the efficiency and accuracy [10, 27, 30].

One way is to choose a finite cluster of the infinite TN and define the environment tensor by contracting the finite TN after taking a pair of $$\tilde {P}^{[L]}$$ and $$\tilde {P}^{[R]}$$ out. One can consider to firstly use the simple update to obtain the spectra and put them on the boundary of the cluster [30]. This is equivalent to using a new boundary condition [27, 29], different from the open or periodic boundary conditions of a finite cluster. Surely, the bigger the cluster becomes, more accurate but more consuming the computation will be. One may also consider an infinite-size cluster, which is formed by a certain number of rows of the tensors in the TN [10]. Again, both the accuracy and computational cost will in general increase with the number of rows. With infinite rows, such a cluster update naturally becomes the full update. Despite the progresses, there are still many open questions, for example, how to best balance the efficiency and accuracy in the cluster update.

4.4 Summary of the Tensor Network Algorithms in Higher Dimensions

In this section, we mainly focused on the iPEPS algorithm that simulates the ground states of 2D lattice models. The key step is to compute the environment tensor, which is to contract the corresponding TN . For several special cases such as trees and fractal lattices, the environment tensor corresponds to an exactly contractible TN, and thus can be computed efficiently (see Sect. 2.​3.​6). For the regular lattices such as square lattice, the environment tensor is computed by the TN contraction algorithms, which is normally the most consuming step in the iPEPS approaches.

The key concepts and ideas, such as environment, (simple, cluster, and full) update schemes, and the use of SVD , can be similarly applied to finite-size cases [31, 32], the finite-temperature simulations [27, 28, 33–39], and real-time simulations [31, 40] in two dimensions. The computational cost of the TN approaches is quite sensitive to the spatial dimensions of the system. The simulations of 3D quantum systems are much more consuming than the 2D cases, where the task becomes to contract the 4D TN. The 4D TN contraction is extremely consuming, one may consider to generalize the simple update [29, 41], or to construct finite-size effective Hamiltonians that mimic the infinite 3D quantum models [29, 42]

Many technical details of the approaches can be flexibly modified according to the problems under consideration. For example, the iPEPO formulation is very useful when computing a 3D statistic model, which is to contract the corresponding 3D TN. As for the imaginary-time evolution, it is usually more efficient to use the two-body evolution operators (see, e.g., [12, 18]) rather than the iPEPO. The environment is not necessarily defined by the tensors; it can be defined by contracting everything of the TN except for the aimed geometrical bond [28, 33]. The contraction order also significantly affects the efficiency and accuracy. One may consider to use the “single-layer” picture [10, 31], or an “intersected” optimized contraction scheme [43].

Creative Commons

Open Access This chapter is licensed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license and indicate if changes were made.

The images or other third party material in this chapter are included in the chapter's Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the chapter's Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.