Let’s recap what we’ve learned so far:
1. The long-term (expected) returns and risks of many kinds of stocks and bonds are well known. Unfortunately, over periods of up to 10 or 20 years, actual returns may be significantly higher or lower than the expected return. The amount of “scatter” from the average value is known as the standard deviation (SD) and is virtually synonymous with risk.
2. Effective portfolio diversification can increase return while reducing risk. Achieving maximal benefit from effective diversification requires periodic rebalancing of portfolio composition back to the target, or “policy” composition. This is often emotionally difficult to do, as it almost always involves moving against market sentiment.
3. Whether you like it or not, you are a money manager. Asset allocation accounts for most of the difference in performance among money managers. Arriving at an effective asset allocation is both critically important and not that hard to do. Long-term success in individual security selection and market timing is difficult to impossible; fortunately, they are nearly irrelevant. The failure of market timing and active security selection will be discussed in Chapter 6.
4. Since the future cannot be predicted, it is impossible to specify in advance what the best asset allocation will be. Rather, our job is to find an allocation that will do reasonably well under a wide range of circumstances.
5. Sticking by your target asset allocation through thick and thin is much more important than picking the right asset allocation.
First of all, let’s be clear about what we mean when we say “optimal allocations.” We can actually be talking about one of three allocations: future, hypothetical, or historical. You cannot know future optimal portfolio composition any more than you can sprout wings and fly, play point guard for the Lakers, or win the Miss America pageant. Anybody who tells you that they know the optimal future allocation belongs in Sing-Sing or Bellevue. (And were you actually able to do this, you sure-as-shootin’ wouldn’t need this book. You would know the future returns of all asset classes, and you wouldn’t need asset allocation. What you would in fact need is a competent pilot for your Gulfstream V to get you back and forth between your villas in Davos, Palm Springs, Jackson Hole, and Martha’s Vineyard.)
Hypothetical optimal allocation refers to the process of postulating a set of returns, SDs, and correlations and then calculating the optimal allocations for these inputs.
Historical optimal allocation, what was optimal in the past, can be calculated. This is an interesting exercise, and one that we shall shortly engage in, but it is a very poor way to determine future allocations.
We’ve already hinted at one method for calculating historical optimal allocations. Recall the portfolio “clouds” in Figures 4-9 and 4-10. The portfolios at the upper left edge of the cloud lay close to the efficient frontier and are very close to being optimal. It is not that difficult to spreadsheet the historical returns and fiddle with your allocations until you are no longer able to improve portfolio return versus risk. In fact, most spreadsheets contain an optimizer tool that will allow you to determine the portfolios which will give you the most (or even least!) return at a given SD level, or the least SD at a given level of return. This is a sort of “poor man’s optimizer.” However, both of these methods are quite slow and cumbersome and are not appropriate for the serious student of portfolio theory. For one thing, it is an enormous amount of work to do “what if” analyses of what happens with variations of an asset’s return or SD, and almost impossible to change its correlation with other assets.
There is a much faster and easier way to optimize portfolios—mean-variance analysis, devised several decades ago by Harry Markowitz (and for which he earned a Nobel Prize). A software application which uses this method is called a mean-variance optimizer (MVO). An MVO will rapidly compute optimal portfolio compositions from three sets of data. These are:
1. The return for each asset
2. The standard deviation of each asset
3. The correlations among all the assets
Until very recently, MVOs were quite expensive and the input data even more so. Because of this, I spent a fair amount of effort describing spreadsheet techniques in this book’s previous versions. Fortunately, this is no longer necessary. MVOs are now available for under $100, and the data has become much easier to obtain as well. See Appendix A for product and vendor information.
MVO’s one disadvantage is that it does not take rebalancing into account, as it is a so-called single-period technique, and rebalancing is a multiple-period phenomenon. However, optimal portfolios are the same whether or not they are rebalanced. Further, it is relatively easy to adjust for rebalancing once the efficient frontier has been calculated.
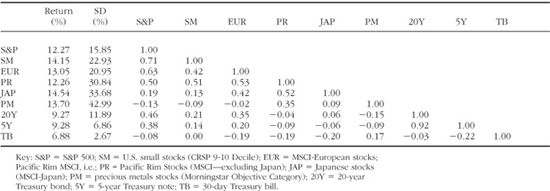
As an example, let’s consider the seven assets for the 1970–1996 period used in Figure 4-10, plus long bonds and T-bills. The complete MVO inputs for this time period are listed in Table 5-1.
Table 5-1. Optimizer Inputs for 1970–1996
The first two columns are the annualized returns and standard deviations. The adjacent columns show the correlations between the annual returns of each asset for the 27 annual-return periods.
These inputs are fed into the optimizer, in this case MVOPlus, produced by Efficient Solutions. Like all Markowitz optimizers, this program utilizes the so-called critical-line technique to produce a series of “corner portfolios,” which define the composition of the efficient frontier for this set of input data. Let’s take a look at the output, shown in Table 5-2. Figure 5-1 shows the actual graphical output from MVOPlus.
Table 5-2. Corner Portfolios 1970–1996
Figure 5-1. Optimizer output, MVOPlus.
Corner 1 is the minimum-variance portfolio; it is the one with the least risk. Notice that it consists of 92.5% T-bills, with the other 7.5% consisting of assets that we would generally consider quite risky. Most of the portfolios in the risk range which most of us would consider reasonable, live between corners 7 and 8. Portfolios 1 through 6 consist almost entirely of short bonds, and above portfolio 8, the portfolios become very risky. Portfolio 10 is the maximum-return portfolio.
MVOPlus has the unique ability to identify the portfolio with the maximum annualized (geometric) return, whereas all other commercially available optimizers will identify the asset with the highest arithmetic return as the last portfolio, which is not the one with the highest geometric return. This is because the difference between the arithmetic and geometric returns is approximately half its variance, or (SD)2/2, and is called variance drag. As we move toward the right on the return-versus-risk plot, variance drag increases to the point where geometric return begins to fall. Remember, you “eat” geometric annualized return, not arithmetic return.
You are not limited to the corner portfolios, of course. If you decide that halfway between portfolios 7 and 8 is where you want to be, then you simply average the compositions of the two portfolios for each asset.
Look at portfolio 7 for a moment. It is about one-third stock and two-thirds five-year Treasuries. So far, so good. But look at the equity composition—almost entirely U.S. small, Japanese, and precious metals stocks. This is not a portfolio that any rational person would own. It is no accident that these are the three assets with the highest returns for the 1970–1996 period. We’ve just run into optimization’s fatal weakness: it is overly fond of assets with a recent history of high returns. In fact, with a bit of practice, it is possible to get the optimizer to spit out almost any portfolio you want. Change the return inputs of most assets by a few percent in either direction and that asset will either dominate the portfolio or completely disappear from it. Do you think that you can predict the future returns of all the major asset classes in your portfolio? If you can, then you are very talented indeed. Hence, the two fundamental laws of optimizers:
An optimizer will heavily favor those assets with high historical or assumed returns.
If you can predict the optimizer inputs well enough to come close to the future efficient frontier, then you don’t need an optimizer in the first place.
The dangers of blindly feeding historical returns, SDs, and correlations into an optimizer should already be apparent from the above example. Asset returns have a tendency to “mean revert” over long time periods; an asset with stellar returns over the past 10 years is more likely than not to have below-average returns in the subsequent 10 years. Some wags have referred to optimizers as “error maximizers” for just this reason.
In order to better understand the pitfalls of optimization, let’s take a look at what actually happens when one uncritically feeds historical data into an optimizer. Let’s divide 1970–1998 into five-year periods with a final four-year period. Next, we’ll optimize each five-year period, and see how the optimal all-stock allocation does in the subsequent five-year period compared to a “coward’s portfolio” consisting of equal parts of all six stock assets (U.S. large cap, U.S. small cap, European, Pacific Rim, Japanese, and precious metals).
We start in 1970–1974. For this period, the optimal return is produced by an allocation of 99.8% precious metals and 0.2% Japan, producing 29.97% annualized. Carrying that allocation forward to 1975–1979 produced a return of 14.71% versus 25.38% for the coward’s portfolio.
For 1975–1979, the optimal allocation was 100% U.S. small stocks, with a return of 39.81% annualized. This allocation actually did pretty well going forward to 1980–1984, with a return of 21.59% versus 14.75% for the coward’s portfolio.
For 1980–1984, the optimal allocation was 73% U.S. small and 27% precious metals with a return of 21.94%. Going forward to 1985–1989 this allocation returned 11.83% versus 24.14% for the cowards.
For 1985–1989, the best allocation was 100% Japanese stocks, producing an astonishing return of 40.24% annualized. The next five years? Negative 3.5% annualized versus to plus 7.54% for the coward’s portfolio.
Again, it’s useful to take a short jaunt in the “wayback machine” to the late 1980s. A few square miles of Tokyo real estate were worth more than all of California, and shortly we were all going to be speaking Japanese. “The Nikkei too expensive at 100 times earnings? Westerners just don’t understand how to value equity on the Tokyo markets.”
And finally, for 1990–1994 the best strategy was 100% Pacific Rim, returning 15.27% annualized. For the next four years (1995–1998) this strategy returned negative 3.22% versus plus 6.61% for the coward’s. And once again, in 1994 “everybody knew” that the Asian Tigers would attain an American standard of living within the decade.
Over the whole 1975–1998 period the above five-year optimization strategy would have returned 8.40% annualized, which is worse than any of the individual stock assets, and much worse than the 15.79% returned annually for the coward’s portfolio.
What you are in effect doing by optimizing historical returns is accepting current conventional wisdom. This is not a coincidence. Markets that have experienced abnormally high returns have usually undergone a substantial increase in price as a multiple of earnings, and this is almost always the result of increasing optimism surrounding that asset.
Where do we stand with our optimizer? In the words of a former president, we are in “deep doo-doo.” We can’t predict returns, SDs, and correlations accurately enough. If we could, we wouldn’t need the optimizer in the first place. And optimizing raw historical returns is a one-way ticket to the poor house.
So, forget about getting the answer from a magic black box. We’ll have to look elsewhere for a coherent allocation strategy.
A well-diversified portfolio is not a free lunch. It does not come anywhere near eliminating risk; economic catastrophes do not respect national borders. The events of 1929–1932 and 1973–1974 involved all markets, and the damage varied only in degree among national markets. Markowitz mean-variance analysis tells us that if one asset has an SD of 20%, then two completely uncorrelated assets (zero correlation) will have an SD of 14.1%, and four mutually uncorrelated assets, an SD of 10%. In practical terms it is nearly impossible to find three mutually uncorrelated assets. Consequently, we cannot hope for a risk reduction of more than about one-quarter to one-third from diversification.
Worse, the correlation coefficients calculated between assets somewhat overstate the diversification benefit because the correlation of below-average returns turns out to be higher than for above-average returns. In other words, the “negative semicorrelations” are greater than the “positive semicorrelations.” Translated into plain English this means that the actual correlation of asset returns in severe bear markets is higher than the “raw” correlation coefficient would suggest. The reduction in SD afforded by diversification often is lost in severe bear markets. Academician Bruno Solnik states simply, “Diversification fails us just when we need it most.” This was well seen on October 19, 1987 and in the fall of 1990 when all of the world’s stock indexes suffered significant losses, in spite of their low correlations in more normal times. This is why simple portfolio backtesting is a valuable supplement to MVO; one can actually see how well a proposed portfolio responded in an actual bear market.
A major argument against international diversification is that of sovereign risk—the possibility that one’s assets will be expropriated by a foreign government or be lost in a war. Consider that before the Second World War two of the world’s major capital markets were Germany and Egypt; one was destroyed in the war and the other nationalized after it. Latin American nations have been defaulting on their debt with near clocklike regularity for the past century. The perils of long-term international investing should not be understated, but it is important to understand the mathematical nature of long-term risk. Let us assume that at some point during a 70-year investment horizon one-half of our capital suddenly and irretrievably disappears. This lowers our long-term return by only 1.0%. Further, consider that while Japanese and German capital disappeared at the beginning of the Second World War, spectacular returns were earned in these markets in the four decades following 1945.
Others argue that because of the globalization of our economy, international diversification has lost its value. No one can doubt that our economic life is becoming increasingly globalized. The events in foreign capital markets seem to exert an instantaneous effect on our own, leading many to predict that the market returns of nations will become increasingly correlated and that the benefits of international diversification will disappear. This argument is so prevalent that it has acquired an aura of fact. Fortunately for the investor, the data indicate otherwise. For example, there is good data for the returns of U.K. and U.S. markets dating from 1919. The 1919–1994 period can be broken down into four periods of 19 years each, and correlations for annual returns can be also calculated for each period:
While the correlation between the U.S. and U.K. markets can be seen to vary widely, there is no pattern of increasing correlation; the lowest correlation is for the last period.
Similarly, it is possible to follow correlations for many individual national market returns for the 1969–1998 period. In general, there is no pattern of increasing correlation. The one exception is the increasing correlations among European markets over the past two decades.
Figure 5-2 is a plot of the correlation coefficient for the S&P 500/EAFE pair for monthly returns (three-year rolling periods) for 1969 to 1998. The correlation is seen to vary widely during this period, but there is certainly no clear-cut increase in this value over time. (There does seem to have been a rise in the correlation over the past two years or so. This was probably caused by the Asian-flu-related volatility of 1997–1998.) There is little evidence to support the notion of an increasing international market correlation resulting from a globalizing economy.
Figure 5-2. S&P 500/EAFE correlations, 1969–1998.
Probably of greater importance than the risk reduction derived from diversification is the “rebalancing bonus,” the extra return produced by rigorous rebalancing. The benefit derived from rebalancing is not only pecuniary, but also psychological. By getting into the habit of profiting by moving in the direction opposite the market’s, the investor gains both a healthy self-reliance and a scorn for market sentiment. This distrust of sentiment and “expert opinion” is one of an investor’s most useful tools.
Yet another psychological benefit of a diversified portfolio results from its limited exposure to any one market segment: you are never “betting the farm” on one asset. If only 5% or 10% of your portfolio is invested in emerging markets stocks, then the inevitable 30% or 50% loss occasionally seen in this area will not hurt too much; it is highly likely that gains in other areas will make up for part or all of the loss. More importantly, your low exposure may make you eager to rebalance, thus “buying cheap.”
Further diversification benefit can be obtained through the use of international small stocks. Consider the correlation grids for large and small stock returns for 1990–1998, shown in Table 5-3. The first number is the correlation for large stocks in the asset class pair, the second for small stocks.
Table 5-3. Correlations of Global Large and Small Stocks, 1990–1998 (Monthly Returns)
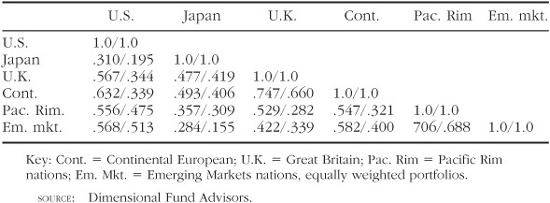
For example, for the Japan and U.S. pair the correlation of monthly returns for large stocks is .310 and .195 for small stocks. In fact, in each case the correlation for small stocks is less than for large stocks. This effect is particularly dramatic for U.S.-U.K. and U.S.-Continental European correlations, the three classes that make up the bulk of most global portfolios. In spite of the fact that small stock indexes of individual nations are considerably more volatile than their larger cousins, a portfolio of global small stocks is only marginally more volatile than a similar portfolio of foreign and domestic large stocks. For example, the SD of the Dimensional Fund Advisors’ global large company index for 1990–1998 was 13.46%, versus 14.37% for the global small company index.
The real risk of small stocks is their tracking error—the propensity to have returns which can be considerably lower, as well as considerably higher, than large stocks. In other words, diversification into this area works whether we want it to or not. This has been particularly painful over the past decade, as large-company stocks have outperformed small-company stocks around the globe, in spite of small stocks’ higher long-term returns.
Rational investors deal with the large-versus-small dilemma in the same way as they deal with the foreign-versus-domestic problem. First and foremost, guard against recency—do not be overly impressed with the last decade’s triumph of domestic over foreign, and of large over small. If anything, these phenomena make it more likely that the opposite will occur in the next decade. Second, hedge your bets with large and small stocks in the same way that Uncle Fred showed you for foreign and domestic stocks. In other words, own all “four corners” of the global equity market: large domestic, large foreign, small domestic, and small foreign.
We are finally ready to allocate your assets. You must ask three questions in sequence:
1. How many different asset classes do I want to own?
2. How “conventional” a portfolio do I want?
3. How much risk do I want to take?
How many different asset classes should you own? You might as well ask the meaning of life. About all one can say is “more than three.” Portfolios come in many degrees of complexity, and the number of assets you employ will depend largely upon how much you tolerate dealing with this complexity. I’ll make a small confession at this point; I’m an asset-class junkie—I just can’t own enough of the things. I enjoy dealing with them, and if I have to manage a portfolio with 20 or 30, that’s all right.
But the law of diminishing returns applies to asset classes. You get the most diversification from the first several. The next several, maybe a bit more. Beyond that you’re probably just amusing yourself.
So here is the hierarchy. I’ll start with level-one portfolio complexity:
U.S. large stocks (S&P 500)
U.S. small stocks (CRSP 9-10, Russell 2000, or Barra 600)
Foreign stocks (EAFE)
U.S. short-term bonds
The CRSP 9-10 is an index of small stocks, produced by the Center for Research in Security Prices, and consists of almost all stocks with market capitalization values in the bottom fifth of the New York Stock Exchange. In fact, most of its companies trade on the Nasdaq. The Russell 2000 consists of the 2000 smallest stocks in the Russell 3000 Index. Finally, the S&P 600 are 600 small companies selected by Standard & Poor’s as representative of the small-cap universe.
If you don’t like investing all that much, and if reading this book is the equivalent of root canal work, then these are the only four assets you really need. You can get most of the diversification of far more complex portfolios from this short list. All four of these asset classes are available as inexpensive index funds. And, as I’ve already said, if history is any guide a portfolio divided equally among these four assets will most likely outperform the overwhelming majority of investment professionals over the next few decades. We’ll discuss later in this chapter what proportions to assign each asset.
U.S. large stocks (S&P 500)
U.S. small stocks (CRSP 9-10, Russell 2000, or Barra 600)
Foreign large stocks
Emerging markets stocks
Foreign small stocks
REITs
U.S. short-term bonds
This palette is for the individual who is serious about diversification and wants its full benefit. You may wish to add other asset classes as well, such as precious metals stocks and international bonds.
I’m not going to list all of the possibilities that the level-three asset palette “true believer” might want to own, since it’s a very long and boring one, but I will instead provide a description. Equity assets can not only be divided according to the size of company (large-versus-small) but also by value versus growth orientation. We’ll talk more about value investing in Chapter 7, but suffice it to say that companies come in two value flavors—growth and value. For growth, think Microsoft, Wal-Mart, and Amazon.com. These are rapidly growing companies selling for upwards of 35 times earnings (if they have any earnings at all!), because these earnings are expected to grow rapidly. For value, think General Motors, Kmart, or J.P. Morgan. These are companies with poor growth prospects, which consequently sell more cheaply than growth stocks.
So, we now have three dimensions of stock characterization—nationality, size, and value versus-growth-orientation. You can easily divide the world up into 10 different regions, and for each you have large versus small and value versus growth. That’s 40 possibilities right there. And that’s not including sectors (REITs, precious metals, natural resources, utilities) or bonds for each nation. Not all of these categories are easily available in the marketplace, but a surprising number are. It is relatively easy to buy an emerging markets small-company fund, for example, if you really want one. One can go even further and buy single-country vehicles, or even individual foreign companies available on the U.S. exchanges as American Depositary Receipts (ADRs).
I don’t recommend the level-three palette for anyone who doesn’t truly enjoy investing and who doesn’t have the time and patience to deal with its complexity.
Let’s start with the level-one palette and assume that you are one of those rare individuals who can tolerate a 100% equity portfolio. Instead of the four assets listed, you only have to consider the first three. Just how do you allocate your assets between U.S. large stocks, U.S. small stocks, and foreign stocks? History tells us that small stocks have higher returns than large stocks and foreign stocks, but with greater risk. Why not simply take the “coward’s way” and divide our assets equally between these three classes?
This is in fact not an unreasonable way to go and should do quite well in the long term. However, remember that whether we like it or not, U.S. large stocks are “the market.” All of us, consciously or subconsciously, compare our own returns to this benchmark, usually the S&P 500.
At times, this “equal mix” also will behave very differently from the benchmark. Therefore, let’s look at a portfolio which is very similar to that used by many institutional investors—60% U.S. large stocks, with 20% each U.S. small and foreign stocks (a “conventional portfolio”) for the six 5-year periods starting 1969. The portfolio compositions and returns are shown in Table 5-4.
TABLE 5-4. Tracking Error of Various Equity Mixes, 1969–1998
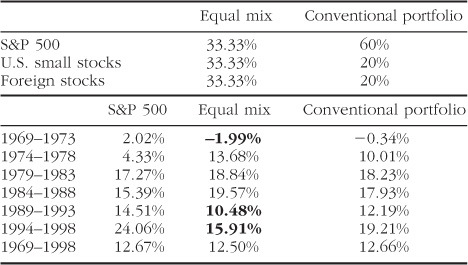
First, note that the long-term returns (last row) of all three portfolios are very similar. Also notice that the coward’s portfolio underperformed the S&P 500 by 4% per year in 1969–1973 and 1989–1993, and by over 8% in the last 5-year period. (These are the boldfaced numbers in the table.) The conventional portfolio lagged the S&P by considerably less.
While it may be true that the long-term returns of a highly diversified portfolio are the same as a more conventional portfolio, from time to time it will seriously underperform it. How much would such temporary underperformance bother you? Presumably many of you already own some small stocks and foreign stocks. How disturbed have you been by their recent laggard performance? If the answer is “very,” then you should choose a portfolio more heavily weighted toward U.S. large stocks. On the other hand, if you can tolerate this sort of “tracking error,” then a more unconventional portfolio heavily weighted toward foreign and small stocks may be appropriate.
As we move toward portfolios of greater complexity, this tracking error becomes more pronounced, and your tolerance to it becomes ever-more important. Recall from Chapter 4 that international small stocks have lagged the S&P 500 by 19% per year since 1990, even though their performance over the past 30 years has been outstanding. In fact, the more exotic asset classes you add to your mix, the higher your tracking error will be. Remember, that tracking error does not mean lower returns, it just means that your portfolio will behave very differently from everyone else’s, and that it will often temporarily underperform everybody else’s.
The third step in the asset allocation process is by far the easiest. You have already done the heavy lifting—deciding what stock asset classes to use, and in approximately what proportion to use them. Now all you have to determine is the overall mix of stocks and bonds. In the first versions of this book, I recommended that the most aggressive investors might consider a 100% equity portfolio. This is because historically stocks have returned several percent more on an annual basis than bonds, albeit at considerably more risk. And yet, as we begin the new millennium, it seems highly likely that over the coming decades stock returns will be at best only slightly higher than bond returns. As already alluded to in Chapter 2, the S&P 500 currently yields about 1.3%, and historically earnings have only grown at a real (inflation-adjusted) rate of 2% per year (discussed in Chapter 2 and shown in Figure 2-12). Some may find it difficult to believe that real corporate earnings have grown at a long-term rate of only 2% per year, but this is in fact the case. In 1920 the Dow Jones Industrial Average earned $9.12 per share, and in 1998 it earned $378.06. This compounds out to just 4.89% per year. During the same period, the inflation rate was 2.87%. Thus, the real return—the difference between these two rates—was almost exactly 2%. (Dividends have grown even more slowly at 1.5% per year in inflation-adjusted terms.) This adds up to an expected real stock return of less than 3.5%. Now consider that Treasury bonds currently yield about 6%. With the inflation rate currently at 1.6%, this results in a real yield of 4.4%. And if you are afraid that an uptick in inflation may wipe out some of those real returns, you can purchase a Treasury Inflation Protected Security (TIPS) at a government-guaranteed 4.1% real yield. In other words, it is quite possible that over the next few decades stock returns may actually be less than bond returns.
For this reason, even the most aggressive investors may wish to hold perhaps 25% bonds, with moderately aggressive investors holding a 50/50 mix of stocks and bonds, and conservative investors in the range of 30% stocks and 70% bonds.
To reiterate, the aggressiveness of your portfolio is reflected in your overall stock and bond mix, not in the kinds of equity you hold, which should be similar at all levels of risk.
Let’s look at a few more examples of how this process works. Assume that you are a bold investor and have answered the three questions posed earlier in the chapter as follows:
1. Complexity: moderate (level-two palette, plus precious metals)
2. Conventionality: low. You have determined that you can tolerate a large amount of tracking error and do not mind at all if your allocation underperforms the S&P 500 for up to a decade, as long as your long-term returns are reasonable.
3. Risk tolerance: high. You have shown an ability to withstand large losses in your portfolio without flinching.
Here’s what such a portfolio might look like:
10% S&P 500
10% U.S. small stocks
10% REITs
10% international large-cap stocks
10% international small-cap stocks
10% emerging markets stocks
10% precious metals stocks
30% U.S. short-term bonds
This portfolio is more or less equally divided between domestic and foreign, and small and large cap. It is extremely unconventional in this regard, and it will have returns that will be radically different from the S&P 500 in many years, in either direction. On the other hand, its long-term returns should be quite high. We hold a fair amount of bonds because the discounted dividend model tells us that stock returns going forward may not be much greater than bond returns. This portfolio is not recommended for all but the hardiest of souls and most independent of thinkers.
Let’s answer the basic portfolio questions a bit differently:
1. Complexity: high. We don’t mind holding more than a dozen asset classes.
2. Conventionality: high. We want adequate diversification and returns, but wish to keep tracking error to a minimum.
3. Risk tolerance: low. We really don’t want to lose more than about 6% of our net worth in a given year.
The following portfolio is taken from the Dimensional Fund Advisors’ (DFAs) “moderate balanced” strategy, with low-to-mid risk. This 40/60 stock/bond portfolio is available from DFA, about which more will be said in Chapter 8:
8% U.S. large-cap growth
8% U.S. large-cap value
4% U.S. small-cap growth
4% U.S. small-cap value
4% REIT
4% international large-cap value
2% international small-cap growth
2% international small-cap value
1.2% emerging markets large-cap growth
1.2% emerging markets large-cap value
1.6% emerging markets small-cap growth
15% one-year corporate bonds
15% two-year global bonds
15% five-year U.S. government bonds
15% five-year global bonds
First, the complexity of this portfolio should satisfy all but the most exacting portfolio buff, with no less than 15 asset classes. Secondly, it is quite conventional, with a 28/12 domestic/foreign split, and it is much heavier in large-cap than small-cap stocks. This portfolio provides adequate safety and diversification, and yet its return only rarely varies more than a half-dozen percent from a domestic 40/60 S&P 500/T-bill mix.
You now have an idea of how the allocation process works. First, decide how many different stock and bond asset classes you are willing to own. Increasing the number of asset classes you employ will improve diversification but will also increase your work load and tracking error. The Gap Portfolio gets around this problem with a heavy weighting of large and domestic stocks in its equity portion.
Second, decide just how much tracking error you can tolerate. If you are unable to tolerate much tracking error, keep your proportion of foreign and small-cap stocks low.
And last, adjust your stock-versus-bond mix according to how much risk you can tolerate, ranging from a maximum of 75% stock for the most aggressive investors down to 25% for the least aggressive.
Up to this point our journey through portfolio analysis has been fairly academic—we have not yet “gotten our fingers dirty” with real investments. In Chapters 6 and 7 we shall examine the nuances of how real markets actually work, and in Chapter 8 we shall explore the nuts and bolts of implementing our asset allocation plan.
1. It is impossible to forecast future optimal portfolios by any technique.
2. Over the long term, a widely diversified global portfolio of small-and large-company stocks should have favorable return-versus risk-characteristics.
3. Your precise asset allocation will depend on three factors: your tolerance to S&P 500 tracking error, the number of assets you wish to own, and your tolerance to risk.
