6
Gases
IDEAL GASES
The three most important gases in brewing are CO2 (carbon dioxide), N2 (nitrogen), and O2 (oxygen). Air is also important; however, it can be treated as an O2 + N2 mixture. Atmospheric air is approximately 21% oxygen and 78% nitrogen plus trace gases (most notably argon).
The kinetic molecular theory (Vincenti and Kruger, 1982) provides the most useful model of gases as far as brewing is concerned. It is based on the following assumptions:
• The gas consists of a large number of very small particles called molecules. Each molecule moves at a constant speed in a straight line. Different molecules can have different velocities.
• The gas molecules are so small that they can be assumed to have no volume. The volume of the gas is, thus, the volume of the container it is in.
• The gas molecules act like billiard balls in the sense that they collide and thereby change directions. Collisions between two molecules are elastic in the sense there is an exchange of kinetic energy (one moves faster than before and the other slower), but the total kinetic energy is conserved.
• The absolute temperature (which is measured from absolute zero [−273.15 °C] in kelvins, K) is proportional to the average kinetic energy of the ensemble of gas molecules. This statement means that as the temperature increases, the gas particles move faster.
• The gas molecules also have collisions with the container walls, and the result of these collisions constitutes the pressure in the system. The greater the number of collisions per unit time, the greater the pressure. The average pressure of the atmosphere at sea level is referred to as one atmosphere (1 atm). It is equal to 14.7 psi (pounds per square inch).
In addition to volume, pressure, and temperature, the concept of a mole is also important to the study of gases, whether in beer, the atmosphere, or wherever a gas occurs. A mole is a set number of molecules of any substance. The substance could be an elemental substance such as argon (Ar) or gold (Au), or it could be a compound such as oxygen (O2), nitrogen (N2), water (H2O), carbon dioxide (CO2), or ethanol (C2H5OH). For any elemental substance, such as gold, 1 mol (mol is the SI symbol for mole) contains 6.02 × 1023 atoms. For any compound, 1 mol contains 6.02 × 1023 molecules. This large number is called Avogadro’s number.
The mass of 1 mol of a compound is equal to its molecular weight in grams (g), e.g., 1 mol of CO2 has a mass of 44 g; 1 mol of N2 has a mass of 28 g; and 1 mole of O2 has a mass of 32 g. The density of a compound is defined as the ratio of mass to volume, e.g., the density of water is 1 g/mL and the density of ethanol is 0.7893 g/mL. The density is distinguished from the specific gravity of a compound; the specific gravity is the ratio of the density of the compound to the density of water at a standard temperature. Thus the specific gravity of ethanol is 0.7893/1 = 0.7893 (the units cancel out).
Thus, there is a relationship between the number (n) of moles—i.e., the amount—of a substance, the mass (m) of the substance in grams, and the molecular weight (MW) of the substance:
![]()
(6.1)
For example, how many moles are represented by 50 g of CO2? As stated, the molecular weight of CO2 is 44 g/mol, so
Conversely, 1.14 mol of N2 has a mass of
![]()
Finally, 44 g of CO2, 28 g of N2, and 32 g of O2 all have the same number of molecules (by definition, because each amount is 1 mol)—namely, the Avogadro’s number.
At the pressures and temperatures typical of brewing, CO2, N2, and O2 behave essentially as ideal gases. For these, volume V (in liters, L), pressure P (in atmospheres, atm), absolute temperature T (in kelvins, K), and number of moles n (in moles, mol) satisfy the relationship
![]()
R has a constant value and is called the universal gas constant. The value of R has been shown to be 0.0821 (L × atm)/(K × mol). Rewriting this equation gives the ideal gas law:
![]()
(6.2)
For example, suppose that a 25 L tank holds 50 g of CO2, and suppose that the temperature is 10 °C. Rearranging equation 6.2 predicts that the pressure in the tank can be calculated as follows:
![]()
Since the mass of CO2 is 50 g, the number of moles (from equation 6.1) is
![]()
In addition, because the absolute temperature (in K) is the temperature in Celsius (°C) plus 273 °C (actually 273.15 °C), the absolute temperature is
![]()
The temperature units °C and K are the same size, i.e., they represent the same change in temperature. The two scales that use them—the Celsius and kelvin (or absolute) temperature scales—just start at different points, 0 °C and 0 K, respectively, and 0 K = −273.15 °C. Thus,
![]()
There are three special cases of the ideal gas law that are expressions of how a fixed mass of gas (i.e., a fixed number of moles n) changes with changes in pressure, volume, and temperature. For this fixed-mass situation, combining two statements of the ideal gas law (i.e., equation 6.2) for a sample of gas at two different conditions yields
![]()
(6.3)
Note that n and R drop out of the calculation. In equation 6.3, P1, V1, and T1 are the pressure, volume, and absolute temperature (in K) of any sample of gas. When changes—e.g., heating or cooling—are made to the sample, new values P2, V2, and T2 result, and these are related to the old values by equation 6.3. The three special cases are shown in Table 6.1.
| Table 6.1 Three Gas Laws for a Fixed Mass of Gas | ||
|---|---|---|
|
Name |
Equation |
Constant |
|
Boyle’s law |
P1V1 = P2V2 |
T1 = T2 |
|
Charles’ law |
V1/T1 = V2/T2 |
P1 = P2 |
|
Gay-Lussac’s law |
P1/T1 = P2/T2 |
V1 = V2 |
In a continuation of the preceding example, suppose that the temperature of the CO2-filled tank is increased from 10 °C to 20 °C. Because a tank is involved, instead of a flexible container such as a balloon, the volume is constant. Table 6.1 indicates that a constant-volume situation is covered by Gay-Lussac’s law. Applying the relationship shown predicts an increase in pressure, as follows:
as already determined, and
![]()
Also, as already determined,
![]()
From Gay-Lussac’s law, it follows that
![]()
APPLICATIONS OF THE LAW OF PARTIAL PRESSURES TO BREWING
In addition to water vapor, mainly produced by vaporization during the boil and not the focus of this chapter, gases in beer are actually present as a mixture of CO2, N2, and O2. Thus it might seem that the ideal gas law would not apply. Fortunately, it does! John Dalton was an English chemist and physicist who lived from 1766 to 1844, and the major feature of his work showed that in a mixture of gases, each molecule acts independently of all others. This statement assumes that the gases do not interact with each other as they might when they are highly compressed. As far as beer is concerned, neither compression nor vaporization is sufficient to void Dalton’s statement, and so this assumed independence of individual gas molecules is a very accurate picture of what actually occurs.
What this concept means is that in a mixture of gases, each component has its own separate PV = nRT relationship and is independent of the action of the other components. The pressure P of an independent component is called the partial pressure of that component. It is the pressure that the component would exert if it were the only gas in the system. The total pressure P is then the sum of the individual partial pressures:
where the individual pressures on the right side of equation 6.4 are the partial pressures of CO2, N2, and O2, respectively. This concept is called Dalton’s law of partial pressures.
In the next three sections, three applications of this basic law are considered. The first deals with the carbonation of beer. The second involves the oxidation of beer, and the last explores the implications of Dalton’s findings for dispensing beer. The dispensing considerations are particularly important to brewers. Indeed, there is nothing more frustrating than to produce a high-quality beer, one for which all the technical issues discussed so far in this book have been correctly resolved, only to have the beer compromised by the way it is dispensed.
CARBONATION OF BEER
The unit generally used for measuring the amount of CO2 dissolved in beer is called volumes (abbreviated Vol.) in the brewing literature. It is defined as follows:
![]()
Table 6.2 gives some representative values of the CO2 content of various types of beer.
| Table 6.2 CO2 Volumes Data | |
|---|---|
|
Volumes (Vol., L/L) |
Beer type |
|
1.0–1.75 |
Real ale |
|
2.2–2.4 |
Draft lager |
|
2.4–2.6 |
U.K. and continental bottle beers |
|
2.6–2.8 |
U.S. lager beer |
|
>3.0 |
Bavarian wheat beers |
Since the density of CO2 at standard temperature and pressure is 1.96 g/L and its molecular weight is 44 g/mol, the number of moles n per liter is determined as follows:
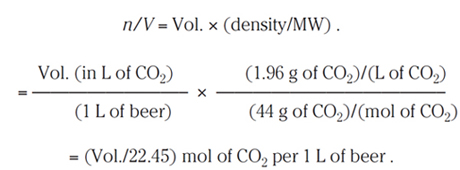
(6.5)
The unit for this kind of expression—the number of moles of a gas per 1 L of liquid—is called the molarity of the gas in the solution. For example, a beer at 2.5 volumes has a molarity of
![]()
Molarity is often expressed by a capital M, e.g., 0.11 M.
The gas laws hold for CO2 in the headspace of a tank or bottle. In particular, if equation 6.5 is mathematically rearranged and P/RT is substituted for n/V (the ideal gas law),
![]()
(6.6)
can be used to compute the molarity and hence the amount of CO2 in the headspace given the partial pressure PCO2 and the temperature T (in K).
For the CO2 actually dissolved in the beer, the situation is considerably more complicated because of gas and liquid interactions. Fortunately, a relationship called Henry’s law applies to this situation. It states that the concentration of a slightly soluble gas (e.g., CO2) is directly proportional to the partial pressure of the gas. Moreover, when a mixture of two gases (e.g., CO2 and O2) is in contact with a solvent (e.g., beer), the amount of each gas that is dissolved is the same as if it were present alone at a pressure equal to its own partial pressure. By using Henry’s law, values for n/V, and hence volumes (Vol.), for various partial pressures P and temperatures T have been worked out (ASBC, 1987). This often-quoted data set is given in part in Table 6.3. For example, if the partial pressure is 14.7 psi = 1 atm and the temperature is 0 °C = 273 K, then by interpolating it can be seen that Vol. = 3.21.
| Table 6.3 Values of CO2 volumes as a function of pressure and temperature | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
4 psi |
8 psi |
12 psi |
14 psi |
16 psi |
20 psi |
33 psi |
34 psi |
35 psi |
36 psi |
|
|
0 °C |
2.05 |
2.48 |
2.90 |
3.11 |
3.30 |
– |
– |
– |
– |
– |
|
2 °C |
1.87 |
2.29 |
2.67 |
2.86 |
3.05 |
– |
– |
– |
– |
– |
|
6 °C |
1.63 |
1.99 |
2.34 |
2.52 |
2.69 |
3.04 |
– |
– |
– |
– |
|
10 °C |
1.41 |
1.74 |
2.06 |
2.21 |
2.38 |
2.70 |
– |
– |
– |
– |
|
25 °C |
– |
– |
– |
– |
1.58 |
1.72 |
2.37 |
2.42 |
2.47 |
2.52 |
|
NOTE: Where no data (–) are listed, the conditions are not relevant to brewing. |
||||||||||
To give a specific case, suppose that a brewer wants to carbonate 100 L of beer in a vessel of 125 L capacity. The 20% headspace is common for carbonation tanks. In addition, suppose that 2.5 volumes of CO2 is required in the finished product. Since approximately 0.2 volumes is lost at the filler, the brewer’s target should be 2.7 volumes. This result means that, under equilibrium conditions,
![]()
is required, or a total of
![]()
Suppose the temperature of the tank is held at 2 °C = 275 K, which is the same as 35 °F. The data in Table 6.3 indicate that to contain 2.7 volumes of CO2 at 2 °C, an equilibrium partial pressure of CO2 of 12 psi is needed. It must be emphasized that time is required for the system to reach equilibrium, and none of the analysis in this example is applicable until the steady state is reached. For direct injection, this time can be significantly reduced by carbonating stones, i.e., diffusers that release CO2 in a spray of tiny bubbles. If the beer is carbonated by addition of new wort (i.e., kraeusening), then equilibrium is usually established shortly after the second fermentation is complete in gas-tight containers.
To compute the total amount of CO2 added, the ideal gas law can be used to determine the amount of CO2 in the tank headspace. Henry’s law shows that the partial pressure of the CO2 in the headspace affects the amount of CO2 in the beer. Thus
![]()
Equation 6.6 predicts that the volumes of CO2 in the headspace is
![]()
or
![]()
Since the tank headspace is 20 L, there are
![]()
in the headspace. Thus a total of 529 + 32 = 561 g of CO2 should be added to the tank. These calculations are summarized as follows:
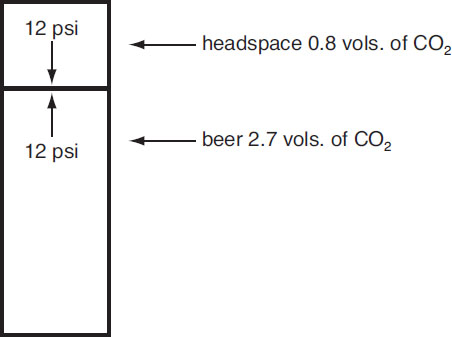
CO2 distribution in beer and headspace
OXIDATION OF BEER
As a second application of Henry’s law, consider the role played by air in packaged beer headspace. Suppose there is a bottle containing 350 mL = 0.35 L of beer with a headspace of 20 mL = 0.02 L. Suppose, that after filling, it was determined that the beer’s headspace air level was 0.5 mL = 0.0005 L. Dalton’s law applies to this situation independent of how much CO2 is involved. In particular, if the version of the gas law due to Boyle (see Table 6.1) is used, the ratio of the partial pressure of air Pair to a reference pressure Pref is proportional to the ratio of the volumes of air Vair in the headspace to the volume of the headspace Vheadspace, i.e.,
![]()
Following the procedures found in Methods of Analysis (American Society of Brewing Chemists, 1987), Pref = 1 atm. Therefore,
![]()
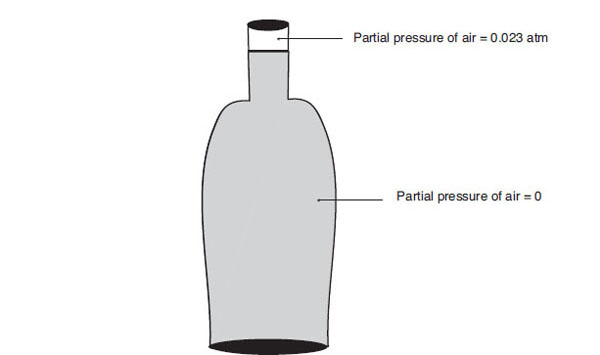
Partial pressure of air in headspace and in beer
Initially, the gases in the headspace will stratify according to weight; i.e., the 0.5 mL volume of air will sit above a CO2 layer. Henry’s law, however, asserts that, at equilibrium, the gases will act as if each were the only gas present. Since the beer was assumed to be free of air at fill, the system is not at equilibrium because there is a concentration differential between the headspace and beer. This forces an air ingress into the beer. If the air were inert in beer, the ingress would continue until the partial pressures balanced. However, beer constituents (e.g., ethanol) will react with the free oxygen in the ways discussed in chapter 4, and the reactions in turn will reduce the partial pressure of the air in the beer, causing more air to diffuse into the beer until ultimately all headspace air is consumed.
It should be noted that the headspace partial pressure, Pheadspace, increases proportionately with the storage temperature (i.e., absolute temperature, in K). This relationship in part explains why the staling rate increases with temperature. As the pressure increases, air is forced into the beer at a greater rate. Since the rate of redox reactions increases exponentially with temperature, the oxygen-bearing components that are absorbed are consumed at greater rates as well.
When one is doing very accurate CO2 measurements, it is necessary to take into account the amount of headspace air just after fill. The above considerations apply here as well. As an example, suppose that a standard air and CO2 tester is used (the tester from the Zahm and Nagle Catalog, Buffalo, New York, for example, which comes with an expanded version of Table 6.3). This is a piercing device that measures the total pressure (i.e., CO2 plus air) in the headspace, the headspace air volume, and the temperature. Measurements with this device are done at 25 °C (77 °F). For instance, suppose that one has 350 mL of beer with 20 mL of headspace and suppose that the Zahm and Nagle instrument reads
![]()
and
![]()
Table 6.3 shows that, ignoring air corrections, this pressure yields 2.52 volumes of CO2. The measured pressure Ptotal = 36 psi is actually the sum of the partial pressure of CO2 and the partial pressure of air. By using both Boyle’s and Dalton’s laws, the partial pressure of air can be computed as follows:
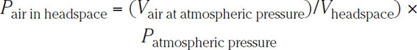
![]()
Thus, the partial pressure due to CO2 is actually
![]()
and interpolating from Table 6.3 at 25 °C gives
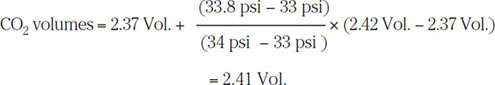
Once the headspace air volumes fall below 1 mL, it is customary to ignore such corrections (ASBC, 1987).
DISPENSING DRAFT BEER
As a final application of the gas laws, consider the proper dispensing of carbonated bottled beer. There are three crucial variables:
1. Equilibrium pressure (PE). This variable is the external pressure required to maintain the beer’s gas content. In the numerical example given next, the beer contains 2.5 vols. of CO2 (no air for this example) and is at 4.5 °C (about 40 °F). Table 6.3 shows that PE is approximately 12 psi in this case.
2. Gravity head (PH). This variable is the pressure to push the beer against gravity from the beer tank to the tap. A widely used rule is that it takes 0.042 psi/in., or equivalently, 1 psi is required to lift beer 2 ft. vertically (Miller, 1992; Wheeler, 1998).
3. Line resistance (PLR). This variable is the pressure required to overcome the resistance in the tubing leading from the beer keg to the tap. For either vinyl or polyethylene hose, a 3/8 in. line provides a resistance pressure of 0.1 psi/ft. whereas lines of 1/4 in. and 3/16 in. diameter require 0.6 and 2.2 psi/ft., respectively (Wheeler, 1998).
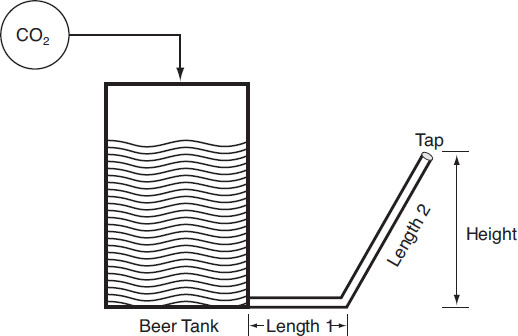
Beer-dispensing system
The effective pressure is defined as
![]()
To prevent overflowing and gushing, the line length is chosen so that the effective pressure is zero (Peff = 0). Then
![]()
This relationship results in a balanced system, and if the exogenous CO2 supply is held at PE, then the system would be in equilibrium. There would be no flow, but at the same time there would be no loss of CO2. A good working rule is that if the supplied CO2 pressure exceeds PE by 2 psi in a balanced system, then a flow rate of 1–1.2 gal./min (2.1–2.6 oz./s) will result. This flow rate is considered ideal; there is no loss of CO2 during dispensing (Miller, 1992; Wheeler, 1998).
To give a numerical example, consider the case of a typical draft box (such as one from the Superior Products Catalog, St. Paul, Minnesota).

Draft box
Suppose that the beer has 2.5 vols. of CO2 and is dispensed at 4.5 °C (about 40 °F). As noted previously, this arrangement gives PE = 12 psi. The gravity head is 2 ft. so,
![]()
Thus, to have a balanced system, one needs
![]()
Suppose a 3/16 in. tubing is used. Then the line length required is
![]()
As noted above, the desired dispensing pressure to achieve balance is
![]()
This analysis does not take into account the possible CO2 pickup in the beer over time by holding 14 psi top pressure on it. This additional CO2 will lead to an unbalanced system—and hence to excess foaming at the tap—in addition to the undesirable increase in beer CO2 volumes. An alternative is to use a CO2 and N2 mix for the driving pressure. The idea is to have sufficient CO2 to balance the equilibrium pressure of beer and to let the N2 overcome the gravity head and line resistance.
As a specific example, suppose that a 75% N2 and 25% CO2 mix is used. In such a mix, the pressure due to CO2 will be roughly 1/3 that of N2. Thus, the desired top pressure is as follows:
|
CO2 pressure |
12 psi |
|
N2 pressure |
36 psi |
|
Top pressure |
48 psi |
This top pressure may seem high at first glance, but it must be kept in mind that the solubility of N2 in beer is a factor of 80 less than CO2. Other numerical examples are in Taylor et al. (1992).
The use of N2 and CO2 mix for carbonating beer is also discussed in Taylor et al. (1992). This approach can be very tricky owing to high gas losses during processing. If these can be managed, however, the result can be a beautiful and highly stable foam stand. This can be explained by partial pressures of the individual gases. First, consider the previous example in which the equilibrium pressure is 12 psi at 40 °F. A typical foam bubble can be described schematically as follows:
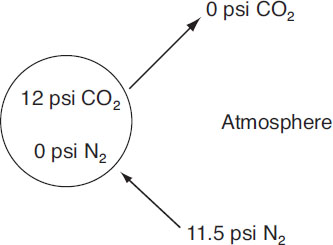
Foam bubble of pure CO2
That is, there is a large partial-pressure differential with the ambient environment leading to CO2 escape and collapsing bubbles. Now consider a 75% N2 and 25% CO2 mix of at 16 psi:
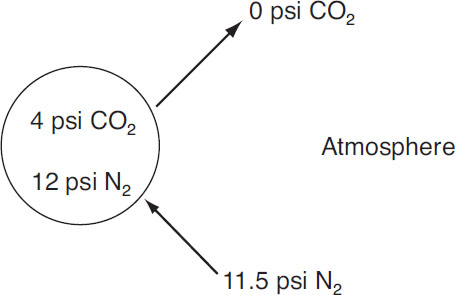
Foam bubble of CO2 and N2
The nitrogen is nearly in equilibrium with the ambient environment, whereas the pressure differential for CO2 has been reduced by a factor of 3. In this situation, the gas loss is considerably less than in the first example and hence provides more support for the foam stand.
I would like to conclude this chapter and indeed this book on a personal note. For me, the dispensing of a new brew is an event of great significance. The beer in the glass is a product that represents a long list of decisions and actions on my part. First of all, there is the choice of brewing materials and the way they are processed. Actually, of greater significance is my choice of yeasts and what I have done to see that they were in appropriate condition to do whatever it is I want them to do. Of even greater significance are the actions I have taken to protect my concoction from adversaries, be they foreign microbes or oxygen. All of this is in that glass and represents the deepest joy of brewing.