 30
30The GMAT problem-solving questions are multiple-choice questions. Each question provides five answer choice options. Most of the questions present a problem situation that requires a single response. Some of the question stems will have Roman numeral options. The five answer options will include various combinations of the Roman numeral options. In either case, you must select the one best answer choice from the five answer choice options.
Start by reading the question stem. Determine what the question is asking. Skim through the answer choices. Decide on an optimum approach for answering the question. Here are some strategic ways to attack problem-solving questions.
For many questions, writing and solving an equation is a straightforward method for determining the answer. Let the variable represent the unknown in the question. When you have more than one unknown in a problem question, you might be able to express one in terms of the other. For instance, if a first unknown is described in terms of a second unknown, it is usually easier to let the variable equal the second unknown. For such problems, you also can choose to assign a variable name to each unknown. Just remember that you will need as many equations as you have variables in order to determine specific values for the variables. Here is an example.
A rectangular swimming pool is twice as long as it is wide. If the perimeter of the pool is 180 feet, what is the length, in feet, of the pool?
 30
30
 60
60
 70
70
 80
80
 90
90
The perimeter, P, of a rectangle is P = 2l + 2w = 2(l + w), where l is the rectangle’s length and w is its width. (See Chapter 10 Geometry Review for formulas of geometric figures).
Method 1: Use one variable.
The length of the pool is described in terms of its width. Let w = the width, in feet, of the pool. Then 2w = the length, in feet, of the pool. Write an equation that represents the facts given in the question.
180 feet = 2(2w + w) or, equivalently, 2(2w + w) = 180 feet
Solve the equation, omitting the units for convenience.
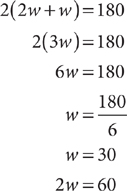
The length of the pool is 60 feet. The correct response is B.
Tip: Make sure you answer the question asked. In this question, after you obtain w, you must calculate 2w to answer the question.
Method 2: Use two variables.
Let w = the width, in feet, of the pool and l = the length, in feet, of the pool. Write two equations that represent the facts given in the question.
(1) l = 2w
(2) 2(l + w) = 180 feet
Simultaneously solve the two equations, omitting the units for convenience.
Using the substitution method, substitute l = 2w from equation (1) into equation (2) to obtain
2(2w + w) = 180
Complete the solution as shown in Method 1.
When you are provided numerical answer choices, you might determine the correct choice by checking the answer choices. Here is an example.
Henry must pay a 7% penalty tax on the portion of the total value of an item that exceeds $100. If Henry paid a penalty tax of $8.75, what was the total value of the item?
 $185
$185
 $225
$225
 $240
$240
 $275
$275
 $300
$300
Before you start checking the answer choices, write an equation to make sure you understand the question. Let x = the total value in dollars of the item. Then x – $100 is the portion of the item that is subject to the 7% penalty tax. Using the information in the question, set up an equation that represents the facts of the question.
7%(x – $100) = $8.75
0.07(x – $100) = $8.75
Now check the answer choices in the equation. The answers are listed in ascending order, so start with choice C. If choice C is incorrect, you might be able to use logical reasoning to eliminate other answer choices as well. This will enable you to determine the correct answer sooner and save time. Check C:
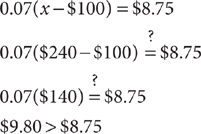
Choice C is too high, so eliminate choices D and E as too high as well. Check B:
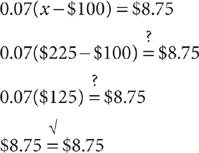
Choice B is the correct response.
When you have questions involving percentages in which the base is not given, you can usually plug in 100 for the base to make the problem easier to work out. Here is an example.
Marvin invested in a stock whose value had increased 5% by the end of 2012, decreased 2% by the end of 2013, and increased 10% by the end of 2014. What is the percent increase in the value of the stock from the end of 2012 to the end of 2014?
 7.80%
7.80%
 8.19%
8.19%
 12.50%
12.50%
 13.00%
13.00%
 17.00%
17.00%
The percent increase in the stock is

For convenience let $100 be the initial value of the stock. Then the value of the stock at the end of 2012 was 105%($100) = $105. By the end of 2013, the value of the stock was 98%($105) = $102.90. By the end of 2014, the value of the stock was 110%(102.90) = $113.19. The percent increase is
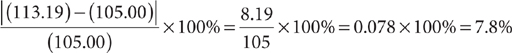
The percent increase in the stock is 7.8%. Choice A is the correct response.
When the question stem and the answer choices both contain one or more variables, you might try evaluating the expressions given in the question stem and answer choices for suitable values of the variables. Make sure the values you select satisfy all the conditions presented in the question. Suitable values are small numbers such as 2, 3, and 4. Avoid using 0 or 1, because these numbers have special properties that might lead you to believe an incorrect answer choice is correct. Look for an answer choice that evaluates to the same value as the expression in the question stem. Tip: You must evaluate all the answer choices to make sure two choices (or possibly more) do not evaluate to the same value as the expression in the question stem. If this occurs, start over and choose different values for the variables. Here is an example.
Which expression is equivalent to 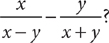
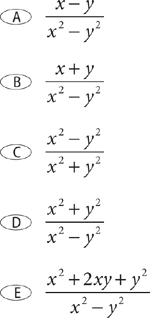
Let x = 3 and y = 2. 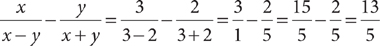
Check A: 
Check B: 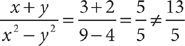
Check C: 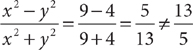
Check D: 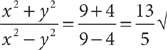
Check E: 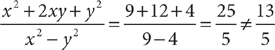
Choice D is the correct response.
In many cases, the most efficient way to answer a problem-solving question is simply to do the math. Here is an example.
4x2 – 8x – 5 = 0
What is the sum of the roots of the preceding quadratic equation?
 –8
–8
 –2
–2
 2
2
 4
4
 8
8
Solve the quadratic equation by factoring.
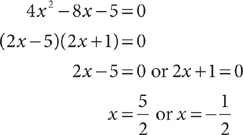
Compute the sum 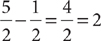 .
.
Choice C is the correct response.
 Use logical reasoning to eliminate answer choices. You can eliminate some answer choices from the outset based on logical reasoning. For instance, if you figure out the answer must be even, you can eliminate all odd answer choices.
Use logical reasoning to eliminate answer choices. You can eliminate some answer choices from the outset based on logical reasoning. For instance, if you figure out the answer must be even, you can eliminate all odd answer choices.
 Make rough sketches for geometry questions. For geometry problems, sketches help you organize the question information. However, make quick rough sketches. Do not spend unnecessary time making them.
Make rough sketches for geometry questions. For geometry problems, sketches help you organize the question information. However, make quick rough sketches. Do not spend unnecessary time making them.
 Know your math. No matter which strategy you use in a problem-solving question, you will need to know and understand math. Most of the math concepts on the GMAT are ones you likely have encountered in the past. However, you might have forgotten some if not most of them. Study the math review in this book to refresh your knowledge and skills.
Know your math. No matter which strategy you use in a problem-solving question, you will need to know and understand math. Most of the math concepts on the GMAT are ones you likely have encountered in the past. However, you might have forgotten some if not most of them. Study the math review in this book to refresh your knowledge and skills.
Select the best of the given answer choices.
1. A grocery store’s electricity cost in January is $1,420. After installing a new energy-efficient heating and cooling system, the manager estimates that the electricity cost will decrease by 2.5% per month over the next six months. Based on this estimate, which expression represents the grocery store’s electricity cost in March of the same year?
 ($1,420)(0.975) + ($1,420)(0.950)
($1,420)(0.975) + ($1,420)(0.950)
 $1,420 – ($1,420)(0.025)(0.025)
$1,420 – ($1,420)(0.025)(0.025)
 $1,420 – ($1,420)(0.025)(0.025)(0.025)
$1,420 – ($1,420)(0.025)(0.025)(0.025)
 ($1,420)(0.975)(0.975)
($1,420)(0.975)(0.975)
 ($1,420)(0.975)(0.950)
($1,420)(0.975)(0.950)
2. Of the 4,800 residents of an apartment complex,  are college students. Suppose the number of college students is reduced by
are college students. Suppose the number of college students is reduced by  . If no other changes occur, what portion of the total remaining residents are college students?
. If no other changes occur, what portion of the total remaining residents are college students?
3. Fifty percent of a couple’s retirement account is invested in stocks, 25% in a mutual fund, and 20% in Treasury bonds. The remaining $20,000 is in certificates of deposit. In the couple’s retirement account, what is the total amount invested?
 $200,000
$200,000
 $300,000
$300,000
 $400,000
$400,000
 $1,000,000
$1,000,000
 $4,000,000
$4,000,000
4. Which of the following expressions has  as a numerical value?
as a numerical value?
I. 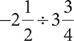
II. 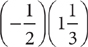
III. 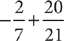
 I only
I only
 II only
II only
 I and II only
I and II only
 II and III only
II and III only
 I, II, and III
I, II, and III
5. The original price of a video game console was $400. The console was reduced by 25% for a sale. After the sale, the price increased to $375. What is the percent increase over the sale price?
 0.2%
0.2%
 0.25%
0.25%
 20%
20%
 25%
25%
 30%
30%
6. Tovia is a delivery person for a specialty frozen food company. Besides her base weekly pay of $350, she makes a 6% commission on all items that she sells to customers. Last week Tovia’s weekly pay plus commissions totaled $920. What amount is the total of Tovia’s sales for last week?
 $604.20
$604.20
 $1,105.80
$1,105.80
 $9,000.00
$9,000.00
 $9,500.00
$9,500.00
 $15,333.33
$15,333.33
7. If the sum of three consecutive integers is doubled, the result is 71 more than  times the third integer. What is the value of the third integer?
times the third integer. What is the value of the third integer?
 19
19
 20
20
 21
21
 22
22
 23
23
8. Lucy is twice as old as Bret. In five years, the sum of their ages will be 52. How old will Lucy be 10 years from now?
 14
14
 24
24
 28
28
 38
38
 43
43
9. If  , then 10x =
, then 10x =



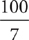

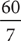
 7
7
 3
3
10. To include a penalty for guessing, the scoring formula for a 60-question, multiple-choice test is  , where s is the score on the test, r is the number of correct responses, and w is the number of incorrect responses. A student answers all 60 questions. Which of the following scores could be the student’s score?
, where s is the score on the test, r is the number of correct responses, and w is the number of incorrect responses. A student answers all 60 questions. Which of the following scores could be the student’s score?
I. –15
II. 10
III. 32
 I only
I only
 I and II only
I and II only
 I and III only
I and III only
 II and III only
II and III only
 I, II, and III
I, II, and III
11. In triangle ABC, sides  and
and  are congruent. The measure of angle C is 36°. What is the measure of angle A?
are congruent. The measure of angle C is 36°. What is the measure of angle A?
 28°
28°
 36°
36°
 72°
72°
 104°
104°
 108°
108°

12. In the preceding figure, lines m and n are parallel and cut by the transversal t. What is the measure of angle θ?
 20°
20°
 40°
40°
 60°
60°
 110°
110°
 120°
120°
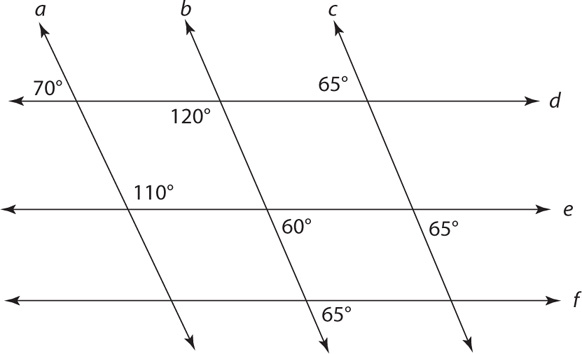
13. Based on the preceding figure, which statement is true?
 a || b
a || b
 a || c
a || c
 b || c
b || c
 d || e
d || e
 d || f
d || f
14. How many triangles are in the preceding figure?
 4
4
 7
7
 8
8
 9
9
 10
10
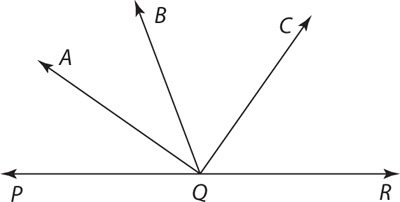
15. In the preceding figure, ∠AQP ≅ ∠AQB and ∠BQC ≅ ∠CQR. What is the measure of ∠AQC?
 100°
100°
 90°
90°
 80°
80°
 75°
75°
 70°
70°
16. A van leaves City A at 9 a.m., moving at an average speed of 50 miles per hour. Without making any stops, the van arrives at City B at 2 p.m. At approximately what time would the van have arrived if the driver had maintained an average speed of 65 miles per hour?
 12:24 p.m.
12:24 p.m.
 12:51 p.m.
12:51 p.m.
 1:24 p.m.
1:24 p.m.
 1:51 p.m.
1:51 p.m.
 2:24 p.m.
2:24 p.m.
17. A candy store owner mixes candy that normally sells for $2.50 per pound and candy that normally sells for $3.75 per pound to make a 90-pound mixture to sell at $3.00 per pound. To make sure that $3.00 per pound is a fair price, how many pounds of the $2.50 candy should the owner use?
 54
54
 50
50
 42
42
 36
36
 30
30
18. Working alone, Annerose can paint a room in 6 hours. Mike working alone can do the same job in 4 hours. If Annerose and Mike work together, how many hours should it take them to paint the room?
 5
5

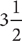
 3
3

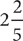

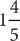
19. The positive integer n is not divisible by 2 or 3. Which could be the remainder when n is divided by 6?
I. 1
II. 3
III. 5
 I only
I only
 I and II only
I and II only
 I and III only
I and III only
 II and III only
II and III only
 I, II, and III
I, II, and III
20. A teacher buys pencils and pens for her classroom. The pencils come 12 in a pack, and the pens come 8 in a pack. The teacher buys the same number of pens as she does pencils, with none left over. What is the least number of each she could buy?
 8
8
 12
12
 24
24
 48
48
 96
96
1. D In February, the electricity cost is $1,420 – 0.025($1,420) = ($1,420)(1–0.025) = ($1,420)(0.975). In March, the electricity cost is ($1,420)(0.975)(1–0.0.025) = ($1,420)(0.975)(0.975).
2. B Calculate the initial number of college students: 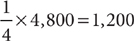 . Calculate
. Calculate  of this number:
of this number: 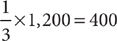 . Calculate the number of college students remaining: 1,200 – 400 = 800. Calculate the number of total residents remaining: 4,800 – 400 = 4,400. Calculate the portion of the total remaining who are college students:
. Calculate the number of college students remaining: 1,200 – 400 = 800. Calculate the number of total residents remaining: 4,800 – 400 = 4,400. Calculate the portion of the total remaining who are college students: 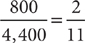 .
.
3. C Let x = The total amount in dollars invested. The percent invested in stocks, the mutual fund, and bonds is 50% + 25% + 20% = 95%. Thus, the percent invested in certificates of deposit is 100% – 95=5%. Write the following percent equation to represent the facts given in the question.
5%x = $20,000
Solve for x, the total amount invested
Method 1: Solve the equation using a conventional procedure, omitting the units for convenience.
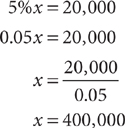
The total amount invested is $400,000.
Method 2: Solve the equation using logical reasoning and mental math. Given 5% of x is $20,000. Then 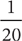 of x is $20,000. So x is $20,000 times 20, which is $400,000. Or given 5% of x is $20,000. Then 10% of x is $40,000. So x is $40,000 times 10, which is $400,000.
of x is $20,000. So x is $20,000 times 20, which is $400,000. Or given 5% of x is $20,000. Then 10% of x is $40,000. So x is $40,000 times 10, which is $400,000.
4. C Eliminate Roman III because, without doing any calculations, you know the sum is positive because  . Eliminate choices D and E because each contains Roman III. Now check Roman I and II.
. Eliminate choices D and E because each contains Roman III. Now check Roman I and II.
Check Roman I: 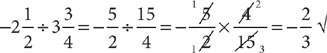
Check Roman II: 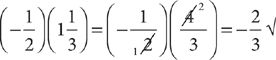
Thus, choice C is correct.
5. D The sale price is $400 minus (25% of $400) =
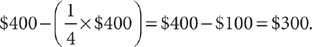
The percent increase is 
6. D Let x = the amount in dollars of Tovia’s total sales last week. Write an equation that represents the facts given in the question.
$350 + 6%x = $920
Method 1: Solve for x using a conventional procedure, omitting the units for convenience.

The amount of Tovia’s total sales last week is $9,500.
Method 2: Check the answer choices. Check C:
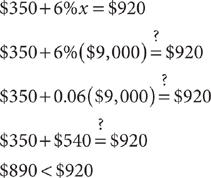
Eliminate choice C as too low. Eliminate choices A and B as too low as well. Check D:
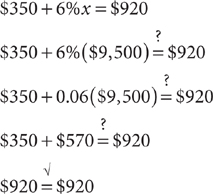
Choice D is the correct response.
7. D Let x, x + 1, and x + 2 represent the three consecutive integers. From the information in the question, set up an equation and solve for x + 2.

Thus, the third integer is x + 2 = 22.
8. D Let x = Bret’s age now, in years. Then 2x = Lucy’s age now, in years. Make a chart to organize the information in the question.

Write an equation that represents the facts given.
(x + 5 years) + (2x + 5 years) = 52 years
Solve the equation, omitting the units for convenience.

2x = 28, Lucy’s age now
28 + 10 = 38, Lucy’s age 10 years from now
9. D Substitute the given value of x, and use your knowledge of exponents to solve for 10x.
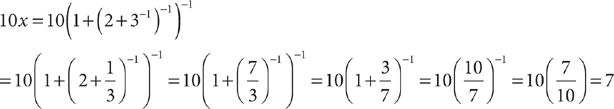
10. B The number of wrong answers, w, is 60 – r (the number of right answers). Therefore, 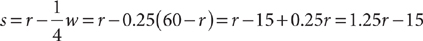 . You know that r is a whole number such that 0 ≤ r ≤ 60. When r = 0, the least score is s = 1.25r – 15 = 1.25(0) – 15 = –15, Roman I. Eliminate choice D because it does not include Roman I. Solving s = 1.25r – 15 for r yields
. You know that r is a whole number such that 0 ≤ r ≤ 60. When r = 0, the least score is s = 1.25r – 15 = 1.25(0) – 15 = –15, Roman I. Eliminate choice D because it does not include Roman I. Solving s = 1.25r – 15 for r yields  . Now use
. Now use 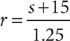 to check the other Roman numeral options to see whether r computes to be a whole number between 0 and 60.
to check the other Roman numeral options to see whether r computes to be a whole number between 0 and 60.
Check Roman II: 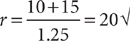 ; eliminate choices A and C because neither includes Roman II.
; eliminate choices A and C because neither includes Roman II.
Check Roman III:  , not a whole number.
, not a whole number.
Eliminate choice E because it includes Roman III. Choice B is the correct response.
11. E Make a sketch, filling in the question information.
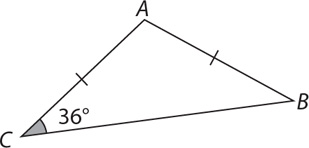
Angles C and B are base angles of an isosceles triangle, so their measures are equal, that is, m∠B = m∠C = 36°. The sum of the angles of a triangle is 180°. Thus, ∠A = 180° – 2(36°) = 180° – 72° = 108°. Note: m∠X denotes the measure of angle X.
12. D θ and 3x + 50° are congruent because they are vertical angles; θ and 2x + 70° are congruent because they are corresponding angles of parallel lines. Thus, θ = 3x + 50° = 2x + 70°, so x = 20°. Thus, θ = 3 · 20° + 50° = 110°.
13. D Check the answer choices. Check A: a || b is false, because the corresponding angles [70° and (180°–120° = 60°] are not congruent. Check B: a || c is false, because the corresponding angles (70° and 65°) are not congruent. Check C: b || c is false, because the corresponding angles (60° and 65°) are not congruent. Check D: d || e is true, because the corresponding angles [70° and (180°–110°) = 70°] are congruent. Because choice D is correct, move on to the next question.
14. C List the triangles, proceeding systematically. You have triangles ABC, ABD, ABE, ACD, ADE, BCD, BCE, and CDE, for a total of 8 triangles.
15. B From the figure, you can see that ∠AQC = ∠AQB + ∠BQC and that m∠AQP + m∠AQB + m∠BQC + m∠CQR = 180°. Given ∠AQP ≅ ∠AQB and ∠BQC ≅ ∠CQR, then 2(m∠AQB) + 2(m∠BQC) = 180°. Dividing both sides of the equation by 2, m∠AQB + m∠BQC = 90° = m∠AQC.
16. B The distance formula is d = rt, where d is the distance traveled at a uniform rate of speed r for a length of time t. The van traveled 5 hours at 50 miles per hour (mph), so the distance, d, from City A to City B is d = rt = (50 mph)(5 hr) = 250 miles. At 65 mph, the time would be
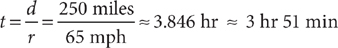
The approximate time of arrival would be 9 a.m. plus 3 hours 51 minutes, which is 12:51 p.m.
17. A Let x = the number of pounds of the candy priced at $2.50 per pound needed. Then 90 – x = the number of pounds of the candy priced at $3.75 per pound needed. Make a chart to organize the information in the question.
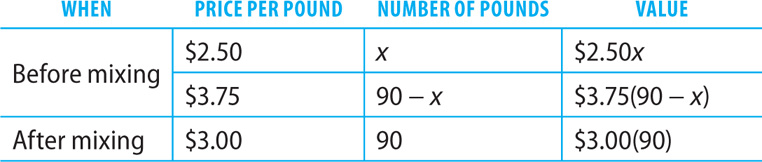
The value of the candy before it is mixed should equal the value after it is mixed. Using the information in the chart, set up an equation that represents the facts given in the question (omitting “pounds” and “per pound” because these units cancel each other).
$2.50x + $3.75(90 – x) = $3.00(90)
Solve for x.
Method 1: Solve the equation using a conventional procedure, omitting the units for convenience.
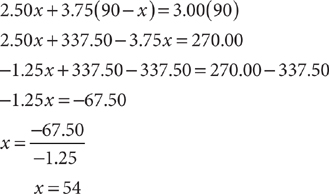
The owner should use 54 pounds of the $2.50 candy.
Method 2: Solve the equation using logical reasoning and mental math. If the owner used half of each type of candy, then the price should be the average of $2.50 and $3.75, which is about $3.13. So, you know that to bring the price down to $3.00 per pound will require more than 45 pounds (half) of the lower-priced candy. Therefore, eliminate choices C, D, and E right away. Now check choice B in the equation:

Choice B doesn’t satisfy the equation. By elimination, choice A is the correct response.
18. D In a “work” problem, it is usually necessary to determine the rate at which someone or something does a task or job. The rate equals the amount of work done divided by the total time worked. Let t = the time (in hours) it will take Annerose and Mike, working together, to paint the room.
Method 1: When you have only two workers, a handy shortcut method for finding the time it will take the two of them to do a job, working together, is to divide the product of their times working alone by the sum of their times working alone. Using the shortcut method and omitting the units for convenience, the time it should take Annerose and Mike, working together, to paint the room is:

It should take Annerose and Mike, working together, 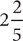 hours to paint the room.
hours to paint the room.
Method 2: Make a chart to organize the information in the question.

Using the information in the chart, set up an equation that represents the facts given in the question. Solve for t.
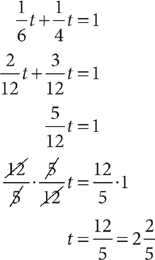
It should take Annerose and Mike, working together, 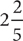 hours to paint the room.
hours to paint the room.
19. C When you divide a positive number by 6, the remainder is 0, 1, 2, 3, 4, or 5. Thus, any nonnegative integer has the form 6k, 6k + 1, 6k + 2, 6k + 3, 6k + 4, or 6k + 5 (k = 0, 1, 2, …). Because n is not divisible by 2 or 3, n must have the form 6k + 1 or 6k + 5. Thus, the remainder when n is divided by 6 is either 1 (Roman I) or 5 (Roman III). Choice C is the correct response.
20. C Solve this problem by finding the least common multiple (LCM) of 12 and 8.
Method 1: Start listing multiples of 12 until you reach one that is also a multiple of 8.
Multiples of 12: 12, 24. Stop because 24 = 3 × 8, a multiple of 8. So, the LCM of 12 and 8 is 24. The teacher bought 24 pencils (2 packs of 12 in a pack) and 24 pens (3 packs of 8 in a pack).
Method 2: The LCM of two numbers is their product divided by their greatest common factor (GCF). The GCF of 12 and 8 is 4. The LCM of 12 and 8 is:
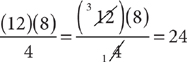 . The teacher bought 24 pencils (2 packs of 12 in a pack) and 24 pens (3 packs of 8 in a pack).
. The teacher bought 24 pencils (2 packs of 12 in a pack) and 24 pens (3 packs of 8 in a pack).
1. The ratio of zinc to copper in a certain alloy is 2 to 5. If 120 grams of copper are used, how many grams of zinc are needed to make this alloy?
 24
24
 48
48
 60
60
 200
200
 300
300
DISTRIBUTION OF STUDENTS AT COMMUNITY COLLEGE X
BY AGE AND GENDER
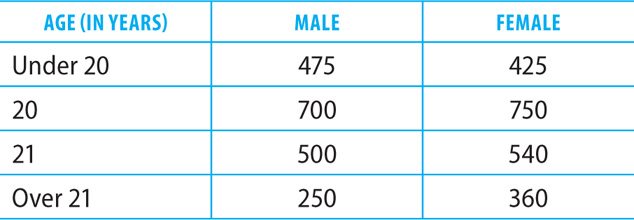
2. The preceding table shows the distribution of students attending Community College X by age and gender. Suppose a student is randomly selected. To the nearest hundredth, what is the probability that the student is male or 21 years or older?
 0.41
0.41
 0.48
0.48
 0.57
0.57
 0.71
0.71
 0.89
0.89
3. In a cooking contest, five judges score each contestant. To calculate a contestant’s final score, the judges discard the highest number and lowest number, and then they take the arithmetic average of the remaining numbers. The five judges score a contestant as 6.3, 7.1, 6.4, 6.5, and 6.2. What is the contestant’s final score?
 6.7
6.7
 6.6
6.6
 6.5
6.5
 6.4
6.4
 6.3
6.3
4. The value of an investment triples every 10 years. By what factor does the value increase over a 30-year period?
 3
3
 6
6
 9
9
 27
27
 30
30
5. What is the units digit of 3102?
 1
1
 3
3
 6
6
 7
7
 9
9
6. Quinn wants a trendy but expensive toy. It goes on sale at a local toy store for 15% less than the original price. Before Quinn can buy the toy, however, the toy store raises the price by 20%. If the 15%-off sale price was $119, the final price is what percent of the original price?
 95%
95%
 98%
98%
 102%
102%
 105%
105%
 120%
120%
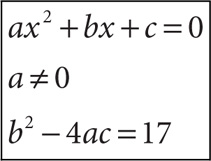
7. From the preceding information given, which statement is true about the equation ax2 + bx + c = 0?
 It has no real roots.
It has no real roots.
 It has exactly one real, rational root.
It has exactly one real, rational root.
 It has exactly one real, irrational root.
It has exactly one real, irrational root.
 It has exactly two real, rational roots.
It has exactly two real, rational roots.
 It has exactly two real, irrational roots.
It has exactly two real, irrational roots.
8. The operation ⊗ is defined on the set of real numbers by a ⊗ b = 2a + ab, where a and b are real numbers and the operations on the right side of the equal sign denote the standard operations for the real number system. What is (3 ⊗ 2)⊗5?
 30
30
 60
60
 74
74
 84
84
 96
96
9. If 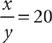 and
and 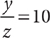 , with y · z ≠ 0, what is the value of
, with y · z ≠ 0, what is the value of 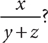
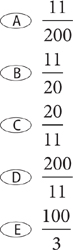
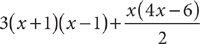
10. Which expression is equivalent to the preceding expression?
 5x2 + 3x – 6
5x2 + 3x – 6
 3x2 + 3x – 6
3x2 + 3x – 6
 –x2 + 3x + 3
–x2 + 3x + 3
 5x2 – 3x + 3
5x2 – 3x + 3
 5x2 – 3x – 3
5x2 – 3x – 3

11. In the preceding figure the lines l, m, and n intersect in a point, the measure of ∠1 is 65°, and the measure of ∠2 is 85°. What is the measure of ∠3?
 20°
20°
 25°
25°
 30°
30°
 35°
35°
 40°
40°
12. Angles a and b are complementary angles, and angles c and d are complementary angles. If angles a and d are congruent, which statement must be true?
 Angles b and c are congruent.
Angles b and c are congruent.
 Angles b and d are congruent.
Angles b and d are congruent.
 Angles a and d are complementary.
Angles a and d are complementary.
 Angles b and c are complementary.
Angles b and c are complementary.
 Angles a and c are congruent.
Angles a and c are congruent.
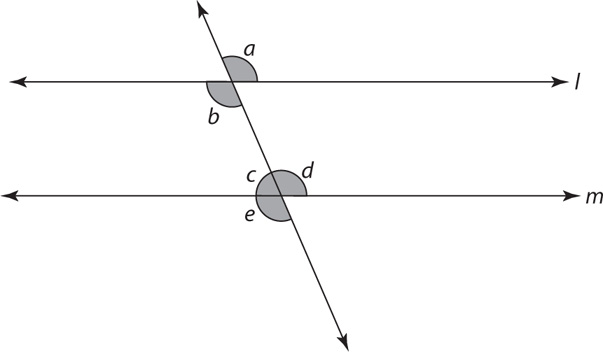
13. In the preceding figure, angles b and c are supplementary. Which statement must be true?
 ∠a ≅ ∠c
∠a ≅ ∠c
 ∠a ≅ ∠d
∠a ≅ ∠d
 ∠b ≅ ∠c
∠b ≅ ∠c
 ∠c ≅ ∠d
∠c ≅ ∠d
 ∠c ≅ ∠e
∠c ≅ ∠e
14. Points R, P, and S lie above line segment  in the relative order given. Line segment
in the relative order given. Line segment  is perpendicular to line segment
is perpendicular to line segment  at the point Q. Hence, Point R lies to the left of
at the point Q. Hence, Point R lies to the left of 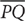 and point S lies to its right. The segment
and point S lies to its right. The segment 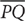 bisects ∠RPS and
bisects ∠RPS and  . The measure of ∠PQS = 35°. What is the measure of ∠RQM?
. The measure of ∠PQS = 35°. What is the measure of ∠RQM?
 35°
35°
 45°
45°
 55°
55°
 65°
65°
 75°
75°
15. In the preceding figure, 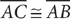 , ∠ABC ≅ ∠ADE, and ∠ACB≅ ∠AED. The measure of ∠ADE is 63°. What is the measure of ∠A?
, ∠ABC ≅ ∠ADE, and ∠ACB≅ ∠AED. The measure of ∠ADE is 63°. What is the measure of ∠A?
 27°
27°
 37°
37°
 44°
44°
 54°
54°
 63°
63°
16. A truck leaves a location traveling due east at a constant speed of 50 miles per hour. One hour later a car leaves the same location traveling in the same direction at a constant speed of 70 miles. If both vehicles continue in the same direction at their same respective speeds, how many hours will it take the car to catch up to the truck?
 1
1
 1.5
1.5
 2
2
 2.5
2.5
 3
3
17. Rhys has $7.50 in dimes and quarters. The total number of coins is 48. How many more dimes than quarters does Rhys have?
 8
8
 12
12
 18
18
 22
22
 30
30
18. For the data shown in the preceding bar graph, what is the median rating of the new product?
 2.0
2.0
 2.5
2.5
 3.0
3.0
 3.5
3.5
 4.0
4.0
19. A chemist is making a 50% alcohol solution. How many milliliters of distilled water must the chemist add to 600 milliliters of an 80% alcohol solution to obtain a 50% solution?
 180
180
 300
300
 360
360
 480
480
 600
600
20. An investor receives interest on two simple interest investments, one at 3%, annually, and the other at 2%, annually. The two investments together earn $900 annually. The amount invested at 3% is $20,000. How much money is invested at 2%?
 $10,000
$10,000
 $12,000
$12,000
 $15,000
$15,000
 $20,000
$20,000
 $35,000
$35,000
1. B Let x = the number of grams of zinc needed. Set up a proportion that represents the facts of the question. Use the first sentence to write the left ratio of the proportion:  (the ratio of zinc to copper). Use the second sentence to write the right ratio of the proportion:
(the ratio of zinc to copper). Use the second sentence to write the right ratio of the proportion:  . Write the proportion:
. Write the proportion: 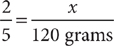 . Solve the proportion, omitting the units for convenience.
. Solve the proportion, omitting the units for convenience.
Method 1: Solve the proportion using a conventional procedure.

48 grams of zinc are needed.
Method 2: Check the answer choices. Eliminate choices D and E. The ratio of zinc to copper is 2 to 5, so the amount of zinc must be less than the amount of copper in the alloy.
Check C:
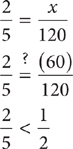
Choice C gave a result that is too large.
Check B:
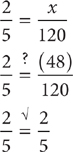
Choice B is the correct response.
2. D Complete the chart by computing the totals in each category.
DISTRIBUTION OF STUDENTS AT COMMUNITY COLLEGE X BY AGE AND GENDER
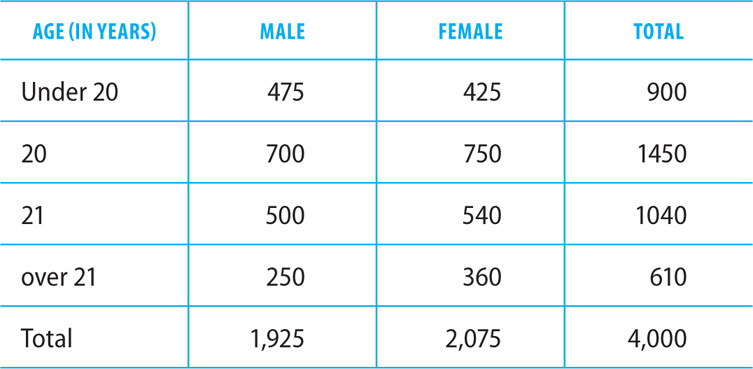
According to the chart, the total number of students is 4,000. There are 1,925 male students and 540 + 360 = 900 female students who are 21 years or older. Thus, of the 4,000 students, there are 1,925 + 900 = 2,825 students who are male or 21 years or older. Tip: Don’t double count the 500 + 250 = 750 male students who are 21 years or older. These students are already counted as part of the 1,925 male students. Therefore, the probability that a randomly selected student is male or 21 years or older is
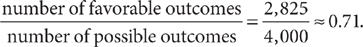
The symbol “≈” is read “is approximately equal to.”
3. D Discarding the highest number (7.1) and the lowest number (6.2) leaves 6.3, 6.4, and 6.5. The arithmetic average of these three numbers, by inspection, is 6.4.
4. D For convenience, suppose the investment is $100. In 10 years, its value will be $300. In 20 years, its value will be $900. Finally, in 30 years, the value of the investment will be $2,700. Because $2,700 is 27 times $100, the investment increased by a factor of 27. Tip: Picking a convenient amount for the investment is a useful strategy in problems like this one.
5. E Looking for a pattern is the best strategy for this problem. Calculate powers of 3:
30 = 1, 31 = 3, 32 = 9, 33 = 27, 34 = 81, and 35 = 243.
Because the units digit of 35 is 3, the next power, 36, will have units digit 9 (because 3 × 3 = 9), and 37 will have units digit 7 (because 9 × 3 = 27). Thus, the units digit for powers of 3 has the pattern 1, 3, 9, 7, 1, 3, 9, 7, and so on. Therefore, 34n has units digit 1. Hence,
3102 = 310032 = 34.2532 = 34.25 .9 has units digit 9.
6. C After the toy store raises the sale price by 20%, the final price is $119 + 20%($119) = $119 + 0.20 ($119) = $119 + $23.80 = $142.80. Let x = original price of the toy in dollars. Set up an equation that represents the facts in the question.
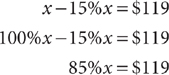
Solve for x, omitting the units for convenience.
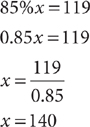
The original price of the toy was $140. Hence,
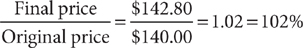
7. E When a ≠ 0, ax2 + bx + c = 0 is a quadratic equation. The quantity b2 – 4ac is its discriminant. The discriminant determines the nature of the roots of the equation. If b2 – 4ac < 0, there are no real roots; if b2 – 4ac = 0, there is exactly one real, rational root; and if b2 – 4ac > 0 (as in this question), there are exactly two real roots. Both of these roots are rational if b2 – 4ac is a perfect square; otherwise, both are irrational. Because 17 is not a perfect square, the equation has exactly two real, irrational roots.
8. D (3⊗2) = 2·3 + 3·2 = 12, so (3⊗2)⊗5=12⊗5=2·12+12·5=24+60=84.
9. D Method 1: To solve, divide every term of  by y. Then substitute terms for which you know the value and simplify.
by y. Then substitute terms for which you know the value and simplify.
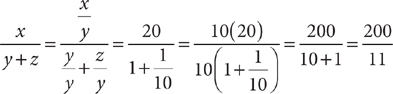
Method 2: Plug in suitable values for x, y, and z. Let x = 400, y = 20, and z = 2. Tip: Be sure to pick values for the variables that satisfy all conditions given in the question. Check: 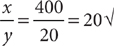 ;
; 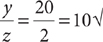 ; y · z = 20·2 = 40 ≠ 0√. Then substitute the values and simplify.
; y · z = 20·2 = 40 ≠ 0√. Then substitute the values and simplify.
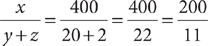
10. E Method 1: Simplify the given expression by performing the indicated operations.
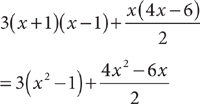
Method 2: Evaluate the expression for a suitable value of x. Then check the answer choices using the same value for x. Let x = 2.
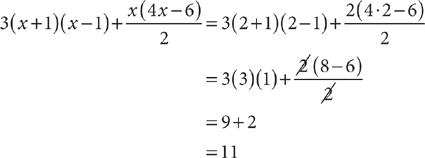
Eliminate A and B because these expressions would evaluate to be even numbers when x = 2. Therefore, neither will evaluate to be 11.
Check C: – x2 + 3x + 3 = –(2)2+3(2)+3=–4+6+3 = 5 ≠ 11
Check D: 5x2 – 3x + 3 = 5(2)2 – 3(2) + 3 = 5(4) – 6 + 3 = 20 – 3 = 17 ≠ 11
Check E: 5x2 – 3x–3 = 5(2)2–3(2)–3=5(4)–6– 3 = 20–9 = 11√
Choice E is the correct response.
11. C ∠3 is congruent to the vertical angle between ∠1 and ∠2. Therefore, m∠1 + m∠3 + m∠2 = 180°. Substitute the measures and solve for m∠3.
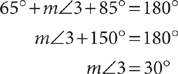
12. A m∠A + m∠B = 90°, and m∠C + m∠D = 90°, so m∠A + m∠B = m∠C + m∠D. If ∠A ≅ ∠D, then their measures are equal, so m∠B + m∠C. Thus, ∠B ≅ ∠C. None of the statements in the other answer choices must be true.
13. B Given angles b and c are supplementary, then lines l and m are parallel. Thus, ∠a ≅ ∠d because they are corresponding angles of parallel lines. None of the statements in the other answer choices must be true.
14. C Make a sketch, filling in the information given in the question.

 , ∠RPQ ≅ ∠SPQ, and
, ∠RPQ ≅ ∠SPQ, and  ; Therefore, ΔPQR ≅ ΔPQS because two sides and the included angle of ΔPQR are congruent to the corresponding parts of Δ PQS. Thus, m∠PQR = m∠PQS = 35° (corresponding parts of congruent triangles are congruent). Given that
; Therefore, ΔPQR ≅ ΔPQS because two sides and the included angle of ΔPQR are congruent to the corresponding parts of Δ PQS. Thus, m∠PQR = m∠PQS = 35° (corresponding parts of congruent triangles are congruent). Given that  is perpendicular to
is perpendicular to  , m∠RQM = 90° – 35° = 55°.
, m∠RQM = 90° – 35° = 55°.
15. D Triangle ABC is isosceles, so m∠ABC = m∠ACB (the base angles of an isosceles triangle are congruent). Given that ∠ABC ≅ ADE and m∠ADE and m∠ADE = 63°, you know that m∠ABC = m∠ACB = 63°. Thus, m∠A = 180° – 2(63°) = 54°.
16. D The distance formula is d = rt, where d is the distance traveled at a uniform rate of speed r for a length of time t. Let t = the time in hours the car will travel before it catches up to the truck. Then t + 1 hour = the time in hours that the truck travels before the car catches up to it. Make a chart to organize the information in the question.
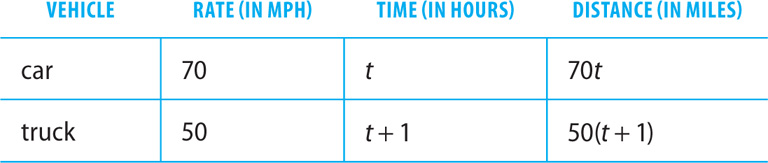
Using the chart, write an equation to represent the facts given in the question. When the car catches up to the truck, both vehicles have traveled the same distance. Thus, 70t = 50(t + 1).
Method 1: Solve for t using a conventional procedure.
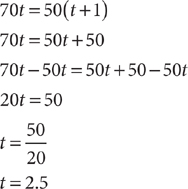
The car will catch up to the truck in 2.5 hours.
Method 2: Check the answer choices. Check C:
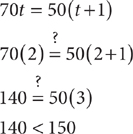
The car has gone 140 miles, but the truck has gone 150 miles. So the time in choice C is too short. Eliminate choices A and B because these times will be too short as well. Check D:
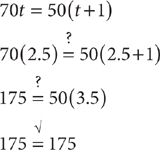
Choice D is the correct response.
17. B Let d = the number of dimes. Let q = the number of quarters. Make a chart to organize the question information.
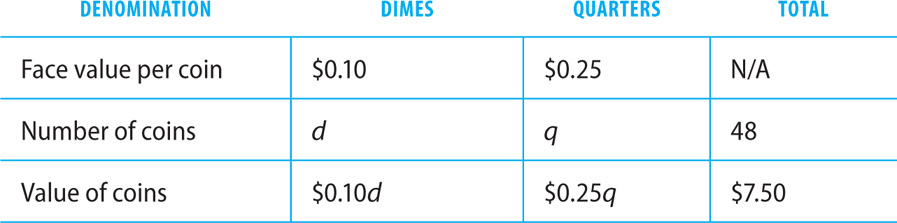
Using the chart, write two equations that represent the facts of the question.
d + q = 48
$0.10d + $0.25q = $7.50
Solve the system, omitting the units for convenience. Using the method of substitution, solve d + q = 48 for q in terms of d.
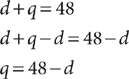
Substitute q = 48 – d into the equation 0.10d + 0.25q = 7.50 and solve for d.
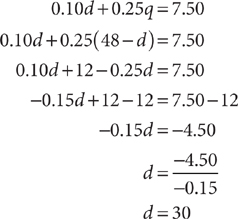
Substitute d = 30 into the equation d + q = 48 and solve for q.
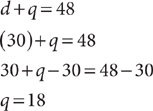
Rhys has 30 dimes and 18 quarters. He has 30 – 18 = 12 more dimes than quarters.
18. C According to the bar graph shown, the new product received eight ratings of 0, four ratings of 1, eight ratings of 2, six ratings of 3, nineteen ratings of 4, and three ratings of 5. In an ordered set of n data values, the location of the median is the  position. For these data,
position. For these data, 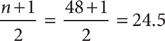 , so the median is halfway between the 24th and 25th data values. From the information in the graph, you can determine that the 24th data value equals the 25th data value, which equals 3, so the median is 3.
, so the median is halfway between the 24th and 25th data values. From the information in the graph, you can determine that the 24th data value equals the 25th data value, which equals 3, so the median is 3.
19. C Let x = number of milliliters of distilled water to be added. Make a chart to organize the information in the question.

The amount of alcohol before mixing equals the amount of alcohol after mixing. Using the information in the chart, set up an equation that represents the facts of the question.
0%x + 80%(600) = 50%(x + 600)
Method 1: Solve for x using a conventional procedure.
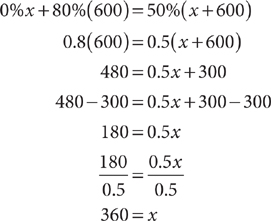
The chemist must add 360 milliliters of distilled water.
Method 2: Check the answer choices. Eliminate choice E because adding 600 milliliters to a 600-milliliter 80% alcohol solution would dilute it to a 40% alcohol solution. Check C:

Choice C is the correct response.
20. C The simple-interest formula is I = PRT, where I is the simple interest earned, P is the amount of the investment, R is the annual interest rate, and T is the time of the investment (in years). Let x = the amount invested at 2% annually. Make a chart to organize the information in the question.
Using the information in the chart, set up an equation that represents the facts in the question.
2%x + 3%($20,000) = $900
Method 1: Solve for x using a conventional procedure, omitting the units for convenience.
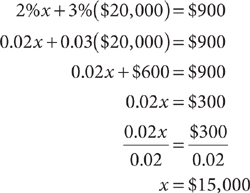
$15,000 is invested at 2%.
Method 2: Check the answer choices. Check C:
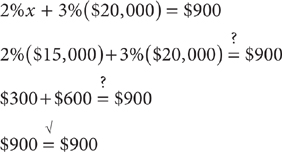
Choice C is the correct response.
1. Three daughters and two sons inherit land from their parents. The older son inherits  of the land, and the oldest daughter inherits
of the land, and the oldest daughter inherits  . The three remaining children equally share the remaining land. What fraction of the land does the younger son inherit?
. The three remaining children equally share the remaining land. What fraction of the land does the younger son inherit?
2. A science book has scale drawings of insects. The scale shows that 1 centimeter in the drawing represents 2.5 centimeters of actual length. What is the length (in centimeters) of the scale drawing of a grasshopper if the grasshopper is actually 9.0 centimeters long?
 3.6
3.6
 4.0
4.0
 4.5
4.5
 18.0
18.0
 22.5
22.5
3. A farmer wants to partition a rectangular 24 feet by 30 feet garden into smaller square plots. What is the length, in feet, of the sides of the largest square plots into which the farmer can partition the garden so that no land is left over?
 2
2
 3
3
 6
6
 8
8
 12
12
4. A college student recently worked four weeks in a new summer job. In the fourth week, the student worked 20% more hours than in the third week. In the third week, the student worked 25% more hours than in the second week. In the second week, the student worked 40% more hours than in the first week. The student worked 42 hours in the fourth week on the job. How many hours did the student work in the first week on the job?
 15
15
 20
20
 25
25
 30
30
 35
35
5. A fast-food restaurant gives a coupon for a free drink to customers who wait in line more than 15 minutes. The dot plot shows the number of minutes 20 customers waited in line one Monday morning at the restaurant.
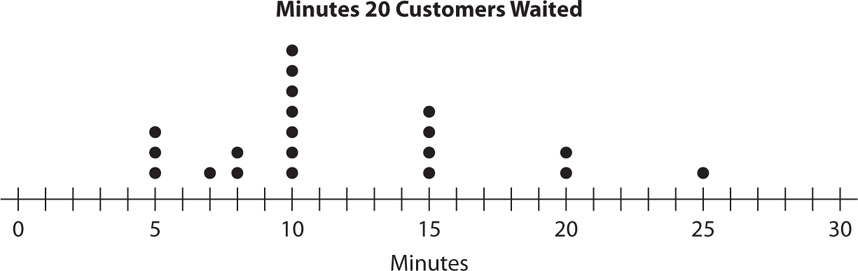
What is the probability that a customer randomly selected from the 20 customers received a coupon for the free drink that Monday morning?
6. Which number line illustrates the solution set of –7 <2x+1<5?

7. If f(x) = x2 + x + 1 and  , then what is the value of
, then what is the value of 
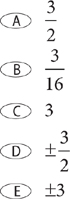
8. When m + n = –6, what is the value of the above expression?
 –52
–52
 –28
–28
 20
20
 28
28
 44
44
2t(t – 2) = 1
9. Which equation shows the preceding equation correctly solved for t?
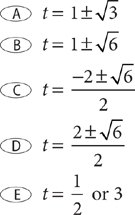
10. For which of the following expressions is x – y a factor?
I. y3 – x3
II. (x2 – y2)5
III. x3 – 3x2y + 3xy2 – y3
 I and II only
I and II only
 I and III only
I and III only
 II only
II only
 II and III only
II and III only
 I, II, and III
I, II, and III
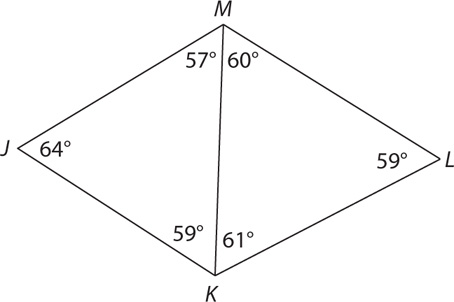
11. In the preceding figure with angle measures as shown, which segment is longest?
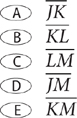
12. Which of the following sets of numbers could NOT be the lengths of the sides of a triangle?
I. 8, 14, 18
II. 6, 16, 24
III. 2, 3, 5
 I only
I only
 I and II only
I and II only
 I and III only
I and III only
 II and III only
II and III only
 I, II, and III
I, II, and III
13. In the preceding figure, which of the following values could be a value of x?
 10
10
 15
15
 25
25
 30
30
 35
35
14. In the preceding figure with the measure of the angles as shown, what is the measure of ∠E?
 85°
85°
 75°
75°
 70°
70°
 65°
65°
 60°
60°
15. If the perimeter of triangle ABC is 60 centimeters, what is the perimeter in centimeters of the triangle formed by connecting the midpoints of the sides of triangle ABC?
 10
10
 15
15
 20
20
 25
25
 30
30
16. The measures of the angles of a triangle are in the ratio 2:3:5. What is the measure of the smallest angle?
 9°
9°
 18°
18°
 36°
36°
 54°
54°
 90°
90°
17. A 50-foot rope is cut into two pieces so that the longer piece is 50% longer than the shorter piece. What is the length, in feet, of the longer piece?

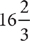
 20
20
 25
25
 30
30

18. A water tank can be filled in 6 hours when the input valve is open and the outlet valve is closed. When the input valve is closed and the outlet valve is open, the same tank can be emptied in 10 hours. If a tank is filled with both valves open, how long, in hours, will it take to fill the tank?
 4
4
 8
8
 12
12
 15
15
 16
16
19. The number of elements in the union of sets A and B is 160, and the number of elements in the intersection of sets A and B is 20. If the number of elements in set A is 50, what is the number of elements in set B?
 30
30
 60
60
 90
90
 110
110
 130
130
20. To estimate the number of turtles in a lake, a team of biologists captures and tags 20 turtles and then releases the turtles unharmed back into the lake. Two weeks later, the team returns to the lake and captures 30 turtles, 6 of which have tags indicating that they are recaptured turtles. Based on this capture-recapture method, what is the best estimate of the number of turtles in the lake?
 200
200
 100
100
 75
75
 50
50
 25
25
1. B The fraction of the land inherited by the older son and oldest daughter together is 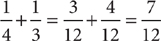 . The fraction remaining is
. The fraction remaining is  . The fraction inherited by each of the three remaining children (including the younger son) is
. The fraction inherited by each of the three remaining children (including the younger son) is 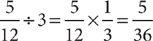 .
.
2. A Let x = the length (in centimeters) of the grasshopper scale drawing. Set up a proportion that represents the facts of the question. Use the first sentence to write the right-side ratio of the proportion:  . Use the second sentence to write the left-side ratio of the proportion:
. Use the second sentence to write the left-side ratio of the proportion:  . Write the proportion:
. Write the proportion: 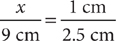 . Solve the proportion, omitting the units for convenience.
. Solve the proportion, omitting the units for convenience.
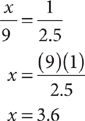
The length of the scale drawing is 3.6 centimeters.
3. C The length of the sides of the square plots into which the farmer can partition the garden must be a factor of both 24 and 30. The largest such factor is the GCF of 24 and 30. Factors of 24 are 1, 2, 3, 4,  , 8, 12, and 24; factors of 30 are 1, 2, 3, 5,
, 8, 12, and 24; factors of 30 are 1, 2, 3, 5, 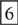 , 10, 15, and 30; GCF is 6. So, 6 feet is the length of the sides of the largest square plots into which the farmer can partition the garden so that no land is left over.
, 10, 15, and 30; GCF is 6. So, 6 feet is the length of the sides of the largest square plots into which the farmer can partition the garden so that no land is left over.
4. B Working backward is the best strategy for this problem. In the fourth week, the student worked 20% more hours than in the third week, so write the following percent equation and solve for x, where x is the number of hours worked in the third week: 42 = 120%x. Thus,  . Change 120% to a fraction, and then divide:
. Change 120% to a fraction, and then divide:
 hours worked in the third week
hours worked in the third week
In the third week, the student worked 25% more hours than in the second week, so write the following percent equation and solve for y, where y is the number of hours worked in the second week: 35 = 125%y. Thus,  . Change 125% to a fraction, and then divide:
. Change 125% to a fraction, and then divide:
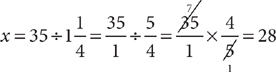 hours worked in the second week
hours worked in the second week
In the second week, the student worked 40% more hours than in the first week, so write the following percent equation and solve for z, where z is the number of hours worked in the first week: 28 = 140%z. Thus, 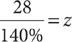 . Change 140% to a fraction, and then divide:
. Change 140% to a fraction, and then divide:
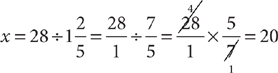 hours worked in the first week
hours worked in the first week
5. C The dot plot shows 1 customer waited 25 minutes and 2 customers waited 20 minutes for a total of 3 of the 20 customers who waited more than 15 minutes. The probability that a randomly selected customer received a coupon for the free drink is  .
.
6. C Solve the double inequality.

7. A Substitute and evaluate.
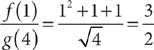
8. C Substitute the value of m + n into the given expression and evaluate.
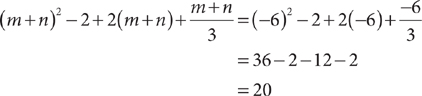
9. D Multiply factors and collect terms so you can use the quadratic formula.
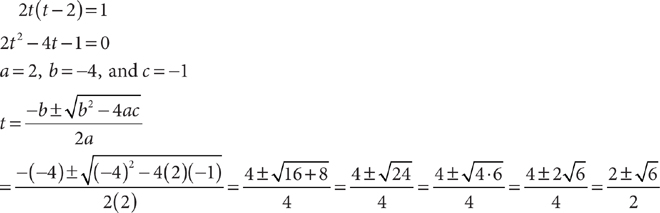
10. E Check each of the given expressions. Check Roman I:
y3–x3=–(x3–y3)=–(x–y)(x2+xy+y2).
So x – y is a factor. Eliminate choices C and D because these choices do not include Roman I. Check Roman II:
(x2 – y2)5 = ((x + y)(x – y))5.
So x – y is a factor. Eliminate choice B because it does not include Roman II. Check Roman III:
x3 – 3x2y + 3xy2 – y3 = (x – y)3.
So x – y is a factor. Choice E is the correct response.
11. C In triangle JKM,  is opposite the largest angle, so it is longer than
is opposite the largest angle, so it is longer than 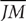 and
and  . In triangle KLM,
. In triangle KLM, 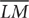 is opposite the largest angle, so it is longer than
is opposite the largest angle, so it is longer than 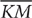 and
and  , making it the longest segment in the figure.
, making it the longest segment in the figure.
12. D In a triangle, the sum of the lengths of any two sides must be greater than the length of the third side (triangle inequality). Only the lengths given in Roman I satisfy this criterion. The lengths given in Roman II and III could not be the lengths of the sides of a triangle. Choice D is the correct response.
13. C 6x°<180° because it is an interior angle of a triangle and 6x°>90° because the measure of an exterior angle of a triangle is greater than the measure of either nonadjacent interior angle. Thus, 90<6x<180, which implies 15<x<30. Of the answer choices, only 25 (choice C) satisfies this inequality.
14. B Start with the angles for which you can find the measure by using the given information. As you determine the measure of each angle, you will gain enough information to find the solution.

The measure of an exterior angle of a triangle equals the sum of the measures of the remote interior angles. Thus, m∠DCA = 105° = 30° + m∠E. Hence, m∠E = 105° – 30° = 75°.
15. E For any triangle, if P, Q, and R are the midpoints of the sides, the perimeter of triangle PQR is one-half the perimeter of the original triangle because the segment between the midpoints of any two sides of a triangle is half as long as the third side. Thus, the perimeter of the triangle formed by connecting the midpoints of the sides of triangle ABC is 30 centimeters.
16. C Let 2x = the measure of the smallest angle, in degrees. Then the measures of the other two angles are 3x and 5x. Given that the angles of a triangle sum to 180°, set up an equation and solve for 2x.
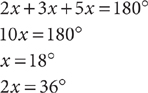
17. D Let x = the length in feet of the shorter piece. Then x + 50%x = 150%x is the length in feet of the longer piece. Because there is a longer and a shorter piece, you know the rope was not cut in half. Therefore, the longer piece has to be longer than 25 feet (half of 50 feet). So, eliminate choices A, B, and C. Check D: If the longer piece is 30 feet, then the shorter piece is 20 feet. Because 30 is 150% of 20 = 1.5(20), choice D is the correct response.
18. D Analyze this problem as a “work problem.” The key idea in a work problem is that the rate at which work is done equals the amount of work accomplished divided by the amount of time worked:  . For the situation in this problem, the work to be done is to fill the tank. However, only the input valve works to fill the tank. The output valve works counter to the input valve because it works to empty the tank. Let t = the time, in hours, it will take to fill the tank with both valves open. To find t, first, determine the rate, rfill, at which the tank can be filled when the input valve is open and the outlet valve is closed and the rate rempty, at which the tank can be emptied when the input valve is closed and the outlet valve is open. Next, write an equation that represents the facts of the question.
. For the situation in this problem, the work to be done is to fill the tank. However, only the input valve works to fill the tank. The output valve works counter to the input valve because it works to empty the tank. Let t = the time, in hours, it will take to fill the tank with both valves open. To find t, first, determine the rate, rfill, at which the tank can be filled when the input valve is open and the outlet valve is closed and the rate rempty, at which the tank can be emptied when the input valve is closed and the outlet valve is open. Next, write an equation that represents the facts of the question.
The rate for filling the tank is 
The rate for emptying the tank is 
Thus, 
Solve for t, omitting the units for convenience.
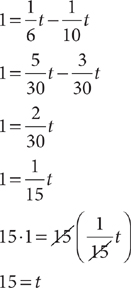
It will take 15 hours to fill the tank.
19. E Sketch a Venn diagram, and add the problem information.
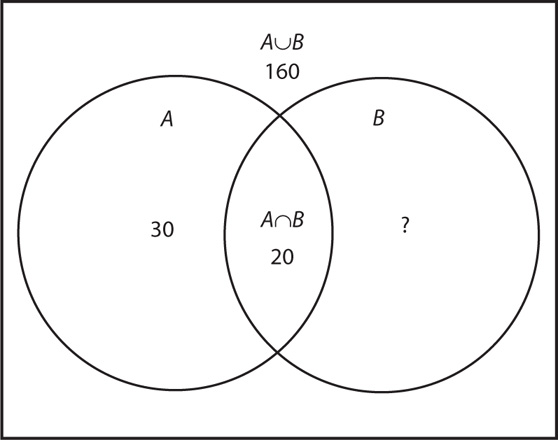
The number of elements that are only in set A is 50 – 20 = 30. Let x = the number of elements that are only in set B. Set up an equation to solve for the number of elements that are only in set B.
30 + 20 + x = 160
x = 160 – 50 = 110
Finally, determine the total number of elements in set B: 110 + 20 = 130.
20. B If all the tagged turtles are still active in the lake when the second group of turtles is captured, the proportion of tagged turtles in the second group should equal the proportion of tagged turtles in the whole population, P, of turtles in the lake. Set up a proportion and solve for P.
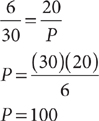
The best estimate of the number of turtles in the lake is 100.
1. A mixture weighs 7.8 grams. It consists of ingredients X, Y, and Z in the ratio 2:5:6, respectively, by weight. How many less grams of ingredient X than ingredient Z are in the mixture?
 0.8
0.8
 1.2
1.2
 1.8
1.8
 2.4
2.4
 3.0
3.0
2. The government allocated $800 million for disaster relief in a hurricane-damaged region. This amount of money is about equal to spending $1 per second for how many years?
 5
5
 25
25
 50
50
 100
100
 150
150
3. What is the least positive integer that is not a factor of 20! and is not a prime?
 19
19
 23
23
 36
36
 46
46
 58
58
4. Which expression is equivalent to 12x + 15x?
 272x
272x
 27x
27x
 3x ·9x
3x ·9x
 3(4x + 5x)
3(4x + 5x)
 3x(4x + 5x)
3x(4x + 5x)
5. The tokens in a game are distributed among five locations in the ratio 5:3:2:4:1. To win the game, a player must collect at least  of the tokens in each of three or more of the five locations. This requirement represents what minimum percent of the total tokens?
of the tokens in each of three or more of the five locations. This requirement represents what minimum percent of the total tokens?
 3%
3%
 4%
4%
 5%
5%
 6%
6%
 7%
7%
6. Which equation shows the preceding equation correctly solved for x?
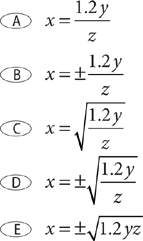
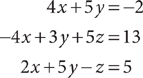
7. For the preceding system of equations, what is the value of y?
 –3
–3
 –1
–1
 1
1
 2
2
 3
3
8. Which of the following sets of ordered pairs is a function?
I. {(–1,3),(1,2)(1,5)(3,8)}
II. {(4,4)}
III. {(1,5),(2,5),(3,5),(4,5)}
 I only
I only
 I and II only
I and II only
 I and III only
I and III only
 II and III only
II and III only
 I, II, and III
I, II, and III
9. Which interval is the solution of |2x – 1| > 7?
 x > –3 and x < 4
x > –3 and x < 4
 x > –4 and x < 3
x > –4 and x < 3
 x < –3 or x > 4
x < –3 or x > 4
 x < –3 or x < 4
x < –3 or x < 4
 x < –4 or x > 3
x < –4 or x > 3
10. Which expression is equivalent to the preceding expression?
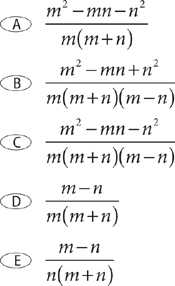
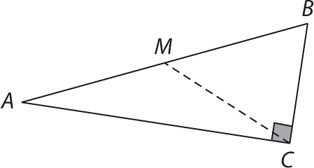
11. In the preceding right triangle ABC, 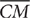 is the median to the hypotenuse. If AC is 24 inches, BC is 10 inches, and AB is 26 inches, what is the measure, in inches, of
is the median to the hypotenuse. If AC is 24 inches, BC is 10 inches, and AB is 26 inches, what is the measure, in inches, of  ?
?
 12
12
 13
13
 14
14
 15
15
 16
16
12. In the preceding trapezoid PQRS,  is the line segment connecting the midpoints of the two nonparallel sides
is the line segment connecting the midpoints of the two nonparallel sides  and
and 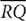 . If PQ = 22 and TU = 14, what is the measure of
. If PQ = 22 and TU = 14, what is the measure of 
 6
6
 7
7
 11
11
 12
12
 18
18
13. How many 4-inch by 4-inch tiles are needed to cover a wall 8 feet by 6 feet?
 6,912
6,912
 1,728
1,728
 864
864
 432
432
 216
216
14. A square and a rectangle have equal areas. The rectangle has dimensions 16 centimeters by 25 centimeters. What is the length, in centimeters, of a side of the square?
 9
9
 18
18
 20
20
 29
29
 40
40
15. If a rhombus has a side of length 16 inches and the measure of one interior angle is 150°, what is the area, in square inches, of the rhombus?
 256
256
 144
144
 128
128
 96
96
 64
64

16. In the preceding figure, x and y are integers. Which of the following is a possible ratio of x to y?
I. 2:1
II. 5:4
III. 10:5
 I only
I only
 II only
II only
 I and III only
I and III only
 II and III only
II and III only
 I, II, and III
I, II, and III
17. What is n if 12 is the greatest common factor of n and 84, and 756 is the least common multiple of n and 84?
 52
52
 108
108
 168
168
 324
324
 378
378
18. Two vehicles leave the same location at exactly the same time, one traveling due north at r miles per hour and the other traveling due south at r + 10 miles per hour. In how many hours will the two vehicles be d miles apart?
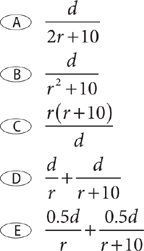
19. Two identical devices can complete a task in 10 hours. How many hours will it take five such devices to do the same task?
 2
2
 4
4
 5
5
 8
8
 20
20
20. The sum of two integers is 168. If the larger integer is three times the smaller integer, what is the value of the larger integer?
 42
42
 56
56
 84
84
 126
126
 252
252
1. D Let 2x, 5x, and 6x equal the weight (in grams) of ingredients X, Y, and Z, respectively, in the mixture. Then 2x + 5x + 6x = 7.8 grams. Simplify and solve for the weights of ingredients X and Z, omitting the units for convenience.

2. B
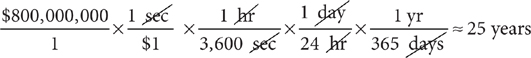
3. D By definition,
20! = 20·19·18·17·16·15·14·13·12·11·10·9·8·7·6·5·4·3·2·1
Hence, you can eliminate A because any positive integer ≤ 20 is a factor of 20!.
Eliminate B because it is a prime. Any positive integer < 20 that can be expressed as the product of factors of 20! is a factor of 20!. For instance, 36 = 2·18 is a factor of 20!, so you can eliminate C. Choice D, 46, is not a prime and 46 = 2·23 is not a factor of 20!, because 23 is not a factor of 20!. Thus, choice D is the correct response. You do not have to check choice E, because 46 < 58.
4. E Factor using your knowledge of exponents.
12x + 15x = (3·4)x + (3·5)x = 3x · 4x + 3x · 5x = 3x(4x + 5x)
5. C For convenience, designate the locations A, B, C, D, and E with tokens in the ratio 5:3:2:4:1, respectively. Letting x be the number of tokens in location E, express the number of tokens in locations A, B, C, D, and E as 5x, 3x, 2x, 4x, and x tokens, respectively. The minimum number of tokens needed to win is  of the tokens in locations B, C, and E (because these locations have the fewest tokens):
of the tokens in locations B, C, and E (because these locations have the fewest tokens):
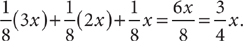
The total number of tokens is 5x + 3x + 2x + 4x + x = 15x. The minimum percent needed to win is therefore:
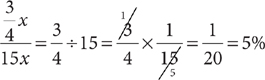
6. D Solve the given equation for x.

7. D For convenience, number the equations.
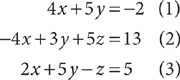
Proceed systematically to eliminate x and z from the equations so you can solve for y. First, to eliminate x from the first two equations, add equations (1) and (2).
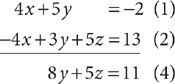
To eliminate x from the third equation, multiply both sides of it by 2 and then add the result to equation (2).
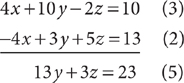
Now eliminate z from equations (4) and (5). Multiply both sides of equation (4) by –3, and multiply both sides of equation (5) by 5. Add the results and then solve for y.
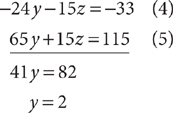
8. D A function is a set of ordered pairs for which each first element is paired with one and only one second element. In other words, in a function, no two ordered pairs have the same first element but different second elements. Only the set of ordered pairs in Roman I fails to satisfy the definition of a function. The ordered pairs (1, 2) and (1, 5) have the same first element but different second elements. Eliminate choices A, B, C, and E. Choice D is the correct response.
9. C |2x – 1| > 7 if and only if 2x – 1 < –7 or 2x – 1 > 7. Solve each condition to find the solution set.
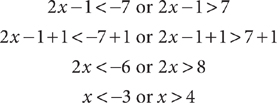
This solution corresponds to choice C.
10. B Method 1: Simplify the expression. To combine the terms, you will need a common denominator.
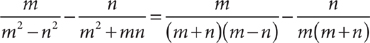
The denominator has one common factor, (m + n). The least common multiple is m(m + n)(m – n).
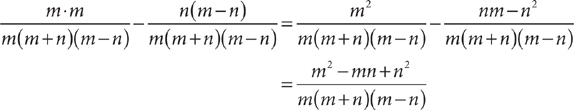
Method 2: Evaluate the expression for suitable values for m and n. Then check all the answer choices using the same values for m and n. Let m = 2 and n = 3.
Check A: 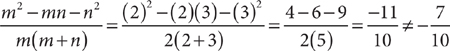
Check B: 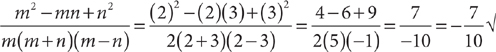
Check C: This choice has the same numerator as choice A, so substitute in the
value. 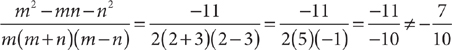
Check D: 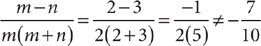
Check E: This choice has the same numerator as choice D, so substitute in the
value. 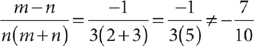
Choice B is the correct response.
11. B In a right triangle, the median to the hypotenuse is one-half the length of the hypotenuse, so the length in inches of  is 13.
is 13.
12. A The length of the segment connecting the midpoints of two nonparallel sides of a trapezoid is one-half the sum of the lengths of its bases. Thus, TU = 14 = 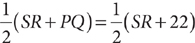 . Solve
. Solve 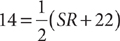 for SR.
for SR.
Method 1: Solve the equation using a conventional procedure.
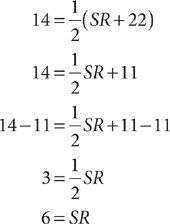
Method 2: Check the answer choices. Check A:
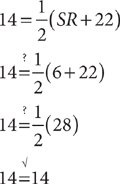
Choice A is the correct response.
13. D The area of the wall in square feet is (8)(6). The area of the wall in square inches is (8 × 12)(6 × 12). The area of one tile in square inches is (4)(4). To find the number of tiles needed, divide the area of the wall in square inches by the area of 1 tile in square inches.
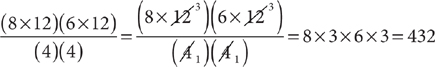
14. C Let x = the length in centimeters of a side of the square. Then x2 = the area of the square in square centimeters. The area of the rectangle in square centimeters = length × width = 16 × 25 = 400. The two areas are equal. Thus, x2 = 400, so  .
.
15. C Make a sketch, filling in the information given in the question.
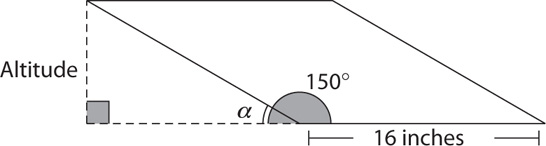
The area A, is A = bh, where b is the base and h is the height (the length of the altitude). The measure of angle α = 180° – 150° = 30°. The indicated altitude is the side opposite the 30° angle in a 30°-60°-90° right triangle that has a hypotenuse of length 16 inches. The sides of a 30°-60°-90° right triangle are in the ratio 1: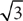 :2. The side opposite the 30° angle is half the hypotenuse. Thus, the altitude’s length in inches is
:2. The side opposite the 30° angle is half the hypotenuse. Thus, the altitude’s length in inches is  · 16 = 8, and the area in square inches is bh = 16 × 8 = 128.
· 16 = 8, and the area in square inches is bh = 16 × 8 = 128.
16. E Check the Roman numeral choices. Check Roman I: If the ratio is 2:1, let 2m = x and 1m = y. The sum of x and y is x + y = 2m + 1m = 3m. Thus, the sum must be a multiple of 3. From the figure, the two angles are supplementary, so their sum is 180°, a multiple of 3. Therefore, the ratio 2:1 is possible. Eliminate choices B and D because these choices do not contain Roman I. By inspection, the ratio in Roman III is equivalent to the ratio in Roman I, so it is a possible ratio of x to y. Eliminate choice A because it does not include Roman III. Check Roman II. If the ratio is 5:4, the sum of x and y must be a multiple of 5 + 4 = 9. Therefore, the ratio 5:4 is possible because 180° is a multiple of 9. Eliminate choice C because it does not include Roman II. Choice E is the correct response.
17. B The least common multiple of two positive integers is their product divided by their greatest common factor. Thus,
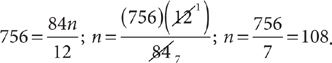
18. A The distance formula is d = rt, where d is the distance traveled at a uniform rate of speed r for a length of time t. Let t = the time in hours that the two vehicles will be d miles apart. Make a chart to organize the information in the question.
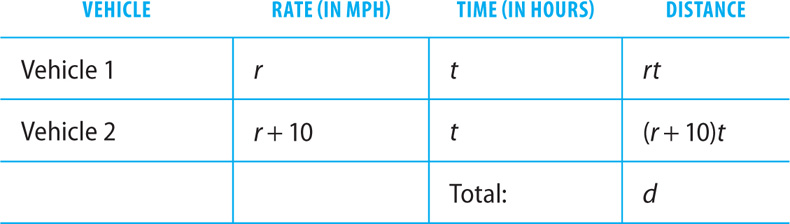
Using the information in the chart, set up an equation and solve for t.
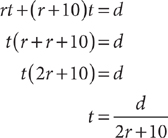
19. B Determine the rate at which one device works. Let r-rate of 1 device; then when 2 devices work together for 10 hours.
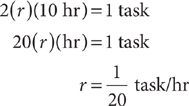
Let t = the time (in hours) it will take 5 devices to do the task.
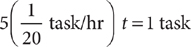
Solve for t, omitting the units for convenience.
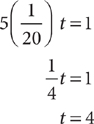
It will take 4 hours for five such devices to do the same task.
20. D Method 1: Let x = the smaller integer. Then 3x = the larger integer. Using the information in the question, set up an equation that represents the facts of the question.
x + 3x = 168
Solve the equation.
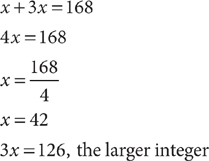
Method 2: Check the answer choices using logical reasoning. Eliminate choice B because 56 is not divisible by 3.
Check C: If the larger integer is 84, the smaller integer is  . Their sum 28 + 84 = 112. So 84 is too small. Eliminate choice A as too small as well. Eliminate E because it is larger than 168.
. Their sum 28 + 84 = 112. So 84 is too small. Eliminate choice A as too small as well. Eliminate E because it is larger than 168.
Check D: If the larger integer is 126, the smaller integer is 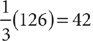 . Their sum
. Their sum 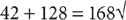 . Choice D is the correct response.
. Choice D is the correct response.
1. What is the value of 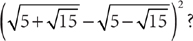
 –10
–10
 0
0





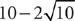
2. Two hundred people will attend a university fund-raiser if tickets cost $30 per person. For each $15 increase in ticket price, 25 fewer people will attend. What ticket price will yield the maximum amount of money for the university?
 $30
$30
 $45
$45
 $60
$60
 $75
$75
 $90
$90
3. A solution of water and sugar is 20% sugar by weight. After several weeks, some of the water evaporates so that the solution is 60% sugar by weight. What is the ratio of the initial weight of water to the final weight of water in the mixture?
 1:6
1:6
 1:4
1:4
 1:3
1:3
 4:1
4:1
 6:1
6:1
4. The football coach at a certain midsized university earns  more in salary than does the university’s basketball coach. The basketball coach’s salary represents what percent of the football coach’s salary?
more in salary than does the university’s basketball coach. The basketball coach’s salary represents what percent of the football coach’s salary?
 125%
125%
 120%
120%
 90%
90%
 80%
80%
 75%
75%
5. Violet inherited a gold and diamond pendant from her grandmother in 2010. In 2011, the value of the pendant decreased by 10%. Its value increased by 20% in 2012 and then decreased by 10% in 2013. How does the 2013 value of the pendant compare with its value in 2010?
 2.8% decrease in value
2.8% decrease in value
 1.4% decrease in value
1.4% decrease in value
 No change
No change
 1.4% increase in value
1.4% increase in value
 2.8% increase in value
2.8% increase in value
6. If  , what is the value of 3x?
, what is the value of 3x?
 0
0



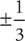
 1
1
 ±1
±1

7. Which values of x are in the solution set of the preceding system of equations?
 0, 4
0, 4
 –4, 0
–4, 0
 –2, 5
–2, 5
 –2, –5
–2, –5
 2, 5
2, 5
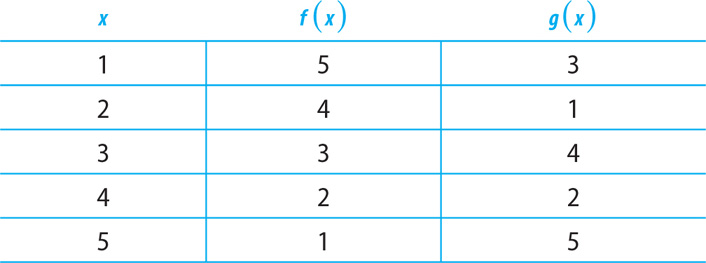
8. The preceding table shows selected values of the functions f and g. What is the value of g(f(4))
 1
1
 2
2
 3
3
 4
4
 5
5
| 2n + 1 | ≤ 6
9. How many integers n satisfy the preceding absolute value inequality?
 Seven
Seven
 Six
Six
 Five
Five
 Four
Four
 None
None
10. If 5 is one solution of the equation x2 – 2x + k = 14, where k is a constant, what is the other solution?
 –5
–5
 –3
–3
 –1
–1
 3
3
 5
5
11. Which of the following sets of numbers could be the lengths of the sides of a right triangle?
I. 7, 10, 13
II. 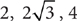
III. 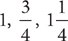
 I only
I only
 I and II only
I and II only
 I and III only
I and III only
 II and III only
II and III only
 I, II, and III
I, II, and III
12. A bike rider leaves camp and travels 7 miles due north, then 3 miles due east, and then 3 miles due south. At this point, the rider stops to rest. What is the rider’s true distance from camp in miles?
 13
13
 10
10
 7
7
 5
5
 4
4
13. A rectangular prism has the dimensions 4 centimeters by 3 centimeters by 12 centimeters as shown in the preceding figure. What is the length, in centimeters, of the diagonal 
 5
5
 11
11
 13
13
 15
15
 25
25
14. What is the area, in square inches, of an equilateral triangle that has altitude of length 12 inches?
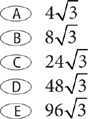
15. In a circle whose radius is 13 centimeters, a chord is 12 centimeters from the center of the circle. What is the chord’s length in centimeters?
 12
12
 10
10
 8
8
 6
6
 5
5
16. A 30-ounce mixture contains cornmeal, wheat germ, and flaxseed by weight in the ratio 5:3:2, respectively. What is the number of ounces of flaxseed in the mixture?
 2
2
 3
3
 6
6
 9
9
 15
15
17. The shaded area of the preceding figure represents a triangular flower bed. A homeowner wants to put decorative bricks around the flower bed. One side of the flower bed is 10 feet long and makes a 45° angle with a walkway that runs east to west. A second side runs parallel to the east-west walkway, and the third side makes a 30° angle with the east-west walkway. What is the perimeter in feet of the flower bed?
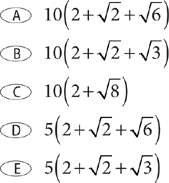
18. Four people are to be seated in four identical chairs placed in a circle. How many different arrangements of the four people (relative to one another) in the four chairs are possible?
 256
256
 128
128
 48
48
 24
24
 6
6
19. Tess and Sunil join different fitness clubs. Tess joins a club that charges a one-time enrollment fee of $50 and $20 for each month of membership. Sunil joins a club that charges a one-time enrollment fee of $70 and $18 for each month of membership. After how many months of membership will Tess and Sunil have paid the same total amount?
 10
10
 15
15
 20
20
 25
25
 30
30
20. Two consecutive angles of a parallelogram have measures x – 30° and 2x + 60°. What is the measure of the smaller angle?
 20°
20°
 40°
40°
 50°
50°
 70°
70°
 160°
160°
1. E Square the expression and simplify.
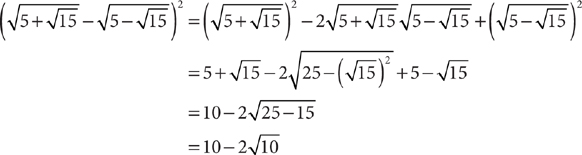
2. D Checking the answer choices is a logical strategy for figuring out the optimum ticket price. Checking A: At $30 per ticket, 200 people will attend, yielding 200 × $30 = $6,000 in ticket sales. Checking B: At $45 per ticket, 175 people will attend, yielding 175 × $45 = $7,875 in ticket sales. Checking C: At $60 per ticket, 150 people will attend, yielding 150 × $60 = $9,000 in ticket sales. Checking D: At $75 per ticket, 125 people will attend, yielding 125 × $75 = $9,375 in ticket sales. Checking E: At $90 per ticket, 100 people will attend, yielding 100 × $90 = $9,000 in ticket sales. So, a $75 ticket price (choice D) will yield the maximum amount of money for the university.
3. E The percent water by weight in the initial solution is 100% – 20% = 80%. For convenience, suppose initially the solution weighed 100 grams. Then it would contain 20 grams (20% of 100) of sugar and 80 grams (80% of 100) of water. After evaporation, the number of grams of sugar is still 20. This represents 60% of the evaporated solution by weight. Write the following percent equation and solve for x, the new weight of the solution (after evaporation).
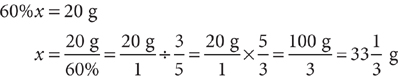
Subtract the weight of the sugar to find the final weight of water in the evaporated solution. 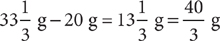 . Use this value to find the ratio of the initial weight to the final weight of water in the solution, omitting the units for convenience.
. Use this value to find the ratio of the initial weight to the final weight of water in the solution, omitting the units for convenience.
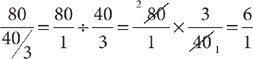
The ratio of the initial weight of water to the final weight of water is 6:1.
4. D For convenience, let $100 = the basketball coach’s salary. Then the football coach’s salary is  . The percent is
. The percent is  . Tip: Picking a value to work with (even if it is not realistic) can simplify a problem.
. Tip: Picking a value to work with (even if it is not realistic) can simplify a problem.
5. A For convenience, let the value of the pendant in 2010 equal $100. In 2011, the value of the pendant was $100 – 10%(100) = $90. In 2012, the value of the pendant was $90 + 20%(90) = $108. In 2013, the value of the pendant was $108 – 10%(108) = $97.20. The percent change is
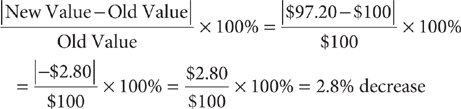
6.  . Square both sides and simplify.
. Square both sides and simplify.
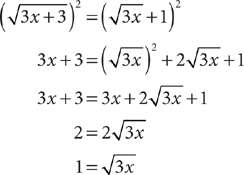
Square both sides.
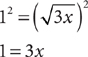
7. A Substitute y = 3x – 5 into the second equation, and solve for x.
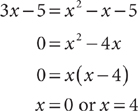
8. A Using the table, f(4) = 2, so g(f(4)) = g(2) = 1.
9. B |2n + 1| ≤ 6 if and only if –6 ≤ 2n + 1 ≤ 6. Solve this double inequality.
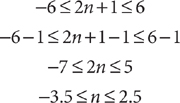
The integers that satisfy this double inequality are –3, –2, –1, 0, 1, and 2. Thus, there are six integers that satisfy |2n + 1| ≤ 6.
10. B First, substitute x = 5 into x2 – 2x + k = 14 and solve for k.
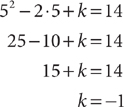
Next, substitute k = –1 into x2 – 2x + k = 14 and solve for x.
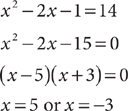
11. D In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. Only the set of numbers in Roman I fail to meet this requirement for a right triangle (72 + 102 = 149 ≠ 169 = 132). Choice D is the correct response.
12. D Let d = the true distance in miles from camp. Make a sketch, filling in the information given in the question.
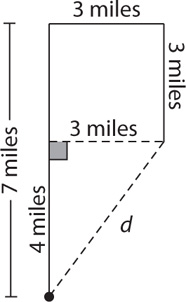
From the sketch, d is the length of the hypotenuse of a right triangle with legs of lengths 3 miles and 4 miles. Therefore, d is 5 miles. Tip: Knowing Pythagorean triples (such as 3, 4, 5) can be very helpful when working with right triangles.
13. C The diagonal 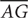 is the hypotenuse of a right triangle with legs
is the hypotenuse of a right triangle with legs  and
and  .
.  is the height of the rectangular prism, and
is the height of the rectangular prism, and  is the diagonal of its base. Omitting the units, AE = 12, and EG = 5 (because it is the hypotenuse of a 3-4-5 right triangle). Therefore,
is the diagonal of its base. Omitting the units, AE = 12, and EG = 5 (because it is the hypotenuse of a 3-4-5 right triangle). Therefore, 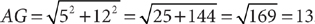 .
.
14. D Make a sketch, filling in the information given in the question.

The angles in an equilateral triangle each measure 60°. Also, in an equilateral triangle, an altitude bisects the angle at the vertex from which it is drawn and the side to which it is drawn. The altitude shown is the leg opposite the 60° angle in a 30°-60°-90° right triangle. The sides of a 30°-60°-90° right triangle are in the ratio 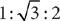 . Omitting the units for convenience, set up a proportion and solve for x and 2x.
. Omitting the units for convenience, set up a proportion and solve for x and 2x.
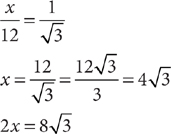
Hence, the area is 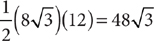 .
.
15. B In a circle, a radius that is perpendicular to a chord bisects the chord. Let x = one-half the length of the chord. Then 2x = the length of the chord. Make a sketch, filling in the question information.
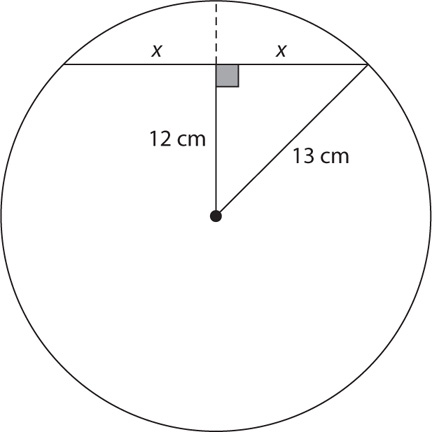
Using the Pythagorean theorem, x2 = 132 – 122 = 169 – 144 = 25. So  , and 2x = 10.
, and 2x = 10.
16. C Let 2x = the number of ounces of flaxseed in the mixture. Then 3x = the number of ounces of wheat germ in the mixture, and 5x = the number of ounces of cornmeal in the mixture. Using the information in the question, write an equation and solve for 2x.
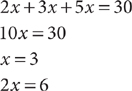
The number of ounces of flaxseed in the mixture is 6 ounces.
17. D Make a quick sketch, and mark on the figure as shown below.
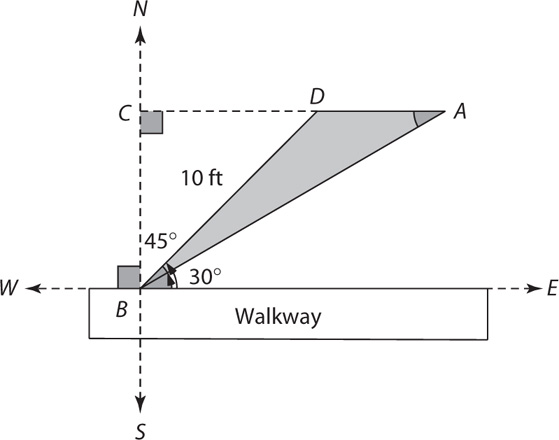
Constructing the perpendicular from A to C creates two right triangles, DCB and ACB. Angle CBD measures 45° (90° – 45°) because  makes a 45° angle with the walkway. Given that
makes a 45° angle with the walkway. Given that  is parallel to the walkway, angle CAB measures 30° because it is congruent with the 30° angle that
is parallel to the walkway, angle CAB measures 30° because it is congruent with the 30° angle that  makes with the walkway (alternate interior angles of parallel lines are congruent). Thus, triangle DCB is a 45°-45°-90° right triangle, and triangle ACB is a 30°-60°-90° right triangle.
makes with the walkway (alternate interior angles of parallel lines are congruent). Thus, triangle DCB is a 45°-45°-90° right triangle, and triangle ACB is a 30°-60°-90° right triangle.
The perimeter of the flower bed in feet equals 10 + BA + DA. In triangle DCB,  and
and  are the legs of a 45°-45°-90° right triangle whose hypotenuse is 10. Because the sides of a 45°-45°-90° right triangle are in the ratio
are the legs of a 45°-45°-90° right triangle whose hypotenuse is 10. Because the sides of a 45°-45°-90° right triangle are in the ratio 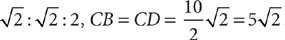 . In 30°-60°-90° right triangle ACB,
. In 30°-60°-90° right triangle ACB, 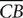 is the side opposite the 30° angle, and
is the side opposite the 30° angle, and  is the side opposite the 60° angle. Because the sides of a 30°-60°-90° right triangle are in the ratio
is the side opposite the 60° angle. Because the sides of a 30°-60°-90° right triangle are in the ratio 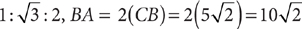 and
and 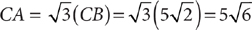 . Thus,
. Thus,  . Therefore, the perimeter is
. Therefore, the perimeter is 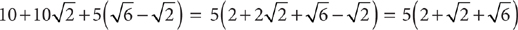 .
.
18. E The people are not assigned to particular seats but are arranged relative to one another only. For instance, the four arrangements shown in the following diagram are the same because the people (P1, P2, P3, and P4) are in the same order clockwise.
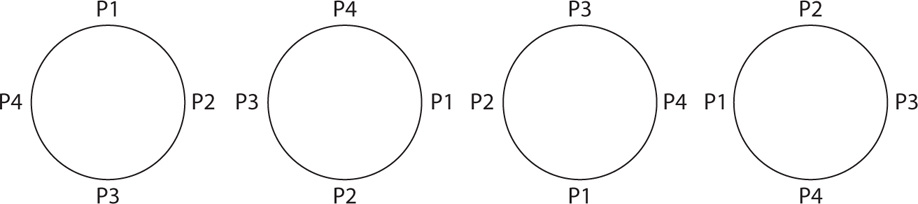
Hence, the position of P1 is immaterial. What counts are the positions of the other three people relative to P1. Therefore, keeping P1 fixed, there are 3·2·1 = 6 different ways to arrange the other three people, so there are 6 different arrangements of the four people in a circle.
19. A Let n be the number of months of membership at which Tess and Sunil will have paid the same total amount. Write an equation to represent the facts.
$50 + $20n = $70 + $18n
Solve for n, omitting the units for convenience.
Method 1: Solve the equation using a conventional procedure.
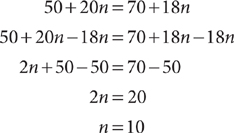
After 10 months, Tess and Sunil will have paid the same total amount.
Method 2: Check the answer choices. Check A:
After 10 months, Tess and Sunil will have paid the same total amount.
20. A Consecutive angles of a parallelogram are supplementary. Write an equation and solve for x.

Use the value of x to find the measure of the smaller angle: x – 30° = 20°.