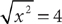
Data sufficiency questions are unique to the GMAT. In these questions, you are presented with a problem question followed by two statements containing additional information. The problem question will be either one to which you can answer yes or no or one that asks for the value of a quantity. Your task is to determine whether the data given are sufficient to answer the problem question posed. When the problem question is a yes or no question, the data given are sufficient only when it is possible to answer with a definite yes or no. In other words, you must be able to answer always yes or always no, not sometimes yes or no. When the problem question asks for the value of a quantity, the data given are sufficient only when it is possible to determine exactly one numerical value for the quantity.
All data sufficiency questions offer you the same five answer choices. Here is an example of a data sufficiency question.
Is x > 3?
(1)
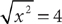
(2) x > 0
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
Start by reading the question stem. The problem question is asking for a yes or no answer. Next, read statement (1). Decide whether the information in statement (1) alone is sufficient to answer the problem question. If statement (1) alone is sufficient, then A or D are the only possible answers. You can cross off B, C, and E as possibilities. On the other hand, if statement (1) alone is not sufficient, then the correct answer cannot be A or D. Consider the question given. Is statement (1) alone sufficient?
(1) 
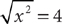
The information in (1) tells you that 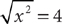. This statement is equivalent to the statement |x|=4. Both –4 and 4 have absolute value equal to 4. Without further information, you do not know whether x is –4 or 4. Hence, you cannot decide whether x > 3; so, statement (1) alone is not sufficient. Therefore, the correct answer is either B, C, or E.
Go on to statement (2). As you make your decision about whether statement (2) alone is sufficient, avoid considering the information given in statement (1). If statement (2) alone is sufficient, then the answer cannot be C or E. Is statement (2) alone sufficient?
(2) x > 0
From the information in (2), you know that x is a positive number, but there is not enough information to determine whether x > 3. For instance, x could be a number between 0 and 3; so, statement (2) alone is not sufficient.
Now consider statements (1) and (2) together. Do they together provide sufficient information for you to answer the problem question? If they do, then the correct answer is C. If they do not, the correct answer is E.
Taking (1) and (2) together, you can determine from (1) that x is either –4 or 4, and then using (2), you can determine that x is 4. Thus, the problem answer is yes, x > 3. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient. Choice C is the correct response.
You should approach every data sufficiency question with the same technique as illustrated in this example. Here is a summary of the process as a decision tree.
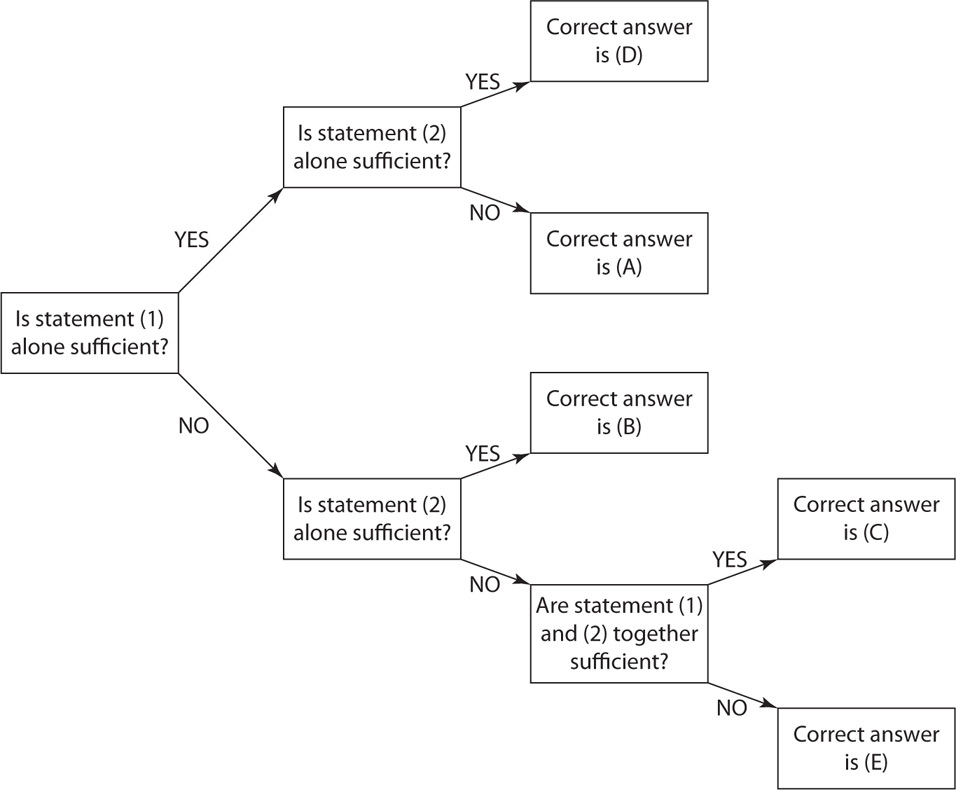
The answer choices for data sufficiency questions do not change. The five options are always the same. Memorize them! You will save valuable time on the test by knowing them without hesitation.
Having a good grasp of math will be of great help to you on data sufficiency questions. Some questions are easily answered when you have an understanding of the math concepts in the question. Also, you can avoid common pitfalls if you are knowledgeable about math concepts. For instance, as shown in the example question, knowing that 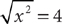is equivalent to |x| = 4 can keep you from making the error of assuming x is 4. Most of the math concepts on the GMAT are ones you likely have encountered in the past. However, you might have forgotten some if not most of them. Study the math review in this book to refresh your knowledge and skills.
In this chapter, even though the solutions to the practice drills include writing equations, most of the time you should not solve the equations. The equations help you organize your thinking and let you know quickly whether you have sufficient data to answer the question. When you have more than one unknown in a problem question, assign a variable name to each unknown. This strategy will help you decide whether you have sufficient information to answer the problem question. In most cases, you will need as many linear equations as you have variables in order to determine single values for variables. Tip: A two-variable linear equation is one that can be written as ax + by = c, where x and y are variables and a, b, and c are real numbers. Be careful though, when you have two variables and two linear equations. Make sure that the two equations are distinct equations. For instance, x + y = 5 and 2x + 2y = 10 are different versions of the same equation. When your two-variable equations are not distinct, you will be unable to obtain a single value as an answer for a target variable. Usually, you can use visual inspection to check the two equations.
Don’t solve equations or work out computations unless doing so is necessary to help you make the correct answer choice. Stop working! Click your answer choice and move on to the next question. For geometry problems, sketches help you organize the question information. Make quick rough sketches. Do not spend unnecessary time making them.
Each problem presents a question and two statements, labeled (1) and (2), in which certain data are given. Using your knowledge of mathematics and everyday facts (such as the number of minutes in an hour or the meaning of the word perpendicular), decide whether the given data are sufficient to answer the question. Then select one of the answer choices that follow.
Note: When a data sufficiency problem asks for the value of a quantity, the data given are sufficient only when it is possible to determine exactly one numerical value for the quantity.
Also, unless otherwise stated, you can assume all of the following.
All numbers used are real numbers.
All figures lie in a plane.
Lines shown as straight are straight lines, and straight lines might sometimes appear jagged.
Figures are drawn accurately, but are NOT necessarily drawn to scale.
All angle measures are greater than zero.
The relative position of points, angles, and regions are in the order shown.
1. A grandson and two granddaughters inherit land from their grandparents. What fraction of the land does the younger granddaughter inherit?
(1) The grandson inherits 
of the land.
(2) The older daughter inherits 50 percent more land than does the younger daughter.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
2. What is the value of the integer n?
(1) LCM(n, 50) = 100
(2) GCF(n, 50) = 50
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
3. On a shelf are 55 fiction and nonfiction books. What is the ratio of fiction to nonfiction books on the shelf?
(1) The number of nonfiction books is 10 more than twice the number of fiction books.
(2) The total number of books on the shelf is 10 more than three times the number of fiction books.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
4. Among a group of university students, all are either science majors or art majors. How many are art majors?
(1) The number of science majors is half the number of art majors.
(2) The number of art majors is half the total number of students in the group.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
5. The funds in a retirement account include $300,000 allocated to municipal bonds and oil stocks. What is the amount invested in municipal bonds?
(1) The amount invested in oil stocks is 150 percent of the amount invested in municipal bonds.
(2) The amount invested in municipal bonds is 24% of the total amount in the retirement account.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
6. A thrift shop has a used-book bin in which paperbacks sell for $2 each and hardcover books sell for $5 each. How many paperback books from the used-book bin did the thrift shop sell last week?
(1) Last week, the number of paperback books sold from the used-book bin was 42 more than twice the number of hardcover books sold from the bin.
(2) Last week, the thrift shop’s sales of paperback books and hardcover books from the used-book bin totaled $309.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
7. If a, b, and c are three consecutive integers (in the order given), what is the value of c?
(1) 2(a+b+c)=6(a+1)
(2) 
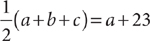
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
8. Gina is twice as old as Oliver. How old will Gina be five years from now?
(1) Five years ago, Gina was the same age as Oliver will be in five years.
(2) The sum of Gina and Oliver’s ages is 30.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
9. What is the value of |x–2|?
(1) x2–4x=12
(2) x<2
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
10. What percent of students at a small community college are male on-campus residents?
(1) Of the male students at the community college, 10 percent are on-campus residents.
(2) Of the female students at the community college, 15 percent are on-campus residents.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
11. In triangle ABC, what is the measure of angle A?
(1) Sides 
and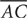 
are congruent.
(2) The measure of angle C is 65°.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
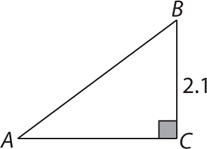
12. What is the perimeter of the preceding right triangle with the measure shown?
(1) AB = 3.5
(2) AC = 2.8
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
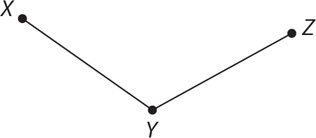
13. Based on the preceding figure, is XZ > 2(YZ)?
(1) 
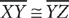
(2) XZ = 7
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
14. In the preceding figure, what is the measure of angle DEC?
(1) m∠BAC = 37°
(2) m∠BEC = 53°
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
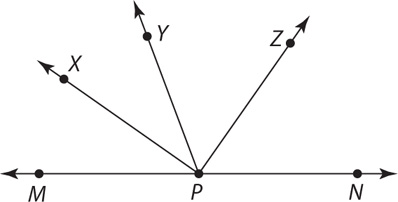
15. In the preceding figure, what is the measure of ∠XPY?
(1) 
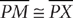
(2) 
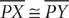
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
16. On the preceding number line, a point between points A and B is randomly selected. What is the probability that the point selected is within 2 units of the point P?
(1) AP = 14
(2) PB = 6
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
17. If x = 6m2 + 4n2, what is the greatest even number that must be a factor of x?
(1) m and n are even.
(2) GCF(m, n) = 2
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
18. Of the 3,600 full-time and part-time positions at a company,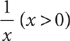 
are part-time. If the company reduces the number of part-time positions by 
, how many part-time positions will it eliminate?
(1) x2 = 9
(2) The number of full-time positions at the company is 2,400.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
19. Yael is making a vegan sandwich consisting of one bread type and one bean-based sandwich filling. If she has a choice of x types of bread and y kinds of fillings, how many different sandwich combinations are possible?
(1) x + y = 13
(2) xy > x2
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. In a league of x teams, each team plays each of the other teams two times during the season. How many total games are played during the season?
(1) x! = 120
(2) There are 10 pairings of the x teams in the league.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
1. C Let x = the portion inherited by the younger granddaughter. From the information in (1), you can determine that the two granddaughters inherit 
of the land, but further information is needed to determine x, the specific fractional portion inherited by the younger granddaughter; so (1) is NOT sufficient. From the information in (2), you know that x + (x + 50%x) is the portion of the land inherited by the two granddaughters together, but further information is needed to determine x, so (2) alone is NOT sufficient. Taking (1) and (2) together, you can determine from (1) that the two granddaughters inherit of the land, and then using (2), you can write and solve the equation 
for a single value of x. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
2. A The information in (1) implies that n cannot be 25 or 50, because LCM(25, 50) = 50 and LCM(50, 50) = 50. Therefore, n ≥100. The multiples of 100 are 100, 200, and so on. The multiples of 50 are 50, 100, 150, and so on. Thus, n = 100, because LCM(100,50) = 100. Thus, (1) is sufficient. The information in (2) implies that n could be 50, 150, 200, or some other multiple of 50; however, there is no further way to distinguish n, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
3. D Let x = the number of fiction books; then 55 – x = the number of nonfiction books. Then the ratio of fiction books to nonfiction books is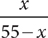 
. From the information in (1), you can write the equation 55 – x = 2x + 10, which you can solve for a single value of x and then compute 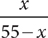. Therefore, (1) is sufficient. From the information in (2), you can write the equation 55 = 3x + 10, which you can solve for a single value of x and then compute 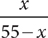. Therefore, (2) is sufficient, so EACH statement ALONE is sufficient.
4. E Let x = the number of art majors, y = the number of science majors, and z = the total number of students in the group. From the information in (1), you can write the equation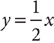 
, which (because you have two variables and only one equation) does not yield a single value for x. Therefore, (1) alone is NOT sufficient. From the information in (2), you can write the equation 
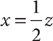, which (because you have two variables and only one equation) does not yield a single value for x. Therefore, (2) alone is NOT sufficient. Taking (1) and (2) together, you have three variables and only two equations, so you cannot determine a single value for x. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
5. A Let x = the amount, in dollars, invested in municipal bonds; then $300,000 – x = the amount invested in oil stocks. From the information in (1), you can write the equation $300,000–x = 150%x, which you can solve for a single value of x. Therefore, (1) alone is sufficient. Let R = the total amount, in dollars, in the retirement account. From the information in (2), you can write the equation 24%R = x, which (because you have two variables and only one equation) does not yield one single value for x. Therefore, (2) alone is NOT sufficient. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
6. C Let x = the number of paperback books sold from the used-book bin last week and y = the number of hardcover books sold from the used-book bin last week. From the information in (1), you have the equation x = 2y + 42, which (because you have two variables and only one equation) does not yield a single value for x, so (1) is NOT sufficient. From the information in (2), you have the equation 2x + 5y = 309, which (because you have two variables and only one equation) does not yield a single value for x, so (2) also is NOT sufficient. Taking (1) and (2) together, you have two linear equations and two variables. You can solve the two equations simultaneously for a single value of x. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
Tip: Use your time wisely, especially the way that is shown in this question. Don’t solve equations or work out computations unless doing so is necessary to help you make the correct answer choice. Stop working! Click your answer choice and move on to the next question.
7. B From the question information, you have b = a + 1, and c = a + 2. You can simplify the information in (1) as (a + b + c) = 3(a + 1), which says the sum of the three integers equals three times the middle integer. This statement is true for any three consecutive integers, so further information is needed, and (1) is NOT sufficient. From the information in (2), you have the equation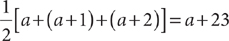 
. You can solve this equation for a single value of a and use that value to obtain c = a + 2, so (2) is sufficient. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
8. D Let x = Oliver’s age now, 2x = Gina’s age now, and 2x + 5 = Gina’s age 5 years from now. From the information in (1), you have 2x – 5 = x + 5. You can solve this equation for a single value of x and use that value to obtain 2x + 5, Gina’s age 5 years from now. Therefore, (1) is sufficient. From the information in (2), you have x + 2x = 30. You can solve this equation for a single value of x and use that value to obtain 2x + 5, Gina’s age 5 years from now, so (2) also is sufficient. Therefore, EACH statement ALONE is sufficient.
9. A You can rewrite the information in (1) as follows:
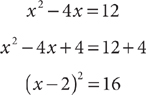
This implies that (x – 2) is either 4 or –4, each of which gives the value 4 for |x – 2|, so (1) is sufficient. From the information in (2), x – 2 < 0, so |x – 2| = –(x – 2) = –x + 2, but further information is needed to determine the value of this expression. Therefore, (2) is NOT sufficient. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
10. E The information in (1) indicates that 10% of the male students are on-campus residents, but neither the total of male students nor the number of students at the college is known. Thus, further information is needed, and (1) is NOT sufficient. The information in (2) is not helpful. It does not give information as to the total number of students at the college or the number of male on-campus residents, so (2) is NOT sufficient. Taking (1) and (2) together, the percent of men who are on-campus residents and the percent of women who are on-campus residents are known, but further information (such as the total number of students at the college and the number of male on-campus residents) is needed to determine the percent of students at the college who are male on-campus residents. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
11. C Sketch a figure.
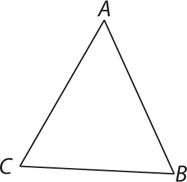
From the question information, m∠A + m∠B + m∠C = 180°. From the information in (1), m∠C = m∠B (base angles of an isosceles triangle are congruent), but further information is needed to determine the measure of angle A, so (1) is NOT sufficient. From the information in (2), m∠A + m∠B + 65° = 180°, which (because you have two unknowns and one equation) does not yield a single value for m∠A, so (2) also is NOT sufficient. Taking (1) and (2) together, you can substitute the equation from (1) into the equation from (2) to obtain m∠A + 65° + 65° = 180°, which you can solve for a single value of m∠A. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
12. D From the figure, BC = 2.1, and triangle ABC is a right triangle with ∠C = 90°. The perimeter, P, of triangle ABC is P = AB + BC + AC. From the information in (1), since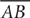 
is the hypotenuse of right triangle ABC and you know that BC = 2.1, you can use the Pythagorean theorem to compute AC and thereafter determine a single value for P. Therefore, (1) is SUFFICIENT. From the information in (2), since 
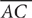is a leg of right triangle ABC and you know the measure of the other leg (BC = 2.1), you can use the Pythagorean theorem to compute AB and thereafter determine a single value for P. Therefore, (2) also is SUFFICIENT. EACH statement ALONE is sufficient.
13. A Sketch triangle XZY.
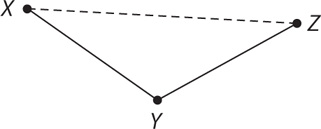
Then by the triangle inequality, XZ < XY + YZ. From the information in (1), XY = YZ, so substitute YZ for XY in the equation: XZ < YZ + YZ, which implies XZ < 2(YZ). Thus, (1) is SUFFICIENT. From the information in (2), 7 < XY + YZ, but further information is needed to answer the question, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
14. B From the information in (1), in triangle ABE, 37° + m∠AEB + m∠ABE = 180°. Because ∠AEB and ∠DEC are vertical angles, you can substitute and rearrange to obtain m∠DEC = 180° – 37° – m∠ABE, which (because you have two unknowns and one equation) does not yield a single value for m∠DEC. Therefore, (1) is NOT sufficient. To apply the information in (2), notice in the figure that ∠BEC and ∠DEC are supplementary angles. Thus, m∠DEC = 180° – 53°, a single value, and (2) is SUFFICIENT. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
15. E The information in (1) concerns segment lengths of the sides of ∠MPX, so by itself it is not useful in finding m∠XPY. Further information about angle measures is needed, and (1) is NOT sufficient. The information in (2) concerns segment lengths of the sides of ∠XPY. You can deduce that if you construct triangle PXY, then m∠PXY = m∠PYX, but without further information about angle measures, you cannot determine m∠XPY. Thus, (2) is NOT sufficient. Taking (1) and (2) together, you have only information about segment lengths. Further information about angle measures is needed to determine m∠XPY. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
16. C (1) Let x = the coordinate of point P and y = the coordinate of point B. Then the probability that the point selected is within 2 units of point P is expressed as follows:
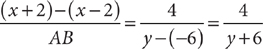
From the information in (1), you can write the equation x –(–6) = x + 6 = 14, from which you can determine x = 8, but you need further information to determine AB = y + 6. From the information in (2), you can write the equation y – x = 6, which implies y = x + 6. Substituting into AB = y + 6 gives AB = x + 6 + 6 = x + 12, but you need further information to determine AB = y + 6 = x + 12. Taking (1) and (2) together, substitute x = 8 into AB = x + 12. This gives AB = 8 + 12 = 20. Now you have the information to solve the expression for probability: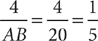 
. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
17. D From the information in (1), you know that both m and n have at least one factor of 2, so you can write m = 2y and n = 2z. Substitute those terms into the given equation: x = 6m2 + 4n2 = 6(2y)2 + 4(2z)2 = 6·22 y2 + 4·22z2 = 2·3·22y2 + 22·22z2. From this expression, you can determine that the greatest even number that must be a factor of x is 23 = 8, so (1) is sufficient. From the information in (2), you know that both m and n have at least one factor of 2, so you can again write m = 2y and n = 2z and find the solution in the same way. Therefore, (2) also is sufficient, and EACH statement ALONE is sufficient.
18. A From the information in (1), because the number of part-time positions that are lost is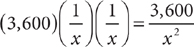 
, you have 
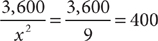. Therefore, (1) is sufficient. From the information in (2), the number of part-time positions is 3,600 – 2,400 = 1,200. Thus, the number of part-time positions that are lost is 
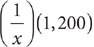. Without further information, 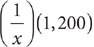cannot be determined. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is NOT sufficient.
19. E The number of possible combinations is xy. The information in (1) tells you that the pair, x and y, is one of a pair of integers that sum to 13. For instance, x = 1 and y = 12 is such a pair whose product is 12, and x = 8 and y = 5 is such a pair whose product is 40. Thus, further information is needed to determine a single value of xy, and (1) is NOT sufficient. From the information in (2), you can assume—based on the question information—that x is positive, so you can determine that y > x, but you need further information to determine xy. Therefore, (2) is NOT sufficient. Taking (1) and (2) together, you know from (1) that the pair, x and y, is one of a pair of integers that sum to 13, and from (2) you can narrow the list of those pairs to ones in which y > x. For instance, x = 1 and y = 12 is such a pair whose product is 12, and x = 2 and y = 11 is such a pair whose product is 22. However, you are unable to determine a single value for xy. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
20. D To apply (1), recall that n! = n(n – 1)(n –2) ···(2)(1). Because 5! = 5·4·3·2·1 = 120, you can determine that x = 5. The number of ways to pair 5 teams is five things taken two at a time, which equals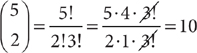 
. Thus, the total number of games played during the season is 2·10 = 20. The information in (1) is sufficient. Tip: You also can figure out the number of ways to pair 5 teams by designating the teams as A, B, C, D, and E. Then systematically list all of the 10 ways to match the teams two at a time: AB, AC, AD, AE, BC, BD, BE, CD, CE, and DE. From the information in (2), you can determine that the total number of games played during the season is 2·10 = 20. Therefore, (2) is sufficient, and EACH statement ALONE is sufficient.
1. An urn contains 15 marbles, all identical except for color. Each marble is either black, green, or red. What is the probability of drawing a black or red marble when a single marble is drawn at random from the urn?
(1) The number of red marbles is 2.
(2) The number of green marbles is 5.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
2. At an appliance store’s going-out-of-business sale, 152 customers bought a washer only, a dryer only, or both a washer and a dryer. If 22 customers bought both a washer and a dryer, how many customers bought only a washer?
(1) Ninety-four customers bought a washer.
(2) Eighty customers bought a dryer.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
3. In October, the amount Jaime spent on food was 
of the amount she spent on rent. The amount Jaime spent on rent was how many times the average (arithmetic mean) of the total amounts she spent on food and clothing?
(1) The amount she spent on clothing was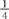 
of the amount she spent on food.
(2) The amount she spent on rent was 250% of the amount she spent on food.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
4. The square of integer m is 20 more than the square of integer n. What is the difference between the two integers?
(1) n2 = 16
(2) m2 = 36
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
5. The sale price of a jacket was $125. After the sale, the price increased. What is the percent increase over the sale price?
(1) The original price was $156.25.
(2) The sale price increased by $25.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
6. The sum of two numbers is 20. What is the value of the larger number?
(1) The product of the two numbers is 96.
(2) The larger number is 20 minus the smaller number.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
7. Myla has only dimes and quarters in a coin bank. How many dimes are in the coin bank?
(1) There are 33 coins altogether.
(2) The face value of the coins is $4.35.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
8. If b, c, and h are constants and x2 + bx + c = (x + h)2, what is the value of c?
(1) h = 5
(2) b = 10
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
9. Working alone, Dylan can paint a room in 3 hours. How many hours does Drake, working alone, take to paint the room?
(1) The time needed for Drake painting alone is 48 minutes longer than for Dylan and Drake painting the room together.
(2) Working together, Dylan and Drake can paint the room in 1 hour 12 minutes.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
10. The majority of the science majors at a small college are freshmen and sophomores, while the remainder are juniors and seniors. What fraction of the science majors are seniors?
(1) Seven-twelfths of the science majors are freshmen and sophomores.
(2) The total number of junior and senior science majors is 150.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
11. In the preceding figure, what is the measure of ∠x?
(1) Lines l and m are parallel.
(2) A and B are regular polygons.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
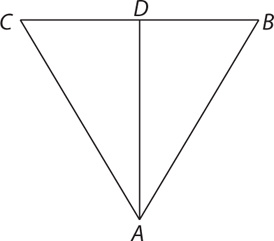
12. In the preceding figure, is ΔABD ≅ ΔACD?
(1) 
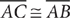
(2) ∠C ≅ ∠B
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
13. In the preceding figure, what is the degree measure of x?
(1) m∠PON = 65°
(2) m∠POM = 115°
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
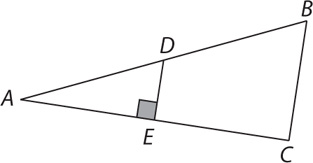
14. In the preceding figure, is triangle ABC similar to triangle ADE?
(1) Angle C is a right angle.
(2) D is the midpoint of .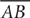
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
15. Given triangle PQR and triangle XYZ such that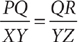 
, are triangles PQR and XYZ similar?
(1) ∠R ≅ ∠Z
(2) ∠Q ≅ ∠Y
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
16. If g(x) is in the domain of f, what is the value of f(g(–1))?
(1) f = {(–1, 2), (1, 5), (3, –4)}
(2) g = {(–4, 2), (–1, 3), (4, –4)}
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
17. A vertical asymptote is a vertical line that corresponds to a value for the variable that produces zero in the denominator of a simplified rational function. At what value of x does the graph of the function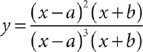 
have a vertical asymptote?
(1) a = 2
(2) b = –3
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
18. What is the value of f(3)?
(1) f(n) = 2f(n – 1) + f(n–2), for n ≥3
(2) f(2) = 2
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
19. For a and b, both positive numbers, what is the value of x if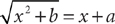 
?
(1) 
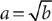
(2) 
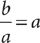
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. If all of the fans at the game are either home-team fans or visiting-team fans, how many of the 6,000 fans at the game are home-team fans?
(1) Twenty percent of the fans at the game are from out of town.
(2) The home-team fans outnumber the visiting-team fans by 540.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
1. B Let x = the number of black marbles, y = the number of green marbles, and z = the number of red marbles. The probability of drawing a black or red marble is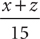 
. Tip: Notice that to determine the solution, you do not need the specific values of x and z, only their sum, x + z. From the information in (1), 
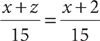, but you cannot compute the probability without knowing x. Therefore, (1) is NOT sufficient. From the information in (2), 15 = x + y + z = x + 5 + z, from which you can reason that x + z = 15 – 5 = 10. Then you can substitute x + z = 10 into 
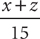to obtain 
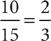. Therefore, (2) is sufficient. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
2. D Let x = the number of customers who bought only a washer. Draw a Venn diagram, using the question information.
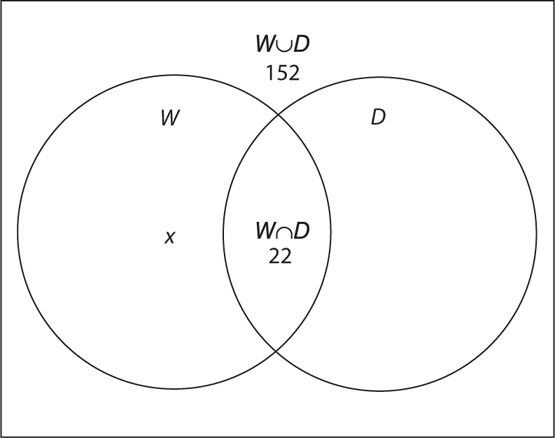
From the information in (1), you can write the equation 94 = x + 22, which you can solve for a single value of x. Therefore, (1) is sufficient. From the information in (2), you can write the equation x + 80 = 152, which you can solve for a single value of x. Therefore, (2) also is sufficient. EACH statement ALONE is sufficient.
3. A Let r = the amount spent on rent, f = the amount spent on food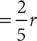 
, and c = the amount spent on clothing. Then the average of the total amounts spent on food and clothing is 
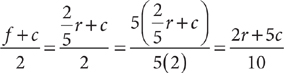. Tip: To eliminate an “unwanted” fraction in the numerator (or denominator) of a fraction, multiply the numerator and denominator of the fraction by the denominator of the unwanted fraction. To answer the question, you will need to determine 
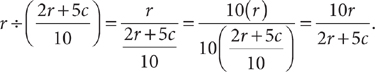From the information in (1), 
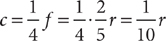. Thus, 
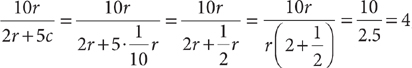, so (1) is sufficient. From the information in (2), you can write the equation r = 250% 
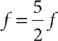, which is equivalent to 
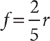, information provided in the question, so (2) is not helpful. In other words, (2) is not sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
4. E From the question information, m2 = n2 + 20. From the information in (1), you can determine that n = ±4 and m = ±6 (because m2 = 16 + 20 = 36). Thus, the difference m – n could be –10, –2, 2, or 10, not one single value; (1) is NOT sufficient. The information in (2) implies that m = ±6 and n = ±4 (because 36 = n2 + 20, n2 = 16). Thus, the difference m – n could be –10, –2, 2, or 10, not one single value; (2) is NOT sufficient. Taking (1) and (2) together, you still know only that n = ±4 and m = ±6, so again the difference could be –10, –2, 2, or 10, not one single value. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
5. B To determine the percent increase over the sale price, you need to compute the following expression:
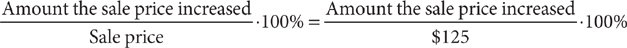
From the information in (1), you cannot determine the amount the sale price increased, so (1) is NOT sufficient. With the information in (2), you are given the amount the sale price increased:
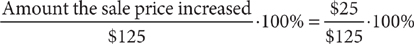
From this information, you can compute the percent increase, so (2) is SUFFICIENT. Thus, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
6. A Let x = the larger number and y = the other number. Then, according to the question, x + y = 20. From the information in (1), xy = 96. From the question information, you can determine that y = 20 – x. Substituting from this equation into xy = 96 gives x(20 – x) = 96, which you can solve as follows:
x(20 – x) = 96
20x – x2 = 96
x2 – 20x + 96 = 0
(x – 8)(x – 12) = 0
Thus, x = 8 with y = 12 (reject because x is the larger number) or x = 12 with y = 8. Thus, 12 is the larger number, and (1) is sufficient. From the information in (2), x = 20 – y, which is equivalent to x + y = 20. Thus, additional information is needed, and (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
7. C Let d = the number of dimes in the coin bank and q = the number of quarters in the coin bank. From the information in (1), d + q = 33, which (because you have two variables and only one equation) does not yield a single value for d. Therefore, (1) is NOT sufficient. From the information in (2), $0.10d + $0.25q = $4.35, which (because you have two variables and only one equation) does not yield a single value for d. Therefore, (2) also is NOT sufficient. Taking (1) and (2) together, you have two linear equations and two variables. You can solve the two equations simultaneously for a single value of d. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
8. D First, x2 + bx +c = (x + h)2 implies that x2 + bx + c = x2 + 2hx + h2, and hence b = 2h and c = h2 (because corresponding coefficients are equal). From the information in (1), c = h2 = 52, so (1) is sufficient. From the information in (2), because b = 2h, 10 = 2h, which implies that h = 5 and c = h2 = 52. Thus, (2) is sufficient. Therefore, EACH statement ALONE is sufficient.
9. B Let x = the time, in hours, it takes Drake to paint the room working alone and t = the time, in hours, it takes Dylan and Drake to paint the room together. From the information in (1), and given that 48 minutes = 0.8 hour, x = t + 0.8 hour. Because you have two variables and only one equation, this does not yield a single value for x, and (1) is NOT sufficient. From the information in (2), given that 12 minutes = 0.2 hour, t = 1.2 hours. According to the question information, Dylan’s room-painting rate is 
of the room per hour. Drake’s room-painting rate is 
of the room per hour. Thus, you can write the equation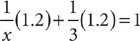 
room, which you can solve for a single value of x. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
10. E From the information in (1), you can determine that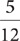 
of the science majors are juniors and seniors, but neither the total number of science majors nor the total number of senior science majors is known. Therefore, (1) is NOT sufficient. The information in (2) gives you the total number of junior and senior science majors, but neither the total number of science majors nor the total number of senior science majors is known. Therefore, (2) is NOT sufficient. Taking (1) and (2) together and letting x = the total number of science majors, you have 
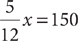, from which you can determine x, the total number of science majors. However, the number of seniors who are science majors is still unknown. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
11. C From the figure, polygon A is a pentagon, and polygon B is a hexagon. You can compute the sum of the measures of the interior angles of each of these polygons by using the formula (n –2)180°, where n is the number of sides. Thus, the sum of the measures of the interior angles of polygon A is (5 – 2)180° = 3·180° = 540°, and of polygon B is (6 – 2)180° = 4·180 = 720°. To organize the angle information in this question, label relevant angles in the figure.
To use the information in (1), knowing that lines l and m are parallel will allow you to identify congruent angles of parallel lines cut by a transversal, but without information about the measures of individual angles in the figure, you cannot determine m∠x. Therefore, (1) is NOT sufficient. To apply the information in (2), remember that in a regular polygon, all interior angles are congruent. Thus,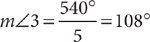 
, and 
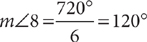. From the figure, ∠1 and ∠3 are supplementary, so m∠1 = 180° – 108° = 72°. Also, m∠x + m∠1 + m∠2 = 180°, which implies that m∠x + 72° + m∠2 = 180°, but without knowing m∠2, you cannot determine m∠x, so (2) also is NOT sufficient. Taking (1) and (2) together, ∠6 and ∠7 are each supplementary with an interior angle of polygon B. Thus, m∠6 = m∠7 = 180° – 120° = 60°. Hence, m∠5 = 180° – 2·60° = 60° (because the sum of the angles of a triangle is 180°). Then m∠4 = m∠5 = 60° (corresponding angles of parallel lines are congruent). Also, m∠4 = m∠2 = 60° (vertical angles are congruent), from which you can determine a single value of m∠x with the following equation: m∠x + 72° + m∠2 = m∠x + 72° + 60° = 180°. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
12. E As you work through this question, recall Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Angle-Angle-Side (AAS) as the four ways to show that two triangles are congruent. From the figure, you can see that 
is a common side in the two triangles. From the information in (1), and the common side, , you have two pairs of corresponding sides congruent to each other. Without further information confirming congruency between the included angles or between the other pair of corresponding sides, you cannot establish congruence, so (1) is NOT sufficient. From the information in (2), you have a pair of corresponding angles congruent to each other. Without further information, you cannot establish congruence, so (2) also is NOT sufficient. Taking (1) and (2) together, two pairs of corresponding sides are congruent and the pair of corresponding nonincluded angles are congruent. You need further information that either the pair of included angles are congruent (SAS) or that the third pair of corresponding sides are congruent (SSS). Therefore, statements (1) and (2) TOGETHER are NOT sufficient. Tip: Side-Side-Angle (SSA) does not guarantee congruence.
13. D From the information in (1), and the figure showing ∠PON and angle (2x + 70°) are supplementary, m∠PON + (2x + 70°) = 65° + (2x + 70°) = 180°. You can solve this equation to determine a single value of x, so (1) is SUFFICIENT. From the information in (2), and the figure showing ∠POM and angle (2x + 70°) are vertical angles, m∠POM = 115° = (2x + 70°). You can solve this equation to determine a single value of x, so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
14. A From the information in (1), ∠A is a common angle in the two right triangles ABC and ADE. Thus, the two triangles are similar (because corresponding angles are congruent), so (1) is SUFFICIENT. From the information in (2), a pair of corresponding sides, 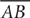and , are proportional in the ratio 2:1. Also, ∠A is common to both triangles. The two triangles would be similar if 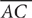and 
could be shown to be proportional in the ratio 2:1, but further information is needed to establish that relationship, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
15. B Sketch a figure.
From the question information, in triangles PQR and XYZ, two pairs of corresponding sides are proportional. From the information in (1), ∠R ≅ ∠Z, but ∠R and ∠Z are not the included angles between the two pairs of corresponding proportional sides. Further information is needed to establish similarity, so (1) is NOT sufficient. From the information in (2), you have that two pairs of corresponding sides are proportional, and the included angles are congruent, so triangles PQR and XYZ are similar, and (2) is SUFFICIENT. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
16. C From the information in (1), the possible values for f(g(–1)) are –4, 2, or 5. This solution is not a single value, so (1) is NOT sufficient. From the information in (2), f(g(–1)) = f(3), but further information is needed to determine f(3). Therefore, (2) is NOT sufficient. Taking (1) and (2) together, from (2), you can determine that f(g(–1)) = f(3), and from (1), you can determine that f(3) = –4. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
17. A Observe that in simplified form,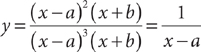 
, which will have a vertical asymptote when x – a = 0, that is, when x = a. From the information in (1), 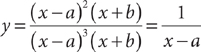will have a vertical asymptote at x = 2, so (1) is SUFFICIENT. The information in (2) is irrelevant to the determination of vertical asymptotes of 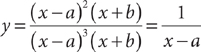, so it is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
18. E From the information in (1), f(3) = 2f(2) + f(1). However, without knowing the values of f(2) and f(1), you cannot determine the value of f(3), so (1) is NOT sufficient. From the information in (2) and without further information, the value of f(3) cannot be determined, so (2) is NOT sufficient. Taking (1) and (2) together, f(3) = 2f(2) + f(1) = f(3) = 2·2 + f(1) = 4 + f(1). However, without knowing the value of f(1), you cannot determine the value of f(3). Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
19. D From the information in (1),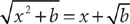 
. Squaring both sides of this equation yields 
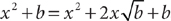, from which you can obtain 
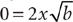. Because b > 0, this equation implies that x = 0. Therefore, (1) is SUFFICIENT. From the information in (2), b = a2, so after substituting, you have 
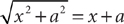. Squaring both sides of this equation yields x2 + a2 = x2 + 2ax + a2, from which you can obtain 0 = 2ax. Because a > 0, this equation implies that x = 0. Therefore, (2) also is SUFFICIENT. EACH statement ALONE is sufficient.
20. B Let x = the number of home-team fans and y = the number of visiting-team fans. Then from the question information, x + y = 6,000. From the information in (1), you know that 20%(6,000) = 1,200 fans are from out of town, but you cannot assume that all of these fans are visiting-team fans, nor can you assume that all of the remaining 4,800 fans are home-team fans, so further information is needed to determine x. Thus, (1) is NOT sufficient. From the information in (2), x = y + 540. With this equation and the equation x + y = 6,000, you have two linear equations and two variables. You can solve the two equations simultaneously for a single value of x, so (2) is SUFFICIENT. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
1. Given m and n are positive integers such that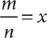 
, then is 5 the remainder when m is divided by n?
(1) m = 85
(2) x = 4.25
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
2. A chemist is making an alloy of tin and copper. How many total grams are in the alloy?
(1) The ratio of tin to copper in the alloy is 1 to 4.
(2) The number of grams of copper in the alloy is 36.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
3. A pet store specializes in selling Scottish terrier dogs. Does the pet store have a greater number of male Scottish terriers?
(1) The number of male Scottish terriers is less than 2 times the number of female Scottish terriers.
(2) One-fourth of the number of female Scottish terriers is less than the number of male Scottish terriers.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
4. If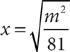 
, what is the value of 
?
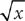(1) m = –4
(2) m is an even integer such that |m| < 10.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
5. The parents of a newborn child allocated $20,000 of their savings to an investment that earns annual interest, compounded monthly. If there were no other transactions in the investment account, what is the amount of money (to the nearest cent) in the account 6 months after the account is opened? The compound-interest formula is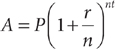 
, where A is the amount accumulated, P is the initial investment, r is the annual rate, n is the number of times interest is compounded per year, and nt is the total number of compounding periods.
(1) The monthly rate on the investment is 0.0625%.
(2) The annual rate, compounded monthly, on the investment is 0.75%.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
6. If x and y are integers, is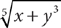 
an integer?
(1) x = 24
(1) x = y3(y2 – 1)
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
7. A sales clerk in a computer store earns a 1% commission on all computer and accessory sales that the clerk makes. Last week, what were the clerk’s total sales?
(1) Last week, the clerk sold two $399 laptop computers and one $249 notebook computer. The clerk also sold suitable accessories to go along with these sales.
(2) Last week, the clerk earned $13.72 in commission.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
8. Is x < 0?
(1) 
(2) x5 + 3 < 0
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
9. Does 5x – 2y = 0?
(1) 
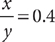
(2) x – y < 0
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
10. What is the perimeter of the rectangle?
(1) The length of the rectangle is 3 meters more than its width.
(2) The perimeter of the rectangle is 6 meters less than 4 times its length.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
11. In ΔABC, what is the smallest possible value for the whole number n?
(1) ∠A ≅ ∠B
(2) AB = 15
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
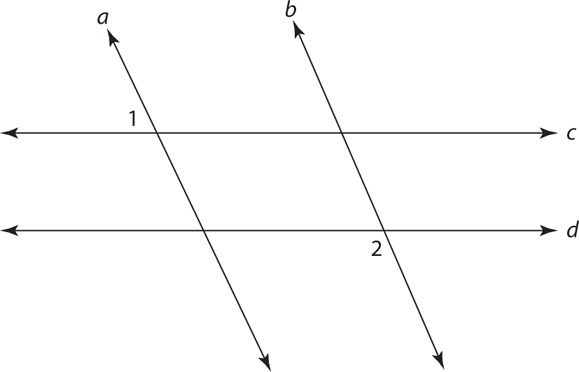
12. In the preceding figure, what is the measure of ∠2?
(1) c || d
(2) m∠1 = 70°
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
13. How many centimeters will a cylindrical barrel roll in 10 revolutions along a smooth surface?
(1) The diameter of the barrel is 56 centimeters.
(2) The radius of the barrel is 28 centimeters.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
14. What is the area (in square inches) of the circle created by the minute hand of a clock as it sweeps an hour?
(1) The minute hand of the clock is 6 inches long.
(2) The hour hand of the clock is 4 inches long.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
15. The figure shown on the grid consists of five rectangles. If the four outer rectangles are folded up and taped to make an open box, what is the box’s volume in cubic centimeters?
(1) The base of the box is a square.
(2) x = 5
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
16. In triangle PQR, triangles RPY and RYQ have areas 90 and 45, respectively. What is the length of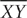 
?
(1) Angle Q is a right angle.
(2) PY = XQ = 10
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
17. A tank for holding water is in the shape of a right circular cylinder. What is the diameter of the base of the cylinder?
(1) When the tank is at full capacity, the volume of water in the tank is 128π cubic feet.
(2) When the tank is 
full, the volume of water in the tank is 96π cubic feet.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
18. In the preceding diagram of circle C, chord 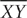intersects chord 
at W. If XW = z + 12, UW = z + 3, and WV = z, what is the length of ?
(1) XW = 6WY
(2) WY = 3
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
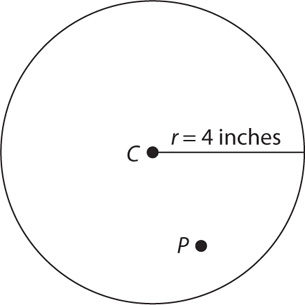
19. If X and P are points in the plane of the preceding circle C, does X lie within circle C?
(1) CX = 3 inches
(2) PX = 2 inches
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. What is the perimeter of rectangle ABCD?
(1) BD = AC = 5
(2) The area of rectangle ABCD is 12.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
1. C From the information in (1), you have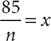 
, but without knowing either n or x, you cannot answer the question. Therefore, (1) is NOT sufficient. From the information in (2), you have 
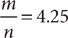, so m = 4.25n, which means 0.25n is the remainder when m is divided by n. But, without knowing n, you cannot determine whether 0.25n is 5. Therefore, (2) is NOT sufficient. Taking (1) and (2) together, you have 
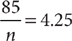, which you can solve for n to obtain n = 20 and 0.25n = 5 (remainder). This latter equation verifies that 5 is the remainder when m is divided by n. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
2. C Let x = the number of grams of tin in the alloy and y = the number of grams of copper in the alloy. To answer the question, you must determine x + y. From the information in (1), you can write the equation 
, but you cannot determine the value of x + y from this relationship. Therefore, (1) is NOT sufficient. From the information in (2), y = 36, so x + y = x + 36, but this does not result in a single value for x + y. Therefore, (2) is NOT sufficient. Taking (1) and (2) together, you can determine from (1) that y = 4x and then substitute this value of y into the equation y = 36 from (2) to obtain 4x = 36. From this equation, you can find x, and thereafter x + y = x + 36. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
3. E Let x = the number of male Scottish terriers and y = the number of female Scottish terriers. From the information in (1), you can write the inequality x < 2y, but this does not tell you whether x or y is greater. For instance, x = 4 and y = 3 satisfies this inequality, and so does x = 2 and y = 3. Therefore, (1) is NOT sufficient. From the information in (2), you can write the inequality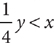 
, but this does not tell you whether x or y is greater. For instance, x = 5 and y = 4 satisfies this inequality, and so does x = 2 and y = 4. Therefore, (2) is NOT sufficient. Taking (1) and (2) together, you can restate the inequalities in terms of y: 
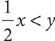and y < 4x. Combining these two inequalities gives 
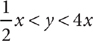, but this does not tell you whether x or y is greater. For instance, x = 4 and y = 3 satisfies this inequality, and so does x = 2 and y = 4. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
4. A The square root symbol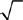 
always denotes the principal (nonnegative) square root. From the information in (1), substitute the given value to find the square root:
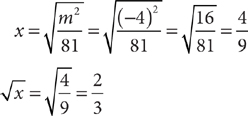
You can find the answer, so (1) is sufficient. From the information in (2), m has a range of values, so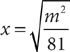 
and, consequently, 
, have a range of values, not a single value. Therefore, (2) is NOT sufficient. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
5. D From the question information, you have 
, so you need either r, the annual rate compounded monthly, or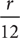 
, the monthly rate, to determine A. The information in (1) gives you the monthly rate, 
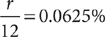, so you can compute A. Therefore, (1) is sufficient. The information in (2) gives you the annual rate, r = 0.75%, so you can compute A. Therefore, (2) also is sufficient. EACH statement ALONE is sufficient.
6. B From the information in (1),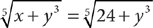 
. Without knowing y, you cannot decide whether this expression equals an integer. For instance, if y = 2, 
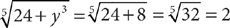, which is an integer, but if 
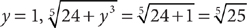, which is not an integer. Therefore, (1) is NOT sufficient. From the information in (2), 
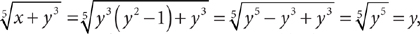an integer. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
7. B Let x = the clerk’s total sales last week. Then 1%x = 0.01x = the clerk’s commission last week. The information in (1) tells you that the clerk’s computer sales were $1,047, but the amount from the accessory sales is not given, so further information is needed. Therefore, (1) is NOT sufficient. From the information in (2), you have 0.01x = $13.72, which you can solve for a single value of x. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
8. D Solve the expression in (1) for x.
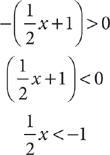
x < –2, so the information in (1) is SUFFICIENT. Tip: Remember to reverse the direction of an inequality when you multiply (or divide) both sides of an inequality by a negative number.
Solve the expression in (2) for x.
x5 + 3 < 0
x5 < –3
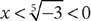, so (2) is SUFFICIENT. Tip: If the index is odd and the radicand is negative, the principal root is negative. (See “Roots and Radicals” in Chapter 8 for a discussion of this topic.)
Therefore, EACH statement ALONE is sufficient.
9. A Solve the equation in (1) for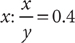 
is equivalent to 
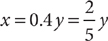. Substituting this result into 5x – 2y = 0 yields 
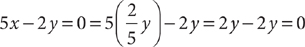, so (1) is SUFFICIENT. From the information in (2), you can determine that x < y, but further information is needed to determine whether 5x – 2y = 0. For instance, x = 1 and y = 2 satisfies this inequality x < y, but 5x – 2y = 5(1) – 2(2) = 5 – 4 = 1 ≠ 0. Thus, (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
10. E Let l = the length of the rectangle and w = the width of the rectangle. Then the perimeter P = 2l + 2w. From the information in (1), l = w + 3, which (because you have two variables and only one equation) does not yield a single value for l or w, so you cannot compute P; (1) is NOT sufficient. From the information in (2), P = 2l + 2w = 4l – 6, which (because you have two variables and only one equation) does not yield a single value for l or w, so you cannot compute P; (2) also is NOT sufficient. Taking (1) and (2) together, you have two linear equations and two variables, but the equation, 2l + 2w = 4l – 6, in (2) simplifies to w = l – 3, which (by inspection) is equivalent to the equation l = w + 3 in (1). Thus, further information is needed to determine P. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
11. C From the information in (1), the triangle is isosceles with base angles A and B. So, AC = BC = n, but further information is needed to determine the value of n, so (1) is NOT sufficient. From the information in (2) and the triangle inequality, n + BC > 15, n + 15 > BC, and 15 + BC > n, but further information is needed to determine the value of n, so (2) also is NOT sufficient. Taking (1) and (2) together, you can use BC = n from (1) and substitute it into n + BC > 15, so n + n > 15 or, equivalently, 2n > 15, and n > 7.5. From this solution, you can identify the smallest possible value for the whole number n (which is 8). Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
12. E From the information in (1), knowing that lines c and d are parallel will allow you to identify congruent angles of parallel lines cut by a transversal, but without information about the measures of angles in the figure, you cannot determine m∠2, so (1) is NOT sufficient. The information in (2) is not helpful, because you cannot establish a relationship between ∠1 and ∠2 without further information, so (2) also is NOT sufficient. Taking (1) and (2) together, you still cannot establish a relationship between ∠1 and ∠2 without further information. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
13. D From the question information, you know that in one revolution, the cylindrical barrel will roll a distance equal to its circumference, πd = 2πr. Thus, in 10 revolutions, the barrel will roll a distance of 10πd = 20πr. From the information in (1), you can substitute d = 56 centimeters into 10πd and then compute a single value for the distance rolled, so (1) is SUFFICIENT. From the information in (2), you can substitute r = 28 centimeters into 20πr and then compute a single value for the distance rolled, so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
14. A From the question information, the area equals πr2, where r is the length of the minute hand. From the information in (1), you can substitute r = 6 inches into πr2 and then compute a single value for the area, so (1) is SUFFICIENT. With the information from (2), you need the length of the minute hand to answer the question, so this information is not useful, and (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
15. B From the question information, the volume of the box is V = lwh, where l = length, w = width, and h = height of the box. The information in (1) tells you about the shape of the base of the box, but you need further information about the dimensions to determine V, so (1) is NOT sufficient. The information in (2) tells you that, by referring to the figure, the length l of the box is 5 centimeters, and it also tells you that each square of the grid has sides of 1 centimeter. Thus, from the figure, l = w = 5 centimeters, and h = 2 centimeters. Now that you have these dimensions, you can determine a single value of V, so (2) is SUFFICIENT. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
16. C From the information in (1), the area of right triangle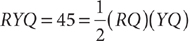 
, which implies that (RQ)(YQ) = 90. Also, the area of right triangle 
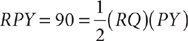, which implies that (RQ)(PY) = 180. Thus, 
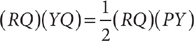, which implies that 
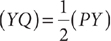. Thus, from the figure, 
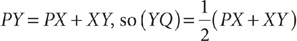, but further information is needed to determine a single value for XY, so (1) is NOT sufficient.
From the information in (2), PX + XY + XY + YQ = 10, which implies that PX = YQ. However, further information is needed to determine a single value for XY, so (2) also is NOT sufficient. Taking (1) and (2) together, you can substitute PY = 10 from (2) into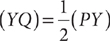 
from (1) to determine that 
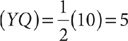. Then you can substitute YQ = 5 into XY + YQ = 10 to obtain XY + 5 = 10, which you can solve for a single value of XY. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
17. E Glancing at (1) and (2), you can see that both mention the volume of the tank. From the question information, the tank is cylindrical. Thus, its volume, V, equals Bh = πr2h, where B is the area of the cylinder’s base, r is the base’s radius, and h is the cylinder’s height. The diameter, d, of the base of the cylinder is 2r. From the information in (1), you know that V = πr2h = 128π cubic feet. This equation implies that r2h = 128 cubic feet, which (because you have two variables and only one equation) does not yield a single value for r, so you are unable to determine d = 2r, and (1) is NOT sufficient.
From the information in (2),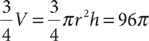 
cubic feet. This equation implies that 
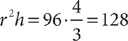cubic feet, which (because you have two variables and only one equation) does not yield a single value for r, so you are unable to determine d = 2r, and (2) also is NOT sufficient. Taking (1) and (2) together, you still end up with r2h = 128 cubic feet, from which you are unable to determine d. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
18. B From the question information, the length of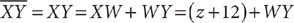 
. Also, because 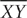and 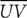are two chords in C intersecting at W, then UW·WV = XW·WY. Substituting the known information into this equation yields (z + 3)(z) = (z + 12)WY. From the information in (1), you can set up the equation XY = XW + WY = 6WY + WY = 7WY, but without knowing WY, you cannot determine a single value for XY. Also, if you substitute XW = 6WY into UW·WV = XW·WY, you obtain (z + 3)(z) = (6WY)(WY), which (because you have two variables and only one equation) does not yield single values for z or WY. So further information is needed to determine XY, and (1) is NOT sufficient. From the information in (2), you can set up the equation XY = (z + 12) + 3. Furthermore, (z + 3)(z) = (z + 12)(3), which simplifies to z2 = 36. Because you can assume that, as a measurement of length, z is positive, this equation yields z = 6, from which you can compute XY = (z + 12) + 3. Thus, (2) is SUFFICIENT. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
19. A From the figure, the radius, r, of the circle is 4 inches. A point will lie within circle C if its distance from the center C is less than 4 inches. From the information in (1), X lies within circle C because CX = 3 inches < 4 inches, so (1) is SUFFICIENT. From the information in (2), you know only that X is 2 inches from P. You need further information to determine whether CX < 4 inches. For instance, suppose that C, P, and X are collinear (in this order) such that CP = 3 inches and PX = 2 inches; then X would lie outside circle C. Thus, (2) is NOT sufficient. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
20. C Sketch a figure.
From the figure, the perimeter, P, is P = 2l + 2w, where the rectangle’s length, l, is AD = BC, and its width, w, is AB = DC. The information in (1) gives you the lengths of the rectangle’s diagonals. Each diagonal forms a right triangle in the rectangle that has legs of lengths l and w and hypotenuse of length 5. Thus, by the Pythagorean theorem, 52 = l2 + w2, which (because you have two variables and only one equation) does not yield single values for l and w, so you are unable to determine P = 2l + 2w; (1) is NOT sufficient. From the information in (2), you know that lw = 12, which (because you have two variables and only one equation) does not yield single values for l and w, so you are unable to determine P = 2l + 2w; (2) also is NOT sufficient. Taking (1) and (2) together, assume that, because they are measurements of distance, l and w are both positive. You can simultaneously solve 52 = l2 + w2 from (1) and lw = 12 from (2), as shown here:
Solve 52 = l2 + w2 for w to obtain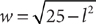 
.
Substitute into lw = 12 to obtain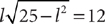 
.
Square both sides to obtain l2(25 – l2) = 144.
Simplify to obtain l4 – 25l2 + 144 = 0.
Factor as you would a quadratic to obtain (l2 – 9)(l2 – 16).
Keeping in mind that l is positive, then from these two equations, l = 3 with w = 4, or l = 4 with w = 3. Either way, P = 2l + 2w = 14. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
1. If x and y are positive integers, is xy a multiple of 18?
(1) x is a multiple of 6.
(2) y is a multiple of 15.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
2. Two friends rented a light-duty moving truck. The rental store charges $19.99 per hour or portion thereof for the truck rental plus $0.55 per mile traveled, with no charge for gasoline. How much did the friends pay for renting the truck?
(1) The total round-trip mileage was 100 miles.
(2) The friends returned the truck after 3 hours 20 minutes.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
3. In a survey of students at a small private college, what percent are taking a foreign language?
(1) Twenty percent of the female students surveyed are taking a foreign language.
(2) Fifteen percent of the male students surveyed are taking a foreign language.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
4. Is the variance of the population set of data values x1, x2, …, x100 equal to 9?
(1) For each data value xi, |xi – μ| = 3, where μ is the mean of the population.
(2) The standard deviation is 3.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
5. A driver makes a trip of d miles. The driver’s average speed is 63 miles per hour for the first part of the trip and 70 miles per hour for the second part of the trip. Was the distance traveled for the second part of the trip longer than the distance traveled for the first part of the trip?
(1) The time for the first part of the trip is 2 hours.
(2) The total time for the entire trip is 3 hours 48 minutes.
Statement (1) ALONE is sufficient, but statement (2) alone is NOT sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
6. To make a 20% alcohol solution, a scientist adds x liters of a 60% alcohol solution to y liters of a 10% solution. What is the value of x?
(1) x + y = 37.5
(2) y = 30
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
7. If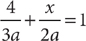 
, where a ≠ 0, what is the value of x?
(1) 3x = 6a – 8
(2) 
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
8. The sum of the reciprocals of two nonzero numbers is 
. What is the value of the larger number?
(1) The larger number is 5 times the smaller number.
(2) Five times the sum of the reciprocals of the two numbers is 3.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
9. An auditorium has only balcony seats and orchestra seats. Tickets for the first performance of a concert at the auditorium are $80 for orchestra seats and $50 for balcony seats. How many balcony seats were sold for the first performance?
(1) The auditorium sold 800 tickets.
(2) Total receipts for tickets for the first performance were $49,000.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
10. A box contains a collection of marbles, all identical except for color. Each marble is either black, red, or white. If a marble is randomly drawn from the box, what is the probability that the marble is white?
(1) The box contains 120 marbles.
(2) There are twice as many black marbles as white marbles in the box.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
11. A quilted shawl is made up of 9-inch by 9-inch squares. What is its perimeter?
(1) The shawl has four rows and six columns.
(2) The shawl consists of 24 squares.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
12. In the preceding figure, what is the length of 
?
(1) 
and 
are medians.
(2) DF = 15
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
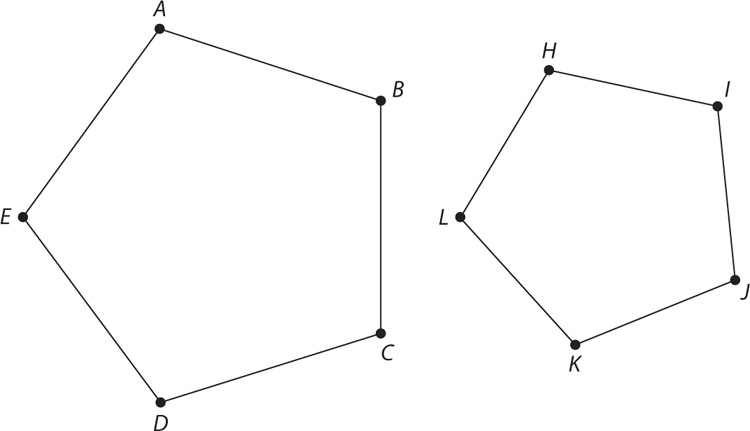
13. In the preceding figure, ABCDE ~ HIJKL. What is the ratio of the area of ABCDE to the area of HIJKL?
(1) 
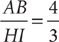
(2) 
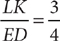
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
14. If a bicycle is traveling at 5 miles per hour, how fast is the bicycle’s front wheel turning in revolutions per minute?
(1) The front wheel has a diameter of 25 inches.
(2) The bicycle is traveling at 440 feet per minute.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
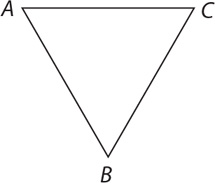
15. What is the area of the preceding triangle ABC?
(1) m∠A = m∠B = m∠C = 60°
(2) AB = 12
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
16. If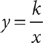 
, where k is a constant, what is the value of y when x = 360?
(1) 
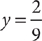when x = 540
(2) xy = k
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
17. A hoodie that usually sells for $85.00 is marked down for an end-of-season clearance sale. If the sales tax rate is 8%, how much does a customer pay for the hoodie at the marked-down price including tax?
(1) Including tax, the customer saves a total of $18.36.
(2) The sales tax on the marked-down price is $5.44.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
18. What is the value of a20 if an = a1 + (n – 1)d?
(1) a4 = 17
(2) a10 = 47
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
19. If x and y are positive integers such that x + y = 10, what is the value of y?
(1) 37 < 5x + 2y < 41
(2) x > 5
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. If the area of a square having sides of length x is equal to the area of a parallelogram having base b, what is the height, h, of the parallelogram to that base?
(1) x = 10
(2) b = 20
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
1. C From the information in (1), x = 6m, for a value of m that is a counting number, but there is no way to determine an exact value for m. Therefore, (1) is NOT sufficient. From the information in (2), y = 15n, for a value of n that is a counting number, but there is no way to determine an exact value for n. Therefore, (2) also is NOT sufficient. Taking (1) and (2) together, combine the two equations by multiplying x = 6m by y = 15n: xy = (6m)(15n) = (6m)(3·5n) = (6·3)(5mn) = 18(5mn). Because 5, m, and n are counting numbers, their product 5mn is a counting number. Thus, xy is a multiple of 18. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
2. C Let t = the number of hours the friends will be charged at $19.99 per hour and d = the total mileage the friends will be charged at $0.55 per mile. Then the cost, C, for the rental is $19.99t + $0.55d. From the information in (1), d = 100 miles, but without knowing t, you cannot compute the cost. Therefore, (1) is NOT sufficient. From the information in (2), t = 4 hours (because they are charged a full hour for a portion of an hour), but without knowing d, you cannot compute the cost. Therefore, (2) also is NOT sufficient. Taking (1) and (2) together, you can substitute the values of t and d into the equation: C = $19.99t + $0.55d = $19.99(4) + $0.55(100), which you can compute to obtain the cost. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
3. E Let x = the number of female students surveyed and y = the number of male students surveyed. Then x + y = the number of students surveyed. The information in (1) tells you that 20%x is the number of female students who are taking a foreign language, but you need further information to determine how many students surveyed are taking a foreign language. Therefore, (1) is NOT sufficient. From the information in (2), you know that 15%y is the number of male students who are taking a foreign language, but you need further information to determine how many students surveyed are taking a foreign language; so (2) also is NOT sufficient. From (1) and (2) taken together,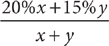 
is the percent of students surveyed who are taking a foreign language. Without further information, this expression cannot be simplified to a single value. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
4. D From the subscripts on the data values, you know there are 100 data values. The variance is a measure of how much these values are spread out relative to the mean, μ, of these numbers. You compute this population variance by subtracting the mean from each data value, squaring each difference, and then summing up the 100 squared differences and dividing by 100. From the information in (1), the variance is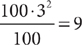 
. Therefore, (1) is sufficient. From the information in (2), the variance equals the square of the standard deviation, so the variance = 32 = 9. Thus, (2) is sufficient. In sum, EACH statement ALONE is sufficient.
5. C The entire distance traveled is d. Let t = the time for the second part of the trip. From the information in (1), the distance traveled for the first two hours of the trip is (63 mph)(2 hr) = 126 miles. The distance traveled for the second part of the trip is d – 126 = 70 mph(t). However, without knowing d or t, you cannot compute the distance traveled for the second part of the trip, so (1) is NOT sufficient. From the information in (2), the time for the first part of the trip is = 3.8 hours – t (Note: 48 minutes is 0.8 hour). Then, omitting the units, the distance traveled for the first part of the trip is 63(3.8 – t) and the distance traveled for the second part of the trip is 70t. But without knowing t, you cannot compare the two distances. Therefore, (2) is NOT sufficient. Taking (1) and (2) together, from (1) the distance traveled for the first two hours of the trip is (63 mph)(2 hr) = 126 miles. From (1) and (2) the time for the second part of the trip equals 3.8 hr. – 2 hr. = 1.8 hr, so the distance traveled for the second part of the trip is (70 mph)(1.8 hr) = 126 miles. Now that you know the two distances are equal, you can answer “No” to the question posed. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
6. D From the information in the question, after mixing, the 20% alcohol solution contains (x + y) liters. From the information in (1), y = 37.5 – x. The amount of alcohol before mixing equals the amount of alcohol after mixing, so 60%x + 10%(37.5 – x) = 20%(37.5), which you can solve to determine a single value of x. Therefore, (1) is SUFFICIENT. From the information in (2), x + y = x + 30. The amount of alcohol before mixing equals the amount of alcohol after mixing. Therefore, 60%x + 10%(30) = 20%(x + 30), which you can solve to determine a single value of x. Therefore, (2) also is SUFFICIENT. EACH statement ALONE is sufficient.
7. B First, simplify the given equation as follows:
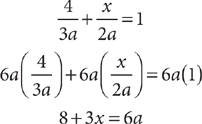
By inspection, you can see that the equation in (1), 3x = 6a – 8, is equivalent to 8 + 3x = 6a, so further information is needed. Therefore, (1) is NOT sufficient. With the equation in (2), that is, 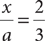(which is equivalent to 3x = 2a), and 8 + 3x = 6a, you have two linear equations and two variables. You can solve the two equations simultaneously for a single value of x. Therefore, (2) is SUFFICIENT. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
8. A Let x = the smaller number and y = the larger number. Then, according to the question,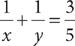 
. From the information in (1), y = 5x. You can substitute from this equation into 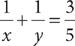to obtain 
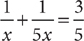. Multiply both sides of this equation by 5x to obtain 6 = 3x, which you can solve for a single value of x. You can substitute your answer into the equation y = 5x to obtain the value of the larger number. Therefore, (1) is SUFFICIENT. From the information in (2), 
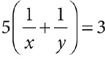, which you can see by inspection is equivalent to 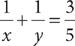, so further information is needed, meaning (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
9. C Let x = the number of balcony seats sold and y = the number of orchestra seats sold. From the information in (1), x + y = 800, which (because you have two variables and only one equation) does not yield a single value for x. Therefore, (1) is NOT sufficient. From the information in (2), $50x + $80y = $49,000, which (because you have two variables and only one equation) does not yield a single value for x. Therefore, (2) also is NOT sufficient. Taking (1) and (2) together, you have two linear equations and two variables. You can solve the two equations simultaneously for a single value of x. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
10. E Let b = the number of black marbles in the box, r = the number of red marbles in the box, and w = the number of white marbles in the box. Then the probability P of randomly drawing a white marble from the box is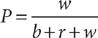 
. From the information in (1), b + r + w = 120, so 
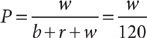, but without knowing w, you cannot determine the probability. Therefore, (1) is NOT sufficient. From the information in (2), b = 2w, so 
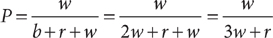, but without knowing r and w, you cannot determine the probability. Therefore, (2) also is NOT sufficient. Taking (1) and (2) together, you can set the two expressions for P equal to each other, giving 
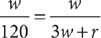. If you divide both sides by w and simplify, you obtain 3w + r = 120, which (because you have two variables and only one equation) does not yield a single value for w, from which you could calculate P. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
Tip: It was permissible to divide both sides of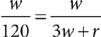 
by w because, in the context of this question, w ≠ 0. Always be careful when you divide by a variable—you need to be confident that the variable has a nonzero value.
11. A From the question information, the perimeter, P, of the shawl is P = 2l + 2w, where l = length and w = width of the shawl. From the information in (1), you can compute l = 6·9 inches and w = 4·9 inches, and with these, you can determine a single value of P = 2(6·9 inches) + 2(4·9 inches). Thus, (1) is SUFFICIENT. From the information in (2), you cannot determine the exact dimensions of the shawl and thereby a single value of P. For instance, if the shawl has four rows and six columns (24 squares), P = 108 inches + 72 inches = 180 inches, but if the shawl has three rows and eight columns (24 squares), P = 144 inches + 54 inches = 198 inches. Thus, (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
12. C Applying the information in (1), the medians in a triangle intersect at a point that is two-thirds of the distance from each vertex to the midpoint of the opposite side, so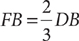 
. However, further information is needed to determine a single value for FB, so (1) is NOT sufficient. From the figure, DB = DF + FB, and applying the information in (2), DB = 15 + FB, but further is needed to determine a single value for FB. Thus, (2) also is NOT sufficient.
Taking (1) and (2) together, because 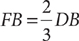and DB = DF + FB, it follows that 
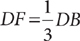. Substituting DF = 15 into this equation, you can determine DB and use that value to calculate 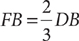. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
13. D From the information in (1), the ratio of the area of ABCDE to the area of HIJKL is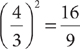 
or 16 to 9, so (1) is SUFFICIENT. From the information in (2), 
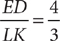. Thus, the ratio of the area of ABCDE to the area of HIJKL is or 16 to 9, and (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
14. A From the information in (1), in one revolution, the wheel will travel a distance equal to its circumference, πd = π(25 inches). Convert 
into revolutions per minute:
You can use this to compute a single value for the answer in revolutions per minute, so (1) is SUFFICIENT. The information in (2) is not helpful, because the speed 440 feet per minute is equivalent to 5 miles per hour, so no additional information is gained; thus, (2) is NOT sufficient. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
15. C From the information in (1), you know that triangle ABC is an equilateral triangle. The formula for the area, A, of an equilateral triangle is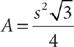 
. Thus, further information is needed to find A, and (1) is NOT sufficient. Tip: If you do not recall that the area of an equilateral triangle is 
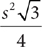, you can construct an altitude of the triangle.
The altitude divides the equilateral triangle into two 30°-60°-90° right triangles. You can use one of these right triangles to determine that the length of the altitude is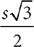 
, so:
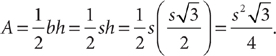
From the information in (2), you can write the area of triangle ABC as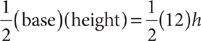 
, but without knowing the height h, you cannot compute a single value for the area, so (2) also is NOT sufficient. Taking (1) and (2) together, you can substitute the length of side AB from (2) into the formula 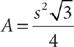based on the information from (1) and then compute a single value for A. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
16. A To answer the question, you need to determine 
. From the information in (1),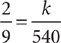 
, from which you can determine k and thereafter, 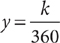. Thus, (1) is sufficient. From the information in (2), 
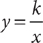, which you know already, so further information is needed, and (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
17. D Let x = the marked-down price. Then x + 8%x = the amount the customer pays for the hoodie at the marked-down price including tax. From the information in (1), you can write the equation ($85 + 8%·$85) – (x + 8%x) = $91.80 – 1.08x = $18.36, which you can solve for a single value of x. Thereafter, you can compute x + 8%x. Therefore, (1) is sufficient. From the information in (2), you can write the equation 0.08x = $5.44, which you can solve for a single value of x. Thereafter, you can compute x + 8%x. Therefore, (2) also is sufficient, and EACH statement ALONE is sufficient.
18. C From the question information, a20 = a1 + (20 – 1)d = a1 + (19)d, so you need the values of a1 and d to determine a20. From the information in (1), a4 = 17 = a1 + 3d, which (because you have two variables and only one equation) does not yield single values for a1 and d, so (1) is NOT sufficient. From the information in (2), a10 = 47 = a1 + 9d, which (because you have two variables and only one equation) does not yield single values for a1 and d, so (2) also is NOT sufficient. Taking (1) and (2) together, you have two linear equations and two variables. You can solve the two equations simultaneously to determine values for a1 and d, and you can use that solution to determine a20. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
19. A From the question information, you can make a table of possible paired values for x and y:
Using the information in (1) and checking through the possible paired values for x and y, only one pair (x = 6 and y = 4) satisfies the double inequality, 37 < 5x + 2y < 41. Thus, (1) is SUFFICIENT. The information in (2) limits the possible paired values for x and y to the four pairs for which x > 5, but further information is needed to determine a single value for y. Thus, (2) is NOT sufficient. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
20. C From the question information, x2 (the area of the square) = bh (the area of the parallelogram). From the information in (1), x2 = (10)2 = 100 = bh, which (because you have two variables and only one equation) does not yield a single value for h, so (1) is NOT sufficient. From the information in (2), x2 = bh = 20h, which (because you have two variables and only one equation) does not yield a single value for h, so (2) also is NOT sufficient. Taking (1) and (2) together, you have 100 = 20h, which you can solve to determine a single value of h. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
1. If m and p are integers, is mp < 0?
(1) m < 0
(2) p is even.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
2. In a survey asking 25 students in a classroom about their juice preferences (apple, orange, grape, and/or none), 15 said they like orange juice, and 10 said they like apple juice. How many students like both orange and apple juice?
(1) One student said she did not like any kind of juice.
(2) Three students said they like grape juice but not orange or apple juice.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
3. What is the smallest of three consecutive odd integers?
(1) The sum of the three integers is 147.
(2) The largest integer is 4 more than the smallest integer.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
4. If the temperature is 20° at 5 a.m. and rises at the rate of y° per hour, what is the value of y?
(1) At 6 a.m., the temperature is 20° + y°.
(2) The temperature at noon is 41°.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
5. A customer makes a deposit of $x and withdrawals of $y and $z from a checking account. If the initial balance was $195 and no other transactions have taken place, what is the customer’s new balance?
(1) $x – ($y + $z) = $135
(2) The difference between $x and $y is $135 more than $z.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
6. What is the value of the larger of two consecutive integers?
(1) The greater integer is odd.
(2) The product of the two integers is 182.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
7. What is the value of 
?
(1) 2x + 2y = 20
(2) x2 + xy = 100 – y2–xy
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
8. What is the value of a–0.6?
(1) 
(2) a2 = 32a
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
9. To the nearest dollar, what is the value of the money in a rectangular box filled to capacity with twenty-dollar bills?
(1) The box measures 24 by 16 by 8 inches.
(2) A stack of 100 twenty-dollar bills is 0.43 inch tall.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
10. How many days will it take four identical machines working together to do a job?
(1) Each machine does 
of the job.
(2) Two such machines can do the job in 8 days.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
11. Can 130° be the measure of an exterior angle of triangle ABC?
(1) m∠B = 55°
(2) m∠C = 65°
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
12. How many sides does the regular convex polygon have?
(1) The measure of each exterior angle is 45°.
(2) The measure of each interior angle is 135°.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
13. In the preceding pentagon ABCDE, what is the measure, in degrees, of the largest angle?
(1) ∠C is the largest angle.
(2) m∠B = 2x
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
14. P and Q are points in a coordinate plane. What is the distance between P and Q?
(1) P has coordinates (–3, 2), and Q has coordinates (3, 4).
(2) The midpoint between P and Q is (0, 3).
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
15. A translation from P(x, y) to P′(x′, y′) is described as “8 units right and 5 units down.” What is the value of x′?
(1) y′ = –1
(2) y = 4
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
16. A box contains cards with the names of boys and girls in a classroom written on them. Only one name is written on each card, and the cards are identical in size and shape. Two cards are randomly drawn from the box, one after the other. What is the probability that the students whose names are drawn are both boys?
(1) The first card drawn is not replaced before the second card is drawn.
(2) The box contains the names of 8 boys and 12 girls.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
17. Is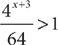 
?
(1) 4x + 3 > 0
(2) 4x > 1
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
18. A collection of coins consists of only nickels, dimes, and quarters. How many quarters are in the collection?
(1) The face value of the coins is $5.
(2) There are 58 coins in all.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
19. Triangle ABC is isosceles. What is its perimeter?
(1) AB = 15
(2) BC = 20
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. What fraction of circle C is shaded?
(1) m∠PCS = 120°
(2) 
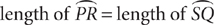
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
EACH statement ALONE is sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
1. B If, according to (1), m is negative, then mp is positive if p is even and negative if p is odd. For instance, if m = –1 and p = 2, then mp = (–1)2 = 1 > 0, and if m = –1 and p = 1, mp = (–1)1 = –1 < 0. Thus, further information is needed, and (1) is NOT sufficient. If, according to (2), p is even, then mp is positive whether m is positive or negative. For instance, if m = –1 and p = 2, mp = (–1)2 = 1 > 0, and if m = 1 and p = 2, mp = (1)2 = 1 > 0. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
2. C From the information in (1), you know that 24 students like some kind of juice, but without further information about the students who like grape juice, you cannot determine how many students like both orange and apple juice. Therefore, (1) is NOT sufficient. From the information in (2), you know that three students like only grape juice, but without further information about the students who do not like any of the three kinds of juices, you cannot determine how many students like both orange and apple juice. Therefore, (2) is NOT sufficient.
Taking (1) and (2) together, let x = the number of students who like both orange and apple juice, o = the number of students who like only orange juice, a = the number of students who like only apple juice, and g = the number of students who like only grape juice. Draw a Venn diagram, using the question information and statements (1) and (2).
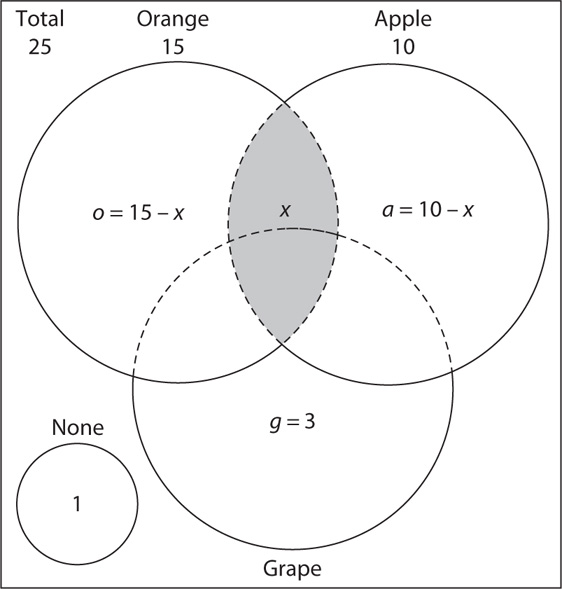
From the Venn diagram, you can write the equation (15 – x) + x + (10 – x) + 3 + 1 = 25, which you can solve for a single value of x, the number of students who like both orange and apple juice. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
3. A Let n, n + 2, and n + 4 be the three consecutive odd integers. From the information in (1), you can write the equation n + (n + 2) + (n + 4) = 147, which you can solve for a single value of n. Therefore, (1) is sufficient. From the information in (2), you can write the equation n + 4 = n + 4, which has an infinite number of solutions, so it is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
4. B From the information in (1), you can determine that the temperature rises y degrees in 1 hour, but additional information is needed to determine y; so (1) is NOT sufficient. From the information in (2), given that noon is 7 hours past 5 a.m., you can write the equation 20° + 7y° = 41°, which you can solve for a single value of y. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
5. D The customer’s new balance is the initial balance plus deposits minus withdrawals, or $195 + $x – $y – $z. From the information in (1), $195 + $x –$y –$z = $195 + $x – ($y + $z) = $195 + $135 = $330. Therefore, (1) is sufficient. From the information in (2), you can write the equation $x – $y = $z + $135, from which you can obtain the equation $x – $y – $z = $135. Substituting this value of $x – $y – $z into the equation for the new balance, you have $195 + $x – $y – $z = $195 + $135 = $330. Therefore, (2) is sufficient, and EACH statement ALONE is sufficient.
6. C Let n = the smaller integer and n + 1 = the greater integer. From the information in (1), you know that n is even and n + 1 is odd, but further information is needed to determine n + 1, so (1) is NOT sufficient. From the information in (2), n(n + 1) = 182, which can be solved as follows:
n(n + 1) = 182
n2 + n – 182 = 0
(n + 14)(n – 13) = 0
Thus, n = –14 with n + 1 = –13, or n = 13 with n + 1 = 14, so further information is needed, meaning (2) also is NOT sufficient. Taking (1) and (2) together, use (1) to pick the solution in (2) where n is even and n + 1 is odd: n = –14 with n + 1 = –13. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
7. D First, observe that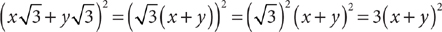 
. From the information in (1), 2x + 2y = 20 is equivalent to 10 x + y = 10, so 
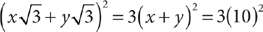, and (1) is SUFFICIENT. From the information in (2), x2 + xy = 100 – y2 – xy is equivalent to x2 + 2xy + y2 = 100, which can be written as (x + y)2 = 100, so 
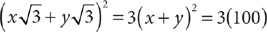, and (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
8. A From the information in (1), a = 25, which you can substitute into the equation given in the problem: a–0.6 = (25)–0.6. You can compute the answer as a single value, so (1) is SUFFICIENT. From the information in (2), a2 – 32a = a(a – 32) = 0, which implies that a = 0 or a = 32. The solution is not a single value, so (2) is NOT sufficient. Tip: You must NOT divide both sides of a2 = 32a by a, because you have no way of determining whether a = 0. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
9. E From the information in (1), the box’s capacity (volume) measures 24 × 16 × 8 cubic inches, but further information is needed to determine how many $20 bills will fit inside of it, so (1) is NOT sufficient. The information in (2) gives you the height of a stack of a hundred $20 bills, but further information is needed to determine how many stacks will fit inside the box, so (2) also is NOT sufficient. Taking (1) and (2) together, you can determine the capacity of the box from (1), but without knowing the length and width of a stack of a hundred $20 bills, in addition to the stack’s height of 0.43 inch from (2), you cannot determine how many stacks will fit inside the box. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
10. B Let d = the number of days it will take four machines to do the job and r = rate at which one machine could do the job working alone. From the information in (1), you know that over the period of d days, each machine does 
of the job, so 
, but further information is needed to determine d. Therefore, (1) is NOT sufficient. From the information in (2), 8 days times 2 machines times r equals 1 job, from which you have 16r = 1 (omitting units). This equation implies that each machine does 
of the job per day. Therefore, if 4 machines working together for d days complete the job, then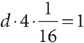 
, which you can solve for a single value of d, so (2) is SUFFICIENT. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
11. C From the information in (1), you know that the measure of the exterior angle that is adjacent to ∠B equals 180° – 55° = 125° ≠ 130°, but you need additional information to determine the measures of the exterior angles at A and C, so (1) is NOT sufficient. From the information in (2), you know that the measure of the exterior angle that is adjacent to ∠C equals 180° – 65° = 115° ≠ 130°, but you need additional information to determine the measures of the exterior angles at A and B, so (2) also is NOT sufficient Taking (1) and (2) together, neither of the exterior angles at B or C can measure 130°. Furthermore, the measure of the exterior angle at A equals the sum of the measures of the two nonadjacent interior angles. Thus, the measure of the exterior angle at A = 55° + 65° = 120° ≠ 130°. So none of the exterior angles of triangle ABC can measure 130°. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
12. D From the information in (1),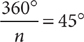 
(because the measure of each exterior angle of a regular convex polygon is 
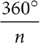). You can solve this equation for a single value of n, so (1) is SUFFICIENT. From the information in (2), 
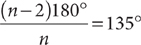(because the measure of each interior angle of a regular convex polygon is 
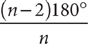). You can solve this equation for a single value of n, so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
13. B From the question information, the sum of the measures of the angles of pentagon ABCDE is (n – 2)180° = (5 – 2)180° = (3)180° = 540°. Thus, (2x – 14) + m∠B + (6x + 2) + (4x – 8) + 6x = 540°. From the information in (1), you know that 6x + 2 is the greatest of the measures of the angles, but further information is needed to determine a single value for 6x + 2, so (1) is NOT sufficient. From the information in (2), you can set up the equation (2x – 14) + (2x) + (6x + 2) + (4x – 8) + 6x = 540°, which you can solve for a single value of x. You can use that value to compute 6x + 2, the measure of the largest angle, so (2) is SUFFICIENT. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
14. A To apply the information in (1), recall that the distance d between two points (x1, y1) and (x2, y2) in a coordinate plane is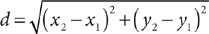 
. Thus, you can substitute the coordinates of P and Q into this formula and determine a single value of d, so (1) is SUFFICIENT. To apply the information in (2), recall that the midpoint between two points (x1, y1), and (x2, y2), in a coordinate plane is the point with coordinates 
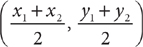. Thus, 
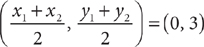, but you need further information to determine the values of x1, y1, x2, and y2, which you can use to determine the distance between P and Q. Thus, (2) is NOT sufficient. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
15. E From the question information, (x′, y′) = (x + 8, y – 5). From the information in (1), you can determine y but not x′, so (1) is NOT sufficient. From the information in (2), you can determine y′ but not x′, so (2) also is NOT sufficient. Taking (1) and (2) together, without having information about x, you cannot determine x′. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
16. C The probability, P, that the students whose names are drawn are both boys is the probability that a boy’s name is drawn first times the conditional probability that a boy’s name is drawn second given that a boy’s name was drawn first. The information in (1) tells you that because the card is not replaced, the outcome of the first draw influences the outcome of the second draw. But, you are unable to determine the desired probability, so (1) is NOT sufficient. From the information in (2), the probability that a boy’s name is drawn first is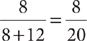 
. However, without knowing whether the first card is replaced, the conditional probability that a boy’s name is drawn second cannot be determined; so (2) is NOT sufficient. Taking (1) and (2) together, 
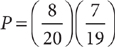, which you can compute. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
17. B Observe that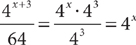 
. The information in (1) is irrelevant because 4 raised to any power is greater than 0, so (1) is NOT sufficient. Applying the information in (2), 
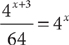, and as given, 4x > 1. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
18. E Let n = the number of nickels, d = the number of dimes, and q = the number of quarters. From the information in (1), $0.05n + $0.10d + $0.25q = $5.00, which (because you have three variables and one equation) does not yield a single value for q, so (1) is NOT sufficient. From the information in (2), n + d + q = 58, which (because you have three variables and one equation) does not yield a single value for q, so (2) also is NOT sufficient. Taking (1) and (2) together, you have you have two equations and three variables, so further information is needed to determine a single value for q. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
19. E From the question information, let x = the length of one of the two congruent sides of triangle ABC and y = the length of the noncongruent side. Then the perimeter, P, of the triangle is P = 2x + y. From the information in (1), you cannot determine whether AB equals x or y. If AB = x, then P = 2·15 + y = 30 + y, but without knowing the value of y, you cannot determine P. Similarly, if AB = y, then P = 2x + 15, but without knowing the value of x, you cannot determine P. Thus, either way, further information is needed, and (1) is NOT sufficient. From the information in (2), you cannot determine whether BC equals x or y. If BC = x, then P = 2·20 + y = 40 + y, but without knowing the value of y, you cannot determine P. Similarly, if BC = y, then P = 2x + 20, but without knowing the value of x, you cannot determine P. Thus, either way, further information is needed, and (2) is NOT sufficient. Taking (1) and (2) together, if AB = x and BC = y, then P = 2·15 + 20 = 50. But if AB = y and BC = x, then P = 2·20 + 15 = 55. Thus, you cannot determine a single value for P. Therefore, statements (1) and (2) TOGETHER are NOT sufficient.
20. A From the information in (1), m∠PCR = m∠PCS = 120° (vertical angles are equal). Thus,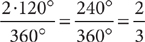 
of the circle is not shaded. Hence, 
of the circle is shaded, so (1) is SUFFICIENT. Knowing from the information in (2) that these two arcs have equal lengths does not provide enough information for you to determine what fractional part of the circle they represent, so (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
