CHAPTER 11
Word Problems
This review of word problems includes the following topics:
Problem-Solving Process
Here is a general process for problem solving on the GMAT.
1. Understand the problem. Ask yourself: What content area (arithmetic, algebra, or geometry) is the question’s primary focus? Is the problem a familiar type (for example, a mixture problem)? Determine what you need to find. Look for words like find, determine, what is, how many, how far, how much, and the like. Decide how many unknowns are in the problem.
2. Make a plan. Decide how you should go about determining a solution. Identify the information in the problem. Is there a formula that you need? If measurement units are given, determine what units the answer should have. Decide whether making a chart or sketching a diagram would be helpful. Try to relate the current problem to practice problems you have worked out. Make sure your plan will result in a solution that answers the question.
3. Carry out the plan. Using the plan you decided upon, work out the solution on the erasable noteboard provided at the testing center. Make sure you copy all information accurately. Write neatly so that you can check over your work. If the answer should have units, check whether your calculations will result in the proper units for the answer. Tip: If you are using an equation to find the solution, you might find it convenient to omit the units while solving the equation, given that you have already checked that the answer will have the proper units.
4. Look back. Verbalize your answer. Did you answer the question that was asked? Check your solution in the context of the problem. Does it make sense? Is it reasonable? Are units needed?
Representing Verbal Phrases and Statements
For many questions, writing and solving an equation is a straightforward method for determining the answer. When you use equations, you must represent verbal phrases and statements using mathematical symbolism. Here are some general guidelines.

Example: Ten less than three times a number is five more than twice the number. What is the number?
Let n = the number. Write an equation that represents the facts.
3n – 10 = 2n + 5
(Keep in mind that “Ten less than three times a number” is not 10 – 3n.) Solve the equation.
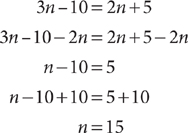
The number is 15.
Sometimes you have two or more unknowns in a problem. For this situation you can use a different variable name for each unknown. On the other hand, you might assign a variable name to one unknown and express the other unknowns in terms of that variable. For instance, if a first unknown is described in terms of a second unknown, let the variable equal the second unknown. In most cases, you will need as many equations as you have variables in order to determine specific values for the variables. No matter whether you go with one variable or two or more variables, ultimately, the process will culminate in a one-variable linear equation (or its equivalent).
The length of a lawn is 6 feet longer than its width. The lawn’s perimeter is 68 feet. What is the lawn’s length, in feet?
Method 1: Use one variable.
The lawn’s length is described in terms of its width. Let w = the lawn’s width, in feet. Then w + 6 feet = the lawn’s length, in feet. Write an equation that represents the facts given in the question.
2[(w +6 feet) + w] = 68 feet
Solve the equation, omitting the units for convenience.
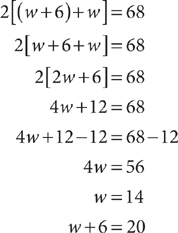
The lawn’s length is 20 feet.
Method 2: Use two variables.
Let w = the lawn’s width, in feet, and l = the lawn’s length, in feet. Write two equations that represent the facts given in the question.
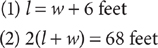
Simultaneously solve the two equations, omitting the units for convenience.
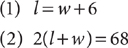
Using the substitution method, substitute l = w + 6 from equation (1) into equation (2) to obtain
2[(w +6) + w] = 68
Complete the solution as shown in Method 1.
Consecutive Numbers
Consecutive integers differ by 1. For these problems, let n = the first integer (the least one), n + 1 = the second integer, n + 2 = the third integer, and so on.
Example: The greatest of three consecutive integers is 10 more than twice the second integer. What is the value of the greatest integer?
Let n = the first integer, n + 1 = the second integer, and n + 2 = the third integer (the greatest one). Write an equation that represents the facts given in the question.
(n + 2) = 2(n + 1) + 10
Solve the equation.
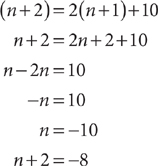
The greatest integer is –8.
Consecutive even integers and consecutive odd integers differ by 2. For these problems, let n = the first even or odd integer, n + 2 = the second even or odd integer, and n + 4 = the third even or odd integer, and so on.
Ratios and Proportions
Ratios
A ratio is a multiplicative comparison of two quantities. If two quantities are in the ratio a to b and you know their sum is c, solve ax + bx = c for x, then compute ax or bx, whichever one is needed.
Example: The ratio of boys to girls in a classroom of 21 students is 3 to 4. How many girls are in the classroom?
Solve 3x + 4x = 21.
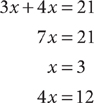
There are 12 girls in the classroom.
Proportions
A proportion is a mathematical statement that two ratios are equal. The statement 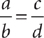 is a proportion and is read “a is to b as c is to d.” The fundamental property of proportions is that
is a proportion and is read “a is to b as c is to d.” The fundamental property of proportions is that 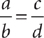 if and only if ad = bc. The numbers a, b, c, and d are the terms of the proportion. The products ad and bc are the cross products (illustrated below).
if and only if ad = bc. The numbers a, b, c, and d are the terms of the proportion. The products ad and bc are the cross products (illustrated below).

If the values of three of the four terms of a proportion are known, the value of the fourth term can be determined by using the fundamental property of proportions. Find a cross product that results in a numerical value, and then divide by the numerical term you didn’t use. For example,
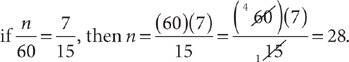
When you have a word problem involving proportions, look for a sentence or phrase in the problem that provides the information you need for the left ratio of the proportion, and then look for another sentence or phrase that gives you the information you need for the right ratio of the proportion.
Example: On a map, the distance between two cities is 13.5 inches. The scale on the map shows that 0.5 inches represents 20 miles. What is the distance, in miles, between the two cities?
Let d = the distance, in miles between the two cities.
Information for the left ratio of the proportion is in the first sentence of the problem (13.5 inches represents d miles on the map), and information for the right ratio of the proportion is in the second sentence (0.5 inches represents 20 miles on the map).
Write the proportion.
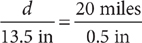
Solve the proportion, omitting the units for convenience.
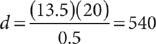
The distance between the two cities is 540 miles.
Percentage
Formula and Terminology
In simple percentage problems use the formula P = RB, where P is the percentage (the “part of the whole”), R is the rate (the quantity with a % sign or the word percent attached), and B is the base (the “whole amount”).
Finding the Percentage
If the percentage is missing, multiply the base by the rate. Here is an example.
Devra works at an electronics store that pays a commission rate of 2% to employees for all sales. Last week, Devra’s sales totaled $2,428. What commission did Devra earn last week?
In this problem, Devra’s commission is P, which is unknown; R is 2%; and B is $2,428. So, P = RB = (2%)($2,428) = (0.02)($2,428) = $48.56.
Devra earned $48.56 in commission last week.
Finding the Base
If the base is missing, divide the percentage by the rate. Here is an example.
An online store offered a 25% discount on all clothing items during a two-day sale. Laura got $74.75 off the price of a coat she purchased during the sale. What was the original price of the coat?
In this problem, the original price of the coat is B, which is unknown; R is 25%; and P is $74.75. So,
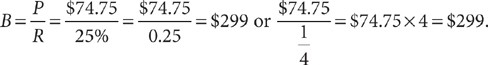

Finding the Rate
If the rate is missing, divide the percentage by the base. Express your answer as a percent.
Example: Aaron paid a sales tax of $9.90 on a camera that cost $120. What was the sales tax rate for the purchase?
In this problem, the sales tax rate is R, which is unknown; P is $9.90, and B is $120. So,
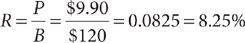
The sales tax rate was 8.25%.
Percentage Increase or Decrease
The percent change (increase or decrease) in the value of an item is
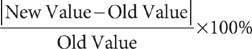
For example, suppose a necklace increased in value from $345.00 to $396.75. Then (omitting the units), the percent increase is
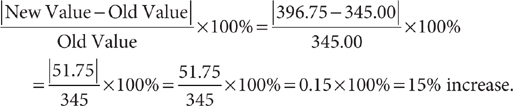
Similarly, suppose a book decreased in value from $25.90 to $23.31. Then (omitting the units), the percent decrease is
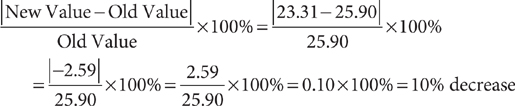
Simple Interest
Simple interest is I = Prt, where I is the simple interest accumulated on a principal, P, at a simple interest rate, r, per time period for t time periods. For example, the simple interest earned on an investment of $10,000 at a 2% annual simple interest rate for 5 years is
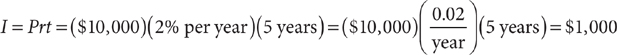
Ages
In age problems, comparisons are usually made in specified time periods (present, future, or past). Make a table to organize the age information to help you understand the question.
Example: Jaylon is twice as old as Kyle. Five years from now the sum of their ages will be 46. How old will Jaylon be in 10 years?
Let K = Kyle’s age, in years, now. Then 2K = Jaylon’s age, in years, now.
Make a table to organize the age information.

Write an equation that represents the facts shown in the table.
(2K + 5 years) + (K + 5 years) = 46 years
Solve the equation, omitting the units for convenience.
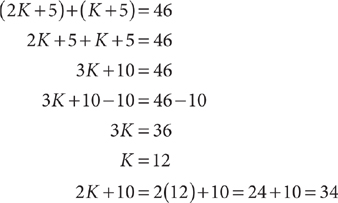
Jaylon will be 34 years old in 10 years.
Mixtures
In a mixture problem, the amount (or value) of a substance before mixing equals the amount (or value) of that substance after mixing. Make a table to organize the mixture information to help you understand the question.
Example: How many milliliters of a 30% alcohol solution must be added to 500 milliliters of a 70% alcohol solution to yield a 40% alcohol solution?
Let x = the number of milliliters of the 30% solution to be added.
Make a table to organize the information in the question.

The amount of alcohol before mixing equals the amount of alcohol after mixing. Write an equation that represents the facts shown in the table.
30%x + 70%(500) = 40%(x + 500)
Solve the equation.
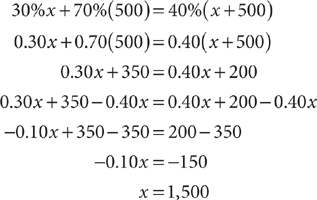
1,500 milliliters of the 30% alcohol solution must be added.
Coins
In a coin problem, the value of a collection of coins equals the sum of the values of the coins in the collection. (Of course, you must assume there are no rare coins in the collection that would be worth more than their face values.) Make a table to organize the coin information to help you understand the question.
Example: Andre has a jar containing 759 U.S. nickels and dimes that have a total value of $53.30. How many nickels are in the jar?
Let n = the number of nickels. Let d = the number of dimes. Make a table to organize the coin information in the question.
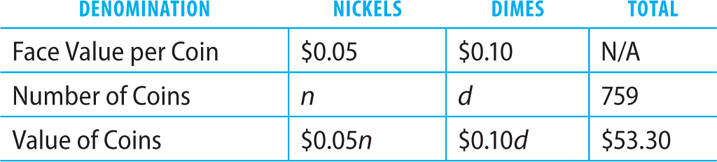
Using the table, write two equations that represent the facts.
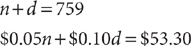
Solve the system, omitting the units for convenience.
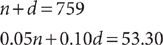
Using the method of substitution, solve the first equation, n + d = 759, for d in terms of n.
d = 759 – n
Substitute the result into the second equation and solve for n.
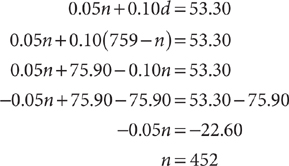
There are 452 nickels in the jar.
Distance-Rate-Time
The distance formula is d = rt, where d is the distance a vehicle travels at a uniform rate of speed, r, for a given length of time, t. Make a table to organize the vehicle information and maybe sketch a rough diagram, if needed, to help you understand the question.
Example: At 8 p.m., a car and a van leave the same location. The car travels due east at 70 miles per hour. The van travels due west at 60 miles per hour. At what clock time will the two vehicles be 325 miles apart?
Let t = the time in hours the two vehicles will be 325 miles apart. Then 8 p.m. plus t = the clock time the two vehicles will be 325 miles apart. Make a chart to organize the information in the question.

Sketch a diagram.

Using the diagram, write an equation that represents the facts.
60t + 70t = 325 miles
Solve the equation, omitting the units for convenience.
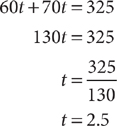
The clock time the two vehicles will be 325 miles apart is 8 p.m. plus 2.5 hours = 10:30 p.m.
Work
In a typical work problem, you are given the time, call it x, that it will take one person (or device) to do a task, working alone, and the time, call it y, that it will take another person (or device) to do the same task, working alone. Then the time it will take both of them, working together, is
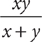
Example: Working alone, Dylan can paint the walls of a long hallway in 4 hours. Jeremy can paint the walls of the hallway in 3 hours, working alone. How long will it take them, working together, to paint the hallway?
Omitting the units, calculate 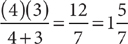 . The time it will take Dylan and Jeremy, working together, to paint the hallway is
. The time it will take Dylan and Jeremy, working together, to paint the hallway is 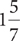 hours.
hours.
Right Triangles
3-4-5 Right Triangles
You will likely see right triangles on the GMAT that have sides of lengths 3, 4, and 5 or of lengths that are multiples of 3, 4, and 5. The reason is that 3, 4, and 5 and any multiple of these numbers (such as 6, 8, and 10 or 30, 40, and 50) satisfy the Pythagorean theorem. That is, 32 + 42 = 52, 62 + 82 = 102, and 302 + 402 = 502.
Example: A wall is 12 feet long and 9 feet high. What is the diagonal length of the wall?
The diagonal is the hypotenuse of a right triangle that has legs of 12 feet and 9 feet. The numbers 12 and 9 are multiples of 4 and 3 by a factor of 3, respectively. Therefore, the hypotenuse is a multiple of 5 by a factor of 3. Thus, the diagonal length of the garden is (3)(5 feet) = 15 feet.
30°-60°-90° Right Triangles
In a right triangle that has acute angles of 30° and 60°, the lengths of the triangle’s three sides are in the ratio 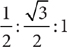 or, equivalently,
or, equivalently, 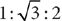 .
.
Example: Find BC in the right triangle shown below.
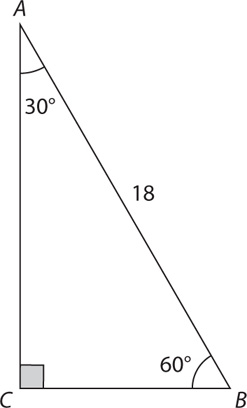
The triangle is a 30°-60°-90° right triangle. 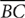 is opposite the 30° angle. Therefore,
is opposite the 30° angle. Therefore, 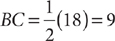 .
.
45°-45°-90° Right Triangles
In an isosceles right triangle that has congruent acute angles of 45°, the lengths of the triangle’s three sides are in the ratio 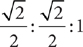 or, equivalently,
or, equivalently, 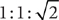 .
.
Example: Find the length of the hypotenuse in the right triangle shown below.
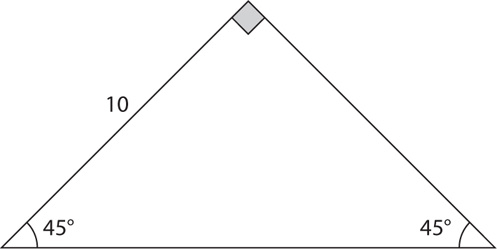
The triangle is a 45°-45°-90° right triangle. The three sides are in the ratio 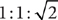 . Therefore, the length of the hypotenuse is
. Therefore, the length of the hypotenuse is 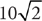 .
.
Divisors and Factors
Divisibility Rules
Here are some useful divisibility rules to know for the GMAT.
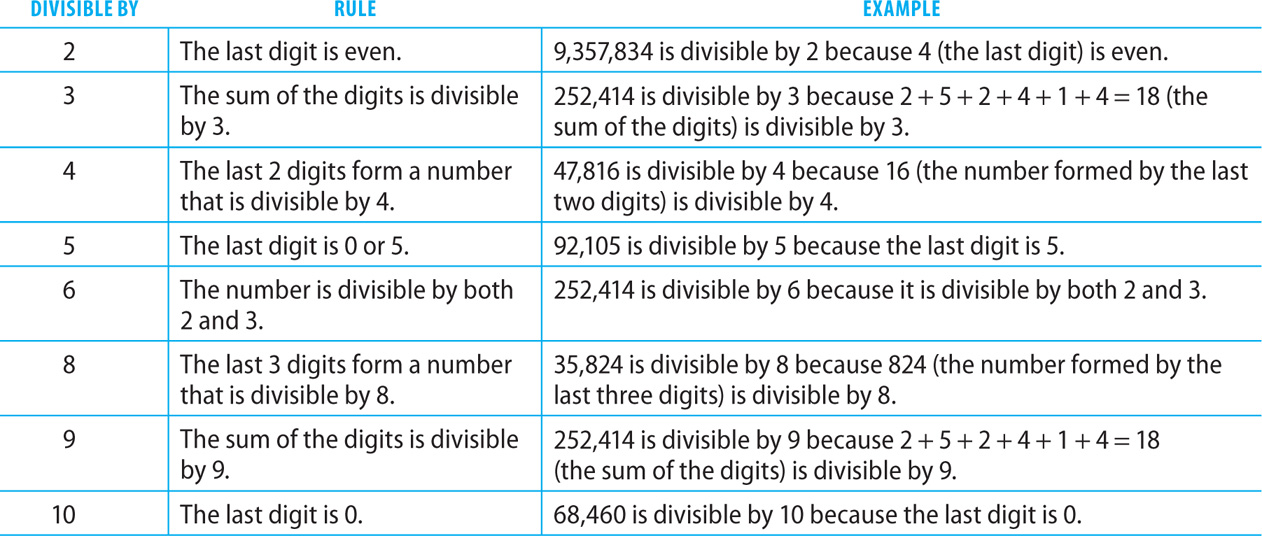
 If an integer divides evenly into n, then it divides evenly into any multiple of n. For instance, 3 divides 594, so it also divides (10)(594) = 5,940.
If an integer divides evenly into n, then it divides evenly into any multiple of n. For instance, 3 divides 594, so it also divides (10)(594) = 5,940.
 If an integer divides evenly into both m and n, then it divides evenly into am + bn, for any integers a and b. For instance, 3 divides evenly into 27 and 3 divides evenly into 60, so 3 divides evenly into (5)(27) + 4(60) = 375.
If an integer divides evenly into both m and n, then it divides evenly into am + bn, for any integers a and b. For instance, 3 divides evenly into 27 and 3 divides evenly into 60, so 3 divides evenly into (5)(27) + 4(60) = 375.
Factors
If the prime factorization of a positive integer n is 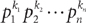 , where the p’s are distinct positive prime numbers and the k’s are their corresponding exponents, then the number of positive factors (or divisors) of n is the product (k1 + 1)(k2 + 1)…(kn + 1). For example, the number of positive factors (or divisors) of n = a4b2c5d, where a, b, c, and d are prime numbers, is (4 + 1)(2 + 1)(5 + 1)(1 + 1) = (5)(3)(6)(2) = 180.
, where the p’s are distinct positive prime numbers and the k’s are their corresponding exponents, then the number of positive factors (or divisors) of n is the product (k1 + 1)(k2 + 1)…(kn + 1). For example, the number of positive factors (or divisors) of n = a4b2c5d, where a, b, c, and d are prime numbers, is (4 + 1)(2 + 1)(5 + 1)(1 + 1) = (5)(3)(6)(2) = 180.
On a smaller scale, the number of positive factors of 24, which equals (23)(3), is (3 + 1)(1 + 1) = (4)(2) = 8. Because integers can have negative factors, the number of factors (positive and negative) of 24 is 2(8) = 16.
Greatest Common Factor and Least Common Multiple
Greatest Common Factor
The greatest common factor (or GCF) of two numbers is the greatest factor common to both numbers. In other words, it is the largest number that evenly divides into each of the two numbers. In GCF word problems you are seeking the greatest common number, the greatest common size, the greatest common measure, and so forth that can be used to evenly divide or distribute the objects or things from two unequal-size sets so that none are left over.
Example: A civic club has 24 boys and 36 girls as members. For a community project, the club’s faculty sponsor wants to evenly divide the boys and girls into groups, so that no one is left out. What is the greatest number of groups the faculty sponsor can make?
The greatest number of groups is the GCF (24, 36) = 12. Each of the 12 groups will have 2 boys and 3 girls in it. Tip: Notice that 5 × 12 = 60, which is the total number of members (24 + 36 = 60).
Least Common Multiple
The least common multiple (or LCM) of two numbers is the least number that is a multiple of both numbers. In other words, it is the minimum number both numbers evenly divide into. In LCM word problems you are seeking the minimum common number, the minimum common time, the minimum common measure, and so forth between two multiple events or items.
Example: At the entrance to an amusement park every 50th person gets a ticket for a free drink and every 75th person gets a ticket for a free ride. What is the minimum number of people who must enter for a person to receive both tickets?
The minimum number of people is the LCM (50, 75) = 150. The 150th person will be the first person to receive both tickets.
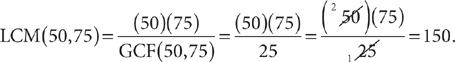
Permutations and Combinations
Permutations
A permutation is a selection in which order is important. That is, different orderings of the same elements are counted separately. For example, two permutations of the numbers from one to five are 12345 and 53142.
On the GMAT, use the product rule for counting to work permutation problems. Make sure that:
 The items from which you select are mutually different items (that is, no two are alike).
The items from which you select are mutually different items (that is, no two are alike).
 You select without replacement.
You select without replacement.
 Different orderings of the same items are counted separately.
Different orderings of the same items are counted separately.
Some situations that indicate you might have a permutation problem are the following: creating codes, passwords, or license plates; making words; assigning roles; filling positions; making ordered arrangements of things (people, objects, colors, and so on), selecting persons or things as first, second, third, and so on; distributing items among several objects or people; and similar scenarios.
For example, the number of different ways a club of 20 members can select a president, vice-president, and secretary from its membership if no person holds more than one office and all members are eligible for any one of the three positions is 20 × 19 × 18 = 6,840. (There are 20 members from which to select a president. After that position is filled, there are 19 members from which to select a vice-president. After the first two positions are filled, there are 18 members from which to select a secretary.)
Combinations
A combination is a selection in which order is not important. For example, the set of vowels a, e, i, o, and u is the same as the set of vowels i, a, u, o, and e. However, two different combination consisting of four vowels are the set a, e, i, and o and the set a, e, i, and u.
On the GMAT, to work combination problems use the combination formula
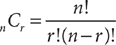
Make sure that:
 The items from which you select are mutually different items (that is, no two are alike).
The items from which you select are mutually different items (that is, no two are alike).
 You select without replacement.
You select without replacement.
 Different orderings of the same items are not distinguished as being different from each other.
Different orderings of the same items are not distinguished as being different from each other.
Some situations that indicate you might have a combination problem are the following: making a collection of things (books, coins, and so on); selecting a committee; choosing questions from a test; counting the number of subsets of a given size from a set; dealing hands from a deck of cards; selecting pizza toppings; listing the combinations from a set of items; choosing students for groups; and similar scenarios.
Example: The number of different ways a club of 20 members can select a 3-member officer-nominating committee from its membership if all members are eligible to serve on the committee is
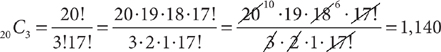
Sequences
A sequence is a list of terms written in a particular order.
In an arithmetic sequence, consecutive terms have a common difference. The sequence has the form a1, a1 + d, a1 + 2d, …, a1 + (n – 1)d, …, where a1 is the first term and d is the common difference between terms. The general term for an arithmetic sequence is an = a1 + (n – 1)d. For example, the first five terms of the arithmetic sequence that has first term a1 = 3 and common difference d = 5 are 3, 8, 13, 18, and 23. The 20th term is a20 = 3 + (20 – 1)(5) = 3 + (19)(5) = 98.
In a geometric sequence, consecutive terms have a common ratio. The sequence has the form a1, a1r, a1r2, …, a1rn–1, …, where a1 is the first term and r is the common ratio. The general term for a geometric sequence is an = a1rn–1. For example, the first five terms of the geometric sequence that has first term a1 = 10 and common ratio r = 2 are 10, 20, 40, 80, and 160. The 10th term is a10 = (10)(210–1) = (10)(29) = (10)(512) = 5,120.
A recursive definition for a sequence includes the value of one or more initial terms and a formula for finding each term from previous terms. The Fibonacci sequence has the following recursive definition: a1 = 1, a2 = 1, and an = an–1 + an–2, for n ≥ 3. The first five terms of the sequence are 1, 1, 2, 3, and 5.
If you encounter sequences on the GMAT, look for a recognizable pattern. Is there a common difference? Is there a common ratio? Are the terms sequential perfect squares or cubes? Are the terms obtained by adding or subtracting the previous terms in some way?
Example: The first five terms of a sequence are 2, 5, 8, 11, and 14. If the sequence continues in the same manner, what is its 50th term?
The terms shown have a common difference of 3 with first term a1 = 2. If this pattern continues in the same manner, the general term is a1 + (n – 1)d = 2 + (n – 1)(3). Thus, the 50th term is a50 = 2 + (50 – 1)(3) = 2 + (49)(3) = 149.
Word Problem Drill
Directions: Select the best answer choice.
1. A candy store owner mixes candy that normally sells for $15.00 per pound and candy that normally sells for $22.50 per pound to make a 90-pound mixture to sell at $18.00 per pound. To make sure that $18.00 per pound is a fair price, how many pounds of the $15.00 candy should the owner use?
 30
30
 36
36
 42
42
 50
50
 54
54
2. Elaine is twice as hold as Trevor. In five years, Trevor will be  as old as Elaine. How old, in years, will Trevor be in five years?
as old as Elaine. How old, in years, will Trevor be in five years?
 20
20
 25
25
 30
30
 40
40
 45
45
3. A collection of 33 U.S. coins amounts to $4.35. If the collection consists of only dimes and quarters and contains no rare coins, how many dimes are in the collection?
 7
7
 13
13
 23
23
 26
26
 30
30
4. A chemist is making a 50% alcohol solution. How many milliliters of distilled water must the chemist add to 1,000 milliliters of a 70% alcohol solution to obtain a 50% solution?
 200
200
 400
400
 600
600
 800
800
 1,000
1,000
5. An investor receives interest on two simple-interest investments, one at 2.5% annually, and the other at 1.5% annually. The two investments together earn $460 annually. If the amount invested at 2.5% is $10,000, how much money is invested at 1.5%?
 $10,000
$10,000
 $12,000
$12,000
 $14,000
$14,000
 $16,000
$16,000
 $18,000
$18,000
6. Two vehicles leave the same location at exactly the same time, one traveling due west at r miles per hour and the other traveling due east at r + 20 miles per hour. In terms of r and d, what is t, the number of hours for the two vehicles to be d miles apart?
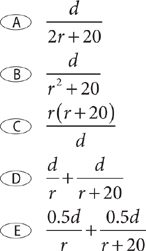
7. Working alone, Angus can paint two rooms in 5 hours. Dimitri working alone can do the same job in 3 hours. If Angus and Dimitri work together, how much time, in hours, should it take them to paint the two rooms?
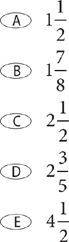
8. Twice the sum of three consecutive integers is 42 more than twice the sum of the first and third integer. Find the value of the second integer.
 19
19
 20
20
 21
21
 22
22
 23
23
9. If the sum of two numbers is 30 and their product is 224, what is the greater number?
 12
12
 14
14
 16
16
 18
18
 20
20
10. A 24-pound mixture of nuts contains peanuts, pecans, and almonds by weight in the ratio 5:2:1, respectively. What is the amount, in pounds, of pecans in the mixture?
 2
2
 3
3
 6
6
 9
9
 12
12
11. Helene and Yannick both swam in the indoor pool at the YOLO Fitness Gym today. Helene swims at YOLO Fitness Gym every 12 days. Yannick swims there every 15 days. If both continue with their regular swimming schedule at YOLO Fitness Gym, the next time both will swim there on the same day is in how many days?
 15
15
 30
30
 60
60
 120
120
 180
180
12. In triangle ABC, the measure of ∠A is 25 degrees more than the measure of ∠B, and the measure of ∠C is 9 degrees less than twice the measure of ∠B. What is the measure of the largest angle?
 36°
36°
 41°
41°
 66°
66°
 73°
73°
 82°
82°
13. A rhombus has sides of length 20 inches, and the measure of one interior angle is 150°. What is the area of the rhombus in square inches?
 400
400
 200
200
 100
100
 80
80
 60
60
14. Two jars of the same brand of blueberry jam have cylindrical shapes. One jar is twice the height of the other jar, but its diameter is one-half the diameter of the shorter jar. What is the ratio of the volume of the taller jar to the volume of the shorter jar?
 1:1
1:1
 1:2
1:2
 1:4
1:4
 2:1
2:1
 4:1
4:1
15. A bank offers its business customers two different plans for monthly charges on checking accounts. With Plan A, the account holder pays a fee of $0.15 per check processed during the month with no monthly service charge on the account. With Plan B, the account holder pays a $10.00 monthly service charge with a fee of $0.05 per check processed during the month. Find the break-even point for the two plans. That is, find the number of checks processed per month for which the costs of the two plans are equal.
 40
40
 50
50
 60
60
 80
80
 100
100
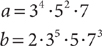
16. For a and b shown above, which of the following expressions represents the greatest common factor of a and b?
 5·7
5·7
 2·3·5·7
2·3·5·7
 34 ·5·7
34 ·5·7
 2·34 ·52 ·73.
2·34 ·52 ·73.
 2·39 ·53 ·74
2·39 ·53 ·74
17. For which of the following numbers would division by 8 result in a remainder of 0?
I. 27,531,808
II. 19,999,064
III. 21,750,548
 I only
I only
 I and II only
I and II only
 I and III only
I and III only
 II and III only
II and III only
 I, II, and III
I, II, and III
Questions 18 to 25 each presents a question and two statements, labeled (1) and (2), in which certain data are given. Using your knowledge of mathematics and everyday facts (such as the number of minutes in an hour or the meaning of the word perpendicular), decide whether the given data are sufficient to answer the question. Then select one of the answer choices that follow.
18. What is the value of a100 if an = a1 + (n – 1)d?
(1) a5 = 30
(2) a20 = 105
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
19. Member of a club are electing a president, a vice-president, and a treasurer. If each club member is eligible for each position and no one can hold two positions, is the number of possible different outcomes greater than 900?
(1) The number of members in the club is greater than 10.
(2) After a president is elected, there are 11 members left from which to choose the other two positions.
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
20. Two vehicles leave the same location at exactly the same time, the first traveling due west and the second traveling due east. In how many hours will the two vehicles be 390 miles apart?
(1) The average speed of the first vehicle is 10 miles per hour faster than the average speed of the second vehicle.
(2) When the two vehicles are 390 miles apart, the second vehicle has gone a distance of 180 miles.
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
21. A sporting goods store marks up the price of an exercise bike from its original cost. What percent of the selling price is the markup?
(1) The selling price of the exercise bike is $450.
(2) The markup on the exercise bike is 25% of the original cost.
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
22. Given consecutive integers a, b, and c, is c > 40?
(1) a + b + c = 126
(2) a < b < c
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
23. Is the prime number x a factor of 48?
(1) x is a factor of 10.
(2) x is a factor of 28.
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
24. How high up the wall will the wire reach?
(1) The wire is anchored on the ground 9 feet from the base of the wall.
(2) The wire is 15 feet long.
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
25. In a social club, the number of members is 56. How many female members are in the club?
(1) The ratio of male members to female members in the club is 3 to 5.
(2) If four additional male members are recruited to the club while the number of female members remains unchanged, the ratio of male members to the number of members in the club will be 5 to 12.
 Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
 Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
 BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
 EACH statement ALONE is sufficient.
EACH statement ALONE is sufficient.
 Statements (1) and (2) TOGETHER are NOT sufficient.
Statements (1) and (2) TOGETHER are NOT sufficient.
Answers
1. E Let x = the number of pounds of the candy priced at $15.00 per pound needed. Then 90 – x = the number of pounds of the candy priced at $22.50 per pound needed. Make a table to organize the candy information in the question.
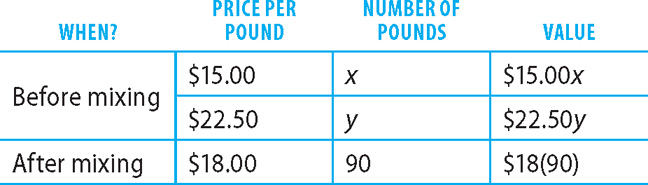
The total number of pounds is 90. The value of the candy before it is mixed should equal the value after it is mixed. Using the table, write two equations that represent the facts (omitting “pounds” and “per pound” because these units cancel each other).
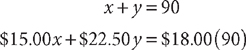
Solve the system, omitting the units for convenience.
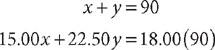
Using the method of substitution, solve the first equation, x + y = 90, for y in terms of x.
y = 90 – x
Substitute the result into the second equation and solve for x.
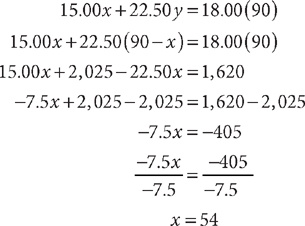
The candy store owner should use 54 pounds of the $15.00 candy.
2. B Let T = Trevor’s age now, in years. Then 2T = Elaine’s age now, in years. Make a table to organize the age information.

Write an equation that represents the facts given.
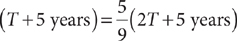
Solve the equation, omitting the units for convenience.
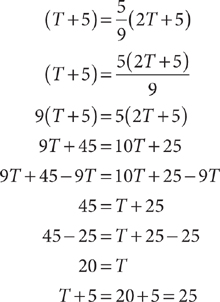
Trevor will be 25 years old in 5 years.
3. D Let d = the number of dimes. Let q = the number of quarters. Make a table to organize the coin information in the question.

Using the table, write two equations that represent the facts.
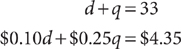
Solve the system, omitting the units for convenience.
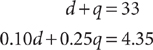
Using the method of substitution, solve the first equation, d + q = 33, for q in terms of d.
q = 33 – d
Substitute the result into the second equation and solve for d.
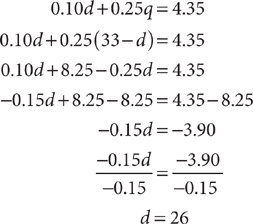
There are 26 dimes in the collection.
4. B Let x = the number of milliliters of distilled water to be added. Make a table to organize the information in the question.
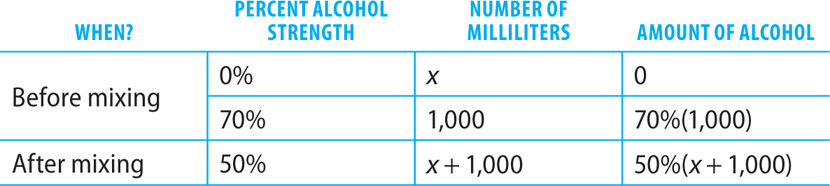
The amount of alcohol before mixing equals the amount of alcohol after mixing. Write an equation that represents the facts shown in the table.
70%(1,000) = 50%(x + 1,000)
Solve the equation.
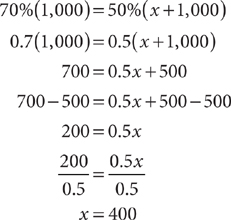
The chemist must add 400 milliliters of distilled water.
5. C Let x = the amount invested at 1.5% annually. Make a table to organize the investment information.
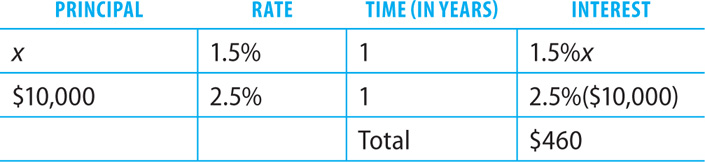
Using the information in the table, write an equation to represent the facts.
1.5%x + 2.5%($10,000) = $460
Solve the equation, omitting the units for convenience.
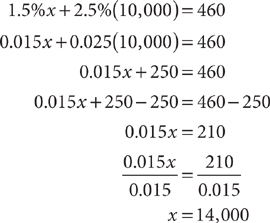
The amount invested at 1.5% is $14,000.
6. A Make a table to organize the vehicle information in the question.

Using the information in the table, set up an equation and solve for t.
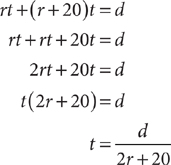
7. B Omitting the units, calculate 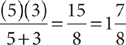 . The time it will take Angus and Dimitri, working together, to paint the two rooms is
. The time it will take Angus and Dimitri, working together, to paint the two rooms is 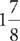 hours. You should eliminate choice E at the outset because the time for Angus and Dimitri working together should be less than either of their times working alone.
hours. You should eliminate choice E at the outset because the time for Angus and Dimitri working together should be less than either of their times working alone.
8. C Let n = the first integer, n + 1 = the second integer, and n + 2 = the third integer. Write an equation that represents the facts given in the question.
2[n + (n + 1) + (n + 2)] = 2[n + (n + 2)] + 42
Solve the equation.
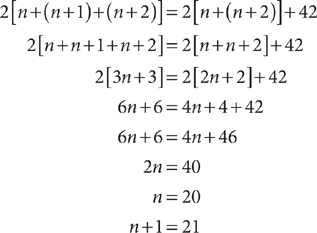
The second integer is 21.
9. C Let x = the greater number and y = the lesser number. Write two equations that represent the facts given in the question.
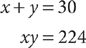
Check the answer choices to solve.
Check C. If x is 16, then x + y = 16 + y = 30. So y is 30 – 16 = 14; and xy is (16)(14) = 224. Thus, C is correct.
10. C Let x = the amount, in pounds, of almonds in the mixture, 2x = the amount, in pounds, of pecans in the mixture, and 5x = the amount, in pounds, of peanuts in the mixture. Using the information in the question, write an equation and solve.
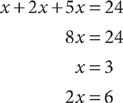
The amount of pecans in the mixture is 6 pounds.
11. C The number of days until the next time is LCM (12, 15) = 60. It will be 60 days before Helene and Yannick both will swim at YOLO Fitness Gym on the same day.
12. D Let x = m ∠B. Then x ∠A + x = 25° = ∠A, and 2x – 9° = m∠C. Given that the angles of a triangle sum to 180°, write an equation and solve, omitting the units for convenience.
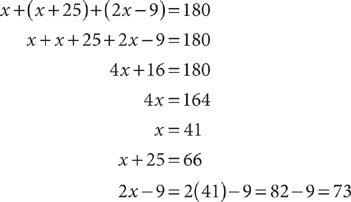
The largest angle has measure 73°.
13. B Make a sketch, filling in the information given in the question.
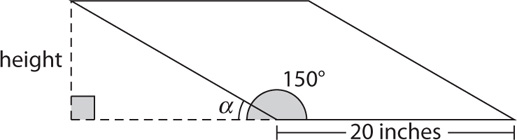
The area is base times height. Angle a = 180° – 150° = 30°. The indicated height is the side opposite the 30° angle in a 30°-60°-90° right triangle. Thus, the height, in inches, is 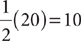 , and the area in square inches is (20)(10)= 200.
, and the area in square inches is (20)(10)= 200.
14. B Let h = height of the shorter jar; then 2h = height of the taller jar. Let r = radius of the taller jar; then 2r = radius of the shorter jar. (The relationship between the radii is the same as that between the diameters.) Find the ratio of Vtaller, the volume of the taller jar, to Vshorter, the volume of the smaller jar:
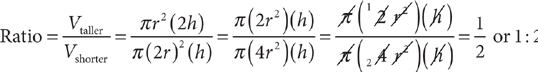
15. E Let x = the number of checks processed per month. For Plan A, the monthly cost is $0.15x. For Plan B, the monthly cost is $0.05x + $10. To find the break-even point, set the costs of the two plans equal to each other and solve for x, omitting the units for convenience.
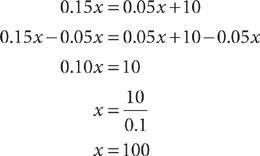
The break-even point for the two plans occurs when the number of checks processed per month is 100 checks.
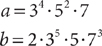
16. C Because a and b have common factors of 34, 5, and 7, the GCF of a and b is 34 ·5·7.
17. B A number is divisible by 8 if the last three digits form a number that is divisible by 8. The numbers in (I) and (II) are divisible by 8 because 808 and 064 are divisible by 8. The number in (III) is not divisible by 8, because 548 is not divisible by 8. Thus, choice B is correct.
18. C From the question information, a100 = a1 +(100–1)d = a1 +(99)d, so you need the values of a1 and d to determine a100. From the information in (1), a5 = 30 = a1 + 4d, which (because you have two variables and only one equation) does not yield single values for a1 and d, so (1) is NOT sufficient. From the information in (2), a20 = 105 = a1 + 19d, which (because you have two variables and only one equation) does not yield single values for a1 and d, so (2) also is NOT sufficient. Taking (1) and (2) together, you have two linear equations and two variables, which you can solve simultaneously to determine values for a1 and d, and you can use that solution to determine a100. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
19. D Let n = the number of members in the club. From the question information, the number of possible outcomes is n(n – 1)(n – 2). From the information in (1), you can determine that n > 10. Therefore, you know that n is at least 11, and the number of possible outcomes is at least 11(10)(9) = 990. Thus, (1) is SUFFICIENT. From the information in (2), you can determine that n is 12, which you can substitute into n(n – 1) × (n – 2) to obtain 12(11)(10) = 1320. Thus, (2) also is sufficient. Therefore, EACH statement ALONE is sufficient.
20. C Let t = the number of hours in which the two vehicles will be 390 miles apart, x = the speed of the first vehicle, and y = the speed of the second vehicle. Omitting the units, the equation xt + yt = 390 expresses the conditions given in the question, so 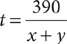 . From the information in (1),x = 10 + y, so
. From the information in (1),x = 10 + y, so 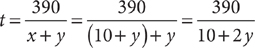 , but without knowing the value of y, you cannot determine the value of
, but without knowing the value of y, you cannot determine the value of 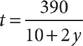 . Therefore, (1) is NOT sufficient. From the information in (2), yt = 180, which implies that
. Therefore, (1) is NOT sufficient. From the information in (2), yt = 180, which implies that 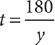 , but without knowing the value of y, you cannot determine the value of
, but without knowing the value of y, you cannot determine the value of 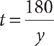 , so (2) is NOT sufficient. Taking (1) and (2) together, you can set the two expressions for t equal to each other, giving
, so (2) is NOT sufficient. Taking (1) and (2) together, you can set the two expressions for t equal to each other, giving 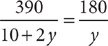 , which you can solve for y. Then you can determine the value of t, using either
, which you can solve for y. Then you can determine the value of t, using either 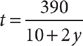 or
or 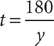 . Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
21. B Let c = the original cost of the exercise bike, m = the markup, and s = c + m = the selling price. Then the markup is 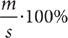 of the selling price. From the information in (1),
of the selling price. From the information in (1), 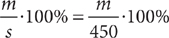 , but without knowing m, you cannot compute the percent, so (1) is NOT sufficient. From the information in (2), m = 25%c = 0.25c and s = c + m = c + 0.25c = 1.25c. Then
, but without knowing m, you cannot compute the percent, so (1) is NOT sufficient. From the information in (2), m = 25%c = 0.25c and s = c + m = c + 0.25c = 1.25c. Then 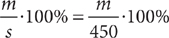 , which you can compute, so (2) is SUFFICIENT. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
, which you can compute, so (2) is SUFFICIENT. Therefore, statement (2) ALONE is sufficient, but statement (1) alone is not sufficient.
22. A Using the information in (1), you can divide the sum by 3 to obtain the value of the middle integer. Using that value, you can obtain the values of the other two integers. Therefore, you have sufficient information to answer definitely “yes” or “no” as to whether c > 40, so (1) is SUFFICIENT. Tip: Notice that it is not necessary to perform calculations to answer the question posed. You should avoid taking time to do unnecessary calculations. However, just for your information, the three integers are 41, 42, and 43, all of which are greater than 40. The information in (2) lets you know the order of the three integers, but it does not provide sufficient information for you to determine whether c > 40. So, (2) is NOT sufficient. Therefore, statement (1) ALONE is sufficient, but statement (2) alone is not sufficient.
23. C From the information in (1), you can determine that x is 2 or 5, the prime factors of 10. If x is 2, then the answer to the question posed is yes, but if x is 5, the answer is no. Thus, (1) is NOT sufficient. From the information in (2), you can determine that x is 2 or 7, the prime factors of 28. If x is 2, then the answer to the question posed is yes, but if x is 7, the answer is no. Thus, (1) is NOT sufficient. Taking (1) and (2) together, x is 2, which is also a factor of 2(10) + 1(28) = 20 + 28 = 48. Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
24. C Make a rough sketch.
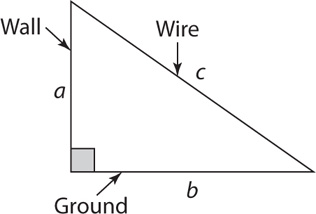
The wire makes a right triangle with portions a and b of the wall and ground, respectively. From the information in (1), you can determine that b is 9 feet, but without further information you cannot determine a, the distance up the wall. Thus, (1) is NOT sufficient. From the information in (2), you can determine that c is 15 feet, but without further information you cannot determine a, the distance up the wall. Thus, (2) is NOT sufficient. Taking (1) and (2) together, you have b = 9 feet and c = 15 feet. Because 9 = 3(3) and 15 = 3(5), you can use your knowledge of 3-4-5 triangles to determine a (or you can determine a using the Pythagorean theorem). Therefore, BOTH statements together are sufficient, but NEITHER statement ALONE is sufficient.
25. D Let f = the number of female members in the club and m = the number of male members in the club. Then from the question information, f + m = 56. From the information in (1), 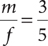 , which is equivalent to 5m = 3f. This equation and the equation f + m = 56 give you two linear equations with two variables, which you can solve simultaneously for a single value of f, so (1) is SUFFICIENT. From the information in (2),
, which is equivalent to 5m = 3f. This equation and the equation f + m = 56 give you two linear equations with two variables, which you can solve simultaneously for a single value of f, so (1) is SUFFICIENT. From the information in (2), 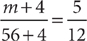 , which you can solve for m. Then you can substitute the value of m into f + m = 56 to find f, so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
, which you can solve for m. Then you can substitute the value of m into f + m = 56 to find f, so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
 Problem-solving process
Problem-solving process Representing verbal phrases and statements
Representing verbal phrases and statements Consecutive Numbers
Consecutive Numbers Ratios and proportions
Ratios and proportions Percentage
Percentage Simple interest
Simple interest Ages
Ages Mixtures
Mixtures Coins
Coins Distance-rate-time
Distance-rate-time Work
Work Right triangles
Right triangles Divisors and factors
Divisors and factors Greatest common factor and least common multiple
Greatest common factor and least common multiple Permutations and combinations
Permutations and combinations Sequences
Sequences
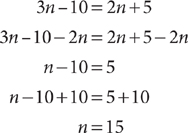
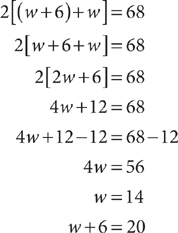
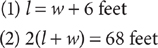
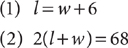
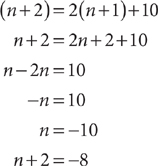
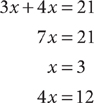
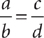 is a proportion and is read “a is to b as c is to d.” The fundamental property of proportions is that
is a proportion and is read “a is to b as c is to d.” The fundamental property of proportions is that 
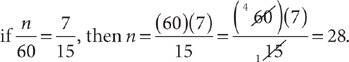
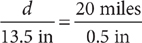
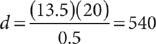
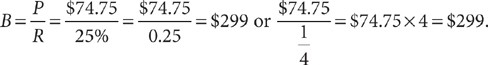

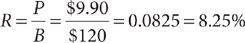

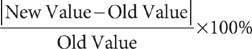
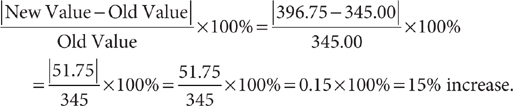
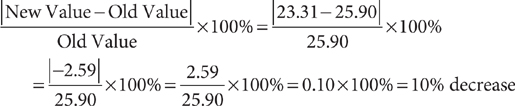

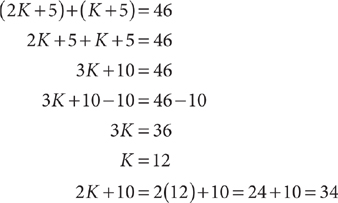

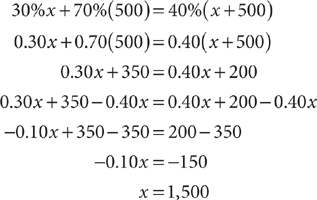

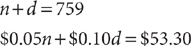
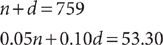
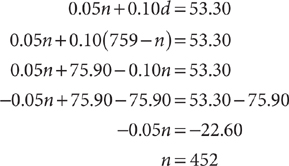


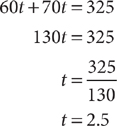
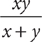
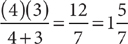 . The time it will take Dylan and Jeremy, working together, to paint the hallway is
. The time it will take Dylan and Jeremy, working together, to paint the hallway is 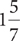 hours.
hours.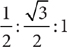 or, equivalently,
or, equivalently, 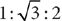 .
.
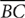 is opposite the 30° angle. Therefore,
is opposite the 30° angle. Therefore, 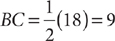 .
.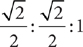 or, equivalently,
or, equivalently, 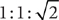 .
.
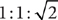 . Therefore, the length of the hypotenuse is
. Therefore, the length of the hypotenuse is 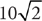 .
.
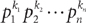 , where the p’s are distinct positive prime numbers and the k’s are their corresponding exponents, then the number of positive factors (or divisors) of n is the product (k1 + 1)(k2 + 1)…(kn + 1). For example, the number of positive factors (or divisors) of n = a4b2c5d, where a, b, c, and d are prime numbers, is (4 + 1)(2 + 1)(5 + 1)(1 + 1) = (5)(3)(6)(2) = 180.
, where the p’s are distinct positive prime numbers and the k’s are their corresponding exponents, then the number of positive factors (or divisors) of n is the product (k1 + 1)(k2 + 1)…(kn + 1). For example, the number of positive factors (or divisors) of n = a4b2c5d, where a, b, c, and d are prime numbers, is (4 + 1)(2 + 1)(5 + 1)(1 + 1) = (5)(3)(6)(2) = 180.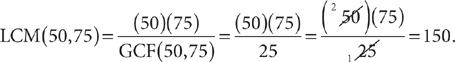
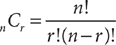
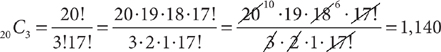
 30
30 36
36 42
42 50
50 54
54 as old as Elaine. How old, in years, will Trevor be in five years?
as old as Elaine. How old, in years, will Trevor be in five years?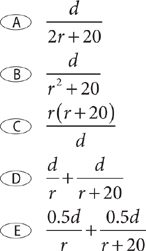
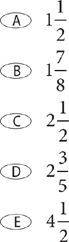
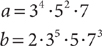

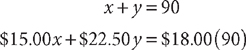
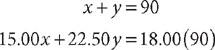
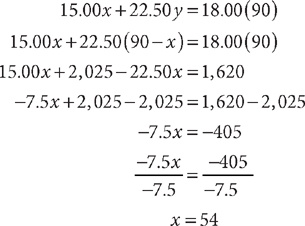

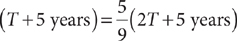
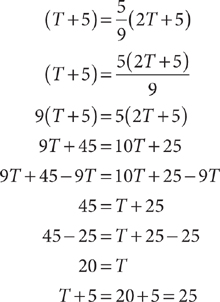

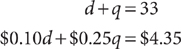
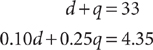
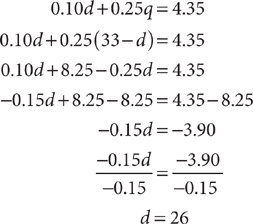

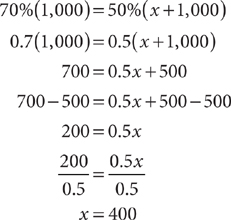

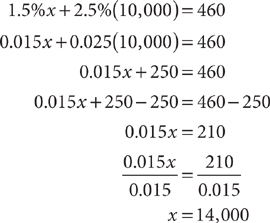

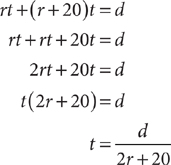
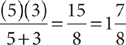 . The time it will take Angus and Dimitri, working together, to paint the two rooms is
. The time it will take Angus and Dimitri, working together, to paint the two rooms is 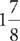 hours. You should eliminate choice E at the outset because the time for Angus and Dimitri working together should be less than either of their times working alone.
hours. You should eliminate choice E at the outset because the time for Angus and Dimitri working together should be less than either of their times working alone.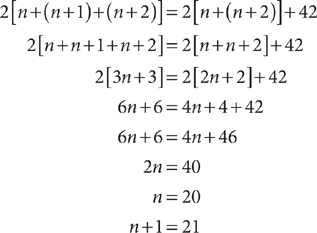
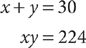
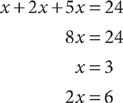
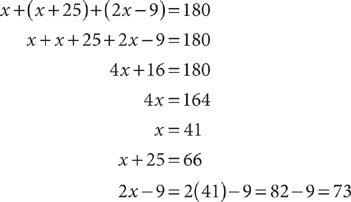

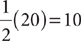 , and the area in square inches is (20)(10)= 200.
, and the area in square inches is (20)(10)= 200.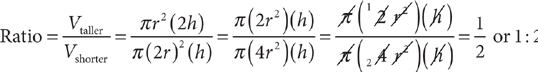
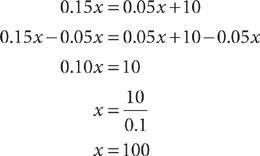
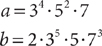
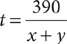 . From the information in (1),x = 10 + y, so
. From the information in (1),x = 10 + y, so 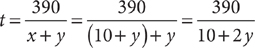 , but without knowing the value of y, you cannot determine the value of
, but without knowing the value of y, you cannot determine the value of 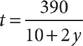 . Therefore, (1) is NOT sufficient. From the information in (2), yt = 180, which implies that
. Therefore, (1) is NOT sufficient. From the information in (2), yt = 180, which implies that 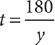 , but without knowing the value of y, you cannot determine the value of
, but without knowing the value of y, you cannot determine the value of 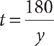 , so (2) is NOT sufficient. Taking (1) and (2) together, you can set the two expressions for t equal to each other, giving
, so (2) is NOT sufficient. Taking (1) and (2) together, you can set the two expressions for t equal to each other, giving 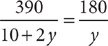 , which you can solve for y. Then you can determine the value of t, using either
, which you can solve for y. Then you can determine the value of t, using either 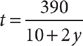 or
or 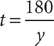 . Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.
. Therefore, BOTH statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient.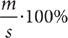 of the selling price. From the information in (1),
of the selling price. From the information in (1), 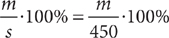 , but without knowing m, you cannot compute the percent, so (1) is NOT sufficient. From the information in (2), m = 25%c = 0.25c and s = c + m = c + 0.25c = 1.25c. Then
, but without knowing m, you cannot compute the percent, so (1) is NOT sufficient. From the information in (2), m = 25%c = 0.25c and s = c + m = c + 0.25c = 1.25c. Then 
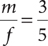 , which is equivalent to 5m = 3f. This equation and the equation f + m = 56 give you two linear equations with two variables, which you can solve simultaneously for a single value of f, so (1) is SUFFICIENT. From the information in (2),
, which is equivalent to 5m = 3f. This equation and the equation f + m = 56 give you two linear equations with two variables, which you can solve simultaneously for a single value of f, so (1) is SUFFICIENT. From the information in (2), 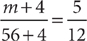 , which you can solve for m. Then you can substitute the value of m into f + m = 56 to find f, so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.
, which you can solve for m. Then you can substitute the value of m into f + m = 56 to find f, so (2) also is SUFFICIENT. Therefore, EACH statement ALONE is sufficient.