ONE-VALUED FUNCTIONS OF A COMPLEX VARIABLE
The meaning of the word “convergent” as applied to series of real numbers has been given in Ch. V., p. 77. A general discussion of the principles of convergence is reserved for the companion volume on Analysis. We give here only what is necessary for the extension of the idea to series of complex numbers.
Absolutely Convergent Series. If the series, ∑|xn|, of positive real numbers
![]()
is convergent, we say that the series, ∑|xn|, of real numbers
![]()
is absolutely convergent.
Thus the series,
![]()
is absolutely convergent, because it is shown on p. 210 that the series, ![]() , is convergent.
, is convergent.
If a series is absolutely convergent, it is necessarily convergent. This may be seen by expressing it as the “difference” between two convergent series ; thus,
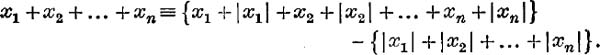
Since ∑|xn| is convergent, the second bracket tends to a limit, say V, when n → ∞; also 0 ≤ (xn + |xn|) ≤ 2|xn|; ![]() the first bracket never decreases as n increases and is always less than 2V ; it therefore tends to a limit ≤ 2V, when n → ∞;
the first bracket never decreases as n increases and is always less than 2V ; it therefore tends to a limit ≤ 2V, when n → ∞; ![]() ∑ xn is convergent.
∑ xn is convergent.
Thus the convergence of ![]() implies the convergence of
implies the convergence of
![]()
But obviously a series may be convergent without being absolutely convergent; for example, ![]() is convergent, with sum to infinity log 2 ; but the series,
is convergent, with sum to infinity log 2 ; but the series, ![]() is divergent, see p. 69. A series which, is convergent, but not absolutely convergent, is called conditionally convergent or sometimes semi-convergent.
is divergent, see p. 69. A series which, is convergent, but not absolutely convergent, is called conditionally convergent or sometimes semi-convergent.
Series of Complex Terms. Consider the series ∑ zn, of complex numbers
![]()
where zn = xn + iyn, and xn, yn are real numbers.
This series is called convergent if the series ∑ xn and ∑ yn are both convergent. If X and Y are the sums to infinity of these series, so that
![]()
X+iY is called the sum to infinity of the series ∑ zn.
For example, since
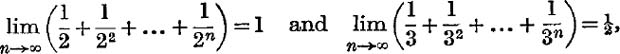
we say that the series
![]()
is convergent, with sum to infinity ![]() .
.
More shortly, we may say that ∑ zn is convergent if
![]()
tends to a limit Z when n → ∞, for this only means that
![]()
tend to limits X and Y and that X + iY is denoted by Z.
Absolute Convergence of Series of Complex Terms. If
![]()
and if the series, ∑ |zn|, of positive real numbers
![]()
is convergent, we say that the series, ∑ zn, of complex numbers
![]()
is absolutely convergent, and it is easy to see that it is then necessarily “ convergent,” in the sense defined above.
For ![]() and similarly | yn | ≤ | zn |; therefore ∑ xn and ∑ yn are absolutely convergent;
and similarly | yn | ≤ | zn |; therefore ∑ xn and ∑ yn are absolutely convergent; ![]() they are convergent;
they are convergent; ![]() ∑ zn is convergent.
∑ zn is convergent.
The Geometric Progression Consider the series
![]()
where z ≡ r (cos θ + i sin θ).
If ϕ(z) ≡ 1 + z + z2 + … + zn–1, we have, as for the G.P. of real numbers, ![]() , provided z ≠ 1.
, provided z ≠ 1.
Hence this series is convergent, and has ![]() for sum to infinity, if
for sum to infinity, if 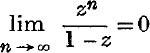 , i.e. if
, i.e. if ![]() , since z ≠ 1.
, since z ≠ 1.
Now zn = rn (cos nθ + i sin nθ) and r is positive. Also if r < 1, lim rn = 0, see p. 78; but |rn cos nθ| ≤ rn and |rn sin nθ| ≤ rn, ![]() if r < 1, lim (rn cos nθ) = 0 and lim (rn sin nθ) = 0 ;
if r < 1, lim (rn cos nθ) = 0 and lim (rn sin nθ) = 0 ; ![]() lim zn = 0.
lim zn = 0.
Thus the geometric progression of complex numbers is convergent when |z| < 1, that is, if it is absolutely convergent.
The values of ϕn(z) and ![]() in terms of r and θ were virtually obtained in Ch. IX., p. 174, where x was used instead of r.
in terms of r and θ were virtually obtained in Ch. IX., p. 174, where x was used instead of r.
The Exponential Series. Consider the series
![]()
where z ≡ x + iy = r(cos θ + i sin θ) and r > 0.
It has been proved in Ch. V that the series of positive numbers
![]()
is convergent for all values of r. Thus the series (1) is absolutely convergent and therefore it is convergent.
In other words, if
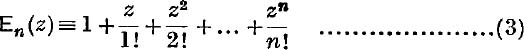
then ![]() exists, for all values of z. This limit may be denoted by E(z), thus
exists, for all values of z. This limit may be denoted by E(z), thus
![]()
If z ≡ x + 0i, the function E(z) corresponds to the function exp (x) of the real variable x, see Ch. V., p. 90, in just the same way that the complex number x + 0i corresponds to the real number x.
For this reason, the function E (z) is usually written exp (z), but it should be understood that exp (z), so used, acquires its meaning by definition as a function of complex algebra. In fact, the definition of equation (41) is replaced by the following definition:
![]()
Proofs of the properties of exp (z) must be based on this definition ; it is not permissible to assume that the properties established for exp (x) hold also for exp (z).
Functional Law for exp (z). If z ≡ 0 + yi, the exponential series is
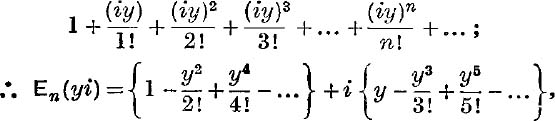
where the series in brackets are finite.
But, by pp. 80, 81, when n → ∞, the expressions in these two brackets tend to cos y and sin y;
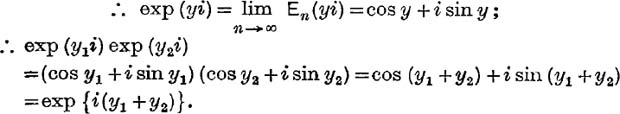
If then z1, z2 are each of the form 0 + iy, the exponential function, exp (z), satisfies the functional law,
![]()
We proceed to prove that this result is true for all complex values of z.
Let z1 ≡ x1 + iy1, z2 ≡ x2 + iy2, and |z1| = r1, |z2| = r2.
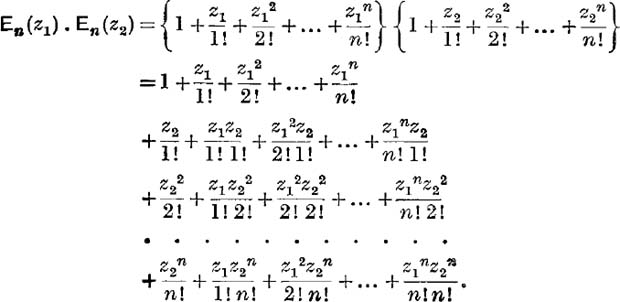
Add up by diagonals ; the terms of order s, where s ≤ n,. give
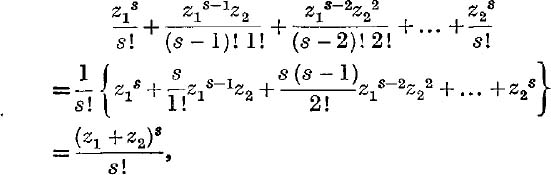
by the binomial theorem for a positive integral index.
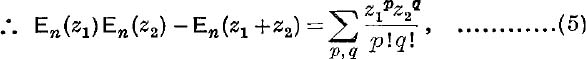
where the summation extends to all values of p, q such that p + q > n, p≤ n, q ≤ n.
In precisely the same way, we have
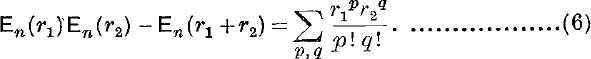
Now from Ch. V., p. 91, when n → ∞, En(r1), En(r2), En(r1 + r2) tend to the limits er1, er2, er1+r2; but er1 er2 = er1+r2;
![]()
Now each term of the ∑ expression in (6) is the modulus of the corresponding term of the ∑ expression in (5) ; also the modulus of a sum ≤ the sum of the moduli;
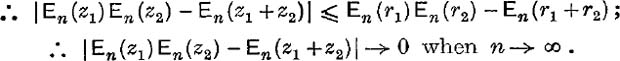
But, when n → ∞, En(z1), En(z2), En(z1 + z2) tend respectively to the limits exp (z1), exp (z2), exp (z1 + z2);
![]()
where z1, z2 are any two complex numbers.
This proof of the functional law for exp (z) suggests an alternative method for developing the theory of the exponential function of a real variable.
We start by proving from first principles that, for all real values of x,
![]()
is an absolutely convergent series. Denote its sum to infinity by E (x).
From equation (6) above, we have, for r1 > 0, r2 > 0,
![]()
Similarly, the product set out above shows that
![]()
equals the sum of a number of positive terms ;
![]()
![]() from (8) and (9), En (r1), En (r2), En (r1 + r2),E2n (r1 + r2).
from (8) and (9), En (r1), En (r2), En (r1 + r2),E2n (r1 + r2).
But when n → ∞, En(r1), En(r2), En(r1 + r2), E2n(r1 + r2) tend respectively to the limits E (r1), E(r2), E(r1 + r2), E(r1 + r2);
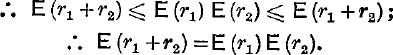
The properties of the exponential function of a real variable can then be deduced from this functional law.
Expression of esp (z) in the Modulus-Ampiitude Form. By equation (7), exp (z) = exp (x + iy) = exp (x + 0i) exp (0 + iy).
But
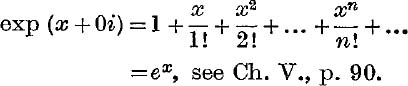
Also, by p. 192, ![]()
![]() exp (z) is a complex number, with modulus ex and amplitude 2nπ + y, and we write
exp (z) is a complex number, with modulus ex and amplitude 2nπ + y, and we write
![]()
Thus we see that the function exp (z) is periodic, with period 2πi. The principal value of the amplitude of exp (x + iy) is obtained by choice of n such that – π < 2nπ + y ≤ π.
The special relations,
![]()
give important forms for cos y and sin y :
![]()
![]()
These forms, however, are merely alternative ways of writing equations (6) and (5) in Ch. V. (pp. 80, 81).
Example 1. Express exp (iα) exp (x cis β), (i) in the modulusamplitude form, (ii) as a power series in x.
What conclusions can be drawn by comparing the two results ?
(i) 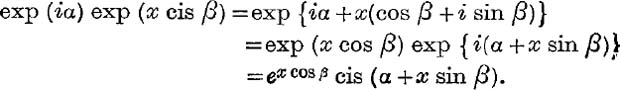
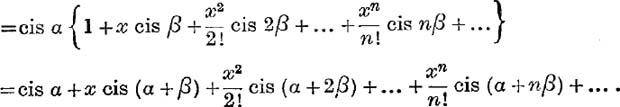
It follows that
![]()
and
![]()
Example 2. Discuss the convergence of the series
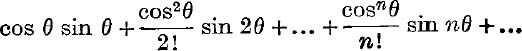
and find the sum to infinity.
Consider the series
![]()
Since |cis nθ| = 1, in the series of moduli the sum to n terms is
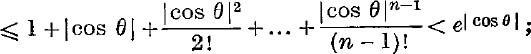
![]() is absolutely convergent. Hence it is vergent, and this implies the convergence of the given series.
is absolutely convergent. Hence it is vergent, and this implies the convergence of the given series.
Also series (i)
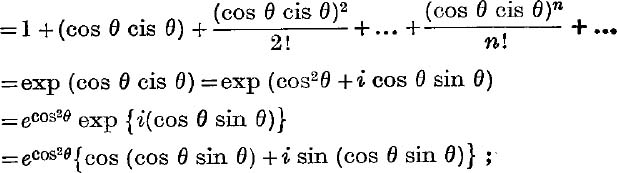
![]() the sum to infinity of the given series = ecos2 θ sin (cos θ sin θ).
the sum to infinity of the given series = ecos2 θ sin (cos θ sin θ).
Note. A direct proof of the absolute convergence of the given series is as follows : | sin nθ| ≤ 1, ![]() the sum to n terms of the series of moduli
the sum to n terms of the series of moduli
![]()
EXERCISE X. a.
Express the following in the form, a + ib :
1. exp (l + iπ).
2. exp (i) + exp (– i).
3. exp (![]() ).
).
4. exp (cos θ + isin θ).
5. exp (a + ib) exp (a – ib).
6. exp (log r + iθ).
7. exp {sec α exp (iα)}.
8. exp (x cis θ) exp (y cis ϕ).
Give simplified values of the following :
9. exp (iπ).
10. exp ( –iπ).
11. exp (cis θ) + exp {cis (– θ)}.
12. exp (cis θ tan θ).
13. exp (i cis θ) – exp {– i cis ( – θ)}.
14. exp {exp (cis θ)}.
15. Prove that exp ( – θ – iϕ) = (ch θ – sh θ) (cos ϕ – i sin ϕ).
16. If X + i Y = exp (x + iy), find the relation between X and Y, (i) if x is constant and equal to c ; (ii) if y is constant and equal to m.
17. Find u, v if 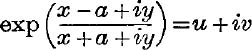 .
.
18. Find u if (1 – a2 cos 2θ – ia2 sin 2θ)–1 exp (iθ) = u + iv.
19. The complex numbers z, z′ are represented by the points P, P′, where z′ = exp (z). Discuss the movement of P, (i) if P′ describes the unit circle, centre the origin, clockwise, starting from the point (– 1, 0), (ii) if P′ describes the negative half of the y′-axis, starting from the origin.
20. Find real numbers a and b such that
![]()
21. Show that the equation, exp x = x + a, where a is real, has no solution of the form, x = iv, where v is real.
If it has a solution, x = u + iv, where v ≠ 0, prove that u is positive.
22. What results can be obtained by equating the first and second parts of the complex numbers in the relation,
![]()
(i) if z = cos α + i sin α;
(ii) if z = 1 + i tan β?
23. Prove that exp [(a + ib)x] – exp [(a – ib)x] = 2i eax sin bx.
Use this relation to find the coefficient of xn when ex cos θ sin (x sin θ) is expanded in powers of x.
24. Express 2eθ cos θ in the form exp (u + iv) + exp (u – iv).
Hence find the coefficient of θn in the expansion of eθ cos θ in powers of θ.
25. Prove that exp {exp (θi)} – exp {– exp (θi)} = a + ib, where a = 2 cos (sin θ) sh (cos θ) and b = 2 sin (sin θ) ch (cos θ).
26. Expand e x sin α sin (x cos α) in ascending powers of x.
Sum to infinity the following series :
27. x cos θ + x2 cos 2θ +x3 cos 3θ + … ; (– 1 < x < 1).
28. x sin α + x2 sin (α + β) + x3 sin (α + 2β) + …; (– l < x < l).
29. ![]() .
.
30. ![]() .
.
31. ![]() .
.
32. ![]() .
.
33. 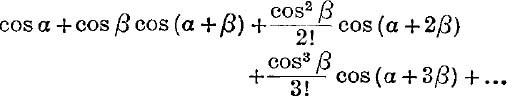 .
.
34. ![]() .
.
35. If ![]() and
and ![]() , prove that C2 + S2 = {ch (cos θ) – cos (sin θ)}2.
, prove that C2 + S2 = {ch (cos θ) – cos (sin θ)}2.
The Generalised Circular Functions. If z is any complex number, cos z and sin z are defined by the relations :
![]()
![]()
Further, we write
![]()
The definitions are equivalent to
![]()
![]()
![]()
The definitions are of course chosen so that formulae established for circular functions of a real variable (defined geometrically) hold also for the generalised functions. The reason that they hold is indicated below :
Results such as cos 0 = 1, sin 0 = 0, cos(–z) = cosz, sin ( – z) = – sin z, are immediately deduced from the definitions, (13), (14) and (42) above.
Suppose it is required to prove that
![]()
Using relations (13), (14) it is necessary to prove that
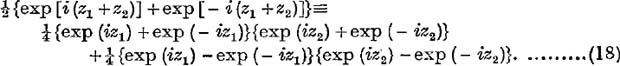
Now we know that, for real values of y1, y2,
![]()
and ![]() from relations (11), (12), p. 194,
from relations (11), (12), p. 194,
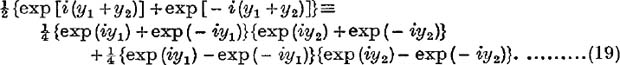
Since the result of simplifying the right side of (19) gives the left side, and since the process of simplification of the right side of (18) corresponds precisely to that of (19), the truth of (19) implies the truth of (18). Hence to every general formula in the trigonometry of the real angle, there corresponds a similar formula for the generalised circular functions of a complex variable.
The Generalised Hyperbolic Functions. If z is any complex number, ch z and sh z are defined by the relations :
![]()
![]()
Further, we write th ![]() , cosech z =
, cosech z = ![]() , etc.
, etc.
These definitions are equivalent to the forms,
![]()
![]()
The definitions are of course chosen so that formulae established for hyperbolic functions of a real variable (see p. 105) hold also for the generalised functions; this fact may bo established by the same method as has just been used for the generalised circular functions.
There is a simple connection between the generalised circular and hyperbolic functions.
![]()
Also
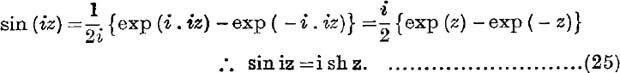
Relations (24), (25) justify the rule given on p. 105 for deducing formulae connecting hyperbolic functions from the corresponding formulae for the circular functions.
For example:
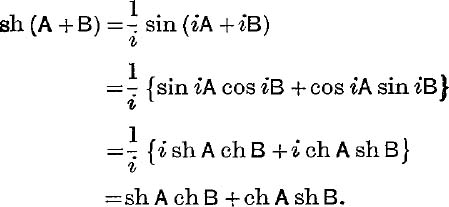
Also a product of sines introduces i2 and so leads to a change of sign in the corresponding formula for hyperbolic functions.
The generalised hyperbolic functions are periodic ; we have from (24) and (25)
![]()
where n is any integer.
Expression of Generalised Circular Functions in the Form, A + iB.
If 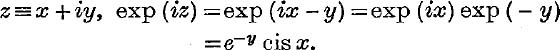
Similarly, exp (– iz) = ey cis ( – x); and so it is easy, by using the definitions (13) and (14), to express cos z and sin z in the form A + iB. But it is more convenient to proceed as follows :
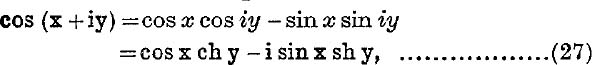
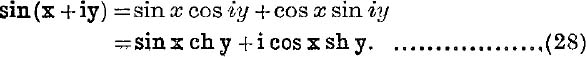
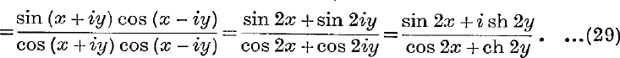
Example 3. If sin (x + iy) = cis α, prove that tan x tan α = th y.
We have also sin (x – iy) = cis ( – a);
![]() by subtraction,
by subtraction, 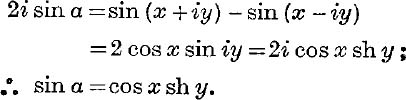
Similarly, by addition, cos α = sin x ch y.
Dividing, we have tan α = cot x th y.
Note. The expressions for sin a and cos a also follow at once from the expansion of sin (x + iy) in (28), viz. cos a + i sin a = sin (x + iy) = sin x ch y + i cos x sh y.
Example 4. Find the sum to infinity of ![]()
Put cis θ for z in equation (23).
Then
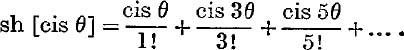
Similarly
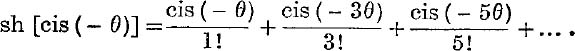
Now cis (nθ) – cis (– nθ) = 2i sin nθ; ![]() by subtraction we get
by subtraction we get
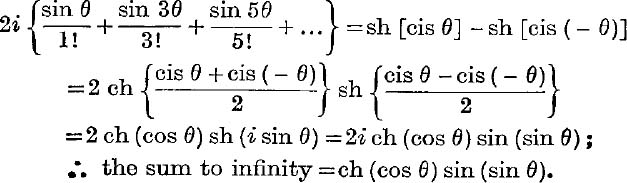
EXERCISE X. b.
1. Deduce the values of cos ![]() and i sin
and i sin ![]() from equations (13), (14).
from equations (13), (14).
2. Verify sin 2z = 2 sin z cos z and cos2z + sin2z = 1 for the generalised functions, directly from the definitions.
3. Prove that ch zi =cos z and sh zi = i sin z.
4. Verify ch(A + B) = ch A ch B + sh A sh B and ![]() , by means of equations (24), (25).
, by means of equations (24), (25).
Express the following in the form a + ib :
5. sin (x – iy).
6. cos2(x + iy).
7. cot (x + iy).
8. ch (x + iy).
9. th (x–iy).
10. cosec (x + iy).
11. exp {sin (x + iy)}.
12. exp {sh (x – iy)}.
13. sh(x – iy) cos (y + ix).
14. Simplify :
(i) ch (x + ![]() );
);
(ii) sh (x + ![]() );
);
(iii) th (x + ![]() );
);
(iv) ch (x + πi);
(v) sh (x + πi);
(vi) th (x + πi).
15. Simplify 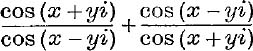 .
.
16. If sin (x + iy) = u + iv prove that
(i) u2 cosec2x – v2 sec2x = 1;
(ii) u2 sech2 y + v2 cosech2 y = l.
17. If cos (x + iy) = cos θ + i sin θ, prove that cos 2x + ch 2y = 2.
18. If tan (x + iy) = u + iv, prove that
(i) (u2 + v2 – 1) tan 2x + 2u = 0;
(ii) (u2 + v2 + l)th 2y – 2v = 0.
19. If ch (x + yi) cos (u + iv) = 1, and if cos y ≠ 0 and cos u ≠ 0, prove that tan u th v = th x tan y.
20. If sin (x + iy) = tan (u + iv), prove that 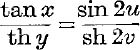 .
.
21. If x + yi = c ch (α + iβ), find the locus of the point (x, y), (i) when α is constant, and (ii) when β is constant. Prove that the loci cut orthogonally.
22. If x + yi = (α + iβ)2 find the loci of (x, y) for α constant and for β constant.
23. If x + yi = f(α + iβ) show that the loci of (x, y) for α constant and β constant cut orthogonally. [Assume that f denotes a function with differential coefficients, and that 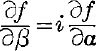 .]
.]
Sum to infinity the following series :
24. ![]() .
.
25. ![]()
26. ![]() .
.
27. ![]() .
.
28. ![]() .
.
29. If z is any complex number, prove that exp (cos z) sin (sin z) is the sum to infinity of ![]() .
.
30. If z is any complex number, express in series of powers of z:
(i) cos z ch z;
(i) sin z ch z;
MISCELLANEOUS EXAMPLES
EXEECISE X. c.
Express the following in the form a + ib:
1. exp {![]() }.
}.
2. exp {(x + iy)2}.
3. tan ![]() .
.
4. sec (x + iy).
5. cosec (x – iy).
6. cosech (x – iy).
7. If sin (α + iβ) = cos θ + isin θ, prove that
![]()
8. If ![]() , prove that
, prove that
(i)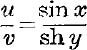 ;
;
(ii) (1 – u2 – v2)ch y = (1 + u2 + v2)cos x.
9. If th x = sin a sech b and tan y = sec a sh b, express ch (x + yi) in terms of a and b.
10. If a exp (θi) + b exp (– 3θi) = c, where a, b, c are real numbers, prove that either a + b = ±c or (a – b)(a2 – b2) = bc2.
Find the sums to infinity of the following series :
11. x sh α + x2 sh 2α + x3 sh 3α + … .
12. 1 – x cos α + x2 cos(α + β) – … .
13. ![]() .
.
14. ![]() .
.
15. ![]() .
.
16. ![]() .
.
17. Prove that ![]() .
.
19. Expand eax cos bx in a series of powers of x.
20. If Z = X + iY, z = x + iy, 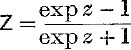 , and
, and ![]() prove that X2 + Y2 < 1.
prove that X2 + Y2 < 1.
21. Find the value of sin α sin β where α and β are the roots of 2x2 – 2xπ + π2 = 0.
22. Simplify exp {exp( θi)} – exp {– exp (– θi)}.
23. Expand excosβ sin (α + x sinβ) in a series of powers of x.
Find the sums to infinity of
24. 2 sin θ + 3 sin θ sin 2θ + 4 sin2 θ sin 3θ + 5 sin3 θ sin4 θ+ …, ![]() .
.
25. ![]() .
.
26. 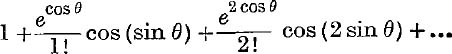 .
.
27. ![]() .
.
28. ![]() .
.
29. Prove that the sum to infinity of
![]()
30. Prove that the sum to infinity of
![]()