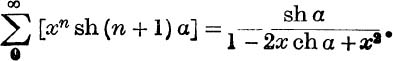CHAPTER VI

THE SPECIAL HYPERBOLIC FUNCTIONS

From the expansions in Ch. V, we have

 

and

 

Therefore, by addition and subtraction,

 

and

 

. These results should be compared with the expansions of cos x and sin x in Ch. V, pp. 80, 81. The precise connection will be explained after complex numbers and functions of a complex variable have been defined. But equations (1) and (2) suggest that the functions (e^x + e^–x) and (e^x – e^–x) possess properties analogous to those of cos x and sin x. We therefore define these functions as the “hyperbolic cosine” and the “hyperbolic sine” of x and we write

 

and we speak of these functions as “cosh x” and “shine x” (or else “sinsh x”): they are sometimes written “cosh x” and “sinh x.”

We therefore have

 

 

We also define the hyperbolic tangent, hyperbolic secant, hyperbolic cosecant, hyperbolic cotangent, which are written th x. sech x, cosech x, coth x, by the relations

 

Note. th x is pronounced “than x” or “tansh x,” and is sometimes written “tanh x.”

Formulae for the Hyperbolic Functions.   Putting e^x = t, we have

 

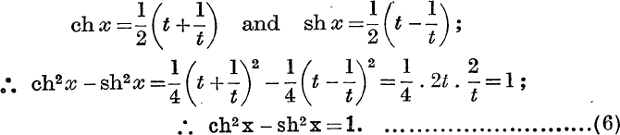
Similarly,

 

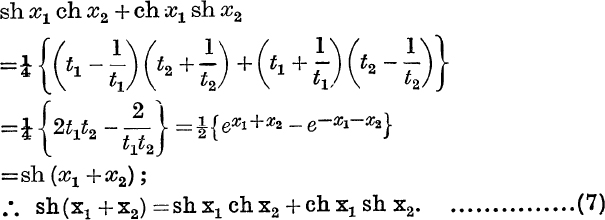
Also

 

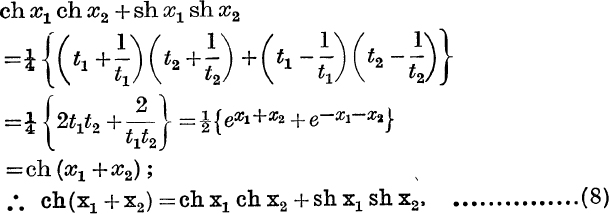
We have also from the definitions the general relations

 

and the special values

 

By comparing formulae (6)-(9) with the corresponding trigonometrical formulae, the reader will see that to every (general) trigonometrical formula there corresponds an analogous formula for the hyperbolic functions which may be written down by Osborn’s rule: In any formula connecting the circular functions of general angles, replace each circular function by the corresponding hyperbolic function and change the sign of every product (or implied product) of two sines.

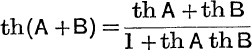Thus, from , we may infer that , since implies a product of two sines.

The rule does not apply to properties depending on the periodicity of the circular functions or the values pf the ratios of special angles ; e.g. the rule must not be used in connection with

 

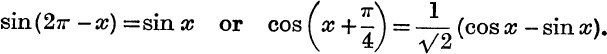
For the present, this rule should be regarded merely as a mnemonic. Its justification is best left till circular functions of a complex variable have been defined, see Chapter X.

EXERCISE VI. a.

Prove some of the following formulae in Nos. 1-10, and check the others by the rule on p. 105.

1. ch( –x) = ch x; sh(–x) = –sh x; th(–x) = – th x.

2. sh2θ = 2 sh θ ch θ.

3. ch 2θ = ch²θ + sh²θ = 2 ch²θ – 1 = 1 + 2 sh²θ.

4. 1 + ch α = 2ch²; 1 – ch α = -2 sh².

5. .

6. .

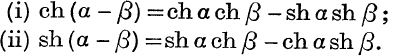7. .

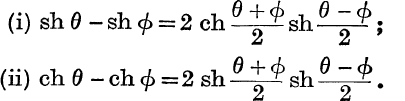Write down the corresponding formulae for sh θ + sh ϕ and ch θ + ch ϕ.

8. .

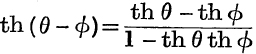9. (i) sh 3θ = 3 sh θ + 4 sh³θ; (ii) ch 3θ = 4 ch³θ – 3 ch θ.

Write down the formula for th 3θ in terms of th θ.

10. sech²x = 1 – th²x. What is the corresponding formula for cosech² x ?

Write down alternative expressions for the following :

11. 1 – coth²x.

12. sh³x.

13. sh²x – sh²y.

14. shθ shϕ.

15. shθ chϕ.

16. chθ chϕ.

17. (ch x – sh x)^–1.

18. (chx + shx)ⁿ.

19. (chx – shx)ⁿ.

20. Expand (x + y + z).

21. Prove that ch(x + y) ch(x – y) = ch²x + sh²y.

22. Prove that .

23. Express ch θ and th θ in terms of sh θ.

24. Express ch θ and sh θ in terms of th θ.

25. Express sh θ and th θ in terms of k, where k = ch 2θ.

26. Express sh θ and ch θ in terms of t, where t = th0.

27. If x = sin u ch v and y = cos u sh v, find a relation between

 

28. Prove that .

29. If tan θ = tan α th β and tan ϕ = cot α th β, prove that

 

30. Prove that ch²(θ + ϕ) – ch²(θ – ϕ) = sh 2θ sh 2θ.

31. Prove that sin²θ ch²ϕ + cos²θ sh²ϕ = (ch 2ϕ – cos 2θ).

32. Simplify .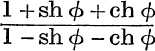

33. Express sh 2x + sh 2y + sh 2z – sh (2x + 2y + 2z) in factors.

34. If sin x ch y = cos α and cos x sh y = sin α, prove that

 

35. Simplify sh (log x) and ch (log x).

36. Prove that ch x + ch 2x + ch 3x + … + ch nx equals

 

Differential Coefficients and Integrals. Using the definitions, we have

 

 

 

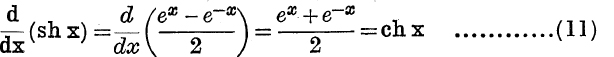
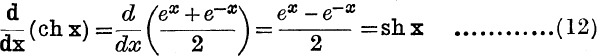
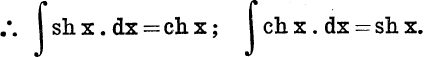
Further,

 

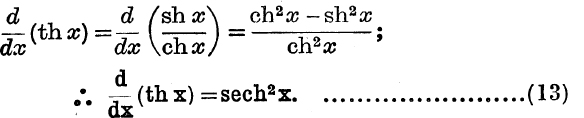
In general, expressions involving the hyperbolic functions are integrated by methods similar to those used for the circular functions.

It should also be noted that the general solution of the equation may be written in the form y = Ash x + B ch x where A, B are arbitrary constants, just as that of may be written in the form y = A sin x + B cos x. (See Ex. VI. b, No. 27.)

Example 1. Find .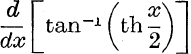

 

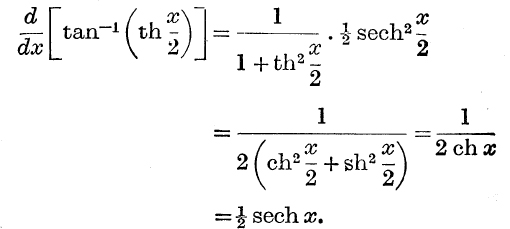
Example 2. Evaluate .

 

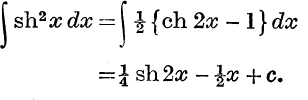
EXERCISE VI. b.

Differentiate with respect to x:

1. sh x + ch x.

2. ch²x.

3. sh²x.

4. sh x ch x.

5. cosech x.

6. sech x.

7. coth x.

8. log(sh x).

9. log(ch x).

10. .

11. tan^–1 (coth x).

12. log (sh x + ch x).

Integrate with respect to x:

13. ch 2x.

14. sh 3x.

15. th x.

16. coth x.

17. sh²x.

18. cosech²x.

19. th²x.

20. coth2 x.

21. sh x sh 2x.

22. cosech x,

23. sh x sh 2x.

24. ch³x.

25. What is (ch x cos x + sh x sin x) ?

26. Find the value of ∫ch x sin x dx.

27. If y = a sh nx + b ch nx where a, b, n are constants, prove that .

28. (Behaviour of sh x and ch x).

(i)  Prove that ch x is always positive and that sh x has the same sign as x.

(ii)   Deduce from (i) that sh x steadily increases as x increases, that ch x steadily decreases if x is negative and steadily increases if x is positive, as x increases.

(iii)  What is the minimum value of ch x ?

(iv)  How does ch x behave when x → ∞ and when x → – ∞ ?

(v)   How does sh x behave when x → ∞ and when x → – ∞ ?

(vi)  Find the limit of when and of when x → + ∞ and of when x → – ∞.

(vii)  Find the limit o when x → + ∞ and of when x → – ∞.

(viii)  Draw in the margin the graphs of sh x and ch x. Compare each with the graphs of e^x and e^–x. [The graph of ch x is called a Catenary, because it is the curve in which a uniform flexible chain with fixed ends hangs.]

29. (Behaviour of thx and coth x).

(i)   Prove that th x and coth x are both odd functions of x.

(ii)  Prove that th x steadily increases as x increases. What conclusion can be drawn from the fact that

 

(iii) Find the limits of th x when x → + ∞ and when x → – ∞. What are the limits of coth x in these cases ?

(iv) Discuss the behaviour of th x when x → 0, (a) through positive values, (b) through negative values.

(v)  What is the slope of y = th x at x = 0 ?

(vi) Prove that |th x| < 1 and |coth x| > 1 for all values of x.

(vii) Draw in the margin the graphs of th x and coth x.

30. Draw the graphs of sech x and cosech x.

Inverse Hyperbolic Functions. If y = sh x, then e^x – e^–x = 2y;

 

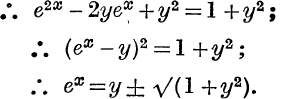
But e^x > 0; is not a possible value of e^x;

 

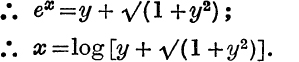
Since sh x increases steadily as x increases from – ∞ to + ∞ , it is clear that for any value of sh x there is only one value of x. If y = sh x, we write x = sh^–1y. The function sh^–1y is therefore a onevalued function of y given by the relation

 

This inverse function, sh^–1y, is therefore not really a new function, but nevertheless the notation is useful.

The reader has seen (Ex. VI. b, No. 28) that, if y = ch x, y has no value less than 1, and that to any value of y greater than 1 there correspond two values of x, numerically equal but of opposite sign.

The function x = ch^–1y is therefore only defined for values of y ≥ 1 and is a two-valued function.

The reader should prove, by the same method as that used above for sh^–1y, that

 

Similarly, the reader will see from the results of Ex. VI. b, No. 29, that, if y = th x, – 1 < y < 1, and that to any value of y in this range there corresponds one value of x.

The function x = th^–1y is therefore only defined for the range of values – 1 < y < 1 and is a one-valued function. By the same method as before, it may be shown that

 

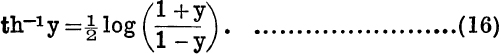
Applications to Geometry and Integration. The equation

 

shows that the coordinates of any point P on the hyperbola

 

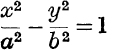
may be written (a ch θ, b sh θ); this is analogous to the use of the eccentric angle for the ellipse, (cf. Ex. VI. c, No. 13). Further, if O is the centre and if A is the vertex (a, 0), it may be shown that the area of the sector AOP is abd (Ex. VI. c, No. 14).

Another important application occurs in integration. Just as integrals involving (1 – x²) or (a² – x²) can often be evaluated by the substitution x = sin θ or x = a sin θ, so integrals involving (1 + x²) or (a² + x²) can often be evaluated by putting x = sh θ or x = a sh θ, and those involving (x² – 1) or (x² – a²) by putting x = ch θ or x = a ch θ.

Example 3. Evaluate .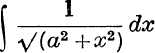

Put ;

 

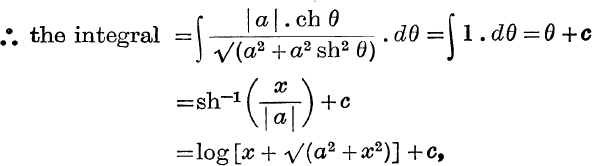
where c is a constant.

Example 4. Evaluate , where x < – 2.

Here it is not possible to put x = 2 ch θ, because x is negative, while 2 ch θ is positive. But we can put x = – 2 ch θ, and we can take θ as positive.

Then (x² – 4) = + 2 sh θ; also dx = – 2 sh θ. dθ

 

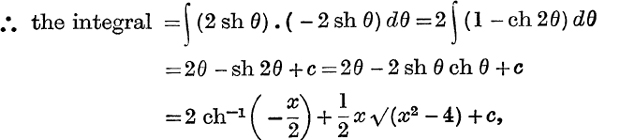
where c is a constant.

The difficulty of sign illustrated in this Example does not arise in numerical work because, if an integral such as 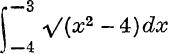occurs, it is natural to begin by substituting x = – ξ, and this reduces the integral to 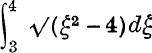, so that ξ is positive throughout the given range of values.

EXERCISE VI. c

1. Prove that, if y ≥ 1, ch ^–l y = ± log{}.

2. Prove that, if |y| < 1, th ^–1 y = .

3. Draw the graphs of ch ^–1 x and sh ^–1 x.

4. Draw the graphs of th ^–1 x and coth ^–1 x.

5. Prove that, if 0 < y ≤ 1, sech ^–1 y = .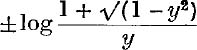

6. Express cosech^–1 y in logarithmic form, (i) if y > 0, (ii) if y < 0.

7. Prove that .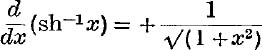

8. Prove that 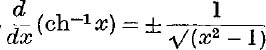, and explain the ambiguous sign, showing how to distinguish between the two cases.

9. Prove that, if |x| < 1, .

10. Prove that, if | x | > 1, .

11. Eliminate u from the equations:

(i) x = a ch u, y = b sh u;

(ii) x = a ch (u + α), y = b sh (u + β).

12. Prove that x = a ch (u + α), y = b ch (u + β) are parametric equations of a hyperbola.

13. Prove that the chord of the hyperbola x² – y² = a² joining the points (a ch θ, a sh θ) (a ch ϕ, a sh ϕ) is

 

14. Prove that the area between the hyperbola , the x-axis, and the ordinate from P, (a ch θ, b sh θ), is and that the area of the sector bounded by the curve, the x-axis and OP is abθ.

15. Evaluate by putting x = a th θ, and compare the result with that obtained by expressing the integrand in partial fractions.

16. Evaluate 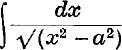where x² > a², (i) for x > 0, (ii) for x > 0.

17. Evaluate .

Evaluate the following integrals :

18. .

19. .

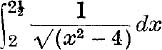20. .

21. .

22. .

23. .

24. Prove that if , and find the corresponding result when (cf. Nos. 9, 10).

EASY MISCELLANEOUS EXAMPLES.

EXERCISE VI. d.

1. Prove that (ch x + sh x)(ch y + sh y) = ch (x + y) + sh (x + y).

2. Prove that ch ⁶ x – sh ⁶ x = 1 + sh ² 2x and express it in terms of ch 4x.

3. Simplify

 

4. Prove that .

Differentiate with respect to x :

5. .

6. .

7. sech ^–1x.

8. .

9. x ^{sh x}.

10. e^ax sh bx.

Integrate with respect to x :

11. e^x (th x +sech²x).

12. sh x sh 2x sh 3x.

13. e^ax sh bx.

14. .

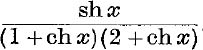15. Find the parabola which most closely approximates to y = ch x near the point (0, 1), and deduce the radius of curvature of the catenary at that point.

16. Find the angle of intersection of the curves y = 1 + ch x and y = e^x.

17. If θ > 0, prove that ch θ > sh θ > θ > th θ.

18. Evaluate 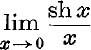and .

19. Evaluate .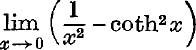

20. Prove that .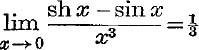

21. Show that sh x – , if x is small.

22. Express x cosech x in terms of powers of x when x is so small that x⁶ is negligible.

23. Prove that ch x < , if |x| < 1.

24. Prove that sh x < , if 0 < x < 1.

25. Prove that 2 (ch x – 1) < x sh x.

26. Show that x = 1·9 is an approximate solution of x = 2 th x, and find a closer approximation.

27. If tanx = th y, prove that 2 tan ^–1 (sin 2x) = tan^–1 (sh 4y).

28. Prove that sh^–1(cot θ) = log (cot θ + | cosec θ |).

29. (i) Express th ^–1x + th^–1 y in the form th ^–1 p ;

(ii) Prove that if x, y are the coordinates of a point P and th^–1x + th ^–1y = c, a constant, then P lies on a hyperbola with asymptotes parallel to the axes.

30. If P, Q are the points (a ch θ, b sh θ), (a ch ϕ, b sh ϕ) on the hyperbola , prove that

(i) the area of the segment cut off by PQ, is ab {sh (θ – ϕ) – θ + ϕ} ;

(ii) the tangent at is parallel to PQ.

(iii) the pole of PQ is .

31. By expressing ch θ, sh θ in terms of , find from x = a ch θ, y = b sh θ, rational algebraic parametric equations to the hyperbola, . Show that two points of the curve on opposite branches cannot be represented by one set of parametric equations in terms of θ, but can be represented by one set of parametric equations in terms of an arbitrary parameter t.

32. Use the formula, 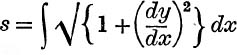to show that y² – s² = 1 for the catenary, y = ch x.

33. What curve is represented by the parametric equations, x = a sh² θ, y = 2a sh θ? Apply the formula, , to show that the length of the arc of this curve, measured from the origin, is a (θ + sh θ ch θ).

HARDER MISCELLANEOUS EXAMPLES.

EXERCISE VI. e.

1. if , find th 2x and tan 2y in terms of a and b.

2. If tan x = tan λ th μ and tan y = cot λ, th μ, prove that

 

3. Prove that .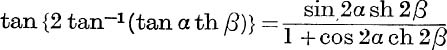

4. If ch u = sec θ, where –π < θ < π, and if uθ is positive, prove that sh u = tan θ, u = log (sec θ + tan θ), and . How are the results affected if uθ is negative ?

5. Evaluate 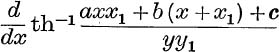, where and .

6. Evaluate 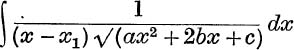by means of No. 5

7. If n > 1, prove that .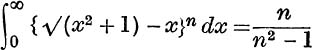

8. Prove that x (2 + ch x) > 3 sh x, for x > 0.

9. Find whether or is the greater when x is small.

10. If θ is small, prove that .

11. Solve the equation .

12. Show that is an approximate solution of

 

where a is small, and find a closer approximation.

13. Prove that sin x = th mx where m is positive, has an infinity of roots, and that the large positive ones occur in pairs near (2n + )π, and that closer approximations are

 

14. Prove that (ch θ + sh θ)ⁿ = ch nθ + sh nθ.

15. Prove that 2 ch nα = (ch α + sh α)ⁿ + (ch α – sh α)ⁿ.

16. Express ch 5x in terms of ch x.

17. Express sh 5x in terms of sh x.

18. Express in terms of sh x.

19. Prove that 64 ch⁷x = ch 7x + 7 ch 5x + 21 ch 3x + 35 ch x, and express sh⁷ x in terms of hyperbolic sines of multiples of x.

20. Express sh⁶x in terms of hyperbolic cosines of multiples of x.

21. Prove that

 

22. Find an expression for (ch θ + sh θ – l)ⁿ similar to that in No. 21.

23. Prove that

 

24. Sum the series sh α + sh 2α + sh 3α + … to n terms.

25. Sum the series ch α + ch(α + β) + ch (α + 2 β) + … to n terms.

26. Sum the series ch θ + 2 ch 2θ + 3 ch 3θ + … to n terms.

27. If n is a positive integer, prove that

 

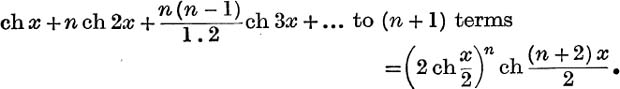
28. Prove that the sum to infinity of

 

29. Find the sum to infinity of

 

30. If 0 < α < β, show that the sum to infinity of

 

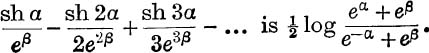
31. If –β < α < β, show that the sum to infinity of

 

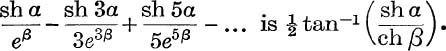
32. Find the sum to infinity of

 

33. If |x| < e^–α, prove that if α > 0