The first book to illuminate the joy of logical deduction was Elements, written around 300 BCE by the Greek mathematician Euclid.
Elements is ostensibly about geometry, that is, the behavior of points, lines, surfaces, and solids. Yet its real significance for the history of human thought was the method Euclid introduced to investigate these concepts. The book begins with a set of definitions, and five basic rules he states we can accept as true. He deduces everything else in the book from these original premises, at each stage showing rigorously how each step follows from the one before. The power of this method is that it constructs a huge edifice of knowledge for which the truth of a few preliminary statements guarantees the truth of everything else. The template of Elements is the template of all subsequent mathematics.
In practical terms, all Euclid started with was a straightedge, for drawing lines, and a compass, for drawing circles. That’s it. Every theorem in the book (and there are hundreds of them) is proved using those two instruments alone.
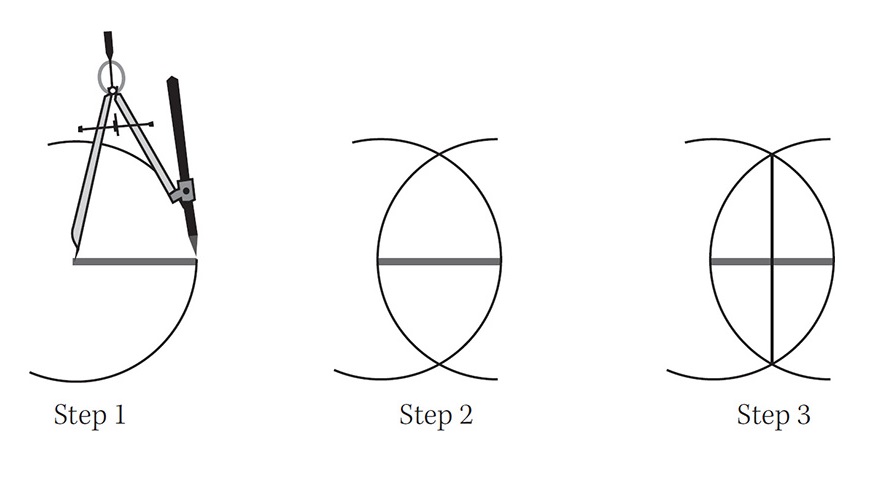
Here, for example, is how you cut a given line in half:
Step 1. Place the compass point at one end of the line, the pencil at the other, and draw a circle.
Step 2. Repeat with the compass point at the other end.
Step 3. Use the straightedge to draw a line between the two intersections of the circles. The line cuts the given line in half.
Each theorem in Elements, in fact, is presented like a problem, and each proof is presented like its solution. It’s a puzzle book in all but name. What I really like about the next problem is that it teases Euclid, the master of conceptual frugality, for having too much equipment in his pencil case.
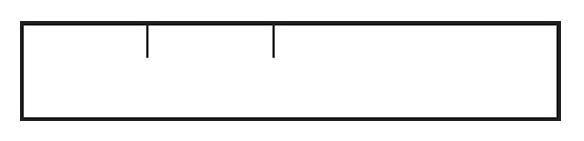
THE LONE RULER
You have a pencil and a ruler but no compass. The ruler has two marks on it, as shown below. Can you draw a line whose length is exactly half the distance between those two marks? In other words, if the distance between the marks is 2 units, can you draw a line 1 unit long?
You can only measure using the ruler—not the pencil or the paper.
The problems I’ve chosen for this chapter are all geometric in the sense that they explore, and have fun with, the properties of lines, shapes, and physical objects. The next one originates from an eighteenth-century edition of Elements that contains notes by William Whiston, Isaac Newton’s successor as Lucasian Professor of Mathematics at Cambridge University. Whiston noted a mathematical oddity that became a particularly celebrated puzzle.
He imagined a man walking around the circumference of the Earth, and remarked how much farther the man’s head would travel than his feet. Can you work out the distance? Assume that the Earth is a perfect sphere.
I’ll do the calculation for you, but first we require a piece of elementary mathematical knowledge: The formula for the circumference of a circle, which is twice pi times the radius, usually abbreviated to 2πr, where pi is approximately 3.14. I’m hoping that introducing a formula here doesn’t put you off what is a delightful and surprising result. Bear with me while we work it out.
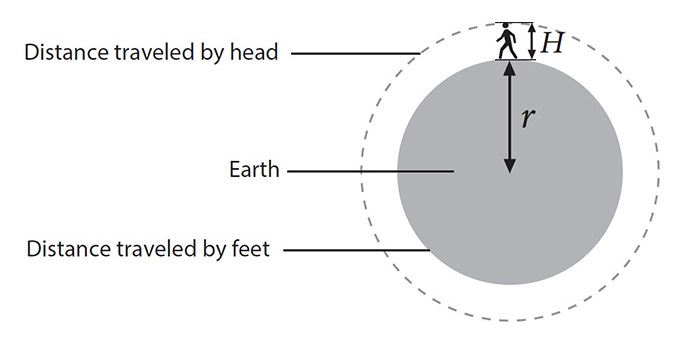
In the diagram above, r is the radius of the Earth and H is the man’s height. Using the formula, the circumference of the Earth (the distance traveled by the man’s feet) is 2πr and the circumference of the dotted circle (the distance traveled by his head) is 2π(r + H), since the radius of the dotted circle is the radius of the Earth plus the man’s height. So, the difference between the two circumferences, which is the distance the head travels further, is:
2π(r + H) – 2πr = 2πr + 2πH – 2πr = 2πH.
The 2πr terms cancel out (hold that thought!) and the answer is 2πH, which is 2 × 3.14 × the man’s height.
So, if the man’s height is, say, 1.8m, the distance his head travels more than his feet is about 11m.
Now we can see why Whiston thought the answer interesting enough to point out. The distance is tiny! The circumference of the Earth is about 40,000km. It is startling to think that after thousands of kilometers of strolling around the Earth the man’s head only travels about 11m more than his feet, or 0.00003 percent of the total journey.
Whiston’s globetrotter is the origin of the following classic puzzle.
ROPE AROUND THE EARTH
A rope lies tightly around the circumference of the Earth. The rope is then extended in length by 1m and raised up at every point from the ground until it is again a taut circle, and every point on the rope is the same height above the ground.
How high is the rope now? What size of animal could crawl under it?
The illustration below shows how this problem is essentially the same as the previous one. Both involve the comparison of two concentric circles, the smaller of which is the circumference of the Earth. In the rope’s case the bigger circle has a circumference that is 1m longer than the smaller circle.
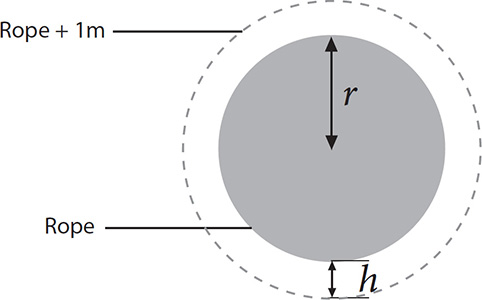
When the problem is phrased in terms of the rope, the counterintuitive answer is even more powerful. By extending the rope by 1m, we will be able to raise it off the ground by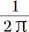 
m, which is about 16cm. (My workings: Let c be the circumference of the Earth, so the length of the extended rope is c + 1. Using the formula for circumference we have two equations: 2πr = c and 2π(r + h) = c + 1. These combine to get 2πh = 1, or h = .)
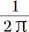Think about this result for a second. We have a rope that is 40,000km long, and we extend it so it is 40,000.001km long. Yet this apparently insignificant increase creates enough slack for the rope to stand 16cm off the ground all the way around the world. What animal will be able to get through? Easily a cat or a small dog.
Now let’s return to that thought, from our discussion of the man walking around the Earth. When we worked out the extra distance the head travels, the two 2πr terms canceled out, leaving the answer as 2π times the man’s height. What is significant here is that the Earth’s radius, r, appears nowhere in the answer, meaning that the extra distance traveled by the head is determined only by the man’s height and not by the size of the Earth. In other words, the size of the Earth makes no difference to the answer. Whiston’s rambler could be walking around any sphere at all, and his head would always cover an extra 11m.
(1) A man walks round an atom. How much further does his head travel than his feet?
(2) A man walks round a football. How much further does his head travel than his feet?
(3) A man walks round Jupiter (circumference: about 400,000km). How much further does his head travel than his feet?
(4) A man walks round the Sun (circumference: 4.4 million km). How much further does his head travel than his feet?
The answer in all cases is only 11m (ignoring, of course, the physical challenges involved). Likewise, if a rope was girdling an atom, a football, Jupiter, or the Sun, an extra meter in length would create enough slack to raise the rope by 16cm at all points. Amazing.
William Whiston lasted only eight years as Lucasian Professor before he was expelled from Cambridge for heresy. (His offence was to reject the idea of the Holy Trinity, arguing instead that Jesus was subordinate to God.) Whiston never returned to academia, instead giving math and science lectures in London’s coffee houses, where he had the tendency to digress into religious rants.
Whiston’s greatest contribution to science was the crucial role he played in persuading the British government to establish the Board of Longitude, which offered prize money to the first person to invent a way to determine a ship’s longitude at sea. Ever hopeful to win the cash, he nevertheless failed in all his attempts to solve the problem. It is beautifully fitting, therefore, that his greatest contribution to math was a puzzle about circumnavigating the Earth.
I prefer Whiston’s phrasing of the problem as a man walking around the Earth to the later version of a rope hovering above the ground, since—although both are obviously absurd—the former scenario seems less contrived. If there was a rope girdling the Earth, and you did extend it by 1m, before even thinking of attempting to levitate it everywhere, surely you would raise it at a single point to see how far it would go. Especially if the purpose was to let animals pass under it!
New problem:
You have a rope that is lying around the circumference of the Earth. You extend it by a meter. Now you raise it upward at a single point until the slack becomes taut. How high does it go? What animal will fit under it now?
Don’t struggle with the calculation, because the answer is only accessible to those with a certain level of math. I have included the question here since the answer is interesting. Have a guess, and peek at the answer in the back.
In fact, do the next question first, and then peek at the answer.
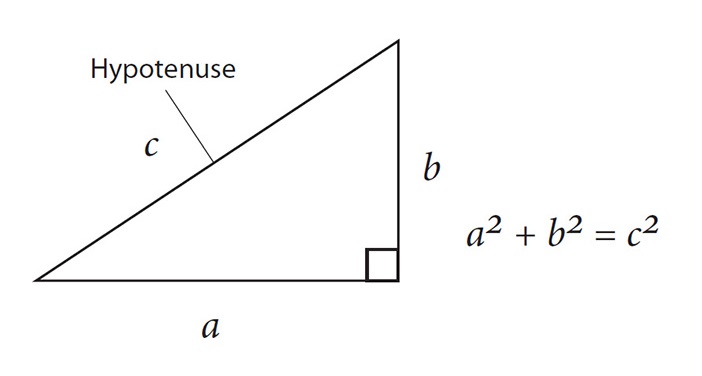
Clue: We will need Pythagoras’s theorem, which states that for all right-angled triangles the square of the hypotenuse is equal to the sum of the squares of the other two sides. (The hypotenuse is the side opposite the right angle.) But you knew that anyway, right?
BUNTING FOR THE STREET PARTY
There will be a party on your street, which is 100m from end to end. You have a 101m line of bunting for the decorations. You attach one end of the bunting to the bottom of a lamp post at one end of the street, and the other end to the bottom of a lamp post 100m away at the other end of the street. You hang the middle of the bunting from the top of a pole halfway down the street.
Assuming there is no slack and no stretching of the bunting, how high will the pole be?
The next three puzzles concern the behavior of rolling circles. They might spin your head if you have never thought about these ideas before, but I guarantee you will appreciate the “wow” however you discover the answers. The puzzles will become more accessible after that, when we visit Japan.
Elements established Euclid as the laureate of logic, the high priest of cold and rigorous deductive thought. This reputation is now shared, and possibly eclipsed, by Sherlock Holmes.
The fictional sleuth aspired to Euclidean rigor—“How often have I said to you that when you have eliminated the impossible, whatever remains, however improbable, must be the truth?”—but he was not as good at math.
In one early Sherlock Holmes caper, The Adventure of the Priory School, Holmes looks at the wheel tracks made by a bicycle and deduces which way it was heading. He explains his reasoning to Watson: “The more deeply sunk impression is, of course, the hind wheel, upon which the weight rests. You perceive several places where it has passed across and obliterated the more shallow mark of the front one. It was undoubtedly heading away from the school.”
I’m not sure I follow. Surely the back wheel would obliterate the front wheel’s mark in whichever direction the cyclist was going?
Holmes creator Sir Arthur Conan Doyle missed a trick. But it is possible to deduce the direction of travel of a bicycle from its tire tracks.
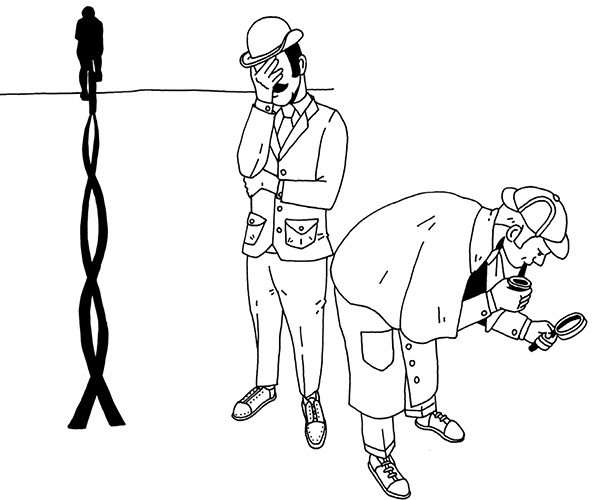
ON YER BIKE, SHERLOCK!
Was the cyclist who left the tracks below going from left to right, or from right to left?
Holmes was correct that you first need to work out which wheel made which track, but you can do this without knowing how deep each impression is.
Here’s another bicycle puzzle. You may instinctively know the answer. One image feels right, and the other doesn’t. But can you work out why?
FUZZY MATH
A photographer is taking a picture of a bicycle in motion. The bike is traveling along a horizontal road either from left to right, or from right to left; the direction doesn’t matter. The wheel is a white disc, with two pentagons marked on it.
Which of the two images below is the photo that the photographer took?
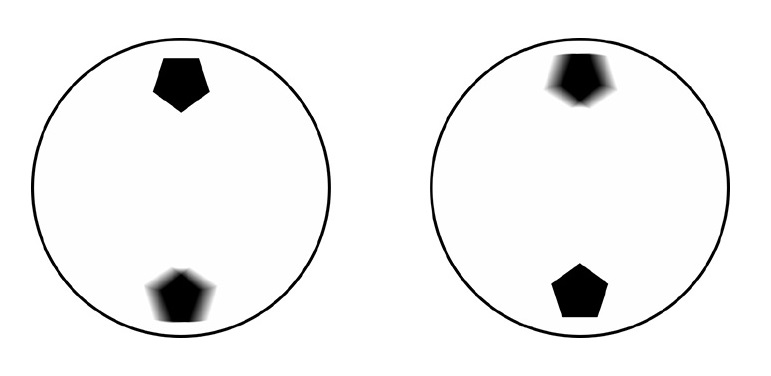
The lesson of the above puzzle is that the behavior of a rolling circle is subtler than at first it appears.
The following question is taken from an SAT general aptitude test that 300,000 Americans took in 1982. Only three students got the correct answer. Will you?
ROUND IN CIRCLES
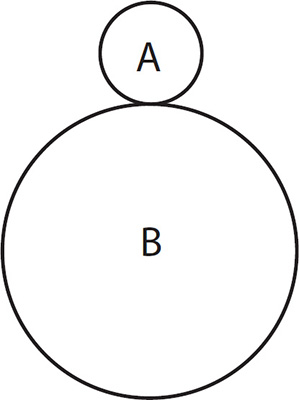
The radius of circle A is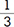 
of the radius of circle B. Circle A rolls around circle B one trip, back to its starting point. How many times will circle A revolve in total?
(a)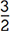 
(b) 3
(c) 6
(d) 
(e) 9
Now for something to scrunch your mind in a different way.
EIGHT NEAT SHEETS
Eight sheets of identically sized square paper are placed on a table. Their edges form the following pattern, with only one sheet, marked 1, completely visible.
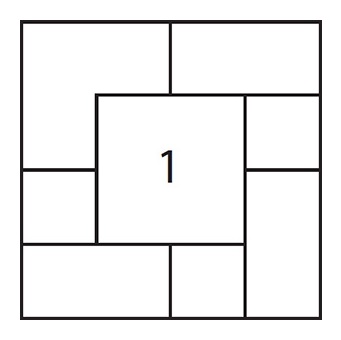
Can you number the other sheets from top to bottom where 2 is the second layer, 3 is the third layer, and so on?
To print this image, visit the book’s webpage and download the PDF.
I first read about the neat sheets in Kobon Fujimura’s brilliant The Tokyo Puzzles. Between the 1930s and the 1970s, Fujimura was Japan’s puzzle king. He published many books, some bestsellers, and in the 1950s he even had his own weekly TV puzzle show. Fujimura’s popularity presaged the modern boom in Japanese pencil puzzles, epitomized by the international success of Sudoku in the 2000s, which I’ll discuss in more detail later in this chapter.
The Japanese have a more playful approach to numbers than we do in the West, or at least this is how it has felt to me the two times I have visited Japan. Schoolchildren recite their times tables with the happy levity of a nursery rhyme. A popular pastime used to be to play games with the numbers on your subway ticket. And the country has turned mental arithmetic into a spectator sport. Learning the abacus is still a popular after-school activity, and there is a tournament circuit for its best practitioners. When I attended the national abacus championship in 2012, the climax was a counting game in which contestants visualizing an abacus had to add fifteen numbers flashed at them in under two seconds. It was tense and exciting!
Here’s another of Fujimura’s puzzles that I really love.
A SQUARE OF TWO HALVES
A big square is divided into sixteen smaller squares. The images below show two ways to cut this big square into two identical pieces.
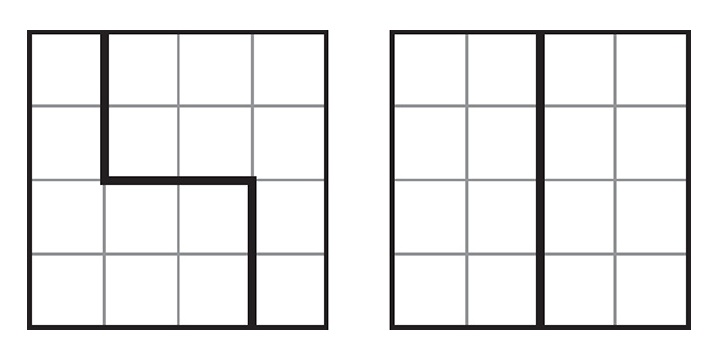
There are four more ways to do this. Can you find them?
To print a blank grid, visit the book’s webpage and download the PDF.
For clarification, you can only cut along the inner lines and the two shapes must be identical, meaning that if they were made of card you would be able to make them align perfectly by sliding one on top of the other and adjusting their positions while always keeping them flat. If you need to turn one shape upside down—that is, take the card off the table and replace it with the top side on the bottom—in order to make it align perfectly with the other card, the shapes are not identical.
Finally, here is a Fujimura puzzle with curves. You may need the formula for the area of a circle, which is pi multiplied by the square of its radius, or πr2.
THE WING AND THE LENS
Illustrated below is a quarter circle that contains two smaller semicircles. Prove that the wing shape A has the same area as the lens shape B.
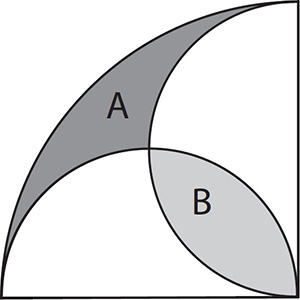
I like this puzzle not only because the image is pretty, but also because it reminds me of the Japanese tradition, between the seventeenth and nineteenth centuries, of hanging decorative wooden tablets containing geometry problems outside shrines and temples. Called sangaku, these mathematical images were both religious offerings and public announcements of the latest discoveries. They made mathematics a public event, a source of visual entertainment and wonder. I saw a sangaku tablet at a temple in Kyoto. It included pictures of circles, triangles, spheres, and other shapes, beautifully painted in white and red. The composition of geometrical shapes in a sangaku is harmonious and artistic, an aesthetic noticeably absent from the purely didactic images you might find in a Western geometry text book. A sangaku tablet usually has just the final image of a problem, with minimal inscriptions underneath. Many hundreds of sangaku survive, such as the one below, dated 1865, from a temple near Nagoya. The problem is credited to a fifteen-year-old boy, Tanabe Shigetoshi.
SANGAKU CIRCLES
The image below shows five sizes of circle. From smallest to largest there are six white circles, seven dark grey ones, three light grey ones, one with a dotted line that sits in the triangle, and a larger one with a solid line.
How many radii of the white circle fit along the radius of the circle with the dotted line?
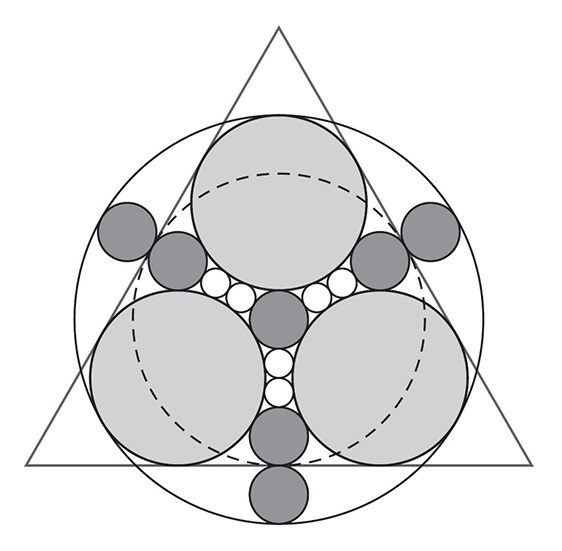
To print this image, visit the book’s webpage and download the PDF.
The puzzle bamboozles you with its splendor. It’s hard to know where to start. But once you find a way to describe the radii of certain circles in terms of the radii of other circles, you’ll discover a really beautiful puzzle.
An even younger Japanese teenager devised the next problem. Thirteen-year-old Sato Naosue’s sangaku was hung in 1847 at a temple about 300 miles north of Tokyo. It is trickier than the last one because—as in almost all problems with right-angled triangles—you need to know Pythagoras’s theorem. (For a refresher on the theorem go back a few pages to Problem 57.)
SANGAKU TRIANGLE 
Below are three sizes of circle: two black, three white, and one grey. Four of the circles are inscribed inside a square, which—together with the other circles—is inscribed inside a triangle. Show that the radius of the grey circle is twice the radius of the black circle.
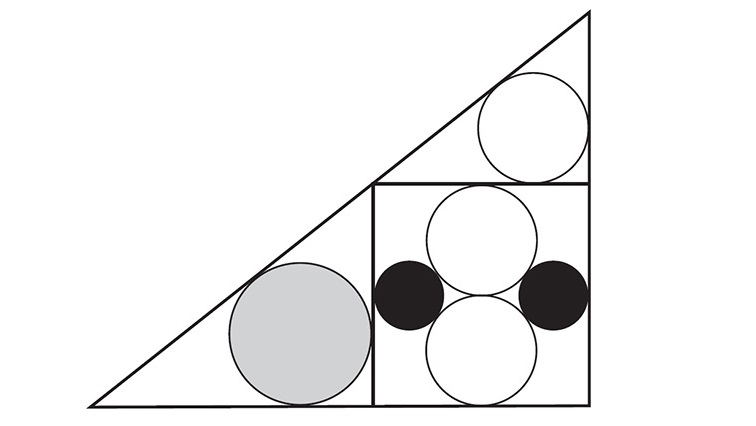
To print this image, visit the book’s webpage and download the PDF.
Another Japanese tradition is the use of tatami mats. Made from woven straw, and so soft that you walk on them without shoes or slippers, they are usually rectangular in shape and twice as long as they are wide.
TREADING ON THE TATAMI
Below is an arrangement of tatami mats. Imagine you are walking from A to B along the edges of the mats. If you want to take the longest path, one idea is to start by following the longest possible straight line—along the top, say, as in the middle image; or down the side, as in the right-hand image.
But there is an even longer path than these two. Can you find it?
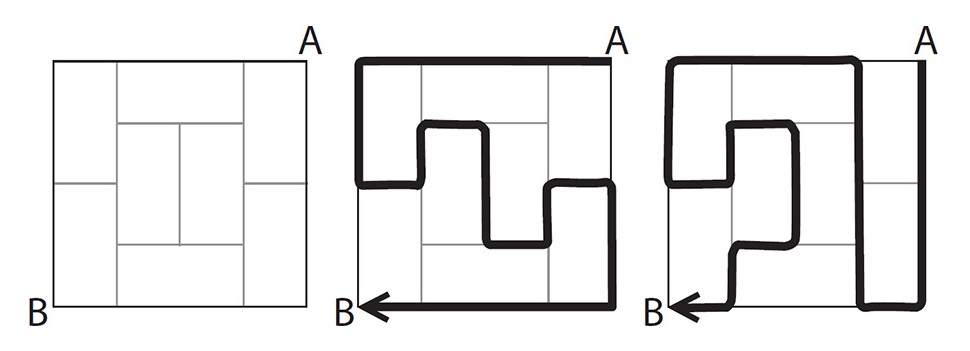
To print this image, visit the book’s webpage and download the PDF.
If you ever want to lay tatami mats, you need to be aware that there is an auspicious and an inauspicious way to do so. The lucky way—as demonstrated in the previous question—is to lay them so that whenever three mats meet they make the shape of a “T.” The unlucky way is to have four mats meeting at the corners, which makes a “+.” Lucky layouts never have four mats meeting at a single point. This superstition makes for some really fun puzzles.
FIFTEEN TATAMI MATS
Tile the room below with fifteen 2 × 1 tatami mats, according to the rule that no four mats can meet at a corner.
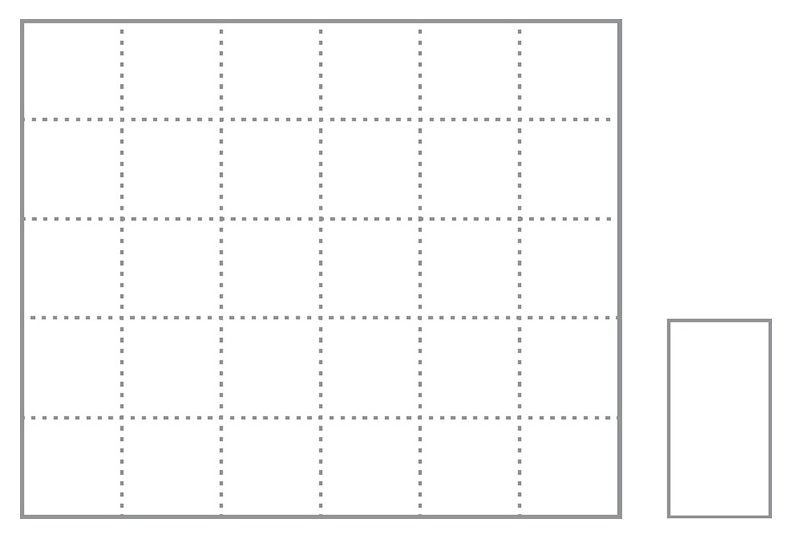
To print this image, visit the book’s webpage and download the PDF.
In this question and the next one, use a pencil so you can rub out wrong turns.
Nob Yoshigahara was a Japanese chemical engineer who turned to writing puzzles after he was burned by a chemical explosion. By the time he died in 2004 he was one of the world’s most influential puzzle people: a columnist, author, toy designer, collector, and international conference organizer. He is remembered by his friends in the global puzzle fraternity as a charismatic, generous, and eternally playful figure. His most successful toy, “Rush Hour,” a logic game in which you must slide plastic cars and buses around a grid, has sold upward of ten million copies around the world.
Yoshigahara devised the “number tree” puzzle that begins this book. He also introduced a new twist to tatami-laying problems. In the pattern below, a straight line (in bold) goes from one side of the room to the other. The next puzzle is about a room where no lines cross the room.
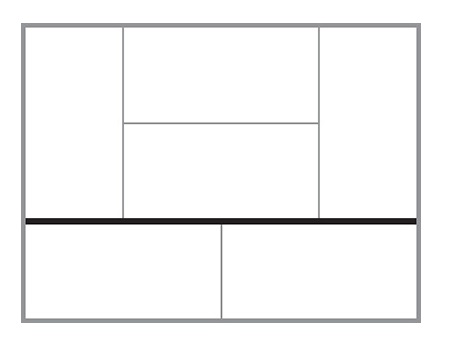
NOB’S MATS
Tile the room from the previous question with fifteen 2 × 1 tatami mats such that no single line goes straight across the room. Mats are allowed to meet four at a corner.
But rooms are not always rectangles! In the next problem, two corner squares are taken up by staircases.
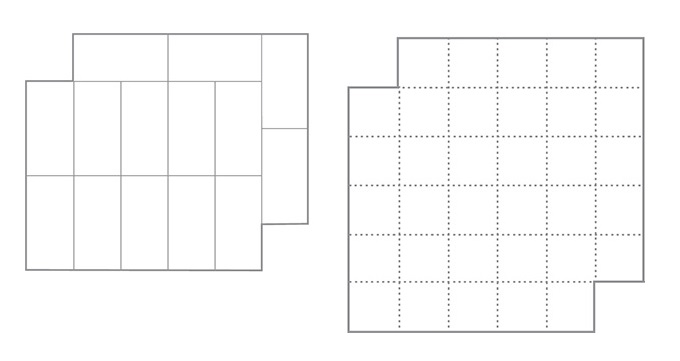
AROUND THE STAIRCASES
When the room from the previous two problems has opposing corners cut off, it is possible to cover it with 14 tatami mats without gaps or overlaps, as shown below left. (The mats can be placed in any position.) Let’s extend the room so it is now 6 × 6, still with two corners cut for the staircases. Prove that you cannot cover the new room with 17 mats without gaps or overlaps.
To print this image, visit the book’s webpage and download the PDF.
But staircases are not always in corners! In the next problem, the positions of the two staircases are chosen at random.
RANDOM STAIRCASES
Architects have decided that they do not want to put two staircases in opposing corners of our 6 × 6 room. If the squares in the room are shaded like a chessboard, as shown below, and if one staircase is in any white square and one staircase is in any shaded square, show that it is possible to tile the room with 17 tatami mats leaving neither gaps nor overlaps. Mats cover two adjacent squares and can be placed in any position as long as they are not in the two squares removed for the staircases.
To print this image, visit the book’s webpage and download the PDF.
In this puzzle you need to show that it is always possible to tile the room, not just provide an example of when it does.
When I posted the next problem in my Guardian column, several architects mocked me for how simple they found it, since the solution is a common design feature of British homes. Their response was the clearest reminder that puzzles that mangle the brains of some solvers can sometimes be almost embarrassingly obvious to others.
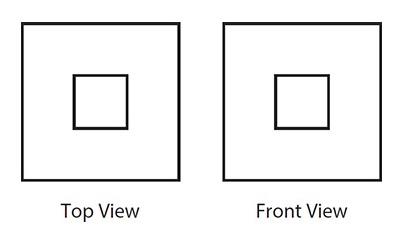
WOODBLOCK PUZZLE
Below are the top and front views of a three-dimensional wooden structure with flat sides. Draw at least one view of the structure from the left-hand side.
All visible edges are marked as lines. Hidden edges must be marked as dotted lines. So, for example, the object below of two square sides with square holes in them, joined at an edge, is not a solution because the side, top and front views of this object would have dotted lines for the hidden edges, as shown below. Of course, it is fine for a side view to have hidden edges. But there can be no hidden edges on the top or front views, since that contradicts the images in the question, which have no dotted lines.
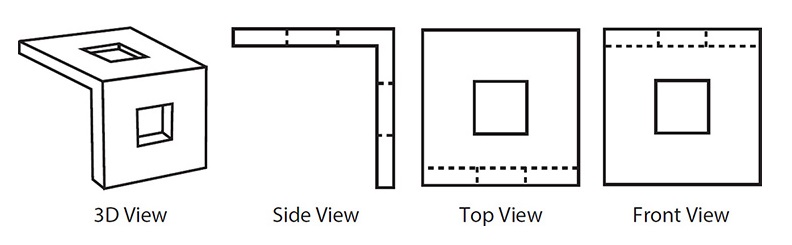
It is important to note that since the object is made of wood, no part of it can have zero thickness.
The next two puzzles take us inside the home.
The Borromean rings are a fascinating mathematical object: three interlocking rings that have the intriguing property that even though they are all linked, when any single ring is taken away, the remaining two are no longer linked, as illustrated below. (If you make the rings from rigid material, the way they overlap forces each ring to face in a slightly different direction than the others, so the diagram is a slight cheat.) I find it pleasingly counterintuitive that no single ring is joined to any other, but that they are inseparable when taken together. The rings are a popular symbol for the interdependence of three parts, and have been used in Christian iconography, for example, to represent the Holy Trinity.
The rings are named after the Borromeo family of Renaissance Italy, who had an image of three interlocking rings on their coat of arms, although the idea of three objects connected in that way predates them. The valknut is a Viking emblem with three interlocking triangles, now most commonly featured in tattoos, pendants, and heavy metal T-shirts.
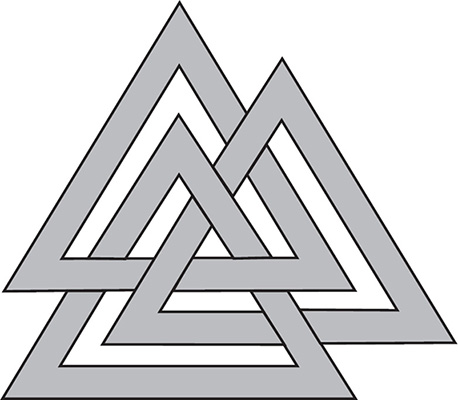
The Borromean rings have three linked elements that fall apart completely when any one of the parts is removed. The same idea is behind the next puzzle.
PICTURE ON THE WALL
The normal way to hang a picture with two nails is to let the string hang over both nails, as shown below.
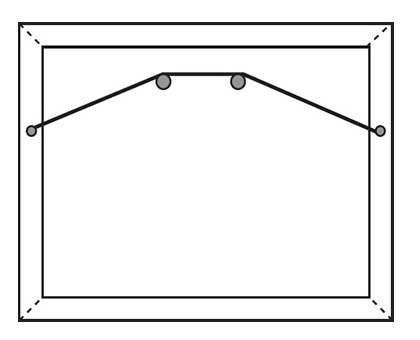
The advantage of two nails is that if one nail comes off the wall the picture stays up, because the string is supported by the other nail.
Can you think of a way to loop the string around the nails such that if either one of the nails fails, the picture will also fall to the floor? (You can increase the length of the string if you need to.)
Rings and home furnishings lead us naturally to the mathematical idea of a “napkin ring”: the shape you get when you drill a cylindrical hole through a sphere, where the center of the hole passes through the center of the sphere. The following is an incredible puzzle because it contains so little information.
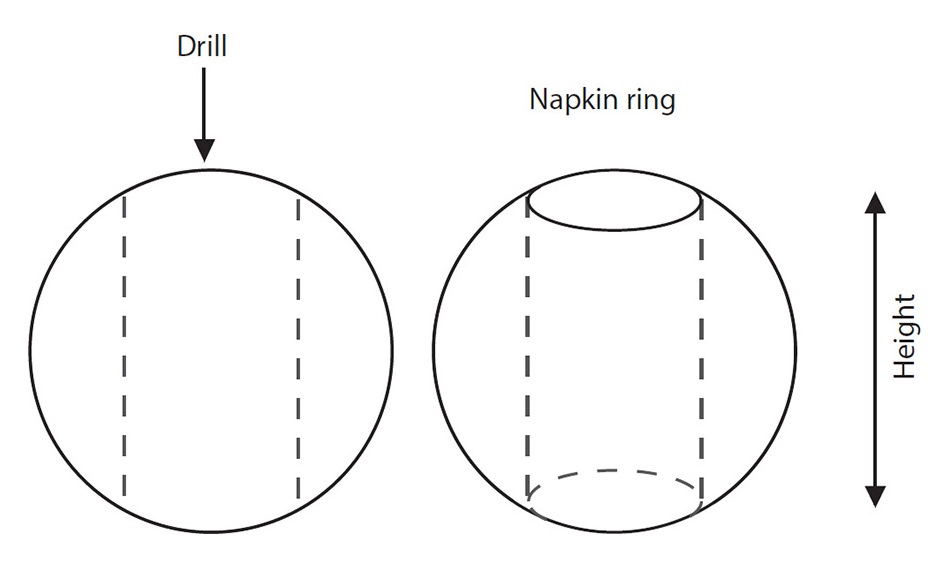
A NOTABLE NAPKIN RING
A napkin ring is 6cm deep. What is its volume?
There is a fair bit of legwork here, but don’t let that deter you. I’ll start you off. Trust me, this is an amazing puzzle.
The volume of the napkin ring is the volume of the sphere minus the volume of the central bit that got removed, which looks like a cylinder with domes on the top and bottom.
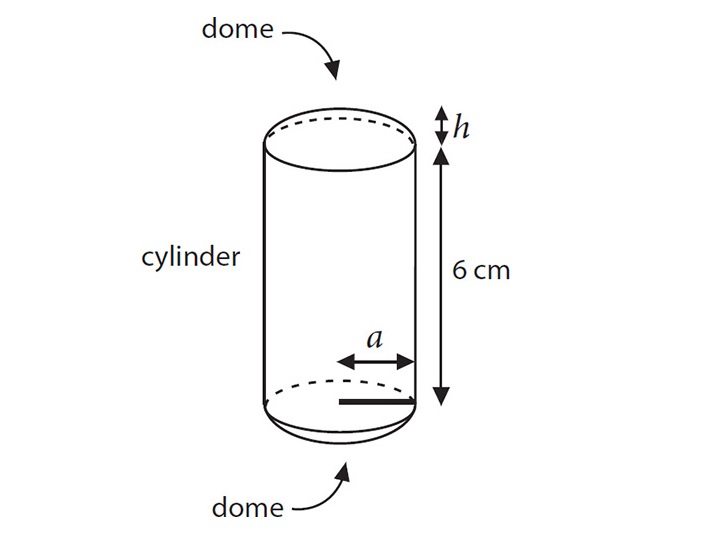
I’ve added the height of the cylinder, which is 6cm. Let the radius of the sphere be r, the dome’s height be h and the radius of the cylinder cross section, which is also the radius of the base of the dome, be a. Now all that you require are the formulae for volume, which I will generously supply here.
The volume of the sphere: (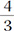
)πr3
The volume of the cylinder: πa2 × 6cm, or 6πa2
The volume of each dome: (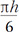
)(3a2 + h2)
We are almost there. The volume of the napkin ring is equal to the volume of the sphere minus the volume of the cylinder minus two times the volume of the dome. Using Pythagoras’s theorem we can write a in terms of r, and we can also write h in terms of r. So, we can write the volume of the ring as an expression in which the only variable is r. The expression will be long and crammed full of rs and πs . . .
What are you waiting for?!
The historian Herodotus wrote that geometry originated with the Egyptian practice of measuring areas of arable land flooded by the Nile. Calculating the areas of squares and rectangles is still one of the first tasks we learn in geometry: All you do is multiply one side by the neighboring side.
This very simple procedure is all you need to solve a Menseki Meiro, or Area Maze, a wonderful puzzle by the Japanese inventor Naoki Inaba.
Here’s a sample question, so you get the hang of it. Your task is to find the missing value. The marked distances are not exact, so you cannot get the answer by measuring.
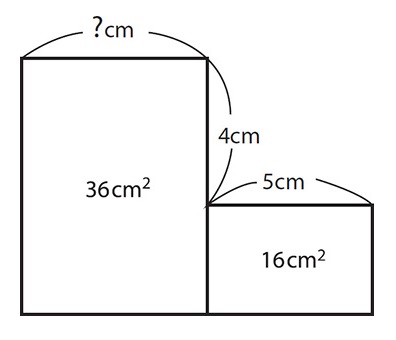
To print this image, visit the book’s webpage and download the PDF.
The beauty of this puzzle is that you must solve it geometrically, and with whole numbers. You are not allowed to spoil your workings with equations or—heaven forbid—fractions. To solve this Area Maze, complete the large rectangle as shown below. The area A must be 20cm, since it is 4cm × 5cm. Which means that the area of A plus the rectangle below it is 20cm + 16cm = 36cm. This area is the same as the large rectangle on the left side. Since they share the same height, they must share the same width—so the missing value is 5cm.
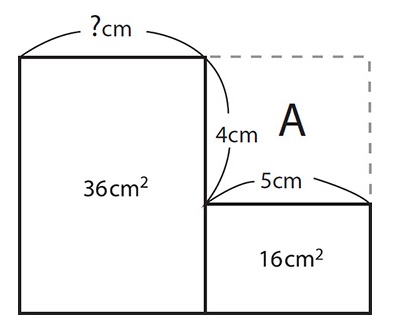
AREA MAZE
Find the missing value.
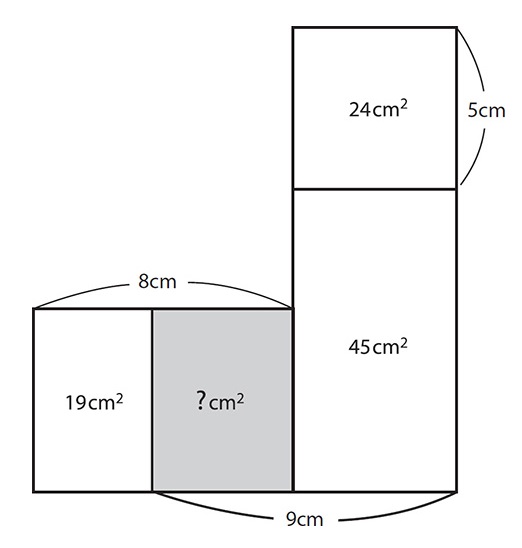
To print this image, visit the book’s webpage and download the PDF.
Naoki Inaba is probably the most prolific and brilliant designer of deduction puzzles working today, although his work is barely known beyond his home country. Japan, in fact, sustains arguably the most vibrant puzzle community in the world, through individuals like Inaba and the magazine publisher Nikoli.
You probably haven’t heard of Nikoli, but you will have heard of Sudoku, which first appeared in the magazine Puzzle Communication Nikoli in the mid-1980s. Sudoku was Nikoli’s rebranding of a puzzle called Number Place from the American magazine Dell Pencil Puzzles and Word Games. In case you have been living under a rock (or tatami mat) for the last decade, the puzzle is based on a 9 × 9 grid. The solver must fill the blanks with the numbers 1 through 9 so that each digit appears once in each row and column and also once in each of the 3 × 3 subsquares within the main grid. Sudoku didn’t attract much attention until 1986, when Nikoli decided to position the given digits in a symmetrical pattern, like letters in crosswords. The tweak worked, and it became a big domestic success. In late 2004, Sudoku appeared in the West for the first time, after an English speaker, Wayne Gould, who had spotted the puzzle while on holiday in Japan, offered Sudoku grids he had made using a computer program to newspapers including The Times in London. Within a few months of Sudoku’s first appearance in The Times, the puzzle was a permanent daily feature in many newspapers around the globe.
It is ironic that Nikoli is best known for a puzzle it didn’t create, because since the launch in 1980 of its quarterly magazine the company has published about 600 new types of puzzle. Its speciality is grid puzzles, like Sudoku, in which a grid, usually square, needs to be filled in. Part of the puzzles’ charm is the attention to detail—the grids are presented beautifully with the elements arranged symmetrically, or, if not, with care given to how they look. The rules are always very simple, and the pleasure of using a pencil to gradually fill in the spaces is satisfying, addictive and, to people like me, as therapeutic as coloring. I’ve chosen four examples to seduce you.
Nikoli’s magazine has a circulation of about 50,000. Its readers are not only solvers but also the creators of many of the puzzles, sending in several hundred suggestions a year. The next in our collection, Shikaku, was an idea sent to Nikoli by 21-year-old university student Yoshinao Anpuku. Later, he joined the company, and is now its executive editorial officer.
SHIKAKU
In Shikaku the aim is to divide a grid into rectangular and square “boxes.” The numbers in the grid determine the area of the box containing that number (as measured by the number of cells).
I’ll work through an example with you. In the illustration below, A is the opening grid and C the completed solution, in which all the rectangular and square boxes are marked. A good way to start is to look for the largest number in the opening grid, since often the shape and position of its box will be restricted. The largest number in this puzzle is 9, and the only possible boxes for a 9 are a 9 × 1 rectangle or a 3 × 3 square. There are no horizontal or vertical lines of nine empty cells, so the box must be the square, and it fits in only one position, illustrated in B. Likewise the only rectangular box of 8 cells that contains the 8, and the only rectangular box of 6 cells that contains the 6, must be in the positions marked. Once some boxes are drawn in, you can deduce the positions of other boxes.
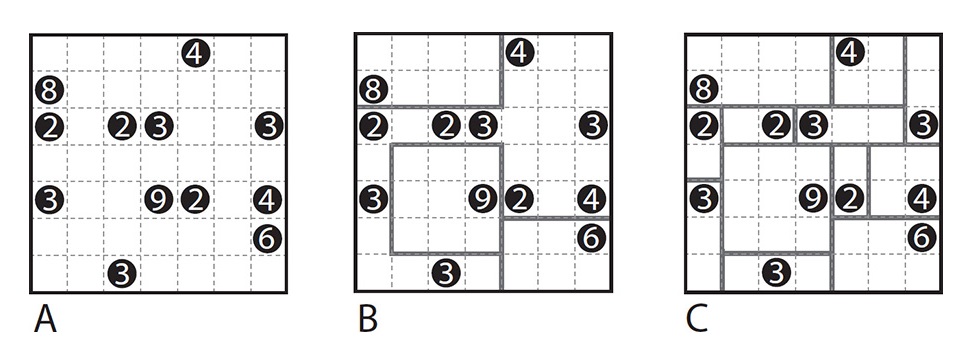
To print this image, visit the book’s webpage and download the PDF.
Nikoli was founded by Maki Kaji, a horse-racing obsessive who named his company after the Irish-trained colt that was the losing favorite in the 1980 Epsom Derby. I first met Kaji at Nikoli’s offices in Tokyo in 2008. He told me about two of his hobbies: collecting rubber bands and taking photos of license plates which display lines in the times tables, such as 23 06 (2 × 3 = 6) and 77 49 (7 × 7= 49). Catching up with him again in 2016, he said his rubber band collection continues to expand, with notable new items from Thailand and Hungary. And he now has pictures of about 85 percent of the lines from the one to nine times tables. “I’m nearing completion. But I have a rule: that I won’t intentionally look for them. I take photos of the ones I come across incidentally.”
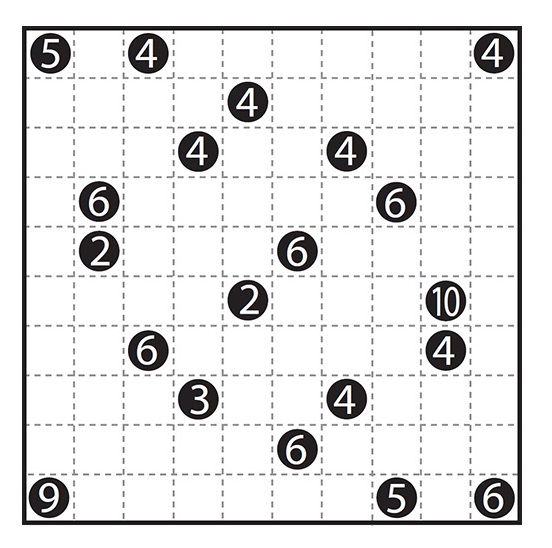
SLITHERLINK
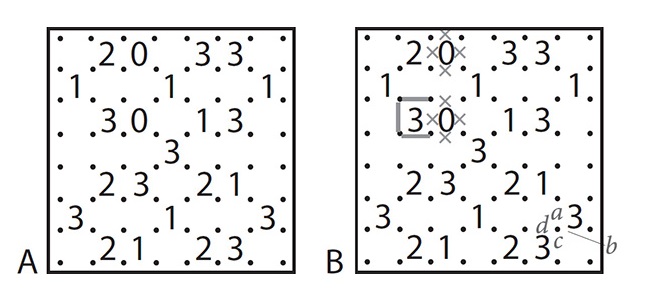
In Slitherlink, the aim is to connect the dots horizontally and/or vertically and to make a single connected loop. The numbers in the grid tell you how many lines surround that number. So, there will be one line around 1, two lines around 2, and so on. You do not know how many lines surround squares with no digits in them. The final loop must never cross itself, nor branch off.
In image A below, the obvious places to start are the 0s, since no lines go around them. Mark little crosses around the 0s to show that no lines can go there, as in image B. One of the crosses is by a 3, leaving only three possible spaces for lines around that number. Fill those lines in. In image C we can continue the loop upward, and there is only one way it can go around the 2. Note that in image B I also marked a, b, c, and d in the spaces where potential lines could come from the dot between two 3s. The loop must pass through this point, since when three lines surround a cell all four dots are used. The loop must pass through either a or b, and either c or d, since if it passes through both a and b or both c and d then the loop will have a branch, which is forbidden. In all cases it must pass through the other two sides of both 3s, so we can mark them in on image C. The full loop is illustrated in image D.
Here’s one for you. Remember there is a single loop, with no crosses or branching. There is only one solution and it can be deduced by logic alone.
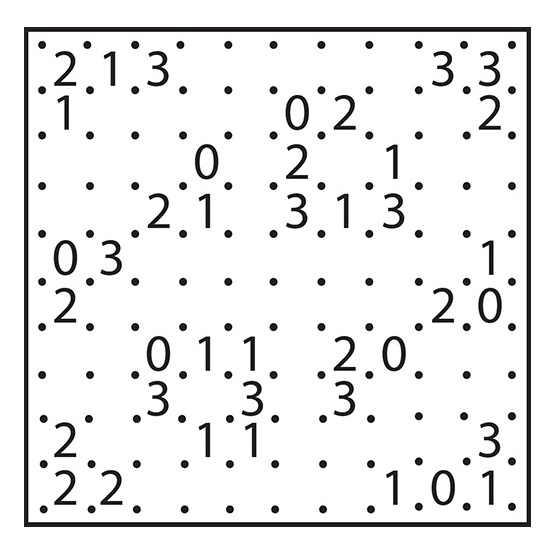
To print this image, visit the book’s webpage and download the PDF.
Slitherlink is one of Kaji’s favorite Nikoli puzzles and it’s one of my favorites too. I love the way you slowly construct the loop, which gradually snakes around the grid. Filling it in is immensely gratifying.
HERUGOLF
Nikoli is constantly introducing new puzzles. Herugolf is a recent offering that was inspired by golf, and how your shots tend to get shorter and shorter as you approach a hole.
In Herugolf you must putt each ball, denoted by a circle, into its correct hole, denoted by an H. The number in the circle is the distance in cells that the first putt of that ball must travel. If the first putt does not reach an H square exactly, the second putt must travel one cell less. If the second putt does not reach an H square exactly, the third putt must travel one cell less, and so on. So, the path of a 3-ball will either travel three squares exactly, or three squares followed by two squares, or three squares followed by two squares followed by one square. The balls can only travel horizontally or vertically. Each new putt can be in the same direction as the previous one, or change direction.
The paths of the balls cannot cross, and balls must reach the holes exactly at the end of each putt. No two balls go into the same hole. The shaded areas are bunkers. A putt can cross a bunker, but cannot land on one.
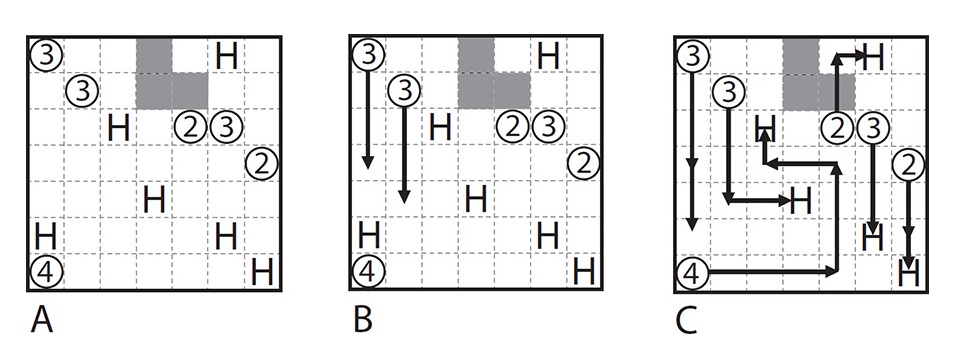
In the example, A is the starting grid. The first thing to do is to see if any balls have their first putt determined. The 3-ball in the top left corner must travel three squares on its first putt. But it cannot go horizontally since it will land on a bunker, so it has to travel vertically down, as in image B. Likewise the 3-ball diagonally adjacent to it will also land in a bunker if putted horizontally, so it must travel down. Each of these balls must continue with a putt that goes only two squares, so the ball from the top left corner is forced to continue down, since the paths cannot cross, and the ball reaches the hole. The other ball must move horizontally, because if it goes down there is no hole it can reach with its following putt, which will be a single square. So it also reaches its hole. Image C shows the completed grid.
To print this image, visit the book’s webpage and download the PDF.
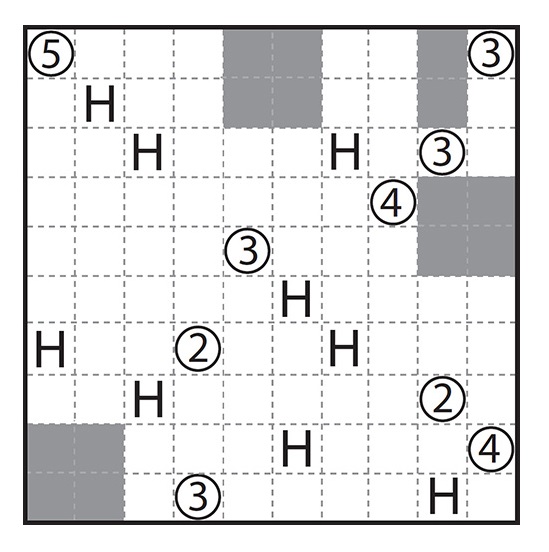
AKARI
My final Nikoli puzzle is also inspired by the real world—in this case bulbs lighting up a room. The aim of Akari is to illuminate the entire grid by placing light bulbs, which are drawn as circles. A black cell with a number indicates how many bulbs need to be positioned in the neighboring cells either directly above, below, to the left, or to the right of that number. Each bulb lights up all unblocked squares in its row and column. Squares that are not adjacent to numbers may or may not have bulbs in them. In the final grid all white squares must be illuminated, and no two bulbs can be in each other’s light path.
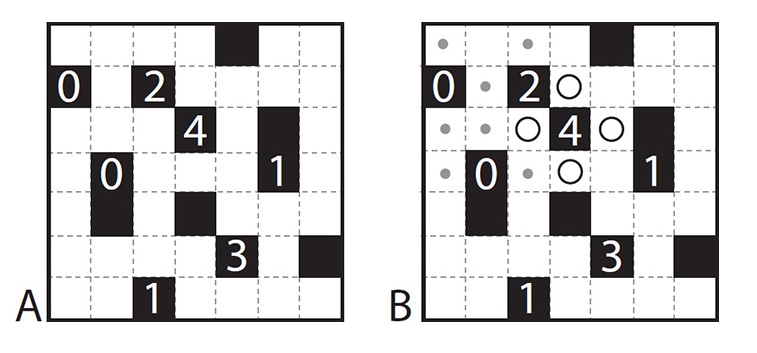
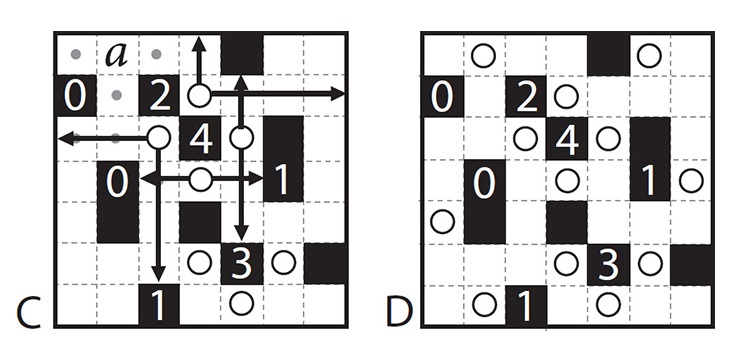
In the example, the empty grid is A. Since each number indicates how many bulbs are next to it vertically and horizontally, we know that there are bulbs in all horizontal and vertical positions next to the 4, and also that there are no bulbs in the horizontal and vertical positions next to both 0s, which I have marked with dots in image B. Since two of the bulbs adjacent to the 4 are also adjacent to the 2, we know that the other sides of the 2 cannot have any bulbs, so I have added an extra dot in the square above the 2. In image C, the arrows show the rows and columns illuminated by the four bulbs placed in the previous image. The square above the 3 cannot have a bulb because it is in the path of another bulb, so the other three sides of the 3 must each have one. We can also deduce that there has to be a bulb in a, since all other positions that would illuminate that square are forbidden from having bulbs, either because we marked them as having no bulb or because they are in the light path of another bulb. The completed puzzle is shown in D.
Now shed some light on these proceedings.
To print this image, visit the book’s webpage and download the PDF.
The placement of light bulbs in interestingly shaped rooms leads us to our final geometrical puzzle.
The image below is the horizontal cross section of a room. The bulb shows the position of the single light source. When the light is switched on, the wall marked in bold remains completely in shadow. (We’re assuming no reflections from the other walls.)
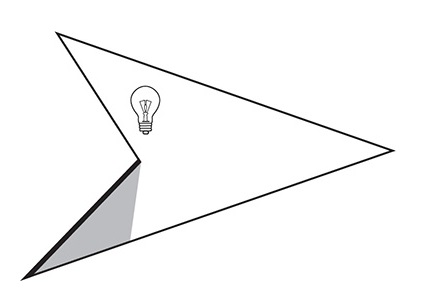
THE DARK ROOM
Design a room with straight walls in which there is a position for a single light source that leaves part or all of every wall in shadow.
The walls of the room must all join. Free-standing walls or edges that stick out are prohibited.
Would the last person to solve this one please turn off the lights.
