The best laid schemes o’ mice an’ men/Gang aft agley.
Robert Burns, poet
This chapter is where we finally face up to uncertainty, only to discover that it comes in two forms: one that we can figure out reasonably well and another that defies all attempts at measurement. Our aim is to provide a practical guide for coping with your daily dose of uncertainty. If that’s cheered you up no end, here’s a tragic tale. It may dampen your spirits, but it will help to explain the two types of uncertainty.
Klaus Bauermeister, originally from Zurich, was working in New York for the private wealth division of a well-known Swiss investment bank, when he planned the fateful trip. In fact, he spent nearly seven months planning it. His son Frank was in his last year of high school and would turn eighteen on June 27, four days after graduation. That was when Klaus planned to hand him the surprise envelope containing the tickets and highly researched itinerary. The holiday would take the whole family (Klaus, his wife, his daughter, and Frank) from New York to Singapore, then to Thailand, where the Bauermeisters would tour the northern forests – partly by elephant – for a week. Next, they’d relax in the resort of Phuket for three days, before returning to Singapore for a weekend of pampering in the Swiss Hotel.
Klaus’s passion for planning and detail was a way of life. Take going to work each morning. He lived on the Upper East Side, at 94th Street between Lexington and 3rd Avenue, and combined walking with taking the subway to his office on the corner of 51st Street and 6th Avenue. Klaus always left at exactly 8.00 am, took exactly the same route and loved recording the time it took door to door each day. The average was almost exactly forty-three minutes – and on all but the exceptional occasions he knew he’d be in the office between thirty-seven and forty-nine minutes from leaving home.
When June 27 (a good day for commuting at thirty-nine minutes) came, Frank whooped with delight, which gave Klaus all the joy he’d planned for. The birthday envelope – handed over with ceremony at the family’s favorite Thai restaurant that evening – was bulging with meticulous detail. From choosing Singapore Airlines for the long-haul flights (it had the best safety record) and getting seats above the wing (in case of an emergency landing), to booking restaurants and hotels, Klaus had thought of everything. He’d spent hours and hours researching it all on the internet. Well, to tell the truth, it was his patient secretary who’d done a lot of the groundwork, but the banker prided himself on having zeroed in on the best options.
Sometimes Klaus’s wife made gently affectionate comments about him being a control freak, but he didn’t mind. Unlike his son, he didn’t like surprises and, anyway, there weren’t many downsides to over-planning. Of course, he remained blissfully unaware that his long-suffering secretary didn’t share this analysis. But in this particular case – taking his precious family so far from home – even she could see that the price of planning was undoubtedly worth paying.
When the family finally arrived in Phuket on July 14, 2006, everything had gone perfectly according to plan. There were no unpleasant surprises of the kind that Klaus hated. No airplane delays, no stray luggage, no mislaid reservations, no upset stomachs. The hotels and restaurants all lived up to his expectations, with the exception of one meal, which had seemed a little over-priced given its quality. There weren’t even any elephant-riding accidents, an activity which had given Klaus a few nightmares at the planning stage. (He’d only made the booking when he discovered the elephant operators adhered to the highest standards of health and safety, with harnesses and helmets for all passengers.) Singapore’s cleanliness and orderliness had been a particular delight and the Swiss banker from New York was looking forward to returning there as he lay on the idyllic beach.
On the third morning in Phuket, he succumbed to the temptation of using his BlackBerry. But not for work purposes, mind you. Klaus had been pondering his pension arrangements in bed the night before and wanted to contact his financial adviser before he forgot. Having woken early so that his family wouldn’t catch him in the act of emailing, he strode out onto the beach and into the brilliant sunshine . . . only to feel the hot rays of risk beating down onto his pale skin. In his enthusiasm for that pensions business, he’d forgotten to apply sun block and, with all those articles in the papers about melanomas, well, you can’t be too careful, can you? So Klaus stepped into the convenient shade of a nearby palm tree, whereupon a coconut promptly dropped on to his head with a resounding thud.
By the time the hotel staff came running, he was no longer breathing. Their efforts to revive him were futile and ten minutes later a Western-trained doctor (whose presence had been one of the plus points for Klaus in choosing the resort) pronounced him dead. As the same doctor later assured Frank and his distraught mother and sister, it had all happened too quickly for Klaus to feel either pain . . . or surprise. Klaus had become one of a very small number of people who suffer death by coconut, a tragic event that even he, the master of planning, couldn’t have predicted.
There is, however, a final twist in Klaus’s story. It isn’t quite a happy ending, but offered some solace to his grieving family. They discovered that, years earlier, Klaus had taken out a life insurance policy for 7.5 million Swiss francs. He’d also recently purchased travel insurance covering any expenses incurred by an accident during the trip, plus three million dollars for death or permanent disability. It turns out that Klaus’s passion for planning had also covered the possibility of his own early death and its unexpected consequences for his family. Though he was powerless to save his own life, he had at least made sure his loved ones would suffer no financial hardship.
Klaus, Frank, and their family are – we’re pleased to report – entirely fictional. But our next story, that of Pierre Dufour, is tragically true, even if it relies on the same kind of awfully bad luck. Dufour, a forty-year-old Canadian, lived in Arizona with his wife and two children. His passion was investments, and he’d put practically all his money into stocks. He was extremely pleased with himself, as his portfolio had done extremely well during the five years he’d been in the USA.
Pierre Dufour died or, more precisely, committed suicide early in the morning of October 20, 1987, the day after Black Monday. The stock market had fallen by more than 22% in just one single day – and his own investments by more than 39%. His wife said that he was still worth many millions, but for Dufour losing more than $4.8 million in a single day was more than he could bear. Even if he’d been able to accept the loss of his money, he couldn’t take the way his beliefs had been shaken. His portfolio consisted mainly of growth stocks and small caps, and had therefore been outperforming the Dow Jones and S&P 500 by more than 6%. Dufour had remained confident it would soon double or triple in value until less than a week before his death.
His confidence was not entirely misplaced. US stock markets had been growing nicely since the early 1980s. Then the market suddenly started falling. It fell 2.7% on October 6, 1987, and by smaller percentages over the next four days. On Tuesday, October 13 (the number 13 was always a lucky one for Pierre Dufour and Tuesday was his favorite day of the week) the decline halted, and the market grew by nearly 2%. Dufour wasn’t particularly bothered by these events, as they were normal stock-market fluctuations. However, the next three days weren’t at all typical. On Wednesday, October 14 the market fell 3%, on Thursday 2.3% and, worse, on Friday, October 16, an additional 5.2%. But Pierre Dufour hoped that the decline was over and that the next week would see another reversal of the downward trend. The US economy was growing strongly, corporate profits were high, and everyone was predicting they were going to increase further in 1988. So, all in all, there were no signs of any trouble and he saw the decline as a way to increase his profits. For these perfectly sound reasons, Dufour borrowed money against his existing portfolio to buy more stocks at bargain prices on the Friday afternoon.
Monday, October 19, however, turned out to be the worst day in the history of the stock market. It was even worse than October 28, 1929, which kick-started the Great Depression. By the time he tragically ended his life, Pierre Dufour had lost more than half of his money in just ten trading days. The shock was as great as if he’d been hit by a falling coconut – and his state of mind darker than the blackest Monday.
Although there have been many suggested explanations for Black Monday, none of them seems quite convincing – even with the benefit of hindsight. Today, it’s only when we hear about events like Pierre Dufour’s suicide that we can begin to imagine how the entire financial world was taken by total and utter surprise on that Monday. The stock-market collapse of 1987 was what former trader Nassim Nicholas Taleb calls – in his excellent book of the same name – a “Black Swan,” a totally unexpected event with mammoth consequences.1 Like the coconut that killed Klaus, no one, including all the experts whose own finances were ruined, saw it coming.
Stock markets have a mind of their own. After October 19, stock prices started rising again as if nothing had happened. Exactly twenty-one months and seven days later, the S&P 500 regained the same value as on October 6, 1987. The upward trend continued for over a decade – until the events that led up to the 2000–2003 market downturn. Today, Black Monday is no more than a blip: a small trough in a graph full of mountainous peaks and low valleys. Had Dufour been alive today, he would have seen his monetary Fortune increase many times over. It even turns out that he’d believed in the right kind of investments. His growth and small-cap stocks gained in value even more significantly than the S&P 500.
But of course, it’s too late for Pierre Dufour. It’s also too late for James Smith of Cedar Rapids, Iowa. He committed suicide after his broker demanded back some of the money he’d borrowed to buy stocks that were now rapidly falling in value (known in the business as a “margin call”). It’s too late as well for the brokerage firm vice-president killed by George King of Durham, North Carolina, after King was asked to repay part of what he had borrowed (another margin call). And too late for King who then went on to kill himself.2 Provided they could have stalled their creditors long enough for the markets to rise again, Smith and King would have been fabulously wealthy men today. The same would have been true of Dufour.
The story of Klaus illustrates the crucial difference between two types of uncertainty. In honor of our fictional friend, we call them “subway” and “coconut” uncertainty, respectively. We go into more detail below, but the main distinction is that you can quantify and model subway uncertainty, while coconuts remain totally and utterly unpredictable. Now, there’s no doubt that we humans have great difficulty coping with uncertainty in any way, shape, or form. But one of our greatest difficulties, for both lay people and statisticians alike, is distinguishing between these two types. More importantly, to believe that “coconuts” can be quantified and modeled as if they were “subways” is not simply misguided. As the story of Pierre Dufour shows, it can also be tragic.
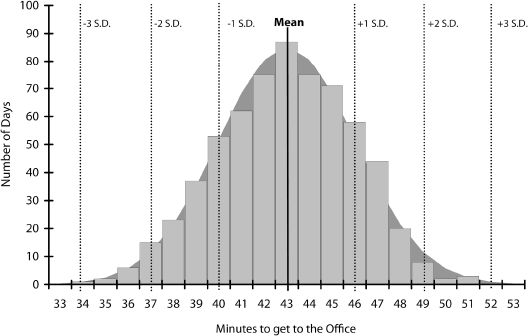
Subway uncertainty was what Klaus experienced each day as he commuted from his home to his office in New York. The uncertainty centered on how long the journey took. Klaus knew that it rarely took exactly the same number of minutes as on the day before. Instead, there were variations due to a whole bunch of uncontrollable factors that each had an independent effect on his travel time. These ranged from mundane train delays caused by crowding on the platforms or obstruction of the closing doors to freak weather conditions or criminal activity. But, thanks to Klaus’s statistical training, he was able to map the situation very clearly. First, he knew his average (or mean) travel time was forty-three minutes. Second, he knew that a little more than two-thirds of his journeys took between forty and forty-six minutes (that is, within three minutes of the average). Third, he knew that about 95% of his journeys took between thirty-seven and forty-nine minutes (that is, within six minutes of the average). He also knew that the remaining 5% of his journeys – apart from some very rare exceptions – were in the range of thirty-four to fifty-two minutes (that is within nine minutes of the average). Finally, his travel times weren’t increasing or decreasing over time: there was no trend.
In words rather than numbers, Klaus’s journey to work was an event that happened very often and the time it took didn’t fluctuate greatly from the average. Although the exact number of minutes remained uncertain when he set off each morning, Klaus could be confident that he would arrive before 9.00 am. In all the years he’d lived in New York, he’d only ever been late twice – and that was because of exceptionally heavy snow falls. What’s more, the factors affecting his travel time were many, various, and – most of the time – independent of each other: a mechanical problem here, a crowd of Japanese tourists there, and maybe an icy patch on the not-so-sunny side of the platform. Being a meticulous kind of guy, Klaus had recorded all his travel times for the last three years and two months in an Excel spreadsheet reproduced in figure 16 with a symmetric bell-shaped curve behind it. This shows, for example, that on eighty-seven days it took him forty-three minutes while on just one day it took him thirty-four minutes and on one other day fifty-two minutes (see figure 16).
Of course, subway uncertainty applies to lots of events that have nothing to do with subways. An obvious example is the game we played in chapter 8 of flipping a coin 100 times. We can forecast the fluctuations, or uncertainty, in our expected gains or losses fairly accurately. Thanks to opinion polls, we’re also pretty good at knowing who’s going to win an election the day before it happens, or even more accurately on the day itself – using exit polls. And, as we saw in the previous chapter, if statistical reasoning is allowed to prevail over emotions, sales data – provided we have enough – allow companies to make reasonable projections into the future and measure the associated uncertainty. Incidentally, amongst the most expert of all forecasters are suppliers of electricity. If the average usage on July days between 11.00 am and 3.00 pm, at a temperature of 32 degrees centigrade, is 12,000 MW, it’s highly unlikely that it will be more than 14,000 MW on such a day in the future. Electricity companies have the art of prediction down to a T – and quite literally in England, where supply is always boosted for the half-time break in national soccer games. That’s when an entire country gets off the sofa and puts the kettle on for a nice, refreshing brew of their favorite beverage.
Figure 16 Klaus’s journey to work
Coconut uncertainty is quite different from subway uncertainty. A “coconut” is the occurrence of a totally unexpected event that has important consequences. It may be something that happens so rarely that it’s impossible to keep an Excel spreadsheet full of statistics. Or it may be something common enough for us to know the likelihood of such an event taking place . . . but with no idea of when or where. The classic example from the natural world is that of large earthquakes. It’s well known that earthquakes tend to occur in parts of the world where there is friction between tectonic plates in the Earth’s crust. In fact, in these regions (such as parts of California) small tremors are a way of life.3 However, from time to time, there are major earthquakes that wreak death and destruction, as in San Francisco in 1906 or Chile in 1960. Today, unfortunately, science cannot tell us when or where in the tremor-prone regions of the world the next big quake will take place or how many people it will kill.4
Having said all that, scientists have uncovered a remarkable statistical correlation between the size of earthquakes and the frequency of their occurrence. There is, of course, a great deal of data about earthquakes and their sizes, as measured on the Richter scale. And it doesn’t take a great deal of analysis to find that, as size increases, frequency decreases in a very consistent manner.
In geological terms, in any given year, there are, on average, roughly 134 earthquakes worldwide measuring 6.0 to 6.9 on the Richter scale, around 17 with a value of 7.0 to 7.9 . . . and one at 8 or above.5 In other words, scientists are pretty sure that there’ll be, on average, one huge earthquake in the world every year. The trouble is, they’re completely in the dark as to when or where it will take place and whether it will occur in a populated region. The underlying reason is that the Earth’s crust is in a so-called “critical state.” This means that conditions are ripe for earthquakes across the globe’s tremor-prone zones, but big ones only occur when there’s a chain reaction of smaller events that multiply into a major natural disaster – a bit like the butterfly effect we saw in chapter 8. We can also apply this model to our lives – each of which can be considered to be in a critical state. That is, a totally unpredictable small event (such as a tropical breeze) can initiate another everyday occurrence (the falling of a coconut), which interacts with a further trivial incident (someone standing under the tree) to produce a fatal accident.
In statistical terms, there are big differences between Klaus’s commuting times and the occurrence of earthquakes. The distribution of the various sizes of earthquakes isn’t nicely centered around the average value with just as many big and small ones on each side (as in Klaus’s commuting graph). Instead, the most frequently occurring size of earthquake is very small, and the larger the earthquake, the less likely it is to occur. On top of that, the occurrence of a destructively huge earthquake in any given tremor-prone region this year is clearly possible, while the likelihood of an extreme commuting event – such as Klaus being two hours later for work – isn’t quite zero, but is astronomically small. When it comes to earthquakes, all we can really do is to wait until the coconut – or more accurately, the roof – falls on our heads. If we’re lucky enough to live on a wealthy fault line, we don’t have much reason to worry. Engineers will have developed building techniques to save us . . . but there’s nothing they can do to stop the quake itself.
Klaus – to his eternal credit – demonstrated that he understood the difference between the two types of uncertainty. His meticulous research and planning showed that he knew how to take advantage of the regularities of subway uncertainty. And by taking out insurance to cover unforeseen disasters far from home, he also proved that he’d considered the possibility of “coconuts.” That he was killed by one shouldn’t diminish our respect for him. It’s simply not possible to avoid coconut uncertainty in our daily lives but, as Klaus showed, it is possible to minimize their negative consequences through planning.
Coconuts, of course, come in many different shapes, sizes and textures. They can be big, red double-decker buses going too fast through the middle of London or small explosive devices on transatlantic flights. They can be as wet as a tsunami, dry as a sandstorm, hot as a volcano, or cold as an avalanche. In this book, we have emphasized coconuts with negative consequences. However, sometimes coconuts can make you jump for joy: winning the jackpot in the Spanish lottery, finding buried treasure in your back yard, getting a hole in one, or even backing a big winner on the stock market.
Although it doesn’t grow on trees, money is one of the most common forms of coconut. In many ways our economy too is in a critical state. We know, for example, that in any given year, there will be many business failures. While most of these will be small firms, we can be pretty sure that there’ll also be big, hairy, audacious bankruptcies on the scale of Lehman Brothers, WorldCom, Enron, or LTCM. Every so often there will be major after-shocks that ripple throughout the global financial markets. And, once in a blue moon, there’ll be a Black Monday or Tuesday. We don’t know when, of course, but we do know that these extreme fluctuations happen rather more often than they theoretically should – especially if we believe the models of subway uncertainty provided by conventional statistical theory. Roughly speaking, the market behaves rationally 95% of the time, under the influence of the wisdom of crowds . . . but 5% of the time the crowd goes crazy. As Alan Greenspan, former Federal Reserve Chairman suggests, in his memoirs The Age of Turbulence, the problem is not simply that collective human nature creates and bursts bubbles. It’s also that our collective memory wipes out the past. He writes: “There’s a long history of forgetting bubbles. But once that memory is gone, there appears to be an aspect of human nature to get cumulative exuberance.”6 Ultimately, it’s mass hysteria and collective loss of memory that transform markets from subways into coconuts.
Before braving a more complex statistical explanation of the difference between subway and coconut uncertainty, let’s take a short detour into statistical history.
As we saw in chapter 8, the human race was a late developer as far as probability and statistics are concerned. The first formal attempts to apply probabilistic reasoning to gambling date from the seventeenth century, and the use of statistics to describe characteristics of human populations only really evolved in the nineteenth century. Curiously, even though public lotteries, annuities (payments of an annual sum of money until a person’s death), and insurance policies were common in the eighteenth and nineteenth centuries, it’s clear that many professionals in these fields really didn’t understand basic statistical concepts. The purchase price of annuities, for example, often didn’t vary according to the age of the purchaser.7 But in the twentieth century, we made significant progress. In particular, we invented computers – which made it a lot easier to use statistical models in decision making.
Even before computers, human beings made some intellectual breakthroughs of their own. Around 300 years after French mathematicians Pascal and Fermat made the first formal analysis of gambling (see chapter 8), the American economist Harry Markowitz published a ground-breaking paper on investments in the Journal of Finance.8 His innovation was to introduce the concept of risk, as well as returns, into portfolio selection. He suggested that if you’re unwilling to accept a larger risk, then you should also be prepared to accept lower returns. He also recommended minimizing risk by building a portfolio of securities whose returns do not co-vary (that is, don’t move up and down together). It’s the same as the traditional, common-sense concept of not putting all of your eggs in the same basket.
But Markowitz went one step further. He suggested using a statistical tool to measure risk. This was the “standard deviation,” a term coined toward the end of the nineteenth century, but a concept that had been around for over 200 years. We won’t go into how to calculate it here, but just say that it’s a statistical measure that tells you how closely the various values of a dataset (for example the times it took Klaus to get to his office, or the daily prices of a given company’s stock over a year) are dispersed around their average or mean. Markowitz was thus equating future risk with past dispersion or volatility, as measured by the standard deviation.
Of course, whether people use formal probabilistic models or not, uncertainty never goes away. Neither do risk or opportunities. Yet Markowitz’s work started an investment revolution. It gave investors a way of quantifying risk (and opportunity) and of tackling uncertainty head-on instead of ignoring the issue. This was an incredible achievement. But was the great economist’s analysis complete? The short answer is “no.”
The spate of statistical modeling unleashed by Markowitz’s paper on the financial markets wasn’t fully accurate. The experts started treating the financial markets as if the fluctuations were like the time taken by Klaus to get to work each day. But unlike Klaus’s commuting times, the values of, say, the DJIA (the Dow Jones Industrial Average) aren’t closely clustered around their average. There are many more big fluctuations than most people – even experts – expect. And some of those people, like Pierre Dufour, can’t take the emotional impact of the biggest fluctuations.
But the road from theory to practice is full of potholes. Nobody (except for Klaus, and he’s both fictional and dead) is going to draw complex graphs or identify statistical models for everyday decision making. Instead we offer you a simple rule of thumb. We could warn you about all the emotional, cognitive, and technical biases which can prevent good decision making. But we’d prefer to focus on the positive for a bit. We’ll suggest following a mechanical routine for handling uncertainty that can overcome these biases. As an analogy, imagine you’re a top golfer about to make a winning putt, or a star tennis player about to serve for the Wimbledon title. The outcome is both crucial and uncertain. And too much thinking, feeling, or technical analysis can be fatal. The way real professionals deal with the situation is to have a well-defined routine and to follow it every time they putt or serve. The tennis player might bounce the ball precisely five times, while the golfer follows a strict ritual of movements. It’s the automated nature of the routine that leads to consistency of execution. Amidst all the pressures, in the intense heat of the moment, it’s still possible to make a winning shot. And the way you handle uncertainty can be the same.
As we mentioned before, subway uncertainty is something that we can quantify or model, whereas coconut uncertainty is extremely difficult if not impossible to quantify or model. Almost all uncertain situations include elements of both subway and coconut uncertainty. Yet another way to think about this – and borrowing from a quote by Donald Rumsfeld (a former US Secretary of Defense) – is to distinguish between known knowns, known unknowns, and unknown unknowns. For example, the return from an insured fixed deposit in a bank is a known known – we know exactly what we will receive in the future. The outcome of a coin toss is an example of a known unknown. We know that the outcome of the coin toss will be heads or tails, but we don’t know which. Similarly, we know that there will be bubbles in financial markets in the future, but we don’t know when or where. Then there are the unknown unknowns, unique and rare events that are completely unexpected and unimagined. These are the Black Swans, so eloquently characterized by Taleb in his book. These can only be identified after their occurrence, for if we could have anticipated them before, they wouldn’t be Black Swans. Looking back at history, the internet was a Black Swan, as was the Great Depression of 1929–1933.
Once we accept that there are known knowns, known unknowns, and unknown unknowns, we can set about thinking about the underlying uncertainty in a more systematic manner. There is no uncertainty associated with known knowns, as we know exactly what will happen. In the case of known unknowns, we may be able to quantify and model the uncertainty for some events but not for all. Going back to our examples above, we can model the uncertainty of a coin toss, but it is impossible to quantify or model the uncertainty concerning future bubbles in the financial markets even though we can clearly expect these to occur. (A senior member of the Chinese government once aptly remarked that a financial market is like champagne – if it did not have bubbles, no one would be willing to drink it!) What this means is that some of the known unknowns involve subway uncertainty (like the coin toss) while others are part of coconut uncertainty (like bubbles in the financial markets). The unknown unknowns are necessarily part of coconut uncertainty. These distinctions are summarized in figure 17.
Figure 17 Subway and coconut uncertainty
Our suggested routine for assessing uncertainty has three steps – all beginning with the letter A. It’s the triple A approach that we mentioned briefly in chapter 1:
1. Accept that you are operating in an uncertain world.
2. Assess the level of uncertainty you are facing using all available inputs, models, and data, even if you’re dealing with an event that seems regular as clockwork.
3. Augment the range of uncertainty just estimated.
Here’s the routine again, in a bit more detail.
Psychologically, we must first accept that uncertainty always exists, whether we like it or not. Ignoring it is not an option. This also means accepting that accurate forecasting is not an option either. Illusory forecasting practices, the extreme example being horoscopes, may be entertaining, but they’re not useful. Believing that experts – from doctors and fund managers to management gurus and fairground clairvoyants – can predict the future may bring comfort in a confusing world. But, as we’ve illustrated many times in this book, our inability to predict the future accurately extends to practically all fields of social science. It’s important to accept, once and for all, that uncertainty cannot be eliminated – even if your forecasts are reasonably accurate and your planning meticulous (think of Klaus). We have no control over a wide range of future events from earthquakes to Black Mondays or Tuesdays.
The key to handling uncertainty is finding ways to picture the range of possible outcomes. Whether your interest is in sales data, stock prices, the weather, earthquakes, or simply getting to work every day, you can’t hope to be realistic about assessing the chances of anything happening, unless you at first identify all the things that could possibly go right or wrong. Once you’ve accepted all the possibilities, you’re ready to move on to the next step.
The world of finance before and after 1952 is a good example of the importance of accepting uncertainty – and then moving on by trying to assess it. As we pointed out in chapters 4 and 5, the majority of financial professionals now realize that accurate forecasting of the markets is impossible. However, this doesn’t stop them giving advice to their clients about achieving the maximum returns for a given level of risk. In some cases, they may even do so for a minimum cost, for example, by recommending index funds or similar vehicles. At the same time other professionals specialize in creating investments with different levels of risk by, for instance, diversifying between bonds and stocks of various degrees of volatility. Today there are many financial products, aimed at all sorts of investors, covering all types of needs and risk profiles: from venture capital to treasury bills and certificates of deposit. This just didn’t happen before 1952, when no one explicitly considered risk.
Skeptics might argue that there’s no point in attempting to control risk if your decisions about the future are based on a model that doesn’t incorporate the considerable number of big fluctuations that occurred in the past. This is a valid criticism. Fortunately – for once in this book – there is a straightforward solution.
First, we suggest that you use the available models to calculate the kinds of outcomes that would be expected with subway uncertainty. Collect all the data you can to figure out as accurately as possible what mean and standard deviation best describes your data. Often people think that what they are predicting is unique, for example, the performance of a newly issued stock over the next six months, or the sales of a novel by an unknown author. Our advice in such cases is to ignore uniqueness. Instead, look at the track record of new issues and the sales of first-time authors in general. You probably have no valid reason to believe that the uncertainty surrounding your new issue or author differs from that of the wider population of new issues and authors to which they belong. What’s the statistical history of the general population? Having answered this question, you’re ready for the next stage.
Whatever your assessment in the previous stage, you can be sure you’ve just underestimated the true level of uncertainty in your situation. We’d like to suggest two ways of augmenting your previous assessment to realistic levels.
In the last chapter we demonstrated that, although people have great difficulty in predicting the future, they have little difficulty in explaining the past. So our first proposal is to exploit this hindsight bias through what we call “future-perfect thinking.” To explain what we mean, here’s an example. Imagine you are fifty years old and are planning investments to ensure your financial future. In particular, you want to estimate how much you’ll have in the way of savings when you reach the age of sixty-five.
Now imagine that you actually are sixty-five – that is, we’ve just fast-forwarded fifteen years into the future. How big is your nest egg now? Unfortunately, it turns out that because of the great Black Friday crash of 2021, your savings – which were mainly invested in US equities – are quite small. How did this state of affairs come to pass? Over to your imagination to find a realistic-sounding story about what “happened.” And most people – with the benefit of “hindsight” – really do come up with a convincing explanation. It’s just a lot easier than looking forward.
Now take a different tack. Imagine once again that you are sixty-five, but this time your savings are three times greater than the amount forecast fifteen years ago when you were fifty. Time to build that swimming pool and buy the yacht! But how “did” this happen? Once again over to you to tell the story. Chances are, it’s going to make this outcome sound a whole lot more likely than it originally seemed.
If you do this kind of exercise a few times you’ll start to develop a feeling for different futures and the fact that they are all plausible. Some of these futures will involve coconuts of different kinds and, though there’s no formal technique for converting plausibility into probability, you can use the insights you gain to develop appropriate risk-protection strategies. This is the essence of future-perfect thinking. It involves using the fluency of hindsight to develop clearer pictures of the future. It’s a way not only to augment your assessment of a coconut occurring but also to devise a plan for coping with it in advance.
The second strategy we suggest is less imaginative and a lot easier for the literal-minded to apply. Let’s illustrate with an example again. As you’re probably well aware by now, a common problem in assessing risk is the lack of data. Consider, for example, having to predict the sales of a brand new product. Just how low or high could the number of units sold be in the first year? One way of answering this question is to ask those involved – the product managers, technical staff, and sales team – to estimate a range of upper and lower values that would include 95% of all possible outcomes. And once they’ve come up with a range, double it!
The reasoning behind this rule of thumb is simple. Extensive empirical evidence shows that the range of such forecasts is typically too narrow. People underestimate uncertainty, perhaps because their powers of imagination are too small or because they don’t know how to use future-perfect thinking. The trick is to use (but not believe) the numbers you’re given and magnify them considerably. Doubling the range will provide a much more accurate estimate of uncertainty.
The same approach can be used when there’s some, but not much, past data available. Here you can use the difference between the largest and smallest observations in the past as an initial estimate of the range . . . but then double this too. Why does this help? The main reason is that, to estimate a range accurately, you need to observe values at the two extremes. However, by definition, extreme values occur only rarely and so in small samples you’re unlikely to observe them. Doubling what you’ve observed in a limited number of past occurrences is a crude but more realistic way of estimating the 95% range.
If, on the other hand, you’ve got a lot of data at hand, you may not need to double the range. Instead you can multiply it by a value ranging from, let’s say, 1.5 to 2. The more data available, the closer you can go to 1.5. These values may sound arbitrary, but we assure you they’re based on empirical observations. If you like, you can experiment yourself by keeping track of your estimates and then calculating the percentage of time that actual values are within your estimated ranges. It’s a shame that so few professional forecasters follow this procedure. It might make them more realistic about their own abilities.
Finally, it’s important to realize that the magnitude of uncertainty increases the longer we forecast into the future. Of course, this depends what your unit of future measurement is. If you’re thinking in terms of sales it could be one year or just one quarter. If it’s your pension you might be thinking in terms of decades.
Once you’ve reached a realistic estimate of uncertainty, how do you go about managing the risk? If stock market investments are involved, for instance, you have to consider the possibility that your stock may fall by as much as 40% in a few days. Here the questions center on whether you’d have enough time on your side and cash in the bank, in case part of your investments are on borrowed money, to ride out the storm or whether you’d need to sell at a loss and move on. If the latter, would you still have enough money to live adequately? Have you thought through the costs and benefits of diversification – both by types of investments and geographically? What reserve funds can you create that might withstand financial earthquakes like Black Monday and Tuesday? Are there different types of insurance that you could investigate? Similarly, when developing new products, a CEO must consider whether the company can survive a complete product failure.
In the final analysis, we can’t take actions to mitigate all the uncertainties we face. If a large meteorite hits the earth and causes a new ice age, there’s nothing we can do – especially as most of us are preparing for the onslaught of global warming. Yet we must continue to live with the possibilities of both types of coconut. On the other hand, we should always pay attention to what we can do. There was nothing that Klaus could have done to avoid dying from the fallen coconut, but there was no reasonable justification for Pierre Dufour to commit suicide. In the long run, as he should have known, markets recover and continue their long-term growth. It would only have been a matter of time before he recovered his losses and saw his personal Fortune grow again. Perhaps that’s what wisdom really is: knowing what our actions do and do not affect.
As so often in life, it’s a writer who sums the situation up. The following quote from G.K. Chesterton explains how both subway and coconut uncertainties interact in affecting our experience of the world:
The real trouble with this world of ours is not that it is an unreasonable world, nor even that it is a reasonable one. The commonest kind of trouble is that it is nearly reasonable, but not quite. Life is not an illogicality; yet it is a trap for logicians. It looks just a little more mathematical and regular than it is; its exactitude is obvious, but its inexactitude is hidden; its wildness lies in wait.9
The quote encapsulates this chapter better than any summary we can produce, but here goes . . . It’s tempting to see nice patterns in the past and fit them to the future. But even when we can trace the patterns, there are no guarantees for the future. All we can do is accept the uncertainty, make a reasonable assessment of our chances, and then augment that assessment, in recognition that life is rarely that simple. But enough summarizing. The wildness of the next chapter lies in wait.