
POSITION, VELOCITY AND ACCELERATION
In a 200 m running race, who is most likely to win, the athlete with the fastest acceleration or the athlete with the highest top speed?

By the end of this chapter you should be able to:
•Describe the different forms of motion and the difference between scalar and vector quantities (for example, displacement vs. distance)
•Calculate average and instantaneous velocity and acceleration given the appropriate displacement/velocity and time data
•Define the direction of a movement
•Build a simple biomechanical model to determine the importance of each segment of a race (for example, acceleration phase vs. top-speed phase)
•Describe how performance improvements and different phases of a race affect the race’s outcome
To answer this question properly, we first need to understand position, velocity and acceleration. I shall also take the opportunity to introduce some very important concepts that will not only help you understand the reasoning behind the answer to the above question but will also be important for your understanding of information presented in other chapters. Some of the information might seem like biomechanics jargon but it is very important. To understand biomechanics, you must read and understand the following passages.
Types of motion
Linear motion (also referred to as translation, as opposed to rotation) can occur either in a perfectly straight line (rectilinear motion) or in a curved line (curvilinear motion). Since a 200 m race is usually partly run on a curved part of the track, it is partly curvilinear and partly rectilinear.
Scalar versus vector quantities
There are two ways to describe how far someone has run: distance and displacement. One is a scalar quantity and the other is a vector quantity. A scalar quantity is a simple measure of magnitude (how big, fast, long or wide something is). That is, you can measure it with a scale of some sort. However, a vector quantity has magnitude and direction (north, 22°, left) so you need to provide more than just the scale or magnitude of the quantity. When describing motion, ‘distance’ is a scalar quantity and refers to the sum of all movements in whatever direction, for example 21 m or 3.2 km, whereas ‘displacement’ refers to the end result of a movement and is described with both magnitude and direction, for example 21 m north or 3.2 km up (see Figure 1.1). We use different symbols to denote them to avoid confusion; s is used to denote displacement, whereas d is used to denote distance.
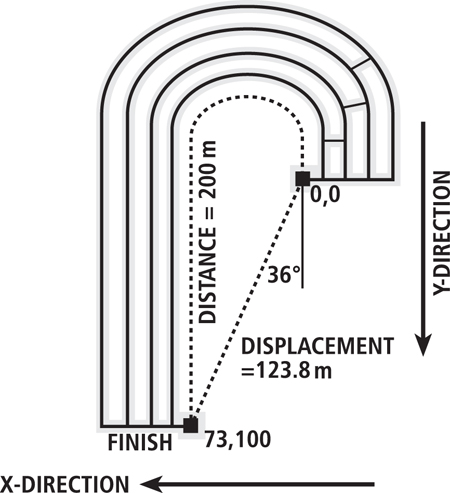
FIG. 1.1 A runner running on the inside lane of an athletics track displaces (s) 123.8 m at an angle of 36°, while covering a distance (d) of 200 m. The distance, a scalar quantity, is more important than the displacement, a vector quantity, in this instance.
If a runner started on a running track (like that in Figure 1.1) at position 0,0 (that is, the runner has moved 0 m in both forward (y) and sideways (x) directions) and finished exactly at the 200 m point, which is at position 73,100 (73 m in the x-direction and 100 m in the y-direction) while running in the inside lane, then the displacement (s) is 123.8 m at an angle of 36° relative to a straight line but the actual distance (d) run is 200 m. So because a 200 m race contains a curvilinear component, we have to choose whether to measure distance or displacement. There is not much point knowing the displacement of the runner, since the idea of a 200 m race is to run 200 m as quickly as possible, so we need only care about distance. Of course, in the rectilinear 100 m race, distance and displacement are the same, although we have to specify a direction if we describe the displacement.
BOX 1.1 CALCULATING VECTOR QUANTITIES
Calculating the displacement of a person or object is relatively easy if movement occurs in two directions, such as in the example in Figure 1. However, if you want to calculate the displacement of something that has travelled along multiple paths, you might consider using the ‘tip-to-tail’ method. We can represent an individual movement as an arrow that has both a length and a direction (remember a vector quantity, such as displacement, has both a magnitude and direction). By placing each arrow’s tail next to the tip of a preceding arrow, you can eventually determine the final displacement (dashed arrow).
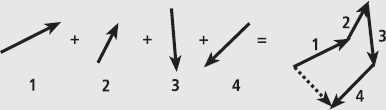
Fig. 1
Consider an orienteer who runs for a certain distance east-north-east, then a little north-north-east, then almost due south, finishing south-west. We can draw arrows representing these four movements (1–4) and thus find the final displacement of the orienteer (dashed line).
In this case, you would measure the displacement and also designate the direction. If you were given magnitudes and directions, you could easily calculate these. For example:
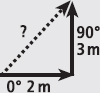
Fig. 2
If a person moved according to Figure 2 above (2 m to the east, designated as an angle of 0°, then 3 m to the north, designated as 90°), you can see that we now have a triangle. We can therefore use Pythagoras’ Theorem (C2 = A2 + B2, where C is the hypotenuse and A and B are other sides) to calculate the hypotenuse, C (read Appendix C to remind you of triganometry basics). C2 = 32 + 22, therefore C2 = 13 and C = 3.6 m (that is, the square root of 13 m).
Every vector quantity has to also have a direction, so what is the resultant direction of our object? This can be calculated easily using sin/cos/tan rules. We now know the length of every side of the triangle and since it is a right-angled triangle we can use any rule we wish to. I’ll use the tan rule, because then I don’t have to calculate the hypotenuse (or if I’ve calculated it wrongly it won’t influence the answer I get for the direction):
tan θ = opposite/adjacent. θ = inv.tan (opposite/adjacent) = inv.tan (3/2) = 56.3° (‘inv’ is short for ‘inverse’ and is a function on any good scientific calculator. It is also known as ‘arctan’).
So, the resultant displacement is 3.6 cm at an angle of 56.3° relative to the first direction of movement. You should remember that you could always calculate the resultant magnitude and direction of a movement by using Pythagoras’ Theorem to calculate the magnitude and the tan rule to calculate the direction (see Appendix C). If there are more than two movements, you just calculate the resultant for the first two movements, then use that as the first movement and add the next movement and so on.
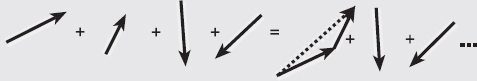
Fig. 3
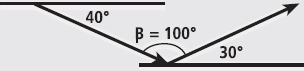
Fig. 4
If the angle between the two movements is not a right angle (as is most often the case; Figure 4) you use the cosine rule: C2 = A2 + B2 – 2(AxB) x cosβ where β is the angle between the two vectors and use θ = inv.tan(A sinβ / (B + Acosβ)) to calculate the angle formed between the two vectors. These equations take a little more time to use but as long as you understand the reasons for their use, you don’t need to memorise them. You can refer to this page when you need to.
You can see that we now have a triangle with a right angle, so we can use Pythagoras’ Theorem and proceed as above.
Scalar |
Vector |
Position (with direction) |
|
Distance |
Displacement |
Speed |
Velocity |
Acceleration |
Acceleration (with direction) |
TABLE 1.1 Scalar-Vector table
The next thing we need to know is how to tell the speed with which someone moved. How quickly did the runner run the 200 m? We can determine how quickly a runner has run (averaged over the whole 200 m) by dividing ‘how quickly’ by ‘how far’ but the value we get depends on whether we want ‘how quickly’ as a scalar or a vector quantity. If we want to know the movement speed over the total distance of 200 m, we would calculate the scalar quantity of speed:
speed = ∆d ÷ ∆t or ∆d/∆t. ‘∆’ means ‘change in’, so ‘∆t’ means ‘change in time’
If we want to know how quickly and in what resultant direction the athlete has moved, we would calculate the vector quantity of velocity:
velocity (v) = ∆s ÷ ∆t. ∆s/∆t, in a given direction that is, displacement(s) per change in time
For these runners, we want to know the average running speed over 200 m, so we use speed = ∆d/∆t. If a runner took 21.2 s to run 200 m, his or her average speed is 200 m/21.2 s = 9.4 m/s. (In scientific notation, this is written as 9.4 m·s-1 – see Box 1.2.) If we calculated the vector quantity instead, we would find a velocity of 5.8 m·s-1 at an angle of 36°.
BOX 1.2 SCIENTIFIC NOTATION IN EQUATIONS
For consistency, it is best to use scientific notation in equations. One way to do this is to change any division signs to multiplication signs. For example, instead of writing s = d/t, we can write s = d·t-1, which literally means ‘multiply d by t to the power of minus one’. ‘Minus one’ means we use the inverse or 1/t. Dividing by a number is the same as multiplying by its reciprocal.
You can check this: in your calculator, enter ‘6/2 =‘ to which the answer is 3, then enter ‘6 × 0.5 =‘, which will also give 3. You’ve divided by a number (2/1 or 2) in the first example and multiplied by its reciprocal (1/2 or 0.5) in the second.
This notation is commonly used to show the units of measurement in the answers to maths problems. For example, we use m·s-1 (metres per second) instead of m/s and m·s-2 rather than m/s/s for acceleration.
You can see it makes a big difference whether we calculate speed (scalar) or velocity (vector). In some instances, it is most useful to calculate the velocity. If a triathlete swam 1.5 km across a lake, what matters is the time taken to move that distance, even if they lose their direction and swim an actual distance of 2 km in getting there!
There is a more advanced method of calculating velocity too. As you can see, by calculating velocity between two time points we can only ever find an average velocity. We can, however, estimate the instantaneous velocity by using more detailed mathematics. The instantaneous velocity is calculated over a very small (close to zero) time period. To do this we need a method of picking out the velocity at a point in time. Consider the graph below (Figure 1.2) of an object moving at a constant velocity. You can see that it moves at constant velocity, travelling at 0.5 units per second. We can therefore calculate the velocity using the average velocity equation as shown in the graph on the right: 3–1.5/5–2 = 1.5/3 = 0.5 units per second. Notice that we have really calculated the slope (gradient) of this line, or the rise/run? This hints that if we can calculate the slope of a line at any specific point, we can calculate the instantaneous velocity.
FIG. 1.2 The velocity of an object at any time point is equal to the slope (gradient) of the displacement–time relation.
The displacement–time data for this object can be fitted perfectly with a straight line. You might remember that the equation for a straight line is: y = ax + b, where a is the slope (or gradient) of the line and b is the y-intercept (i.e. where the line crosses the y or vertical axis). So the equation for the data above would be: y = 0.5x + 0, because the slope or gradient is 0.5 units per second and it crosses the y-axis at 0. In this example it is easy to see that the gradient is 0.5 so the velocity is constantly 0.5 units per second. However, you might also notice that the gradient is equal to the derivative of this line. Those of you who have a bit of a mathematics background will remember that to find the derivative of any line where N is the power term for x, you multiply N by x to the power of N-1. . .
so 0.5x + 0 becomes (0.5 × 1) × (x(1-1)) + (0 × 0) × x(0-1) (0.5x is really 0.5x1)
= 0.5 × 1 + 0
= 0.5
This method makes more sense when we have a more complex velocity curve. If the equation of the curve was 3x2 + 5x + 7, then differentiation would yield:
(3 × 2) × x(2-1) + (5 × 1) × x(1-1) + (7 × 0) × x(0-1)
= 6x + 5
Then if I asked what the velocity was at time = 3.2 s, you would put 3.2 into the equation where x is (remember time was on the x-axis) and the result would be that velocity = 19.2 + 5 = 24.2 units per second. We can assume here that displacement was measured in metres, so we can call it 24.2 m·s-1. So as long as you have the equation to the displacement–time curve (or at least the part that you’re interested in) you can calculate the instantaneous velocity. If you haven’t got a reasonable background in mathematics, this might seem a little complex. But you should understand the idea behind it (i.e. determining the slope of the line at a specific time point), and you can consult a basic mathematics text or website to learn more about differentiation if this is a tool you’ll require for your course of study or work.
The next thing we need to understand is the concept of acceleration; the rate of change of velocity. Acceleration (a) = ∆v/∆t (this can be read as ‘change in velocity over a change in time’) or v·t-1. Velocity is measured in m·s-1 (metres per second) and acceleration in m·s-2 (metres per second per second).
Actual rates of acceleration can’t be measured directly from the information in Figure 1.1 because we only know that the athlete’s average speed over 200 m was 9.4 m·s-1; to calculate acceleration we need to know speeds at many points in the race.
BOX 1.3 HOW FAST IS FAST?
Sometimes, when we see numbers, it is difficult to imagine how big or fast or small they are. By way of comparison, the table below shows the estimated top speeds and accelerations of some of the fastest land animals.
Animal |
Speed (m·s-1) |
Speed (km·h-1) |
Animal |
Acceleration (m·s-2) |
Humana |
12.3 |
44.3 |
Humana |
5.1 |
Cheetah |
29 |
104.5 |
Lionb |
9.5 |
Lion |
22 |
80 |
Gazelleb |
4.5 |
Gazelle |
22 |
80 |
|
|
Hunting dog |
20 |
72 |
|
|
Ostrich |
18 |
64 |
|
|
Domestic cat |
13 |
48 |
|
|
Elephant |
11 |
40 |
|
|
Data adapted from: Natural History magazine, Copyright Natural History Magazine, Inc., 1974.
a Data of Usain Bolt measured by Radar in the World Championships 100 m, Berlin, 2009.
b Data from Elliott et al., 1977, In: Alexander, R.M. Principles of Animal Locomotion, Princeton University Press.
If we determined the runner’s speed at the 10 m mark as 5.9 m·s-1 and it took them 1.8 s to get there, then the average acceleration would be calculated as 5.9 m·s-1/1.8 s = 3.3 m·s-2 (that is, ∆v/∆t = 3.3 m·s-2 – remember to read this as ‘change in velocity over a change in time’). Of course, we can also measure the instantaneous acceleration by finding the derivative of the velocity–time curve, just like we found the instantaneous velocity as the derivative of the displacement–time curve.
In many sports, the calculation of acceleration is very important: for example sports in which chasing-catching is important (e.g. rugby, Australian/American football, basketball/netball), the athlete who can most quickly change direction and accelerate will usually win. If you want some idea of how rapidly this athlete accelerated, compare the rate of 3.3 m·s-2 to the acceleration of animals listed in Box 1.3.
Describing movement direction
The final thing we have to know is how to describe changes in displacement/distance, velocity/speed and acceleration. If we move away from a designated point, we say that we have increased our distance from it or displaced ourselves further. If we then move back, this reduces the displacement but increases the distance. (You can’t have a negative displacement but you can have displacement in positive and negative directions.)
FIG. 1.3 Examples of calculations of scalar and vector quantities describing object movement. The arrow represents the movement of the object (left column), the time over which movement takes place is included in the middle column (i.e. t = 2 s) and the calculations are shown in the right column.
If we drew a diagram of an athlete moving across this page (from A to B in Figure 1.3), we might say that they move in a positive direction if they move from left to right, and they move in a negative direction if from right to left. Their overall displacement is the sum of all of the displacements, with a positive value denoting a net movement from left to right.
We don’t use this terminology for distance, because it’s a scalar quantity and has no direction. The total distance is the sum of all displacements as if they were all positive (see the first example in Figure 1.3). It’s the same for velocity and speed: our velocity is positive if we move at a known speed to the right but negative if we change direction and move to the left.
Acceleration is a little more complicated. Generally, if we speed up we say that acceleration is positive but if we slow down we say that acceleration is negative. However, we have to be more specific when we include either positive or negative direction. If we move to the right (or positive direction) at a constant rate, the acceleration is zero. If we get faster in the positive direction then we are accelerating positively and if we slow down we are accelerating negatively (see the examples in Figure 1.3).
If we then turn around and accelerate back towards our starting point, that is, in the negative direction, we again are accelerating negatively. Acceleration in the negative direction (or negative acceleration) is what would happen if we continued to apply a force that opposed our original direction of movement. Think of a light trolley rolling forwards and then being slowed by a gust of wind coming from the other direction: the wind would first slow it and then eventually push it backwards. The acceleration is always in the same, negative, direction, although we see the trolley slow down and then speed up. If the wind stopped and the trolley (which is now moving backwards) slowed and came to a stop, it would be accelerating negatively in the negative direction (that is, decelerating in the negative direction), which is positive acceleration – two negatives make a positive. You can see an athlete accelerating positively and negatively in Figure 1.4.

FIG. 1.4 In the agility task above, the athlete accelerates positively to his left (our right) from picture A to B then accelerates negatively from B to C and D. Acceleration is positive again from D to E. Photos B to C and D to E show the athlete ‘decelerating’.
It is probably easiest (and indeed is very common) to use the terms accelerate and decelerate to indicate speeding up or slowing down, then explain the direction of travel as positive and negative. However, you should understand the terms so that you don’t get confused. If an object is getting faster while moving in the positive direction or slowing down in the negative direction it is accelerating positively but if it is slowing down while moving in the positive direction or speeding up in the negative direction it is accelerating negatively.
A simple test will determine whether you truly understand position, displacement/distance, velocity/speed and acceleration. (This test makes more biomechanists come unstuck than a million maths-problems-to-be-solved-without-the-use-of-a-calculator.) The test is to see if you can draw velocity and displacement curves – in that order – from a graph of acceleration. Figure 1.5 is an acceleration graph and below it are two graphs that you should cover up with a piece of paper. Without peeking, see if you can first work out what the velocity graph should look like, using the information from the acceleration graph. Then, from the velocity graph, try to work out what the displacement graph would look like.
FIG. 1.5 The above graphs are drawn from data representing the fastest 10 m split times for a world-class male (dark bold lines and numbers) and female (dashed lines and lighter numbers) sprinter. The athletes’ reaction times are not included. As usual, the acceleration graph varies greatly, with the variation being less for speed and less again for position/distance. It can also be seen that the female sprinter accelerated similarly to the male early (up to 10 m or 20 m), but attained a lower top speed, which they both seem to hold equally well. The greater top speed allows the man to reach each 10 m point sooner than the woman, ultimately leading to him finishing the 100 m much faster. Of interest is that these graphs show that if you took the fastest segments run by either runner and put them together, the 100 m could be completed in 9.46 s by the man and in 10.20 s by the woman. With a reaction time of 0.1 s (the fastest legal reaction time under current IAAF regulations), it seems the man (9.56 s) and woman (10.30 s) would have been capable of running the 100 m faster than the current (2009/10) world records of 9.58 s and 10.54 s, for men and women respectively. As a side issue, the units for position/distance, speed and acceleration are not included on the graphs . . . what units should be used and what abbreviations are common for these?
Don’t worry if you don’t get it first time. Even Albert Einstein had to go through things more than once. He even failed the exam to get into technical college to study electrical engineering!
THE ANSWER
But who will run the fastest 200 m? Well now we have all the knowledge we need to answer the question. One way to work it out is to set up an experiment and collect data. First, we set up a timing system to measure the time it takes for our well-trained runner to run 200 m. We also set up the system to record the time to 50 m (acceleration time), the time between 50 and 150 m (maximum speed time) and the time from 150 to 200 m (which we’ll call the deceleration time, since this is the part of the race where athletes suffer fatigue and often fail to maintain their top running speed). We’ll record three trials to try to be certain we have a ‘good’ trial from our runner.
We can then see how running time might differ if we ran each section a little more quickly or slowly. Such manipulation, to gauge the impact of altering some part of a performance, is called modelling; we will use this technique again in other chapters. The recorded times are presented in the left column of Table 1.2. I then manipulated each section of the race to see how it might have affected overall performance.
Race phase |
Actual Time (s) |
Accel. – 3% |
Max. – 3% |
Decel. – 3% |
Max. and Decel. – 3% |
Acceleration (0–50 m) |
5.90 |
5.72 |
5.90 |
5.90 |
5.90 |
Maximum Speed (50–150 m) |
9.70 |
9.70 |
9.41 |
9.70 |
9.41 |
Deceleration (150–200 m) |
5.30 |
5.30 |
5.30 |
5.14 |
5.14 |
Average Speed (m·s-1) |
9.60 |
9.65 |
9.70 |
9.64 |
9.78 |
Total Time (s) |
20.90 |
20.72 |
20.61 |
20.74 |
20.45 |
TABLE 1.2 Actual and ‘manipulated’ running times for a well-trained sprint runner. Times in the final four columns have been altered based on a 3% greater running performance. Times have been adjusted for the acceleration phase only (Accel. – 3%), maximum speed phase only (Max. – 3%), deceleration phase only (Decel. – 3%) and for both maximum speed and deceleration phases (Max. and Decel. – 3%). Changes to running times are emboldened. The greatest improvements in running time are achieved by improving average speed, which is most affected by improvements in maximum running speed.
Looking at the average speeds and total times for running 200 m, we can see that improving the maximum speed phase by 3% has a more profound effect on the average speed, and therefore on the total time, than improving any other individual phase. This is largely due to the maximum speed phase being twice as long (100 m) as the acceleration or deceleration phases (both 50 m).
However, one might expect that if a runner had a faster maximum speed, they would also have a faster deceleration phase, even if they slowed down by the same degree as another runner (that is, the same deceleration but from a higher speed). This idea is incorporated in the final column and shows more clearly that improving top speed leads to a greater improvement in overall running time than improvement of any other phase.
So, the answer is: the runner who improves their average running speed the most will run the fastest 200 m, and this can be best done by improving the maximum running speed. It is for this reason that modern sprinters use a running technique at the start that allows them to attain a good technique in the top-speed phase, rather than using a technique that may be faster at the start but which makes it difficult to reach high top speeds later in the race.
HOW ELSE CAN WE USE THIS INFORMATION?
Such analyses can be used by biomechanists to better understand the factors influencing performance in many sports. In the 100 m sprint, the relative phases are of different durations and they therefore influence performance differently. In swimming, the time spent turning and accelerating out of the turn is very small in relation to the time spent swimming, so swimming time is clearly of great importance. However, you should be mindful that small improvements in performance in the small parts of races can make a substantial difference to a result. As an example, Kieran Perkins’ swimming time (that is, the collective time to swim from 5 to 45 m of each 50 m lap) in the 1500 m event at the Atlanta Olympic Games in 1996 was less than Grant Hackett’s but Hackett’s turn times (that is, the time from 5 m from the end of each lap to 5 m into each lap) were shorter. Grant Hackett won the gold medal; Kieran Perkins finished second (Mason, 2005), even though Hackett was only better in the smallest portion of the race.
Understanding position, velocity and acceleration can also help us work out tactics for many individual and team sports. For example, what strategies can we use in sports like rugby, netball, football (soccer) or basketball? Usually, the athlete with the greatest acceleration will be the most successful. It takes humans about five seconds to reach top speed. Within that time, we would gain ground on our opponent if our acceleration were faster, because, at any point, our velocity would be higher. Only when we reached top speed and our faster opponent continued to accelerate would he or she finally get away. So, if we are close enough to our opponent to start with and we have a faster acceleration we will normally catch them. (You should be aware, however, that if you are running more quickly than your opponent and he or she swerves just as you are about to catch them, they will usually evade you. To find out why, you’ll have to read Chapter 8.)
speed = ∆d/∆t
acceleration (a) = ∆v/∆t
convert m·s-1 to km·h-1: x m·s-1/1000 × 3600
convert km·h-1 to m·s-1: x km·h-1 × 1000/3600
convert km to miles: x km × 0.625 or km/1.6
convert miles to km: x miles × 1.6
Reference
Mason, B. (2005). ‘Biomechanical Support in Sport’. Lancet, 266: 525–6
Related Websites
Minddrops.com (http://www.minddrops.com/LearningObjects/Kinematics/mdlinearmotion.html). Simulation page to aid the understanding of linear motion.
Hyperphysics (http://hyperphysics.phy-astr.gsu.edu/hbase/mot.html). Basic and advanced discussions on linear motion, including maths simulations and calculations.
Physics30 (http://physics30.edcentre.ca/kindyn/distdisp.html). Lesson and questions on displacement/distance, from beginner to more advanced.
Physics30 (http://physics30.edcentre.ca/kindyn/speedvelocity.html). Lesson and questions on speed/velocity, from beginner to more advanced.
Physics30 (http://physics30.edcentre.ca/kindyn/acceleration.html). Lesson and questions on acceleration, from beginner to more advanced.
ZonaLand: National Science Teachers Association (http://zonalandeducation.com/mstm/physics/mechanics/mechanics.html). Clear descriptions and animations of the basic principles of mechanics.
The Physics Classroom – Tutorials (http://www.physicsclassroom.com/Class/). Lessons on basic physics concepts.
The Physics Classroom – Multimedia tools (http://www.physicsclassroom.com/mmedia). Interactive tools and movies depicting basic physics concepts.
The Physics of Sports (http://www.topendsports.com/biomechanics/physics.htm). Website investigating the applications of physics in sports.