Chapter 8

Gravity and Satellite Motion

GOALS

By the end of this chapter, you will be able to:

• Define the gravitational force

• Use Newton’s Law of Gravitation to find the gravitational force between objects

• Apply Kepler’s Laws to understand satellite motion

Lesson 8.1
Gravity

We’ve discussed gravity as it pertains to the weight of objects near the surface of the Earth already. However, this was simply an application of Newton’s Second Law: The mass of an object is multiplied by the acceleration it would feel due to gravity near the Earth’s surface. The fact is that all objects with mass interact gravitationally, not just near the surface of the Earth. The Earth interacts with the Sun, the Moon, with the Earth, and in fact the whole solar system interacts with the center of our galaxy. In order to discuss gravity over large distances, where the acceleration varies greatly, we need a general definition for gravity itself.

Newton published what is referred to as his Law of Universal Gravitation in the Principia along with his force laws. This states that the gravitational force between a mass m1 and a mass m2, separated by a distance r, is

Equation 8.1

where G is known as the gravitational constant, and is

G = 6.67 × 10−11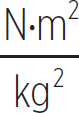

EXAMPLE

Let’s say you drop a 4 kg mass onto a 10 kg table from a height of 1 m. Does the gravitational force between the mass and the table dramatically affect the acceleration of the mass downward?

Well, first take a look at the acceleration produced by the gravitational force between the table and the mass, and then see how it compares to 9.8 m/s2. Second, calculate the gravitational force between the objects:

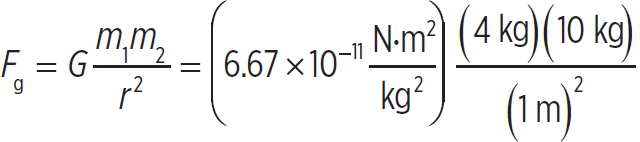= 2.7 × 10−9N

So, the acceleration of the mass is

a = = 6.7 × 10−10m/s2

You can see that this is a significantly smaller acceleration than 9.8 m/s2, so no, it does not have a dramatic affect on the overall acceleration of the mass downward.

In the context of gravity, we have another definition of mass: gravitational mass. Gravitational mass defines an object’s inherent ability to interact gravitationally. The larger an object’s gravitational mass, the larger the gravitational force it can apply on another object. This definition is distinct from inertial mass, but it turns out that the inertial mass and the gravitational mass are the same quantity.

This is our first example of what is referred to as an inverse square relation. These relations appear over and over again in physics. It simply means that whatever value you are interested in decreases with distance, but not linearly. If you double the distance, you decrease the value by 1/4. If you triple the distance, the value is decreased by 1/9. If a measurement A “drops off” as 1/r2, then we would say

where ∝ means “proportional to.”

Equation 8.1 gives only the magnitude of the gravitational force. Gravity is an attractive force, always, so the force always points from one mass to another. This is illustrated in the following figure.

Figure 8.1: Gravitational Force Between Two Masses

Something that is important to note about the above figure. The gravitational force originates at the center of uniformly distributed objects. For our purposes, we will consider all masses as being uniformly distributed throughout an object. This means that the radius r in Equation 8.1 is not from the surface of one object to the surface of another, but from the center of one object to the center of another. The point on any mass that the gravitational force is generated from is known as the center of mass. This is an important point to know, because if you need to calculate the torque produced by gravity, for instance, you need to know the point on the object that it is generated, so you can measure the lever arm.

Instead of using the magnitude-direction form of the gravitational force, you can also represent it algebraically, in component form. All you need to do is define the direction of the vector. Since we call the distance between the objects as r, we can define the vector displacement between the objects as , the unit vector defining this direction as . Then, the displacement would be = r . Using this, we can say that the gravitational force is

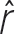or, = / r,

Equation 8.2

EXAMPLE

Consider the masses in the following figure. What is the gravitational force that the 7 kg mass puts on the 5 kg mass? What is the magnitude of that force?

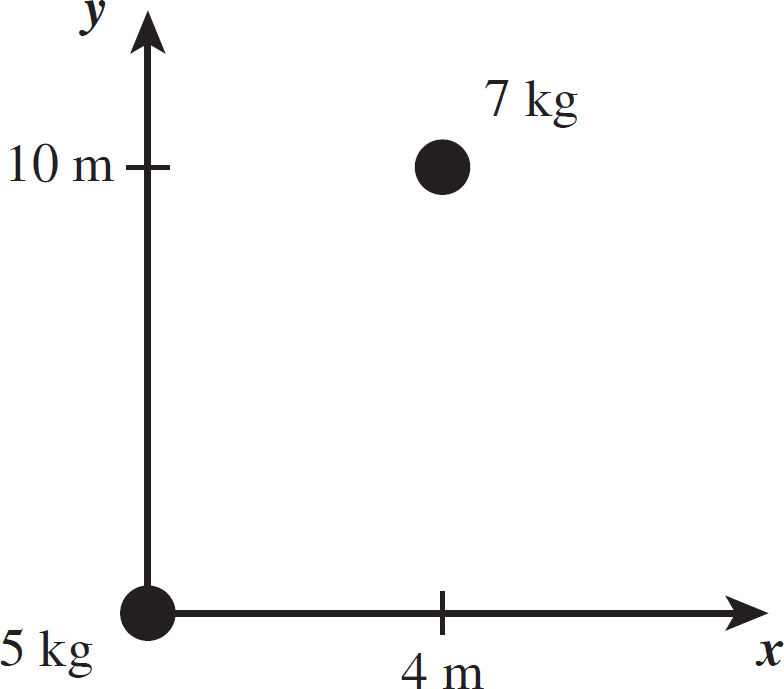
So, there are two things we need from this diagram before you can proceed: the distance between the masses, r, and the vector displacement between them, . It is important to remember that you are looking for the force that the 7 kg mass puts on the 5 kg mass. While the distance between the two is the same, the force will point from the 5 kg mass to the 7 kg, so we have to construct in this same manner. First, find , which is simply

= (4 m)î + (10 m)ĵ

So,

r = 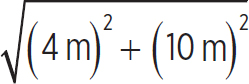= 10.8m

Using Equation 8.2,

The magnitude can be found in one of two ways: You can take the magnitude of the above result, or you can use Equation 8.1 to find the magnitude. Find the magnitude of the above result:

Fg = 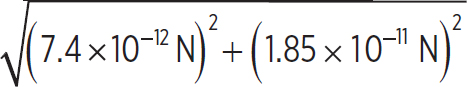= 1.99 × 10−11N

Now that we know the force of gravity in general, we can discuss the acceleration due to gravity. Let’s say there are two masses, m and M. The acceleration on m due to the gravity of M is simply

Equation 8.3

where r is the distance between m and M.

EXAMPLE

Say there exists a planet out in the universe called planet X, which has twice the Earth’s mass and twice its radius. What would the gravitational acceleration be on the surface of planet X?

Refer to Equation 8.3. If the mass is double, then the acceleration is double, and if the radius is double, then the acceleration is 1/4. The result of this is that the acceleration on the surface of planet X is half that of Earth, or 4.9 m/s2.

It is interesting how we arrive at the result in the above example. Notice that we applied Newton’s Second Law on the gravitational force, removing one of the masses from the equation for universal gravitation. It is a matter of nuance, but the mass that appears in Newton’s Second Law is the inertial mass, whereas the mass that appears in the gravitational force is the gravitational mass. One of the most interesting things about physics is that these two masses represent the same quantity. If you think about it, why should it? Why should the quantity that defines an object’s resistance to changes in velocity be the same as the quantity that defines the object’s ability to interact gravitationally? Einstein proposed the equivalence principle in his subject of general relativity that addresses this, but that is much beyond the scope of this text.

As we know, the gravitational force is conservative and has associated potential energy. We described the potential energy in Lesson 6.2 by finding the work done by gravity near the surface of the Earth. In general, the potential energy due to the gravitational force between two masses m1 and m2 separated by a distance of r is

Equation 8.4

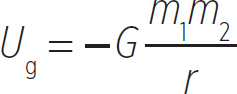
Any potential energy that is negative describes a force that is attractive, whereas any potential energy that is positive describes a force that is repulsive. Since mass is always positive, the above equation states that the gravitational force is always attractive, as we already know.

EXAMPLE

A rocket is resting on the surface of the Earth. What speed would it need to achieve to escape Earth’s gravity? This is known as the escape velocity. Consider the mass of the Earth to be ME and the radius to be RE.

In order for an object to escape the gravitational force of the Earth, it means that when it gets very far away from the Earth, and there is no more gravitational interaction, the object still has to have kinetic energy. Initially, the kinetic energy is

K1 = mv2

and the potential energy is

U1 =

Now, very far away, the potential energy due to gravity approaches zero. So,

K1 + U1 > 0

This means that very far away, when the potential energy is zero, the object still has some kinetic energy left. You can say that the limiting case (the minimum speed required) is when the above energy equals 0. Any speed above that will result in a leftover kinetic energy. So,

Any speed above this will allow the rocket to have a kinetic energy when it is very far away from the Earth, thus escaping its gravity. For Earth, this happens to be about 11,000 m/s, or about 25,000 mph.

In general, any mass M that has a radius of R has an escape velocity of

Equation 8.5

In celestial mechanics, which is the field of mechanics that deals with the movement of celestial bodies (planets, moons, stars, galaxies, etc.), it is rare that a gravitational interaction of interest takes place between two objects of similar mass and size. It is more common that you have one smaller mass interacting with a significantly larger mass. The smaller mass is known as a satellite, and its motion as a result of the gravitational interaction is known as satellite motion. While satellite motion will be investigated more thoroughly in the next section, we will describe it briefly here.

In the case of one small mass interacting with a much larger mass, the motion of the larger mass will not be affected by the gravitational interaction.

EXAMPLE

Take an object dropped from some height toward the Earth with a mass of 1 kg. The Earth’s mass is 6 × 1024 kg. What is the gravitational force between them?

Since we are discussing some physical example of dropping an object, we’ll consider a small height, on the order of tens or even hundreds of meters. In either case, the Earth’s radius is 6.4 million meters, which is significantly larger than whatever height the object is dropped from, so we can just consider r to be the radius of the Earth. In this case, the gravitational force is

So the force on both the Earth and the 1 kg mass is 9.8 N (this is due to Newton’s Third Law). Now, what is the acceleration? Well, you know for the 1 kg object, it should be 9.8 m/s2. And if you take the 9.8 N force on it and divide it by 1 kg, you do get 9.8 m/s2. But what about the acceleration of the Earth? Well,

aE = = 1.6 × 10−24m/s2

This means that if the 1 kg object took, say, 1 s to hit the ground, the Earth would move a whopping 0.8 × 10−24 m. It is very difficult to describe just how small this is. The diameter of a hydrogen atom is roughly 1 Ångström (named after the Swedish physicist Anders Jonas Ångström), Å, or 10−10 m. This makes the diameter of a hydrogen atom 100 trillion times larger than the distance the Earth moves. So, as you can see, when an object has a significantly smaller mass than another, the larger mass is unaffected by the smaller one. This is an important concept in satellite motion.

Now, what does satellite motion actually look like? Well, consider the case in the following figure:

Figure 8.2: Satellite Motion

Since the satellite’s velocity is perpendicular to the force, the force will change just the direction of the satellite, not its speed. After a small time, Δt, the satellite will have curved around the large mass and will now be in a new position. However, in this new position, gravity will still be perpendicular to the velocity. Gravity will always be perpendicular to the velocity as the satellite orbits the mass, so the motion produced is uniform circular motion.

The reason that gravity produces uniform circular motion is because it is a centripetal force, or more properly a central force—a force that always points to the center of a rotation. Since the satellite is so much smaller than the attracting body, it can just orbit without affecting the body’s motion. The Moon’s motion around the Earth is an example of satellite motion, as is the planets’ motions around the Sun. Gravity is the most important force in the universe. It is responsible for planets orbiting the star in every solar system. It is responsible for providing the conditions in the Sun necessary to burn its fuel and stay lit. It is responsible for holding galaxies together.

The next section will cover satellite motion in depth.

Lesson 8.2
Satellite Motion

You already know what basic satellite motion can look like: uniform circular motion. Now it’s time to discuss satellite motion in depth. Three important features of general satellite motion are collectively known as Kepler’s Laws. Kepler’s laws are named after the German mathematician and astronomer Johannes Kepler, who published these laws between 1609 and 1619. Newton showed in his Principia that his Universal Law of Gravitation accurately describes Kepler’s laws. While these were originally intended to explain the motion of planets around the Sun, they can be applied to any satellite.

Kepler’s Laws

1. The orbit of a satellite around an attracting mass is an ellipse, with the attracting body at one of the foci of the ellipse.

2. A line drawn from the attracting mass at one focus to the satellite covers equal areas during equal time intervals.

3. The orbital period of the satellite is proportional to the semi-major axis of the orbit to the power of 3/2.

In order to understand these laws, we must first discuss ellipses. Imagine a circle with a radius r. If you were to draw two perpendicular lines through the center of the circle, they would each reach the rim of the circle after a distance r from the center. An ellipse is a circle-like shape, but instead of the two perpendicular lines having the same distance from the center, they have different distances. An ellipse doesn’t have a randomly changing radius, though. If you were to draw a line across the shortest diameter of an ellipse and a line across the largest diameter, they will be perpendicular. An ellipse and a circle are compared in the following figure.

Figure 8.3: Circle vs. Ellipse

Technically, an ellipse is defined as a curve that surrounds two evenly spaced foci, such that the distance from one focus and the distance from the other focus to the same point on the curve always adds to the same number. This is illustrated in the next figure.

Figure 8.4: Ellipse Definition

The shortest distance from the center of an ellipse to the rim is known as the semi-minor axis, b, and the longest distance from the center to the rim is known as the semi-major axis, a. The foci of an ellipse always lie along the semi-major axis.

One can define a quantity known as the eccentricity of an ellipse as

e =

For an ellipse, the eccentricity has to be between 1 and 0 (since the semi-minor axis, b, is always smaller than the semi-minor axis, a). For a circle, the semi-major axis a equals the semi-minor axis b, so the eccentricity is zero. The eccentricity describes the “elliptical-ness” of a curve, since a circle has no eccentricity.

Now, let’s address each of Kepler’s Laws individually. The first law is fairly straightforward. As a satellite orbits an attracting mass, it does not necessarily undergo uniform circular motion with the attracting body in the center. Rather, it undergoes an elliptical motion with the attracting body at one of the foci. In the solar system, planetary orbits are almost circular. They have very low eccentricities. For instance, the eccentricity of Earth’s orbit is 0.017. Often questions will simplify planetary motion as uniform circular motion because of how close to uniform circular motion the motion of the planets is.

The distance from the attracting mass to the satellite, as a function of angle θ, is given by the following equation

Equation 8.6

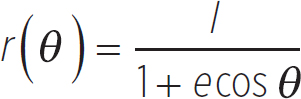
where l is given by

with M being the mass of the attracting body, m being the satellite mass, and L being the orbital angular momentum of the satellite. As will be discussed shortly, the angular momentum of the satellite doesn’t change as it orbits the attracting mass. The quantity l has a geometric definition. It is known as the semi-latus rectum, which is the distance of a line drawn parallel to the semi-minor axis from the focus to the rim of an ellipse.

The second law is a little less straightforward. Consider the following figure. In this figure, a satellite moves from position 1 to position 2 in time Δt1. The line drawn from the focus to the object covers an area A1 during this time. Then, at a future time, the satellite moves from position 3 to position 4 during a time Δt2, and the line drawn from the focus to the satellite covers an area A2. If the time intervals Δt1 and Δt2 are equal, then the areas swept by the line A1 and A2 must also be equal.

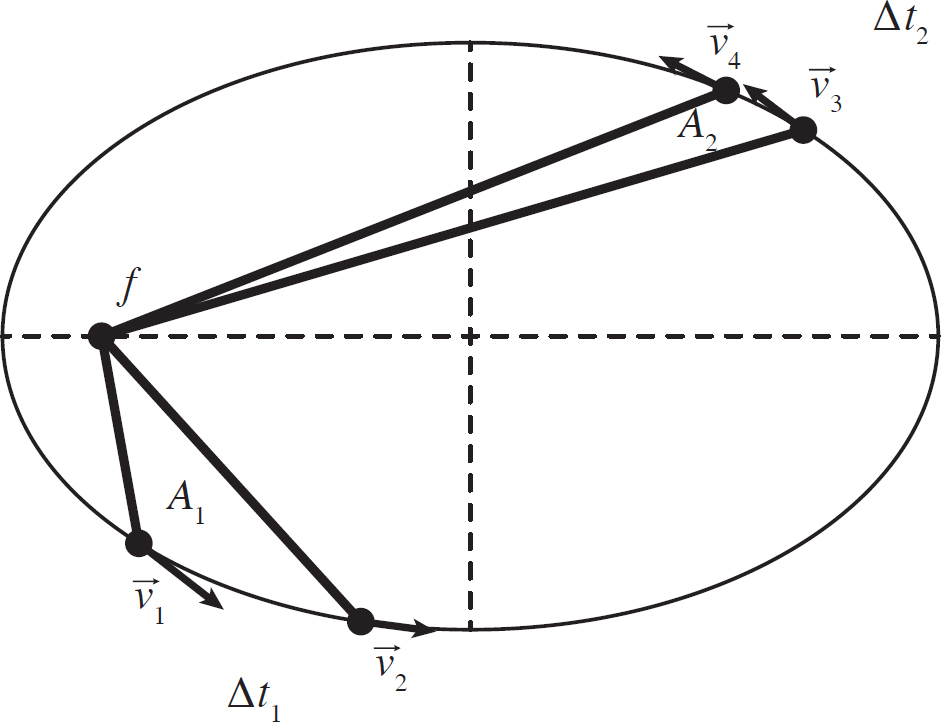
Figure 8.5: Kepler’s Second Law

Kepler’s Second Law is a direct result of conservation of angular momentum. Recall that if there is no net torque acting on an object, then its angular momentum must be a constant. The only force acting on a satellite orbiting an attracting mass is the gravitational force, which is always pointed centrally. This means that the gravitational force acts along the lever arm, and therefore produces no torque. So you know for an orbiting satellite that the net torque is always zero. If you treat the satellite as a point mass, then you know that its moment of inertia is

I = mr2

So, as the distance of the satellite changes with respect to the attracting mass, its moment of inertia changes. In order to conserve angular mometum, the angular speed has to change to compensate. For instance, as the satellite gets further away from the attracting mass, the moment of inertia increases and therefore the angular speed must decrease. As the satellite gets closer, the moment of inertia decreases and the angular speed increases. This means that in a time Δt, the closer you are to the mass, the faster you change your angle, so the wider the area is. But since the satellite is closer, the shorter the area is. The opposite is true when a satellite is further from the attracting mass. The area will not be very wide, but it will be very tall because of how far out the satellite is. Refer to the previous image to see this. A1 looks like a short, fat triangle, whereas area A2 looks like a tall, skinny triangle.

The rate at which the area is swept by this line is given by

Equation 8.7

= r2ω

which is a constant, per Kepler’s Second Law.

Now, Kepler’s Third Law relates the orbital period to the semi-major axis of the orbit. Kepler’s Third Law is simply a mathematical relationship:

Equation 8.8

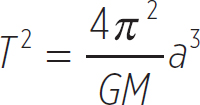
where M is the mass of the attracting body.

EXAMPLE

Derive Kepler’s Third Law for a circular orbit.

You know that Kepler’s First Law states that satellite motion is elliptical, but planetary orbits are almost circular. First, consider the gravitational force as the centripetal force producing the uniform circular motion of the satellite. This means that gravitational acceleration is the centripetal acceleration:

ag = ar

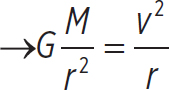
Use the equation v = rω to relate the linear speed to the angular speed, as well as ω = 2πf to relate the angular speed to the frequency of orbits:

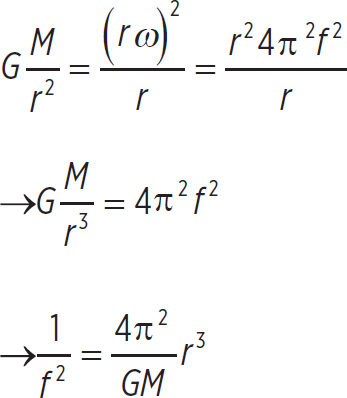
Finally, substitute the period for the frequency, T = 1/f:

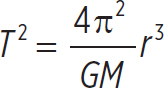
You can see that this result is identical to Equation 8.8 for a circle (when the semi-major axis is just the radius of the circle).

 

DRILL

CHAPTER 8 PRACTICE QUESTIONS

Click here to download a PDF of Chapter 8 Practice Questions.

Directions: Complete the following problems as specified by each question, and then check your work using the solutions that follow. For extended, step-by-step solutions, access your Student Tools online.

1. The displacement between a mass m1 = 2 kg and a mass m2 = 5 kg is , point from m2 toward m1. What is the vector gravitational force on m1 due to m2?

2. What is the altitude above the Earth’s surface that satellites undergo geosynchronous orbits? Recall that a geosynchronous orbit is one in which the satellite is always above the same point on the Earth’s surface. Note that the radius of the Earth is 6.4 × 106 m and the mass is 5.97 × 1024 kg.

3. Planet X has a mass twice that of the Earth and a radius half that of the Earth. Without looking up the mass or radius of the Earth, what is the gravitational acceleration on X at the surface? What about at an altitude equal to half the Earth’s radius?

4. If an astronaut could jump to a height of 50 cm on the Earth, should he worry that jumping on the Moon would cause him to leave the surface and never fall back down? Note that the mass of the Moon is 7.35 × 1022 kg and the radius is 1.74 × 106 m.

5. What speed would you have to throw a baseball to get it to orbit the Earth just above its surface?

6. A comet is a relatively small body in orbit around the Sun. Haley’s comet is a comet that passes by Earth every 75 years or so (the last passing was in 1986 and the next passing will be in 2061). Haley’s comet has an extremely high eccentricity, 0.967. The apogee (the furthest distance from the attracting body) of Haley’s comet is 5.25 × 1012 m, and its perigee (the shortest distance from the attracting body) is 8.77 × 1010 m. What is:

(a)    The semi-major axis?

(b)    The semi-minor axis?

(c)    Its orbital period? Note that the mass of the Sun is 1.99 × 1030 kg.

(d)    To think about: A comet is visible because it begins glowing in the night’s sky. This glowing is known as the comet’s coma, which is a very hot outgas being emitted from the comet. A comet is not visible at all points in its orbit, but only a certain point in its orbit. What point do you think this is?

7. A 1 × 1013 kg comet has an angular momentum of 1 × 1030 J · s around the Sun. The eccentricity of its orbit is 0.9. If its semi-major axis is 1.5 × 1012 m, what is its tangential speed at apogee? At perigee? Note that the distance on an ellipse between the center and the focus is ae (the semi-major axis times the eccentricity).

SOLUTIONS TO CHAPTER 8 PRACTICE QUESTIONS

1. Use the equation

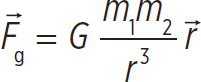
However, if you want to find the gravitational force on m1 due to m2, you need to find the vector which points from m1 toward m2. This is just the negative of the vector given in the problem, or -(4 m)ĵ. Obviously, the magnitude r is just 4 m. So,

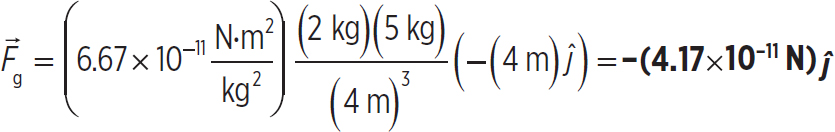
2. You know Kepler’s Third Law for circular orbits is

So, the radius of the orbit is

The only thing to figure out, then, is the period. In order for a satellite to stay above the same point on the ground at all times, it has to rotate at the same speed as the Earth. This means it has the same period as the Earth, or 1 day, which is 86,400 s. So

So, the altitude above the surface of the Earth is just this answer (which is the distance from the center of the Earth) minus the radius of the Earth:

h = 42.2 × 106 m − 6.4 × 106 m = 35.8 × 106 m

which is 35,800 km.

Recall that in the end-of-chapter drills for Chapter 4, it was stated that geosynchronous orbits were at an altitude of 36,000 km.

3. Recall that the gravitational acceleration is equal to

ag = G

So, if the mass doubles, the acceleration doubles. If the radius is 1/2, then the acceleration quadruples. This means that the gravitational acceleration at the surface of X is 8 times that of the Earth, or 78.4 m/s2. But what about at altitude? Well, at an altitude of half the radius of the Earth, this is a mass that is double that of Earth but a radius equal to that of Earth (the radius of X is half the radius of Earth and so is the altitude, so the total distance is the radius of Earth). This means that the gravitational acceleration is just twice that of Earth, or 19.6 m/s2. A second way of looking at this is from the surface of X to altitude, you doubled your radius, so the gravitational acceleration is 1/4 what it was at the surface.

4. On Earth, if the astronaut can jump to a height of 50 cm, then his jump velocity is easily solved for. You can use kinematics or energy physics to do so. Try using kinematics,

v2 = v02 − 2gΔy = 0

The escape velocity of the Moon is

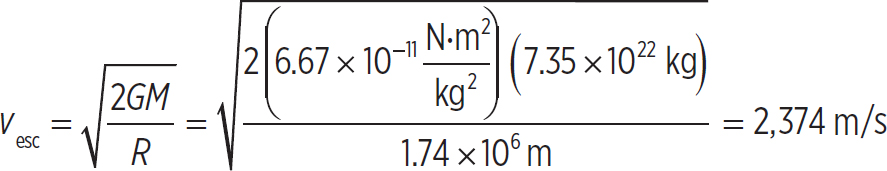
Notice that the astronaut can generate only about 0.1% of the required speed to escape the gravity of the Moon. So, no, he should not be worried at all about leaving the Moon’s surface and floating off into space if he jumps.

5. In order for the baseball to undergo uniform circular motion, the gravitational acceleration has to exactly equal its centripetal acceleration. This means

ar = ag

This is roughly 17,500 mph. Obviously, you cannot throw a baseball this fast. A 100 mph throw is extremely fast.

6. (a) The sum of the apogee and perigee equals the furthest distance across an ellipse, which is twice the semi-major axis. So,

a = = 2.67 × 1012m

(b) You know the eccentricity, and the relationship between eccentricity and the two axes, so

(c) You just need to use Kepler’s Third Law:

T 2 = (2.67 × 1012m)3 = 5.66 × 1018 s2

So, the period is 2.38 × 109 s, which is 27,546.3 days, or 75.5 years. You could have also just read the problem which stated that Haley’s comet appears in the sky every 75 years or so.

(d) The comet is visible in the night sky because of its coma, which is a hot outgas emitted by the comet. A comet is normally made up of ice, and as it passes near the Sun, this ice begins to melt and vaporize. This incredibly hot gas then escapes the comet and illuminates the sky. So, the comet cannot be seen far away from the Sun, because it won’t have a coma. The comet is seen only near its perigee.

7. First, you have to recall that angular momentum is a conserved quantity in satellite motion, so if the angular momentum is 1 × 1030 J•s at any point, it is 1 × 1030 J•s at the apogee and at the perigee. The next step is to figure out what the apogee and the perigee are. First, the distance from the center of the ellipse to the focus (where the Sun is located) is

ae = (1.5 × 1012 m) (0.9) = 1.35 × 1012 m

The apogee (the furthest distance from the focus) is going to be this distance plus the semi-major axis, or

ae + a = 1.35 × 1012 m + 1.5 × 1012 m = 2.85 × 1012 m

The perigee (the closest distance from the focus) is going to be the semi-major axis minus ae:

a − ae = 1.5 × 1012 m − 1.35 × 1012 m = 1.5 × 1012 m

Now, at both the perigee and apogee, the tangential velocity is perpendicular to the line connecting the satellite to the Sun (the lever arm). This means that the orbital angular momentum is just

L = mrvt

Normally it is this times sin θ, but θ is 90° at both the perigee and apogee. So, at the apogee, the tangential speed is

vap 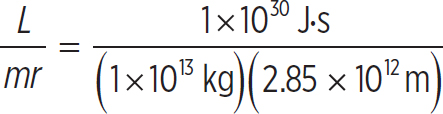= 35,088 m/s

or about 35 km/s. The tangential speed at the perigee is

Vper = 666,672 m/s

or about 667 km/s. Very, very fast.

REFLECT

Congratulations on completing Chapter 8!

Here’s what we just covered.

Rate your confidence in your ability to:

• Define the gravitational force

1 2 3 4 5

• Use Newton’s Law of Gravitation to find the gravitational force between objects

1 2 3 4 5

• Apply Kepler’s Laws to understand satellite motion

1 2 3 4 5

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.