Chapter 10

Waves and Sound

GOALS

By the end of this chapter, you will be able to:

• Explain what a wave is

• Describe wave properties

• Apply knowledge of waves to mechanical waves on a string

• Apply knowledge of waves to sound

• Describe standing waves

Lesson 10.1
What Is a Wave?

A wave is not a physical object, which was the focus of mechanics, so we need different rules to govern how waves act, much like we needed thermodynamics to describe the properties of heat and heat exchange. A wave is an oscillation that carries energy. Most waves require a medium to travel through. A mechanical wave is a wave that requires a solid medium to propagate through. For instance, you can take a rope and tie one end to a wall. If you were to whip your hand up and down quickly, you would produce a mechanical wave on that rope that would travel from your hand to the wall with some amount of energy.

Sound is another instance of a wave, which propagates within a fluid or a solid medium with some amount of energy. You can easily produce a sound by clapping your hands together, or speaking, but you will not be able to see the sound, as you would the mechanical wave on the rope. In the case of the mechanical wave, it is the position of the solid that oscillates. It is clear to see that the rope moves up and down as the wave passes along it. For sound, what oscillates is the pressure of the medium that it is in. Oscillating pressure is not something you can see, but the oscillating pressure produces a force that increases and decreases on your eardrum, which is interpreted as sound.

Light is a third form of wave, but light is unique in the sense that it does not require a medium to propagate in (light can propagate in a vacuum). This was one of the most important discoveries of the 20th century, and led to Albert Einstein constructing the Theory of Relativity between 1905 (when his Special Theory of Relativity was published) and 1916 (when his General Theory of Relativity was published). Light is composed of oscillating electric and magnetic fields. While these have not been discussed, they are responsible for producing the electric and magnetic forces, as we will discuss over the next few chapters.

Lesson 10.2
Mechanical Waves

A mechanical wave is an example of a transverse wave, a wave whose oscillations take place perpendicular to its propagation. Consider a vibrating string. The string’s height will change as it moves up and down, and the wave will propagate along the string. This is shown in the following figure.

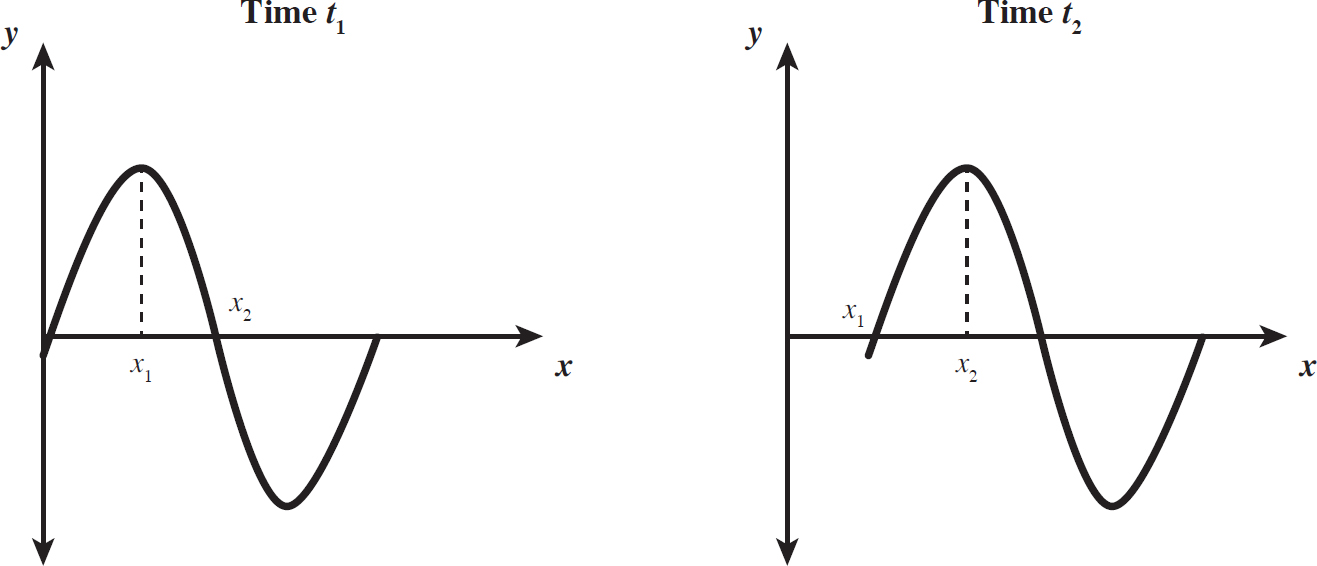
Figure 10.1: Mechanical Wave on a String

In this figure, the peak of the wave is at position x1 at time t1, while position x2 has no height. Then, at a further time t2, the peak of the wave is now at position x2, while the wave is no longer affecting position x1 because it has moved on. This is an example of a single, discrete wave. You could imagine a continuous wave, in which there isn’t simply one peak and valley (known as a trough), but an infinite number of them, as shown on the following page.

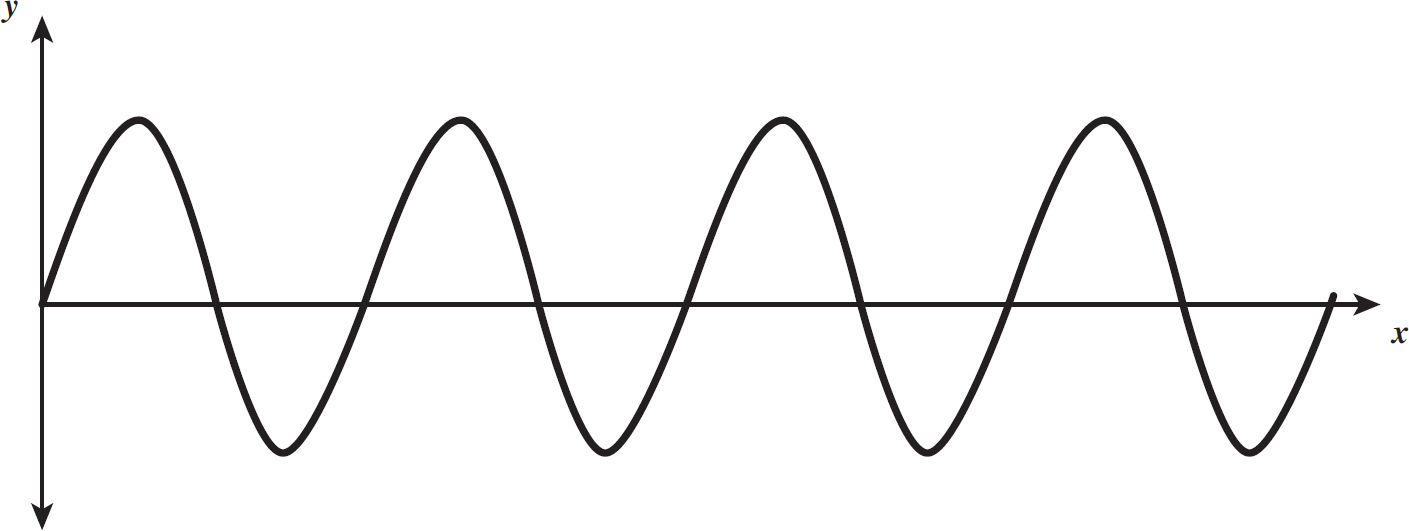
Figure 10.2: Continuous Wave

A wave is very similar in construction to that of simple harmonic motion. Imagine an oscillating mass on a spring. Its vertical position would change over time much like that of a wave on a string. However, the horizontal position of the mass would not change. But imagine we moved the equilibrium point of the spring at some velocity v. Then, not only would the vertical position of the mass be oscillating in time, but its horizontal position would also be changing with time, identical to a wave. In fact, if you were to plot the height versus horizontal position of an oscillating mass on a moving spring, you would get a figure identical to Figure 10.2.

Because of this, we have to define the period and frequency of a wave much like we did in simple harmonic motion. The period of a wave is how long it takes a wave to complete one cycle. One cycle of a wave is defined as the motion undergone by the wave to start at a point and end back at that point with the same velocity it started with. This means that if you considered some height y1, with the wave ascending, a cycle is not complete until the wave returns to the height y1 and is also ascending. A cycle is described in the following picture.

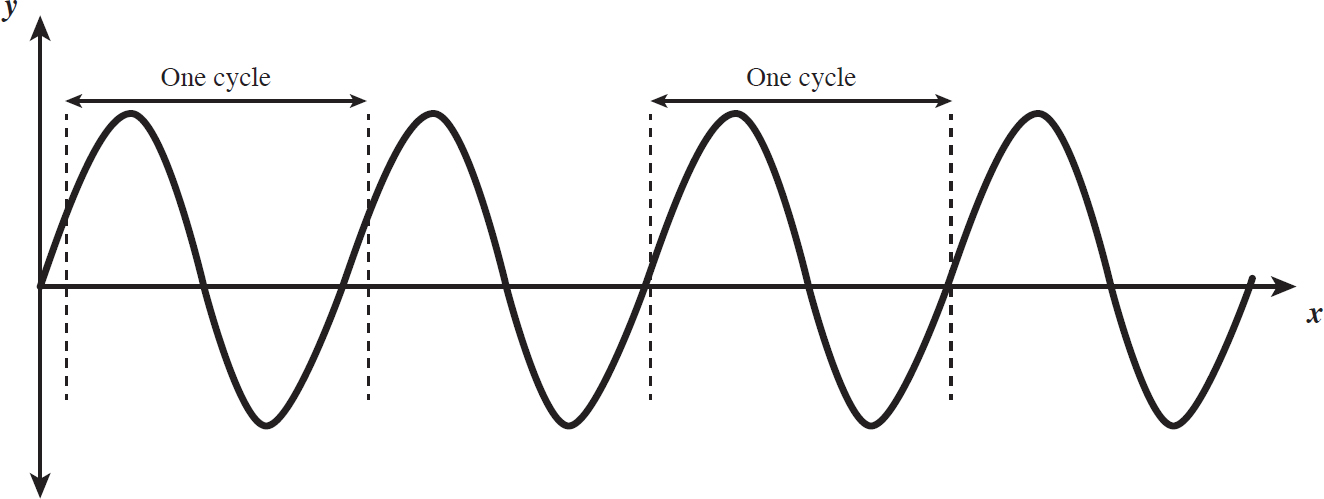
Figure 10.3: Cycles of a Wave

The frequency of a wave refers to the number of cycles it can complete per second, as you would expect, and is still related to the period by

f =

We need to define a new variable for waves, though, that we did have for simple harmonic motion: the wavelength. The wavelength, λ, is the distance that the wave travels in one period. On a y versus x graph, as shown above, the wavelength is just the distance between two peaks or two troughs (which would define one cycle). On a y versus t graph, the period is just the distance between two peaks or two troughs.

In general, the height of a mechanical wave is given by the equation

Equation 10.1

y(x, t) = A sin(kx − ωt)

where A is the amplitude of the wave (the maximum height it reaches), k is known as the wavenumber, and ω is the angular frequency of the wave. The wavenumber is defined as

Equation 10.2

k =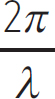

and the angular frequency is defined as

Equation 10.3

ω = 2πf

Notice that angular frequency has the same relationship to frequency that angular speed has to frequency in uniform circular motion. In uniform circular motion, the angular frequency and the angular speed have the same conceptual definition. Thus, angular frequency is defined by the same Greek letter, ω.

Equation 10.1 is of a different form than most equations we’ve seen: It has two inputs. It’s simple to use if you want a numeric result. Put in both the position, x, and the time, t, and you will get your number, assuming you know the wavelength and frequency of the wave. However, if you want to plot the equation, it’s not as straightforward. If you want to plot y versus x, you have to consider t a constant, and if you want to plot y versus t, you have to consider x a constant. What this means is that you can plot y versus x for only a single time t, and you can plot y versus t at only a single position, x.

The velocity of the wave in the y-direction is given by

Equation 10.4

vy(x, t) = Aω cos(kx − ωt)

The sign is important to calculate the velocity, because it will tell you if the wave is moving up or down, but it is not important for the speed.

Finally, if the wave moves a distance λ in the x-direction in a time T, then the speed in the x-direction must be λ/T, or

Equation 10.5

vx = λf

This speed is typically referred to as the propagation speed of a wave, or just the speed. If the speed in the y-direction is asked for, it will be asked for explicitly, but often vx is simply stated as the “speed” of the wave.

Something important to know about the above equation is that it determines the relationship between wavelength and frequency. Meaning, for a particular wave speed, the wavelength and frequency have a set relationship with one another. Neither the wavelength nor the frequency has any affect on the speed of the wave.

There are two important rules to know about waves:

1. A wave’s propagation speed is determined by the type of wave it is and by the properties of the medium it is in, but not by its wavelength or its frequency.

2. A wave’s frequency remains the same as a wave passes between two media.

Combining the first and second rules, we can see that as a wave passes between two media (which will change the wave speed), the wavelength must change. This is because if the speed changes between media, as per the first rule, but the frequency does not, as per the second rule, then the wavelength must change, to satisfy Equation 10.5.

EXAMPLE

A wave propagates at a speed of 12 m/s with a wavelength of 120 nm. What is the wave’s new frequency and wavelength if it passes into a medium where it has half the speed?

So, you know that the frequency of the wave does not change from one medium to another. The original frequency of the wave is

f = 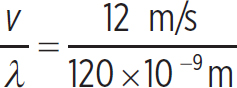= 1.0 × 108s−1

When it passes into the new medium, the wave has a speed of 6 m/s (half its value in the old medium), and thus has a wavelength of

λ = = 6.0 × 10−8m = 60 nm

The speed of a mechanical wave on a string is

Equation 10.6

v =

where T is the tension in the wave (don’t confuse this with the period of the wave) and μ is the mass per unit distance along the string.

EXAMPLE

What is the frequency of a mechanical wave on a 15 kg/m string with a wavelength of 11 cm if the tension in the string is 500 N?

First, the speed of the wave is

v = 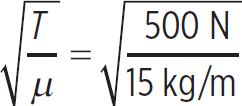= 5.77 m/s

So, the frequency of the wave is

f = 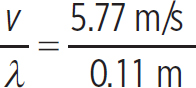= 52.5 s−1

The energy that one wavelength of a mechanical wave on a string carries is given by the equation

Equation 10.7

Eλ = μω2A2λ

EXAMPLE

Consider a system that produces mechanical waves on a spring with a flapping paddle that oscillates a string upward and downward. If the tension in the string is 50 N, and the mass per unit length is 20 g/cm, what does the power output of the system need to be in order to produce 2 wavelengths per second at an amplitude of 1 cm?

First, sift through the information given in the problem. You know that the energy carried by one wavelength is given by Equation 10.7, so the power output of the system needs to be two of that quantity per second, so the power output of the system is

Psys = 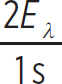= μω2A2 = μω2A2v

So, you need to figure out the frequency as well as the speed of the wave. First, it says it is producing two wavelengths per second, which means that the frequency is 2 s−1. Second, the speed of the wave is

v = 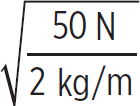= 5 m/s

So, the power required by the system is

Psys = (2 kg/m)(2 s−1)2(0.01 m)2(5 m/s) = 0.004 W

An interesting phenomenon occurs when you produce propagating waves on a string that is anchored to something (a wall, let’s say). As the waves propagate from their origin point, they eventually hit the anchor point, in this case a wall, and are reflected backward. This occurs at the same frequency as the waves were originally produced at. When you overlay two waves propagating in opposite directions with the same frequency, you produce what are known as standing waves. These waves are so called because they have no propagational speed: They simply “stand” still.

While propagating waves can come with any frequency or wavelength, standing waves cannot. Consider a guitar string. If you pluck a guitar string, you will produce a standing wave. However, it will oscillate with only a specific frequency. This is because on a guitar string, each end of the string is fixed, meaning the ends do not oscillate. These end points are known as nodes, or points of no displacement. The middle of the guitar string, where you pluck it, will be an antinode, or a point of maximum displacement.

Consider a string fixed at both ends. We would call this a node-node configuration (both ends are nodes). Only specific wavelengths are allowed, as shown in the following figure.

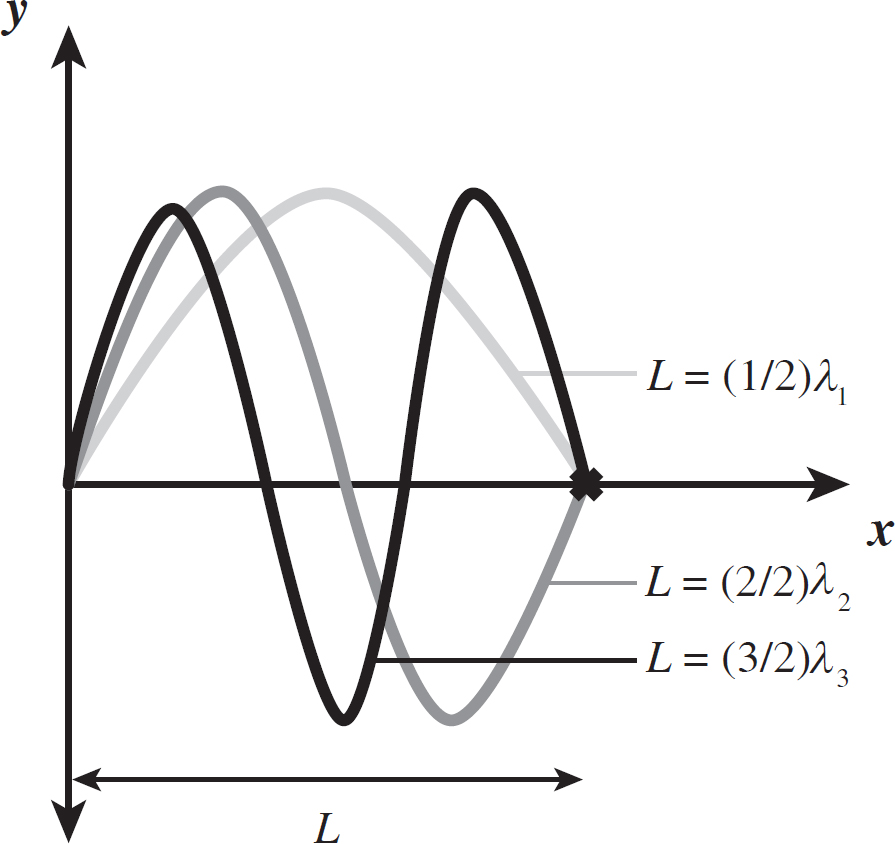
Figure 10.4: Node-Node Standing Waves

There is a trend developing:

L =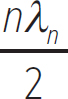

or

Equation 10.8

λn =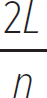

n is known as the harmonic number, and it defines how many wavelengths you can fit into the length of the string. As is clear from the figure, imagine only certain wavelengths (and therefore frequencies) are allowed to exist as standing waves. For instance, you cannot have a wavelength equal (3/4)L, because while this wavelength might start at a node, it will not finish at a node. For node-node standing waves, the harmonic number can be any integer.

Knowing that the speed of the wave to produce this standing wave is v, the frequency of the wave is just

Equation 10.9

fn =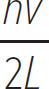

So, clearly standing waves on a string can be produced only at specific frequencies and with specific wavelengths. Sometimes the harmonic number n is referred to as the vibrational mode of the string.

EXAMPLE

Consider a 1 m string with 10 N of tension tied at both ends to anchor points. What are the first, second, and third harmonic frequencies of this string if the mass per unit length of the string were 150 g/m?

In order to calculate harmonic frequencies, you need to know the speed of the propagating wave that would be produced on this string:

v = 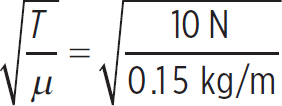= 8.16 m/s

Now, the first vibrational frequency is

f1 = 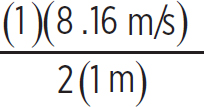= 4.08 s−1

This frequency is known as the fundamental harmonic, and all harmonic frequencies are multiples of it. So, the second harmonic frequency is just

f2 = 2f1 = 8.16 s−1

and the third harmonic frequency is

f3 = 3f1 = 12.2 s−1

As mentioned in the example above, the nth harmonic frequency can be given by

Equation 10.10

fn = nf1

which means that the nth harmonic wavelength can be given by

Equation 10.11

λn =

where λ1 is the fundamental harmonic wavelength.

EXAMPLE

Consider a string that forms a loop of radius r. What are the different harmonic wavelengths that are allowed on this string?

In this case, the vibrations are node-node, except that the two separate ends of an open string are now the same end on a closed string. In this case, the wavelength has to be a multiple of the circumference of the string, or

C =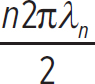

This is just as before, when we said L = nλ/2 for an open string with both ends fixed. Now, if the loop has a radius r, then C = 2πr and

2πr = nπλn → =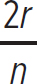

Another type of standing wave that can be produced is a node-antinode standing wave. In this case, all waves must start at a node but end at an antinode. This is illustrated in the following figure.

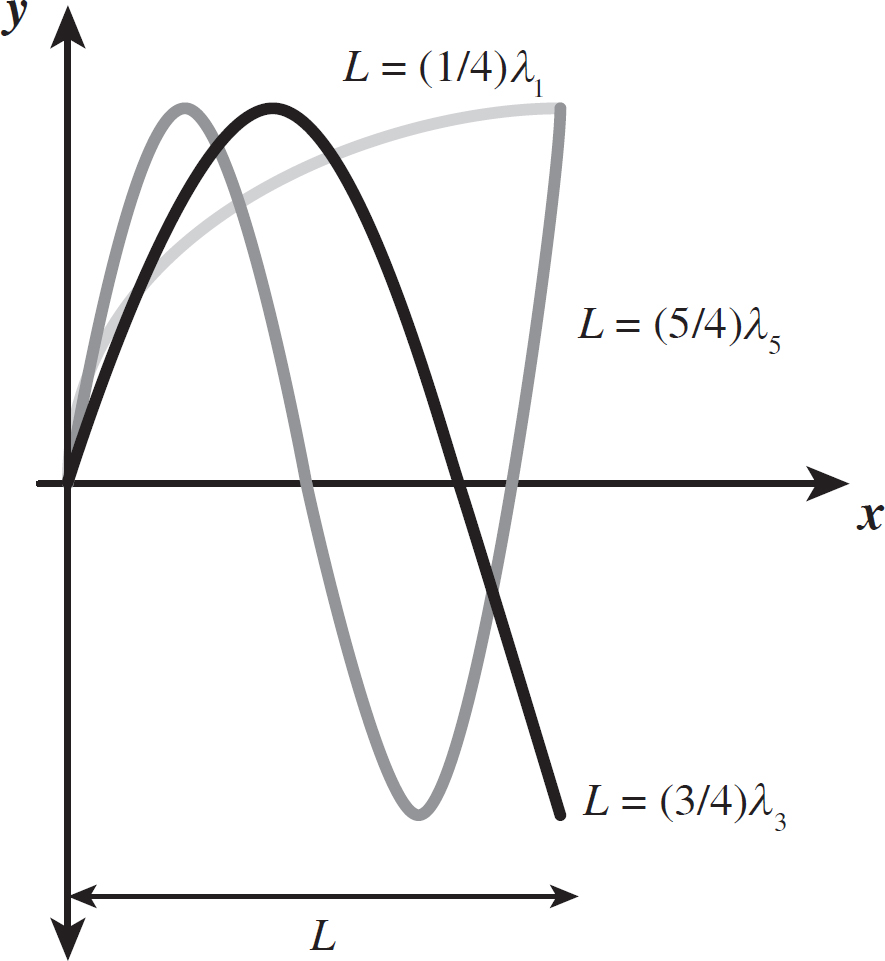
Figure 10.5: Node-Antinode Standing Waves

For node-antinode waves, it is clear that

Equation 10.12

λn =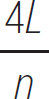

However, in this case, the harmonic number n can be only an integer. This is important to remember, because when you are dealing with node-node standing waves, the harmonic number can be any integer. Furthermore, the frequency of node-antinode standing waves will be

Equation 10.13

fn =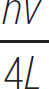

where, once again, the harmonic number n can only be an integer.

EXAMPLE

Consider holding a rope in your hand, which is anchored to a wall on the opposite side. You can produce a standing wave on this string by rapidly moving your hand up and down, but only at certain frequencies. What is the third-lowest frequency you can produce a standing wave at if the rope has a tension of 50 N, a length of 50 cm, and a mass per unit length of 1 kg/m?

First, the speed of the waves you would produce on this rope would be

v = 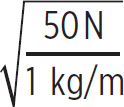= 7.1 m/s

These waves would quickly be reflected off the wall backward to produce standing waves. But only certain frequencies are allowed. These standing waves would be node-antinode, since the anchor point at the wall acts as a node and your hand acts as an antinode. So, the third-lowest harmonic frequency would have a harmonic number of 5 (remember, only odd harmonic numbers are allowed for node-antinode standing waves), so

f5 = = 17.8 s−1

Lesson 10.3
Wave Interference

When two of the same type of waves meet in the same place, they undergo a phenomenon known as interference. Consider two mechanical waves occupying the same place, plotted in the following figure.

Figure 10.6: Interacting Waves

The displacement of each wave sums at each position, resulting in a new wave

Equation 10.14

yint(x, t) = y1(x, t) + y2 (x, t)

Interference is commonly referred to as being one of two types. Constructive interference occurs when the displacement of the two waves is in the same direction (either up or down), resulting in a displacement greater than either of the two waves. Destructive interference occurs when the displacement of one wave is in the opposite direction of the other, resulting in a displacement that is less than that of either wave at that point. A few locations of constructive and destructive interference of the above example are indicated in the figure on the following page.

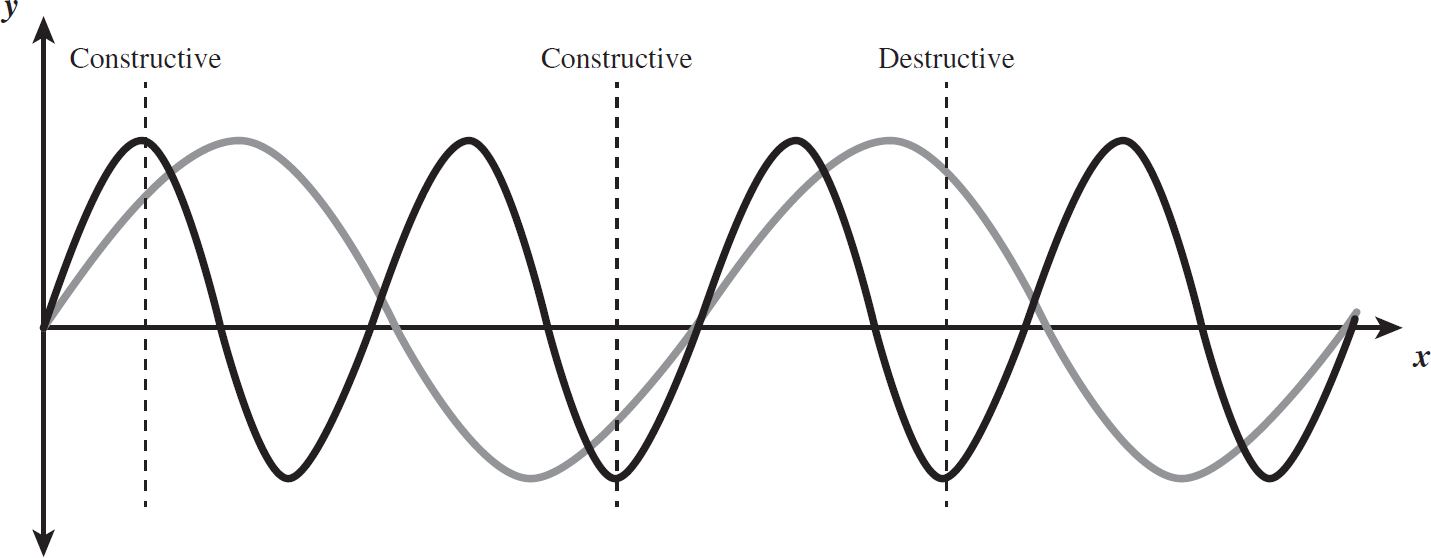
Figure 10.7: Constructive and Destructive Interference

As you have seen, the energy carried by a wave depends upon the amplitude of the wave. This means that the power does, as well. We will look at a new quantity later, known as the intensity of a wave, which depends upon the power carried by the wave. Because interference between two waves results in a new wave of differing amplitude, it affects the energy, power, and therefore intensity of the wave.

EXAMPLE

Consider two waves. The first wave has an amplitude of 5 cm and a wavelength of 4 cm. The second wave has an amplitude of 3 cm and a wavelength of 7 cm. What is the displacement of the interference wave at a position of 2 cm at t = 0?

Consider these two waves to be produced in phase. If they are produced in phase, it means that both waves start at the same position with the same direction of velocity. This is how the waves are depicted in Figure 10.7, where the two waves both start at (0, 0) with their velocities in the +y-direction.

Applying Equations 10.1 and 10.14, you can find the height of the interfered wave:

This will just be

yint (t = 0) = y1 (t = 0) + y2 (t = 0) = A1sin(k1x) + A2sin(k2x)

= (5 cm)sin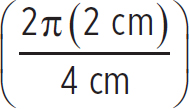 + (3 cm)sin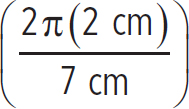

= 2.92 cm

Technically, you cannot apply this method to waves that begin out of phase, because their shapes are not the same. Both waves in Figure 10.7 start as sine waves at the origin, so it is fine to use Equation 10.1. But if the waves did not start in phase, they could not both be described by sine waves, and the problems gets cumbersome and more complicated.

Lesson 10.4
Sound

Sound is a new type of wave that we have not discussed yet, known as a longitudinal wave. Longitudinal waves are waves whose oscillations occur along the direction of propagation, opposite to that of transverse waves. Recall that sound is produced by oscillations between high and low pressure in the medium that it is produced in. This is illustrated in the following figure, where pressure waves are drawn as vertical lines. The closer the pressure waves are, the higher the ambient pressure. The further they are apart, the lower the ambient pressure.

Figure 10.8: Sound Waves

Since the pressure oscillates along the direction of propagation, sound waves are longitudinal waves. However, the dynamics that govern waves still apply to sound. We can still say that if the speed of the sound were v, then the wavelength and the frequency would be related by

v = λf

exactly as before. Sound moves at about 342 m/s in air at sea level. As your altitude increases, air pressure decreases, so the speed of sound also decreases. Representing an object’s speed in factors of speed sound is known as the Mach number of the object, after the Austrian physicist Ernst Mach. For instance, if an object moves at 1.5 times the speed of sound, it moves at Mach 1.5.

The speed of sound at any density ρ is given by the Newton-Laplace equation:

Equation 10.15

vs =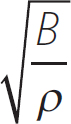

where B is the bulk modulus of the medium and ρ is the density of the medium. The bulk modulus defines the elasticity of the medium (its ability to change volume and then return to its original volume). The larger the bulk modulus, the harder it is to change the volume of the medium due to either compression or expansion. For ideal gases, the bulk modulus is

B = 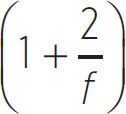P

where f is the number of degrees of freedom of the gas and P is the pressure of the gas, as in Chapter 9.

EXAMPLE

What is the speed of sound of 50 kg of atomic hydrogen in a 1 m3 container at a pressure of 1.0 × 105 Pa?

First, the density of this sample is

ρ = 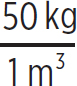= 50 kg/m3

Next, the bulk modulus of this gas is

B = 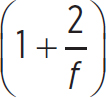P = 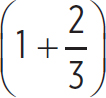(1.0 × 105 Pa) = 1.7× 105 Pa

So, the speed of sound of this sample of gas is

vs = 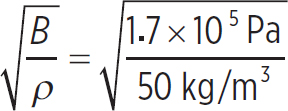= 58.3 m/s

Imagine a person standing near a sound-emitting object, with no relative velocity between the two. The sound-emitting object emits a sound with some wavelength λ, which can be described by the following figure.

Figure 10.9: Sound with No Relative Velocity

Now, imagine there are two people, one in front of the object and one behind the object, with the object moving toward the person in front. This scenario is shown in the next figure. What’s important to notice about the figure is that each wavefront of sound is produced where the object was at the time, not where it is now. This causes wavefronts to move closer together on the front of the object and move further apart on the back of the object, changing the wavelength for each. This is known as the Doppler effect (named after Austrian mathematician Christian Doppler): The wavelength, and therefore frequency, of an emitted sound changes when there is a relative motion to the source of the sound. Since the person in front of the object gets sound with a smaller wavelength, she hears a higher frequency, and the person behind the object vice-versa.

Figure 10.10: Sound with Relative Velocity

Before giving the equation for the shift in frequency due to the Doppler effect, we want to introduce a bit of notation. First, the source has a natural frequency, the frequency that would be heard if you were at rest with respect to the source. This will be referred to as fS. The frequency that someone would hear will be referred to as the detected frequency, fD. Now, the velocity of the source will be vS, and the velocity of the detector will be vD. In this case, the detected frequency will be

Equation 10.16

fD = 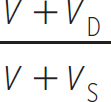fs

where v is the speed of the sound in the medium. Since we are dealing with velocities, there has to be an established coordinate system, so that you can choose whether or not the velocities are positive or negative. The coordinate system for this problem has to be with the detector at the origin and the positive axis drawn from the detector to the source, in order to get the signs correct in Equation 10.16.

For instance, if the detector were moving toward the source, it would have a positive velocity, and if the source were moving toward the detector, it would have a negative velocity. Thus, the numerator of Equation 10.16 would increase and the denominator would decrease, resulting in a detected frequency that is larger than the natural frequency of the source, as expected.

EXAMPLE

If a source emits a sound at 200 Hz and is moving at a speed 20 m/s away from the detector, what is the detected frequency if the detector is moving at 15 m/s toward the source?

In this case, the detector is moving toward the source, so its velocity is positive. Since the source is moving away from the detector, its velocity is also positive, so

fD = 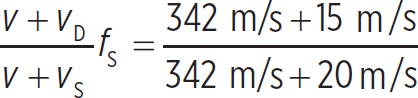(200 Hz) = 197 Hz

This result makes sense. Since the source is moving away from the detector faster than the detector is moving toward the source, they are moving apart, and so the detected frequency should be less than the source frequency.

What happens if you travel faster than the speed of sound? Well, then the Doppler effect equation no longer works. This is illustrated in the figure on the next page.

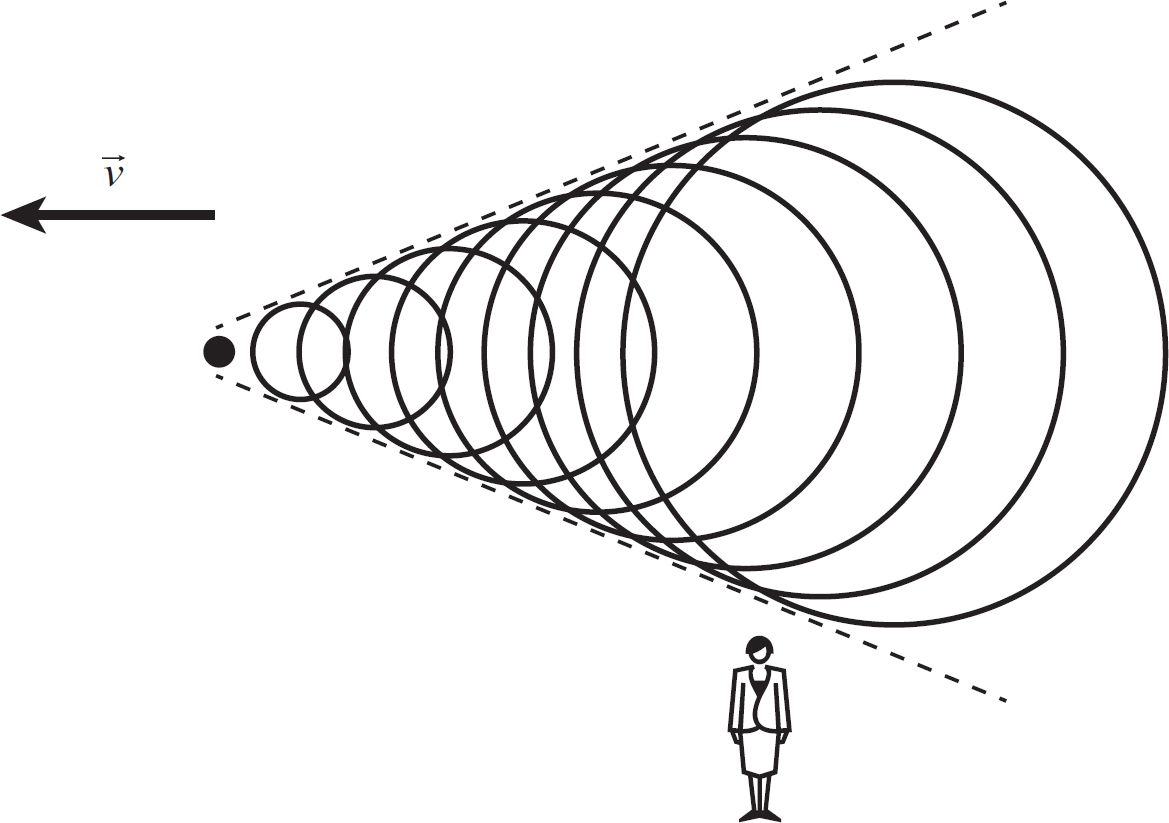
Figure 10.11: Doppler Effect for Supersonic Speeds

In this case, an observer in front of the object will never hear any sound (because the object is moving faster than the sound). Only an observer behind the object will hear anything, and it will be at a really low frequency (the supersonic speeds pull the wavefronts very far apart). This really low frequency sound heard is known as a sonic boom. The loudness of a sonic boom is due to the incredible pressures built up when these wavefronts stack up on top of one another.

The next thing we should talk about is the volume of a sound. Volume, referred to as intensity level, is given by the following equation:

Equation 10.17

β = (10 dB)log

where dB is the decibel (named after the Scottish scientist Alexander Graham Bell, inventor of the telephone), the unit of volume, I is the intensity of the sound, and I0 is the lowest intensity sound a human ear can hear,

I0 = 10 −12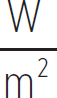

The intensity of any wave is the power carried by the waves over the surface area that the emitted waves occupy. In the case of sound, the intensity drops off as 1/r2, or

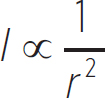
Notice that this is another appearance of an inverse-square relationship. This means that if a sound has some intensity I1 at r1, then the intensity I2 at r2 is given by

Equation 10.18

EXAMPLE

You are 1 m away from a source and hear a sound at 40 dB. If you were to move 9 m further away from the source, what would the volume of the sound be there?

First, you know

(10 dB)log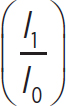 = 40 dB

Now, the volume heard at position 2 is

β2 = (10 dB)log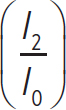

where

I2 =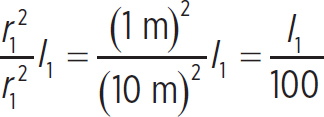

So,

β2 = (10 dB)log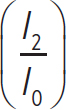 = (10 dB)log

= (10 dB)log − (10 dB)log(100) = 40 dB− 20 dB = 20 dB

In the previous section, we discussed the fact that when waves appear together at the same position, they undergo interference, and the resulting amplitude of the interfered wave is just the sum of the amplitudes of the individual waves. Well, if two sounds are emitted at different frequencies, then the two waves also undergo interference.

However, since these waves are at different frequencies, something interesting happens. They cycle between undergoing constructive and destructive interference. When the waves are undergoing constructive interference, the amplitude grows. This means that the energy, power, and intensity grow, which means that the volume must increase as well. When the waves are undergoing destructive interference, the amplitude decreases, and so the volume does as well.

It turns out that this cycling between constructive and destructive interference occurs at a constant frequency, known as the beat frequency. The beat frequency between two waves of frequencies f1 and f2 is

Equation 10.19

fbeat = |f1 − f2|

EXAMPLE

Two speakers sit near each other, one emitting a frequency of 350 Hz and one emitting an unknown frequency. If the beat frequency you hear is 20 Hz, what is the frequency of the unknown speaker?

Notice the equation for beat frequency is the absolute value of the difference between frequencies. This is because one frequency will always be larger than the other, and no matter what you call f1 or f2, a frequency cannot be negative. This leads to a problem: The beat frequency just measures the difference between the two frequencies, but it cannot tell us which speaker is at the higher frequency. So, is the unknown speaker emitting at a frequency of 330 Hz or a frequency of 370 Hz? It is impossible to tell.

EXAMPLE

Going back to the previous example, let’s say that the first speaker has a variable frequency. You change it from 350 Hz to 360 Hz and the beat frequency drops from 20 Hz to 10 Hz. What is the frequency of the second speaker?

Now you can solve this problem. Since the frequency of the first speaker was increased, and the beat frequency decreased, the second speaker must be at a higher frequency, meaning 370 Hz. Notice that if the second speaker were at 330 Hz, and you increased the first speaker to 360 Hz, the beat frequency would have been 30 Hz, not 10 Hz. So, 330 Hz could not possibly be the frequency of the second speaker.

Lastly, we need to discuss standing sound waves. These are produced by sounds in tubes. There are two types of tubes that would produce standing sounds waves: a tube with two open ends, and a tube with one closed and one open end. The tube with two closed ends produces node-node standing waves, and the tube with one closed and one open end produces node-antinode standing waves. The equations for standing sound waves in tubes are identical to those of standing mechanical waves.

EXAMPLE

What is the fundamental frequency of a 3 m tube of air with an open end?

If one end of the tube is open, it produces node-antinode standing waves, so

f1 = 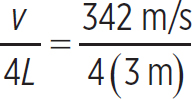= 28.5 Hz

Examples of musical instruments utilizing two open ends are recorders and trumpets. One end is open that allows air to flow in, and one end is open to allow air to flow outward. You can have either pipes with two open ends or pipes with a stopped end in an organ.

 

DRILL

CHAPTER 10 PRACTICE QUESTIONS

Click here to download a PDF of Chapter 10 Practice Questions.

Directions: Complete the following problems as specified by each question, and then check your work using the solutions that follow. For extended, step-by-step solutions, access your Student Tools online.

1. If the bulk modulus of air is 1.43 × 105 Pa, what is the density of air at sea level?

2. Sound travels from air to water, where the bulk modulus is 2.2 × 109 Pa. If a sound was emitted above the surface of a pool of water at 5 mm, what would the wavelength be underwater? Note that the density of water is 1000 kg/m3.

3. What is the displacement of a mechanical wave at a distance of 5 cm from the origin of the wave after 2 s? Consider the amplitude to be 6 cm, the wavelength to be 1 cm, and the period to be 5 s.

4. Let’s say you have a rope that is elastic, meaning that when it stretches it obeys Hooke’s Law. If the force constant was 50 N/m, and you were to stretch the rope by 50 cm, what would the speed of a wave be on the rope? For this rope, the natural length is 1 m and the mass is 2 kg.

5. A string is fixed at both ends and has a tension of 100 N, a mass of 100 g, and a length of 10 cm. What is the lowest frequency standing wave you could produce on the string? What about the largest frequency?

6. You have a small speaker that emits a constant sound of 100 Hz. You then throw it into the air so that it reaches 3 m above where you release it. What is the frequency you hear right when you let it go? What about at the top of the trajectory? What about when it has fallen to the same height that you released it at? Assume in this problem that you’ve released the speaker above your head.

7. You drop a speaker emitting a sound at 150 Hz down a deep well. Once the speaker has dropped for 3 s, what is the beat frequency you hear from the sounds coming up from the well?

8. You can hear that a speaker produces a sound of intensity of 0.1 W/m2 at your current location. What is the volume of that sound? What would the volume be if you doubled your distance from the speaker?

9. An organ has two pipes of identical length, 2 m, one with an open end and one with a stopped end. What is the beat frequency you would hear if each pipe emitted sound at its second-lowest harmonic frequency?

SOLUTIONS TO CHAPTER 10 PRACTICE QUESTIONS

1. Using the equation for the speed of sound and noting that the speed of sound at sea level is 342 m/s,

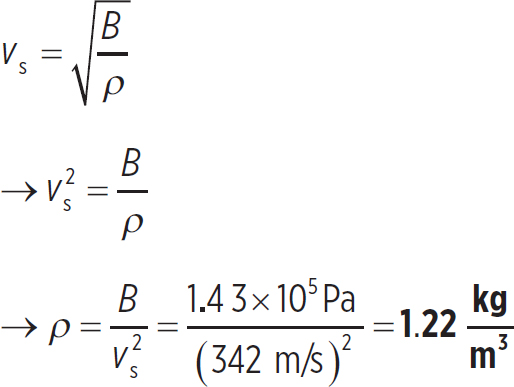
2. First, the speed of sound in water is

vw = 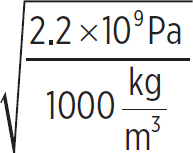= 1483 m/s

Now, when the sound travels from the air into the water, its frequency remains the same, but the wavelength and speed change. Setting the frequencies equal to one another gives us

fa = fw

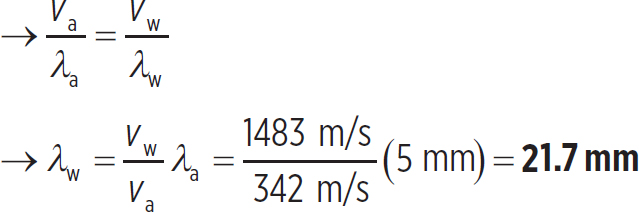
3. In order to solve this, you need to know the wavenumber and the angular frequency of the wave. First, the wavenumber is

k = 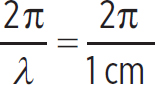= 6.28 cm−1

Next, the angular frequency is

ω = 2πf = 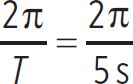= 1.26 s−1

So, the displacement at x = 5 cm and t = 2 s is

y(5 cm, 2 s) = A sin(kx − ωt)

= (6 cm) sin((6.28 cm−1)(5 cm) − (1.26 s−1)(2 s))

= −3.42 cm

4. If the rope is elastic, then the tension in it is just equal to the Hooke force. When it is stretched a distance of 50 cm from its natural length, the tension is

T =kx =(0.5 m) = 25 N

To calculate the speed of the rope, you also need to know the mass per unit length. Now, this is not for the rope at its natural length, but for the rope at its current length, which is 1.5 m:

μ =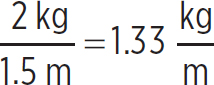

So, the speed of a wave on this rope would be

v = 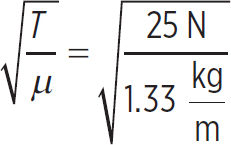= 4.3 m/s

5. First, you need to know the speed of a wave on this string. It would be

v = 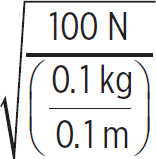= 10 m/s

Now, the lowest frequency harmonic, or the fundamental harmonic, is

f1 = 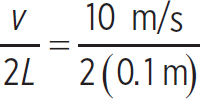= 50 Hz

Note that all harmonics are of the form nf1. There is no upper-limit to n, so there is no “largest” harmonic frequency. The opposite is true for the wavelength. The harmonic wavelength is given by λ1/n, so there is a largest harmonic wavelength, but no smallest.

6. In order for the speaker to reach a height of 3 m, it needed to have an initial speed of

v0 = = 7.67 m/s

Since it is moving away from you at this point, the frequency you hear is

fD = = 97.8 Hz

At the peak, there is no relative motion between you and the speaker, so the frequency you hear is 100 Hz. After it drops 3 m to its original height, it has the same speed that it was launched with, 7.67 m/s, but now its coming toward you instead of moving away from you, so the frequency you hear is

fD = 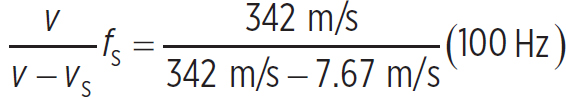= 102.3 Hz

7. As the speaker falls down the well, it is gaining speed away from you, so you are progressively hearing a lower and lower frequency. After it has fallen for 3 s, its speed is

v = gt = (9.8 m/s2)(3 s) = 29.4 m/s

Since the speaker is moving away from you, you hear a frequency of

fD = 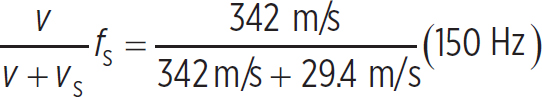= 138 Hz

However, and here’s why this problem seems tricky, the speaker is also moving toward the bottom of the well. This means that sound is “detected” by the bottom of the well with a frequency of

f = 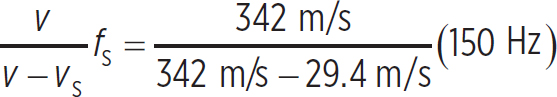= 164 Hz

Once this sound hits the bottom of the well, it is then reflected back upward at the same frequency. This means you can also hear this echo coming up from the bottom of the well. Thus, the beat frequency you would hear is

fbeat = 164 Hz − 138 Hz = 26 Hz

8. The volume of the sound at your current location is

β1 = (10 dB)log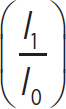 = (10 dB)log 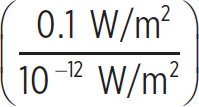= 110 dB

When you double your distance, you reduce the intensity by a factor of 4. Doing this same calculation, but for an intensity of 0.025 W/m2, you get

β2 = (10 dB)log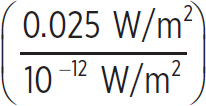 = 104 dB

9. For the pipe that is open at both ends, you know that standing waves produced are node-node, so the second-lowest frequency will have a harmonic number of 2 and will be

f0,2 = 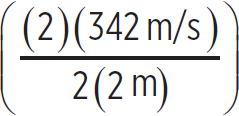= 171 Hz

For the pipe that is stopped, you know that the standing waves produced are going to be node-antinode. This means that the second-lowest frequency is the third harmonic, because harmonic numbers have to be odd for node-antinode standing waves. This is

fc,3 = 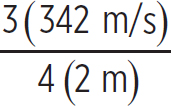= 128 Hz

So, the beat frequency heard is

fbeat = 171 Hz − 128 Hz = 43 Hz

REFLECT

Congratulations on completing Chapter 10!

Here’s what we just covered.

Rate your confidence in your ability to:

• Explain what a wave is

1 2 3 4 5

• Describe wave properties

1 2 3 4 5

• Apply knowledge of waves to mechanical waves on a string

1 2 3 4 5

• Apply knowledge of waves to sound

1 2 3 4 5

• Describe standing waves

1 2 3 4 5

If you rated any of these topics lower than you’d like, consider reviewing the corresponding lesson before moving on, especially if you found yourself unable to correctly answer one of the related end-of-chapter questions.