• V •
27. Relations, their domains and counter-domains; relations and sentential functions with two free variables
In the previous chapters we have already met with a few RELATIONS between things. As examples of relations between two things we may take, for instance, identity (equality) and diversity (inequality). We sometimes read the formula:
x = y
as follows:
x has the relation of identity to y
or also:
the relation of identity holds between x and y,
and we say that the symbol “=” designates the relation of identity. In an analogous way, the formula:
x ≠ y
is sometimes read:
x has the relation of diversity to y
or:
the relation of diversity holds between x and y,
and one says that the symbol “≠” designates the relation of diversity. We have further encountered certain relations holding between classes, namely, the relations of inclusion, of overlapping, of disjointness, and so on. We will now discuss several concepts belonging to the general THEORY OF RELATIONS, which constitutes a special and very important part of logic, and in which relations of an entirely arbitrary character are considered and general laws concerning them are established.1
To facilitate our considerations, we introduce special variables “R”, “S”, … which serve to denote relations. In place of such phrases as:
the thing x has the relation R to the thing y
and:
the thing x does not have the relation R to the thing y
we shall employ symbolic abbreviations:
x R y
and (to use the negation sign of sentential calculus, cf. Section 13)
~(x R y),
respectively.
Any thing having the relation R to some thing y we call a PREDECESSOR WITH RESPECT TO THE RELATION R; any thing y for which there is a thing x such that
x R y
is called a SUCCESSOR WITH RESPECT TO THE RELATION R. The class of all predecessors with respect to the relation R is known as the DOMAIN and the class of all successors as the COUNTER-DOMAIN (or CONVERSE DOMAIN) OF THE RELATION R. Thus, for example, any individual is both a predecessor and a successor with respect to the relation of identity, so that the domain and counter-domain of this relation are both the universal class.
In the theory of relations—just as in the theory of classes—we may distinguish relations of different orders. The RELATIONS OF THE FIRST ORDER are those which hold between individuals; the RELATIONS OF THE SECOND ORDER are those which hold between classes, or relations, of the first order; and so on. The situation is here all the more complicated as we must often consider “mixed” relations whose precedessors are, say, individuals, and its successors classes, or whose predecessors are, for instance, classes of the first order and its successors classes of the second order. The most important example of a relation of this kind is the relation which holds between an element and a class to which it belongs; as we recall from Section 21, this relation is denoted by the symbol “![]() ”.—As in the case of classes, our considerations concerning relations will refer primarily to those of the first order, although the concepts discussed here can and, in a few cases, will be applied to relations of higher orders.
”.—As in the case of classes, our considerations concerning relations will refer primarily to those of the first order, although the concepts discussed here can and, in a few cases, will be applied to relations of higher orders.
We assume that, to every sentential function with two free variables “x” and “y”, there corresponds a relation holding between the things x and y if, and only if, they satisfy the given sentential function; in this connection it is said of a sentential function with the free variables “x” and “y” that it expresses a relation between the things x and y. Thus, for instance, the sentential function:
x + y = 0
expresses the relation of having the opposite sign or, briefly, of being opposite; the numbers x and y have the relation of being opposite if, and only if, x + y = 0. If we denote this relation by the symbol “O”, then the formulas:
x O y
and
x + y = 0
are equivalent. Similarly, any sentential function containing the symbols “x” and “y” as the only free variables may be transformed into an equivalent formula of the form:
x R y
where, in place of “R”, we have a constant which designates some relation. The formula:
x R y
may, therefore, be considered as the general form of a sentential function with two free variables, just as the formula:
![]()
could be looked upon as the general form of a sentential function with one free variable (cf. Section 22).
28. Calculus of relations
The theory of relations is one of the farthest developed branches of mathematical logic. One part of it, the CALCULUS OF RELATIONS, is akin to the calculus of classes, its principal object being the establishment of formal laws governing the operations by means of which other relations are constructed from given ones.
In the calculus of relations we consider, in the first place, a group of concepts which are exact analogues of those of the calculus of classes; they are usually denoted by the same symbols and governed by quite similar laws. (In order to avoid ambiguity, we might, of course, employ a different set of symbols in the calculus of relations, taking, for instance, the symbols of the calculus of classes and placing a dot over each.)
We have thus in the calculus of relations two special relations, the UNIVERSAL RELATION ∨ and the NULL RELATION ∧, the first of which holds between any two individuals, and the second between none.
We have, further, various relations between relations, for instance, the RELATION OF INCLUSION; we say that the relation R is INCLUDED in the relation S, in symbols:
R ⊂ S,
if, whenever R holds between two things, S holds between them likewise; or, in other words, if, for any x and y, the formula:
x R y
implies:
x S y.
We know, for instance, from arithmetic that, whenever
x < y,
then
x ≠ y;
hence the relation of being smaller is included in the relation of diversity.
If, at the same time,
R ⊂ S and S ⊂ R,
that is to say, if the relations R and S hold between the same things, then they are identical:
R = S.
We have, further, the SUM or UNION OF TWO RELATIONS R AND S, in symbols:
R ∪ S,
and the PRODUCT or INTERSECTION OF R AND S, in symbols:
R ∩ S.
The first, R ∪ S, holds between two things if, and only if, at least one of the relations R and S holds between them; in other words, the formula:
x(R ∪ S)y
is equivalent to the condition:
x R y or x S y.
Similarly the product of two relations is defined, using only the word “and” instead of “or”. Thus, for example, if R is the relation of fatherhood (that is, a relation holding between two persons x and y if, and only, x is the father of y), and S the relation of motherhood, then R ∪ S is the relation of parenthood, while R ∩ S is, in this case, the null relation.
We have, finally, the NEGATION or the COMPLEMENT OF A RELATION R denoted by:
R′.
It is a relation which holds between two things if, and only if, the relation R does not hold between them; in other words, for any x and y, the formulas:
x R′ y and ~(x R y)
are equivalent. It should be noted that, if a relation is designated by a constant, then its complement is frequently denoted by the symbol obtained from that constant by crossing it by a vertical or oblique bar. The negation of the relation <, for example, is usually denoted by “![]() ”, and not by “<′”.
”, and not by “<′”.
In the calculus of relations there occur also entirely new concepts, without analogues in the calculus of classes.
We have here, first, two special relations, IDENTITY and DIVERSITY between individuals (which are, incidentally, familiar to us from earlier considerations). In the calculus of relations they are denoted by special symbols, e.g., “|” and “D”, and not by the symbols “=” and “≠” used in other parts of logic. We write, thus:
x | y and x D y
instead of :
x = y and x ≠ y.
The symbols “=” and “≠” are used in the calculus of relations only to denote the identity and diversity between relations.
We have here, further, a very interesting and important new operation, with the help of which we form, from two relations R and S, a third relation called the RELATIVE PRODUCT or COMPOSITION OF R AND S (as opposed to it, the ordinary product is sometimes called the ABSOLUTE PRODUCT). The relative product of R and S is denoted by the symbol:
R/S;
it holds between two things x and y if, and only if, there exists a thing z such that we have at the same time:
x R z and z S y.
Thus, for instance, if R is the relation of being husband and S the relation of being daughter, then R/S holds between two persons x and y if there is a person z such that x is husband of z and z is daughter of y; the relation R/S, therefore, coincides with the relation of being son-in-law.—We have here, in addition, another operation of a similar character, whose result is called the RELATIVE SUM OF TWO RELATIONS. This operation does not play a very great role and will not be defined here.
Finally, we have an operation similar to that of forming R′, namely, an operation with the help of which, from a relation R, we form a new relation called the CONVERSE OF R and denoted by:
![]() .
.
The relation ![]() holds between x and y if, and only if, R holds between y and x. If a relation is denoted by a constant, then for denoting its converse we often employ the same symbol printed in the opposite direction. The converse of the relation <, for instance, is the relation >, since, for any x and y, the formulas:
holds between x and y if, and only if, R holds between y and x. If a relation is denoted by a constant, then for denoting its converse we often employ the same symbol printed in the opposite direction. The converse of the relation <, for instance, is the relation >, since, for any x and y, the formulas:
x < y and y > x
are equivalent.
In view of the rather specialized character of the calculus of relations, we shall here not go any further into the details of it.
29. Some properties of relations
We now turn to that part of the theory of relations whose task it is to single out and investigate special kinds of relations with which one meets frequently in other sciences and, in particular, in mathematics.
We shall call a relation R REFLEXIVE IN THE CLASS K, if every element x of the class K has the relation R to itself:
x R x;
if, on the other hand, no element of this class has the relation R to itself:
~(x R x),
then the relation R is said to be IRREFLEXIVE IN THE CLASS K. The relation R is called SYMMETRICAL IN THE CLASS K if, for any two elements x and y of the class K, the formula:
x R y
y R x.
If, however, the formula:
x R y
always implies:
~(y R x),
then the relation R is said to be ASYMMETRICAL IN THE CLASS K. The relation R is called TRANSITIVE IN THE CLASS K if, for any three elements x, y and z of the class K the conditions:
x R y and y R z
always imply:
x R z.
If, finally, for any two different elements x and y of the class K, at least one of the formulas:
x R y and y R x
holds, that is, if the relation R subsists between two arbitrary distinct elements of K in at least one direction, the relation is called CONNECTED IN THE CLASS K.
In case K is the universal class (or, at any rate, the universe of discourse of the science in which we happen to be interested—cf. Section 23) we usually speak, more briefly, not of relations reflexive, symmetrical, and so on, in the class K, but simply of reflexive relations, symmetrical relations, and so on.
30. Relations which are reflexive, symmetrical and transitive
The above-mentioned properties of relations frequently occur in groups. Very common, for instance, are those relations which are reflexive, symmetrical, and transitive as well. A typical example of this type is the relation of identity; Law II of Section 17 expresses that this relation is reflexive, by Law III identity is a symmetrical relation, and according to Law IV it is transitive (and this accounts for the names of these laws that were given in Section 17). Numerous other examples of relations of this kind may be found within the field of geometry. Congruence, for instance, is a reflexive relation in the set of all line segments (or of arbitrary geometrical configurations), since every segment is congruent to itself; it is symmetrical, since, if a segment is congruent to another segment, the other is congruent to the first; and, finally, it is transitive, since, if the segment A is congruent to the segment B, and B to C, then the segment A is also congruent to the segment C. The same three properties belong to the relations of similarity among polygons or of parallelism among straight lines (assuming any line to be parallel to itself), or—outside the domain of geometry—to the relations of being equally old among people, or of synonymity among words.
Every relation which is at the same time reflexive, symmetrical and transitive is thought of as some kind of equality. Instead of saying, therefore, that such a relation holds between two things, one can, in this sense, also say that these things are equal in such and such a respect, or—in a more precise mode of speech—that certain properties of these things are identical. Thus, instead of stating that two segments are congruent, or two people equally old, or two words synonymous, it may just as well be stated that the segments are equal in respect of their length, that the people have the same age, or that the meanings of the words are identical.
*By way of an example we will give an indication of how it is possible to establish a logical basis for such a mode of expression. For this purpose let us consider the relation of similarity among polygons. We will denote the set of all polygons similar to the given polygon P (or, to use a slightly more current terminology, the common property which belongs to all polygons similar to P and to no others) as the shape of the polygon P. Thus shapes are certain sets of polygons (or properties of polygons; cf. remarks at the end of Section 22). Making use of the fact mentioned above that the relation of similarity is reflexive, symmetrical and transitive, we can now easily show that every polygon belongs to one and only one such set, that two similar polygons belong always to the same set, and that two polygons which are not similar belong to different sets. From this it follows at once that the two statements:
the polygons P and Q are similar
the polygons P and Q have the same shape (that is, the
shapes of P and Q are identical)
are equivalent.
The reader will notice immediately that, in the course of the preceding considerations, we have once before applied an analogous procedure, namely in Section 26 in making the transition from the expression:
the classes K and L are equinumerous
to the equivalent one:
the classes K and L have the same cardinal number.
It can be shown with little difficulty that the same procedure is applicable to any reflexive, symmetrical and transitive relation. There is even a logical law, called the PRINCIPLE OF ABSTRACTION, that supplies a general theoretical foundation for the procedure which we have been considering, but we shall here forego the exact formulation of this principle.*
There is, so far, no universally accepted term denoting the totality of relations which are at the same time reflexive, symmetrical and transitive. Sometimes they have generally been called EQUALITIES or EQUIVALENCES. But the term “equality” is also sometimes reserved for particular relations of the category under consideration, and two things are then called equal if such a relation holds between them. For instance, in geometry, as has been pointed out in Section 19, congruent segments are often referred to as equal segments. We will emphasize here once more that it is preferable to avoid such expressions altogether; their use merely leads to ambiguities, and it violates the convention in accordance with which we consider the terms “equality” and “identity” as synonymous.
31. Ordering relations; examples of other relations
Another very common kind of relation is represented by those which are asymmetrical, transitive and connected in a given class K (they must then, as can be shown, also be irreflexive in the class K). Of a relation with these properties we say that it ESTABLISHES AN ORDER IN THE CLASS K; we say also that the class K is ORDERED BY THE RELATION R. Consider, for example, the relation of being smaller (or, the relation less than, as we shall say occasionally); it is asymmetrical in any set of numbers, for, if x and y are any two numbers and if
x < y
then
![]()
it is transitive, since the formulas:
x < y and y < z
always imply:
x < z;
finally, it is connected, since, of any two distinct numbers, one must be smaller than the other (and it is also irreflexive, since no number is smaller than itself). Any set of numbers, therefore, is ordered by the relation of being smaller. Likewise, the relation of being greater represents another ordering relation for any set of numbers.
Let us now consider the relation of being older. One can easily verify that this relation is irreflexive, asymmetrical and transitive in any given set of people. However, it is not necessarily connected; for it can happen, perchance, that the set contains two people having exactly the same age, that is to say, who were born at the same moment, so that the relation of being older does not hold between them in either direction. If, on the other hand, we consider a set of people in which no two are of exactly the same age, the relation of being older establishes an order in that set.
Many instances of relations are known that belong to neither of the two categories discussed in the present section and in the preceding one. Let us consider a few examples.
The relation of diversity is irreflexive in any set of things, since no thing is different from itself; it is symmetrical, for, if
x ≠ y,
y ≠ x;
it fails to be transitive, however, since the formulas:
x ≠ y and y ≠ z
do not imply the formula:
x ≠ z;
it is, on the other hand, connected, as can be seen at once.
The relation of inclusion between classes, by the law of identity and one of the laws of syllogism (cf. Section 24), is reflexive and transitive; it is, further, neither symmetrical nor asymmetrical, since the formula:
K ⊂ L
neither implies nor excludes the formula:
L ⊂ K
(these two formulas are fulfilled simultaneously if, and only if, the classes K and L are identical); finally, it can be seen with ease that it is not connected. Thus, the relation of inclusion differs in its properties from other relations thus far considered.
32. One-many relations or functions
We will now deal in some detail with another particularly important category of relations. A relation R is called a ONE-MANY or FUNCTIONAL RELATION or simply a FUNCTION if, to every thing y, there corresponds at most one thing x such that x R y; in other words, if the formulas:
x R y and z R y
always imply the formula:
x = z.
The successors with respect to the relation R, that is, those things y for which there actually are things x such that
x R y,
are the ARGUMENT VALUES, the predecessors are the FUNCTION VALUES or, simply, the VALUES OF THE FUNCTION R. Let R be an arbitrary function, y any one of its argument values; the unique value x of the function corresponding to the value y of the argument we will denote by the symbol “R(y)”; consequently we replace the formula:
x R y
by:
x = R(y).
It has become the custom, especially in mathematics, to use, not the variables “R”, “S”, …, but other letters such as “f”, “g”, … to denote functional relations, so that we find formulas like these:
x = f(y), x = g(y), …;
the formula:
x = f(y),
for instance, is read as follows:
the function f assigns (or correlates) the value x to the
argument value y
or
x is that value of the function f which corresponds to (or is
correlated with) the argument value y.
(There is also another custom, of using the variable “x” for denoting the argument value and the variable “y” for denoting the value of the function. We shall not adhere to this custom, and continue to use “x” and “y” in the opposite order, because this is more convenient in connection with the general notation used in the theory of relations.)
In many elementary textbooks of algebra a definition of the concept of a function is to be found that is quite different from the definition adopted here. The functional relation is there characterized as a relation between two “variable” quantities or numbers: the “independent variable” and the “dependent variable”, which depend upon each other in so far as a change of the first effects a change of the second. Definitions of this kind should no longer be employed today, since they are incapable of standing up to any logical criticism; they are the remains of a period in which one tried to distinguish between “constant” and “variable” quantities (cf. Section 1). He who desires to comply with the requirements of contemporary science and yet does not wish to break away completely from tradition, may, however, retain the old terminology and use, beside the terms “argument value” and “function value”, the expressions “value of the independent variable” and “value of the dependent variable”.
The simplest example of a functional relation is represented by the ordinary relation of identity. As an example of a function from everyday life let us take the relation expressed by the sentential function:
x is father of y.
It is a functional relation, since, to every person y, there exists but one person x who is father of y. In order to indicate the functional character of this relation, we insert the word “the” in the above formulation:
x is the father of y,
instead of which we might also write:
x is identical with the father of y.
Such an alteration of the original expression, involving the insertion of the definite article, serves, in ordinary language, exactly the same purpose as the transition from the formula:
x R y
to the formula:
x = R(y)
in our symbolism,
The concept of a function plays a most important role in the mathematical sciences, There are whole branches of higher mathematics devoted exclusively to the study of certain kinds of functional relations. But also in elementary mathematics, especially in algebra and trigonometry, we find an abundance of functional relations. Examples are the relations expressed by such formulas as:
x + y = 5,
x = y2,
x = log10y,
x = sin y,
and many others. Let us consider the second of these formulas more closely. To every number y, there corresponds only one number x such that x = y2, so that the formula really does represent a functional relation. Argument values of this function are arbitrary numbers, values of the function, however, only non-negative numbers. If we denote this function by the symbol “f”, the formula:
x = y2
assumes the form:
x = f(y).
Evidently “x” and “y” may here be replaced by symbols designating definite numbers. Since, for instance,
4 = (−2)2,
it may be asserted that
4 = f(−2);
thus, 4 is the value of the function f corresponding to the argument value −2.
On the other hand, and again in elementary mathematics already, we encounter numerous relations which are not functions. For example, the relation of being smaller is certainly not a function, since, to every number y, there are infinitely many numbers x such that
x < y.
Nor is the relation between the numbers x and y expressed by the formula:
x2 + y2 = 25
a functional relation, since, to one and the same number y, there may correspond two different numbers x for which the formula is valid; corresponding to the number 4, for instance, we have both the numbers 3 and −3. It may be noted that relations between numbers which, like the one just considered, are expressed by equations and correlate with one number y two or more numbers x are sometimes called in mathematics two- or many-valued functions (in opposition to single-valued functions, that is, to functions in the ordinary meaning). It seems, however, inexpedient—at least on an elementary level—to denote such relations as functions, for this only tends to blot out the essential difference between the notion of a function and the more general one of a relation.
Functions are of particular significance as far as the application of mathematics to the empirical sciences is concerned. Whenever we inquire into the dependence between two kinds of quantities occurring in the external world, we strive to give this dependence the form of a mathematical formula, which would permit us to determine exactly the quantity of the one kind by the corresponding quantity of the other; such a formula always represents some functional relation between the quantities of two kinds. As an example let us mention the well-known formula from physics:
s = 16.1 t2
expressing the dependence of the distance s, covered by a freely falling body, upon the time t of its fall (the distance being measured in feet and the time in seconds).
*In conclusion of our remarks on functional relations we want to emphasize that the concept of a function which we are considering now differs essentially from the concepts of a sentential and of a designatory function known from Section 2. Strictly speaking, the terms “sentential function” and “designatory function” do not belong to the domain of logic or mathematics; they denote certain categories of expressions which serve to compose logical and mathematical statements, but they do not denote things treated of in those statements (cf. Section 9). The term “function” in its new sense, on the other hand, is an expression of a purely logical character; it designates a certain type of things dealt with in logic and mathematics. There is, no doubt, a connection between these concepts, which may be described roughly as follows. If the variable “x” is joined by the symbol “=” to a designatory function containing “y” as the only variable, e.g. to “y2 + 2y + 3”, then the resulting formula (which is a sentential function):
x = y2 + 2y + 3
expresses a functional relation; or, in other words, the relation holding between those and only those numbers x and y which satisfy this formula is a function in the new sense. This is one of the reasons why these concepts are so often confused.*
33. One-one relations or biunique functions, and one-to-one correspondences
Among the functional relations particular attention should be paid to the so-called ONE-ONE RELATIONS or BIUNIQUE FUNCTIONS, that is, to those functional relations in which not only to every argument value y only one function value x is correlated, but also conversely only one argument value y corresponds to every value x of the function; they might also be defined as those relations which have the property that their converses (cf. Section 28) as well as the relations themselves are one-many.
If f is a biunique function, K an arbitrary class of its argument values, and L the class of function values correlated with the elements of K, we say that the function f MAPS THE CLASS K ON THE CLASS L IN A ONE-TO-ONE MANNER, or that it ESTABLISHES A ONE-TO-ONE CORRESPONDENCE BETWEEN THE ELEMENTS OF K AND L.
Let us consider a few examples. Suppose we have a half-line issuing from the point O, with a segment marked off indicating the unit of length. Further let Y be any point on the half-line. Then the segment OY can be measured, that is to say, one can correlate with it a certain non-negative number x called the length of the segment. Since this number depends exclusively on the position of the point Y, we may denote it by the symbol “f(Y)”; we consequently have:
x = f(Y).
But, conversely, to every non-negative number x, we may also construct a uniquely determined segment OY on the half-line under consideration, whose length equals x; in other words, to every x, there corresponds exactly one point Y such that
x = f(Y).
The function f is, therefore, biunique; it establishes a one-to-one correspondence between the points of the half-line and the non-negative numbers (and it would be equally simple to set up a one-to-one correspondence between the points of the entire line and all real numbers). Another example is supplied by the relation expressed by the formula:
x = −y.
This is a biunique function since, to every number x, there is only one number y satisfying the given formula; it can be seen at once that this function maps, for instance, the set of all positive numbers on the set of all negative numbers in a one-to-one manner. As a last example let us consider the relation expressed by the formula:
x = 2y
under the assumption that the symbol “y” here denotes natural numbers only. Again we have a biunique function; it correlates with every natural number y an even number 2y; and vice versa—to every even natural number x there corresponds just one number y such that 2y = x, namely, the number ![]() . The function thus establishes a one-to-one correspondence between arbitrary natural numbers and even natural numbers.—Numerous examples of biunique functions and one-to-one mappings can be drawn from the field of geometry (symmetric, collinear mappings, and so on).
. The function thus establishes a one-to-one correspondence between arbitrary natural numbers and even natural numbers.—Numerous examples of biunique functions and one-to-one mappings can be drawn from the field of geometry (symmetric, collinear mappings, and so on).
* Owing to the circumstance that we have the notion of a one-to-one correspondence at our disposal, we are now in a position to lay down an exact definition of a term which, earlier on, we had only been able to characterize intuitively rather than with precision. It is the concept of equinumerous classes (see Section 26). We shall now say that two classes K and L are equinumerous, or that they have the same cardinal number, if there exists a function which establishes a one-to-one correspondence between the elements of the two classes. On the basis of this definition it follows, in connection with the examples considered above, that the set of all points of an arbitrary half-line is equinumerous with the set of all non-negative numbers; and likewise, that the set of positive numbers and the set of negative numbers are equinumerous, and that the same holds for the set of all natural numbers and the set of all even natural numbers. The last example is particularly instructive; for it shows that a class may be equinumerous with a proper subclass of itself. To many readers this fact may seem most paradoxical at a first glance, because usually only finite classes are compared with respect to the numbers of their elements, and a finite class has, indeed, a greater cardinal number than any of its parts. The paradox disappears on calling to mind that the set of natural numbers is infinite and that we are, by no means, justified to ascribe properties to infinite classes that we have observed exclusively in connection with finite classes.—It is noteworthy that the property of the set of natural numbers of being equinumerous with one of its parts is shared by all infinite classes. This property is, therefore, characteristic of infinite classes, and it permits us to distinguish them from finite classes; a finite class can simply be defined as a class which is not equinumerous with any one of its proper subclasses. (However, this definition entails a certain logical difficulty, a discussion of which we will not enter into here.)2*
34. Many-termed relations; functions of several variables and operations
We have, so far, considered exclusively TWO-TERMED (or BINARY) RELATIONS, that is, relations holding between two things. However, one also meets frequently with THREE-TERMED (or TERNARY) and, in general, MANY-TERMED RELATIONS within various sciences. In geometry, for instance, the relation of betweenness constitutes a typical example of a three-termed relation; it holds between three points of a line, and is expressed symbolically by the formula:
A/B/C
which is read:
the point B lies between the points A and C.
Arithmetic, too, supplies numerous examples of three-termed relations; it may suffice to mention the relation between three numbers x, y and z, consisting in the fact that the first number is the sum of the other two:
x = y + z,
as well as similar relations, such as are expressed by the following formulas:
x = y − z,
x = y · z,
x = y : z.
As an example of a four-termed relation let us point to the relation holding between four points A, B, C and D if, and only if, the distance of the first two equals the distance of the last two, in other words, if the segments AB and CD are congruent. Another example is the relation holding between the numbers x, y, z and t whenever they form a proportion:
x : y = z : t.
Of particular importance among the totality of many-termed relations are the many-termed functional relations, which correspond to the two-termed functional relations. For reasons of simplicity we shall restrict ourselves to a discussion of three-termed relations of this type. R is called a THREE-TERMED FUNCTIONAL RELATION if, to any two things y and z, there corresponds at most one thing x having this relation to y and z. This uniquely determined thing, provided it exists at all, we denote either by the symbol:
R(y, z)
or else by the symbol:
y R z
(which now assumes a different meaning from what it had in the theory of two-termed relations). Thus, for the purpose of expressing that x stands to y and z in the functional relation R, we have two formulas at our disposal:
x = R(y, z) and x = y R z.
Corresponding to this twofold symbolism we have a twofold mode of expression. When using the notation:
x = R(y, z),
the relation R is called a FUNCTION. In order to differentiate between two-termed and three-termed functional relations, we speak, in the first case, of FUNCTIONS OF ONE VARIABLE or of FUNCTIONS WITH ONE ARGUMENT, and, in the second, of FUNCTIONS OF TWO VARIABLES or of FUNCTIONS WITH TWO ARGUMENTS. Similarly, four-termed functional relations are called FUNCTIONS OF THREE VARIABLES or FUNCTIONS WITH THREE ARGUMENTS, and so on. In designating functions with any number of arguments it is customary to employ the variables “f”, “g”, …; the formula:
x = f(y, z)
is read:
x is that value of the function f which is correlated with the
argument values y and z.
When the symbolism:
x = y R z
is employed, the relation R is usually referred to as an OPERATION or, more specifically, a BINARY OPERATION, and the above formula is read as follows:
x is the result of the operation R carried out on y and z;
in place of the letter “R” we tend to use, in this case, other letters, especially the letter “O”. The four fundamental arithmetical operations of addition, subtraction, multiplication and division may serve as examples, and also such logical operations as addition and multiplication of classes or relations (see Sections 25 and 28). The content of the two concepts of a function of two variables and of a binary operation is evidently exactly the same. It should, perhaps, be noted that functions of one variable are sometimes also called operations, and, in particular, UNARY OPERATIONS; in the calculus of classes, for instance, the forming of the complement of a class is usually thought of, not as a function, but as an operation.
Although the many-termed relations play an important part in various sciences, the general theory of these relations is yet in its initial stage; when speaking of a relation, or of the theory of relations, one usually has only two-termed relations in mind. A more detailed study has so far only been made of one particular category of three-termed relations, namely, a category of binary operations, as the prototype of which we may consider the ordinary arithmetical addition. These investigations are carried on within the framework of a special mathematical discipline known as the theory of groups. We shall get acquainted with certain concepts from the theory of groups—and thereby also with certain general properties of binary operations—in the second part of this book.
35. The importance of logic for other sciences
We have discussed the most important concepts of contemporary logic, and in doing so we have got acquainted with some laws (very few, by the way) concerning these concepts. It had not been our intention, however, to give a complete list of all logical concepts and laws of which one avails oneself within scientific arguments. This, incidentally, is not necessary, as far as the study and promotion of other sciences are concerned, even of mathematics which is especially closely related to logic. Logic is justly considered the basis of all other sciences, if only for the reason that in every argument we employ concepts taken from the field of logic and that every correct inference proceeds in accordance with the laws of that discipline. But this does not imply that a thorough knowledge of logic is a necessary condition for correct thinking; even professional mathematicians, who, in general, do not commit errors in their inferences, usually do not know logic to such an extent as to be conscious of all logical laws of which they make unconscious use. All the same, there can be no doubt that the knowledge of logic is of considerable practical importance for everyone who desires to think and infer correctly, since it enhances the innate and acquired faculties to this effect and, in particularly critical cases, prevents the committing of mistakes. As far as, in particular, the construction of mathematical theories is concerned, logic plays a part of far-reaching importance also from the theoretical point of view; this problem will be discussed in the next chapter.
Exercises
1. Give examples of relations from the fields of arithmetic, geometry, physics, and everyday life.
2. Consider the relation of being father, that is to say, the relation expressed by the sentential function:
x is father of y.
Do all human beings belong to the domain of this relation? And do they all belong to the counter-domain?
3. Consider the following seven relations among people, namely, of being father, mother, child, brother, sister, husband, wife. We denote these relations by the symbols “F”, “M”, “C”, “B”, “S”, “H”, “W”. By applying various operations defined in Section 28 to the relations, we obtain new relations for which we sometimes find simple names in ordinary language; “H/C”, for instance, as can be seen very easily, denotes the relation of being son-in-law. Find, if possible, simple names for the following relations:
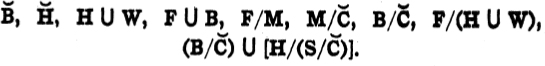
Express with the help of the symbols “F”, “M”, and so on, together with the symbols of the calculus of relations, the relations of being parent, sibling, grand-child, daughter-in-law and mother-in-law.
Explain the meanings of the following formulas, and determine which of them are true:
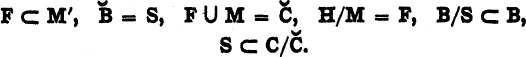
4. Consider the following two formulas of the calculus of relations:
![]() .
.
Show by means of an example that the first is not always satisfied, and try to prove that the second is satisfied by arbitrary relations R and S.
Hint: Consider what it means to say that the relation ![]() (that is, the converse of the relation R/S) or the relation
(that is, the converse of the relation R/S) or the relation ![]() holds between two things x and y.
holds between two things x and y.
5. Formulate in symbols the definitions of all terms of the calculus of relations that were discussed in Section 28.
Hint: The definition of the sum of two relations, for instance, has the following form:
[x (R ∪ S) y] ↔ [(x R y) ∨ (x S y)].
6. Which among the properties of relations discussed in Section 29 are possessed by the following relations:
(a) the relation of divisibility in the set of natural numbers;
(b) the relation of being relatively prime in the set of natural numbers (two natural numbers being called relatively prime if their greatest common divisor is 1);
(c) the relation of congruence in the set of polygons;
(d) the relation of being longer in the set of line segments;
(e) the relation of being perpendicular in the set of straight lines of a plane:
(f) the relation of intersecting in the set of geometric configurations;
(g) the relation of simultaneity in the class of physical events;
(h) the relation of temporally preceding in the class of physical events;
(i) the relation of being related in the class of human beings;
(k) the relation of fatherhood in the class of human beings?
7. Is it true that every relation is either reflexive or irreflexive (in the given class), and either symmetrical or asymmetrical? Give examples.
8. We shall call the relation R INTRANSITIVE IN THE CLASS K if, for any three elements x, y and z of K, the formulas:
x R y and y R z
imply the formula:
~(x R z).
Which of the relations listed in Exercises 3 and 6 are intransitive? Give other examples of intransitive relations. Is every relation either transitive or intransitive?
*9. Show how to make the transition from the expression:
the lines a and b are parallel
to the equivalent one:
the directions of the lines a and b are identical,
and how, in this connection, to define the expression “the direction of a line”.
Solve the same problem for the following two expressions:
the segments AB and CD are congruent
and
the lengths of the segments AB and CD are equal.
What logical law has to be applied here?
Hint: Compare the remarks in Section 30 concerning the concept of similarity.
10. Let us agree to call two signs, or two expressions consisting of several signs, EQUIFORM, if they do not differ as far as their shape is concerned, but merely possibly with respect to their position in space, that is, with respect to the place at which they are printed; otherwise let us call them NON-EQUIFORM. For instance, in the formula:
x = x,
the variables on the two sides of the equality sign are equiform whereas we have non-equiform variables in the formula:
x = y.
Of how many signs does the formula:
x + y = y + x
consist? Into how many groups can these signs be divided, such that two equiform signs belong to the same group and two non-equiform signs belong to different groups?
Which of the properties discussed in Section 29 belong to the relations of equiformity and non-equiformity?
*11. Explain, on the basis of the results of the preceding exercise, why it may be said of equiform signs that they are equal with respect to their FORM, or that they have the same form, and how the term “the form of the given sign” is to be defined (compare Exercise 9).
It is a very common usage to call equiform signs simply equal and even to treat them as if they were one and the same sign. It is, for instance, often said that in an expression like:
x + x
one and the same variable occurs on both sides of the symbol “+”. How should this be expressed with greater exactness?
*12. The inexact mode of speech which was pointed out in Exercise 11 has also been employed several times in this book (after all, we do not want to contend over deeply rooted usages). Show that inexactitudes of this kind occur on pp. 12 and 56, and explain how they could be avoided.
Another example of an inexact mode of speech of this kind is the following: when speaking of sentential functions with one free variable one means functions in which all free variables are equiform. How can the expression:
sentential functions with two free variables
be formulated more exactly?
13. Given a point in a plane, consider the set of all circles in that plane with the given point as their common center. Show that this set is ordered by the relation of being a part. Would this be true too, if the circles did not lie in the same plane, or if they were not concentric?
14. We consider a relation among words of the English language which will be called the relation of PRECEDING (IN LEXICOGRAPHICAL ORDER). We shall explain here the meaning of this term by means of examples. The word “and” precedes the word “can”, since the first begins with “a”, the second with “c”, and “a” has an earlier place in the English alphabet than “c”. The word “air” precedes the word “ale”, since they have the same first letter (or, rather, equiform first letters—cf. Exercise 10), while the second letter of the first word, that is “i”, has an earlier place in the English alphabet than the second letter of the second word, that is “l”. Analogously, “each” precedes “eat”, and “timber” precedes “time”. Finally, “war” precedes “warfare”, since the first three letters of these words are the same, while the first word has only these letters, and the second more than these; and analogously “mean” precedes “meander”.
Write the following words in a line so that, of any two words, the one on the left precedes the one on the right:
care, arm, salt, art, car, sale, trouble, army, ask.
Try to define the relation of preceding among words in a quite general way. Show that this relation establishes an order in the set of all English words. Point out some practical applications of this relation and explain why it is said to establish a lexicographical order.
15. Consider an arbitrary relation R and its negation R′. Show that the following statements of the theory of relations are true:
(a) if the relation R is reflexive in the class K, then the relation R′ is irreflexive in that class;
(b) if the relation R is symmetrical in the class K, then the relation R′ is also symmetrical in that class K;
*(c) if the relation R is asymmetrical in the class K, then the relation R′ is reflexive and connected in that class;
*(d) if the relation R is transitive and connected in the class K, then the relation R′ is transitive in that class.
Are the converses of these statements likewise true?
16. Show that, if the relation R has one of the properties discussed in Section 29, the converse relation ![]() possesses the same property.
possesses the same property.
*17. The properties of relations which were introduced in Section 29 can easily be expressed in terms of the calculus of relations, provided the class K to which they refer is the universal class. The formulas:
![]()
for instance, express that the relation R is transitive and connected, respectively. Explain why; recall the meaning of the symbol “D” of Section 28. Express similarly that the relation R is symmetrical, asymmetrical, or intransitive (cf. Exercise 8). What property of relations discussed in the present chapter is expressed by the formula:
![]()
18. Which of the relations expressed by the following formulas are functions:
(a) 2x + 3y = 12,
(b) x2 = y2,
(c) x + 2 > y − 3,
(e) x is mother of y,
(f) x is daughter of y ?
Which of the relations considered in Exercise 3 are functions?
19. Consider the function expressed by the formula:
x = y2 + 1.
What is the set of all argument values, and what is the set of all function values?
*20. Which of the functions in Exercise 18 are biunique? Give other examples of biunique functions.
*21. Consider the function expressed by the formula:
x = 3y + 1.
Show that this is a biunique function and that it maps the interval [0, 1] on the interval [1, 4] in a one-to-one manner (cf. Exercise 6 of Chapter IV). What conclusion may be drawn from this concerning the cardinal numbers of those intervals?
*22. Consider the function expressed by the formula:
x = 2y.
Using this function show, along the lines of the preceding exercise, that the set of all numbers and the set of all positive numbers are equinumerous.
*23. Show that the set of all natural numbers and the set of all odd numbers are equinumerous.
24. Give examples of many-termed relations from the fields of arithmetic and geometry.
25. Which of the three-termed relations expressed by the following formulas are functions:
(a) x + y + z = 0,
(b) x · y > 2z,
(d) x + 2 = y2 + z2 ?
26. Name a few laws of physics that state the existence of a functional relation between two, three and four quantities.
1 DE MORGAN and PEIRCE (cf. footnotes 6 on p. 52 and 2 on p. 14) were first to develop the theory of relations, especially that part of it known as the calculus of relations (cf. Section 28). Their work was systematically expanded and completed by the German logician E. SCHRÖDER (1841–1902). SCHRÖDER’S Algebra und Logik der Relative (Leipzig 1895), which appeared as the third volume of his comprehensive work Vorlesungen uber die Algebra der Logik, is still the only exhaustive account of the calculus of relations.
2 The first to call attention to the property of infinite classes discussed here was the German philosopher and mathematician B. BOLZANO (1781–1848) in his book Paradoxien des Unendlichen (Leipzig 1851, posthumously published); in this work we already find the first beginnings of the contemporary theory of sets. The above property was later employed by PEIRCE (cf. footnote 2 on p. 14) and others in order to formulate an exact definition of a finite and of an infinite class.