• IX •

METHODOLOGICAL CONSIDERATIONS ON THE CONSTRUCTED THEORY

55. Elimination of superfluous axioms in the original axiom system

The two preceding chapters were devoted to an outline of the foundations of an elementary mathematical theory which constitutes a fragment of arithmetic. In the present chapter we shall proceed to considerations of a methodological nature, concerning the system of axioms and primitive terms upon which that theory is based.

We shall begin with concrete examples illustrating the remarks of Section 39 concerning such problems as arbitrariness in the selection of axioms and primitive terms, the possible omission of superfluous axioms, and so on.

Let us start out with the question whether our system of Axioms 1–11—it will briefly be referred to as SYSTEM —possibly contains any superfluous axioms, that is, axioms which can be derived from the remaining axioms of the system. We shall see at once that it is easy to answer this question, and, moreover, affirmatively. In fact, we have:

Three of the axioms of System , namely, one of the Axioms 4 or 5, Axiom 6, and one of the Axioms 10 or 11, can be derived from the remaining axioms.

PROOF. We show first that

(I)      either of the Axioms 4 or 5 can be derived from the other
with the help of Axioms 1–3.

In fact, we observe that the proof of Theorem 3 was based exclusively—whether directly or indirectly—upon Axioms 1–3. If, on the other hand, we already have Theorem 3 at our disposal, we may derive Axiom 5 from Axiom 4 (or vice versa) by the following mode of inference:

If

x > y    and    y > z,

then, by Theorem 3,

y < x    and    z < y;

hence, by applying Axiom 4 (with “x” having been replaced by “z”, and “z” by “x”), we obtain:

z < x,

which, again by Theorem 3, implies:

x > z,

and this is the conclusion of Axiom 5.

Similarly it can be shown that:

(II)      either of the Axioms 10 or 11 can be derived from the
other with the help of Axioms 1–3.

Finally, we have:

(III)      Axiom 6 can be derived from Axioms 7–9.

*The proof of this latter assertion is not quite simple and resembles the second proof of Theorem 11. Two arbitrary numbers x and y are given; by a fourfold application of Axiom 9, four new numbers u, w, z, and v are introduced one by one, satisfying the following formulas:

From (1) we have, by the commutative law,

y = u + y;

combining this equation with (4) and arguing as in the case of the proof of Theorem 11, we obtain, by the associative law,

From (5) and (2) we obtain:

z = (x + w) + z,

and hence, again by the associative law,

z = x + (w + z)

which, in view of (3), yields:

We have thus shown that, for any two numbers x and y, there exists a number z for which (6) holds; and this is just the content of Axiom 6.

It might be added that the mode of inference sketched above applies, not only to addition, but—in accordance with the general remarks of Sections 37 and 38—also to any other operation; an operation O which is commutative, associative and right-invertible in a class K is also performable in that class, and the class K, therefore, forms an Abelian group with respect to the operation O (cf. Section 47).*

We have seen now that System contains at least three axioms which are superfluous and may therefore be omitted. Consequently, System may be replaced by the system consisting of the following eight axioms:

AXIOM 1⁽¹⁾.    For any numbers x and y we have:    x = y    or    x < y    or    x > y.

AXIOM 2⁽¹⁾.    If    x < y,    then    .

AXIOM 3⁽¹⁾.    If    x > y,    then    .

AXIOM 4⁽¹⁾.    If x < y    and    y < z,    then    x < z.

AXIOM 5⁽¹⁾.    x + y = y + x.

AXIOM 6⁽¹⁾.    x + (y + z) = (x + y) + z.

AXIOM 7⁽¹⁾.    For any numbers x and y there exists a number z such that    x = y + z.

AXIOM 8⁽¹⁾.    If    y < z,    then    x + y < x + z.

We shall refer to this axiom system as SYSTEM , and we now have the following result:

Systems and are equipollent.

In comparison with the original system, the new simplified axiom system has certain shortcomings, both from the esthetic and the didactical points of view. It is no longer symmetric with respect to the two primitive symbols “<” and “>”, certain properties of the relation < being accepted without proof, while quite analogous properties of the relation > have first to be demonstrated. Also, in the new system, Axiom 6 is missing which was of a very elementary and intuitively evident character, while its derivation from the axioms contained in System offers some difficulties.

56. Independence of the axioms of the simplified system

The question now arises whether there are any further superfluous axioms contained in System . It will turn out that this is not the case:

is a system of mutually independent axioms.

In order to establish the methodological statement just formulated, we employ the method of proof by interpretation, which has already been used in a particular case in Section 37.

We are to show that no axiom of System is derivable from the remaining axioms of this system. Let us consider, for example, Axiom 2⁽¹⁾. Suppose we replace the symbol “<” in the axioms of System throughout by “”, without altering the axioms in any other way. As a result of this transformation, no axiom, with the exception of Axiom 2⁽¹⁾, loses its validity; in fact, Axioms 3⁽¹⁾, 5⁽¹⁾, 6⁽¹⁾ and 7⁽¹⁾, since they do not contain the symbol “<”, are left unaltered, and Axioms 1⁽¹⁾, 4⁽¹⁾ and 8⁽¹⁾ go over into certain arithmetical theorems whose proofs on the basis of System or and the Definition 1 of the symbol “” (cf. Section 46) present no difficulties. It may, therefore, be asserted that the set N of all numbers, the relations and >, and the operation of addition form a model of the Axioms 1⁽¹⁾ and 3⁽¹⁾–8⁽¹⁾; the system of these seven axioms has thus found a new interpretation within arithmetic. On the other hand, it can be seen at once that the sentence resulting from Axiom 2⁽¹⁾ by the transformation is false, for its negation can easily be proved in arithmetic; the formula:

does not always exclude:

,

for there are numbers x and y simultaneously satisfying the two inequalities:

(this, of course, is the case if, and only if, x and y are equal). If, therefore, one believes in the consistency of arithmetic (cf. Section 41), one has to accept the fact that the sentence obtained from Axiom 2⁽¹⁾ is not a theorem of this discipline. And from this it follows that Axiom 2⁽¹⁾ is not derivable from the remaining axioms of System ; for otherwise this axiom could not fail to be valid in the case of any interpretation in which the other axioms hold (cf. analogous considerations in Section 37).

By using the same method of reasoning but by applying other, suitable interpretations, we can obtain the same result for any of the other axioms.

*In general, the method of proof by interpretation can be described as follows. It is a question of showing that some sentence A is not a consequence of a certain system of axioms or other statements of a given deductive theory. For this purpose, we consider an arbitrary deductive theory of which we assume that it is consistent (it may, in particular, be the same theory to which the statements of the system belong). We then try to find, within this theory, an interpretation of the system of such a kind that not the sentence A itself but its negation becomes a theorem (or possibly an axiom) of the theory . If we are successful in doing so, we may apply the law of deduction stated in Section 38. As we know, it follows from this law that, if the sentence A could be derived from the statements of the system , it would remain valid for any interpretation of this system. Consequently, the very fact of the existence of an interpretation of for which A is not valid is a proof that this sentence cannot be derived from the system . More strictly speaking, it is a proof of the conditional sentence:

if the theory is consistent, then the sentence A cannot be
derived from the statements of the system .

The reason why we must include the hypothesis that the theory is consistent is easily seen. For otherwise the theory could contain two contradictory sentences among its axioms and theorems, and we could not conclude that did not contain the sentence A (or rather the interpretation of A), from the mere fact that did contain the negation of A; thus our argument would no longer be valid.

In order to arrive, in the above way, at an exhaustive proof of the independence of a given axiom system, the method described has to be applied as many times as there are axioms in the system in question; each axiom in turn is taken as the sentence A, while consists of the remaining axioms of the system.*

57. Elimination of superfluous primitive terms and subsequent simplification of the axiom system; concept of an ordered Abelian group

We return once more to the axiom system . Since this system is independent, it does not permit of any further simplification by the omission of superfluous axioms. Nevertheless, a simplification can be achieved in a different way. For it turns out that the primitive terms of System are not mutually independent. In fact, either one of the two symbols “<” and “>” may be stricken from the list of primitive terms, and then it can be defined in terms of the other. This is easily seen from Theorem 3; on account of its form, this theorem may be considered as a definition of the symbol “>” by means of the symbol “<”, and if in this theorem we exchange the two sides of the equivalence, we may look upon it as a definition of the symbol “<” by means of the symbol “>”. (In either case it is desirable to have the phrase “We say that” precede the theorem; cf. Section 11.) From the didactical point of view, this reduction of the primitive terms might provoke certain objections; for the terms “<” and “>” are equally clear in their meaning and the relations denoted by them possess entirely analogous properties, so that it would appear slightly artificial to consider one of these terms immediately comprehensible while the other has first to be defined with the help of the first. But these objections carry little conviction.

If now, in disregard of any didactical considerations, we resolve to eliminate one of the symbols in question from the list of primitive terms, the task arises of giving our axiom system a form in which no defined terms occur in it. (This is a methodological postulate, by the way, which in practice is frequently disregarded; in geometry, especially, the axioms are usually formulated with the help of defined terms in order to enhance their simplicity and evidence). This task does not present any difficulties; we simply replace in the axiom system every formula of the type:

x > y

by the formula:

y < x

which, by Theorem 3, is equivalent to it. It is then easily seen that Axiom 1 may be replaced by the law of connexity, i.e. Theorem 4, since each follows from the other on the basis of general laws of logic (of sentential calculus, that is); Axiom 3 now becomes a simple substitution of Axiom 2, and may hence be omitted altogether. In this way we arrive at the system consisting of the following seven axioms:

AXIOM 1⁽²⁾.    If    ,    then    x < y    or    y < x.

AXIOM 2⁽²⁾.    If    x < y,    then    .

AXIOM 3⁽²⁾.    If    x < y    and    y < z,    then    x < z.

AXIOM 4⁽²⁾.    x + y = y + x.

AXIOM 5⁽²⁾.    x + (y + z) = (x + y) + z.

AXIOM 6⁽²⁾.    For any numbers x and y there exists a number z such that    x = y + z.

AXIOM 7⁽²⁾.    If    y < z,    then    x + y < x + z.

This axiom system, called SYSTEM , is thus equipollent to either of the two former Systems and . However, in saying this, we commit one inexactitude; for it is impossible to derive from the axioms of System those sentences of Systems or which contain the symbol “>”, unless System is enlarged by adding the definition of this symbol. We may, as we know, give this definition the following form:

DEFINITION 1⁽²⁾.    We say that    x > y    if, and only if,    y < x.

We also know that this last sentence can be proved on the basis of Systems or , if it is treated, not as a definition, but as an ordinary theorem (omitting, in this case, the initial phrase “We say that”). The fact of the equipollence of the three systems in questions can now be formulated as follows:

System together with Definition 1⁽²⁾ is equipollent to
each of the Systems and .

An equally cautious mode of formulation is indicated whenever two axiom systems are compared which, though equipollent, contain, at least partly, different primitive terms.

The axiom system is distinguished advantageously by the simplicity of its structure. The first three axioms concern the relation less than, and together they assert that the set N is ordered by this relation; the next three axioms are concerned with addition, and they assert that the set N is an Abelian group with respect to addition; the last axiom finally—the law of monotony—states a certain dependence between the relation less than and the operation of addition. A class K is said to be an ORDERED ABELIAN GROUP WITH RESPECT TO THE RELATION R AND THE OPERATION O if (i) the class K is ordered by the relation R, (ii) the class K is an Abelian group with respect to the operation O, and (iii) the operation O is monotonic in the class K with respect to the relation R. In accordance with this terminology we can say that the set of numbers is characterized by the axiom system as an ordered Abelian group with respect to the relation less than and the operation of addition.

The following facts concerning System can be established:

System is an independent axiom system, and moreover, all its primitive terms, namely “N”, “<” and “+”, are mutually independent.

We omit the proof of this statement. We remark only that, in order to establish the mutual independence of the primitive terms, one has again to apply the method of proof by interpretation, which in this case, however, assumes a more involved form; lack of space prevents us from going into the modifications of that method which would be required for this purpose.

58. Further simplification of the axiom system; possible transformations of the system of primitive terms

System can obviously be replaced by any system of sentences equipollent to it. We will here give a particularly simple example of such a system, which may be called SYSTEM , and which contains the same primitive terms as . It consists of only five sentences:

AXIOM 1⁽³⁾.    If    ,    then    x < y    or    y < x.

AXIOM 2⁽³⁾.    If    x < y,    then    .

AXIOM 3⁽³⁾.    x + (y + z) = (x + z) + y.

AXIOM 4⁽³⁾.    For any numbers x and y there exists a number z such that    x = y + z.

AXIOM 5⁽³⁾.    If    x + z < y + t,    then    x < y    or    z < t.

We shall show that

Systems and are equipollent.

PROOF. We observe, first of all, that all the axioms of System are either contained in System (thus, Axiom 2⁽³⁾ coincides with Axiom 2, and Axiom 4⁽³⁾ with Axiom 9), or else have been proved on its basis (Axioms 1⁽³⁾, 3⁽³⁾ and 5⁽³⁾ are coincident with Theorems 4, 9 and 14, respectively). But since the axiom systems and are equipollent, as we know from Section 57 (Definition 1⁽²⁾, after all, can always be added to System ), we may conclude that all the sentences of System can be proved on the basis of System . It remains to derive those sentences of System from the axioms of System which are absent in , that is Axioms 3⁽²⁾, 4⁽²⁾, 5⁽²⁾ and 7⁽²⁾. This task is not quite so simple.

*We begin with Axioms 4⁽²⁾ and 5⁽²⁾.

(I)      Axiom 4⁽²⁾ can be derived from the axioms of System .

For, given two numbers x and y, we can apply Axiom 4⁽³⁾ (with “x” put in place of “y”, and vice versa); there is, therefore, a number z such that

If now, in Axiom 3⁽³⁾, we replace “y” by “x”, we obtain:

In view of (1), “x + z” may here be replaced by “y” on both sides, and we arrive at Axiom 4⁽²⁾:

x + y = y + x

(II)      Axiom 5⁽²⁾ can be derived from the axioms of System .

In fact, by Axiom 3⁽³⁾ we have (if “y” is substituted for “z”, and conversely):

x + (z + y) = (x + y) + z;

on account of the commutative law, which has already been derived by (I), we may here replace “z + y” by “y + z”, and we obtain Axiom 5⁽²⁾:

x + (y + z) = (x + y) + z.

In order to facilitate the derivation of Axioms 3⁽²⁾ and 7⁽²⁾, we shall first show how some of the axioms and theorems stated in the preceding chapters may be proved on the basis of System .

(III)      Theorem 1 can be derived from the axioms of System .

We merely observe that the proof of Theorem 1 given in Section 44 is based exclusively upon Axiom 2, which in turn coincides with Axiom 2⁽³⁾ of System .

(IV)      Axiom 6 can be derived from the axioms of System .

In fact, we saw in Section 55 that Axiom 6 can be deduced from Axioms 7, 8 and 9. Axioms 7 and 8 are the same as Axioms 4⁽²⁾ and 5⁽²⁾, and can therefore, by (I) and (II), be derived from the axioms of System . Axiom 9, on the other hand, occurs as Axiom 4⁽³⁾ in System . Hence, Axiom 6 is a consequence of the axioms of .

(V)      Theorem 11 can be derived from the axioms of System .

In the second proof of Theorem 11, as given in Section 49, only Axioms 7, 8 and 9 were used. Theorem 11 is therefore derivable from the axioms of System for the same reason as Axiom 6; see (IV).

(VI)      Theorem 12 can be derived from the axioms of System .

For, suppose the hypothesis of Theorem 12 holds:

x + y < x + z;

we apply Axiom 5⁽³⁾, having replaced “z”, “y” and “t” by “y”, “x” and “z”, respectively. It follows that one of the formulas:

x < x    or    y < z

must hold; the first possibility has to be rejected because it contradicts Theorem 1 which has already been shown to be derivable from System ,—cf. (III). Hence the conclusion of Theorem 12 must hold:

y < z.

(VII)      Axiom 3⁽²⁾ can be derived from the axioms of System .

Let us assume the hypothesis of Axiom 3⁽²⁾, that is, the formulas:

and

If now we had:

y + x = y + z,

it would follow by Theorem 11, which has already been derived by (V), that

x = z.

Thus in (1) “x” might be replaced by “z”, which would lead to:

z < y.

This inequality would contradict (2) by virtue of Axiom 2⁽³⁾ and must therefore be rejected. We thus have:

Since, by Axiom 6, y + x and y + z are numbers, we may, by Axiom 1⁽³⁾, infer from (3) that one of these two cases must hold:

Considering the second of the formulas (4), we may replace in it “y + x” by “x + y” by virtue of Axiom 4⁽²⁾ which has already been derived; we thus arrive at:

y + z < x + y.

To this formula we apply Axiom 5⁽³⁾, where we replace “x” and “t” by “y”, and “y” by “x”. We arrive in this way at the following consequence:

y < x    or    z < y.

But this has to be rejected, since, on account of Axiom 2⁽³⁾, it contradicts (1) and (2) which constitute the hypothesis of Axiom 3⁽²⁾. We therefore return to the first of the formulas (4) and apply Theorem 12 derived above by (VI), with “x” replaced by “y”, and conversely; we obtain thus:

x < z,

and this is the conclusion of Axiom 3⁽²⁾.

(VIII)      Axiom 7⁽²⁾ can be derived from the axioms of System .

The procedure is here similar to the one just applied, but much simpler. We assume the hypothesis of Axiom 7⁽²⁾:

If now we had:

x + y = x + z,

it would follow by Theorem 11 that

y = z;

in (1) we might therefore replace “y” by “z” and arrive at a contradiction to Theorem 1, derived above by (III). Hence we must have:

x + y ≠ x + z,

from which, by Axiom 1⁽³⁾, it follows that

In view of Theorem 12, the second of these inequalities leads to:

z < y,

but this contradicts our hypothesis (1) by virtue of Axiom 2⁽³⁾. Consequently we have to accept the first of the inequalities (2):

x + y < x + z,

and this is the conclusion of Axiom 7⁽²⁾.*

We have seen in this manner that all sentences of System are consequences of System , and conversely; the two axiom systems and are thus really established as equipollent.

System , no doubt, is simpler than System , and hence still simpler than Systems or . Particularly interesting is a comparison between Systems and ; as a result of the successive reductions that have been carried out, the original number of axioms has been diminished by more than one half. On the other hand, it should be noted that some of the sentences of System (namely, Axioms 3⁽³⁾ and 5⁽³⁾) are less natural and simple than the axioms of the other systems, and also that the proofs of some, even very elementary, theorems are here comparatively more difficult and involved than on the basis of those other systems.

Just like a system of axioms, a system of primitive terms may be replaced by any equipollent system. This applies, in particular, to the system of the three terms “N”, “<” and “+” which occur as the only primitive terms in the axioms last considered. If, for instance, in this system we replace the symbol “<” by “”, we obtain an equipollent system; for the second of these symbols was defined in terms of the first, and Theorem 8 tells us how the first may be defined by means of the second. But such a transformation of the system of primitive terms would be in no way advantageous; in particular, it would contribute nothing to a simplification of the axioms, and to the reader, who is possibly more familiar with the symbol “<” than with the symbol “”, it might even appear rather artificial. Another equipollent system can be obtained by replacing in the original system the symbol “+” by “−”; but, again, this transformation would not be at all expedient. In conclusion we should note that other systems of primitive terms are known which are equipollent to the system in question and consist of but two terms.

59. Problem of the consistency of the constructed theory

We shall now briefly touch on some other methodological problems concerning the fragment of arithmetic considered above; these are the problems of consistency and of completeness (cf. Section 41). Since it is quite irrelevant whether we refer our remarks to one or another of several equipollent axiom systems, we shall now always speak of System .

If we believe in the consistency of the whole of arithmetic (and this assumption has been made previously and will be made again in our further considerations), then we must all the more accept the fact that

The mathematical theory based on System is consistent.

But while the attempts to give a strict proof of the consistency of the whole of arithmetic have met with essential difficulties (cf. Section 41), a proof of this kind for System is not only possible but even comparatively simple. One reason for this is the fact that the variety of theorems which can be derived from the axiom system is very small indeed; it is, for instance, not possible to give, on its basis, an answer to the very elementary question as to whether any numbers exist at all. This circumstance facilitates considerably the proof of the fact that the part of arithmetic considered does not contain a single pair of contradictory theorems. With the means here at our disposal, however, it would be a hopeless undertaking to sketch the proof of the consistency or even to try to acquaint the reader with its fundamental idea; this would require a much deeper knowledge of logic, and an essential preliminary task would be the reconstruction of the part of arithmetic in question as a formalized deductive theory (cf. Section 40). It may be added that, if System is enriched by a single sentence to the effect that at least two distinct numbers exist, then the attempt to prove the consistency of the axiom system thus extended will meet with difficulties of the same degree as are encountered in the case of the entire system of arithmetic.

60. Problem of the completeness of the constructed theory

In comparison with the question of the consistency, that of the completeness of System can be dealt with much more readily.

There are numerous problems, formulated exclusively in logical terms and in primitive terms of System , that do not in any way admit of a decision on the basis of this system. One such problem has already been mentioned in the preceding section. Another example is given by the sentence stating that to any number x, there exists a number y such that

x = y + y.

On the basis of the axioms of System alone, it is impossible either to prove or to disprove this sentence. That this is so can be seen from the following consideration. By the symbol “N” we have denoted the set of all real numbers; that is to say, the set N comprehends the integers as well as the fractions, the rational numbers as well as the irrational ones. But it can be seen at once that none of the axioms and, hence, none of theorems following from them would lose their validity if by the symbol “N” we were to denote either the set of all integers (the positive and negative ones including the number 0), or the set of all rational numbers; that is to say, all these statements would remain valid if the word “number” meant either “integer” or “rational number”. In the first case, the sentence mentioned above, which states that for any given number there is another number half as large, would be false; in the second case it would be true. If, therefore, we succeeded in proving this sentence on the basis of System , we would arrive at a contradiction within the arithmetic of integers; if, on the other hand, we were able to disprove it, we would find ourselves involved in a contradiction within the arithmetic of rational numbers.

The argument sketched just now falls under the category of proofs by interpretation (cf. Sections 37 and 56); in order to make this clear let us reformulate the argument slightly. Let “I” denote the set of all integers, and “R” the set of all rational numbers. We shall now give two interpretations of System within arithmetic. The symbols “<”, “>” and “+” remain unchanged in both interpretations, while the symbol “N” which occurs explicitly or implictly in each of the axioms is to be replaced by “I” in the first and by “R” in the second interpretation. (We disregard here the remarks made in Section 43 concerning the possible elimination of the symbol “N”, since this would slightly complicate our reasoning.) All axioms of System retain their validity in both interpretations; the sentence:

for every number x there exists a number y such that
x = y + y,

however, is fulfilled only in the case of the second interpretation, while in the case of the first interpretation its negation holds:

not for every number x is there a number y such that
x = y + y.

On the assumption of the consistency of arithmetic we conclude from the first interpretation that the sentence in question cannot be proved on the basis of System , and from the second interpretation we conclude that it also cannot be disproved.

We have thus shown that there exist two contradictory sentences, formulated exclusively in logical terms and in primitive terms of the mathematical theory which we have been considering, with the property that neither of them can be derived from the axioms of that theory. Consequently we have:

The mathematical theory based on System is incomplete.

Exercises

1.  Let us agree that the formula:

means the same as:

x + 1 < y.

Now replace, in the axioms of System of Section 57, the symbol “<” throughout by “”, and determine which of the axioms retain their validity and which do not, and hence infer that Axiom 1⁽²⁾ cannot be derived from the remaining axioms. What is the name of the method of inference here applied?

2.  Following the lines of the independence proof sketched in Section 56 for Axiom 2⁽¹⁾, show that Axiom 2⁽²⁾ cannot be derived from the remaining axioms of System .

3.  Let the symbol “” designate the set consisting of the three numbers 0, 1 and 2. Among the elements of this set we define a relation , stipulating that it should hold only in these three cases:

Further, we define the operation on the elements of the set by the following formulas:

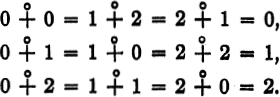
Now replace, in the axioms of System , the primitive terms of that system by “”, “” and “” respectively (and the word “number” by the expression “one of the three numbers 0, 1 and 2”); show, by doing so, that Axiom 3⁽²⁾ cannot be derived from the remaining axioms.

4.  In order to show by means of a proof by interpretation that Axiom 4⁽²⁾ is not derivable from the remaining axioms of System , it is sufficient to replace the symbol of addition in all axioms by the symbol of a certain one among the four operations mentioned in Exercise 3 of Chapter VIII. Which is the operation that has to be used?

5. Consider the operation ⊕ satisfying the following formula:

x ⊕ y = 2 · (x + y).

Show, with the help of this operation, that Axiom 5⁽²⁾ cannot be deduced from the other axioms of System .

6.  Construct a set of numbers of such a kind that, together with the relation < and the operation +, it fails to satisfy Axiom 6⁽²⁾ but forms a model of the remaining axioms of System . What conclusion may, therefore, be drawn with respect to the possibility of deriving Axiom 6⁽²⁾?

7.  In order to show that Axiom 7⁽²⁾ is not a consequence of the other axioms of System , one can proceed by replacing in all axioms two of the primitive terms of the system by corresponding symbols introduced in Exercise 3, leaving the third primitive term unchanged. Determine which term should be left unchanged.

8.  The results obtained in Exercises 1–7 go to show that none of the axioms of System can be derived from the remaining axioms of that system. Carry out analogous independence proofs for the axiom systems of Section 55 and of Section 58 (using, in part, the interpretations applied in the preceding exercises).

9.  Show, on the basis of the axiom system , that any set of numbers which is an Abelian group with respect to the operation of addition is at the same time an ordered Abelian group with respect to the relation less than and the operation of addition. Give examples of sets of numbers of this kind.

10.  In Exercise 5 of Chapter VIII several sets of numbers were given which form Abelian groups with respect to multiplication. Which of these sets are ordered Abelian groups with respect to the relation less than and the operation of multiplication, and which are not?

11.  Use the result obtained in Exercise 10 for a new proof of the independence of Axiom 7⁽²⁾ from the remaining axioms of System (cf. Exercise 7).

*12.  On the basis of the axiom system prove the following theorem:

if there are at least two different numbers, then there is, for
any number x, a number y such that    x < y.

As a generalization of this result, prove the following general group-theoretical theorem:

if the class K is an ordered Abelian group with respect to the relation R and the operation O, and if K has at least two elements, then, for any element x of K, there exists an element y of K such that x R y.

Show with the help of this theorem that no class which is an ordered Abelian group can consist of exactly two, or three, and so on, elements. Can it consist of just one element? (Cf. Exercise 8 of Chapter VIII.)

*13.  Show that the system of Axioms 1⁽²⁾–3⁽²⁾ (of Section 57) is equipollent to the system consisting of Axiom 1⁽¹⁾ and the following sentence:

if    x < y,    y < z,    z < t,    t < u    and    u < v,    then    .

As a generalization of this result establish the following general law of the theory of relations:

for the class K to be ordered by the relation R it is necessary and sufficient that R is connected in K and that it satisfies the following condition:

if x, y, z, t, u and v are any elements of K, and if    x R y,    y R z,    z R t,    t R u    and    u R v,    then it is not the case that    v R x.

*14.  Using the considerations of Sections 48, 55 and 58, show that the following three systems of sentences are equipollent:

        (a) the system of Axioms 6–9 of Section 47;

        (b) the system of Axioms 4⁽²⁾–6⁽²⁾ of Section 57;

        (c) the system of Axioms 3⁽³⁾ and 4⁽³⁾ of Section 58.

Generalizing this result, formulate new definitions of the expression:

the class K is an Abelian group with respect to the operation O,

that are equivalent to, but simpler than, the definition given in Section 47.

*15.  Consider the system consisting of the following five axioms:

AXIOM 1⁽⁴⁾.    If    ,    then    x < y    or    y < x.

AXIOM 2⁽⁴⁾.    If    x < y,    y < z,    z < t,    t < u    and    u < v,    then    .

AXIOM 3⁽⁴⁾.    x + (y + z) = (x + z) + y.

AXIOM 4⁽⁴⁾.    For any numbers x and y there exists a number z such that    x = y + z.

AXIOM 5⁽⁴⁾.    If    y < z,    then    x + y < x + z.

Using the results of Exercises 13 and 14, show that System is equipollent to each of the Systems and .

16.  In Section 58 it was asserted that the system of the three primitive terms “N”, “<” and “+” is equipollent to the system of the terms “N”, “” and “+”; to this assertion it should really have been added that these systems are equipollent with respect to a certain system of sentences, for instance, with respect to System of Section 58 and Definition 1 of Section 46. Consider why such an addition is indispensable. In general, why is it necessary always to refer to a particular system of sentences when intending to establish the equipollence of two systems of terms (in the sense of Section 39)?

*17.  Consider the system consisting of the following seven sentences:

AXIOM 1⁽⁵⁾.    For any numbers x and y we have:        or    .

AXIOM 2⁽⁵⁾.    If        and    ,    then    x = y.

AXIOM 3⁽⁵⁾.    If        and    ,    then    .

AXIOM 4⁽⁵⁾.    x + y = y + x.

AXIOM 5⁽⁵⁾.    x + (y + z) = (x + y) + z.

AXIOM 6⁽⁵⁾.    For any numbers x and y there exists a number z such that    x = y + z.

AXIOM 7⁽⁵⁾.    If    ,    then    .

Show that the axiom systems (of Section 57) and become equipollent systems of sentences, if Definition 1 of Section 46 is added to the first, and Theorem 8 of Section 46 to the second, considering the latter theorem as a definition of the symbol “<”. Why may we not simply say that Systems and are equipollent?

18.  Following the line of argument taken in Section 60, show that, on the basis of System , the following sentence can be neither proved nor disproved:

if    x < z,    then there exists a number y for which    x < y    and    y < z.

*19.  Show that, on the basis of System , the following sentence can be neither proved nor disproved:

for any number x there exists a number y such that    x < y.

*20.  In the present chapter we have used the method of proof by interpretation in order to establish the independence or incompleteness of an axiom system. The same method is also employed in investigations concerning its consistency. In fact we have the following methodological law at our disposal which represents a consequence of the law of deduction:

If the deductive theory has an interpretation in the deductive theory and the theory is consistent, then the theory is also consistent.

Show that this statement is correct. In Section 38 some remarks have been made concerning possible interpretations of arithmetic and geometry; applying the law just given, deduce from these remarks consequences concerning the consistency of arithmetic and geometry and its connection with the consistency of logic.