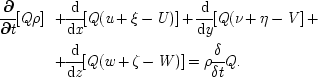Introduction
Philosophers distinguish phenomenological from theoretical laws. Phenomenological laws are about appearances; theoretical ones are about the reality behind the appearances. The distinction is rooted in epistemology. Phenomenological laws are about things which we can at least in principle observe directly, whereas theoretical laws can be known only by indirect inference. Normally for philosophers 'phenomenological' and 'theoretical' mark the distinction between the observable and the unobservable.
Physicists also use the terms 'theoretical' and 'phenomenological'. But their usage makes a different distinction. Physicists contrast 'phenomenological' with 'fundamental'. For example, Pergamon Press's
Encyclopaedic Dictionary of Physics says, 'A phenomenological theory relates observed phenomena by postulating certain equations but does not enquire too deeply into their fundamental significance.'
1
The dictionary mentions observed phenomena. But do not be misled. These phenomenological equations are not about direct observables that contrast with the theoretical entities of the philosopher. For look where this definition occurs—under the heading 'Superconductivity and superfluidity, phenomenological theories of'. Or notice the theoretical entities and processes mentioned in the contents of a book like
Phenomenology of Particles at High Energies (proceedings of the 14th Scottish Universities Summer School in Physics): (1) Introduction to Hadronic Interactions at High Energies. (2) Topics in Particle Physics with Colliding Proton Beams. (3) Phenomenology of Inclusive Reactions. (4) Multihadron Production at High Energies: Phenomenology and Theory.
2
end p.1
Francis Everitt, a distinguished experimental physicist and biographer of James Clerk Maxwell, picks Airy's law of Faraday's magneto-optical effect as a characteristic phenomenological law.
3 In a paper with Ian Hacking, he reports, 'Faraday had no mathematical theory of the effect, but in 1846 George Biddell Airy (1801-92), the English Astronomer Royal, pointed out that it could be represented analytically in the wave theory of light by adding to the wave equations, which contain second derivatives of the displacement with respect to time, other
ad hoc terms, either first or third derivatives of the displacement.'
4 Everitt and Hacking contrast Airy's law with other levels of theoretical statement—'physical models based on mechanical hypotheses, . . . formal analysis within electromagnetic theory based on symmetry arguments', and finally, 'a physical explanation in terms of electron theory' given by Lorentz, which is 'essentially the theory we accept today'.
Everitt distinguishes Airy's phenomenological law from the later theoretical treatment of Lorentz, not because Lorentz employs the unobservable electron, but rather because the electron theory explains the magneto-optical effect and Airy's does not. Phenomenological laws describe what happens. They describe what happens in superfluids or meson-nucleon scattering as well as the more readily observed changes in Faraday's dense borosilicate glass, where magnetic fields rotate the plane of polarization of light. For the physicist, unlike the philosopher, the distinction between theoretical and phenomenological has nothing to do with what is observable and what is unobservable. Instead the terms separate laws which are fundamental and explanatory from those that merely describe.
The divide between theoretical and phenomenological commonly separates realists from anti-realists. I argue in these essays for a kind of anti-realism, and typically it is an anti-realism that accepts the phenomenological and rejects the theoretical. But it is not theory versus observation that I reject. Rather it is the theoretical as opposed to the phenomenological.
end p.2
In modern physics, and I think in other exact sciences as well, phenomenological laws are meant to describe, and they often succeed reasonably well. But fundamental equations are meant to explain, and paradoxically enough the cost of explanatory power is descriptive adequacy. Really powerful explanatory laws of the sort found in theoretical physics do not state the truth.
I begin from the assumption that we have an immense number of very highly confirmed phenomenological laws. Spectra-physics Incorporated continuously runs a quarter of a million dollars' worth of lasers to death to test their performance characteristics. Nothing could be better confirmation than that. But how do the fundamental laws of quantum mechanics, which are supposed to explain the detailed behaviour of lasers, get their confirmation? Only indirectly, by their ability to give true accounts of lasers, or of benzene rings, or of electron diffraction patterns. I will argue that the accounts they give are generally not true, patently not true by the same practical standards that admit an indefinite number of commonplace phenomenological laws. We have detailed expertise for testing the claim of physics about what happens in concrete situations. When we look to the real implications of our fundamental laws, they do not meet these ordinary standards. Realists are inclined to believe that if theoretical laws are false and inaccurate, then phenomenological laws are more so. I urge just the reverse. When it comes to the test, fundamental laws are far worse off than the phenomenological laws they are supposed to explain.
The essays collected in this volume may be grouped around three different but interrelated arguments for this paradoxical conclusion.
(1) |
The manifest explanatory power of fundamental laws does not argue for their truth.
|
(2) |
In fact the way they are used in explanation argues for their falsehood. We explain by ceteris paribus laws, by composition of causes, and by approximations that improve on what the fundamental laws dictate. In all of these cases the fundamental laws patently do not get the facts right.
|
(3) |
The appearance of truth comes from a bad model of
|
end p.3
|
explanation, a model that ties laws directly to reality. As an alternative to the conventional picture I propose a simulacrum account of explanation. The route from theory to reality is from theory to model, and then from model to phenomenological law. The phenomenological laws are indeed true of the objects in reality—or might be; but the fundamental laws are true only of objects in the model.
|
1. Against Inference to Best Explanation
I will argue that the falsehood of fundamental laws is a consequence of their great explanatory power. This is the exact opposite of what is assumed by a well-known and widely discussed argument form—inference to the best explanation. The basic idea of this argument is: if a hypothesis explains a sufficiently wide variety of phenomena well enough, we can infer that the hypothesis is true. Advocates of this argument form may disagree about what counts as well enough, or how much variety is necessary. But they all think that explanatory power, far from being at odds with truth, leads us to it. My first line of argument in these essays denies that explanation is a guide to truth.
Numerous traditional philosophical positions bar inferences to best explanations. Scepticism, idealism, and positivism are examples. But the most powerful argument I know is found in Pierre Duhem's
Aim and Structure of Physical Theory,
5 reformulated in a particularly pointed way by Bas van Fraassen in his recent book
The Scientific Image.
6 Van Fraassen asks, what has explanatory power to do with truth? He offers more a challenge than an argument: show exactly what about the explanatory relationship tends to guarantee that if
x explains
y and
y is true, then
x should be true as well. This challenge has an answer in the case of
causal explanation, but
only in the case of causal explanation. That is my thesis in 'When Explanation Leads to Inference'. Suppose we describe the concrete causal process by which a phenomenon is brought about. That kind of explanation
end p.4
succeeds only if the process described actually occurs. To the extent that we find the causal explanation acceptable, we must believe in the causes described.
For example, consider the radiometer, invented by William Crookes in 1853. It is a little windmill whose vanes, black on one side, white on the other, are enclosed in an evacuated glass bowl. When light falls on the radiometer, the vanes rotate. At first it was assumed that light pressure causes the vanes to go round. Soon it was realized that the pressure of light would not be nearly great enough. It was then agreed that the rotation is due to the action of the gas molecules left inside the evacuated bowl. Crookes had tried to produce a vacuum in his radiometer. Obviously if we accept the agreed explanation, we infer that Crookes's vacuum was imperfect; the explanation demands the presence of molecules in the jar.
There were two rival hypotheses about what the molecules did. Both ideas are still defended by different camps today. A first proposal was that the vanes are pushed around by pressure of the molecules bouncing more energetically from the black side than the white. But in 1879 James Clerk Maxwell, using the kinetic theory of gases, argued that the forces in the gas would be the same in all directions, and so could not push the vanes. Instead differential heating in the gas produces tangential stresses, which cause slippage of the gas over the surface. As the gas flows around the edge, it pulls the vanes with it. In his biography of Maxwell, Francis Everitt urges the superiority of Maxwell's account over the more widely accepted alternative.
7 His confidence in Maxwell's causal story is reflected in his ontological views. His opponents think the tangential stresses are negligible. But unlike them, Everitt believes that if he builds a radiometer big enough he will be able to measure the flow of gas around the edge of the vanes.
The molecules in Crookes's radiometer are invisible, and the tangential stresses are not the kinds of things one would have expected to see in the first place. Yet, like Everitt, I believe in both. I believe in them because I accept Maxwell's
end p.5
causal account of why the vanes move around. In producing this account, Maxwell deploys certain fundamental laws, such as Boltzmann's equation and the equation of continuity, which I do not believe in. But one can reject theoretical laws without rejecting theoretical entities. In the case of Maxwell's molecules and the tangential stresses in the radiometer, there is an answer to van Fraassen's question: we have a satisfactory causal account, and so we have good reason to believe in the entities, processes, and properties in question.
Causal reasoning provides good grounds for our beliefs in theoretical entities. Given our general knowledge about what kinds of conditions and happenings are possible in the circumstances, we reason backwards from the detailed structure of the effects to exactly what characteristics the causes must have in order to bring them about. I have sometimes summarized my view about explanation this way: no inference to best explanation; only inference to most likely cause. But that is right only if we are very careful about what makes a cause 'likely'. We must have reason to think that this cause, and no other, is the only practical possibility, and it should take a good deal of critical experience to convince us of this.
We make our best causal inferences in very special situations—situations where our general view of the world makes us insist that a known phenomenon has a cause; where the cause we cite is the kind of thing that could bring about the effect and there is an appropriate process connecting the cause and the effect; and where the likelihood of other causes is ruled out. This is why controlled experiments are so important in finding out about entities and processes which we cannot observe. Seldom outside of the controlled conditions of an experiment are we in a situation where a cause can legitimately be inferred.
Again the radiometer illustrates. Maxwell is at odds with the standard account. To resolve the debate, Maxwell's defender, Everitt, proposes not further theoretical analysis, but rather an experiment. He wants to build an enormous radiometer, where he can control the partial vacuum and its viscosity, vary the coefficient of friction on the vanes, vary their widths, take into account winds in the jar, and
end p.6
finally determine whether the tangential stresses are really the major cause of rotation.
The dispute about normal and tangential stresses highlights a nice point about observation. Philosophical debate has focused on entities. Instrumentalists, who want to believe only in what they can see, get trapped in footling debates: do we really 'see' through a microscope? An electron microscope? A phase-interference light microscope? Even with the naked eye, do we not in any case see only effects? But many of the things that are realities for physics are not things to be seen. They are non-visual features—the spin of the electron, the stress between the gas surface, the rigidity of the rod. Observation—seeing with the naked eye—is not the test of existence here. Experiment is. Experiments are made to isolate true causes and to eliminate false starts. That is what is right about Mill's 'methods'.
Where can such an idea make a difference? I think these are just the kinds of considerations that need to be brought to current philosophical debates about quantum electrodynamics. Nobody denies the enormous organizing and predictive power of this theory, especially since the development in the last few years of gauge field theories, which unify weak and electromagnetic phenomena. Many think that quantum electrodynamics is the most impressive theory we have ever had in these respects. But as elementary particle physicist James Cushing remarks,
When one looks at the succession of blatantly
ad hoc moves made in QFT [quantum field theory] (negative-energy sea of electrons, discarding of infinite self energies and vacuum polarizations, local gauge invariance, forcing renormalization in gauge theories, spontaneous symmetry breaking, permanently confined quarks, color, just as examples) and of the picture which emerges of the 'vacuum' (aether?), as seething with particle-antiparticle pairs of every description and as responsible for breaking symmetries initially present, one can ask whether or not nature is
seriously supposed to be like that.
8 Does the success of quantum field theory argue for the existence of negative energy electrons, permanently confined quarks, and a vacuum 'seething with particle-antiparticle
end p.7
pairs of every description'? Debate among philosophers has tended to focus on the coherence of the theory, or on the true extent of is successes.
9 I think we should instead focus on the causal roles which the theory gives to these strange objects: exactly how are they supposed to bring about the effects which are attributed to them, and exactly how good is our evidence that they do so? The general success of the theory at producing accurate predictions, or at unifying what before had been disparate, is no help here. We can believe in the unexpected entities of quantum electrodynamics if we can give them concrete causal roles; and the rationality of that belief will depend on what experimental evidence supports the exact details of those causal claims.
Although I claim that a successful causal explanation gives good reason to believe in the theoretical entities and theoretical properties it postulates, I have repeatedly said that I do not believe in theoretical laws. But do not properties and laws go hand-in-hand? Bas van Fraassen asks: are not 'inferences to causes after all merely inferences to the truth of propositions describing general characteristics of . . . the things the propositions are about'?
10 The answer to van Fraassen's question is, undoubtedly, yes. But the propositions to which we commit ourselves when we accept a causal explanation are highly detailed causal principles and concrete phenomenological laws, specific to the situation at hand, not the abstract equations of a fundamental theory. Maxwell says that the vanes are dragged around by gas sliding over the edge. They are not pushed by light pressure or the normal force of the gas on the surface. The acceptability of his account depends on a host of general claims about what happens in radiometers.
Here is one phenomenological law—in this case a causal principle—which Maxwell uses:
[The] velocity (with which the gas slides over the surface) and the corresponding tangential stress are affected by inequalities of temperature
end p.8
at the surface of the solid, which give rise to a force tending to make the gas slide along the surface from colder to hotter places.
11 Here is another, this one critical to his argument that the vanes are not pushed by pressure normal to the surface:
When the flow of heat is steady, these forces (the total forces acting in all directions) are in equilibrium.
12 Maxwell's explanation of exactly how the motion in radiometers takes place will not be right unless these principles are true. But these are not fundamental laws. Maxwell sets his particular causal story into the framework of the developing kinetic theory of gases. It is useful to contrast the two specific laws quoted, about what happens in radiometers, with two fundamental equations from this basic theory which Maxwell uses. In his derivation, he employs both Boltzmann's equation
- (1)
-

and the general equation of continuity
- (2)
-
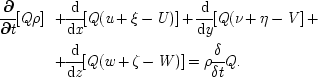
These are general, abstract equations; they are not about any particular happenings in any particular circumstances. The contrast is like that between moral principles, as Aristotle sees them in the
Nicomachean Ethics, Book II, Chapter 7, 'Among statements about conduct those which are general apply more widely, but those which are particular are more genuine.'
end p.9
Explanatory power is no guarantee of truth, unless van Fraassen's challenge can be met. I argue that, in the very special case of causal explanation, the challenge is met. In causal explanations truth is essential to explanatory success. But it is only the truth of low-level causal principles and concrete phenomenological laws. Is there no further account that secures the truth of abstract laws as well; no story of explanation that shows that abstract laws must be true if they are to explain? There are two models of theoretical explanation that could do so. I discuss them in Essay
6. Both have serious flaws. The other essays in this volume that argue against inference to the best explanation are 'When Explanation Leads to Inference', and 'The Reality of Causes in a World of Instrumental Laws'.
Since I make such heavy use of the notion of causal principles—a notion which empiricists will be wary of—one earlier paper is included. 'Causal Laws and Effective Strategies' argues that causal laws are quite as objective as the more Humean laws of association. One standard point of view maintains that causal laws are required to account for explanatory asymmetries. If only laws of association are admitted, the length of the shadow can as well explain the height of the flagpole as the reverse. In The Scientific Image van Fraassen argues persuasively that these asymmetries are not genuine. I think he is mistaken. But his case is powerful, and it might persuade us to give up certain explanatory strategies. But we will not so easily be persuaded to give up our strategies for action, which are essential to practical life. Perhaps there is no fact of the matter about what explains what. But there is no doubt that spraying swamps is an effective way to stop the spread of malaria, whereas burning the blankets of malarial patients is not. The essay on causation argues that laws of association are insufficient to account for the facts about effective strategies. Causal laws are required as well. Besides defending this central philosophical thesis the first essay re-introduces Simpson's paradox to the philosophical literature and it finds in Simpson's paradox the underlying source of a variety of different counterexamples that philosophers have proposed against probabilistic models of causation.
end p.10
give causal explanations of isolated events, I shall discuss here only explanations for kinds of events that recur in a regular way, events that can be described by phenomenological laws. I am thinking of the kinds of explanation that are offered in highly mathematical theories.
I said in the last section that there are two quite different kinds of things we do when we explain a phenomenon in physics. First, we describe its causes. Second, we fit the phenomenon into a theoretical frame. Ever since the earliest expositions of the covering-law model, it has been objected that its account of the first kind of explanation is inadequate. I have been strongly influenced by the criticism due to Michael Scriven
19 and Alan Donagan,
20 but many others make similar points as well. At present Wesley Salmon
21 is developing an alternative account of this kind of explanation, which focuses on singular causal processes and on causal interactions. Here I consider only the second kind of explanatory activity. How do we fit a phenomenon into a general theoretical framework?
Prima facie, the covering-law model seems ideally suited to answer: we fit a phenomenon into a theory by showing how various phenomenological laws which are true of it derive from the theory's basic laws and equations. This way of speaking already differentiates me from the covering-law theorist. I do not talk about explaining a feature of a phenomenon by deriving a description of that feature; but rather of treating a phenomenon by deriving a variety of phenomenological laws about it. But this is not the primary difference. The 'covering' of 'covering-law model' is a powerful metaphor. It teaches not only that phenomenological laws can be derived from fundamental laws, but also that the fundamental laws are laws that govern the phenomena. They are laws that cover the phenomena, perhaps under a more general or abstract description, perhaps in virtue of some
end p.16
hidden micro-structural features; but still the fundamental laws apply to the phenomena and describe how they occur.
I propose instead a 'simulacrum' account. That is not a word we use any more, but one of its dictionary definitions captures exactly what I mean. According to the second entry in the Oxford English Dictionary, a simulacrum is 'something having merely the form or appearance of a certain thing, without possessing its substance or proper qualities'. On the simulacrum account, to explain a phenomenon is to construct a model which fits the phenomenon into a theory. The fundamental laws of the theory are true of the objects in the model, and they are used to derive a specific account of how these objects behave. But the objects of the model have only 'the form or appearance of things' and, in a very strong sense, not their 'substance or proper qualities'.
The covering-law account supposes that there is, in principle, one 'right' explanation for each phenomenon. The simulacrum account denies this. The success of an explanatory model depends on how well the derived laws approximate the phenomenological laws and the specific causal principles which are true of the objects modelled. There are always more phenomenological laws to be had, and they can be approximated in better and in different ways. There is no single explanation which is the right one, even in the limit, or relative to the information at hand. Theoretical explanation is, by its very nature, redundant. This is one of the endemic features of explanation in physics which the deductive-nomological (D-N) account misses, albeit with the plea that this annoying feature will no longer be present when the end of physics is achieved.
'Fitting Facts to Equations' is full of examples of the kinds of models we use in explaining things in physics. I offer the simulacrum account in the next essay as an alternative which provides a better description of actual explanatory practice than do conventional covering-law accounts. It obviously serves my attack on fundamental laws. The 'simulacrum' aspect is intended seriously: generally the prepared and unprepared descriptions cannot be made to match. But only the prepared descriptions fall under the
end p.17
basic laws. The lesson for the truth of fundamental laws is clear: fundamental laws do not govern objects in reality; they govern only objects in models.
2. What Difference Does It Make?
Debate between realists and non-realists has been going on for a long time. Does the outcome have any practical consequence? I think it does. The last essay in this volume provides one example. I have argued that many abstract concepts in physics play merely an organizing role and do not seem to represent genuine properties. Unitarity has the earmarks of being just such a concept in quantum mechanics.
Unitarity is a property of operators. Those operators that are unitary represent motions that are indeterministic. Unitarity plays no causal role in the theory; nothing else about its use argues for interpreting it as a real property either. Yet there is a tendency to think of it not only as a mathematical characteristic of operators, but also as a genuine property of the situations represented by the operators. This, I claim, is the source of the notorious measurement problem in quantum mechanics. Unitarity marks no real property in quantum theory, and if we do not suppose that it must do so we have no interesting philosophical problem about measurement.
Essay
9 is concerned exclusively with the measurement problem, and not with the other conceptual difficulty in quantum mechanics that philosophers commonly discuss, the Einstein-Podolsky-Rosen paradox. These two problems tend to sit at opposite ends of a balance: philosophical treatments that offer hope for solving one usually fare badly with the other. This is certainly the case with the programme I propose. If it should work, it would at best eliminate the measurement problem, which I believe to be a pseudo-problem. But it would have nothing to say regarding the very perplexing facts about locality brought out by the EPR paradox.
end p.18
3. Conclusion
The picture of science that I present in these essays lacks the purity of positivism. It is a jumble of unobservable entities, causal processes, and phenomenological laws. But it shares one deep positivist conviction: there is no better reality besides the reality we have to hand. In the second sentence of this introduction I characterized the distinction between phenomenological and theoretical laws: phenomenological laws are about appearances; theoretical ones about the reality behind the appearances. That is the distinction I reject. Richard Feynmann talks about explaining in physics as fitting phenomena into 'the patterns of nature'. But where are the patterns? Things happen in nature. Often they happen in regular ways when the circumstances are similar; the same kinds of causal processes recur; there are analogies between what happens in some situations and what happens in others. As Duhem suggests, what happens may even be organized into natural kinds in a way that makes prediction easy for us (see the last section of 'When Explanation Leads to Inference'). But there is only what happens, and what we say about it. Nature tends to a wild profusion, which our thinking does not wholly confine.
The metaphysical picture that underlies these essays is an Aristotelian belief in the richness and variety of the concrete and particular. Things are made to look the same only when we fail to examine them too closely. Pierre Duhem distinguished two kinds of thinkers: the deep but narrow minds of the French, and the broad but shallow minds of the English. The French mind sees things in an elegant, unified way. It takes Newton's three laws of motion and turns them into the beautiful, abstract mathematics of Lagrangian mechanics. The English mind, says Duhem, is an exact contrast. It engineers bits of gears, and pulleys, and keeps the strings from tangling up. It holds a thousand different details all at once, without imposing much abstract order or organization. The difference between the realist and me is almost theological. The realist thinks that the creator of the universe worked like a French mathematician. But I think that God has the untidy mind of the English.
end p.19
Guide for the Reader
The last essay on quantum mechanics shows how anti-realism can be put to work. The first essay defends causes. The principal arguments for theoretical entities and against theoretical laws are in the middle essays. Although the essays argue in favour of theoretical entities and against theoretical laws, the main emphasis is on the latter theme. This book is a complement, I think, to the fine discussions of representation, experimentation, and creation of phenomena in Ian Hacking's
Representing and Intervening.
22 Hacking provides a wealth of examples which show how new entities are admitted to physics. Essay
6 here has some detailed examples and many equations that may not be of interest to the reader with pure philosophic concerns; but the general point of the examples can be gleaned by reading the introductory sections. Although Essay
9 is about quantum mechanics, it is not technical and readers without expert knowledge will be able to follow the argument.
end p.20