Understanding what motivates choices is at the root of understanding how consumers make them. Economists assume that consumers maximize utility. Utility is a measure of the satisfaction that the consumer enjoys from the consumption of goods and services (you can think of it as “happiness”). And while consumers seek as much utility as possible, they are constrained by a limited budget, which forces them to make choices within that constraint.
In this chapter, we first discuss what are known as utility functions, and then move to budget constraints. We then combine these to get a rule for how consumers maximize utility across all items that they choose to purchase.
CHAPTER OBJECTIVES
After completing this chapter, the student should be able to:
1. Distinguish between the total utility received from the consumption of a good and the marginal utility received from the consumption of the next unit of that good.
2. Explain the concept of diminishing marginal utility and how it predicts when a person will stop consuming units of a good.
3. Draw a budget constraint to show the limits of a person’s consumption possibilities.
4. Find the combination of two goods that maximizes a consumer’s utility given a budget constraint.
Some people receive utility from watching college football on an autumn Saturday; other people would rather use their Saturdays to go to the movies or read a book. Every consumer has different preferences for goods and services, so it is impossible to measure one person’s utility function against another person’s utility function. At first, this might imply that it is impossible to study consumer behavior because each consumer has unique preferences. However, to understand how consumers behave, we don’t need to know each person’s preferences; we simply need to assume that, given those preferences, each person seeks as much utility as possible. In other words, each consumer is a total utility maximizer.
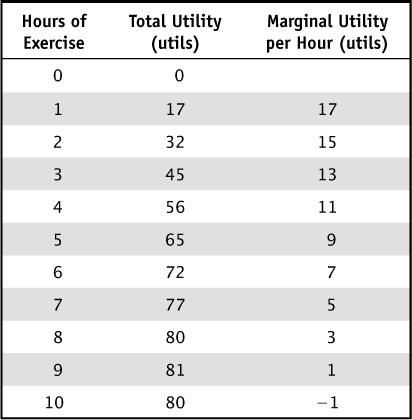
For example, suppose Lily enjoys exercising at her campus fitness center every week. In economics lingo, her utility is a function of how much weekly exercise she consumes. Economists use a fictional unit of measurement, the util, to measure how much total utility a person receives, and that total utility is represented by the second column in Table 2-1. The first two columns show the amount of total utility Lily gets from each unit of exercise. The third column in the table shows the marginal utility she enjoys with each additional hour of exercise. For example, when she exercises for one hour, she receives 17 utils, but when she exercises for two hours, she receives 32 utils. Therefore, the marginal utility of the second hour of exercise is 15 additional, or marginal, utils.
TABLE 2-1 Lily’s Utility per Hour of Exercise
Figure 2-1 shows a graph of Lily’s total utility function, with utils on the vertical axis. We can see that Lily’s total utility rises with more exercise, but peaks at nine hours of exercise and then begins to fall with the tenth hour. Why? Because it turns out that consuming more and more of something doesn’t always make you happier and happier.
FIGURE 2-1 • Lily’s Total Utility
When you’re very thirsty, the first glass of water is incredible! The second glass is also pretty thirst-quenching, but the fourteenth glass of water might actually be enough to make you sick. In other words, the first glass provides a lot of marginal utility, the second provides a little less, and the fourteenth provides much less (so much less that drinking it makes you worse off). This illustrates a nearly universal truth that economists recognize as the principle of diminishing marginal utility: marginal utility declines as more units of a good are consumed.
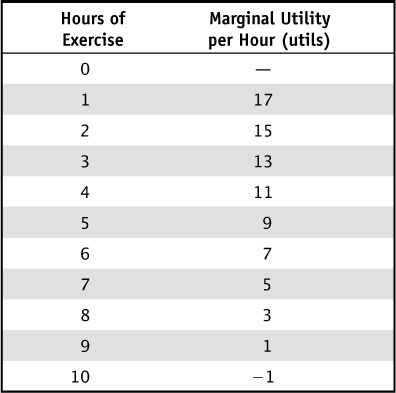
We can see this both in Table 2-2 and in Figure 2-2, both of which show Lily’s marginal utility. Each additional hour of exercise adds fewer utils to Lily’s total utility than the hours that came before. In fact, at the tenth hour, she is actually losing utility, and we see this as marginal utility that dips below zero. Once the marginal utility becomes negative, you are actually making yourself worse off if you increase your consumption. To maximize her total utility, it is clear that Lily should continue to exercise until the ninth hour and should never consume the tenth hour. This is important because it tells us that, even when we don’t have to pay to consume each unit, we will eventually stop consuming.
FIGURE 2-2 • Lily’s Marginal Utility
TABLE 2-2 Lily’s Marginal Utility per Hour of Exercise
When people first learn about marginal utility, a common mistake that they make is to assume that once marginal utility begins to diminish, a consumer should stop consuming units of that good. It is important to understand that marginal utility is the additional total utility received from the next unit of a good. If total utility will increase with the next unit of a good, the consumer is wise to consume that unit. So while marginal utility may be diminishing, so long as it is greater than zero, the next unit consumed will still increase the consumer’s total utility.
We have seen that the principle of diminishing marginal utility predicts that a consumer will stop his consumption before the marginal utility becomes negative, even if a good is free. Most of the time, however, consumers must pay a monetary price to consume goods and services, and they must be mindful of how much money they have to spend on those items. We now introduce the concept of a budget constraint for a consumer. In the real world, there are many different goods at many different prices that we must choose among. To keep it simple, though, we will start with a consumer who chooses between only two items.
Suppose that our college student, Lily, had to pay $10 for each visit to the fitness center, that she also consumed meals at the campus center at $5 each, and that she had a weekly income of $50 to divide between these two things. Assuming that Lily cannot spend more than her income (she cannot borrow), we can create an equation for her budget constraint:
Income ≥ spending on exercise + spending on meals
Her spending on exercise is simply the price of each visit ($10) multiplied by the number of times she goes to the fitness center (E). Likewise, her spending on meals is the price of each meal ($5) multiplied by how many meals (M) she buys. And recalling that she only has $50 of income, we can rewrite her budget constraint equation as:
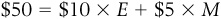
Still Struggling
Why did we switch from a “≥” sign to an “=” sign? Recall that Lily’s objective is to maximize her utility. Since we have only two goods, it doesn’t make sense for her not to spend all of her money (we assume that she cannot save, and that she doesn’t get utility from money itself, but only from the goods that money buys). Therefore, if we assume that Lily is rational, she will always spend all of her money.
Table 2-3 shows six possible consumption bundles (labeled points A through F) for these two goods that would use exactly her income. Figure 2-3 shows these consumption possibilities in a graph in which the budget constraint is shown as a downward-sloping line that separates the bundles that are affordable from those that are unaffordable. Combinations that lie below the budget line, like point X, use less than $50 of her income. Assuming that Lily would be happier spending more of her income on these two goods, a point like X would not maximize her utility. Combinations that lie beyond the budget line, like point Z, would probably make Lily happier, but would require more than $50 to purchase.
TABLE 2-3 Lily’s Consumption Bundles for Meals and Exercise
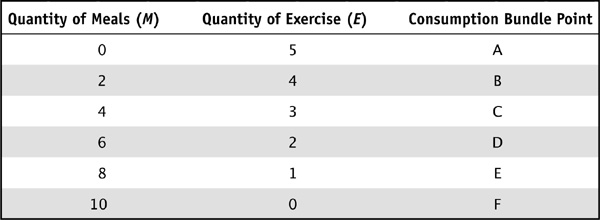
FIGURE 2-3 • Consumption Possibilities
If Lily knows her budget constraint, which consumption bundle should she choose so that she achieves the maximum amount of utility that is possible within that constraint? To answer that, we need a little more information.
Table 2-4 shows how much utility Lily receives from the consumption of several different combinations of meals and exercise and what each of these would cost.
TABLE 2-4 Lily’s Utility and Cost
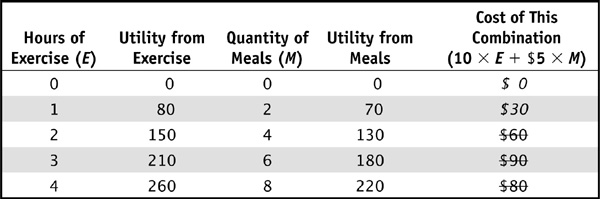
Note that some of these combinations (the ones that are crossed out) are unaffordable and therefore unattainable, so we shouldn’t even consider them as options. Some combinations (the ones that are in italics) aren’t spending all of her money, so we shouldn’t consider those either. Instead, we need to focus only on the combinations that lie on the budget line. For example, suppose Lily chooses point B, where 
, 
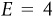, and she enjoys 330 utils. If she can reshuffle her consumption along the budget line and increase her utility, then she should do so. As we can see in Table 2-5, maximum utility of 390 utils is received when she buys four meals and exercises for three hours.
TABLE 2-5 Lily’s Maximum Utility
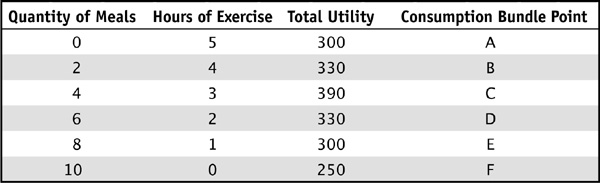
Another way to think about Lily’s problem is to think about her spending decision incrementally. We can ask the question: if Lily has $1 to spend, how should she best spend that dollar? She should probably spend it on the item that will increase her utility by the most utils. If she goes through life spending her next $1 on the thing that gives her the highest marginal utility for that dollar, she is bound to maximize her utility! We modify Table 2-4 to create marginal utility per dollar spent. Before we do that, let’s introduce a very minor bit of math: marginal utility per dollar.
Marginal utility (MU) for some good X is defined as the change in total utility (ΔTU) divided by the change in the units of X consumed (ΔX). Mathematically, this creates the ratio
So, for example, when Lily goes from two meals to four meals, her total utility increases from 330 to 390:
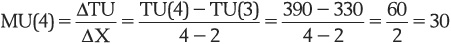
and to get MU per dollar for that fourth meal (m), we just divide this by the price:
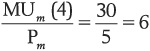
This tells us that each dollar that Lily spends on the fourth meal gives her 6 additional utils. When we fill out the rest of the table in a similar fashion, we get Table 2-6.
TABLE 2-6 Lily’s Marginal Utility per Dollar
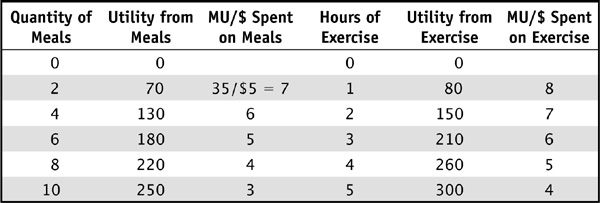
We already know from trial and error that Lily maximizes her utility by consuming 4 meals and 3 hours of exercise. Going through the process of trial and error would be tedious, but luckily we can see in this table that this bundle has an interesting outcome: the marginal utility per dollar is equal for both goods. This condition is often described as the utility maximization rule. The consumer should spend all of her income on two goods, X and Y, such that:
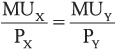
As long as one good provides more utility per dollar than another, the consumer will buy more of the first good; as more of the first product is bought, its marginal utility diminishes until the amount of utility per dollar just equals that of the other product.
Why is this a utility maximization rule? It makes sense on two levels. Mathematically, this turns out to be the combination that makes total utility the highest possible. Note from Tables 2-5 and 2-6 that any combination for which the utility maximization rule doesn’t hold results in a lower level of utility.
Second, on an intuitive level, it makes sense that you spend your money in such a way that you are getting the same “bang for the buck” for everything you buy. If you are consuming at a point where you are getting a different bang for each good, you should reallocate your consumption. For example, what if the following were true?
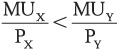
In other words, you are getting more “bang for the buck” with good Y, so you should consume more of good Y! This requires that you decrease your consumption of X in order to stay within your budget constraint. For example, consider the consumption bundle of 6 meals and 2 units of exercise. From Table 2-6, we can calculate that the marginal utility of the sixth meal is 25 and the marginal utility of the second unit of exercise is 70, so
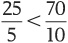
Since you are getting more bang for the buck from exercising, you should increase your consumption of exercise.
What happens to MUY when you consume more? The principle of diminishing marginal utility says that MUY falls. And as you consume fewer units of X, MUX increases. The theory of consumer choice predicts that this kind of reshuffling will cease when the ratios are equal again, and the net result is that total “happiness” increases.
Utility maximization can tell us what a rational consumer will do in order to make herself as happy as possible. When consumers are faced with consumption decisions, they go through this process (although probably on a more intuitive level than sitting down and calculating it all). However, mapping it out in this manner turns out to be very useful for the economist. For instance, if we go through this process, we can figure out how much a consumer will change her consumption of a good in response to a change in the price of that good. This is something that we will see in the next chapter.
Still Struggling
Working with the utility maximization rule can be difficult at first. Some students find it easier to locate the correct bundle of goods X and Y by rearranging the rule in the following way:
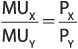
This tells us that we need to limit our search to combinations of X and Y that produce a ratio of marginal utilities (MUX/MUY) that is equal to the ratio of the prices. In the example we have been using,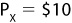 
and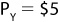 
, and so the ratio 
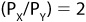. Any combination of X and Y that does provide a ratio of marginal utilities equal to 2 is a candidate for the combination that maximizes utility. Once you limit the search to only those combinations, find the one that uses up exactly the consumer’s income and you’ve solved the problem.
This chapter describes how economists measure the “happiness” that consumers get from consumption as utility, and assumes that consumers seek to maximize their utility. The additional utility received from the consumption of the next unit of a good is known as marginal utility, and the law of diminishing marginal utility assumes that buyers receive less and less additional utility from each additional unit that they consume. A budget constraint shows how a consumer’s income and the prices of two goods, X and Y, limits the combinations of X and Y that the consumer can afford. Consumers are believed to maximize their utility given the limits of the budget constraint. The utility maximization rule states that the best (utility-maximizing) combination of goods to consume will be the one where the marginal utility per dollar spent on each good will be the same for all goods. Mathematically, this rule is expressed as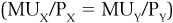 
.
Is each of the following statements true or false? Explain.
1. When you consume more of a good, both your total utility and your marginal utility will always increase.
2. Utility can be thought of as the dollar value of happiness.
3. If a consumer gets 80 marginal units of happiness from consuming Gams, which cost $4 each, and 100 marginal units of happiness from consuming Ferbs, which also cost $4 each, the consumer would be better off if he increased his consumption of Ferbs.
4. If the marginal utility of the next unit is less than zero, that unit should not be consumed.
For each of the following, choose the answer that best fits.
5. The Table 2-7 shows Sissy’s total utility from the consumption of fried chicken livers. Given the information in the table, the marginal utility of the fourth chicken liver is:
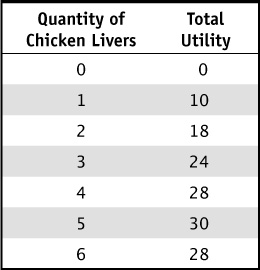
A. 28 utils.
B. 7 utils.
C. 4 utils.
D. zero utils.
6. Table 2-7 shows Sissy’s total utility from the consumption of fried chicken livers. Sissy also buys cans of soda and is receiving six utils per dollar from her soda consumption. Given the information in this table, if Sissy is maximizing her utility by consuming three chicken livers, the price of chicken livers must be:
A. $1
B. $2
C. $6
D. $5
7. Jamaal is currently spending all of his income on coffee and doughnuts. The price of coffee is $2 per cup, and the price of doughnuts is $3 each. Suppose that Jamaal’s current marginal utility for a cup of coffee is 5 utils and his marginal utility for a doughnut is 9 utils. Is there a way for Jamaal to adjust his consumption to increase his utility?
A. Yes. He should consume more doughnuts and less coffee.
B. Yes. He should consume more coffee and less doughnuts.
C. No. He has already maximized his utility.
D. Yes. He should consume more coffee and more doughnuts.
8. A consumer has $100 of income to spend on goods X and Y. The price of good X is $4, and the price of good Y is $5. Which of the following combinations of X and Y lies on the consumer’s budget line?
A. 10X and 5Y.
B. 25X and 20Y.
C. 12X and 10Y.
D. 10X and 12Y.
9. A consumer has $100 of income to spend on goods X and Y. The price of good X is $10, and the price of good Y is $2. Which of the following combinations of X and Y is currently unaffordable?
A. 10X and 0Y.
B. 6X and 25Y.
C. 4X and 20Y.
D. 5X and 25Y.
10. Grace really enjoys cupcakes. In fact, the graph of her total utility curve from eating cupcakes is a straight line that always rises by 5 utils for every cupcake she eats. This tells us that her marginal utility curve:
A. Also rises 5 utils with every cupcake she eats.
B. Begins at 5 utils for the first cupcake, but diminishes with more cupcakes.
C. Is a horizontal line at 5 utils for all cupcakes eaten.
D. Initially rises for the first cupcake, is highest at 5 utils, then diminishes with more cupcakes.
