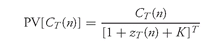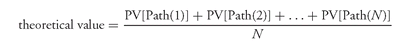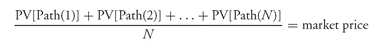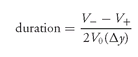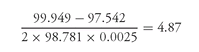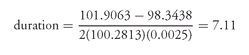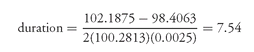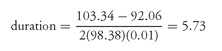CHAPTER 12
VALUING MORTGAGE-BACKED AND ASSET-BACKED SECURITIES
I. INTRODUCTION
In the two previous chapters, we looked at mortgage-backed and asset-backed securities. Our focus was on understanding the risks associated with investing in these securities, how they are created (i.e., how they are structured), and why the products are created. Specifically, in the case of agency mortgage-backed securities we saw how prepayment risk can be redistributed among different tranches to create securities with a prepayment risk profile that is different from the underlying pool of mortgages. For asset-backed securities and nonagency mortgage-backed security, we saw how to create tranches with different degrees of credit risk.
What we did not discuss in describing these securities is how to value them and how to quantify their exposure to interest rate risk. That is, we know, for example, that a support tranche in a CMO structure has greater prepayment risk than a planned amortization class (PAC) tranche. However, how do we determine whether or not the price at which a support tranche is offered in the market adequately compensates for the greater prepayment risk? In this chapter, we will describe and then apply a methodology for valuing mortgage-backed securities and some types of asset-backed securities—Monte Carlo simulation. As we stressed in Chapter 9, a byproduct of a valuation model is the option-adjusted spread. We will see how the option-adjusted spread for a mortgage-backed or an asset-backed security is computed and applied. From a valuation model the effective duration and effective convexity of any security can be computed. We will explain how to compute effective duration and effective convexity using the Monte Carlo simulation model. However, in the case of mortgage-backed securities, there have been several alternative measures of duration used by practitioners. These measures will be identified along with their advantages and disadvantages.
Admittedly, the majority of this chapter is devoted to the valuation of mortgage-backed securities and by extension to all real estate-related asset-backed securities. They are the most difficult asset-backed products to value and to quantify in terms of interest rate exposure. At the end of this chapter, we provide a framework for determining which analytical measures discussed in this chapter are appropriate for valuing any asset-backed security. In fact, the principles apply to all fixed income products.
II. CASH FLOW YIELD ANALYSIS
Let’s begin with the traditional analysis of mortgage-backed and asset-backed securities—cash flow yield analysis. As explained in Chapter 6, the yield on any financial instrument is the interest rate that makes the present value of the expected cash flow equal to its market price plus accrued interest. When applied to mortgage-backed and asset-backed securities, this yield is called a cash flow yield. The problem in calculating the cash flow yield of a mortgage-backed and asset-backed securities is that the cash flow is unknown because of prepayments. Consequently, to determine a cash flow yield, some assumption about the prepayment rate must be made. And, in the case of all but agency mortgage-backed securities, an assumption about default rates and recovery rates must be made.
The cash flow for mortgage-backed and asset-backed securities is typically monthly. The convention is to compare the yield on mortgage-backed and asset-backed securities to that of a Treasury coupon security by calculating the security’s
bond-equivalent yield. As explained in Chapter 6, the bond-equivalent yield for a Treasury coupon security is found by doubling the semiannual yield to maturity. However, it is incorrect to do this for a mortgage-backed or an asset-backed security because the investor has the opportunity to generate greater reinvestment income by reinvesting the more frequent (i.e., monthly) cash flows. The
market convention is to calculate a yield so as to make it comparable to the yield to maturity on a bond-equivalent basis. The formula for annualizing the monthly cash flow yield for a monthly-pay product is therefore:
bond-equivalent yield = 2[(1 + iM)6 − 1]
where
iM is the monthly interest rate that will equate the present value of the projected monthly cash flow equal to the market price (plus accrued interest) of the security.
To illustrate the calculation of the bond-equivalent yield, suppose that the monthly yield is 0.6%. That is, iM is 0.006. Then
bond-equivalent yield = 2[(1.006)6 − 1] = 0.0731 = 7.31%
A. Limitations of Cash Flow Yield Measure
All yield measures suffer from problems that limit their use in assessing a security’s potential return. The yield to maturity has two major shortcomings as a measure of a bond’s potential return. To realize the stated yield to maturity, the investor must:
1. reinvest the coupon payments at a rate equal to the yield to maturity, and
2. hold the bond to the maturity date
As explained in Chapter 6, the reinvestment of the coupon payments is critical and for long-term bonds can be as much as 80% of the bond’s return. Reinvestment risk is the risk of having to reinvest the interest payments at less than the computed yield. Interest rate risk is the risk associated with having to sell the security before its maturity date at a price less than the purchase price.
These shortcomings are equally applicable to the cash flow yield measure:
1. the projected cash flows are assumed to be reinvested at the cash flow yield, and
2. the mortgage-backed or asset-backed security is assumed to be held until the final payout based on some prepayment assumption.
The importance of reinvestment risk, the risk that the cash flow will have to be reinvested at a rate less than the cash flow yield, is particularly important for many mortgage-backed and asset-backed securities because payments are monthly and both interest and principal must be reinvested. Moreover, an additional assumption is that the projected cash flow is actually realized. If the prepayment, default, and recovery experience is different from that assumed, the cash flow yield will not be realized.
B. Nominal Spread
Given the computed cash flow yield and the average life for a mortgage-backed or asset-backed security based on some prepayment, default, and recovery assumption, the next step is to compare the yield to the yield for a comparable Treasury security. “Comparable” is typically defined as a Treasury security with the same maturity as the security’s average life. The difference between the cash flow yield and the yield on a comparable Treasury security is called the nominal spread.
Unfortunately, it is the nominal spread that some managers will use as a measure of relative value. However, this spread masks the fact that a portion of the nominal spread is compensation for accepting prepayment risk. For example, CMO support tranches have been offered at large nominal spreads. However, the nominal spread embodies the substantial prepayment risk associated with support tranches. The manager who buys solely on the basis of nominal spread fails to determine whether or not that nominal spread offered adequate compensation given the substantial prepayment risk faced by the holder of a support tranche.
Instead of nominal spread, managers need a measure that indicates the potential compensation after adjusting for prepayment risk. This measure is called the option-adjusted spread. We discussed this measure in Chapter 9 where we covered the valuation of corporate and agency bonds with embedded options. Before discussing this measure for structured products, we describe another spread measure commonly quoted for structured products called the zero-volatility spread, a measure described in Chapter 9.
III. ZERO-VOLATILITY SPREAD
As explained earlier, the proper procedure to compare any security to a U.S. Treasury security is to compare it to a portfolio of Treasury securities that have the same cash flow. The value of the security is then equal to the present value of all of the cash flows. The security’s value, assuming the cash flows are default-free, will equal the present value of the replicating portfolio of Treasury securities. In turn, these cash flows are valued at the Treasury spot rates.
The
zero-volatility spread is a measure of the spread that the investor would realize over the entire Treasury spot rate curve if the mortgage-backed or asset-backed security is held to maturity. It is not a spread off one point on the Treasury yield curve, as is the nominal spread. The zero-volatility spread (also called the
Z-spread and the
static spread) is the spread that will make the present value of the cash flows from the mortgage-backed or asset-backed security when discounted at the Treasury spot rate plus the spread equal to the price of the security. A trial-and-error procedure (or search algorithm) is required to determine the zero-volatility spread. We illustrated this in Chapter 6.
158Also as explained at Level I, in general, the shorter the maturity or average life of a structured product, the less the zero-volatility spread will differ from the nominal spread. The magnitude of the difference between the nominal spread and the zero-volatility spread also depends on the shape of the yield curve. The steeper the yield curve, the greater the difference.
One of the objectives of this chapter is to explain when it is appropriate to use the Z-spread instead of the OAS. What will be seen is that if a structured product has an option and the borrower tends to take advantage of that option when interest rates decline, then the OAS should be used. If the borrower has an option but tends not to take advantage of it when interest rates decline, then the Z-spread should be used.
IV. MONTE CARLO SIMULATION MODEL AND OAS
In Chapter 9, we discussed one model that is used to value callable agency debentures and corporate bonds, the binomial model. This valuation model accommodates securities in which the decision to exercise a call option is not dependent on how interest rates evolved over time. That is, the decision of an issuer to call a bond will depend on the level of the rate at which the issue can be refunded relative to the issue’s coupon rate, and not the path interest rates took to get to that rate. In contrast, there are fixed income securities and derivative instruments for which the periodic cash flows are “interest rate path-dependent.” This means that the cash flow received in one period is determined not only by the current interest rate level, but also by the path that interest rates took to get to the current level.
For example, in the case of passthrough securities, prepayments are interest rate path-dependent because this month’s prepayment rate depends on whether there have been prior opportunities to refinance since the underlying mortgages were originated. This phenomenon is referred to as “prepayment burnout.” Pools of passthroughs are used as collateral for the creation of CMOs. Consequently, there are typically two sources of path dependency in a CMO tranche’s cash flows. First, the collateral prepayments are path-dependent as discussed above. Second, the cash flows to be received in the current month by a CMO tranche depend on the outstanding balances of the other tranches in the deal. Thus, we need the history of prepayments to calculate these balances.
Conceptually, the valuation of agency passthroughs using the Monte Carlo model is simple. In practice, however, it is very complex. The simulation involves generating a set of cash flows based on simulated future mortgage refinancing rates, which in turn imply simulated prepayment rates.
Valuation modeling for agency CMOs is similar to valuation modeling for passthroughs, although the difficulties are amplified because the issuer has distributed both the prepayment risk and the interest rate risk into different tranches. The sensitivity of the passthroughs comprising the collateral to these two risks is not transmitted equally to every tranche. Some of the tranches wind up more sensitive to prepayment risk and interest rate risk than the collateral, while some of them are much less sensitive.
The objective is to figure out how the value of the collateral gets transmitted to the tranches in a deal. More specifically, the objective is to find out where the value goes and where the risk goes so that one can identify the tranches with low risk and high value: the tranches a manager wants to consider for purchase. The good news is that this combination usually exists in every deal. The bad news is that in every deal there are usually tranches with low value and high risk that managers want to avoid purchasing.
A. Simulating Interest Rate Paths and Cash Flows
To generate these random interest rate paths, the typical model used by Wall Street firms and commercial vendors takes as input today’s term structure of interest rates and a volatility assumption. (We discussed these topics in Chapter 9.) The term structure of interest rates is the theoretical spot rate (or zero coupon) curve implied by today’s Treasury securities. The simulations should be calibrated so that the average simulated price of a zero-coupon Treasury bond equals today’s actual price.
On-the-run Treasury issues are often used in the calibration process. Some dealers and vendors of analytical systems use the LIBOR curve instead of the Treasury curve—or give the user a choice to use either the Treasury curve or the LIBOR curve. The reason is that some investors are interested in spreads that they can earn relative to their funding costs and LIBOR for many investors is a better proxy for that cost than Treasury rates. (We will discuss the different types of investors later.)
As explained in Chapter 9, every dealer and vendor of analytical systems employs an interest rate model. This is a model that assumes how interest rates will change over time. The interest rate models employed by most dealers and vendors of analytical systems are similar. However, one input to all interest rate models is the interest rate volatility assumption. It is that assumption that varies by dealer and vendor. As will be illustrated later in this chapter, it is a critical input.
The volatility assumption determines the dispersion of future interest rates in the simulation. Today, many dealers and vendors do not use one volatility number for the yield of all maturities of the yield curve. Instead, they use either a short/long yield volatility or a term structure of yield volatility. A short/long yield volatility means that volatility is specified for maturities up to a certain number of years (short yield volatility) and a different yield volatility for longer maturities (long yield volatility). The short yield volatility is assumed to be greater than the long yield volatility. A term structure of yield volatilities means that a yield volatility is assumed for each maturity.
Based on the interest rate model and the assumed volatility, a series of interest rate paths will be generated. We will see shortly how a security is valued on each interest rate path. However, there is nothing that we have explained thus far that assures us that the values produced by the model will be arbitrage free. Recall from Chapter 9 that the binomial interest rate tree by design is constructed to be arbitrage free. That is, if any of the on-the-run issues that were used to construct the binomial interest rate tree are valued using the tree, the model would produce a value for that on-the-run issue equal to its market value. There is nothing we described so far about the Monte Carlo simulation to assure this.
More specifically, in the case of Monte Carlo simulation for valuing mortgage-backed and asset-backed securities, the on-the-run Treasury issues are typically used. What assurance is there that if an on-the-run Treasury issue is valued using the Monte Carlo simulation model it will be arbitrage free? That is, what assurance is there that the value produced by the model will equal the market price? Nothing. That’s right, nothing. What the model builder must do is “adjust” the interest rate paths so that the model produces the correct values for the on-the-run Treasury issues. A discussion of this adjustment process is not important to us. In fact, there are very few published sources that describe how this is done. The key point here is that no such adjustment is necessary in a binomial model for valuing corporate and agency bonds with embedded options because the tree is built to be arbitrage free. In the case of the Monte Carlo simulation model, the builder must make an arbitrary adjustment to the interest rate paths to get the model to be arbitrage free.
The simulation works by generating many scenarios of future interest rate paths. As just explained, the “raw” interest rate paths that are simulated must be “adjusted” so as to make the model generate arbitrage-free values for whatever benchmark interest rates are used—typically, the on-the-run Treasury issues. So, in the remainder of this chapter, when we refer to interest rate paths it is understood that it is the “adjusted” interest rate paths where “adjusted” means that each interest rate path is adjusted so that the model will produce arbitrage-free values.
In each month of the scenario (i.e., path), a monthly interest rate and a mortgage refinancing rate are generated. The monthly interest rates are used to discount the projected cash flows in the scenario. The mortgage refinancing rate is needed to determine the cash flows because it represents the opportunity cost the borrower (i.e., mortgagor) is facing at that time.
If the refinancing rates are high relative to the borrower’s original coupon rate (i.e., the rate on the borrower’s loan), the borrower will have less incentive to refinance, or even a disincentive (i.e., the homeowner will avoid moving in order to avoid refinancing). If the refinancing rate is low relative to the borrower’s original coupon rate, the borrower has an incentive to refinance.
Prepayments are projected by feeding the refinancing rate and loan characteristics into a prepayment model. Given the projected prepayments, the cash flows along an interest rate path can be determined.
To make this more concrete, consider a newly issued mortgage passthrough security with a maturity of 360 months.
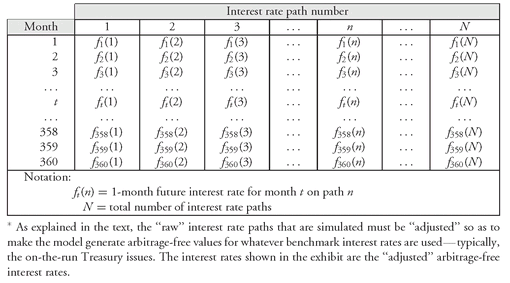
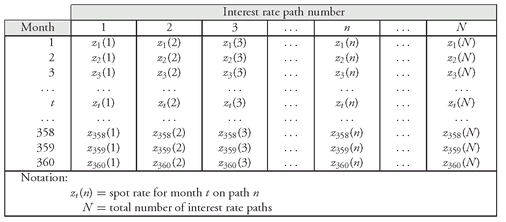
Exhibit 1 shows
N “adjusted” simulated interest rate path scenarios—adjusted to be arbitrage free. Each scenario consists of a path of 360 simulated 1-month future interest rates. (The number of paths generated is based on a well known principle in simulation which will not be discussed here.) So, our first assumption that we make to get
Exhibit 1 is the volatility of interest rates.
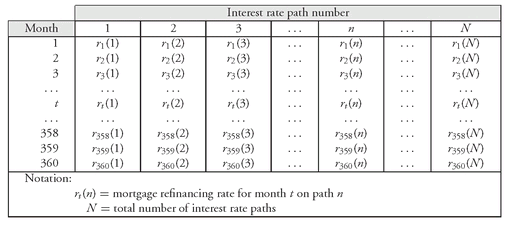
Exhibit 2 shows the paths of simulated mortgage refinancing rates corresponding to the scenarios shown in
Exhibit 1. In going from
Exhibit 1 to
Exhibit 2, an assumption must be made about the relationship between the Treasury rates and refinancing rates. The assumption is that there is a constant spread relationship between the rate that the borrower will use to determine whether or not to refinance (i.e., the refinancing rate) and the 1-month interest rates shown in
Exhibit 1. For example, for 30-year mortgage loans, model builders use the 10-year Treasury rate as a proxy for the refinancing rate.
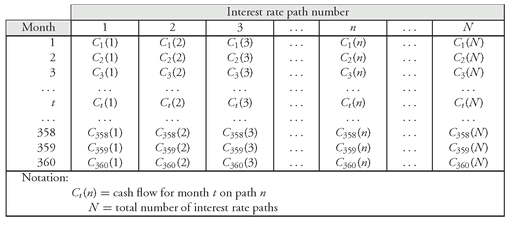
Given the mortgage refinancing rates, the cash flows on each interest rate path can be generated. For agency mortgage-backed securities, this requires a prepayment model. For asset-backed securities and nonagency mortgage-backed securities, this requires both a prepayment model and a model of defaults and recoveries. So, our next assumption is that the output of these models (prepayments, defaults, and recoveries) are correct. The resulting cash flows are depicted in
Exhibit 3.
B. Calculating the Present Value for an Interest Rate Path
EXHIBIT 1 “Adjusted” Simulated Paths of Arbitrage-Free 1-Month Future Interest Rates
∗
EXHIBIT 2 Simulated Paths of Mortgage Refinancing Rates
EXHIBIT 3 Simulated Cash Flows on Each of the Interest Rate Paths
Given the cash flows on an interest rate path, the path’s present value can be calculated. The discount rate for determining the present value is the simulated spot rate for each month on the interest rate path plus an appropriate spread. The spot rate on a path can be determined from the simulated future monthly rates. The relationship that holds between the simulated spot rate for month
T on path
n and the simulated future 1-month rates is:
zT(n) = {[1 + f1(n)][1 + f2(n)] ··· [1 + fT(n)]}1/T − 1
where
zT(n) = simulated spot rate for monthT on path n
ft(n) = simulated future 1-month rate for montht on path n
In Chapter 6 we explained the relationship between spot rates and forward rates.
Consequently, the interest rate path for the simulated future 1-month rates can be converted to the interest rate path for the simulated monthly spot rates as shown in
Exhibit 4. Therefore, the present value of the cash flows for month
T on interest rate path
n discounted at the simulated spot rate for month
T plus some spread is:
where
The spread, K , reflects the risks that the investor feels are associated with realizing the cash flows.
The present value for path
n is the sum of the present value of the cash flows for each month on path
n. That is,
PV[Path(n)] = PV[C1(n)] + PV[C2(n)] + · · · + PV[C360(n)]
where PV[Path(
n)] is the present value of interest rate path
n.
C. Determining the Theoretical Value
The present value of a given interest rate path can be thought of as the theoretical value of a passthrough if that path was actually realized. The theoretical value of the passthrough can be determined by calculating the average of the theoretical values of all the interest rate paths. That is, the theoretical value is equal to
where
N is the number of interest rate paths. The theoretical value derived from the above equation is based on some spread,
K . It follows the usual practice of discounting cash flows at spot rates plus a spread—in this case the spread is
K .
This procedure for valuing a passthrough is also followed for a CMO tranche. The cash flow for each month on each interest rate path is found according to the principal repayment and interest distribution rules of the deal.
EXHIBIT 4 “Adjusted” Simulated Paths of Monthly Arbitrage-Free Spot Rates
D. Selecting the Number of Interest Rate Paths
Let’s now address the question of the number of scenario paths, N , needed to value a security. The number of interest rate paths determines how “good” the estimate is, not relative to the truth but relative to the model used. The more paths, the more the average value produced tends to converge. It is simply a statistical sampling problem.
Most models employ some form of variance reduction to cut down on the number of sample paths necessary to get a good statistical sample.
159 Several vendor firms have developed computational procedures that reduce the number of paths required but still provide the accuracy of a full Monte Carlo analysis. The procedure is to use statistical techniques to reduce the number of interest rate paths to sets of similar paths. These paths are called
representative paths. For example, suppose that 2,000 sample paths are generated. Using a certain statistical technique, these 2,000 sample paths can be collapsed to, say, 16 representative paths. The security is then valued on each of these 16 representative paths. The theoretical value of the security is then the
weighted average of the 16 representative paths. The weight for a path is the percentage of that representative path relative to the total sample paths. Vendors often give the investor or portfolio manager the choice of whether to use the “full Monte Carlo simulation” or to specify a number of representative paths.
E. Option-Adjusted Spread
In Chapter 9, we explained the option-adjusted spread (OAS). Specifically, we explained (1) how to compute the OAS for corporate and agency bonds with embedded options and (2) how to interpret the OAS and apply it in relative analysis. Below we cover the same issues for the OAS computed for mortgage-backed securities.
1. Computing the OAS In the Monte Carlo model, the OAS is the spread that when added to all the spot rates on all interest rate paths will make the average present value of the paths equal to the observed market price (plus accrued interest). Mathematically, OAS is the value for
K (the spread) that will satisfy the following condition:
where
N is the number of interest rate paths. The left-hand side of the above equation looks identical to that of the equation for the theoretical value. The difference is that the objective is to determine what spread,
K , will make the model produce a theoretical value equal to the market price.
The procedure for determining the OAS is straightforward and involves the same search algorithm explained for the zero-volatility spread. The next question, then, is how to interpret the OAS. Basically, the OAS is used to reconcile value with market price. On the right-hand side of the previous equation is the market’s statement: the price of a structured product. The average present value over all the paths on the left-hand side of the equation is the model’s output, which we refer to as the theoretical value.
2. Interpreting the OAS and Relative Value Application What an investor or a portfolio manager seeks to do is to buy a mortgage-backed security where value is greater than price. By using a valuation model such as the Monte Carlo model, a portfolio manager could estimate the value of a security, which at this point would be sufficient in determining whether to buy a security. That is, the portfolio manager can say that this security is 1 point cheap or 2 points cheap, and so on. The model does not stop here. Instead, it converts the divergence between price and value into some type of spread measure since most market participants find it more convenient to think about spreads than price differences.
The OAS was developed as a measure of the spread that can be used to convert dollar differences between value and price. As we explained in Chapter 9, in the binomial model a spread is measured relative to the benchmark interest rates used to generate the interest rate tree and which is therefore used to make the tree arbitrage free. The same is true in the case of the Monte Carlo simulation model. The spread is measured relative to the benchmark interest rates that were used to generate the interest rate paths and to adjust the interest rate paths to make them arbitrage free. Typically, for a mortgage-backed security the benchmark interest rates are the on-the-run Treasury rates. The OAS is then measuring the average spread over the Treasury spot rate curve, not the Treasury yield as explained in Chapter 9. It is an average spread since the OAS is found by averaging over the interest rate paths for the possible Treasury spot rate curves. Of course, if the LIBOR curve is used, the OAS is the spread over that curve.
This spread measure is superior to the nominal spread which gives no recognition to the prepayment risk. As explained in Chapter 9, the OAS is “option adjusted” because the cash flows on the interest rate paths are adjusted for the option of the borrowers to prepay. While we may understand the mechanics of how to compute the OAS and why it is appropriate to use the OAS rather than the nominal spread or Z-spread, the question is what does the spread represent? In Chapter 9, a discussion of what compensation the OAS reflects for corporate and agency bonds with embedded options was presented. The compensation is for a combination of credit risk and liquidity risk. The compensation depends on the benchmark interest rates used in the analysis. For example, consider the use of Treasury interest rates and more specifically the Treasury spot rate curve since this is the benchmark typically used in the calculation of an OAS for a mortgage-backed security. If there is an OAS computed using the Treasury benchmark, then what is that OAS compensating?
Consider first Ginnie Mae mortgage passthrough securities. As explained earlier (Chapter 3), Ginnie Mae is an arm of the U.S. government. The securities it issues are backed by the full faith and credit of the U.S. government. Effectively, a Ginnie Mae mortgage-backed security is a Treasury security with prepayment risk. The OAS removes the prepayment risk (i.e., the option risk). Additionally, if the benchmark is Treasury rates, the OAS should not be compensation for credit risk. That leaves liquidity risk. While Ginnie Mae mortgage passthrough securities may not be as liquid as on-the-run Treasury issues, they are fairly liquid as measured by the bid-ask spread. Nevertheless, part of the OAS should reflect compensation for liquidity risk. There is one more risk that was not the focus of Chapter 9, modeling risk. In our explanation of the Monte Carlo model, there were several critical assumptions and parameters required. If those assumptions prove incorrect or if the parameters are misestimated, the prepayment model will not calculate the true level of risk. Thus, probably a good part of the compensation for a Ginnie Mae mortgage passthrough security reflects payment for this model uncertainty.
If we consider CMOs issued by Ginnie Mae rather than the mortgage passthrough securities, the OAS would reflect the complexity associated with a particular tranche. For example, a planned amortization class (PAC) tranche would be less exposed to modeling risk than a support tranche in the same CMO structure. Hence, compensation for modeling risk would be greater for a support tranche than a PAC tranche in the same structure. Moreover, PAC tranches have greater liquidity than support tranches, so compensation is less for the former relative to the latter.
As we move from Ginnie Mae issued mortgage products to those issued by Freddie Mac and Fannie Mae, we introduce credit risk. As explained in Chapter 3, Freddie Mac and Fannie Mae are government sponsored enterprises (GSEs). As such, there is no requirement that a GSE be bailed out by the U.S. government. The GSEs are viewed as triple A rated. Consequently, in addition to modeling risk and liquidity risk, a portion of the OAS reflects credit risk relative to Treasury securities.
Moving on to nonagency mortgage-backed securities and real estate backed asset-backed securities, the OAS is compensating for: (1) credit risk (which varies depending on the credit rating for the tranche under consideration), (2) liquidity risk (which is greater than for Ginnie Mae, Fannie Mae, and Freddie Mac mortgage products), and (3) modeling risk.
F. Option Cost
The implied cost of the option embedded for a mortgage-backed or asset-backed security can be obtained by calculating the difference between the option-adjusted spread at the assumed volatility of interest rates and the zero-volatility spread. That is,
option cost = zero-volatility spread − option-adjusted spread
The Option cost,option cost measures the prepayment (or option) risk embedded in the security. Note that the cost of the option is a byproduct of the option-adjusted spread analysis, not valued explicitly with some option pricing model.
G. Illustrations
We will use two deals to show how CMOs can be analyzed using the Monte Carlo model/OAS procedure discussed above—a simple structure and a PAC/support structure.
1601. Simple Structure The simple structure analyzed is Freddie Mac (FHLMC) 1915. It is a simple sequential-pay CMO bond structure. The structure includes eight tranches, A, B, C, D, E, F, G, and S. The focus of our analysis is on tranches A, B, and C. All three tranches were priced at a premium.
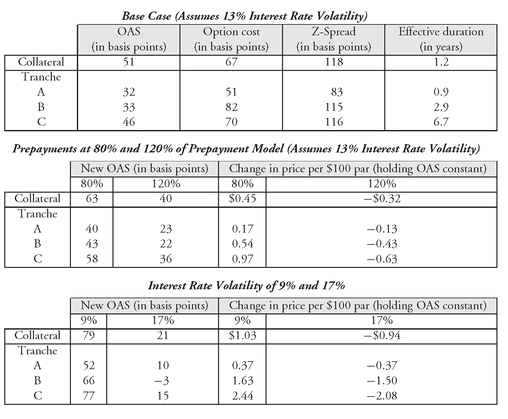
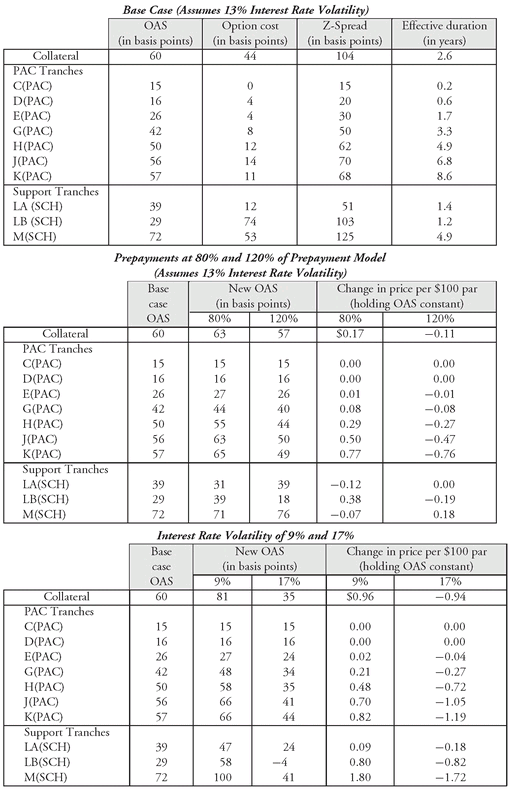
The top panel of
Exhibit 5 shows the OAS, the option cost, and effective duration
161 for the collateral and the three tranches in the CMO structure. However, tranche A had the smallest effective duration and tranche C had the largest effective duration. The OAS for the collateral is 51 basis points. Since the option cost is 67 basis points, the zero-volatility spread is 118 basis points (51 basis points plus 67 basis points).
At the time this analysis was performed, March 10, 1998, the Treasury yield curve was not steep. We explained that when the yield curve is relatively flat the zero-volatility spread will not differ significantly from the nominal spread. Thus, for the three tranches shown in
Exhibit 5, the zero-volatility spread is 83 basis points for A, 115 basis points for B, and 116 basis points for C.
Notice that the tranches did not share the OAS equally. The same is true for the option cost. Both the Z-spread and the option cost increase as the effective duration increases. Whether or not any of these tranches were attractive investments requires a comparison to other tranches in the market with the same effective duration. While not presented here, all three tranches offered an OAS similar to other sequential-pay tranches with the same effective duration available in the market. On a relative basis (i.e., relative to the other tranches analyzed in the deal), the only tranche where there appears to be a bit of a bargain is tranche C. A portfolio manager contemplating the purchase of this last cash flow tranche can see that C offers a higher OAS than B and appears to bear less of the risk (i.e., has lower option cost), as measured by the option cost. The problem portfolio managers may face is that they might not be able to go out as long on the yield curve as tranche C because of effective duration, maturity, and average life constraints relative to their liabilities, for example.
Now let’s look at modeling risk. Examination of the sensitivity of the tranches to changes in prepayments and interest rate volatility will help us to understand the interaction of the tranches in the structure and who is bearing the risk. How the deal behaves under various scenarios should reinforce and be consistent with the valuation (i.e., a tranche may look “cheap” for a reason).
We begin with prepayments. Specifically, we keep the same interest rate paths as those used to get the OAS in the base case (the top panel of
Exhibit 5), but reduce the prepayment rate on each interest rate path to 80% of the projected rate. As can be seen in the second panel of
Exhibit 5, slowing down prepayments increases the OAS and price for the collateral. The exhibit reports two results of the sensitivity analysis. First, it indicates the change in the OAS. Second, it indicates the change in the price, holding the OAS constant at the base case.
EXHIBIT 5 OAS Analysis of FHLMC 1915 Classes A, B, and C (As of 3/10/98) All three tranches were trading at a premium as of the date of the analysis.
To see how a portfolio manager can use the information in the second panel, consider tranche A. At 80% of the prepayment speed, the OAS for this tranche increases from 32 basis points to 40 basis points. If the OAS is held constant, the panel indicates that the buyer of tranche A would gain $0.17 per $100 par value.
Notice that for all of the tranches reported in
Exhibit 5 there is a gain from a slowdown in prepayments. This is because all of the sequential tranches in this deal are priced over par. (An investor in a tranche priced at a premium benefits from a slowdown in prepayments because the investor receives the higher coupon for a longer period and postpones the capital loss from a prepayment.) Also notice that while the changes in OAS are about the same for the different tranches, the changes in price are quite different. This arises because the shorter tranches have less duration. Therefore, their prices do not move as much from a change in OAS as a longer average life tranche. A portfolio manager who is willing to go to the long end of the yield curve, such as tranche C, would realize the most benefit from the slowdown in prepayments.
Also shown in the second panel of the exhibit is the second part of our experiment to test the sensitivity of prepayments: the prepayment rate is assumed to be 120% of the base case. The collateral loses money in this scenario because it is trading above par. This is reflected in the OAS of the collateral which declines from 51 basis points to 40 basis points. Now look at the three tranches. They all lost money because the tranches were all at a premium and the speeding of prepayments adversely affects the tranche.
Before looking at the last panel that shows the effect of a change in interest rate volatility on the OAS, let’s review the relationship between expected interest rate volatility and the value of a mortgage-backed security. Recall that the investor in a mortgage-backed security has sold an option to homeowners (borrowers). Thus, the investor is short an option. As will be explained in Chapter 14, the value of an option depends on expected interest rate volatility. When expected interest rate volatility decreases, the value of the option embedded in a mortgage-backed security decreases and therefore the value of a mortgage-backed security increases. The opposite is true when expected interest rate volatility increases—the value of the embedded option increases and the value of a mortgage-backed security decreases.
Now let’s look at the sensitivity to the interest rate volatility assumption, 13% in the base case. Two experiments are performed: reducing the volatility assumption to 9% and increasing it to 17%. These results are reported in the third panel of
Exhibit 5.
Reducing the volatility to 9% increases the dollar price of the collateral by $1.03 and increases the OAS from 51 in the base case to 79 basis points. However, this $1.03 increase in the price of the collateral is not equally distributed among the three tranches. Most of the increase in value is realized by the longer tranches. The OAS gain for each of the tranches follows more or less the effective durations of those tranches. This makes sense, because the longer the duration, the greater the risk, and when volatility declines, the reward is greater for the accepted risk. At the higher level of assumed interest rate volatility of 17%, the collateral is severely affected. The longer the duration, the greater the loss. These results for a decrease and an increase in interest rate volatility are consistent with what we explained earlier.
Using the Monte Carlo simulation/OAS analysis, a fair conclusion that can be made about this simple structure is: what you see is what you get. The only surprise in this structure is the lower option cost in tranche C. In general, however, a portfolio manager willing to extend duration gets paid for that risk in this structure.
2. PAC/Support Tranche Structure Now let’s look at how to apply the methodology to a more complicated CMO structure, FHLMC Series 1706. The collateral (i.e., pool of passthroughs) for this structure is Freddie Mac 7s (7% coupon rate). A partial summary of the deal is provided in
Exhibit 6. That is, only the tranches we will be discussing in this section are shown in the exhibit.
162 While this deal looks complicated, it is relatively simple compared to many deals that have been issued. Nonetheless, it brings out all the key points about application of OAS analysis, specifically, the fact that most deals include cheap bonds, expensive bonds, and fairly priced bonds. The OAS analysis helps identify how a tranche should be classified. A more proper analysis would compare the OAS for each tranche to a similar duration tranche available in the market.
All of the tranches in
Exhibit 6 were discussed in Chapter 10. At issuance, there were 10 PAC tranches, three scheduled tranches, a floating-rate support tranche, and an inverse floating-rate support. Recall that the “scheduled tranches” are support tranches with a schedule, referred to in Chapter 10 as “PAC II tranches.”
The first two PAC tranches in the deal, tranche A and tranche B, were paid off at the time of the analysis. The other PAC tranches were still available at the time of the analysis. The prepayment protection for the PAC tranches is provided by the support tranches. The support tranches in this deal that are shown in
Exhibit 6 are tranches LA, LB, and M. There were other support tranches not shown in
Exhibit 6. LA is the shortest average life support tranche (a scheduled (SCH) bond).
EXHIBIT 6 Summary of Federal Home Loan Mortgage Corporation—Multiclass Mortgage Participation Certificates (Guaranteed), Series 1706
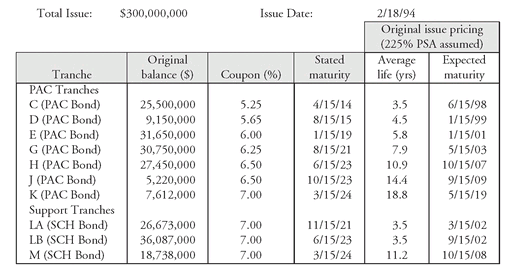
The collateral for this deal was trading at a premium. That is, the homeowners (borrowers) were paying a higher mortgage rate than available in the market at the time of the analysis. This meant that the value of the collateral would increase if prepayments slow down but would decrease if prepayments increase. What is important to note, however, is that a tranche could be trading at a discount, par, or premium even though the collateral is priced at a premium. For example, PAC C had a low coupon rate at the time of the analysis and therefore was trading at a discount. Thus, while the collateral (which was selling at a premium) loses value from an increase in prepayments, a discount tranche such as tranche C would increase in value if prepayments increase. (Recall that in the simple structure analyzed earlier, the collateral and all the tranches were trading at a premium.)
The top panel of
Exhibit 7 shows the base case OAS, the option cost, and the effective duration for the collateral and tranches in
Exhibit 6. The collateral OAS is 60 basis points, and the option cost is 44 basis points. The Z-spread of the collateral to the Treasury spot curve is 104 basis points.
The 60 basis points of OAS did not get equally distributed among the tranches—as was the case with the simple structure analyzed earlier. Tranche LB, the scheduled support, did not realize a good OAS allocation, only 29 basis points, and had an extremely high option cost. Given the prepayment uncertainty associated with this tranche, its OAS would be expected to be higher. The reason for the low OAS is that this tranche was priced so that its cash flow yield is high. Using the Z-spread as a proxy for the nominal spread (i.e., spread over the Treasury yield curve), the 103 basis point spread for tranche LB is high given that this appears to be a short average life tranche. Consequently, “yield buyers” (i.e., investors with a preference for high nominal yield, who may not be attentive to compensation for prepayment risk) probably bid aggressively for this tranche and thereby drove down its OAS, trading off “yield” for OAS. From a total return perspective, however, tranche LB should be avoided. It is a rich, or expensive, tranche. The other support tranche analyzed, tranche M, had an OAS of 72 basis points and at the time of this analysis was similar to that offered on comparable duration tranches available in the market.
EXHIBIT 7 OAS Analysis of FHLMC 1706 (As of 3/10/98)
The analysis reported in the top panel of
Exhibit 7 help us identify where the cheap tranches are in the deal. The long average life and effective duration tranches in the deal are the PAC tranches G, H, J, and K. These tranches have high OAS relative to the other tranches and low option cost. They appear to be the cheap tranches in the deal. These PAC tranches had well protected cash flows and exhibited positive convexity (i.e., these tranches lose less in an adverse scenario than they gain in a positive scenario).
The next two panels in
Exhibit 7 show the sensitivity of the OAS and the price (holding OAS constant at the base case) to changes in the prepayment speed (80% and 120% of the base case) and to changes in volatility (9% and 17%). This analysis shows that the change in the prepayment speed does not affect the collateral significantly, while the change in the OAS (holding the price constant) and price (holding OAS constant) for each tranche can be significant.
Tranches C and D at the time of the analysis were priced at a discount with short average lives. The OAS and price of these two tranches were not affected by a slowing down or a speeding up of the prepayment model. Tranche H was a premium tranche with a medium-term average life at the time of the analysis. Because tranche H was trading at a premium, it benefits from a slowing in prepayments, as the bondholder will receive the coupon for a longer time. Faster prepayments represent an adverse scenario. The PAC tranches are quite well-protected. The longer average life PACs will actually benefit from a reduced prepayment rate because they will be earning the higher coupon interest longer. So, on an OAS basis, the earlier conclusion that the long PACs were allocated a good part of the deal’s value holds up under our first stress test (i.e., changing prepayments).
The sensitivity of the collateral and the tranches to changes in volatility are shown in the third panel of
Exhibit 7. A lower volatility increases the value of the collateral, while a higher volatility reduces its value (This is consistent with our option cost equation in Section IV.E.) The long average life PACs continue to be fairly well-protected, whether the volatility is lower or higher. In the two volatility scenarios they continue to get a good OAS on a relative value basis, although not as much as in the base case if volatility is higher (but the OAS still looks like a reasonable value in this scenario). This reinforces the earlier conclusion concerning the investment merit of the long PACs in this deal. Note, however, that PAC tranches H, J, and K are more sensitive to the volatility assumption than tranches C, D, E, and G and therefore the investor is accepting greater volatility risk (i.e., the risk that volatility will change) with tranches H, J, and K relative to tranches C, D, E, and G.
V. MEASURING INTEREST RATE RISK
As explained in Chapter 9, duration and convexity can be used to estimate the interest rate exposure to parallel shifts in the yield curve (i.e., a measure of level risk). In this section we will discuss duration measures for mortgage-backed securities. There are several duration measures that are used in practice. Two researchers who have done extensive work in measuring duration, Lakhbir Hayre and Hubert Chang, conclude that “No single duration measure will consistently work well for mortgage securities.”
163 To that conclusion should be added that there are some measures that do not work at all.
A. Duration Measures
Duration is a measure of the price sensitivity to changes in interest rates. We have seen how to compute the duration of a security by shocking rates up and down and determining how the price of the security changes. Duration is then computed as follows:
where
Δy = change in rate used to calculate new values (i.e., the interest rate shock)
V+ = estimated value if yield is increased byΔy
V− = estimated value if yield is decreased byΔy
V0 = initial price (per $100 of par value)
For bonds with embedded options such as mortgage-backed securities, the appropriate measure is effective duration and to capture the negative convexity of a bond with an embedded option, effective convexity should be computed. We will see how to calculate the effective duration for a mortgage-backed security using the Monte Carlo simulation model. Then we will see how the assumptions of the model impact the duration estimate. Dealers and vendors use other measures of duration that will be described later.
1. Effective Duration To calculate effective duration, the value of the security must be estimated when rates are shocked up and down a given number of basis points. In terms of the Monte Carlo model, the yield curve used (either the Treasury yield curve or LIBOR curve) is shocked up and down and the new curve is used to generate the values to be used in the effective duration and effective convexity formulas. This is analogous to the process we used to compute effective duration and effective convexity using the binomial model in Chapter 9.
In generating the prices when rates are shocked up and down, there is an assumption that the relationships assumed in generating the initial price do not change when rates are shocked up and down. Specifically, the yield volatility is assumed to be unchanged to derive the new interest rate paths for a given shock (i.e., the new
Exhibit 1), the spread between the mortgage rate and the 10-year Treasury rate is assumed to be unchanged in constructing the new
Exhibit 2 from the newly constructed
Exhibit 1, and the OAS is assumed to be constant. The constancy of the OAS comes into play because when discounting the new cash flows (i.e., the cash flows in the new
Exhibit 3), the current OAS that was computed is assumed to be the same and is added to the new rates in the new
Exhibit 1.
We’ll use an illustration by Lakhbir Hayre and Hubert Chang to explain the calculation of effective duration for a mortgage-backed security, a FNMA 7.5% TBA passthrough on May 1, 1996.
164 On that day, the base mortgage rate was 7.64%. The price of the issue at the time was 98.781 (i.e., 98-25). The OAS was 65 basis points. Based on a shock of 25 basis points, the estimated prices holding the OAS constant at 65 basis points were as follows:
V− = 99.949 for a decrease in the yield curve of 25 basis points
V+ = 97.542 for an increase in the yield curve of 25 basis points
The effective duration based on a
Δy of 0.0025 is then
There are differences in the effective durations for a given mortgage-backed security reported by dealers and vendors of analytical systems. Several practitioners have explained and illustrated why there are differences in effective duration estimates reported by dealers and vendors. The differences result from, among others:
165 1. differences in the amount of the rate shock used
2. differences in prepayment models
3. differences in option-adjusted spread
4. differences in the relationship between short-term interest rates and refinancing rates
Earlier, we discussed the first reason. As explained, the rate shock is the amount interest rates are increased and decreased to obtain the two values that are inserted into the effective duration formula. If the change is too large, there is the problem with picking up the effect of convexity.
Prepayment models differ across dealers and vendors. Some dealer models consistently forecast slower prepayments relative to other dealer models and others the reverse.
The effective duration is dependent on the OAS computed. Recall that the calculation of the OAS is a byproduct of the Monte Carlo model. Therefore, the computed value for the OAS depends on all of the assumptions in the Monte Carlo model. Specifically, it depends on the yield volatility assumed and the prepayment model employed. Dealers and vendors make different assumptions regarding yield volatility and use proprietary prepayment models. These can result in differences in OAS. Since the OAS is added to the new simulated short-term rates to compute the new values for V− and V+, a different OAS will result in different effective durations.
Finally, recall that in explaining the Monte Carlo simulation model that we stated that in moving from
Exhibit 1 (the simulated short-term rates) to
Exhibit 2 (the refinancing rates), an assumption must be made about the relationship between short-term rates and the 10-year Treasury rate (i.e., the rate used as a proxy for refinancing). Differences in models about how large the spread between these rates will be affects the value of a mortgage-backed security and therefore the values used in the duration equation when rates are shocked.
2. Other Duration Measures There have been other measures proposed for estimating the duration of a mortgage-backed security. These measures include
cash flow duration, coupon curve duration, and
empirical duration. The first two duration measures are forms of effective duration in that they do recognize that the values that should be used in the duration formula should take into account how the cash flows may change due to changes in prepayments when interest rates change. In contrast, empirical duration is a duration that is computed statistically using observed market prices. Below we describe how each of these duration measures is calculated, as well as the advantages and limitations of each.
a. Cash Flow Duration Recall from the general duration formula that there are two values that must be substituted into the numerator of the formula—the value if rates are decreased (
V−) and the value if rates are increased (
V+). With effective duration, these two values consider how changes in interest rates change the cash flow due to prepayments. This is done through the Monte Carlo simulation by allowing for the cash flows to change on the interest rate paths.
For
cash flow duration, there is recognition that the cash flow can change but the analysis to obtain the cash flow is done following a static methodology. Specifically, the cash flow duration is calculated as follows:
Step 1: Calculate the cash flow based on some prepayment assumption.
Step 2: From the cash flow in Step 1 and the market price (V0), compute the cash flow yield.
Step 3: Increase the cash flow yield by Δy and from a prepayment model determine the new prepayment rate at that higher cash flow yield. Typically, the prepayment rate will be lower than in Step 1 because of the higher yield level.
Step 4: Using the lower prepayment rate in Step 3 determine the cash flow and then value the cash flow using the higher cash flow yield as the discount rate. This gives the value (V+).
Step 5: Decrease the cash flow yield by Δy and from a prepayment model determine the new prepayment rate at that lower cash flow yield. Typically, the prepayment rate will be higher than in Step 1 because of the lower yield level.
Step 6: Using the higher prepayment rate in Step 5 determine the cash flow and then value the cash flow using the lower cash flow yield as the discount rate. This gives the value (V−).
From the change in basis points (Δy), the values for V+ and V− found in Steps 4 and 6, and the initial value V0, the duration can be computed.
We can use the hypothetical CMO structure in Chapter 10 to illustrate how to calculate cash flow duration. Specifically, in FJF-2, there were four tranches, A, B, C, and Z. Let’s focus on tranche C. Suppose that the price for this tranche is 100.2813. Then the cash flow duration is computed as follows:
Step 1: Suppose that the assumed prepayment rate for this tranche is 165 PSA.
Step 2: Based on the assumed prepayment rate of 165 PSA and the price of 100.2813, it can be demonstrated that the cash flow yield is 7%.
Step 3: Suppose that the cash flow yield is increased (i.e., shocked) by 25 basis points (from 7% to 7.25%) and suppose that some prepayment model projects a prepayment rate of 150 PSA. (Note that this is a slower prepayment rate than at 7%.)
Step 4: Based on 150 PSA, a new cash flow can be generated. The cash flow is then discounted at 7.25% (the new cash flow yield). It can be demonstrated that the value of this tranche based on these assumptions would be 98.3438. This is the value V+.
Step 5: Suppose that the cash flow yield is decreased (i.e., shocked) by 25 basis points (from 7% to 6.75%) and suppose that some prepayment model projects a prepayment rate of 200 PSA. (Note that this is a faster prepayment rate than at 7%.)
Step 6: Based on 200 PSA, the new cash flow can be generated. The cash flow is then discounted at 6.75% (the new cash flow yield). It can be demonstrated that the value of this tranche based on these assumptions would be 101.9063. This is the value V−.
Now we have the following information:
V0 = 100.2813
V+ = 98.3438
V− = 101.9063
Δ y = 0.0025
Then using the general form of duration, we obtain:
What type of duration measure is the cash flow duration—effective duration or modified duration? Technically, it is a form of effective duration because notice that in Steps 3 and 5 when the rate is changed, the cash flow is allowed to change. However, as has been stressed throughout, the valuation model that is used to get the new values to substitute into the duration formula is critical. The valuation model in the case of the cash flow duration is based on the naive assumption that there is a single prepayment rate over the life of the mortgage-backed security for any given interest rate shock. This is in contrast to the values produced by the Monte Carlo simulation model that does more sophisticated analyses of how the cash flow can change when interest rates change.
Why bother discussing the cash flow duration if it is an inferior form of effective duration? The reason is that it is a commonly cited duration measure and practitioners should be aware of how it is computed. Likewise, we did discuss in detail yield calculations despite their limitations.
An interesting question is how does this form of duration compare to modified duration. Recall from Chapter 7 and Chapter 9 that modified duration does not assume that cash flows will change when rates are shocked. That is, in the steps discussed above to obtain cash flow duration, in Steps 3 and 5 it is assumed that the prepayment rate is the same as in Step 1.
To illustrate this, we’ll once again use tranche C in FJF-2. In Step 3, the prepayment rate assumed is still 165 PSA despite the fact that rates are assumed to increase. That is, the cash flow is not assumed to change. Based on a cash flow yield of 7.25% and a prepayment rate of 165 PSA, the value of this tranche would decline to 98.4063. When the cash flow yield is assumed to decline to 6.75%, the prepayment rate is still assumed to be 165 PSA and the value of this tranche would be 102.1875. Then to calculate the modified duration we know:
V0 = 100.2813
V+ = 98.4063
V− = 102.1875
Δy = 0.0025
The modified duration is then:
Thus, the modified duration is greater than the cash flow duration for this tranche.
It is important to reiterate that the modified duration is inferior to the cash flow duration because the former gives absolutely no recognition to how prepayments may change when interest rates change. While cash flow duration is commonly cited in practice, it is a form of effective duration that does give some recognition that prepayments and therefore cash flow may change when interest rates change, but it is based on a naive assumption about how prepayments may change. The effective duration as computed using Monte Carlo simulation is superior to cash flow duration.
b. Coupon Curve Duration The
coupon curve duration uses market prices to estimate the duration of a mortgage-backed security. This approach, first suggested by Douglas Breeden,
166 starts with the coupon curve of prices for similar mortgage-backed securities. The coupon curve represents generic passthrough securities of a particular issuer with different coupon rates. By rolling up and down the coupon curve of prices, the duration can be obtained. Because of the way it is estimated, this approach to duration estimation was referred to by Breeden as the “roll-up, roll-down approach.” The prices obtained from rolling up and rolling down the coupon curve of prices are substituted into the duration formula.
To illustrate this approach, suppose that the coupon curve of prices for a passthrough security for some month is as follows:
| Coupon | Price |
|---|
| 6% | 85.19 |
| 7% | 92.06 |
| 8% | 98.38 |
| 9% | 103.34 |
| 10% | 107.28 |
| 11% | 111.19 |
Suppose that the coupon curve duration for the 8% coupon passthrough is sought. If the yield declines by 100 basis points, the assumption is that the price of the 8% coupon passthrough will increase to the price of the current 9% coupon passthrough. Thus, the price will increase from 98.38 to 103.34. Similarly, if the yield increases by 100 basis points, the assumption is that the price of the 8% coupon passthrough will decline to the price of the 7% coupon passthrough (92.06). Using the duration formula, the corresponding values are:
V0 = 98.38
V+ = 92.06
V− = 103.34
Δy = 0.01
The estimated duration based on the coupon curve is then:
Breeden tested the coupon curve durations and found them to be relatively accurate in estimating the interest rate risk of generic passthrough securities.
167 Bennett Golub reports a similar finding.
168While the advantages of the coupon curve duration are the simplicity of its calculation and the fact that current prices embody market expectations, there are disadvantages. The approach is limited to generic mortgage-backed securities and difficult to use for mortgage derivatives such as CMOs.
c. Empirical Duration When computing effective duration and cash flow duration, the values to be substituted into the duration formula are those based on some valuation model. For coupon curve duration, the observed market prices are used in the duration formula. In contrast,
empirical duration is estimated statistically using historical market prices and market yields.
169 Regression analysis is used to estimate the relationship. Some firms such as PaineWebber use empirical duration, also called
implied duration, as their primary measure of the duration of an MBS.
There are three advantages to the empirical duration approach.
170 First, the duration estimate does not rely on any theoretical formulas or analytical assumptions. Second, the estimation of the required parameters is easy to compute using regression analysis. Finally, the only inputs that are needed are a reliable price series and Treasury yield series.
There are disadvantages.
171 First, a reliable price series for the mortgage security may not be available. For example, there may be no price series available for a thinly traded mortgage derivative security or the prices may be matrix priced (i.e., priced by a pricing service based on issues with similar characteristics) or model priced rather than actual transaction prices. Second, an empirical relationship does not impose a structure for the options embedded in a mortgage-backed security and this can distort the empirical duration. This may occur after a sharp and sustained shock to interest rates have been realized. Finally, the volatility of the spread to Treasury yields can distort how the price of a mortgage-backed security reacts to yield changes.
VI. VALUING ASSET-BACKED SECURITIES
From the description of the Monte Carlo model, it can be seen that the valuation process is complex. Rather than build their own valuation model, portfolio managers typically use a model of a third-party vendor of analytical systems or a model of a dealer firm to value mortgage-backed securities. But mortgage-backed securities are only one type of structured product. Asset-backed securities are also structured products. Is it necessary to use the Monte Carlo model for all asset-backed securities? Below we will explain the circumstances as to when the Monte Carlo model must be used and when it is sufficient to use the Z-spread.
The model that should be used for valuing an asset-backed security (ABS) depends on the characteristic of the loans or receivables backing the deal. An ABS can have one of the following three characteristics:
Characteristic 1: The ABS does not have a prepayment option.
Characteristic 2: The ABS has a prepayment option but borrowers do not exhibit a tendency to prepay when refinancing rates fall below the loan rate.
Characteristic 3: The ABS has a prepayment option and borrowers do exhibit a tendency to prepay when refinancing rates fall below the loan rate.
An example of a Characteristic 1 type ABS is a security backed by credit card receivables. An example of a Characteristic 2 type ABS is a security backed by automobile loans. A security backed by closed-end home equity loans where the borrowers are high quality borrowers (i.e., prime borrowers) is an example of a Characteristic 3 type ABS. There are some real-estate backed ABS we discussed in Chapter 11 where the verdict is still out as to the degree to which borrowers take advantage of refinancing opportunities. Specifically, these include securities backed by manufactured housing loans and securities backed by closed-end home equity loans to borrowers classified as low quality borrowers.
There are two possible approaches to valuing an ABS. They are the
1. zero-volatility spread (Z-spread) approach
2. option-adjusted spread (OAS) approach
For the Z-spread approach the interest rates used to discount the cash flows are the spot rates plus the zero-volatility spread. The value of an ABS is then the present value of the cash flows based on these discount rates. The Z-spread approach does not consider the prepayment option. Consequently, the Z-spread approach should be used to value Characteristic 1 type ABS. (In terms of the relationship between the Z-spread, OAS, and option cost discussed earlier in this chapter, this means that the value of the option is zero and therefore the Z-spread is equal to the OAS.) Since the Z-spread is equal to the OAS, the Z-spread approach to valuation can be used.
The Z-spread approach can also be used to value Characteristic 2 type ABS because while the borrowers do have a prepayment option, the option is not typically exercised. Thus, as with Characteristic 1 type ABS, the Z-spread is equal to the OAS.
The OAS approach—which is considerably more computationally extensive than the Z-spread approach—is used to value securities where there is an embedded option and there is an expectation that the option is expected to be exercised if it makes economic sense for the borrower to do so. Consequently, the OAS approach is used to value Characteristic 3 type ABS. The choice is then whether to use the binomial model (or a comparable model) or the Monte Carlo simulation model. Since typically the cash flow for an ABS with a prepayment option is interest rate path dependent—as with a mortgage-backed security—the Monte Carlo simulation model is used.
VII. VALUING ANY SECURITY
We conclude this chapter with a summary of the approaches to valuing any fixed income security using the two approaches that we discussed in the previous section—the Z-spread approach and the OAS approach.
Below we match the valuation approach with the type of security.
1. For an option-free bond the correct approach is the Z-spread approach.
2. For a bond with an embedded option where the cash flow is not interest rate path dependent (such as a callable corporate or agency debenture bond or a putable bond) the correct approach is the OAS approach. Since the backward induction method can be used for such bonds, the binomial model or its equivalent should be used.
3. For a bond with an embedded option where the cash flow is interest rate path dependent (such as a mortgage-backed security or certain real estate-backed ABS) the correct approach is the OAS approach. However, because of the interest rate path dependency of the cash flow, the Monte Carlo simulation model should be used.