What a wonderful and amazing scheme have we here of the magnificent vastness of the universe!
CHRISTIAAN HUYGENS, COSMOTHEOROS
’Tis all in pieces, all coherence gone.
JOHN DONNE, “AN ANATOMIE OF THE WORLD”
An Extraterrestrial Age
It will perhaps come as no surprise that even the elimination of its most vocal proponent failed to do away with the cosmology of an infinite universe and its infinite worlds. To be sure, Giordano Bruno’s execution in 1600 encouraged a degree of caution for a number of decades, especially among Catholic scholars on the Continent, but for the most part the seventeenth century witnessed a veritable explosion of treatises concerning the existence of other worlds.1 This explosion can be attributed in part to the exceedingly public nature of Bruno’s trial and execution, which arguably circulated Bruno’s heretical cosmology more widely than it would have been otherwise and which lent to it a certain harrowing caché.2 Even more significantly, this fascination with the possibility of other worlds was fomented by the publication in 1610 of Galileo’s telescopic discoveries.3 In them lay the observational proof that the earth was just one of many planets orbiting the sun. Karl Guthrie therefore credits Galileo Galilei (1564–1642) with having lit the fire of seventeenth-century “pluralism,”4 explaining that “the lay public was not sufficiently convinced by Copernicus’s theory until Galileo had actually seen through his telescope in 1609/10 that the surface of the moon was extremely similar to that of the Earth; that Jupiter was circled not by one moon (like the Earth) but by four, which could only shine on Jupiter’s inhabitants; and that the stars of the Milky Way were suns.”5
Galileo’s success in this regard is clear from the Inquisition’s only having condemned “Copernicanism” six years after the publication of Galileo’s Sidereus nuncius (1610). After the emergence of his Dialogue Concerning the Two Chief World Systems (1632), the Inquisition then tried and convicted Galileo himself, placing him under lifelong house arrest and his writings on the burgeoning Index of Prohibited Books.6 In spite of the church’s best efforts, however, this sentencing only intensified the anxious excitement stirred up by Bruno’s fate, an excitement that seems to have been unfazed by Galileo’s abject apology and recantation (“I neither did hold nor do hold as true the condemned opinion of the earth’s motion and the sun’s stability”).7 Apology notwithstanding, the Dialogue had clearly demonstrated the superiority of the heliocentric model, leaving geocentrism all but indefensible. Hence the infamous lore of Galileo’s having recanted his recantation with a softly muttered “eppur si muove”: “and yet it moves.”8
Not incidentally, it was this era that also staged a spirited retrieval of the long-demonized Atomists. With Aristotelian cosmology definitively thrown in the Copernico-Galilean dustbin, the intellectuals of the late Renaissance and baroque periods turned to Lucretius in particular to provide a heliocentrically viable alternative. The resulting neo-Atomist movement, which seems to have had its earliest roots in England’s Northumberland Circle,9 finds its best-known elaboration in the Syntagma (1647) of Pierre Gassendi (1592–1655), a philosopher, astronomer, and Roman Catholic priest who sought to reconcile Epicurus with Christianity.10 His most significant move in this regard was to deny the eternity and infinity of atoms, asserting instead that God had created a finite number of them out of nothing, set them in motion, and used them to form the planets and suns of the universe.11 Strikingly, Gassendi also rejected the Atomist doctrine of a plurality of worlds, calling it both incompatible with scripture and beyond the reach of observational verification.12 In line with Marin Mersenne and the late Scholastics, Gassendi argued that an infinite cause need not produce an infinite effect and that God’s omnipotence is reflected not in the volume of his creation, but in his ability to bring it out of nothing.13
Even as Gassendi insisted that “this world is the only one,” however, he postulated that the other planets in our solar system are most likely inhabited, with the more perfect creatures living close to the sun and the less perfect creatures living farther from it.14 At this point, then, we run into a bit of a semantic difficulty concerning the definition of world. Gassendi denies emphatically that there are other kosmoi, let alone an infinite number of them, but he is happy to assent to the existence of any number of inhabited planets, and many other thinkers (Nicholas of Cusa, for one) would call an inhabited planet a “world.” But this fuzziness is not merely definitional; rather, it serves as an index of a significant conceptual shift among the pluralists of the seventeenth century. During this period, even the scholars who did affirm a “plurality of worlds” were affirming not a plurality of self-contained systems strewn throughout infinite space, but a plurality of inhabited planets orbiting a plurality of suns.15 “Worlds,” in other words, became the specific bodies that could be seen through a telescope.
The invention of the telescope therefore had the duplicitous effect of both extending and narrowing the cosmological vision of western Europe. As it became possible to see all the way out to the craters on the moon and the satellites of Jupiter, the question of “other worlds” was pulled within those observational limits. As a consequence, the meditations on “other worlds” became far more concrete than they had ever been, if no less speculative. Rather than wondering whether worlds were perishable or imperishable or whether one earth might in principle be drawn to the center of multiple kosmoi, the seventeenth-century pluralists wondered whether there was life on the moon or on Jupiter or Mars and what it might look like. This is not to say that such questions had never been asked before—here we might recall Cusa’s brief but spirited catalog of different cosmic residents16—but is simply to say that these residents received new and intensified focus in the seventeenth century. Observationally speaking, this newfound fascination with extraterrestrials was indeed conditioned by Galileo’s construction of an “astronomically useful telescope.”17 But philosophically and even theologically, it had been conditioned a century and a half earlier with Europe’s “discovery” of the Americas.
In his inexhaustible City of God (413–426), Augustine devotes one brief chapter to “the fabled ‘antipodes,’ men, that is, who [are said to] live on the other side of the earth.” From the outset, he insists that “there is no rational ground” for believing that such people exist because scripture tells us that all humanity came from one man, and “it would be too ridiculous to suggest that some men might have sailed from our side of the earth to the other.”18 Although debates on this issue would reopen during the twelfth and thirteenth centuries, the church’s official position for more than a thousand years after Augustine was that “antipodeans” did not exist.19 This teaching was called into question rather dramatically after the voyages of Columbus, and it was finally abolished in 1573 when Pope Paul III declared that the natives of the lands encountered in these voyages could not be enslaved (and could be converted) because they were, in fact, “human.”20 The so-called antipodean debate therefore provided a blueprint for the seventeenth-century pluralists: If humans existed on “the other side” of this planet, what would stop them from existing on other planets as well? This line of reasoning took flight following Tommaso Campanella’s Apologia pro Galileo (1622), which dubs Galileo “the new Columbus” and suggests that it would be as ridiculous to deny the existence of people on other planets as it would be to deny the existence of people in the Americas.21
And sure enough, the unfolding extraterrestrial debate opened a number of anthropological and theological questions that were remarkably similar to those concerning non-European humans. To what extent could the inhabitants of other planets be considered “rational”? Were they less or more intelligent than Europeans?22 Were their bodies like “ours” or different?23 Were they darker, lighter, taller, shorter?24 Were they descendants of Adam or members of some other species entirely?25 Had they fallen when Adam fell, or had they somehow remained sinless? Did Christ save Venusians when he died on a cross on the earth, or would he have to jump from planet to planet to be born again, teach for a while, and die at the hands of some alien Pontius Pilate?26 Could a Lunarian be baptized with the water in a crater on the moon?27 In short, seventeenth-century pluralism both reflected and enacted a massive anxiety over the place of “European man” not only on the globe but throughout the universe, the vast expanse of which threatened to render him insignificant.
A distraught John Donne gave voice to the state of things in “An Anatomie of the World” (1611):
And new Philosophy calls all in doubt,
The element of fire is quite put out;
The sun is lost, and th’earth, and no mans wit
Can well direct him where to looke for it.
And freely men confesse that this world’s spent,
When in the Planets and the Firmament
They seeke so many new; they see that this
Is crumbled out againe to his Atomies.
’Tis all in peeces, all cohaerence gone;
All just supply and all Relation.28
For Donne, the Atomist revival was shattering the cosmos, “crumbling” the heavens into particles, and leaving humanity without any solid point of orientation: “The sun is lost,” he mourns, “and th’earth.” A similar anxiety surfaces half a century later in Blaise Pascal’s Pensées. Contemplating humanity’s position between the endlessness revealed by the telescope and the endlessness revealed by the microscope, Pascal confesses, “The eternal silence of these infinite spaces terrifies me.”29 In the French, this infamous utterance is followed immediately by the exclamation, “How many kingdoms know us not!” Here we might remember Alexander the Great weeping when he learned of “the infinity of kosmoi” or Thomas Aquinas worrying that an infinite world would compromise the integrity of an infinite God (see chap. 2, sec. “Accident and Infinity,” and chap. 3, sec. “Ending the Endless”). For better or worse, cosmic infinity always seems to undermine sovereignty—whether human or divine.
“The World and Its Prisons”: The Curious Case of Johannes Kepler
Provoked by the telescopic unfolding of “these infinite spaces,” the cosmological writings of the seventeenth century display a dizzying combination of anthropological fascination, existential revulsion, scientific restraint, and theological innovation. Such a combination is perhaps nowhere more apparent than in the work of Johannes Kepler (1571–1630), who is best known for his three laws of planetary motion. The first of these laws is that planets orbit the sun in ellipses rather than circles. This discovery improved the predictive power of Copernicanism dramatically, establishing Kepler as something of a heliocentric hero. His position on cosmic plurality, however, was complicated. On the one hand, he shared his pluralist contemporaries’ conviction that the earth was not the only inhabited planet in the solar system; he even wrote a fictional account of a journey to the moon called Somnium, which imagined and cataloged numerous species of lunar creatures.30 On the other hand, Kepler refused to speculate about life beyond our solar system or even about solar systems beyond our solar system, insisting that our sun occupied the center of a finite universe, bounded by a ring of fixed stars.
For this reason, Kepler was disinclined to trust “the speculations of the Cardinal of Cusa” and was downright horrified by the “dreadful philosophy” of “the unfortunate [Giordano] Bruno,” who had “made the world so infinite that [he posited] as many worlds as there are fixed stars.”31 Faced with such a prospect, Kepler went so far as to express sympathy for Aristotle, who may have been wrong about the position of the earth, but who was right, he said, to demolish the Atomists’ execrable infinity of worlds. Anticipating the sentiments expressed by Donne and Pascal, Kepler wrote that “the very cogitation [of infinite worlds] carries with it I don’t know what secret, hidden horror; indeed one finds oneself wandering in this immensity, to which are denied limits and center and therefore all determinate places.”32 In order to close down the “immensity” that Bruno had reopened, Kepler suggested that one could always appeal to scripture, which never mentions any worlds other than our own. Yet he cautioned that, in essence, “the question we are discussing is not a dogmatic one,” and so the problem of Bruno’s “immeasurabilities” would have to be “dealt with … by scientific reasoning.”33
Kepler executed this scientific reasoning along two major lines. First, he attacked the cosmic homogeneity that Bruno’s infinite universe implied. As we will recall from Cusa and Bruno alike, an unbounded universe has no absolute center or periphery. Rather, every place looks like every other place, such that the inhabitants of any planet would see themselves at the center of the universe, surrounded by a dense ring of stars. But Kepler countered that observation had shown this not to be the case: of all the stars in the sky, he argued, our sun appears to be brightest, and therefore (according to his own interpretation of Galileo’s findings) it is the largest. Because all other stars are smaller than our sun, the view from anywhere else in the universe would be totally different from ours.34 We must therefore live in an immense cavity in the sky: a unique clearing in which a few planets orbit this one brilliant sun, surrounded by a shell of stars. And because these stars cannot be said to be suns—because, in fact, “the body of our Sun is brighter beyond measure than all the fixed stars together”—Kepler was able to conclude that “this world of ours does not belong to an undifferentiated swarm of countless others.”35 In effect, he countered Bruno’s neo-Epicureanism with a modulated dose of early Stoicism: the world for Kepler was a singular, bounded whole in the midst of a giant void. The modulation, of course, was that this universe would neither disappear in fire nor reemerge from it; both temporally and spatially, the Keplerian cosmos must be unique.
Kepler’s second approach to reigning in Bruno’s cosmology was simply to insist that astronomy must limit itself to observable phenomena. An infinity of other worlds is in principle unobservable, he maintained, and therefore of no scientific use.36 In De stella nova (1606), Kepler therefore expressed the fervent wish that “Astronomy herself” might cure “this madness of the philosophers” by limiting “her” imagination to the visible and the measurable. Only proper scientific restraint could bring an errant philosophy “back within the bounds of the world and its prisons…. Surely,” he cautioned, “it is not good to wander through that infinity.”37 Nevertheless, by allowing observation to maintain the walls of the cosmic “prison,” Kepler also allowed observation to move or demolish those walls. He knew this, of course, and had been particularly worried that four recently discovered “planets” might be seen to orbit one of the fixed stars—in which case the fixed stars might indeed be “suns” in their own right.
To Kepler’s relief, this was not the case: in 1610, Galileo reported that all the new “planets” he had seen were moons of Jupiter. Just a few months later, an exuberant Kepler exclaimed in a written response to Galileo, “I rejoice that I am to some extent restored to life by your work. If you had discovered any planets revolving around one of the fixed stars, there would be waiting for me chains and a prison among Bruno’s innumerabilities.” Perhaps realizing how inapt this metaphor was (after all, the Stella nova had commended the “prisons” of the bounded cosmos), Kepler immediately reversed it: “I should rather say, exile to [Bruno’s] infinite space. Therefore, by reporting these four planets revolve, not around one of the fixed stars, but around the planet Jupiter, you have for the present freed me from the great fear which gripped me as soon as I heard about your book.”38 For the present, Kepler was free to be confined within a singular and finite cosmos. For the present, he would not have to think about anything he could not observe.
Well, not quite “anything.” As Karl Guthrie has shown, Kepler added an appendix to his cosmic travelogue Somnium well after he had learned about Galileo’s discoveries.39 And although Galileo himself had considered “false and damnable the view of those who would put inhabitants on Jupiter, Venus, and the Moon,”40 Kepler used the occasion of Galileo’s observations to offer even more details about the many varieties of Lunarians—whom no one had ever seen. Even more puzzlingly, the young Kepler in particular indulged in some remarkably constructive theologizing, finding in his rebounded cosmos a perfect image of the Trinity. As the central and brightest body in the universe, as the source of its light and life, the sun was for Kepler the created image of the Father. The fixed stars on the periphery could be said to embody the Son. And the interstellar space between them, “the relationship between the point and the circumference,” reflected the Holy Spirit.41 As it was for both Bruno and Cusa, then, the universe for Kepler was the created expression of God Godself. Yet thanks to an intricate implication of existential panic, ecclesiastical bullying, and scientific rigor, Kepler fled the infinity of Bruno and the boundlessness of Cusa, contracting even the contracted universe back into a stubbornly finite cosmos.
His trinitarian vision notwithstanding, what we begin to see in Kepler is a new disciplinary separation between scientific and humanist approaches to cosmology. As Steven Dick has shown, the question of a plurality of worlds began to move in the mid-seventeenth century out of the realm of astronomy and “into the domain of philosophical explorations, both secular and religious.”42 Strikingly, the “religious” branch of this philosophical inquiry generated far less drama in the second half of the seventeenth century than it had during the time of Copernicus, Bruno, and Galileo. With a few vocal exceptions, it simply became commonplace to assert that a universe filled with inhabited cosmic bodies was more befitting of an omnipotent God than one lonely planet or solar system would be.43
Chief among these vocal exceptions was Walter Charleton (1619–1707), whose neo-Epicurean Physiologia (1654) not only denies any plurality of worlds but even suggests that “Democritus and Epicurus” themselves never taught such a thing, “proposing it as a necessary Hypothesis” rather than as a cosmic reality.44 Charleton raises a number of objections to this doctrine in the Physiologia, but they can for all intents and purposes be grouped into two: first, he finds the notion theologically offensive, and, second, he thinks it an affront to reason. Everyone agrees, Charleton begins, that God could have created worlds apart from this one. But to claim that God has done such a thing would be downright blasphemous. To say, for example, that there are more atoms in creation than were needed to compose this world would be to imply that God does not know how “to proportion the quantity of his materials to the model or platform of his structure.” And to say that there is an infinite “Residue” of such material would be to imply that God’s creation is somehow “equal to Himself” and, consequently, that God has “an Imperfection in his Nature.”45
We have already heard both of these arguments in defense of the singularity of God. The line of attack more unique to Charleton, on which he spends far more time, concerns the unreasonableness of the doctrine of a plurality of worlds—a charge that will be leveled against modern multiverse theorists (see conclusion). According to Charleton, it simply makes no sense to posit other worlds beyond our own; there is no reason to do such a thing. He admits that both cosmic pluralists and cosmic monists lack observational evidence that might support their positions; there is no way to see that the world is either unique or one of many. But Charleton finds this inability all the more reason to affirm the “Unity of the world”; in the absence of evidence, he argues, the monists ground their position “upon that stable criterion, our Sense,” and the pluralists “found theirs upon the fragil [sic] reed of wild Imagination.”46 To make matters worse, the pluralists spend so much time attending to invisible worlds that they fail to understand the one world that they can see. Charleton finds it painfully ironic that “there were whole Schools of Philosophers, who fiercely contended for a Plurality of Worlds, when, indeed, their Understandings came so short of conquering all the obvious Difficulties of this one, that even the grass they trod on, and the smallest of Insects, a Handworm, must put their Curiosity to a stand.” To anyone who might feel seduced into cosmic pluralism, Charleton therefore prescribes a “Remedy.” Contemplate the handworm, he suggests, or a dandelion or the motion of leaves in the wind: “The most inquisitive may find Difficulties more than enough within the Little World of their own Nature”; what is more, their efforts “will prove more advantageous to the acquisition of Science, then [sic] the most acute metaphysical Discourse.”47
In Charleton, then, we see a remarkable concordance between a particularly Scholastic style of conservative theology and an early modern scientific commitment to observation and common sense. When it came to the question of a plurality of worlds, the new scientists followed a very similar approach, resolving along with Kepler to “avoid the march to the infinite.”48 In the meantime, a new breed of Brunian theologians and philosophers joyfully entertained what they regarded as an unproblematic proposition: an infinite God can be glorified only in an infinite number of worlds. Strikingly, then, “sacred” and “secular” attitudes toward cosmic multiplicity swapped places in the seventeenth century: the new theology began to revel in the pluriversal glory of God, whereas “Astronomy herself” remained confined—from the second half of the seventeenth century to the second half of the twentieth—to the one world that astronomers could measure and see. Nevertheless, the growing philotheopoetic body of cosmic pluralism was not without scientific grounding. Even as the infinite worlds of “mad philosophy” were reviled by figures such as Kepler and Charleton, they found rational support in the cosmology of René Descartes.
The Ambivalent Pluralist: René Descartes
In the British Isles and on the Continent alike, the latter half of the seventeenth century produced an increasing number of “pluralist” treatises, the majority of which were to some degree based on the cosmology of René Descartes (1596–1650).49 By all accounts, this Cartesian-inspired pluralism reached its apex in the flamboyant prose of Bernard le Bovier de Fontenelle (1657–1757), whose immensely popular Conversations on the Plurality of Worlds (1686) proclaims an infinite number of solar systems inhabited by a staggering variety of creatures.50 These conversations, addressed to a “Marquise de G***,” are presented in plain (if melodramatic) prose so that even women might understand them (“I only ask of the ladies,” Fontenelle writes in the preface, “for this whole System of Philosophy, the same amount of concentration that must be given to the Princess of Clèves”).51 The Dutch astronomer Christiaan Huygens (1629–1695) offers a similarly delightful journey through multiply inhabited planets in the popular, posthumously published Cosmotheoros (1698).52 Having made his way from the earth to the other planets and moons in our solar system and then to the (most likely infinite) multitude of orbited suns beyond it, Huygens exclaims, “What a wonderful and amazing scheme have we here of the magnificent vastness of the universe! So many suns, so many earths, and every one of them stocked with so many herbs, trees, and animals, and adorned with so many seas and mountains! And how must our wonder and admiration be increased when we consider the prodigious distance and multitude of the stars!”53 Like Fontenelle, Huygens grounds his ecstatic journey through the ranks of an infinite universe in Descartes’s “vortex” theory.54 What is strange about calling either of these works “Cartesian,” however, is that Descartes himself either avoided or denied each of his own theory’s most thrilling cosmic implications. He would never say whether he thought there might be life on other planets,55 he refused to call the universe “infinite,”56 and he said quite explicitly that “there cannot be a plurality of worlds.”57 Nevertheless, his universal theory of “vortices” seemed to indicate otherwise.
In a letter to none other than the anti-Brunian Marin Mersenne, Descartes wrote, “I have resolved to explain all the phenomena of nature, that is, all of physics.”58 The year was 1629, Descartes was thirty-three years old, and he had just begun working on a book he would come to call Le monde, ou Traité de la lumière (The World, or a Treatise on Light). This book, which sets forth a full heliocentric cosmology and cosmogony (Stephen Dick calls it the “first complete physical system … since Aristotle”),59 took Descartes far longer to complete than he had expected it to. As he explained to Mersenne, he was plagued by concerns not only that his physics might be wrong, but also that his theology might be poorly received—especially his conviction that once matter is created, it goes on to form a world with no further help from God.60 Descartes therefore resolved to publish the treatise anonymously, “principally because of theology, which has been so subjected to Aristotle that it is almost impossible to set out another philosophy without its appearing at first contrary to faith.”61
But just as Descartes had finally completed the manuscript in 1633, he learned that Galileo had been placed under house arrest, his books condemned and burned. In a letter to Mersenne that never reached its destination, Descartes wrote, “[T]his has so astonished me that I am almost resolved to burn all my papers, or at least not to let anyone see them.”62 Although Descartes had foreseen the controversy that his cosmology might generate concerning God’s function in the universe, it seems that he had not known how staunchly opposed the church remained to heliocentrism, on which his little treatise depended entirely: “I confess that if [the motion of the earth] is false, all the foundations of my philosophy are also…. It is so linked to all parts of my treatise that I cannot detach it without rendering the rest completely defective.”63 And so the manuscript was suppressed until after Descartes’s death in 1650. Nevertheless, he managed to scatter some of its central ideas throughout the formally dry, almost neo-Scholastic Principia philosophiae (Principles of Philosophy, 1644), thereby circulating an attenuated version of his vortex theory while he was still alive.
Descartes’s first major cosmological move in the Principia is to sidestep the Brunian controversy over infinity by returning to the Cusan solution. “We should never enter into arguments about the infinite [numquam disputandum esse de infinito],” he writes; “things in which we observe no limits—such as the extension of the world, the division of the parts of matter [partium materiae], the number of the stars, and so on—should instead be regarded as indefinite [pro indefinitis habenda].”64 Descartes insists on this distinction not only in the Principia, but also in the controversial Le monde and throughout his written correspondence—most notably with the enthusiastic English pluralist Henry More, who tried at length to convince him to abandon it.65 Depending on the context, Descartes offers one of two different reasons for maintaining that the world is indefinite rather than infinite. The first is theological: in short, it allows Descartes “to reserve the term ‘infinite’ for God alone”;66 here he reminds us of Thomas’s distinction between a limitlessness that is strictly “privative” and one that is fully “negative” (although Descartes somewhat confusingly calls the negative infinity “positive”). The second reason is epistemological: to call the world and its matter “indefinite” is to say that we do not know how to ascribe limits to them. “Whether they are simpliciter infinite or not,” he wrote to More, “I confess not to know. I only know that I do not discern in them any end.”67 This may sound like a kind of Cusan ignorantia, but Descartes has no desire to call the universe (or anything else) unknowable. Rather, this admission of nonknowledge becomes for Descartes the condition of knowledge: it is only when we admit that we do not know about infinity that we will refrain from getting lost in it, stand on determinate ground, and gain certainty about everything else.
It is this epistemological strategy that Descartes is employing in Le monde when he invites us to imagine with him the creation of a world. A signal of how long it has been since western Europe has had a proper cosmogony, Descartes prefaces his own by hearkening back to Plato. “In order … to make the length of this discourse less boring for you,” he begins, “I want to wrap part of it in the cloak of a fable [dans l’invention d’une fable].”68 Much like Timaeus, Descartes offers us a “likely story.” In this newer fable, however, the storyteller is also the demiurge. “For a short time,” he entreats us, “allow your thought to wander beyond this world to view another, wholly new one, which I shall cause to be born [que je feray naistre] before you in imaginary space” (49, translation altered, emphasis added). Lest we get lost in this imaginary space, however, Descartes is careful to circumscribe its limits: “In order that infinity not impede us and not embarrass us, let us not try to go all the way to the end; let us enter only so far in that we can lose from view all the creatures that God made five or six thousand years ago and [stop] there in some fixed place [en quelque lieu déterminé]” (51). We seem, then, to be back behind the biblical creation, with nothing more than Descartes, ourselves, and a finite, “fixed place.”
For the sake of having a place to start, we can think of this “fixed place” as place itself: the place in which the world will come to be. Here, again, Descartes reminds us in Le monde that it will do no good to think of this place as infinite, proposing instead that we “purposely [à dessein] restrict it to a determinate space that is no greater, say, than the distance between the earth and the principal stars of the firmament” (51). And as we have already seen, restricting ourselves to a determinate space is, for Descartes, the condition for our knowing anything about the world at all. In fact, he suggests, because “we” are making this cosmos in the first place, we can just declare that “there is absolutely nothing” about it “that anyone cannot know as perfectly as possible” (51–53). So we have a very large but perfectly comprehensible place, and this place constitutes the most primitive state of the cosmos. Crucially, however, this state is not empty. Rather, our determinate place is filled with “the matter that God shall have created … out to an indefinite distance” (51, emphasis added).
This little passage is doing an extraordinary number of things. First, it suddenly reintroduces God, who is absent from the beginning of the story and then is excised as soon as he is mentioned. In fact, the story begins and rebegins with nothing more than Descartes, our imaginations, and a fixed place. As the story develops, however, Descartes concedes that it cannot begin at the beginning because it must assume that God “shall have created” matter already along with the space that it occupies. Theologically, this concession allows Descartes to suggest (although he never actually says it) that God created matter out of nothing. Literarily, it allows him to begin right where Timaeus begins: with a demiurge (in this case, Descartes) who finds a disordered material already there. And, epistemologically, it saves Descartes from preemptive ruin by giving him some precosmic material, for, in the words of two twenty-first-century cosmologists, “there are no rigorous physical principles that dictate how to go from ‘nothing’ to ‘something.’”69
Second, this passage repudiates the Atomist void, indicating that there is no “place” without matter—no time when space will not already have been filled. This is to say, as Descartes explains in the Principia, that “there is no real distinction between space … and the corporeal substance contained in it.”70 For even if we were to remove a stone from a place, we would not thereby remove the extension of the place itself, and anything extended is material. In terms of his cosmogony, then, Descartes is beginning not with a void—the very notion of which he calls “a contradiction” insofar as there is no difference between matter and space71—but with a “plenum,” a space so “filled” with matter that it is matter itself.
Third, with no void, there can be no atoms moving within it. This is another point that Descartes clarifies in the Principia: no unit of matter is indivisible (a-tomos). “For if there were any atoms,” he reasons, “then no matter how small we imagined them to be, they would necessarily have to be extended; and hence we could in our thought divide each of them into two or more smaller parts.”72 In other words, insofar as “an indivisible unit of matter” is already the product of our imagination, the very fact that we can imagine dividing it amounts to its divisibility. Besides, Descartes adds, even if there existed a particle so small that no human could divide it, God could divide it, and so it would be in principle divisible.73 As it was for Aristotle, then, matter for Descartes is infinitely divisible—or as he scrupulously phrases it, “indefinitely divisible.”74 By rejecting atoms as well as the infinite, however, Descartes ironically allows himself to configure matter in units that are genuinely discrete. As we may recall from Bruno in particular, nothing infinite can be divided into real parts; rather, any “part” of the infinite must itself be infinite. Hence Bruno’s (and Cusa’s and even Lucretius’s) total holography: if creation is infinite, then “all things are in all things”—the universe in a grain of sand or, for that matter, in an atom. Such a riot of in(ter)distinction will clearly not do for Descartes, whose “things” must be clear and distinct. Therefore, his units of matter are not “atoms,” but “parts” or “particles” (parties); his universe not infinite but indefinite.
This distinction leads to the final implication of the same short passage, which is that the “matter that God shall have created” in (and as) our “fixed space” extends “to an indefinite distance.” Now it seems here that Descartes wants conflicting things. On the one hand, he insists that the “place” we are imagining is “determinate”; on the other hand, he says that it is indefinite. So either Descartes is contradicting himself, or he is suggesting that the indefinite is determinate—that the indefinite, unlike the infinite, can be clarified, distinguished, and known. Hence the discrete “parts” rather than the holographic atoms. Moreover, the indefinite extension of matter prevents any hypothetical Atomist or even Stoic from suggesting that there might be a void beyond Descartes’s fixed place. To say that the plenum extends indefinitely is to say that there is no outside, that the plenum is what there is. And, of course, this is the reason “there cannot be a plurality of worlds”: because there is nowhere else for them to be.75
To return to our fable in Le monde, then, Descartes has taken us to his cosmic primordium: a determinate, indefinite, corporeal space. This is the Cartesian “chaos” (cahos), but our demiurge insists that it is a perfectly comprehensible chaos. In fact, “there is nothing simpler nor easier to know among inanimate creatures,” for whereas our knowledge of all other bodies relies on the famously unreliable faculty of sense perception, our knowledge of “the matter from which I have composed the chaos” relies on intellect alone (55). All we need to do, then, is to subtract the qualities we know through sense perception—such as wetness and heat and color and light—and assume the chaos to be bare extension itself: “Let us [then] conceive of it as a real, perfectly solid body, which uniformly fills the entire length, breadth, and depth of the great space at the center of which we have halted our thought” (53). A body with no qualities might seem hard to imagine, but Descartes assures us that it is not. In fact, precisely because it possesses no qualities, he claims, this chaos is clearer and more distinct than anything we can see, smell, or taste. Or, as he puts it here, “chaos contains nothing that is not so perfectly known to you that you could even pretend not to know it” (55).
How, then, does a solid lump of chaos become a cosmos? Descartes backtracks again: it turns out that we need a bit more from God. In order to imagine that unqualified matter can form a world, we must also assume that when God creates the material, he divides it into parts (parties) of different size and shape and that he sets these parts in motion, making “some begin to move in one direction and others in another, some faster and some slower (or indeed, if you wish, none at all)[.]” “[T]hereafter,” Descartes concludes, “he makes them continue their motion according to the ordinary laws of nature” (55). At this point, then, God can leave the scene, for once he “so wondrously establishes” these laws, they will be “sufficient to make the parts of that chaos untangle themselves [se démélent d’elles mesmes] … [into] a most perfect world” (55).
This is how it works: because there is no such thing as empty space, the chaos particles that God will have made must “touch one another on all sides, without there being any void in between” (60). This means that they cannot move in a straight line, as they would otherwise “naturally” do, and so must begin to move in circles instead, forming a vortex (tourbillon) (71, 79). But because God also made these particles distinct from one another, endowing them with different types of motion, “we should not imagine that they all came together to turn around a single center,” forming one vortex alone. Rather, the particles begin to collect “around many different [centers], which we may imagine to be diversely situated with respect to one another” (79–81). The centers of Cartesian vortices, unlike those of Democritean vortices, are occupied by the lightest particles, which are most “agitated” and therefore move in the tightest circles. They are then held in place by the heavier particles, which move in slower circles around them and whose sheer bulk prevents the light particles from moving toward the peripheries (81–83, 109–11). And once the different kinds of particles have winnowed out in this manner, they have become the three basic elements that Descartes discerns in the cosmos. The lightest particles become the “luminous element” that composes the stars; the heaviest particles constitute the “opaque element” that composes the planets; and the “middling” particles form the “transparent element” that fills the heavens: “the element of air” (37–39). Each vortex, in other words, becomes a solar system, whose planets orbit a central star through a vast expanse of space.
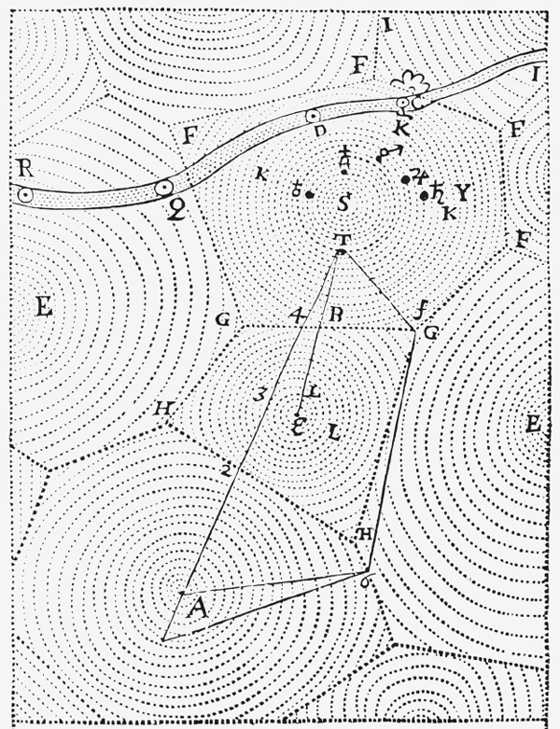
Even in this state, however, space is never empty, and so the vortices are not exactly separate. Rather, they border one another by means of a “surface without thickness,” which Descartes calls the “firmament” (87). As we can see in figure 4.1, the firmament (the line stretching from H to H, for example) is a permeable membrane, and so bodies can travel between vortices. Most of these traveling bodies are the phenomena we call “comets” (see the river-shaped path at the top of the image). Furthermore, the permeability between vortices means that the sun of one vortex can be seen from the planets of other vortices. This explains why the residents of the earth can see so many stars: each of the stars in “our” sky occupies the center of its own vortex. Descartes’s hesitations and protestations notwithstanding, then, one can begin to see why his vortices became so popular among his pluralist contemporaries—and why they were quickly condemned in the French universities. Although Descartes might have maintained that this indefinite expanse of things is the only indefinite expanse of things, he also filled it with innumerable systems, each revolving around a center resembling our sun.76 And for this reason, even as he insists that there is only one “world,” Descartes imagines, as he tells us in Le monde, that “there are as many heavens [cieux] as there are stars, and, since the number of stars is indefinite, so too is the number of the heavens” (87). This brief gesture toward the vast plurality of the universe, along with the instability of the term indefinite, set Fontenelle, Huygens, and their enthralled audiences wondering: What sort of plants, animals, atmospheres, and astronomers might inhabit such an “indefinite” number of worlds? The possibilities seemed infinite.
Grace and Gravity in Isaac Newton
As history would have it, however, the craze over Cartesian cosmology was as short-lived as it was fervent. Just one year after the appearance of Fontenelle’s Cartesian Conversations, Isaac Newton (1642–1727) published Principia (1687), whose synthesis of Galileo’s physics and Kepler’s orbital laws left Descartes’s vortices in ruin.77 In this work, Newton offers his Law of Universal Gravitation, which says, first, that the force keeping planets in orbit is the same as the force keeping our feet on the ground, and, second, that the magnitude of this force is determined by the mass of bodies and the distance between them (F = gMm/r2).78 Against Descartes, then, Newton showed that bodies need not touch one another to influence one another. In fact, he argued, a seamless fabric of particles such as those Descartes describes would prevent planetary motion altogether. In order for bodies to remain in orbit, gravity must pull them through empty space.79 Newton therefore reinstated the distinction that Descartes had abolished between matter and space, arguing that “absolute space” is an inert, extended background through which objects may or may not move. Similarly, he insisted, “absolute time” flows universally and inexorably, “without regard to anything external.”80
Gottfried Leibniz (1646–1716) rigorously contested Newton’s “absolute” view of space and time, insisting that these terms were just descriptions of relations between objects. Space and time, Leibniz argued, have no independent existence; they are, as he wrote to the Newtonian Samuel Clarke in 1716, “purely relative” to each other and to the matter “within” them.81 As we will see in chapter 5, Leibniz’s more Cartesian view would be vindicated two hundred years later by Einstein’s theory of general relativity, which, according to the Times article that broke the story, rendered “Newtonian ideas overthrown.”82 In the meantime, however, “Newtonian ideas” had won: Newton’s absolute matrix was far more commonsensical than Leibniz’s odd relations, and at the scales to which Newton was confined, it worked.83 Although Newton infamously had no idea what gravity was (he steadfastly refused to formulate such a “hypothesis”),84 he could predict its behavior with remarkable accuracy. By the end of the seventeenth century, then, Newton’s principles had become entrenched as the new laws of cosmic motion.
Frustratingly for many would-be Newtonians, however, Newton never provided a cosmogony, primarily because he believed that the laws he had discovered were insufficient to such a task. Gravitation alone could neither create nor sustain the universe. This insufficiency comes across most clearly in the four letters that Newton wrote in the winter of 1692/1693 to Richard Bentley, a Cambridge theologian in the process of delivering a lecture series titled “A Confutation of Atheism.” Bentley was convinced that Newtonian mechanics provided the most helpful combination of “natural laws” and “supernatural acts”; in other words, Newton’s laws constituted scientific proof of the existence of an extracosmic God.85 Newton opened his first letter with an enthusiastic endorsement of such a project: “[N]othing,” he wrote, “can rejoice me more than to find it useful for that purpose.”86
And, indeed, over the course of the letters to Bentley, Newton uncovered three significant gaps in his gravitational theory—gaps that, he believed, could be filled only by appealing to God. The first concerns the division of matter “into two sorts”—that is, “shining” and “opaque,” or stars and planets. Are the two substances created differently from the outset? Do shining bodies begin as opaque but then light up through some mysterious process along the way? “I do not think [the two types of matter] explicable by meer [sic] natural causes,” Newton professed, “but am forced to ascribe it to the counsel and contrivance of a voluntary agent…. Why there is one body in our solar system qualified to give light and heat to all the rest, I know no reason, but because the author of the system thought it convenient.”87
The second Newtonian phenomenon that requires a divine supplement, we learn, is planetary motion itself. Under the influence of gravity, Newton explained to Bentley, matter is attractive. So gravity alone can account for the planets’ movement toward the sun, but not for their movement around it; in fact, left to its own devices, gravity would cause all the opaque cosmic bodies to crash into the shining one. So “gravity may put the planets in motion,” he reasoned, “but without the divine power it could never put them into such a circulating motion as they have about the sun.”88 Orbital motion, he concluded, requires an “intelligent agent.”
Finally, assuming that the “fixt stars” are bodies akin to our sun and that they may or may not have their own systems of planets and moons miraculously processing around them, Newton found it remarkable that they all were sufficiently far apart from one another to avoid attracting one another. Much as unassisted gravity would cause the planets to crash into the sun, it would also cause the suns to crash into one another, forming one giant “mass” of shining material. Something, then, must have separated these systems from the outset and must continue to keep them separate. This “something,” interestingly enough, is not only or even primarily God. Rather, the first principle Newton invoked to save the universe from gravitational collapse is infinity.
Cosmic infinity is, in fact, the matter with which Newton opened his first letter to Bentley. If the cosmos were finite, he began, then “the matter on the outside of this space would by its gravity tend towards all the matter on the inside, and by consequence fall down in the middle of the whole space, and there compose one great spherical mass.”89 What Newton was envisioning here is similar to the phenomenon that twentieth-century physicists would come to call a “big crunch”—except that for Newton, space itself would remain extended throughout such an event, whereas for the post-Einsteinian (and neo-Leibnizian) tradition, a “big crunch” would draw space-time itself into a gravitational collapse. At any rate, Newton had come to believe that if the cosmos were finite, gravity would cause all the matter in the universe to implode.90 If, however, the universe were infinite and homogeneous—if space and matter were to extend forever—then “it would never convene into one mass, but some of it would convene into one mass and some into another, so as to make an infinite number of great masses, scattered at great distances from one another throughout all that infinite space.”91 In this brief passage, one can detect the sketchy beginnings of a cosmogonic narrative: once God has created, distinguished, and distributed matter throughout an infinite universe, gravity draws the opaque bodies toward the shining ones. But, again, Newton never pursued this line of thinking. His central concern was rather to establish cosmic infinity as a kind of outward “push” to counteract the gravitational “pull.” Once the fixed stars are created, however they are created, they never collide because they are equally attracted to one another in all directions forever.
The infamous atheist Edmund Halley (1656–1742), Newton’s friend and collaborator, attested that this explanation does, in fact, ensure the noncollapsing nature of the cosmos. As Halley explained it, “[I]f the whole be infinite, all the parts of it would be nearly in equilibrio, and consequently each fixt star, being drawn by contrary powers, would keep its place; or move, till such time, as … it found its resting place.”92 For Newton, however, Halley’s “nearly” amounted to impending chaos; as he went on to explain to Bentley, an infinite universe would be highly unstable and would remain in equilibrium only if each component of the universe were not “nearly” but absolutely equally attractive, in all directions, forever. Absolute stability, however, is difficult to attain; as Newton confessed, “I reckon this as hard as to make not only one needle only, but an infinite number of them (so many as there are particles in infinite space) stand accurately poised upon their points.” So it is here that he appealed, once more, to God. It is impossible for gravity alone to keep the cosmic bodies balanced on their needle points, “yet I grant it possible, at least by a divine power; and if they were once to be placed … they would continue in that posture without motion for ever, unless put into new motion by the same power.”93
In sum, then, Newton appealed to God in order to account for the creation, distribution, and repulsion of matter—the same functions for which Descartes appealed to God. Unlike Descartes, however, Newton believed that God was required to keep the cosmos in balance. Whereas Descartes was happy to call God onto the stage at the beginning and then push him off for the rest of the cosmic show, Newton thought that the laws of nature could not function on their own; in particular, they depended on God to intervene periodically and correct irregularities. This was another point on which Leibniz would disagree vehemently with Newton: “[A]ccording to [his] doctrine,” Leibniz chided Clarke, “God Almighty needs to wind his watch from time to time, otherwise it would cease to move. He did not, it seems, have sufficient foresight to make it a perpetual motion.”94 But, again, theology was not Newton’s primary or even secondary concern (it is telling, for example, that he delegated to Clarke the responsibility of debating these points). And considering how reluctant he was to imagine the origins of this world, Newton certainly had no desire to imagine the birth of other worlds. He did briefly entertain the notion in his penultimate letter to Bentley that “there might be other systems of worlds before the present ones, and others before those and so on to all past eternity.”95 There might, in other words, be Stoic cycles built into the infinite, quasi-Epicurean universe. But just like the rest of Newton’s cosmological principles, such cyclicality could be accomplished only by God: “[T]he growth of new systems out of old ones, without the mediation of a divine power, seems to me apparently absurd.”96
Although Newton did not write a cosmogony, then, he opened the possibility of such a thing through his brief references to an infinite universe filled with infinite worlds—worlds, moreover, that might undergo periodic destruction and re-creation. And although a number of astronomers and theologians, including Bentley himself, would go on to explore these tenuous openings,97 the most extravagant Newtonian cosmogony would emerge in the early writings of Immanuel Kant.
Failure to Launch
Published anonymously when Immanuel Kant (1724–1804) was thirty-one years old, the Universal Natural History and Theory of the Heavens (1755) announces itself as “an essay on the constitution and mechanical origin of the whole universe [Weltgebäude], treated according to Newtonian Principles.”98 In the words of the philosopher Milton Munitz, this book “ventures where Newton feared to tread,” offering a full cosmogony based on the law of gravitation: a Newtonian replacement for Descartes’s demolished vortices.99 Unlike Descartes’s cosmogony, however, Kant’s was almost completely unknown in his own time. Just after printing the Natural History, his publisher went bankrupt and was forced to impound all the unsold copies. A year later, the book was reprinted under Kant’s own name and dedicated to Frederick the Great, but neither the king nor anyone else seemed to notice. Johann Lambert (1728–1777) had not even heard of Kant’s Natural History when he published many similar (and many different) ideas in Cosmologische Briefe (1761); and even after Lambert’s book gained a degree of recognition, Kant’s did not.100
As Munitz has written, the Natural History “had to wait for more than a century for its true greatness to be appreciated.”101 And appreciated it has been: it is now not uncommon to hear Kant’s early theory hailed as “the first scientific cosmology”—a cosmology, moreover, that anticipates “the essence of modern models.”102 But, of course, not everybody shares this view. The book is almost never taught in philosophy or history of science curricula, and there is painfully little secondary material on it—especially compared with the vast body of work on Kant’s three critiques, Religion Within the Limits of Reason Alone, and late essays.103 Perhaps the book’s most trenchant modern critic has been Stanley Jaki, who in a lengthy introduction to his own translation of the Natural History charges Kant with displaying a “tenacious amateurism” in physical science, indulging in “willful and confused speculations,” and “constantly referring to Newton without ever studying him seriously.” In short, Jaki concludes, “Kant’s parading in Sir Isaac’s cloak [is] a shabby performance,” and whatever modern principles he anticipated are the result of a “lucky guess.”104
But the most likely reason for this text’s continued obscurity is neither that it was ahead of its time nor that it was behind in its science, but that it ventured beyond “the limits of reason alone.” As numerous scholars have noted, the wildly imaginative Natural History of Kant’s youth is not only overshadowed by his later work but invalidated by it.105 After all, the critiques confine our epistemological reach to “phenomena,” things as they appear, whereas the Natural History accounts not only for things as they are, but also for the process by which all things have come to be in the first place. As Kant himself admits in a preface to the work, “[S]uch ideas seem to surpass very far the forces of human reason.”106 And yet, he assures us, “I do not despair. I have ventured, on the basis of a slight conjecture, to undertake a dangerous journey and I already see the promontories of new lands” (81/39).
Atomism, Enlightened
Like any good cosmogonist, Kant starts the Natural History with chaos: “I set the first state of matter [Zustand der Natur] … in the universal dispersion of the basic stuff [Urstoff], or atoms [Atome]” (85/45). And so we are back with the Atomists, to whom Kant is inexorably drawn throughout this work, no matter how fiercely he assails them.107 Their godlessness is loathsome; their principle of “accident,” a joke. Yet “even in the most senseless opinions,” Kant concedes, “one can at times notice something true” (85/45). This, it should be said, is a colossal understatement. The “something true” that Kant can “at times notice” in the Atomists is nothing less than Atomism itself, right up to its infinite universe and infinite worlds. The only significant difference is that the whole thing is set in motion by God and executed according to “necessary laws” (86/46). Kant calls these laws “Newtonian” and offers them as a correction to the “blind concourse” of the Epicureans. Nevertheless, the laws are Epicurean.
To return to our cosmogony, what we have so far is a chaos of uniformly distributed atoms. Kant continues: “Epicurus posited a gravity which drove these elemental particles to sink” (85/45). Here, we might note that Kant is calling to mind the “second” type of Lucretian chaos: rather than a primordial tempestas, we have the downward cascade, what Michel Serres calls the “laminar flow” that pulls atoms down “in a straight line through the void.”108 Kant calls this falling force “gravity” (Schwere) because it “seems not to be very different from the Newtonian attraction [Anziehung], which I assume” (85/45). This, then, is the way Kant will cosmogonize Newton: by mapping gravity onto Lucretius’s laminar flow. As we will recall, however, laminar flow alone will never make a world. The atoms have to “swerve a little.”109 And so Kant borrows from the Epicureans a certain “deviation [Abweichung] from the rectilinear motion of the fall”—even though he calls their account of it “absurd” (85/45). Kant’s swerve will happen not by chance, but by “the repulsive force of the particles [der Zurückstoβungskraft der Teilchen],” which acts in tension with the attractive force of gravity (85/46, translation altered slightly).
Unfortunately for Kant, however, there is no Newtonian equivalent of this “repulsive force”—as we have seen, in fact, this lack was part of what prevented Newton from thinking cosmogonically himself. Gravity accounts for matter’s attraction, but not for its dispersion or rotation, and so as Newton wrote to Bentley, he could never explain how matter “became evenly spread throughout the heavens, without a supernatural power.”110 In this light, Kant’s appeal to a naturally “repulsive force” constitutes a significant deviation from Newton in two senses: it introduces a non-Newtonian law, and that law has nothing to do with a “supernatural power.” But it falls right in line with the Epicureans. In effect, Kant’s repulsive force is none other than the Epicurean “swerve.” And when atoms are subjected to the attraction that makes them fall and the repulsion that makes them swerve, Kant tells us, they form a vortex (Wirbel), and a vortex makes a world (85/46).
Being “Newtonian” (and Epicurean), Kant’s vortices differ significantly from those of Descartes. First, they form not in a gapless plenum, but “in a non-resistant space,” which Kant, himself swerving around the void debate, describes as “completely empty, or at least as good as empty.”111 Second, Kant’s vortices are not the places of solar systems, but the processes that produce them. And third, they form not around the fastest particles, but around the most attractive ones.
Beginning again from the laminar flow, Kant imagines a “point” (Punkt) in the midst of a “very large space … where the attraction of elements … works stronger than anywhere else” (115/89). This most attractive point will draw innumerable atoms toward itself, forming “a body in that center of attraction which grows … from an infinitely small seed” into an increasingly massive core, whose weight draws even more particles toward itself (115/90). As the body grows, it begins to pull particles toward itself from greater and greater distances, at which point even the slightest repulsion between them can “bend” their velocity “sideways,” producing “great vortices of particles [groβe Wirbel von Teilchen]” (116/90). At first, these vortices intersect one another, the flood of particles colliding in different circles through all imaginable planes. But this very conflict gradually brings the particles “into equilibrium” so that they all begin to move in the same direction in “horizontal, that is, parallel-running orbits” around this strongly attractive body at the center, which has become a sun (116/90). The bodies moving in orbits, of course, become the planets, moons, and comets.
Theological Detour
This, then, is the way a solar system comes into being for Kant, and it is striking that God does not seem to figure into the process at all, let alone the particular places that Newton had reserved for God. In his preface to Natural History, Kant explains that this godlessness had been a significant concern from the moment he began the project at hand. If a chaos of atoms can bring itself into perfect order, if “nature is sufficient to herself,” then it seems to have no room for God: “[D]ivine government is unnecessary, Epicurus lives again in the midst of Christendom and an unholy philosophy [Weltweisheit] tramples underfoot the faith which … enlighten[s] philosophy itself” (82/40). This, we may recall, is precisely what Lucretius says Epicurus has done: freed himself from the “crushing weight of religion” to leave it “trampled underfoot.” Such trampling allows Lucretius to travel “beyond the fiery ramparts” of the world to see an infinite number of others,112 and indeed, this seems to be the passage Kant is channeling when he tells us his “dangerous journey” has allowed him to “see the promontories of new lands” (81/39). Finally, just as Epicurus’s journey made him “a god,”113 Kant promises that those “who have the courage to continue the investigation” will “designat[e] with their own names” the lands that they find there—mastering, naming, and in that sense possessing them all (81/39). All this notwithstanding, Kant insists that his account does not do away with the existence of a “highest being” but, to the contrary, proves it.
Kant proves the existence of God not by filling mechanical gaps with the deity, but by demonstrating God’s evidence within the whole cosmogonic process. Impishly, Kant accomplishes this task by using the Atomists’ two antitheistic principles, accident and infinity, against them. In the face of the Atomist doctrine of “accident,” Kant sets forth a straightforward teleological proof (the very one that Lucretius undermines, David Hume ridicules, William Paley reasserts, and Kant himself will dismantle less than a decade after writing the Natural History).114 The order and harmony among the elements of the universe, Kant argues, testify to its having been designed by a supremely intelligent, good, and powerful creator. To the objection that his own physics seems to indicate otherwise, Kant cleverly replies that the very appearance of a lack of design is a proof of design. That is, the sheer fact that a primal cacophony of particles can produce anything at all is “undeniable proof” of their having originated in a brilliant being with a master plan. In short, “there is a God precisely because, even in chaos, nature can proceed in no other way than regularly and orderly” (86/47, translation altered slightly, emphasis in original).115 Kant then goes on to unravel the Atomists’ atheism through their principle of “infinity.” In an infinite universe, Lucretius tells us, everything that can happen will happen, so there is no need to appeal to the gods when asking why things are as they are; rather, everything is bound to happen somewhere, given enough time and space.116 Again, Kant’s response is that this boundless field of possibilities demonstrates precisely what Lucretius thinks it repudiates: the very infinity of creation is “a witness of that power which can be measured by no standard.”117 In other words, nothing but an infinite cause could produce an infinite effect, and so the infinite universe must be the product of divine contrivance.
It is a strong sign of the times that Kant does not hesitate at all to call the creation “infinite.” Unlike Descartes, who a little more than a hundred years earlier called the universe “indefinite” to signal its inferiority to God, Kant insists in the Natural History that the revelation (Offenbarung) of God is just as infinite as God himself (151/145). One can even hear Brunian echoes as Kant says that anything short of an infinite creation would be an insult to an infinite God: “Now it would be senseless to set Godhead in motion with an infinitely small part of his creative ability and to imagine his infinite force … locked up in an eternal absence of exercise” (151/144). It is “far more proper,” Kant concludes—even “necessary”—to find the infinite glory of God reflected in an infinite creation (151/144). What, then, does Kant’s infinite creation look like?
Cosmic Ascent
We embarked on the foregoing theological detour after having witnessed the formation of a sun and its planets. Together, Kant explains in Natural History, these bodies constitute a “system” because they move in a common plane around a common center (112/85). The resulting “solar world” (Sonnenwelt) is sustained by the continued operation of our two primeval forces: the attractive force that pulls bodies toward the center and the repulsive force that pushes them away (98/65). It is the steady tension between these forces that keeps the planets and moons in orbit, with the attractive force preventing them from flying outward into infinity and the repulsive force preventing them from crashing into the sun. Moreover, Kant explains, the repulsive force provides the “small deviation” from circularity that results in Kepler’s ellipses (118/94).
From here, Kant throws off Newton’s typical restraint on the matter, announcing with little fanfare that our solar world cannot possibly be the only one. Rather, “the fixed stars, as so many suns, are centers of similar systems in which all may be arranged just as greatly and orderly as ours” (101/70). Thus begins an ascending meditation on the staggering scope of creation, an “infinite cosmic space [that] swarms with worlds [von Weltgebäuden wimmele] whose number and excellence has a relation to the inexhaustibility of their creator” (101/70). Now, as far as Kant is concerned, the plurality of solar systems is simply not up for debate; everyone “since Huygens’ time believes that [all] the fixed stars are … suns” (101/70). What is less clear is whether these suns bear any relation to one another; indeed, from the seemingly haphazard positions of the stars, most people are led to think that they exist in no order at all (101/70).118 But the notion that systematic regularity might apply only on “the small scale” and not “among the members of the universe [Weltall] at large” is perplexing to Kant. He therefore appeals to Thomas Wright of Durham, whose Original Theory or New Hypothesis of the Universe (1750) proposes that the stars of the Milky Way compose a system analogous to our solar system. The book had been reviewed a year after its publication in a German periodical, and although Kant had not read the work itself, the review had made such an impression on him that he credits Wright with having “first” given him “the prompting to look upon the fixed stars not as a scattering swarm with no visible order, but as a system” (88/50–51). Yet Wright, Kant claims, was not clear about the shape of this system, nor had he articulated a resemblance between the Milky Way and other cosmic phenomena.119
In order to “improve” upon Wright, Kant therefore employs a mixture of observational tactics and strange geometry, the conclusion of which is that all the stars of the Milky Way occupy a common plane. For Kant, this means that they constitute a system; in effect, the Milky Way is a solar world writ huge, an ordered set of relations that Kant calls a “world-system” (Weltsysteme) (103/72–73). By the rule of analogy, he infers that this higher system must be sustained by the same forces that order the solar world. Mindful, however, of how far one star is from any other, Kant postulates that each of them cannot exert a gravitational pull on each of the others. Rather, “the attraction of the sun should reach to about the nearest fixed star,” which in turn tugs on its neighbor in what William James might call a “strung-along” fashion, so that “the entire host of [stars] would be driven to approach one another” through the attractions each exerts on its nearest neighbors (103/73). But, Kant reminds us, the attractive power of gravity alone would cause the “world-system” of the Milky Way to “fall together sooner or later into one lump,” just as it would do in our solar system, if there were not that other non-Newtonian force, the Epicurean repulsive force that Kant now also calls “centrifugal.” This repulsive force works against gravity to produce “the eternal orbital motions whereby the edifice of creation is secured from collapse and made fit for an imperishable duration” (103–4/73–74).
If it is the case that the Milky Way is a “system” analogous to (but greater than) our solar system, then three further conclusions follow. The first is that the galaxy must have a center (Kant proposes the star Sirius as the most likely candidate) (104/74). The second is that the “fixed stars” must actually move around this center—not once a day, as they did around the Ptolemaic earth, but perhaps one degree every four thousand years (which would explain why twenty-five hundred years of observations had not recorded any change) (105/76).120 And the third is that just as our solar system is not the only solar system, the Milky Way cannot be the only Milky Way (106–7/77–78).
With this last conclusion, Kant had come upon a truly new idea. Wright had not proposed it directly (although he had gestured toward it in his penultimate and more or less unexplained diagram [figure 4.2]), Johann Lambert stopped short of it, and no one much before them would have had the language to propose it.121 In 1786, the observational astronomer William Heschel would present evidence that the nebulae were “no less than whole siderial systems, [which might] well outvie our Milky Way in grandeur.”122 Nevertheless, this multigalactic proposal would lose all credence during the nineteenth century. As we will see in chapter 5, Albert Einstein believed for half of his life that there was only one galaxy; it was not until Edwin Hubble’s discoveries of the Andromeda and Triangulum galaxies in the early 1920s that a different view became plausible. Unlike Hubble, of course, Kant did not observe other galaxies directly; rather, he reasoned to them from analogy. If the Milky Way is structured like a solar system, he argued, and if there are countless other solar systems, then surely there are countless other Milky Ways as well. In an infinite universe, what would prevent that from being the case? And would countless Milky Ways not reflect the omnipotence of God far better than a lone galaxy would?
But Kant’s conjecture is not strictly analogical (or, for that matter, theological). With help from Pierre-Louis Moreau de Maupertius’s astronomical descriptions (published mostly in the 1740s),123 he reasons in the Natural History that if there were another Milky Way, it would be so distant from us that it would appear “as a small space illuminated by a weak light, [a space] whose figure will be circular when its plane presents itself directly to the eye, and elliptically when it is seen from the side” (106/77–78). And, of course, such phenomena do exist. They are the cloudy figures astronomers call “nebulae,” which Galileo thought were small clusters of stars and Maupertius thought were single stars that were “less luminous” than others and “somewhat flattened.”124 Kant’s reasoning is that if the nebulae were single stars, and if they were as distant as the other stars, then they would have to be immense in order to appear so large to us. But if they were immense, then why would they look so pale? Kant therefore proposes that the nebulae are neither giant stars nor small clusters of stars, but galaxies—vast structures of “so many thousands” of stars separated by vast stretches of space (107/97).125 Again, this idea would not be taken seriously until a century and a half later, when Hubble realized that all the nebulae are structures like the Milky Way, so that far from there being only one galaxy in existence, there are “hundreds of thousands” of them.126 But Kant does not stop there.
Why, he wonders in the Natural History, should galaxies be considered the highest-order systems? The law of analogy (along with the findings of somewhat more tenuous observation) can lead one, Kant reckons, to produce the “conjecture that even these higher world-orders are not without relation to one another and … constitute a still more immeasurable system” (108/79–80).
At this juncture, Kant ventures momentarily beyond the bounds of reason, leading his reader on an upward journey through the successive ranks of cosmic systems—a journey that fills him with increasing wonder. “If the greatness of a planetary world-edifice [Weltgebäude], in which the earth as a grain of sand is hardly noticed, moves the intellect to admiration [Verwunderung],” he begins,
with what astonishment [Erstaunen] will one be enchanted if one considers the infinite [unendlich] amount of worlds and systems which fill the total of the Milky Way; but how this astonishment increases when one realize[s] that all these immeasurable star-orders again form the unit of a number whose end we do not know and which perhaps just as the former is inconceivably great and yet again is only the unit of a new number system. We see the first members of a progressive relation of worlds and systems, and the first part of this infinite [unendlich] progression makes already known what one must conjecture about the whole. There is no end here but an abyss [Abgrund] of a true immeasurability in which all ability of human concepts sinks. (108/80)
In a striking topographical reversal, the journey upward ultimately casts Kant down. The higher he is able to climb through the power of intellect, the more dramatically he finds himself sinking into the unintelligible. So “human concepts” will never be able to grasp the entirety of this “progressive relation of worlds and systems,” plunging us instead into “an abyss of a true immeasurability.” The only options, it seems, are to fall silent in astonishment or to try to dust oneself off from the journey and resolve to measure the immeasurable. Kant opts for the latter.
Climbing down from his mountain and up from his abyss, Kant tells us that if the space of creation is infinite, if the stuff of creation is infinite, and if cosmic bodies are arranged in greater and greater systems, then “the cosmic space will be enlivened with worlds without number and without end” (152/146). As we have just seen, however, our philosopher—much like those in the century that preceded him—is both amazed and terrified by these worlds without end. So one way to overcome this riot of emotion is to ask whether this endless progression of systems might itself constitute a system—whether there might be an übersystem within which all the supergalaxies, galaxies, and solar systems are somehow nestled. As Kant phrases the question, “[W]ill now that systematic connection extend also to the whole and hold together the entire universe [Universum], the all of nature [das All der Natur], in one such system through the connection of attraction with centrifugal force?” He answers immediately, “I say yes” (152/146). And so here Kant begins a complicated retreat from infinity.
Out of the Abyss
There must be a single System of systems, Kant reasons in the Natural History, because if there were none, then there would be no overarching force to regulate the attractions among different systems. Left to the whims of gravitational variation (we have heard this story before), the bodies of a hypothetically polysystematic universe would fall into a massive cosmic implosion. And even if these separate systems happened to have equal gravitational force, Kant imagines, then “the smallest displacement in the universe would … hand it over … to collapse” (152/146). This would make the continued existence of the universe a perpetual miracle (Wunder), and Kant, taking a sudden Leibnizian swipe at Newton, says that God does not work by means of intermittent wonder working or by holding up the stars on needle points. “One … hits the mark far more appropriately,” he declares, “if one makes from the entire creation a single system” so that the harmonious order among cosmic bodies becomes a function of the laws of nature themselves (152/146). Kant therefore decides that the endless “chain of members” he has been contemplating cannot be “truly infinite [wirklich unendlich]”; rather, it finds its end in a single, universal System (152/146, emphasis added). In other words, the world is not “immeasurable” at all, and “human concepts” need not give way to helpless astonishment.
Back on solid ground, Kant continues: if God has indeed made the world a single System, then he has made “related to a single center all worlds and world-orders [Welten und Weltordnungen] that fill the entire infinite space” (152/146, emphasis added). This regrounded line of thinking immediately runs into a serious difficulty, though. In order to say that there is one universal System, Kant has decided that the progression of worlds cannot be “truly infinite.” Now, just a few sentences later, he says that space is infinite, so presumably the progression of worlds could in principle go on forever, yet Kant insists that the whole thing ends in one all-embracing System. At what point, then, does the endless progression end? Where, in infinite space, might one find the border of the übersystem (and what happens if Lucretius throws a spear at it)? Kant diverts our attention from this problem by focusing not on the periphery of this System, but on its “single center,” a Mittelpunkt around which “all worlds and world-orders” must be organized. But this middle point is equally perplexing: as any reader of Cusa or Bruno knows, an infinite universe has no center.
Kant does acknowledge that, geometrically speaking, there is no center in an infinite universe. But if there is no center, then there is no System, and there must be a System. So Kant resolves to designate as “center” the place where creation began: that “lump of … exceptionally large attraction” that first pulled the falling atoms toward itself (152/147). Because worlds first began to form around this lump, Kant tells us, they will be more densely clustered there, growing sparser as they get farther away. And because the “primeval stuff [is] piled up considerably thicker … and increases in its scattering with distances from that point,” Kant concludes that “such a point can have the privilege to be called a center” (153/148). In effect, he just displaces the spatial problem temporally, “centering” the infinite around its purported place of origin. But where, exactly, can an infinite universe be said to have begun?
In a footnote to this perplexing sentence, translator Stanley Jaki writes that “this reasoning shows Kant a most uncritical thinker, though neither the first or [sic] the last of those who, being infatuated with infinity, lose their critical faculties” (284n.23). I would suggest, however, that the problem is not Kant’s infatuation with infinity, but his fear of it. The problem is Kant’s infatuation not with infinity, but with oneness, which requires him to have an all-encompassing System, which requires him to posit a center, which necessitates his retreat from the infinite. Moreover, I would submit that the error seems to stem not from Kant’s having lost his critical faculties, but from his desperate attempt to regain them. He makes no such blunder as he is ascending in amazement through an infinite progression of worlds. It is when he comes back down and tries to assemble them into a single, nested System that he goes wrong and tries to center the centerless.127
Either way, however, Kant thinks that he has managed to organize the infinite universe around one gravitational center. He believes this center to be the starting point of creation, with worlds, galaxies, and supergalaxies fanning out from it in all directions, becoming sparser and sparser the farther they find themselves from the center. Of course, if worlds began to form at one place in one time, and if they thin out from that “center,” then there may be an immense number of them, but there is not an infinite number of them. Space, as it turns out, is infinite for Kant, but the worlds within it are numbered.128 Because these worlds are not genuinely innumerable, one might therefore conclude that creation is not as infinite as its creator. It is perhaps to prevent our drawing this conclusion that Kant, at this late stage, suddenly adds another major principle to his cosmogony. “Creation is never completed,” he asserts. “Though it has once started[, it] will never cease. It is always busy in bringing forth more scenes of nature, new things, and new worlds” (155/150). This, then, is the sense in which there are an infinite number of worlds: worlds are temporally infinite. As Kant puts it, creation “needs nothing less than eternity … to enliven the entire limitless reaches of infinite space with worlds without number and without end” (155/150–51).
If one were able to see the Kantian universe as a whole, it would therefore look like a vast sphere expanding into infinite space, with fully formed worlds, galaxies, and supergalaxies at the center; half-formed world-systems around them; and chaos on the periphery—where an infinite number of atoms lie (or fall) in wait, ready to form a never-ending number of new worlds (155/151).
Just as we have begun to wrap our minds around this image, however, Kant tosses in yet another new principle. Having established that creation is never finished, he suddenly announces that “every world that has been brought to completion gradually shows [a tendency] toward its destruction.”129 So it seems that systems do not enjoy “imperishable duration,” as he said earlier, in line with Bruno and Plato (103–4/73–74). Now he channels Lucretius instead to tell us that just as animals and plants perish, so will worlds themselves (157/154). The corollary, of course, is that just as nature brings forth new plants and new animals, so does it build “new formations in other celestial regions … repairing the loss with gain” (157/154). Therefore, the death of the old worlds is compensated by the birth of the young ones. And assuming that worlds live longer than the time it takes to make them, Kant figures there will always been a net gain of kosmoi (159/157).
So with this new insight, a revised bird’s-eye view of the universe would show a vast sphere expanding into infinite space, with destroyed worlds, galaxies, and supergalaxies at the center; older world-systems in a ring around them; younger world-systems in a ring around them; half-formed world-systems in a ring around them; and an infinite sea of Urstoff (basic material) on the periphery. The upshot of all this is that “the developed world finds itself confined between the ruins of a collapsed nature and the chaos of an undeveloped one” (159/157, translation altered slightly).
Lest we think that this is the final vision, however, Kant adds one last big idea to the end of his increasingly extravagant cosmology. The idea, he says, is “just as probable” as the notion that worlds perish in one place to be created elsewhere, and it is just as “befitting the constitution of divine works” (159/157). It has to do with those ruins that the dead worlds leave behind. “Can one not believe,” he asks, “that nature, which was capable of placing herself from chaos into regular order and a skillful system, will not be in the position to restore herself from the new chaos … and to renew the first combination?” (159/157). Can one not believe, in other words, in the eternal return of the same? So, with very little warning, Zeno is back on the scene, now mingling awkwardly with Newton, Leibniz, and Lucretius. In case we are uncertain that there really is a Stoic in our midst, Kant proceeds to tell us how this cosmic recycling will take place. When the systems of our world break down and come to a standstill, he explains, all the “planets and comets” (presumably still under the force of gravity) will crash into the sun. The sun, in turn, will “obtain an immeasurable increase through the mixture of so many and great lumps” (159/157). The resulting conflagration will “not only dissolve again everything into the smallest elements, but these will again expand and scatter … into these same distant spaces which they occupied before the first formation of nature” (159/157). Thus rebegins the cosmogony, with “a new world-edifice” emerging from the ashes of the old “through the combination of … attraction and repulsion” (160/158). And toward the end of this very strange paragraph, Kant calls the “astonishing” phenomenon he has just introduced “the phoenix of nature” (160/158).
He unfortunately says very little else about this phoenix, pausing just long enough to make it clear (pace Augustine) that human souls do not undergo such cycles before he ends the section (161/159–60). And so we do not learn, for example, whether this conflagration happens just at the level of solar systems, whether it extends out to galaxies, or whether it involves the whole universe. Nor do we learn how to reconcile this sudden cyclicality with the remaining sections of the Natural History, which go on to arrange the inhabitants of Kant’s “worlds without end” into an Enlightenment-flavored Great Chain of Being, with the least intelligent beings in the old worlds toward the center and the most intelligent in the new worlds on the periphery (167–68/169–70). One is therefore left wondering: After the conflagration, do the old worlds become new? Does the center thereby become the periphery? Might a fuller reflection on the phoenix somehow save Kant from his strange hierarchy, his impossible center, his infatuation with oneness? Kant never lets us know.
What he offers us instead is a riot of incompatible elements, a swarm of cosmological contradictions that has been gathering throughout this treatise and that gets louder and more frenetic as it ends: “Newtonian” gravity with a Lucretian swerve; Lucretian cosmogony with an omnipotent God; Leibnizian theology in Newtonian space; Timaean eternity with an Atomist demise; Brunian infinity with a Ptolemaic center; endless worlds in a Thomistic hierarchy; and, at the end of it all, a Stoic conflagration that burns the world into Epicurean atoms, pulling material bodies toward itself only to fling them, in a burst of fire, out to the infinite. In this final contradiction and expulsion, one can moreover detect proleptic hints of the oscillating big bang model, but Kant’s retention of Newtonian space prevents it; space, for Kant, stands still, whereas matter is drawn to the “center” of infinity and then somehow thrown outward again. The Natural History, in the end, is remarkably, ingeniously crowded: a late Enlightenment kitchen sink of past, present, and future cosmologies. You might even call it chaos.
 4
4 

