![]()
3.141592653589…
Circular Reasoning
We began the last chapter with some problems designed to challenge your geometric intuition pertaining to rectangles and triangles, ending with a problem that involved a rope connecting two goalposts at the opposite ends of a football field. In this chapter our focus will be on circles, and we’ll begin with a problem that starts by putting a rope around the Earth!
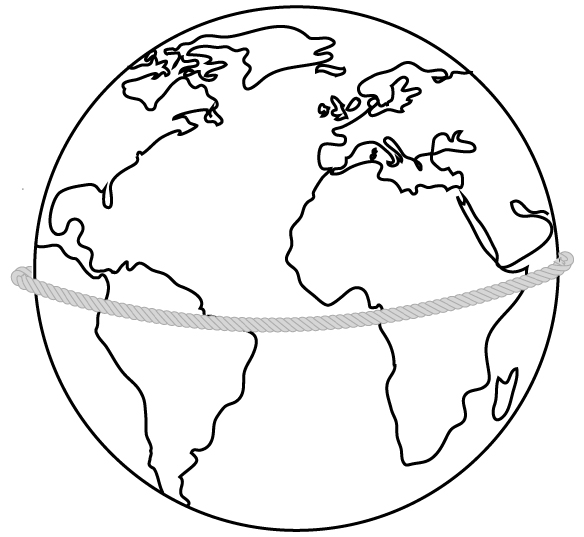

Question 1. Imagine that a rope is about to be tied around the Earth’s equator (approximately 25,000 miles long). Before tying the ends together, an extra 10 feet of rope is added. If we now somehow lift the rope so that it hovers over each point of the equator by the same distance, about how high will the rope be?
A) Less than one inch off the ground.
B) Just high enough to crawl under.
C) Just high enough to walk under.
D) High enough to drive a truck under.
Question 2. Two points X and Y are fixed on a circle, as in the figure below. We wish to choose a third point Z on the circle somewhere on the major arc (the long arc between X and Y, not the short arc). Where should we choose the point Z to maximize the angle ∠XZY?
A) Point A (opposite the midpoint of X and Y).
B) Point B (the reflection of X through the center of the circle).
C) Point C (as close to X as we can).
D) It doesn’t matter. All angles will have the same measure.
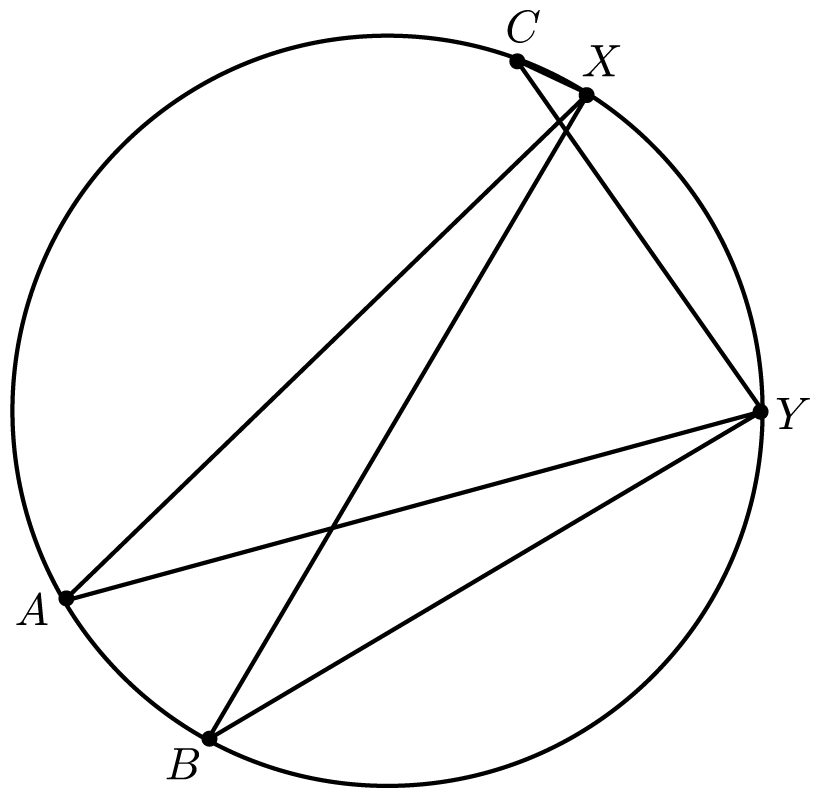

Which point on the major arc between X and Y results in largest angle? Is it angle ∠XAY, ∠XBY, ∠XCY, or are they all the same?
To answer these questions, we need to improve our understanding of circles. (Well, I suppose you don’t need circles to read the answers. The answers are B and D, respectively. But in order to appreciate why these answers are true, we need to understand circles.) A circle can be described by a point O and a positive number r so that every point on the circle has a distance r away from O, as shown on the opposite page. The point O is called the center of the circle. The distance r is called the radius of the circle. As a mathematical convenience, a line segment 
![]() from O to a point P on the circle is also called a radius.
from O to a point P on the circle is also called a radius.
Circumference and Area
For any circle, its diameter D is defined to be twice its radius, and is the distance across the circle. That is,
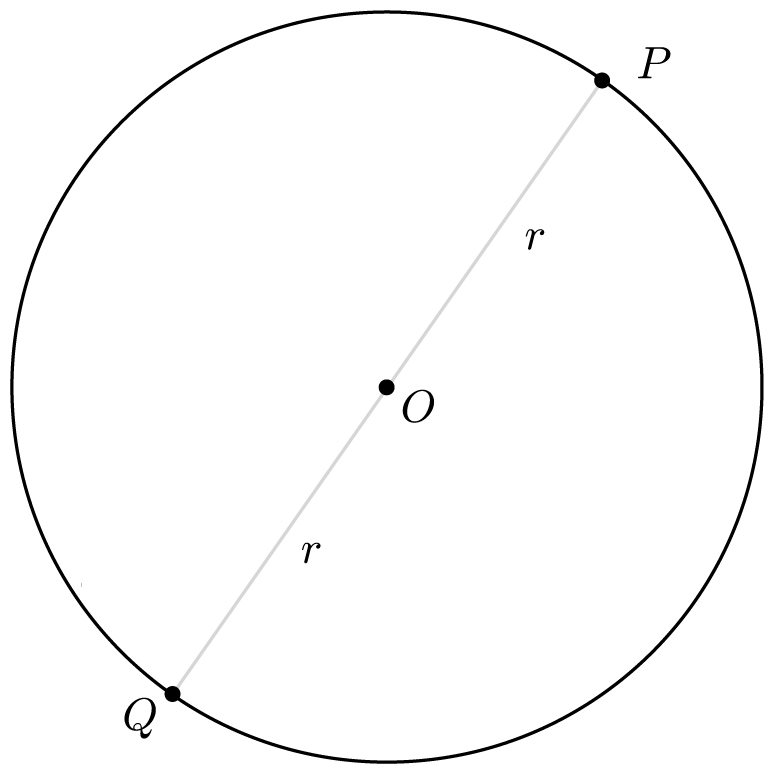

A circle with center O, radius r, and diameter D = 2r
D = 2r
The perimeter of a circle (its distance around) is called the circle’s circumference, denoted by C. From the picture, it is clear that C is bigger than 2D, since the distance along the circle from P to Q is bigger than D and the distance from Q back to P is also bigger than D. Consequently, C > 2D. If you eyeball it, you might even convince yourself that C is a little bigger than 3D. (But to see it clearly, you might need to wear 3-D glasses. Sorry.)
Now, if you wanted to go about comparing a circular object’s circumference to its diameter, you might wrap a string around the circumference. Then divide the length you measured by the diameter. You’ll find, regardless of whether you are measuring a coin, the base of a glass, a dinner plate, or a giant hula hoop, that
C/D ≈ 3.14
We define the number π (pi, pronounced “pie”; the Greek letter for the “p” sound) to be the exact constant that represents the ratio of a circle’s circumference to its diameter. That is,
π = C/D
and π is the same for every circle! Or if you prefer, you can write this as a formula for the circumference of any circle. Given the diameter D or radius r of any circle, we have
C = πD
or
C = 2πr
The digits of π begin as follows:
π = 3.14159 . . .
We will provide more digits of π and discuss some of its numerical properties later in this chapter.
Aside
Interestingly, the human eye is not so good at estimating circumferences. For example, take any large drinking glass. What do you think is bigger, its height or its circumference? Most people think the height is bigger, but it’s usually the circumference. To convince yourself, put your thumb and middle finger on opposite sides of a glass to determine its diameter. You will likely see that your glass is less than 3 diameters tall.
We can now answer question 1 from the beginning of the chapter. If we think of the equator of the Earth as a perfect circle with circumference C = 25,000 miles, then its radius must be
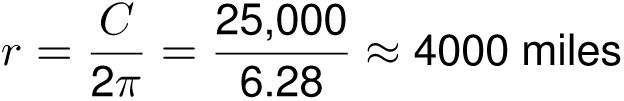
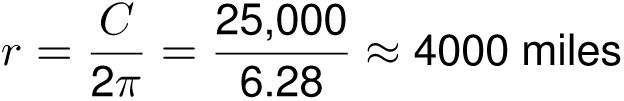
But we don’t actually need to know the value of the radius to answer this question. All we really need to know is how much the radius will change if we increase the circumference by 10 feet. Adding 10 feet to the circumference will create a slightly larger circle with a radius that is larger by exactly 10/2π = 1.59 feet. Hence there would be enough space beneath the rope that you could crawl under it (but not walk under it, unless you were quite a limbo dancer!). What is especially surprising about this problem is that the answer of 1.59 feet does not depend at all on the Earth’s actual circumference. You would get the same answer with any planet or with a ball of any size! For example, if we have a circle with circumference C = 50 feet, then its radius is 50/(2π) ≈ 7.96. If we increase the circumference by 10 feet, then the new radius is 60/(2π) ≈ 9.55, which is bigger by about 1.59 feet.
Aside
Here’s another important fact about circles.
Theorem: Let X and Y be opposite points on a circle. Then for any other point P on the circle, ∠XPY = 90º.
For example, in the figure below, angles ∠XAY, ∠XBY, and ∠XCY are all right angles.
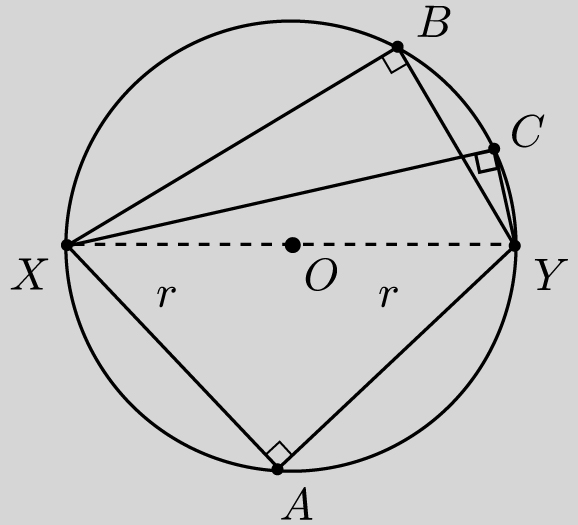
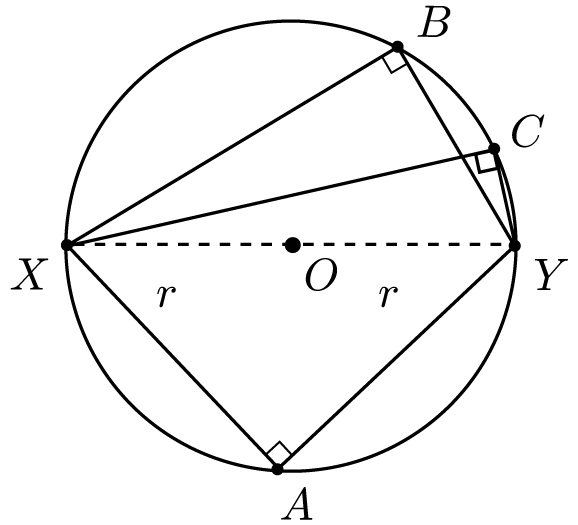
Proof: Draw the radius from O to P, and suppose that ∠XPO = x and ∠YPO = y. Our goal is to show that x + y = 90°.

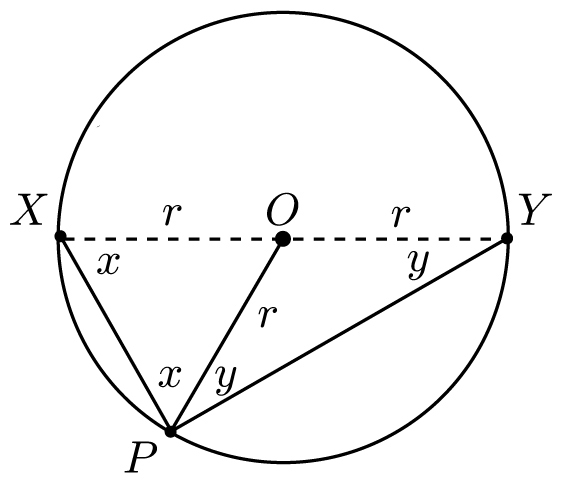
Since 
![]() and
and 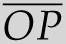
![]() are radii of the circle, they both have length r, and therefore triangle XPO is isosceles. By the isosceles triangle theorem, ∠OXP = ∠XPO = x. Similarly,
are radii of the circle, they both have length r, and therefore triangle XPO is isosceles. By the isosceles triangle theorem, ∠OXP = ∠XPO = x. Similarly, 
![]() is a radius and ∠OYP = ∠YPO = y. Since the angles of triangle XYP must sum to 180°, we have 2x + 2y = 180°, and therefore x + y = 90°, as desired.
is a radius and ∠OYP = ∠YPO = y. Since the angles of triangle XYP must sum to 180°, we have 2x + 2y = 180°, and therefore x + y = 90°, as desired.

![]()
The theorem above is a special case of one of my favorite theorems from geometry — the central angle theorem, described in the next aside.
Aside
The answer to question 2 from the beginning of the chapter is revealed by the central angle theorem. Let X and Y be any two points on the circle. The major arc is the longer of the two arcs connecting X and Y. The shorter arc is called the minor arc. The central angle theorem says that the angle ∠XPY will be the same for every point P on the major arc between X and Y. Specifically, angle ∠XPY will be half of the central angle ∠XOY. If Q is on the minor arc from X to Y, then ∠XQY = 180º − ∠XPY.

For example, if ∠XOY = 100º, then every point P on the major arc from X to Y has ∠XPY = 50º, and every point Q on the minor arc from X to Y has ∠XQY = 130º.
Once we know the circumference of a circle, we can derive the important formula for the area of a circle.
Theorem: The area of a circle with radius r is πr2.
This is a formula that you probably had to memorize in school, but it is even more satisfying to understand why it is true. A perfectly rigorous proof requires calculus, but we can give a pretty convincing argument without it.
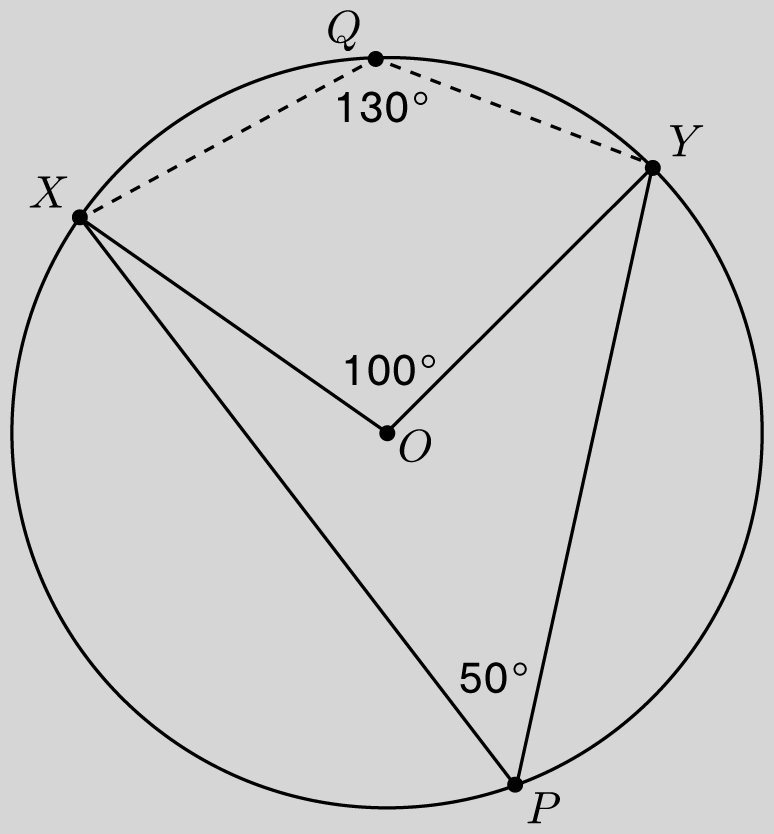
Proof 1: Think of a circle as consisting of a bunch of concentric rings, as pictured on the following page. Now cut the circle from the top to its center, as shown, then straighten out the rings to form an object that looks like a triangle. What is the area of this triangular object?

The area of a circle with radius r is πr2
The area of a triangle with base b and height h is 
![]() . For the triangle-like structure the base is 2πr (the circumference of the circle) and the height is r (the distance from the center of the circle to the bottom). Since the peeled circle becomes more and more triangular as we use more and more rings, then the circle has area
. For the triangle-like structure the base is 2πr (the circumference of the circle) and the height is r (the distance from the center of the circle to the bottom). Since the peeled circle becomes more and more triangular as we use more and more rings, then the circle has area
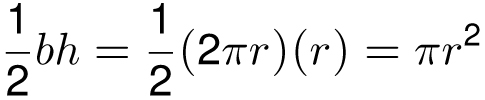
as desired.

![]()
For a theorem so nice, let’s prove it twice! The last proof treated the circle like an onion. This time we treat the circle like a pizza.
Proof 2: Slice the circle into a large number of equally sized slices, then separate the top half from the bottom half and interweave the slices. We illustrate with 8 slices, then with 16 slices, on the next page.
As the number of slices increases, the slices become more and more like triangles with height r. Interlacing the bottom row of triangles (think stalagmites) with the top row of triangles (stalactites) gives us an object that is very nearly a rectangle with height r and base equal to half the circumference, namely πr. (To make it look even more like a rectangle, instead of a parallelogram, we can chop the leftmost stalactite in half and move half of it to the far right.) Since the sliced circle
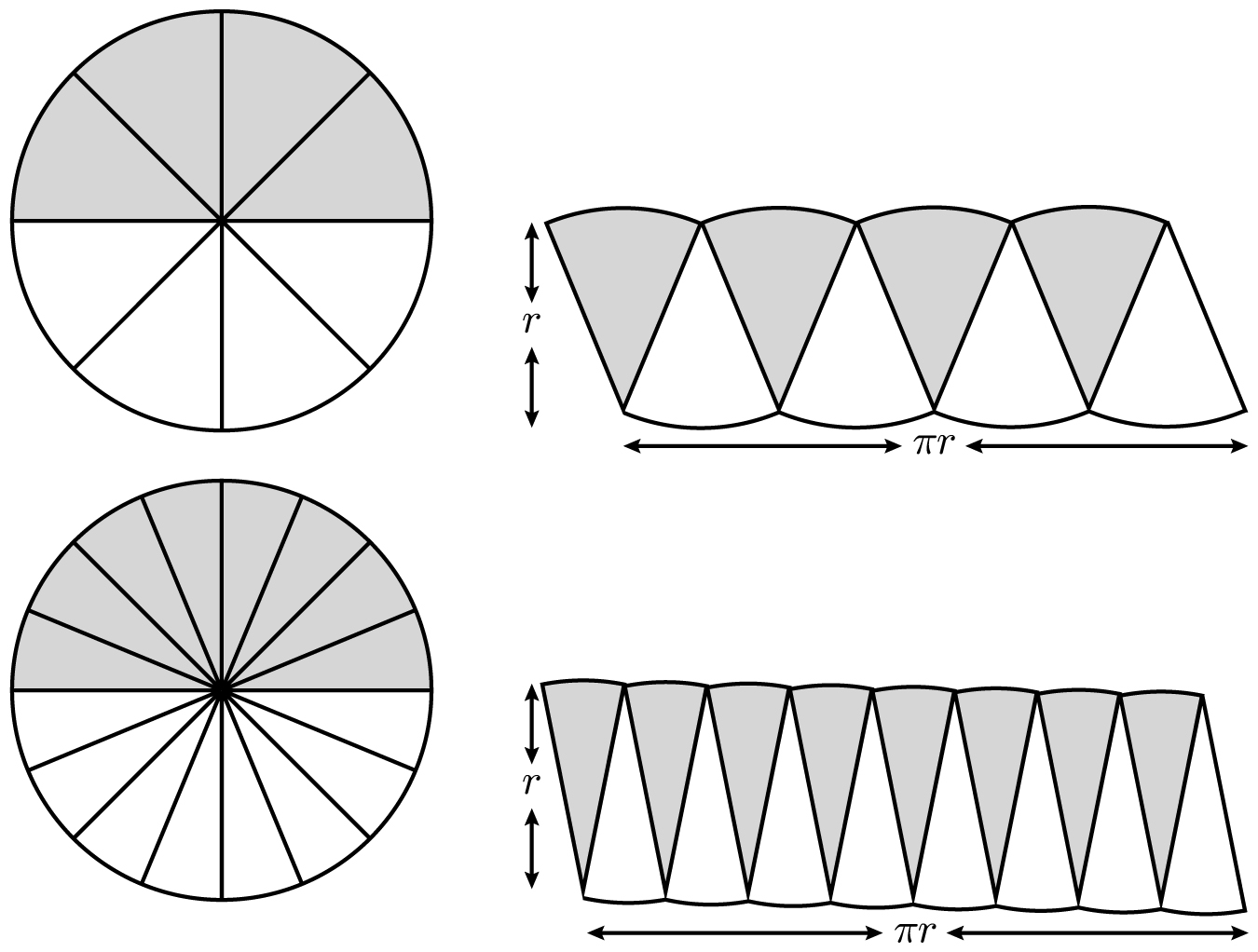

Another proof (by pizza pi?) that the area is πr2
becomes more and more rectangular as we use more and more slices, the circle has area
bh = (πr)(r) = πr2
as predicted.

![]()
We often want to describe the graph of a circle on the plane. The equation to do so for a circle of radius r centered at (0, 0) is
x2 + y2 = r2
as seen in the graph on the next page. To see why this is true, let (x, y) be any point on the circle, and draw a right triangle with legs of length x and y and hypotenuse r. Then the Pythagorean theorem immediately tells us that x2 + y2 = r2.
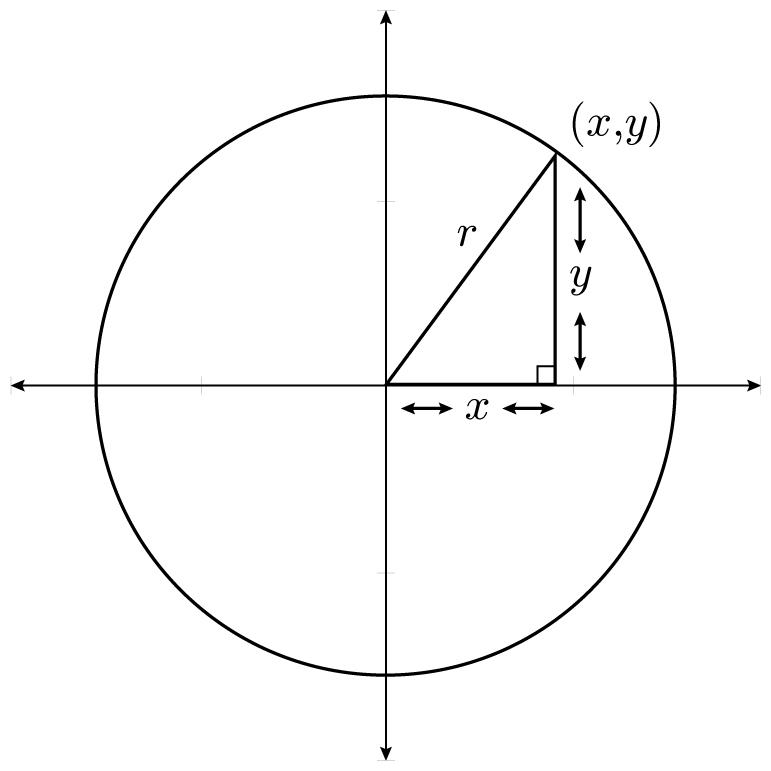

A circle of radius r centered at (0, 0) has formula x2 + y2 = r2 and area πr2
When r = 1, the above circle is called the unit circle. If we “stretch” the unit circle by a factor of a in the horizontal direction and by a factor of b in the vertical direction, then we get an ellipse, like the one below.
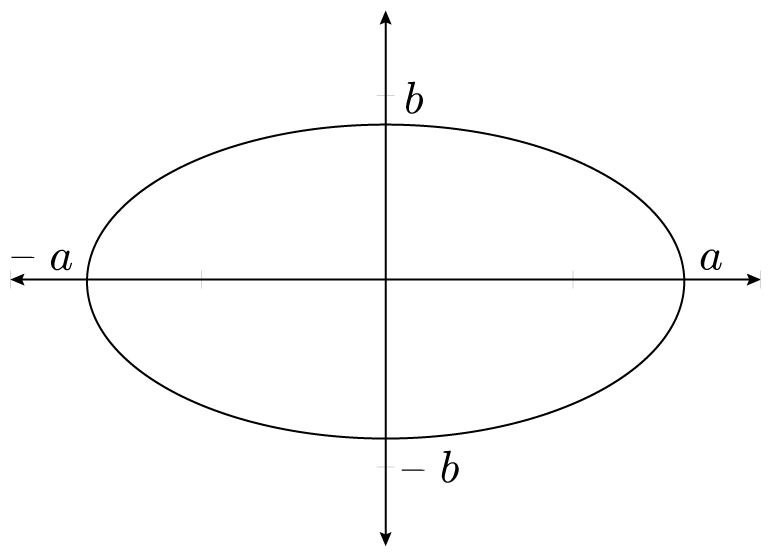

The area of an ellipse is πab
Such an ellipse has the formula
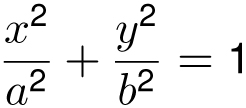
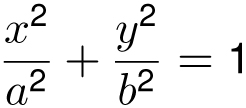
and has area πab, which makes sense, because the unit circle has area π and the area has been stretched by ab. Notice that when a = b = r, we have a circle of radius r and the πab area formula correctly gives us πr2.
Here are some fun facts about ellipses. You can create an ellipse by taking two pins, a loop of string, and a pencil. Stick two pins on a piece of paper or cardboard and wrap the string around the pins with a little bit of slack. Place your pencil at one part of the string and pull the string taut so that the string forms a triangle, as in the figure below. Then move the pencil around the two pins, keeping the string taut the entire time. The resulting diagram will be an ellipse.
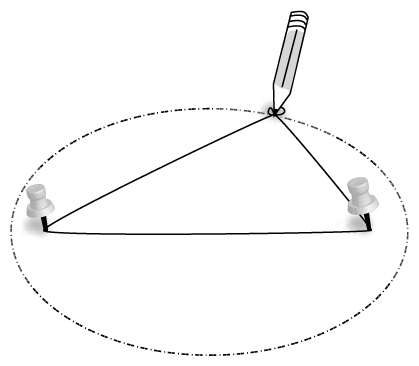

The positions of the pins are called the foci of the ellipse, and they have the following magical property. If you take a marble or billiard ball and place it at one focus, then hit the ball in any direction, after one bounce off the ellipse it will head straight to the other focus.


Heavenly bodies like planets and comets travel around the sun in elliptical paths. I can’t resist the following rhyme:
Even eclipses
Are based on ellipses!
Aside
Interestingly, there is no simple formula for the circumference of an ellipse. But the mathematical genius Srinivasa Ramanujan (1887–1920) established the following excellent approximation. The circumference of an ellipse, as described above, is approximately
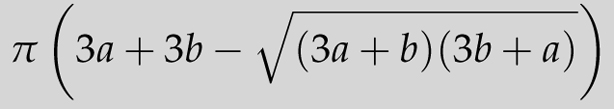
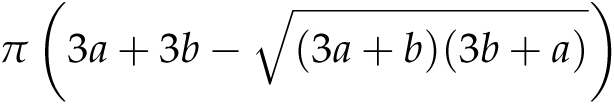
Notice that when a = b = r, this reduces to 
![]() , the circumference of a circle.
, the circumference of a circle.
The number π appears in three-dimensional objects as well. Consider a cylinder, such as a can of soup. For a cylinder of radius r and height h, its volume (which measures how much room the shape takes up) is
Vcylinder = πr2h
This formula makes sense, since we can think of the cylinder as made up of circles with area πr2 stacked one on top of another (like a stack of round coasters at a restaurant) to a height of h.
What is the surface area of the cylinder? In other words, how much paint would be necessary to paint its exterior, including the top and bottom? You do not need to memorize the answer since you can figure it out by breaking the cylinder into three pieces. The top and bottom of the cylinder each have an area of πr2, so they contribute 2πr2 to the surface area. For the rest of the cylinder, cut the cylinder with a straight cut from bottom to top and flatten the resulting object. The object will be a rectangle with height h and base 2πr, since that’s the circumference of the surrounding circle. Since this rectangle has area 2πrh, the total surface area of the cylinder is
Acylinder = 2πr2 + 2πrh
A sphere is a three-dimensional object where all points are a fixed distance away from its center. What is the volume of a sphere of radius r? Such a sphere would fit inside a cylinder of radius r and height 2r, so its volume must be less than πr2 (2r)= 2πr3. As luck (and calculus) would have it, the sphere occupies exactly two-thirds of that space. In other words, the volume of a sphere is
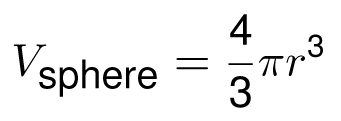
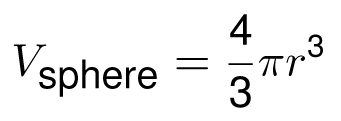
The surface area of a sphere has a simple formula that is not so simple to derive:
Asphere = 4πr2
Let’s end this section with examples of where π appears in ice cream and pizza. Imagine an ice cream cone with height h, and where the circle at the top has radius r. Let s be the slant height from the tip of the cone to any point on the circle, as shown below. (We can calculate s from the Pythagorean theorem, since h2 + r2 = s2.)
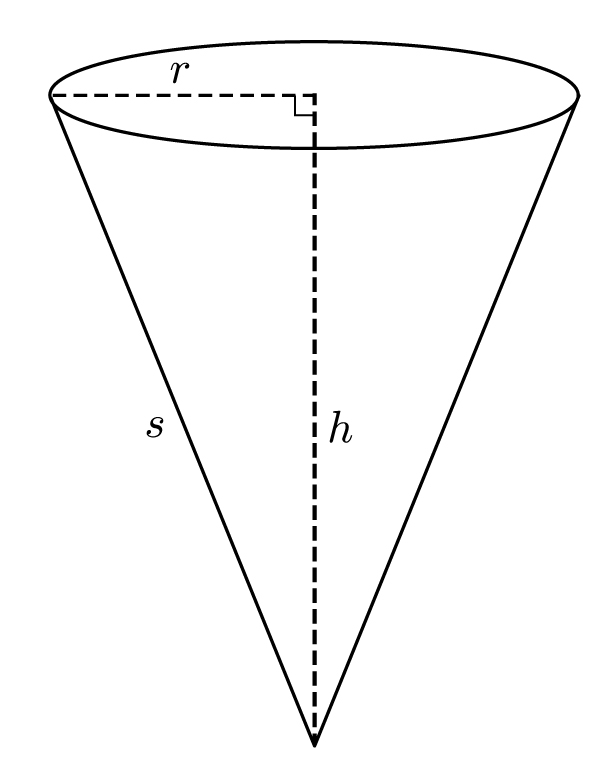

The cone has volume πr2h/3 and surface area πrs
Such a cone would fit inside a cylinder with radius r and height h, so it is no surprise that the cone’s volume is less than πr2h. But it is a surprise (and completely unintuitive without using calculus) that the volume is exactly one-third of that number. In other words,
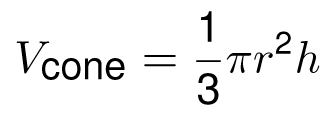
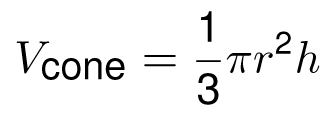
Although we can derive the surface area without calculus, we just display it for its elegance and simplicity. The surface area of a cone is
Acone = πrs
Finally, consider a pizza with radius z and thickness a, as shown below. What would its volume be?
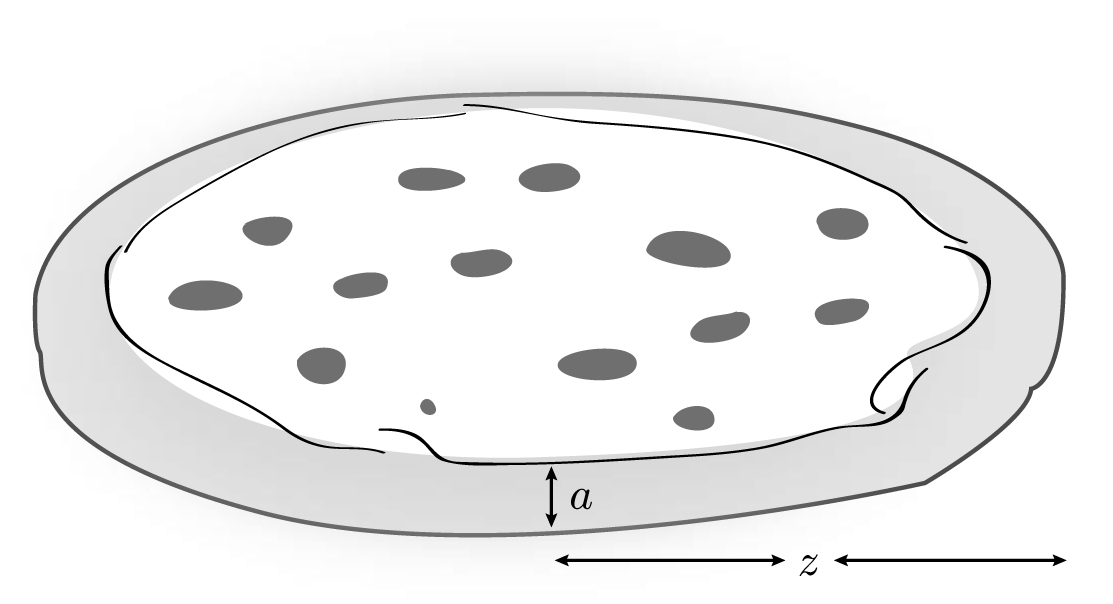

What is the volume of this pizza with radius z and thickness a?
The pizza can be thought of as an unusually shaped cylinder with radius z and height a, so its volume must be
V = πz2 a
But the answer was really staring you in the face all along, since if we spell out the answer more carefully we get
V = pi z z a
Some surprising appearances of π
It’s no surprise to see π show up in areas and circumferences of circular objects like the ones we have seen. But π shows up in many parts of mathematics where it doesn’t seem to belong. Take, for example, the quantity n!, which we explored in Chapter 4. There is nothing particularly circular about this number. It is largely used for counting discrete quantities. We know that it’s a number that grows extremely fast, and yet there is no efficient shortcut for computing n!. For instance, computing 100,000! still requires many thousands of multiplications. And yet there is a useful way to estimate n! using Stirling’s approximation, which says that


where e = 2.71828 . . . (another important irrational number that we will learn all about in Chapter 10). For instance, a computer can calculate that to four significant figures, 64! = 1.269 × 1089. Stirling’s approximation says that 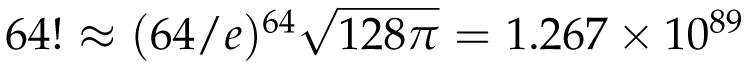
![]() . (Is there a shortcut to raising a number to the 64th power? Yes! Since 64 = 26, you just start with 64/e, and square it six times.)
. (Is there a shortcut to raising a number to the 64th power? Yes! Since 64 = 26, you just start with 64/e, and square it six times.)
The famous bell curve, pictured below, which appears throughout statistics and all of the experimental sciences, has a height of 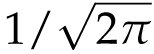
![]() . We’ll say more about this curve in Chapter 10.
. We’ll say more about this curve in Chapter 10.
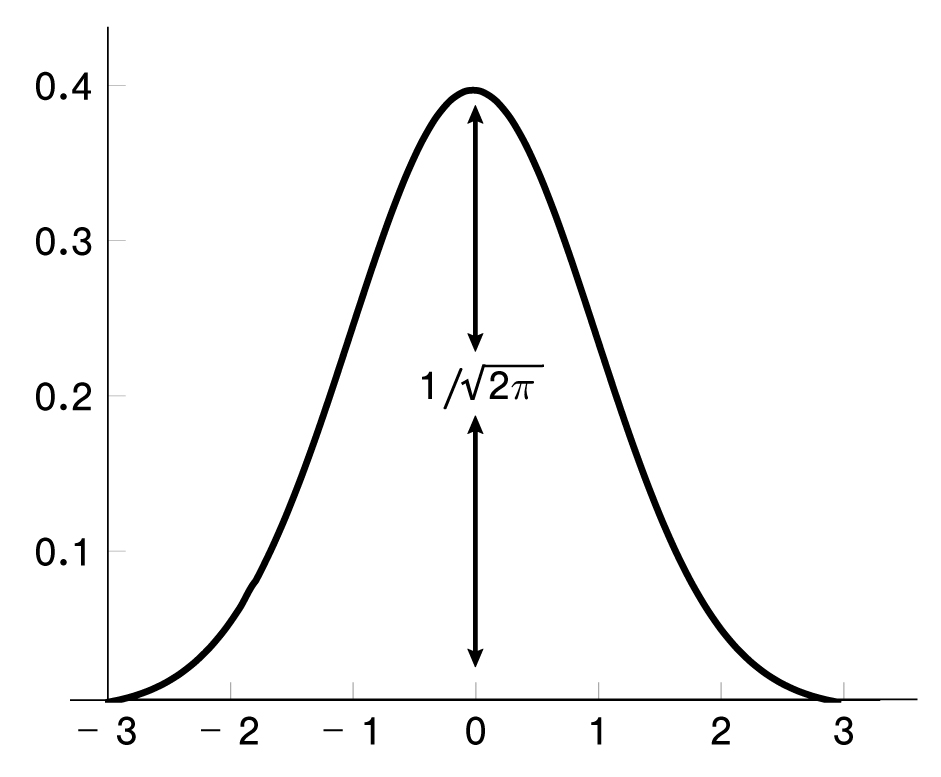

The height of the bell curve is 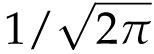
![]()
The number π also often appears in infinite sums. It was Leonhard Euler who first showed that when we add the squares of the reciprocals of the positive integers, we get
1 + 1/22 + 1/32 + 1/42 + · · · = 1 + 1/4 + 1/9 + 1/16 + · · · = π2/6
And if we square each of the above terms, the sum of the reciprocals of fourth powers turns out to be
1 + 1/16 + 1/81 + 1/256 + 1/625 + · · · = π4/90
In fact, there are formulas for the sum of reciprocals of every even power 2k, producing an answer of π2k, multiplied by a rational number.
What about powers of odd reciprocals? In Chapter 12, we will show that the sum of the reciprocals of the positive integers is infinite. With odd powers bigger than 1, like the sum of the reciprocals of the cubes,
1 + 1/8 + 1/27 + 1/64 + 1/125 + · · · = ???
the sum is finite, but nobody has figured out a simple formula for the sum.
Paradoxically, π pops up in problems pertaining to probability. For example, if you randomly choose two very large numbers, the chance that they have no prime factors in common is a little over 60 percent. More precisely, the probability is 6/π2 = .6079 . . . . It is no coincidence that this is the reciprocal of the answer to one of our earlier infinite sums.
Digits of π
By doing your own careful measurements, you can experimentally determine that π is a little bit bigger than 3, but two questions naturally arise. Can you prove that π is near 3 without the use of physical measurements? And is there a simple fraction or formula for π?
We can answer the first question by drawing a circle of radius 1, which we know has area π12 = π. In the figure below, we have drawn a square with sides of length 2 that completely contains the circle. Since the area of the circle must be less than the area of the square, this proves that π < 4.
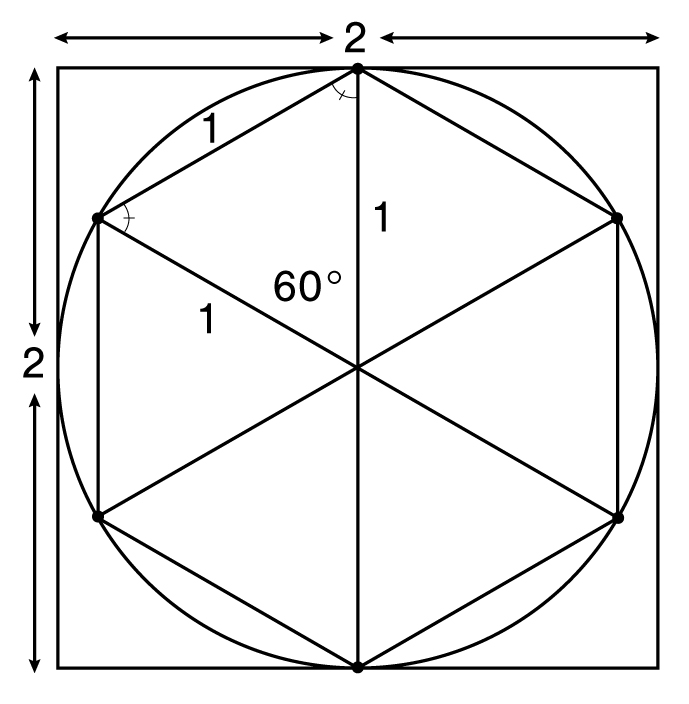

A geometrical proof that 3 < π < 4
On the other hand, the circle also contains a hexagon at six equally spaced points along the circle. What is the perimeter of the inscribed hexagon? The hexagon can be broken into 6 triangles, each with a central angle of 360° /6 = 60°. Two sides of each triangle are radii of the circle with length 1, so the triangle is isosceles. By the isosceles triangle theorem, the other two angles are equal, and must therefore also be 60°. Hence, these triangles are all equilateral with sides of length 1. The perimeter of the hexagon is 6, which is less than the circumference of 2π. Thus 6 < 2π, and so π > 3. Putting it all together, we have
3 < π < 4
Aside
We can restrict π to a smaller interval by using polygons with more sides. For example, if we surround the unit circle with a hexagon instead of a square, we can prove that 
![]() . . . .
. . . .
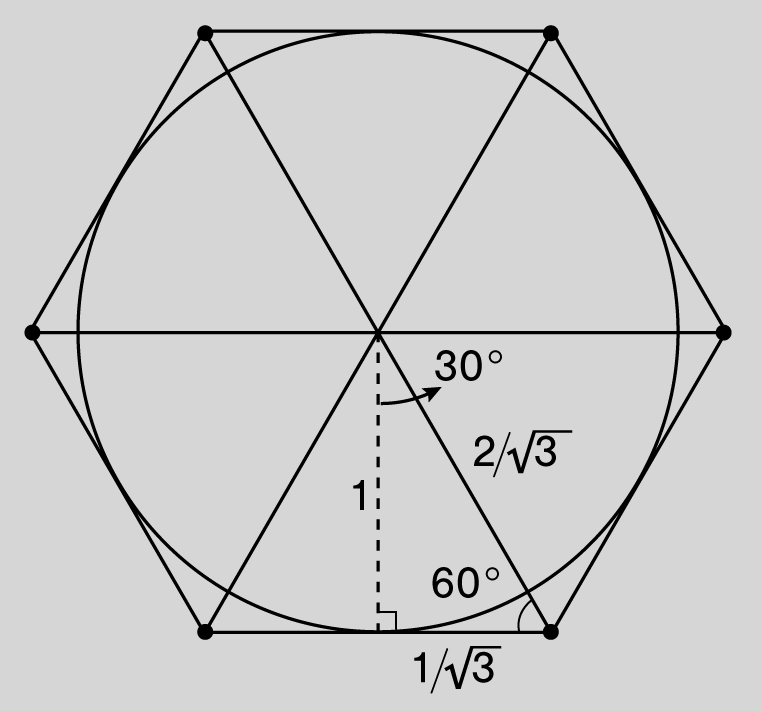
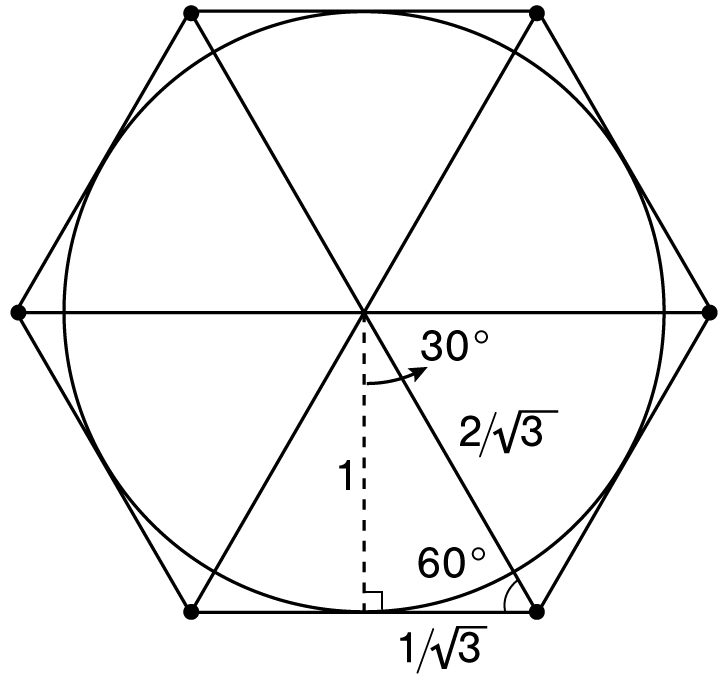
Once again, the hexagon can be subdivided into six equilateral triangles. Each of these triangles can be subdivided into two congruent right triangles. If the short leg has length x, then the hypotenuse has length 2x, and by the Pythagorean theorem, x2 + 1 = (2x)2. Solving for x gives us 
![]() . Consequently, the perimeter of the hexagon is
. Consequently, the perimeter of the hexagon is 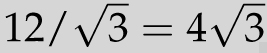
![]() , and since this is greater than the circle’s circumference, 2π, it follows that
, and since this is greater than the circle’s circumference, 2π, it follows that 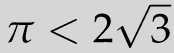
![]() . (Interestingly, we reach the same conclusion by comparing the area of the circle to the area of the hexagon.)
. (Interestingly, we reach the same conclusion by comparing the area of the circle to the area of the hexagon.)
The great ancient Greek mathematician Archimedes (287 to 212 BC) built on this result to create inscribed and circumscribed polygons with 12, 24, 48, and 96 sides, leading to 3.14103 < π < 3.14271 and the simpler looking inequality

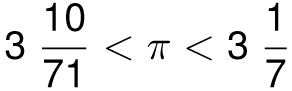
There are many simple ways to approximate π as a fraction. For example,


I particularly like the last approximation. Not only does it correctly give π to six decimal places, but it also uses the first three odd numbers twice: two 1s, two 3s, and two 5s, in order!
Naturally, it would be interesting to find a fraction that gave us π exactly (where the numerator and denominators are integers; otherwise we could simply say 
![]() ). In 1768, Johann Heinrich Lambert proved that such a search would be futile, by showing that π is irrational. Perhaps it could be written in terms of square roots or cube roots of simple numbers? For example,
). In 1768, Johann Heinrich Lambert proved that such a search would be futile, by showing that π is irrational. Perhaps it could be written in terms of square roots or cube roots of simple numbers? For example, 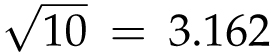
![]() . . . is pretty close. But in 1882, Ferdinand von Lindemann proved that π is more than just irrational. It is transcendental, which means that π is not the root of any polynomial with integer coefficients. For example,
. . . is pretty close. But in 1882, Ferdinand von Lindemann proved that π is more than just irrational. It is transcendental, which means that π is not the root of any polynomial with integer coefficients. For example, 
![]() is irrational, but it is not transcendental, since it is a root of the polynomial x2 − 2.
is irrational, but it is not transcendental, since it is a root of the polynomial x2 − 2.
Although π cannot be expressed as a fraction, it can be expressed as the sum or product of fractions, provided we use infinitely many of them! For example, we will see in Chapter 12 that


The formula above is beautiful and startling, yet it is not a very practical formula for calculating π. After 300 terms, we are still not any closer to π than 22/7 is. Here’s another astounding formula, called Wallis’s formula, where π is expressed as an infinite product, although it also takes a long time to converge.
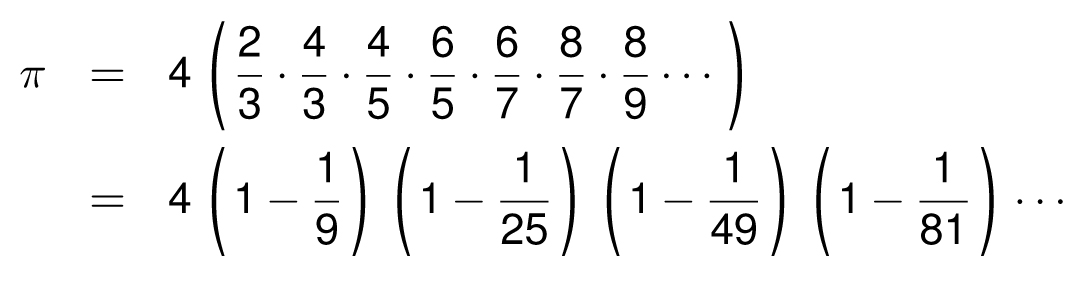
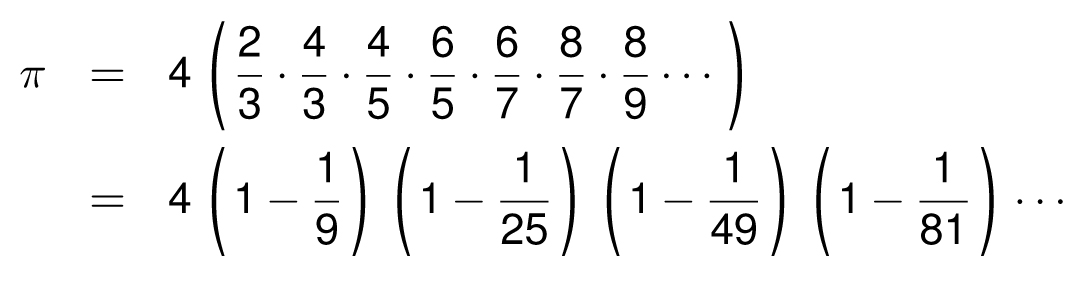
Celebrating and Memorizing π (and τ)
Because of people’s fascination with π (and as a way to test the speed and accuracy of supercomputers), π has been calculated to trillions of digits. We certainly don’t need to know π to that level of accuracy. With just forty digits of π, you can measure the circumference of the known universe to within the radius of a hydrogen atom!
The number π has developed almost a cult following. Many people like to celebrate the number π on Pi Day, March 14 (with numeric representation 3/14), which also happens to be the birthdate of Albert Einstein. A typical Pi Day event might consist of mathematically themed pies for display and consumption, Einstein costumes, and of course π memorization contests. Students generally memorize dozens of digits of π, and it is not unusual for the winner to have memorized over a hundred digits. By the way, the current world record for π memorization belongs to Chao Lu of China, who in 2005 recited π to 67,890 decimal places! According to the Guinness Book of World Records, Lu practiced for four years to reach this many digits, and it took him a little over twenty-four hours to recite all the digits.
Behold the first 100 digits of π:
π = 3.141592653589793238462643383279502884197169399375
105820974944592307816406286208998628034825342117067 . . .![]()
Over the years, people have come up with creative ways to memorize the digits of π. One method is to create sentences where the length of each word gives us the next digit of π. Some famous examples include “How I wish I could calculate pi” (which yields seven digits: 3.141592) and “How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics” (which provides fifteen digits).
A most impressive example was written in 1995 by Mike Keith, who generated 740 digits in an amazing parody of Edgar Allan Poe’s poem “The Raven.” The first stanza, along with the title, generates 42 digits. The stanza’s “disturbing” ten-letter word generates the digit 0.
Poe, E. Near a Raven
Midnights so dreary, tired and weary.
Silently pondering volumes extolling all by-now obsolete lore.
During my rather long nap—the weirdest tap!
An ominous vibrating sound disturbing my chamber’s antedoor.
“This,” I whispered quietly, “I ignore.”
Keith went on to extend this masterpiece by writing a 3835-digit “Cadaeic Cadenza.” (Note that if you replace C with 3, A with 1, D with 4, and so on, then “cadaeic” becomes 3141593.) It begins with the “Raven” parody, but also includes digital commentaries and parodies of other poems such as Lewis Carroll’s “Jabberwocky.” His most recent contribution to this genre is Not a Wake: A Dream Embodying π’s Digits Fully for 10000 Decimals. (Note the word lengths in the book’s title!)
The word length method for memorizing π suffers from a significant problem. Even if you could memorize the sentences, poems, and stories, it is not so easy to instantly determine the number of letters in each word. Or as I like to say, “How I wish I could elucidate to others. There are often superior mnemonics!” (which yields thirteen digits).
My favorite way to memorize numbers is through the use of a phonetic code called the major system. In this code, every digit is represented by one or more consonant sounds. Specifically,
1 = t or d
2 = n
3 = m
4 = r
5 = l
6 = j, ch, or sh
7 = k or hard g
8 = f or v
9 = p or b
0 = s or z
There are even mnemonics for memorizing this mnemonic system! My friend Tony Marloshkovips offers the following suggestions. The letter t (or its phonetically similar d) has 1 downstroke; n has 2 down-strokes; m has 3 downstrokes; “four” ends in the letter r; displaying 5 fingers, you see an L between your index finger and your thumb; a backward 6 looks like a j; two 7s can be drawn to form a K; a skater does a figure 8; turning the 9 backward or upside down, you obtain p or b; “zero” begins with z. Or if you prefer, you can put all the consonants in order, TNMRLShKVPS, and you get my (fictitious) friend’s name: Tony Marloshkovips.
We can use this code to turn numbers into words by inserting vowel sounds around the associated consonant sounds. For example, the number 31, which uses consonants m and t (or m and d), can be turned into words like
31 = mate, mute, mud, mad, maid, mitt, might, omit, muddy
Notice that a word like “muddy” or “mitt” is acceptable, since the d or t sound only occurs once. Spelling doesn’t matter. Since the consonant sounds of h, w, and y are not represented on the list, then it is acceptable to use those sounds as freely as vowels. Thus, we could also turn 31 into words like “humid” or “midway.” Notice that although a number can often be represented by many different words, a word can only be represented by a single number.
The first three digits of π, with consonant sounds m, t, and r, can become words like
314 = meter, motor, metro, mutter, meteor, midyear, amateur
The first five digits 31415, can become “my turtle.” Extending this to the first twenty-four digits of π, 314159265358979323846264 can become
My turtle Pancho will, my love, pick up my new mover Ginger
I turn the next seventeen digits 33832795028841971, into
My movie monkey plays in a favorite bucket
I like the next nineteen digits, 6939937510582097494, since they allow some long words:
Ship my puppy Michael to Sullivan’s backrubber
The next eighteen digits of π, 459230781640628620, could give us
A really open music video cheers Jenny F. Jones
followed by twenty-two more digits, 8998628034825342117067:
Have a baby fish knife so Marvin will marinate the goose chick!
Thus, with five silly sentences, we have encoded the first one hundred digits of π!
The phonetic code is quite useful for memorizing dates, phone numbers, credit card numbers, and more. Try it, and with a little bit of practice, you will vastly improve your ability to remember numbers.
All mathematicians agree that π is one of the most important numbers in mathematics. But if you look at the formulas and applications that use π, you will find that most of them have π multiplied by 2. The Greek letter τ (tau, rhymes with “wow”) has been adopted to represent this quantity
τ = 2π
Many people believe that if we could go back in time, mathematical formulas and key concepts in trigonometry would be expressed more simply using τ instead of π. These ideas have been elegantly and entertainingly expressed in articles by Bob Palais (“π is Wrong!”) and Michael Hartl (“The Tau Manifesto”). The “central point” of the argument is that circles are defined in terms of their radius, and when we compare the circumference to the radius, we have C/r = 2π = τ. Some textbooks are now labeled as “τ-compliant” to indicate that they will express formulas in terms of both π and τ. (Although switching to this constant may not be “easy as pie,” many students and teachers will agree that τ is easier than π.) It will be interesting to see what happens to this movement in the coming decades. Supporters of τ (who call themselves tauists) earnestly believe that they have the truth on their side, but they are tolerant of the more traditional notation. As they like to say, tauists are never pious.
Here are the first one hundred digits of τ with spaces inserted for the mnemonics given afterward. Note that τ begins with the numbers 6 and 28, both of which are perfect numbers, as described in Chapter 6. Is that a coincidence? Of course! But it’s a fun tidbit anyway.
τ = 6.283185 30717958 64769252 867665 5900576 839433 8798750 211641949 8891846 15632 812572417 99725606 9650684 234135 . . .![]()
In 2012, thirteen-year-old Ethan Brown established a world record by memorizing 2012 digits of τ as a fund-raising project. He used the phonetic code, but instead of creating long sentences, he created visual images, where each image contained a subject, an action (always ending in -ing) and an object being acted upon. The first seven digits, 62 831 85, became “An ocean vomiting a waffle.” Here are his images for the first one hundred digits of τ.
An ocean vomiting a waffle
A mask tugging on a bailiff
A shark chopping nylon
Fudge coaching a cello
Elbows selling a couch
Foam burying a mummy
Fog paving glass
A handout shredding a prop
FIFA beautifying the Irish
A doll shooing a minnow
A photon looking neurotic
A puppy acknowledging the sewage
A peach losing its chauffeur
Honey marrying oatmeal
To make the images even easier to remember, Brown adopted the memory palace approach by imagining himself wandering through his school, and as he walked down certain passageways and entered various classrooms, there would be three to five objects doing silly things in each room. Ultimately, he had 272 images split up among more than 60 locations. It took him about 4 months of preparation to recite the 2012 digits, which he did in 73 minutes.
Let’s end this chapter with a musical celebration of π. I wrote this as a lyrical addition to Larry Lesser’s parody, “American Pi.” You should only sing the song once, because π doesn’t repeat.
A long, long, time ago,
I can still remember how my math class used to make me snore.
’Cause every number we would meet
Would terminate or just repeat,
But maybe there were numbers that did more.
But then my teacher said, “I dare ya
To try to find the circle’s area.”
Despite my every action,
I couldn’t find a fraction.
I can’t remember if I cried,
The more I tried or circumscribed,
But something touched me deep inside
The day I learned of pi!
Pi, pi, mathematical pi,
Twice eleven over seven is a mighty fine try.
A good old fraction you may hope to supply,
But the decimal expansion won’t die.
Decimal expansion won’t die.
Pi, pi, mathematical pi,
3.141592653589.
A good old fraction you may hope to define,
But the decimal expansion won’t die!