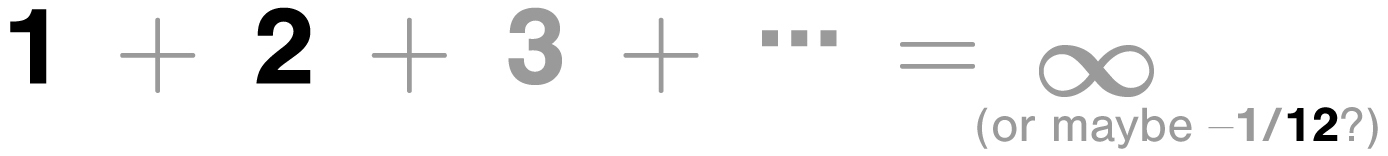
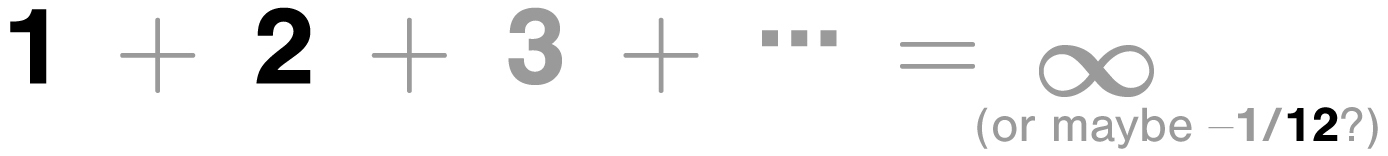
The Magic of InfinityThe Magic of Infinity
Infinitely Interesting
Last, but certainly not least, let’s talk about infinity. Our journey began in Chapter 1 with the sum of the numbers from 1 to 100:
1 + 2 + 3 + 4 + · · · + 100 = 5050
and we eventually discovered formulas for the sum of the numbers from 1 to n:
and we discovered formulas for other sums with a finite number of terms. In this chapter, we will explore sums that have an infinite number of terms like
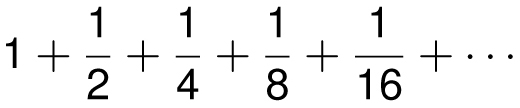
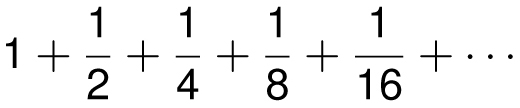
which, I hope, I will convince you has a sum that is equal to 2. Not approximately 2, but exactly equal to 2. Some sums have intriguing answers, like
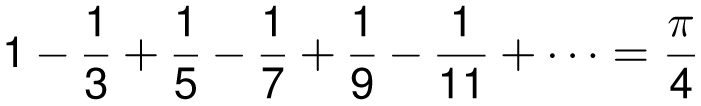
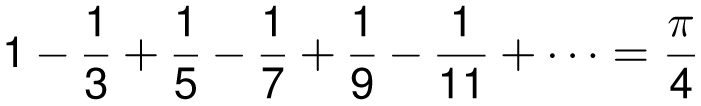
And some infinite sums, like
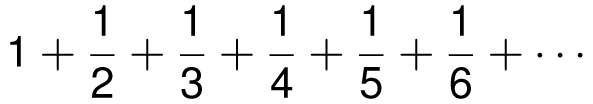
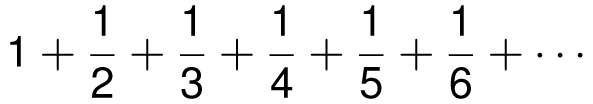
don’t add up to anything. We say that the sum of all the positive numbers is infinity, denoted
1 + 2 + 3 + 4 + 5 + · · · = ∞
which means that the sum grows without bound. In other words, the sum will eventually exceed any number you wish: it will eventually exceed one hundred, then one million, then one quadrillion, and so on. And yet, by the end of this chapter, we shall see that a case could be made that
Are you intrigued? I hope so! As we shall see, when you enter the twilight zone of infinity, very strange things can happen, which is part of what makes mathematics so fascinating and fun.
Is infinity a number? Not really, although it sometimes gets treated that way. Loosely speaking, mathematicians might say:
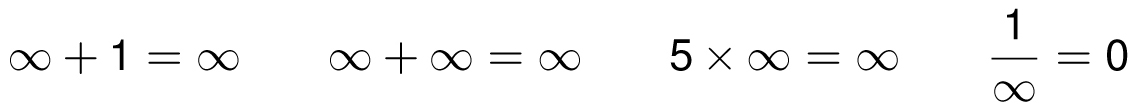
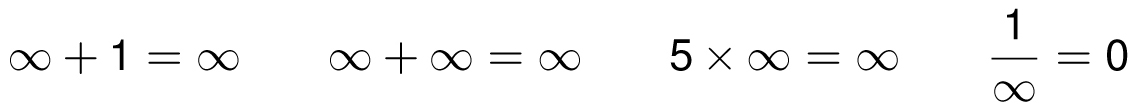
Technically, there is no largest number, since we can always add 1 to obtain a larger number. The symbol ∞ essentially means “arbitrarily large” or bigger than any positive number. Likewise, the term − ∞ means less than any negative number. By the way, the quantities ∞ − ∞ (infinity minus infinity) and 1/0 are undefined. It is tempting to define 1/0 = ∞, since when we divide 1 by smaller and smaller positive numbers, the quotient gets bigger and bigger. But the problem is that when we divide 1 by tiny negative numbers, the quotient gets more and more negative.
An Important Infinite Sum: The Geometric Series
Let’s start with a statement that is accepted by all mathematicians, but seems wrong to most people when they first see it:
0.99999 . . . = 1
Everyone agrees that the two numbers are close, indeed extremely close, but many still feel that they should not be considered the same number. Let me try to convince you that the numbers are in fact equal by offering various different proofs. I hope that at least one of these explanations will satisfy you.
Perhaps the quickest proof is that if you accept the statement that
then when you multiply both sides by 3 you get
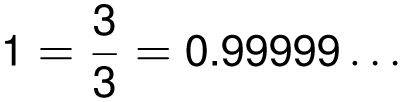
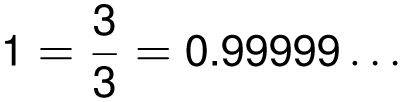
Another proof is to use the technique that we used in Chapter 6 to evaluate repeating decimals. Let’s denote the infinite decimal expansion with the variable w as follows:
w = 0.99999 . . .
Now if we multiply both sides by 10, then we get
10w = 9.99999 . . .
Subtracting the first equation from the second gives us
9w = 9.00000 . . .
which means that w = 1.
Here’s an argument that uses no algebra at all. Do you agree that if two numbers are different, then there must be a different number in between them (for instance, their average)? Then suppose, to the contrary, that 0.99999 . . . and 1 were different numbers. If that were the case, what number would be in between them? If you can’t find another number between them, then they can’t be different numbers.
We say that two numbers or infinite sums are equal if they are arbitrarily close to one another. In other words, the difference between the two quantities is less than any positive number you can name, whether it be 0.01 or 0.0000001 or 1 divided by a trillion. Since the difference between 1 and 0.99999 . . . is smaller than any positive number, then mathematicians agree to call these quantities equal.
It’s with the same logic that we can evaluate the infinite sum below:
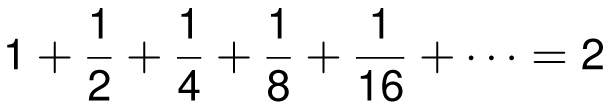
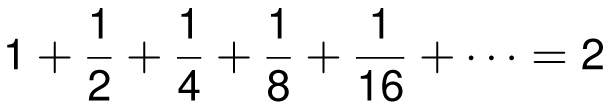
We can give this sum a physical interpretation. Imagine you are standing two meters away from a wall, and you take one big step exactly one meter toward the wall, then another step half a meter toward the wall, then a quarter of a meter, then an eighth of a meter, and so on. After each step, the distance between you and the wall is cut exactly in half. Ignoring the practical limitations of taking tinier and tinier steps, you eventually get as close to the wall as desired. Hence the total length of your steps would be exactly two meters.
We can illustrate this sum geometrically, as in the figure below. We start with a 1-by-2 rectangle with area 2, then cut it in half, then half again, then half again, and so on. The area of the first region is 1. The next region has area 1/2, then the next region has area 1/4, and so on. As n goes to infinity, the regions fill up the entire rectangle, and so their total area is 2.
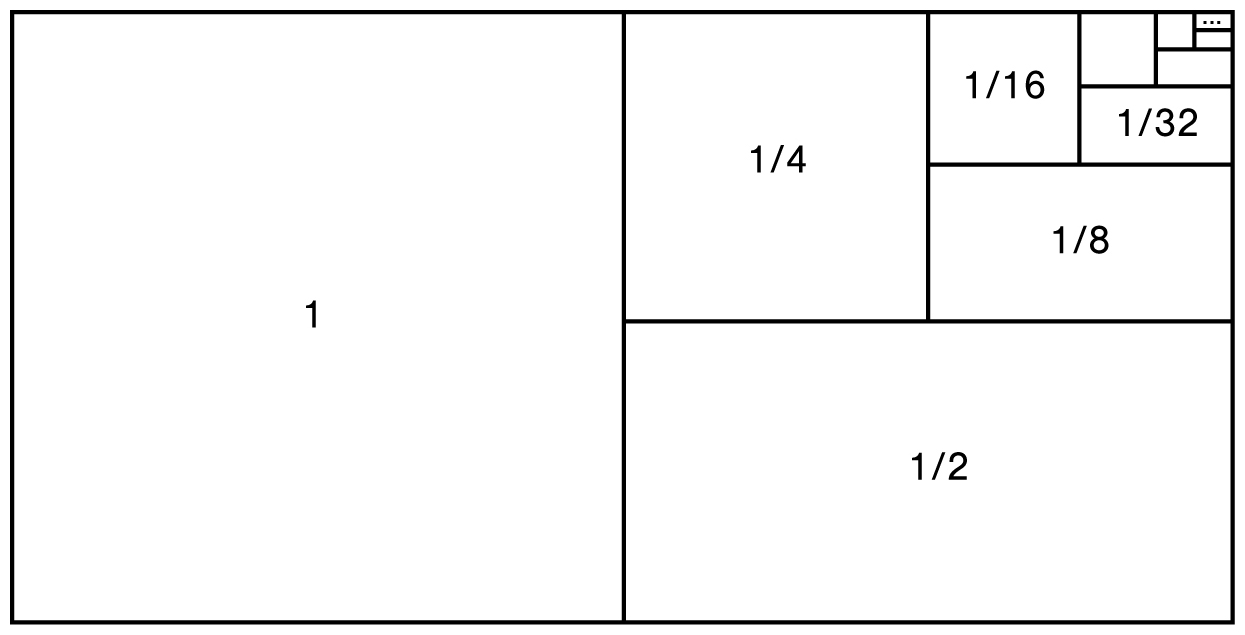
A geometric proof that 1 + 1/2 + 1/4 + 1/8 + 1/16 + · · · = 2
For a more algebraic explanation, we look at the partial sums, as given in the table below.
The pattern seems to indicate that for n ≥ 0,
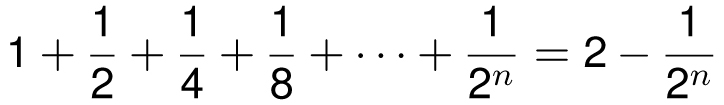
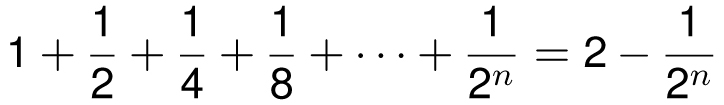
We can prove this by induction (as we learned in Chapter 6) or as a special case of the finite geometric series formula below.
Theorem (finite geometric series): For x ≠ 1 and n ≥ 0,
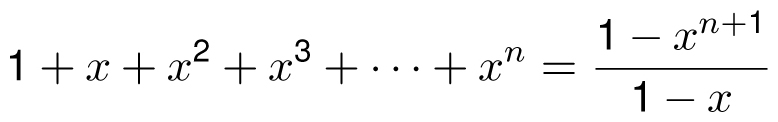
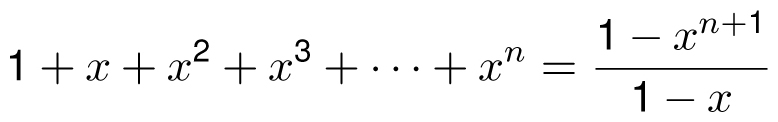
Proof 1: This can be proved by induction as follows. When n = 0, the formula says that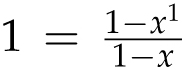 
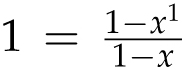, which is certainly true. Now assume the formula holds when n = k, so that
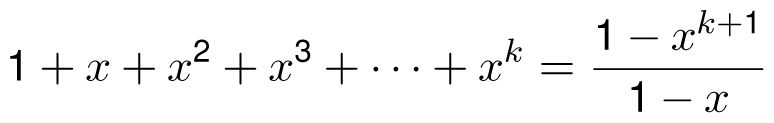
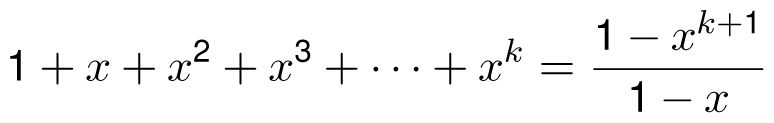
Then the formula will continue to be true when n = k + 1, since when we add xk+1 to both sides, we get
as desired.
Alternatively, we can prove this by shifty algebra, as follows.
Proof 2: Let
S = 1 + x + x2 + x3 + · · · + xn
Then when we multiply both sides by x we get
xS = x + x2 + x3 + · · · +xn + xn+1
Subtracting away the xS (pronounced “excess”), we have massive amounts of cancellation, leaving us with
S − xS = 1 − xn+1
In other words, S(1 − x) = 1 − xn+1, and therefore
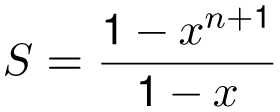
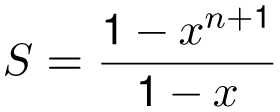
as desired.
Notice that when x = 1/2, the finite geometric series confirms our earlier pattern:
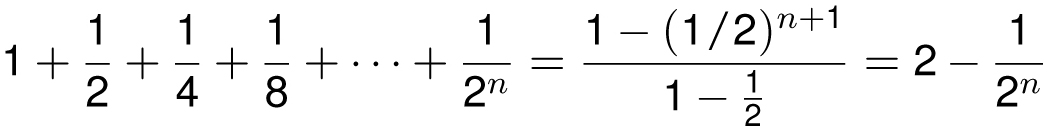
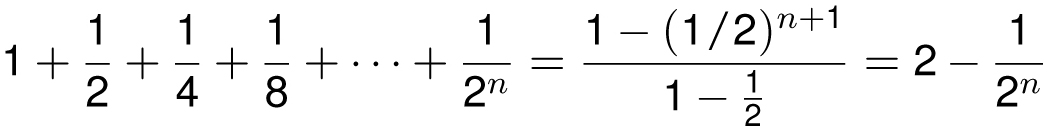
As n gets larger and larger, (1/2)n gets closer and closer to 0. Thus, as n → ∞, we have
Aside
Here’s a joke that only mathematicians find funny. An infinite number of mathematicians walk into a bar. The first mathematician says, “I’d like one glass of beer.” The second mathematician says, “I’d like half a glass of beer.” The third mathematician says, “I’d like a quarter of a glass of beer.” The fourth mathematician says, “I’d like an eighth of a glass. . . .” The bartender shouts, “Know your limits!” and hands them two beers.
More generally, any number between −1 and 1 that gets raised to higher and higher powers will get closer and closer to 0. Thus we have the all-important (Infinite) geometric series.
Theorem (geometric series): For −1 < x < 1,
The geometric series solves the last problem by letting x = 1/2:
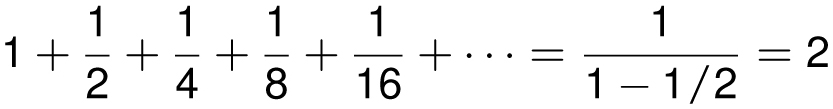
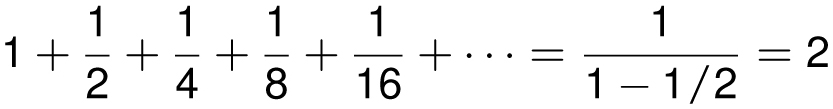
If the geometric series looks familiar, it’s because we encountered it at the end of the last chapter when we used calculus to show that the function y = 1/(1 − x) has Taylor series 1 + x + x2 + x3 + x4 + · · ·.
Let’s see what else the geometric series tells us. What can we say about the following sum?
When we factor the number 1/4 out of each term, this becomes
so the geometric series (with x = 1/4) says that this simplifies to
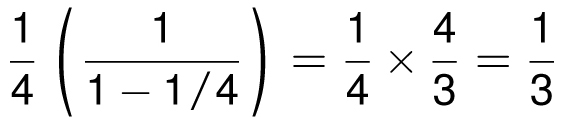
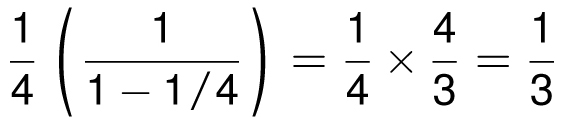
That series has a particularly beautiful proof without words as shown on the next page. Notice that the dark squares occupy exactly one-third of the area of the big square.
We can even use the geometric series to settle the 0.99999 . . . question, since an infinite decimal expansion is just an infinite series in disguise. Specifically, we can use the geometric series with x = 1/10 to get
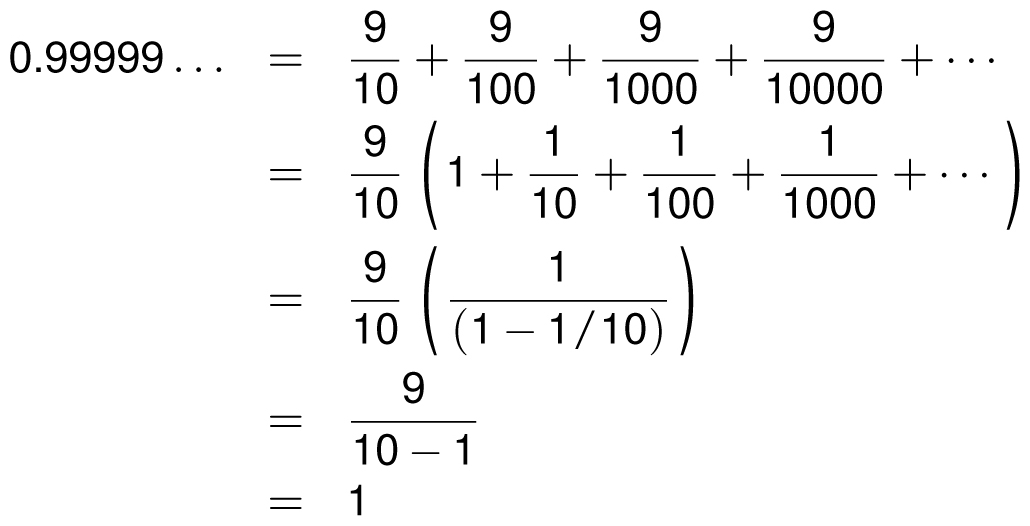
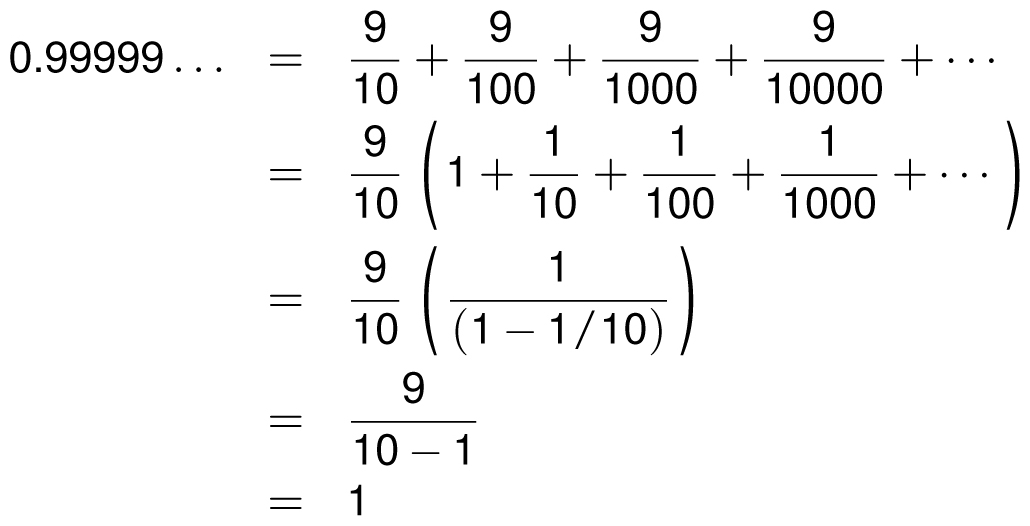
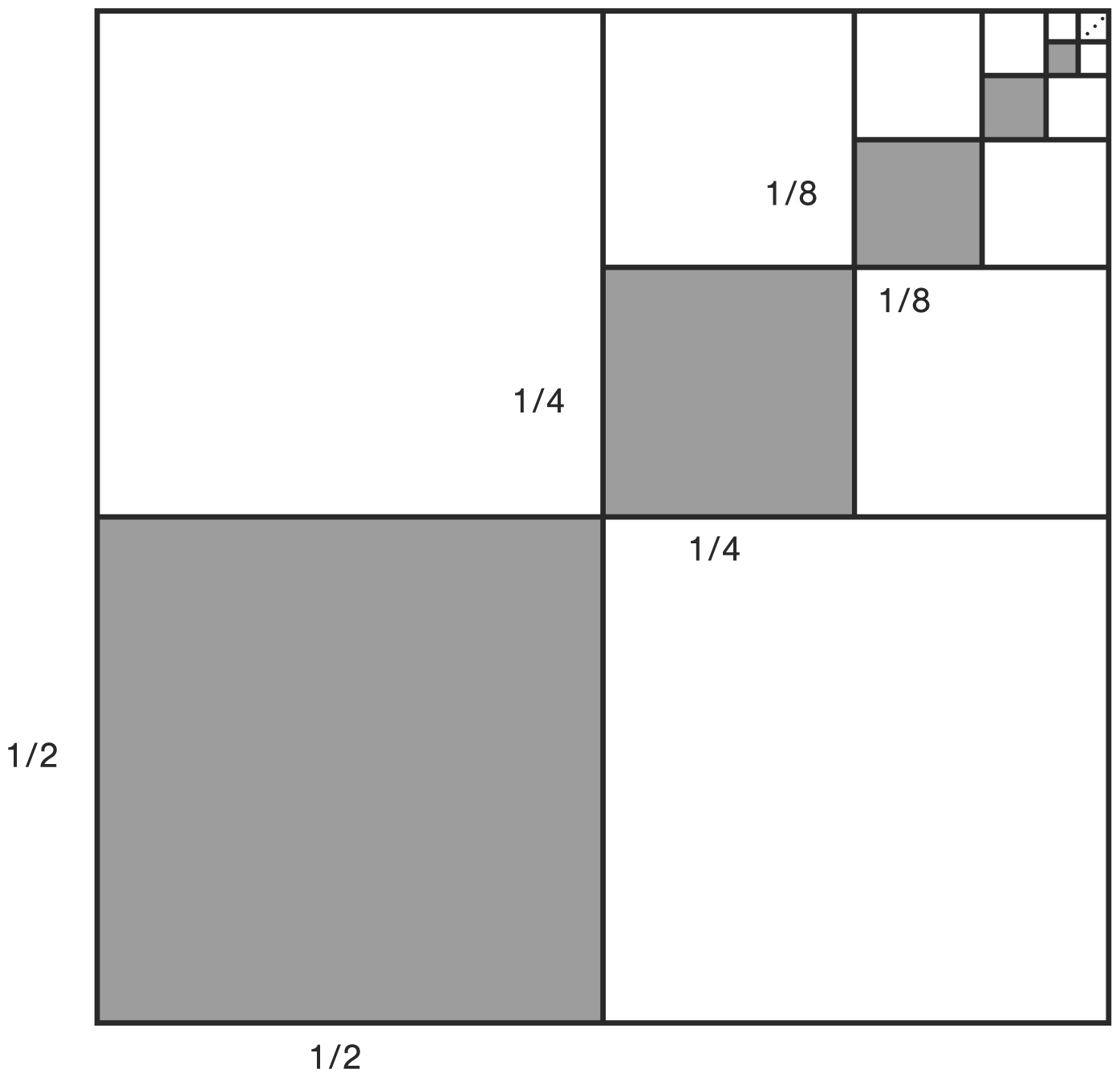
Proof without words: 1/4 + 1/16 + 1/64 + 1/256 + · · · = 1/3
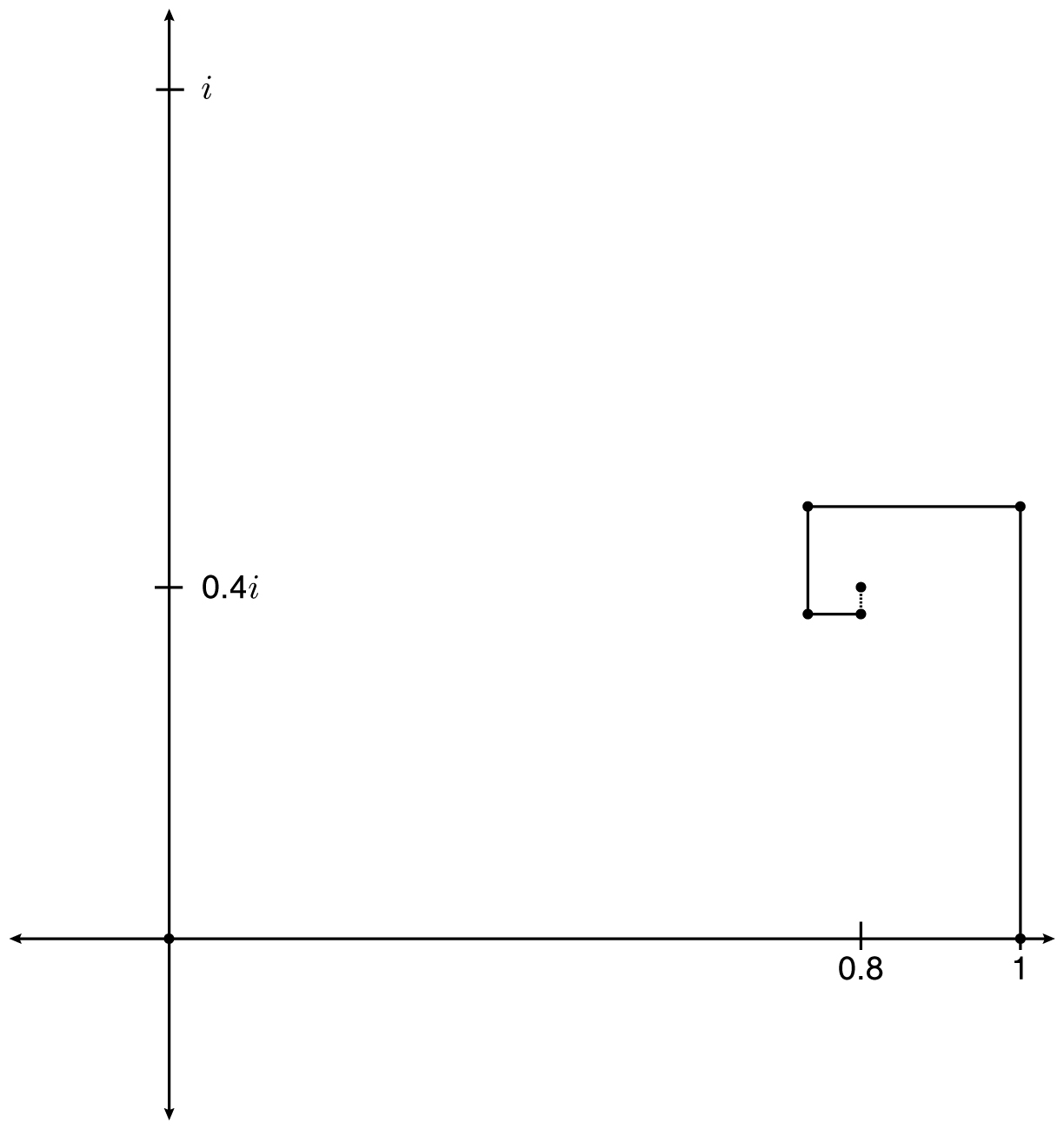
The geometric series formula even works when x is a complex number, provided that the length of x is less than 1. For example, the imaginary number i/2 has length 1/2, so the geometric series tells us that
which we illustrate on the next page on the complex plane.
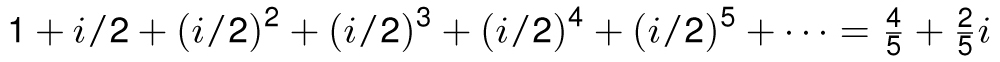
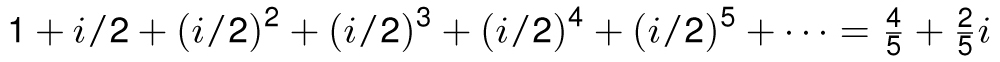
Although the finite geometric series formula is valid for all values of x ≠ 1, the (infinite) geometric series formula requires that |x| < 1. For example, when x = 2, the finite geometric series correctly tells us (as we derived in Chapter 6) that
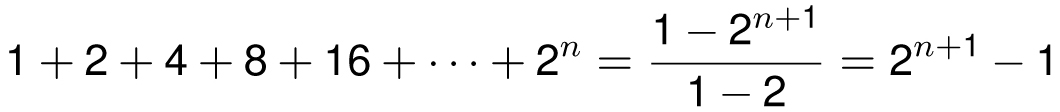
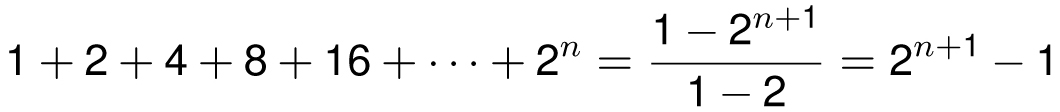
but substituting x = 2 in the geometric series formula says that
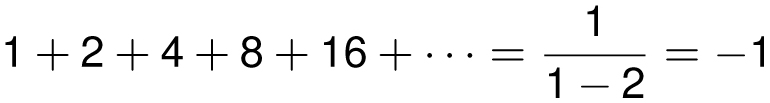
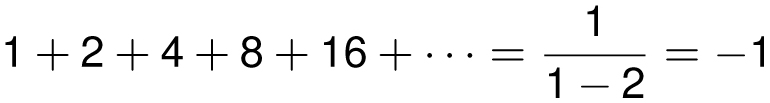
which looks ridiculous. (Although looks can be deceiving. We will actually see a plausible interpretation of this result in our last section.)
Aside
There are infinitely many positive integers:
1, 2, 3, 4, 5 . . .
There are also infinitely many positive even integers:
2, 4, 6, 8, 10 . . .
Mathematicians say that the set of positive integers and the set of even positive integers have the same size (or cardinality or level of infinity) because they can be paired up with one another:
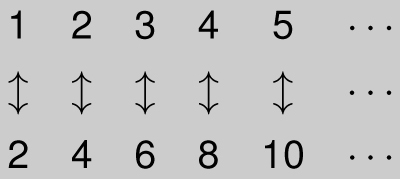
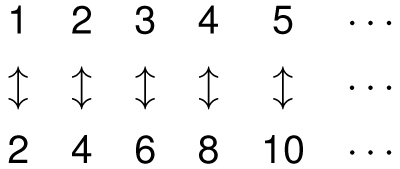
A set that can be paired up with the positive integers is called countable. Countable sets have the smallest level of infinity. Any set that can be listed is countable, since the first element in the list is paired up with 1, the second element is paired up with 2, and so on. The set of all integers
. . . − 3, −2, −1, 0, 1, 2, 3 . . .
can’t be listed from smallest to largest (what would be the first number on the list?), but they can be listed this way:
0, 1, −1, 2, −2, 3, −3 . . .
Thus the set of all integers is countable, and of the same size as the number of positive integers.
How about the set of positive rational numbers? These are the numbers of the form m/n where m and n are positive integers. Believe it or not, this set is countable too. They can be listed as follows:
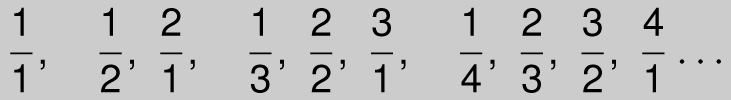
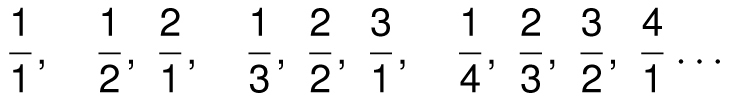
where we first list the fractions according to the sum of their numerators and denominators. Since every rational number appears on the list, the positive rational numbers are countable too.
Aside
Are there any infinite sets of numbers that are not countable? The German mathematician Georg Cantor (1845–1918) proved that the real numbers, even when restricted to those that lie between 0 and 1, form an uncountable set. You might try to list them this way:
0.1, 0.2, . . . , 0.9, 0.01, 0.02, . . . , 0.99, 0.001, 0.002, . . . 0.999, . . .
and so on. But that will only generate real numbers with a finite number of digits. For instance, the number 1/3 = 0.333 . . . will never appear on this list. But could there be a more creative way to list all the real numbers? Cantor proved that this would be impossible, by reasoning as follows. Suppose, to the contrary, that the real numbers were listable. To give a concrete example, suppose the list began as
We can prove that such a list is guaranteed to be incomplete by creating a real number that won’t be on the list. Specifically, we create the real number 0.r1r2r3r4 . . . where r1 is an integer between 0 and 9 and differs from the first number in the first digit (in our example, r1 ≠ 3) and r2 differs from the second number in the second digit (here r2 ≠ 7) and so on. For instance, we might create the number 0.2674 . . . . Such a number can’t be on the list anywhere. Why is it not the millionth number on the list? Because it differs in the millionth decimal place. Hence any example of a list you create is guaranteed to be missing some numbers, so the real numbers are not countable. This is called Cantor’s diagonalization argument, but I like to call it proof by Cantor-example. (Sorry.)
In essence, we have shown that although there are infinitely many rational numbers, there are considerably more irrational numbers. If you randomly choose a real number from the real line, it will almost certainly be irrational.
Infinite series arise frequently in probability problems. Suppose you roll two 6-sided dice repeatedly until a total of 6 or 7 appears. If a 6 occurs before a 7 occurs, then you win the bet. Otherwise, you lose. What is your chance of winning? There are 6 × 6 = 36 equally likely dice rolls. Of these, 5 of them have a total of 6 (namely (1, 5), (2, 4), (3, 3), (4, 2), (5, 1)) and 6 of them have a total of 7 ((1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)). Hence it would seem that your chance of winning should be less than 50 percent. Intuitively, as you roll the dice, there are only 5 + 6 = 11 rolls that matter—all the rest require us to roll again. Of these 11 numbers, 5 of them are winners and 6 are losers. Thus it would seem that your chance of winning should be 5/11.
We can confirm that the probability of winning is indeed 5/11 using the geometric series. The probability of winning on the first roll of the dice is 5/36. What is the chance of winning on the second roll? For this to happen, you must not roll a 6 or 7 on the first roll, then roll a 6 on the second roll. The chance of a 6 or 7 on the first roll is 5/36 + 6/36 = 11/36, so the chance of not rolling 6 or 7 is 25/36. To find the probability of winning on the second roll, we multiply this number by the probability of rolling a 6 on any individual roll, 5/36, so the probability of winning on the second roll is (25/36)(5/36). To win on the third roll, the first two rolls must not be 6 or 7, then we must roll 6 on the third roll, which has probability (25/36)(25/36)(5/36). The probability of winning on the fourth roll is (25/36)3(5/36), and so on. Adding all of these probabilities together, the chance of winning your bet is
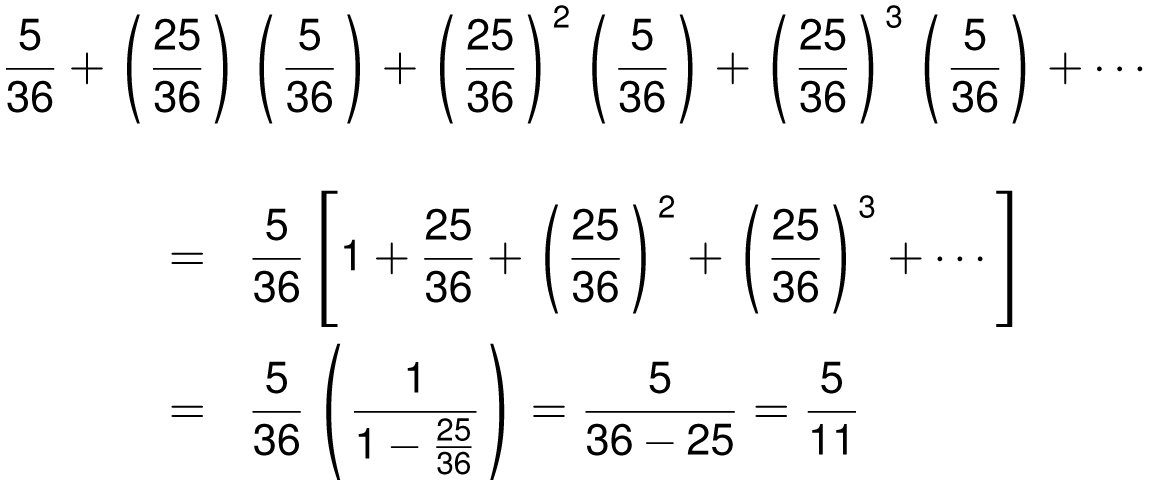
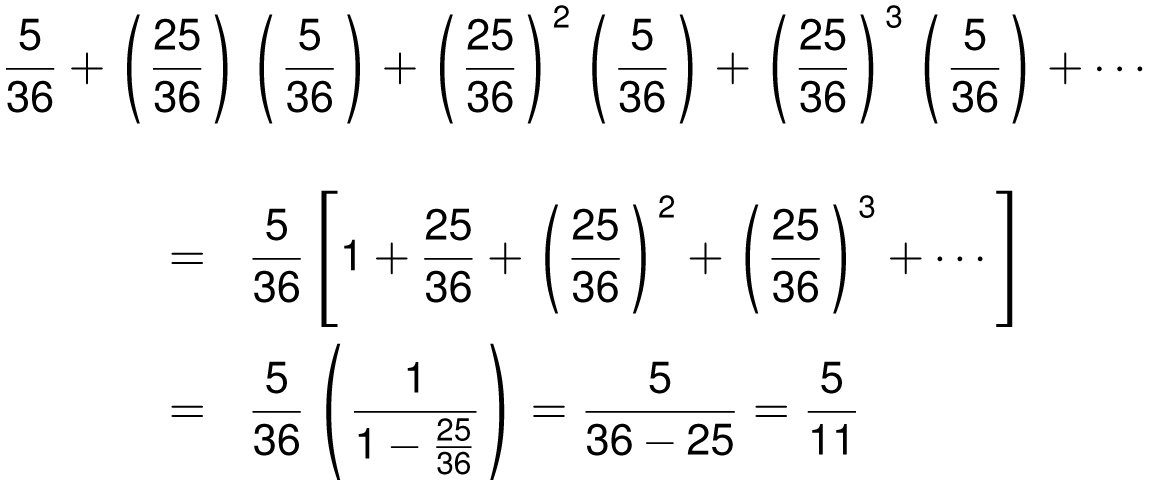
as predicted.
The Harmonic Series and Variations
When an infinite series adds up to a (finite) number, we say that the sum converges to that number. When an infinite series doesn’t converge, we say that the series diverges. If an infinite series converges, then the individual numbers being summed need to be getting closer and closer to 0. For example, we saw that the series 1 + 1/2 + 1/4 + 1/8 + · · · converged to 2, and notice that the terms 1, 1/2, 1/4, 1/8 . . . are getting closer and closer to 0.
But the converse statement is not true, since it is possible for a series to diverge even if the terms are heading to 0. The most important example is the harmonic series, so named because the ancient Greeks discovered that strings of lengths proportional to 1, 1/2, 1/3, 1/4, 1/5, . . . could produce harmonious sounds.
Theorem: The harmonic series diverges. That is,
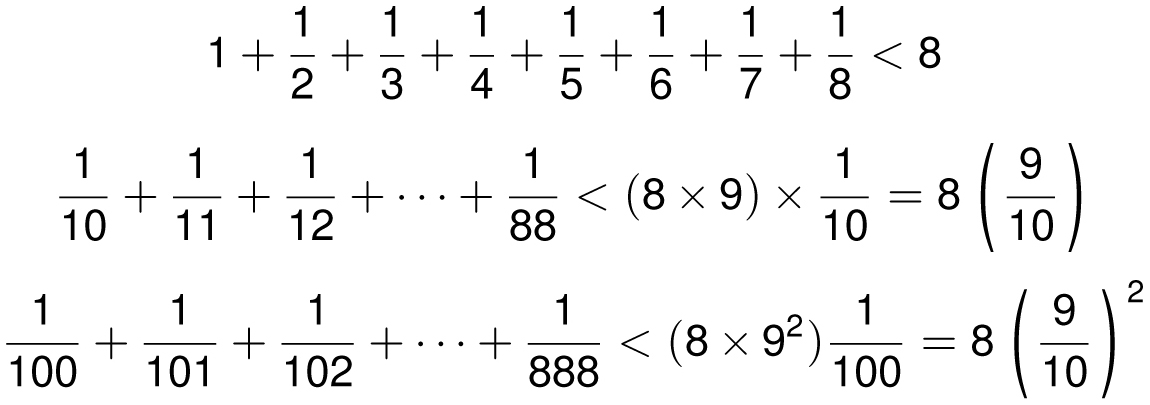
Proof: To prove that the sum is infinity, we need to show that the sum gets arbitrarily large. To do this we break up our sum into pieces based on the number of digits in the denominator. Notice that since the first 9 terms are each bigger than 1/10, therefore
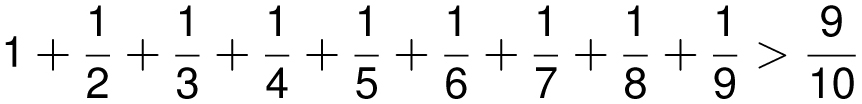
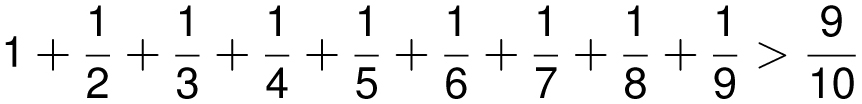
The next 90 terms are each bigger than 1/100, and so
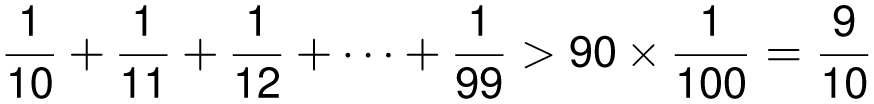
Likewise, the next 900 terms are each bigger than 1/1000. Thus,
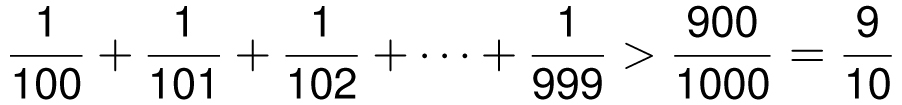
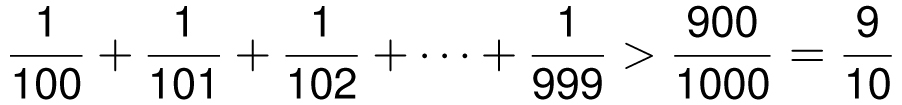
Continuing this way, we see that
and so on. Hence the sum of all of the numbers is at least
which grows without bound.
.
Aside
Here’s a fun fact:
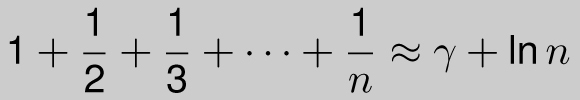
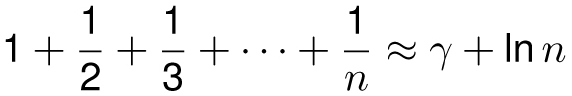
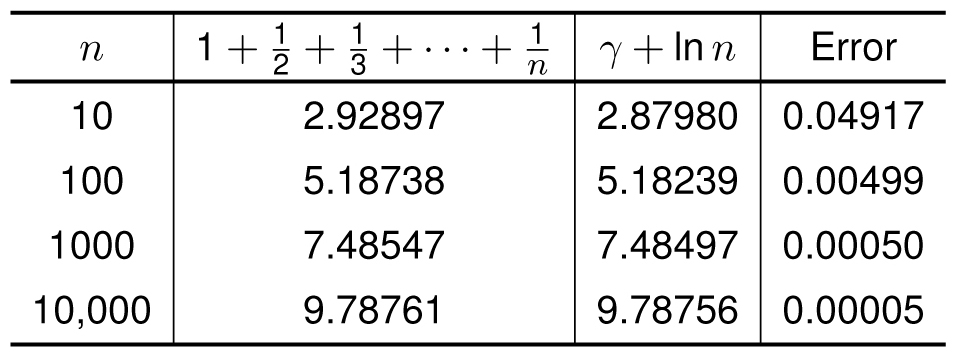
where γ is the number 0.5772155649 . . . (called the Euler-Mascheroni constant) and ln n is the natural logarithm of n, described in Chapter 10. (It is not known if γ, pronounced “gamma,” is rational or not.) The approximation gets better as n gets larger. Here is a table comparing the sum with the approximation.
Equally fascinating is the fact that if we only look at prime denominators, then for a large prime number p,
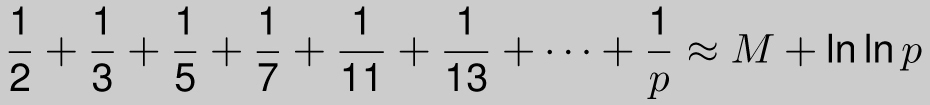
where M = 0.2614972 . . . is the Mertens constant and the approximation becomes more accurate as p gets larger.
One consequence of this fact is that
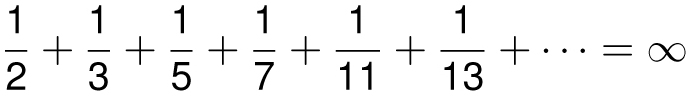
but it really crawls to infinity because the log of the log of p is small, even if p is quite large. For instance, when we sum the reciprocals of all prime numbers below googol, 10100, the sum is still below 6.
Let’s see what happens when you modify the harmonic series. If you throw away a finite number of terms, the series still diverges. For example, if you throw away the first million terms 
, which sums to a little more than 14, the remaining terms still sum to infinity.
If you make the terms of the harmonic series larger, then the sum still diverges. For example, since for 
we have
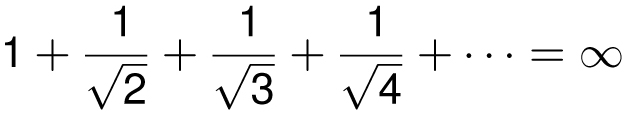
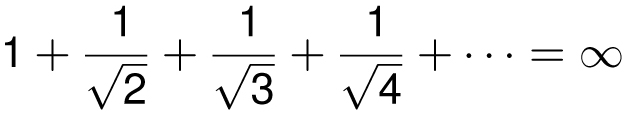
But making each term smaller does not necessarily mean that the sum will converge. For example, if we divide each term in the harmonic series by 100, it still diverges, since
Yet there are changes to the series that will cause it to converge. For instance, if we square each term, the series converges. As Euler proved,
In fact, it can be shown (through integral calculus) that for any p > 1,
converges to some number below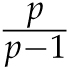 
. For example, when p = 1.01, even though the terms are just slightly smaller than the terms of the harmonic series, we have a convergent series
Suppose we remove from the harmonic series any number with a 9 in it somewhere. In this situation, we can show that the series does not sum to infinity (and therefore must converge to something). We prove this by counting the 9-less numbers with denominators of each length. For instance, we begin with 8 fractions with one-digit denominators, namely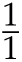 
through 
. There are 8 × 9 = 72 two-digit numbers without 9, since there are 8 choices for the first digit (anything but 0 or 9) and 9 choices for the second digit. Likewise, there are 8 × 9 × 9 three-digit numbers without 9s, and more generally, 8 × 9n−1 n-digit numbers without 9s. Noting that the largest of the one-digit fractions is 1, the largest two-digit fraction is 
, and the largest three-digit fraction is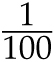 
, we can break our infinite series into blocks as follows,
and so on. The sum of all of the numbers is at most
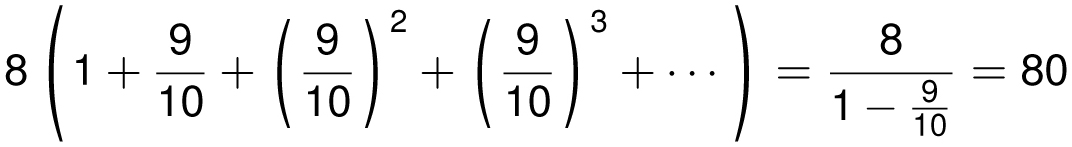
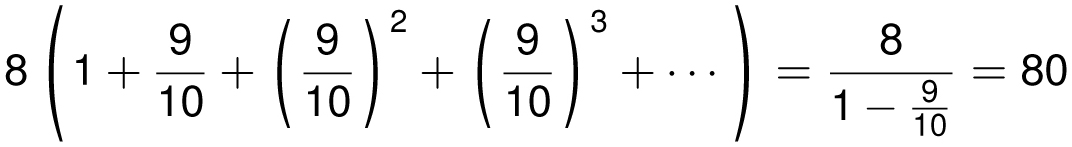
by the geometric series. Hence, the 9-less series converges to a number less than 80.
One way to think of the convergence of this series is that almost all large numbers have a 9 in them somewhere. Indeed, if you generate a random number with each digit randomly chosen from 0 to 9, the chance that the number 9 was not among the first n digits would be (9/10)n, which goes to 0 as n gets larger and larger.
Aside
If we treat the digits of π and e as random strings of digits, then it is a virtual certainty that your favorite integer appears somewhere in those numbers. For example, my favorite four-digit number, 2520, appears as digits 1845 through 1848 of π. The first 6 Fibonacci numbers 1, 1, 2, 3, 5, 8, appear beginning at digit 820,390. It’s not too surprising to see this among the first million digits, since with a randomly generated number, the chance that the digits of a particular six-digit location matches your number is one in a million. So with about a million six-digit locations, your chances are pretty good. On the other hand, it is rather astonishing that the number 999999 appears so early in π, beginning at digit 763. Physicist Richard Feynman once remarked that if he memorized π to 767 decimal places, people might think that π was a rational number, since he could end his recitation with “999999 and so on.”
There are programs and websites that will find your favorite digit strings inside π and e. Using one of these programs, I discovered that if I memorized π to 3000 decimal places, it would end with 31961, which is amazing to me because March 19, 1961, happens to be my birthday!
Intriguing and Impossible Infinite Sums
Let’s summarize some of the sums we have seen so far.
We began this chapter by investigating
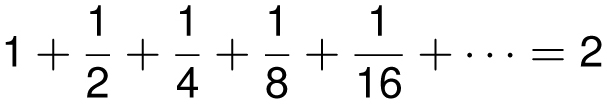
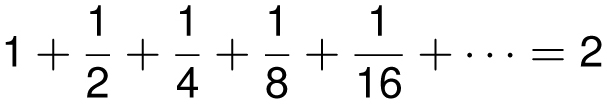
We saw that this was a special case of the geometric series, which says that for any value of x where −1 < x < 1,
Notice that the geometric series also works for negative numbers between 0 and −1. For instance, when x = −1/2, it says
A series that alternates between positive and negative numbers that are getting closer and closer to zero is called an alternating series. Alternating series always converge to some number. To illustrate with the alternating series above, draw the real line and put your finger on the number 0. Then move it to the right by 1, then go to the left by 1/2, then go to the right by 1/4. (At this point, your finger should be on the point 3/4.) Then go to the left by 1/8 (so that your finger is now on the point 5/8), and so on. Your finger will be homing in on a single number, in this case 2/3.
Now consider the alternating series
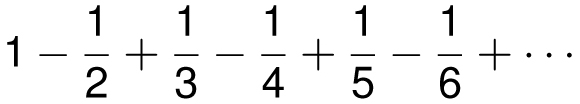
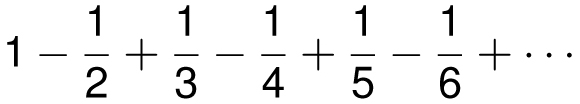
After four terms, we know that the infinite sum is at least 1 − 1/2 + 1/3 − 1/4 = 7/12 = 0.583 . . . , and after five terms, we know that it is at most 1 − 1/2 + 1/3 − 1/4 + 1/5 = 47/60 = 0.783. . . . The eventual infinite sum is a little more than halfway between these two numbers, namely 0.693147. . . . Using calculus, we can find the real value of this number.
As a warm-up exercise, take the geometric series:
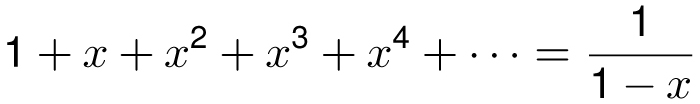
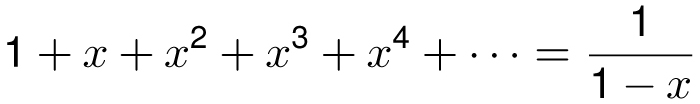
and let’s see what happens when we differentiate both sides. Recall from Chapter 11 that the derivatives of 1, x, x2, x3, x4, and so on are, respectively, 0, 1, 2x, 3x2, 4x3, and so on. Thus, if we assume that the derivative of an infinite sum is the (infinite) sum of the derivatives, and use the chain rule to differentiate (1 − x)−1, then we get for −1 < x < 1,
Next let’s take the geometric series with x replaced by −x, so that for −1 < x < 1,
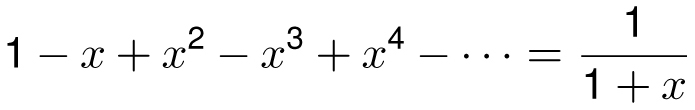
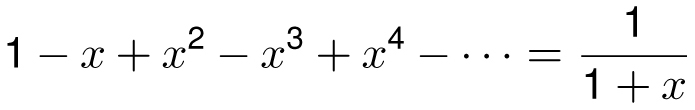
Now we take the anti-derivative of both sides, known to calculus students as integration. To find the anti-derivative, we go backward. For instance, the derivative of x2 is 2x, so going backward, we say that the anti-derivative of 2x is x2. (As a technical note for calculus students, the derivative of x2 + 5, or x2 + π, or x2 + c for any number c, is also 2x, so the anti-derivative of 2x is really x2 + c.) The anti-derivatives of 1, x, x2, x3, x4, and so on are, respectively x, x2/2, x3/3, x4/4, x5/5, and the anti-derivative of 1/(1 + x) is the natural logarithm of 1 + x. That is, for −1 < x < 1,
(Technical note for calculus students: the constant term on the left side is 0, since when x = 0, we want the left side to evaluate to ln 1 = 0.) As x gets closer and closer to 1, we discover the natural meaning of 0.693147 . . . , namely
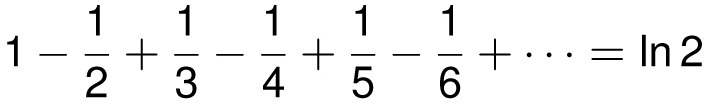
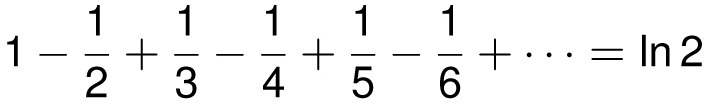
Aside
If we write the geometric series with x replaced with −x2, we get, for x between −1 and 1,
In most calculus textbooks, it is shown that y = tan−1 x has derivative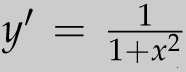 
. Thus, if we take the anti-derivative of both sides (and note that tan−1 0 = 0), we get
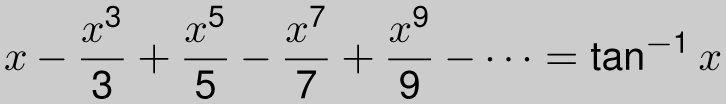
Letting x get closer and closer to 1, we get
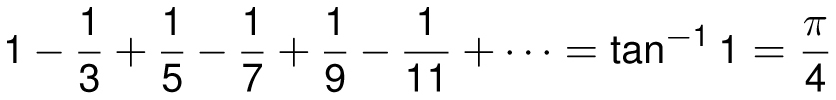
We have seen how the geometric series can be used, now let’s see how it can be abused. The formula for the geometric series says that
for values of x where −1 < x < 1. Let’s look at what happens when x = −1. Then the formula would tell us that
Of course that’s impossible; since we are only adding and subtracting integers, there is no way that they should sum to a fractional value like 1/2, even if the sum converged to something. On the other hand, the answer isn’t entirely ridiculous, because when we look at the partial sums we have
and so on. Since half of the partial sums are 1 and half of the partial sums are 0, the answer 1/2 isn’t too unreasonable.
Using the illegal value x = 2, the geometric series says
This answer looks even more ridiculous than the last sum. How can the sum of positive numbers possibly be negative? And yet maybe there is a reasonable interpretation for this sum too. For instance, in Chapter 3, we encountered ways in which a positive number could act like a negative number, with relationships like
10 ≡ −1 (mod 11)
allowing us to make statements like 10k ≡ (−1)k (mod 11).
Here’s a way to understand 1 + 2 + 4 + 8 + 16 + · · · that requires thinking out of the box a little. Recall that in Chapter 4, we observed that every positive integer can be represented as the sum of powers of 2 in a unique way. This is the basis for binary arithmetic, which is the way digital computers perform calculations. Every integer uses a finite number of powers of 2. For instance, 106 = 2 + 8 + 32 + 64 uses just four powers of 2. But now suppose that we also allowed infinite integers, where we could use as many powers of 2 as we wanted. A typical infinite integer might look like
1 + 2 + 8 + 16 + 64 + 256 + 2048 + · · ·
with powers of 2 appearing forever. What these numbers would represent is unclear, but we could come up with consistent rules for doing arithmetic with them. For instance, we could add such numbers provided that we allowed carries to occur in the natural way. For instance, if we add 106 to the above number, we would get
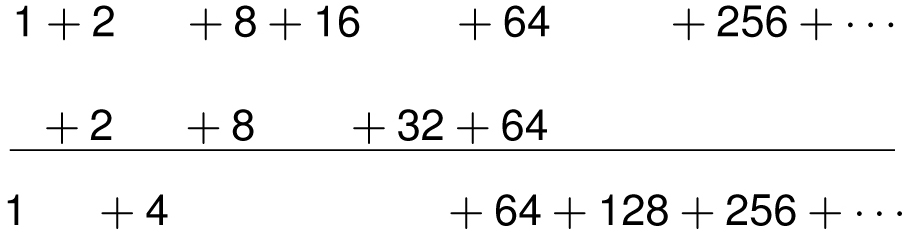
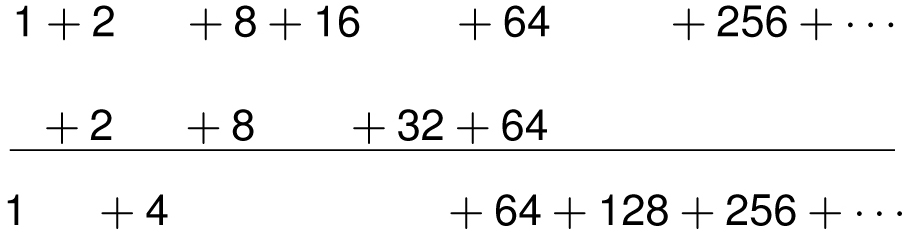
where the 2 + 2 combine to create the 4; next, the 8 + 8 forms 16, but when added to the next 16 creates a 32, which when added to the next 32 creates 64, which when added to the two 64s creates 64 and 128. Everything from 256 onward is unchanged. Now imagine what happens when we take the “largest” infinite integer and add 1 to it.
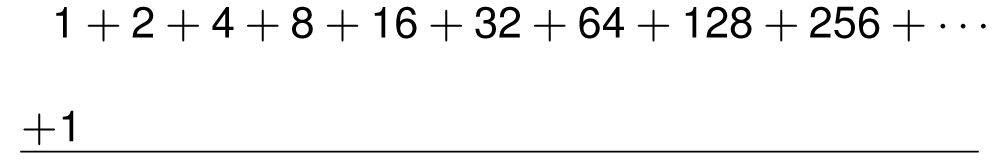
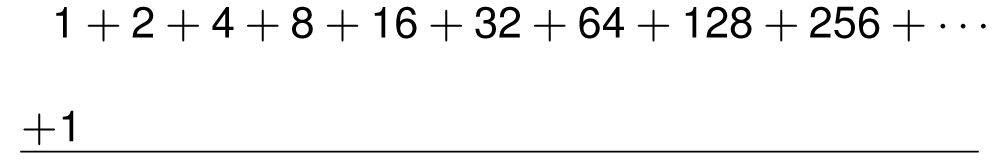
The result would be a never-ending chain reaction of carrying with no power of 2 appearing below the line. Hence, the sum can be thought of as 0. Since (1 + 2 + 4 + 8 + 16 + · · ·) + 1 = 0, then subtracting 1 from both sides suggests that the infinite sum behaves like the number −1.
Here is my favorite impossible infinite sum:
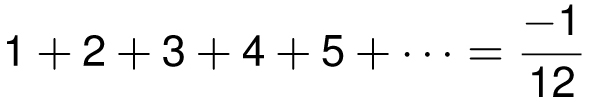
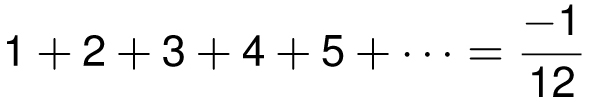
We “prove” this by the shifty algebra approach that we used in the second proof of the finite geometric series. Although the shifty approach is valid for finite sums, it can lead to nonsensical-looking results for infinite sums. For instance, let’s first use shifty algebra to explain an earlier identity. We write the sum twice, but shift the terms over by one space in the second sum as follows:
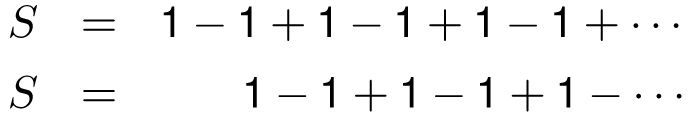
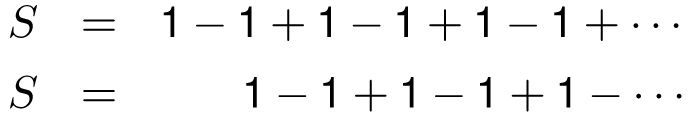
Adding these equations together gives us
2S = 1
and therefore S = 1/2, as we asserted earlier, when we set x = −1 in the geometric series.
Aside
We can use the shifty algebra approach to give a quick, but not quite legal, proof of the geometric series formula.
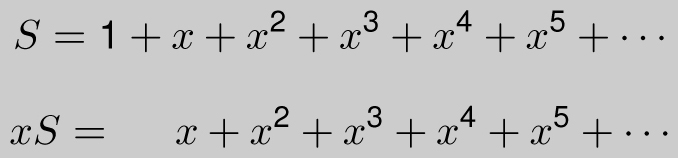
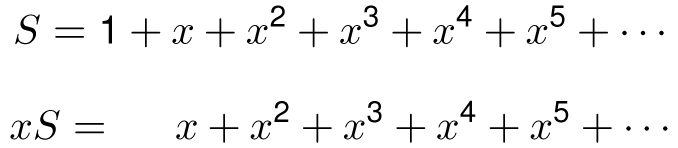
Subtracting these two equations gives us
S(1 − x) = 1
and therefore
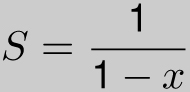
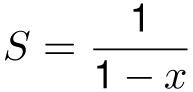
Next we claim that the alternating version of our desired sum also has an interesting answer, namely
Here’s the shifty algebra proof. Writing the sum twice, we get
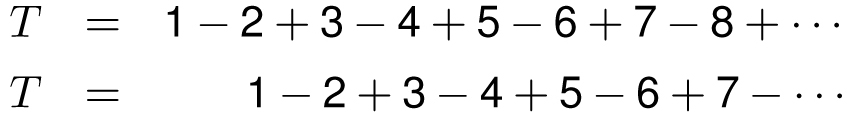
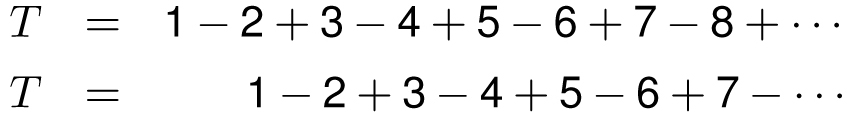
When we add these equations we get
2T = 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 + ···
Therefore 2T = S = 1/2 and so T = 1/4, as claimed.
Finally, let’s see what happens when we write the sum of all positive integers as U and underneath that we write the previous (and unshifted) sum T.
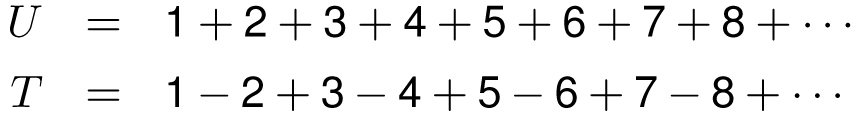
Subtracting the second equation from the first one reveals
U − T = 4 + 8 + 12 + 16 + · · · = 4(1 + 2 + 3 + 4 + · · ·)
In other words,
U − T = 4U
Solving for U, we get 3U = −T = −1/4, and therefore
U = −1/12
as claimed.
For the record, when you add an infinite number of positive integers, the sum diverges to infinity. But before you dismiss all of these finite answers as pure magic with no redeeming qualities, it is possible that there is a context where this actually makes sense. By expanding our view of numbers, we saw a way in which the sum 1 + 2 + 4 + 8 + 16 + · · · = −1 was not so implausible. Recall also that when we confined numbers to the real line, it was impossible to find a number with a square of −1, yet this became possible once we viewed complex numbers as occupants of the plane with their own consistent rules of arithmetic. In fact, theoretical physicists who study string theory actually use the sum 1 + 2 + 3 + 4 + · · · = −1/12 result in their calculations. When you encounter paradoxical results like the sums shown here, you could just dismiss them as impossible and be done with it, but if you allow your imagination to consider the possibilities, then a consistent and beautiful system can arise.
Let’s end this book with one more paradoxical result. At the beginning of this section we saw that the alternating series
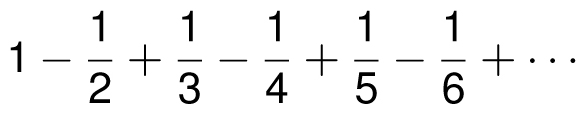
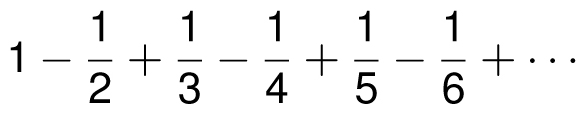
converged to the number ln 2 = 0.693147. . . . If you add these numbers in a different order, you would naturally expect to still get the same sum, since the commutative law of addition says that
A + B = B + A
for any numbers A and B. And yet, look what happens when we rearrange the sum in the following way:
Note that these are the same numbers being summed, since every fraction with an odd denominator is being added and every fraction with an even denominator is being subtracted. Even though the even numbers are being used up at twice as fast a rate as the odd numbers, they both have an inexhaustible supply, and every fraction from the original sum appears exactly once in the new sum. Agreed? But notice that this equals
which is one-half of the original sum! How can this be? How is it possible that when we rearrange a collection of numbers, we can get a completely different number? The surprising answer is that the commutative law of addition can actually fail when you are adding an infinite number of numbers.
This problem arises in a convergent series whenever both the positive terms and the negative terms form divergent series. In other words, the positive terms add to ∞ and the negative terms add to −∞. Such was the case with our last example. These sequences are called conditionally convergent series and, amazingly, they can be rearranged to obtain any total you desire. How would we rearrange the last sum to get 42? You would add enough positive terms until the sum just exceeds 42, then subtract your first negative term. Then add more positive terms until it exceeds 42 again. Then subtract your second negative term. Repeating this process, your sum will eventually get closer and closer to 42. (For instance, after subtracting your fifth negative term, −1/10, you will always be within 0.1 of 42. After subtracting the fiftieth negative term, −1/100, you will always be within 0.01 of 42, and so on.)
Most of the infinite series that we encounter in practice do not exhibit this strange sort of behavior. If we replace each term with its absolute value (so that each negative term is turned positive), then if that new sum converges, then the original series is called absolutely convergent. For example, the alternating series we encountered earlier,
is absolutely convergent, since when we sum the absolute values we get the familiar convergent series
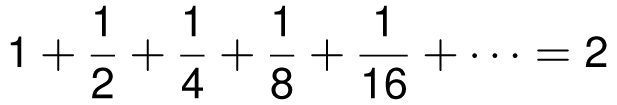
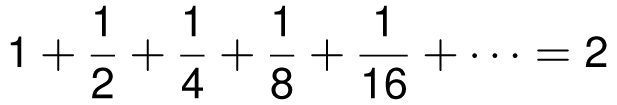
With absolutely convergent series, the commutative law of addition will always work, even with infinitely many terms. Thus in the alternating series above, no matter how thoroughly you rearrange the numbers 1, −1/2, 1/4, −1/8 . . . , the rearranged sum will always converge to 2/3.
Unlike an infinite series, a book has to end sometime. We don’t dare to try to go beyond infinity, so this seems like a good place to stop, but I can’t resist one last mathemagical excursion.
Encore! Magic Squares!
As a reward for making it all the way to the end of the book, here is one more magical mathematical topic for your enjoyment. It has nothing to do with infinity, but it does have the word “magic” squarely in its title: magic squares. A magic square is a square grid of numbers where every row, column, and diagonal add to the same number. The most famous 3-by-3 magic square is shown below, where all three rows, all three columns, and both diagonals add to 15.
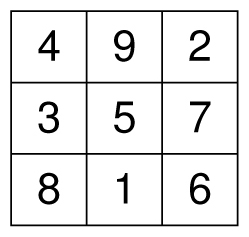
A 3-by-3 magic square with magic total 15
Here’s a little-known fact about this magic square that I call the square-palindromic property. If you treat each row and column as a 3-digit number and take the sum of their squares, you will find that
4922 + 3572 + 8162 = 2942 + 7532 + 6182
4382 + 9512 + 2762 = 8342 + 1592 + 6722
A similar phenomenon occurs with some of the “wrapped” diagonals, too. For instance,
4562 + 3122 + 8972 = 6542 + 2132 + 7982
Magic “squares” indeed!
The simplest 4-by-4 magic square uses the numbers 1 through 16 where all rows, columns, and diagonals sum to the magic total of 34, like the one below. Mathematicians and magicians like 4-by-4 magic squares because they usually contain dozens of different ways to achieve the magic total. For instance, in the magic square below, every row, column, and diagonal adds to 34, as does every 2-by-2 square inside it, including the upper left quadrant (8, 11, 13, 2), the four numbers in the middle, and the four corners of the magic square. Even the wrapped diagonals sum to 34, as do the corners of any 3-by-3 square inside.
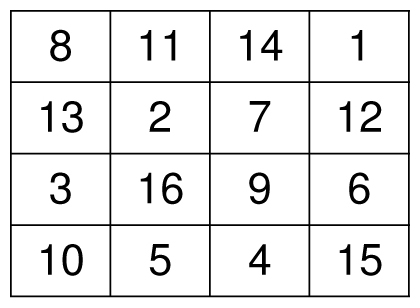
A magic square with total 34. Every row, column, and diagonal sums to 34, as do nearly every other symmetrically placed four squares.
Do you have a favorite two-digit number bigger than 20? You can instantly create a magic square with total T just by using the numbers 1 though 12, along with the four numbers T − 18, T − 19, T − 20 and T − 21 as shown on the next page.
For example, see the magic square on the next page with a magic total of T = 55. Every group of four that used to add up to 34 will now add up to 55, as long as the group of 4 includes exactly one (not two, not zero) of the squares that use the variable T. So the upper right squares will have the correct total (35 + 1 + 7 + 12 = 55) but the middle left squares will not (34 + 2 + 3 + 37 ≠ 55).
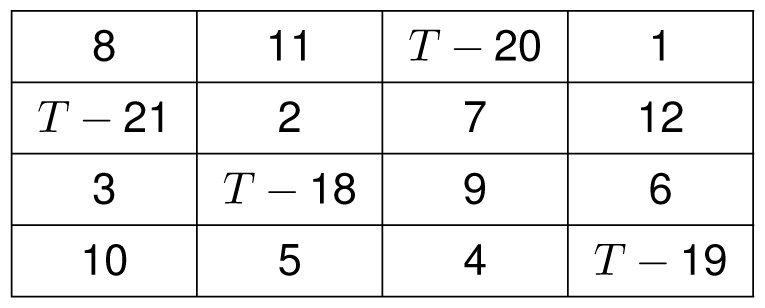
A quick magic square with magic total T
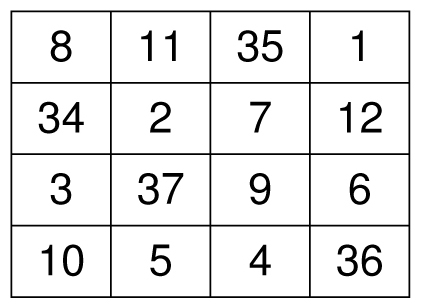
A magic square with total 55
Although not everyone has a favorite two-digit number, everyone does have a birthday, and I find that people appreciate personalized magic squares that use their birthdays. Here is a method that I use for creating a “double birthday” magic square, where the birthday actually appears twice: in the top row and in the four corners. If the birthday uses the numbers A, B, C, and D, then you can create the following magic square. Notice that every row, column, and diagonal, and most symmetrically placed groups of four squares, will add to the magic total A + B + C + D.
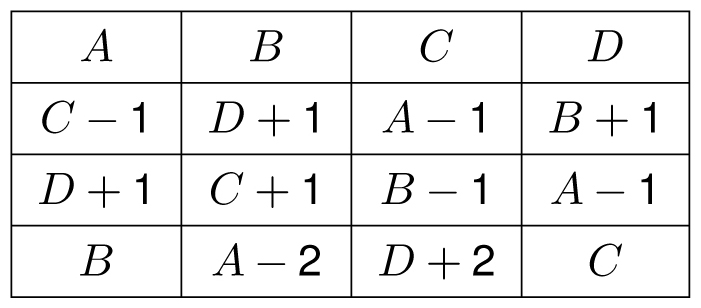
A double birthday magic square. The date A/B/C/D appears in the top row and four corners.
For my mother’s birthday, November 18, 1936, the magic square looks like this:
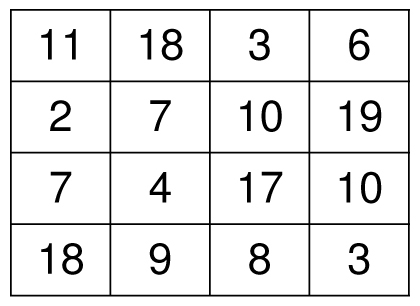
A birthday magic square for my mother: 11/18/36, with magic total 38
Now create a magic square based on your own birthday. If you follow the pattern given above, your birthday total will appear more than three dozen times. See how many you can find.
Although 4-by-4 magic squares have the most combinations, there are techniques for creating magic squares of higher order. For example, here is a 10-by-10 magic square using all the numbers from 1 to 100.
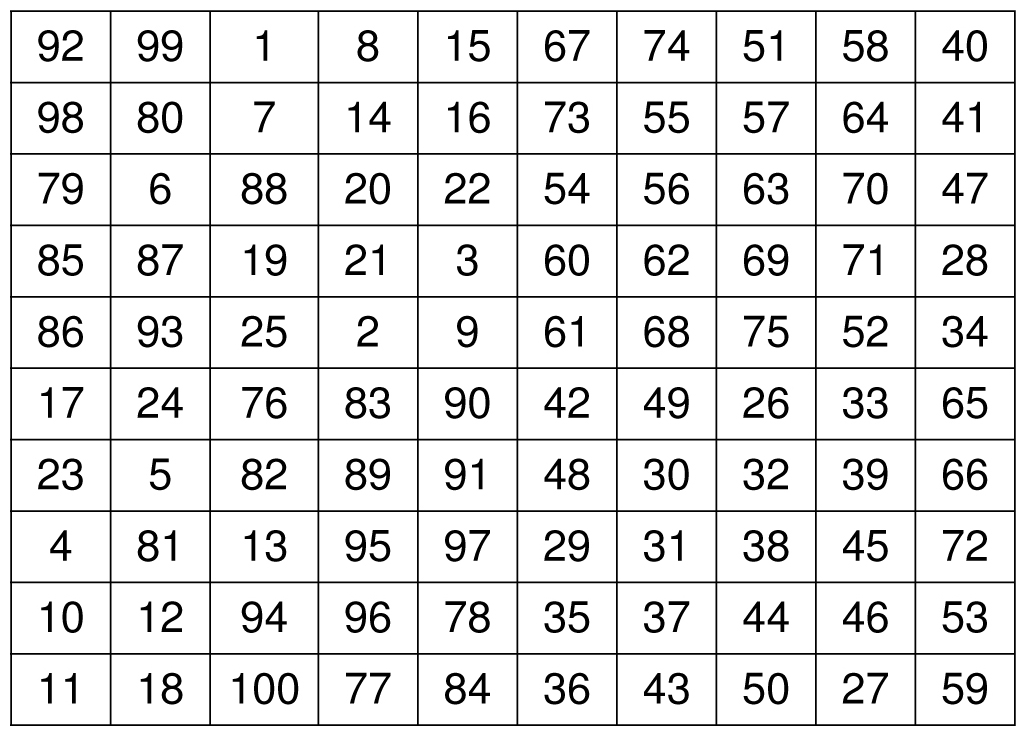
A 10-by-10 magic square using numbers 1 through 100
Can you figure out the magic total of each row, column, and diagonal without adding up any of the rows? Sure! Since we showed a long time ago that numbers 1 through 100 add to 5050, each row must add to one-tenth of that. Hence the magic total must be 5050/10 = 505. This book began with the problem of adding the numbers from 1 to 100, and so it seems appropriate that we end here as well. Congratulations (and thank you) for reading to the end of the book. We covered a great many mathematical topics, ideas, and problem-solving strategies. As you go back through this book and read other books that rely on mathematical thinking, I hope you find the ideas presented in this book to be useful, interesting, and magical.