Storms at sea, and the violent waves they produce, have terrorized seamen since they first ventured onto the oceans millennia ago. Until recently, only the wisdom of ships’ captains, built from many years of battling the seas and experiencing the wrath of the capricious waves, provided any help in surviving these storms. Since the 1930s, meteorologists have been able to provide increasing support in predicting the wind patterns. With constantly improving networks of weather stations, and more recently with satellites, meteorologists have been able to forecast storm winds and icing conditions several days in advance.
But until the 1960s, predictions of the effect of these winds on the ocean waves were rudimentary, and forecasts of wave heights during storms were quite unreliable. Mariners were still under threat from giant waves they could not anticipate. Forecasters vowed to do better. But as we have seen, just understanding how high a wind can raise the waves has been a daunting challenge.
Over the last 60 years oceanographers have learned, painfully at first, to forecast the heights and periods of storm waves as much as a few days in advance. In this chapter we’ll see how they developed and tested their techniques, beginning in World War II. But to get a feeling for how far along they have come in their quest, we take a moment to remember one of their greatest successes—and failures: Hurricane Katrina.
The residents of New Orleans and of other cities along the U.S. Gulf Coast will never forget Hurricane Katrina. Katrina was born on August 23, 2005, near the Bahamas as a tropical depression and grew rapidly in intensity as it swept across Florida into the unusually warm waters of the Gulf. On August 28 Katrina became a monster category 5 storm with sustained winds of 175mph. These hurricane-force winds extended 105 miles out from the center. A buoy 50 miles off the coast recorded waves 55 feet tall in the open sea.
At 4:00 p.m. CDT, Max Mayfield, director of the National Hurricane Center in Miami, issued a warning that a storm surge of 18 to 22 feet above normal tide level could be expected, with 28 feet in some localities. (A storm surge is a hill of water that is raised by the low atmospheric pressure in a hurricane and driven shoreward by the wind.) He cautioned that “some levees in the Greater New Orleans area could be overtopped.”
Katrina had declined to a category 3 storm when she made landfall at Buras-Triumph, Louisiana, on August 29. But she still retained tremendous energy and record breadth (240 miles across) for a Gulf hurricane. Now the storm’s waves rode atop a storm surge (also known as a storm tide) that the swirling winds had piled up. It was this combination of battering waves and a high storm surge that caused most of the record devastation inland.
Max Mayfield, in a March 7, 2007, interview on YouTube, recalled that he expected the storm surge to weaken after the winds of Katrina dropped to a category 3, but in fact the surge remained powerful because of the sheer size of Katrina. As bad as the winds of a category 3 hurricane are, it was that massive surge that caused the flooding of 80% of New Orleans as it raced through the narrow water channels to the city and broke through 53 levees.
Katrina caused over $75 billion of property damage and took more than 1,800 lives throughout the Gulf states. A third of the population of New Orleans left the city permanently, and reconstruction efforts were still under way more than 7 years after the disaster. The city of New Orleans will probably never fully recover from this storm.
Katrina could have caused many more fatalities if forecasters at the National Hurricane Center in Miami had not been able to predict both the path and the intensity of the storm days in advance and warn the population. Moreover, forecasts of the height of the waves that topped the storm surge proved to be vital. However, not even the forecasters anticipated the devastating power of the surge—a wall of water pushing relentlessly against puny levees and floodwalls.
New Orleans will always be under threat from hurricanes; even the most sophisticated hurricane forecasting that tries to model the complex interactions between wind, water, and land still cannot predict the possible course of a hurricane’s destruction.
Like many other advances, the science of forecasting waves was launched during World War II. In 1942 Harald Sverdrup and Walter Munk at the Scripps Institution of Oceanography were working on antisubmarine detection for the U.S. Navy. Sverdrup was the director of Scripps, and Munk was a freshly minted Ph.D. from the California Institute of Technology and Sverdrup’s former student.
In an interview in June 1986, Munk recalled that while working temporarily at the Pentagon in 1943, he had learned that practice landings for an amphibious invasion of North Africa had to be cancelled whenever the swell was higher than 7 feet. The reason was that the landing craft would turn sideways and swamp in such a swell. Munk visited the Army practice site in the Carolinas to see for himself. He returned to Washington to look up the wave statistics for North Africa and realized that high swell could be a real problem for the invasion. Many troops would drown while landing unless the swell was lower than 7 feet. Practice landings could always be cancelled at the last minute, but real landings, involving thousands of troops, boats, and supplies, were irreversible.
Apparently nobody had realized that this could be a problem. When Munk warned his superiors, he was scoffed at. He was only a junior oceanographer. Surely, they told him, “someone” was dealing with the problem. Munk would not be rebuffed. He called his mentor, Harald Sverdrup, the director of the Scripps Institution of Oceanography and told him of his fears. Sverdrup came to Washington immediately and warned the generals. Because of his scientific credentials, he was taken seriously. The two men were assigned the task of finding a solution to the problem.
So Munk and Sverdrup began to work to predict the height of the swell in North Africa. To do so, they had to examine the whole process by which storm waves grow and turn into swell, how swell travels great distances, and how offshore topography can focus wave energy from swell into high surf.
Observations had shown that as a wind blows over a lake, the wave heights and periods at the upwind shore quickly reach a steady state. If the wind blows long enough, a steady-state region expands over the whole lake, with higher waves at the downwind shore owing to the longer fetch. But if the fetch is unlimited, as may happen over the ocean, waves grow in height at the same rate everywhere. These facts helped to guide Munk and Sverdrup as they created their theory.
First, they had to learn how to estimate the wind’s characteristics on a chosen day. By examining the isobars (the lines connecting points of equal atmospheric pressure) on a weather map, they could determine the direction, speed, and fetch of the wind. Maps from two or more days allowed them to determine the duration of the wind as well.
They then introduced the concept of “significant wave height,” which they defined as the average (root mean square) height of the highest third of a set of waves. These waves appear to carry most of the energy in a stormy sea, and this term is now commonly used when discussing wave heights. As Munk explained in an interview (Finn Aaserud, La Jolla, Calif., June 30,1986):
I think that we invented that [term], and it came about as follows: after returning to Scripps we were monitoring practice landings under various wave conditions by the Marines at Camp Pendleton, California. After each landing we would ask the coxswains of the landing crafts to estimate today’s wave height, 7 feet one day, 4 feet the next day. We would make simultaneous wave records, and compute root mean square [rms] elevations. It turned out that the coxswains’ wave heights far exceeded twice the rms elevations. It was easier to define a new statistical quantity than to modify the mindset of a Marine coxswain, so we introduced “significant wave height” as being compatible with the Marines’ estimates. To our surprise that definition has stuck till today.
Next, Sverdrup and Munk focused on the rate at which the wind transmits energy to waves with significant heights. With nothing better in hand at the time, they adopted Harold Jeffreys’s “sheltering” theory, which held that the wind would push on the windward side of a crest and leap over the next trough. The difference in air pressure from front to back of a crest would amplify a wave.
Then they formulated two energy balance equations, in which energy gained from the wind was balanced by the growth of wave heights and of wave speeds. One equation was valid when the fetch was effectively infinite and the wind blew for a limited time. The other equation was valid when the duration of the wind was very long but the fetch was limited. The two men assumed that, depending on the fetch and the duration of the wind, the wave heights would reach a steady state. From their theory they could then estimate the significant wave height and period. Next, they calculated how these waves escaped the storm area as swell and estimated how much the swell decayed because of air resistance as it traveled long distances toward a coast.
Their research was ready for use a few months before the invasion of North Africa and later Normandy in June 1945. As Munk recounted (CBS 8, San Diego, Calif., Feb. 18, 2009): “Eventually in collaboration with the British Met Service a prediction was made for the Normandy landing, where it played a crucial and dramatic role. The prediction for the first proposed day of landing was that it would be impossible to have a successful landing. As I understand, the wave prediction persuaded Eisenhower to delay for 24 hours. For the next day the prediction was ‘very difficult but not impossible.’ Eisenhower decided not to delay the second day, because the secrecy would be lost in waiting two weeks for the next tidal cycle.” Because Sverdrup and Munk’s information resulted in a delay of the invasion until June 6, when the swell was tolerable, their forecasts certainly saved many lives.
During the war Sverdrup and Munk also prepared charts and tables to guide amphibious landings elsewhere in Europe and Africa and taught young forecasters how to use them. Although many of their assumptions have since been superseded, their emphasis on energy balance laid the foundations of the science of wave forecasting and stimulated much postwar research.
In the 1950s Willard Pierson, Gerhard Neumann, and Richard James introduced a more rigorous approach to forecasting. They based their scheme on Munk’s concept of energy balance but also introduced wave spectra and statistics. Pierson, a professor at New York University whom we met in chapter 5, developed a formal mathematical description of wave generation and propagation in 1952. To simplify the problem he introduced the concept of the “fully developed sea,” in which the energy input of the wind would be exactly balanced by losses due to a number of causes. With certain strong assumptions, his team could calculate the shape of this final equilibrium wave energy spectrum. The spectra they derived for winds of different speeds have the peaked shapes we saw in figure 5.1. Wave frequencies around a “significant” frequency contain the most energy, while other higher and lower frequencies tail off rapidly in energy.
From such spectra the three scientists could derive the significant wave height and period of interest to mariners. In fact, assuming a bell-shaped distribution of wave heights, they could determine the fraction of waves that had any height of interest. They were also able to estimate these quantities when the wind is limited either in fetch or in duration.
These three authors published a manual for U.S. Navy forecasters written in simple, clear language for ordinary seamen. It presented the novice forecaster with a set of charts and tables with which to predict wave heights and periods in a high wind with a minimum of calculation. A forecaster only needed to know a few characteristics of the prevailing wind, such as its speed, fetch, and duration, to deal with any situation in the deep ocean. A test of their method showed agreement with wave height observations to only 50%—not high precision, it is true, but a step in the right direction. Their manual was used for over 20 years to design structures on vulnerable coasts and to avoid the worst of storms at sea.
The success of the manual was somewhat surprising in retrospect. Pierson and colleagues had made the basic assumption that the shape of the fully developed wave spectrum depends solely on wind speed and does not depend on wind fetch or duration. They assumed they could correct for limited fetch, for example, by cutting off a fully developed spectrum at a specific long wavelength. In order to test these assumptions and improve the accuracy of the method, new observations would be necessary and a more detailed theory would be required for the generation of storm waves.
In 1955 Roberto Gelci, a marine forecaster at the French National Weather Service, independently conceived the energy balance approach to forecasting. Like Pierson, he proposed that the wave energy spectrum be calculated by balancing energy gains and energy losses. But he avoided the assumption of a steady-state, fully developed sea. He would instead try to calculate the evolution of the spectrum.
His scheme assumed that each wavelength would gain energy from the prevailing wind at a particular rate fixed by an empirical formula and would lose energy at some other rate. Gelci had no theory to guide him (this was 1955), so he had to extract empirical formulas for energy gains from crude archival observations. In addition, he could only assume that waves lost energy by spreading away from the wind direction. That would require him to calculate the paths of many different wave trains in order to predict their evolution. The final result was hardly a polished theory. At best, it was a recipe for calculating the changes in space and time of ocean waves in a strong wind.
With all the uncertainties entering his method, Gelci’s predictions were far from accurate. But the idea of including the directions of wave propagation was novel, and many other investigators saw its potential.
In the 1950s there was still a great deal of controversy about which physical processes were involved in raising waves on a flat sea. The situation improved in 1957 when Owen Phillips and John Miles published their resonance theories of wave generation. As you will recall from chapter 3, Phillips predicted a constant initial rate of growth from a flat sea; Miles predicted exponential growth beginning with small waves.
Both men tried to extend their theories from these “capillary” waves to predict the final equilibrium spectrum of gravity waves in a stronger wind. Phillips was able to predict at least the shape of the high-frequency tail of the spectrum by assuming that waves with frequencies near the peak of the spectrum reach energy equilibrium. But a comparison with observation showed that these theories predicted growth rates 10 times too small. So the theory of wave generation still remained more art than science, despite a flurry of theoretical attempts to improve the underlying physics.
Despite the success of the Pierson-Neumann-James manual, the reality of a fully developed sea was debated vigorously in the 1960s. Does the sea ever reach this kind of equilibrium? it was asked. Are both the fetch and the duration of a steady wind ever large or long enough to ensure a fully developed sea?
In 1964 Willard Pierson and Lionel Moskowitz claimed that they could find many examples of a fully developed sea in the records of ships at sea. Moreover, they showed that the shape of the spectrum of such a sea depends solely on the wind speed and that all the spectra can be transformed into a universal shape. They are “self-similar,” as the Soviet scientist S. A. Kitaigorodskii had predicted. This demonstration helped to establish the Pierson-Moskowitz universal spectrum as a valuable working tool for forecasting. One needed to know only the wind speed, they argued, in order to predict the wave spectrum and therefore the significant wave height and period.
These developments marked what one could call the first generation of forecasting models. Then in 1960, Klaus Hasselmann entered the forecasting field. At that time he was still a physics student in Hamburg, working on wave resistance to ships. After he read some papers by John Miles and by Owen Phillips on the transfer of energy among waves, he decided to investigate for himself. As we have already seen in chapter 4, he showed that energy transfers could occur only among sets of four waves that are related in frequency and direction. He claimed that such transfers could be a dominant process in wave growth, but without empirical verification, his claim remained controversial. Hasselmann also doubted that a fully developed sea (with a final steady energy spectrum) would ever be achieved in nature: the spectrum would continue to evolve, even in a constant wind, because of the transfer of energy among waves.
The 1968 JONSWAP campaign in the North Sea, organized by Hasselmann (see chapter 5), was a turning point in oceanography and the science of forecasting. It yielded high-quality observations of the wave spectra at a series of fetches and wind speeds. It also revealed that the changes in the shape of the energy spectrum with increasing fetch were “self-similar,” which was a clue to the underlying physics.
The critical result for forecasting was that the empirical JONSWAP spectra could all be described by one universal empirical formula, in which the wind speed and the fetch are adjustable parameters. If one knew the wind speed and the fetch in a hurricane, one could predict the storm’s wave spectrum by a simple modification of the universal formula. These test results were markedly different from the Pierson-Moskowitz spectrum of a “fully developed sea,” where wind speed was the only necessary factor. The JONSWAP spectrum contained four times the energy of the Pierson-Moskowitz spectrum at the same peak frequency. That would be crucial in estimating potential storm damage.
Moreover, the JONSWAP campaign revealed that nonlinear transfers of energy among waves were essential in the growth of waves, just as Hasselmann had claimed. The wind deposits its energy to waves in the midrange of wavelengths, and these transfer energy to waves with longer and shorter wavelengths.
The JONSWAP spectra are observational data that can be summarized by a universal formula, but they do not, in themselves, reveal the underlying physics that produces them. Oceanographers wanted to understand the forces that produce the observed spectra. Only then could they devise a theoretically sound forecasting scheme.
As with all other forecasting methods, their basic tool was the energy equation that balances the energy gains and losses of a specific wavelength as a function of time. However, they expanded the sources of energy gains and losses: a wave gains energy both from the wind and from other waves. It loses energy by spreading, by whitecapping, and perhaps by other mechanisms. To make progress, it would be necessary to find formulas that describe each of these processes. One way to start would be to try to extract trial formulas from the observations.
In effect, that is what happened. Using the JONSWAP data, oceanographers like Hasselmann tried out different approximations for the energy gains, losses, and transfers in the energy equation to see which combinations seemed to best fit the data. Then throughout the 1980s, they devised a variety of numerical forecasting models using the various approximations. This burst of activity initiated the second generation of forecasting models. One of the first examples is the Spectral Ocean Wave Model (SOWM) that Willard Pierson and colleagues constructed for the U.S. Navy. It was first applied to the Mediterranean Sea and later to the Atlantic and Pacific Oceans.
In 1981, a conference (the Sea Wave Modeling Program, or SWAMP—scientists love to create droll acronyms) was held to compare the performance of nine models in realistic exercises. Each model used the same input of wind conditions. The results were sobering: for a specified hurricane wind, the predictions of significant wave heights in the different models varied from 8 to 25m—not a very comforting outcome.
Two of the weakest links in the models were identified: the approximations used for the dissipation of waves due to whitecapping and for the transfer of energy among waves. Hasselmann had written down the complicated formal mathematics for the transfer effect, but the computers of the day were unable to evaluate the effect within the time constraints of a daily forecast. Therefore, each expert adopted a different approximate formula for the effect, with the result that the models produced very different predictions. Hasselmann and colleagues would work furiously over the next decade to find a suitable approximate formula for the critical wave-wave interaction.
The third generation of models began with the formation in 1984 of the Wave Modeling Group (WAM) under the leadership of Klaus Hasselmann. Over the next decade these researchers strived to produce a forecasting model that would avoid arbitrary choices of a limiting spectrum and would incorporate the best practical formulas for the wave-wave energy transfer. They also improved predictions of the spreading of storm waves away from the direction of the wind. The guiding principles of these third-generation models were that first principles must be used, rather than empirical “fitting” of data; that the wave energy spectrum would be created from these first principles, rather than have an assumed shape; and that the resulting nonlinear equations had to be solved explicitly, and not approximated.
The 1968 JONSWAP experiment had been fetch-limited and therefore could not establish whether a fully developed sea exists in nature; in the early 1980s the issue was still controversial. Therefore, in 1984 the Dutch scientist Gebrand Komen and other members of the WAM group performed a critical test of the latest WAM model (3GWAM). They wanted to see whether any tuning of the parameters of the model would result in a fully developed sea. They used a realistic model of the wind profile, a crude description of white-capping, and better modeling of the spreading of waves. They found that indeed a steady-state spectrum is possible but is very sensitive to the way in which waves spread.
By the mid-1980s weather agencies and navies in several countries began to develop their own wave forecasting computer programs based on the energy balance concepts in the third-generation models. For example, the University of Technology in Delft, Holland, created the WAVEWATCH I program. It went through two revisions at the U.S. National Centers for Environmental Prediction and was eventually adopted as the standard forecasting tool. Similarly, the U.K. National Center for Ocean Forecasting developed the full Boltzmann forecast program, and the Canadians created the Ocean Wave model. Not to be outdone, the U.S. Navy’s Fleet Numerical Meteorological and Oceanic Center published its own third-generation programs.
In the 1990s, satellite observations of wave heights and winds began to be available. Forecasters made heroic efforts to incorporate real-time satellite observations in their numerical prediction schemes. However, the interpretation of satellite radar images turned out to be a formidable task.
Third-generation forecasting programs require huge computer resources and became feasible only with the advent of supercomputers in the 1990s and early 2000s. At that point several nations could collaborate in producing daily or hourly forecasts tailored to specific areas in the global ocean. In the mid-1990s six European nations established a continent-wide center at Reading, U.K.—the European Centre for Medium-Range Weather Forecasts (ECMWF). Drawing on the pooled weather observations of member nations, the ECMWF issued forecasts for the continent and surrounding waters. Part of its charter was the twice-daily prediction of wave heights in the North Atlantic using third-generation models. By 2007, 34 nations had joined the ECMWF collaboration, and wave height predictions were being made for most of the world’s oceans.
The U.S. National Weather Service has taken an independent path. It currently issues forecasts of weather and wave heights every 6 hours for seven large regions in the Western Hemisphere: the Western North Atlantic, the Caribbean, the Central Pacific, and the central and eastern parts of the North and South Equatorial Pacific. Predictions of wave heights are made with the updated WAVEWATCH III program.
As an example, here is an excerpt from the forecast for June 19, 2011, 1630 hours UTC.
HIGH SEAS FORECAST FOR MET AREA IV
1630 UTC SUN JUN 19 2011
SEAS GIVEN AS SIGNIFICANT WAVE HEIGHT . . . WHICH IS THE AVERAGE HEIGHT OF THE HIGHEST 1/3 OF THE WAVES. INDIVIDUAL WAVES MAY BE MORE THAN TWICE THE SIGNIFICANT WAVE HEIGHT
NORTH ATLANTIC NORTH OF 31N TO 67N AND WEST OF 35W
GALE WARNING
.INLAND LOW 48N65W 1002MB MOVING E 10 KT. FROM 38N TO 50N BETWEEN 57W AND 60W WINDS 25 TO 35 KNOTS SEAS TO 9 FT.
.24 HOUR FORECAST LOW 47N60W 1000MB. FROM 39N TO 51N BETWEEN 50W AND 58W WINDS 25 TO 35 KNOTS SEAS TO 12 FT.
.48 HOUR FORECAST LOW 47N53W 1004MB. CONDITIONS DESCRIBED WITH LOW 44N49W BELOW.
Forecasting models, like palm readings, are valuable only if they produce reliable predictions. There is no way to know which models, if any, make accurate predictions without comparing them with independent observations. To test their models, forecasters play a game called hindcasting. It consists of trying to predict the heights and periods of waves in a past storm using wind observations made during the storm. Then they compare their hindcasts with observations of waves made during the storm. Literally dozens of such exercises have been carried out with varying results. We’ll examine a few of them.
The most pressing need for good forecasting arises during the hurricane season in the Gulf of Mexico. The National Hurricane Center in Miami, Florida, tracks these great storms with satellites and radar and attempts to forecast the path and strength of the winds and waves when the hurricane hits the coast. The U.S. Gulf Coast is densely populated with permanent tethered buoys that provide a continuous record of winds and waves. These observations have been compiled in a huge database that supplies forecasters with the input and ground truth for hindcasting.
In 1988 the WAM Development and Implementation (WAMDI) group carried out one of the first hindcasting tests with a third-generation model (3GWAM). They “predicted” the significant wave heights and periods for six North Atlantic storms and three Gulf of Mexico hurricanes: Camille (1969), Anita (1977), and Frederick (1979).
As an example of the kind of challenge these forecasters faced, consider Hurricane Camille. She was a category 5 storm when she entered the Gulf of Mexico on August 16, 1969. Her maximum sustained winds may never be known because she destroyed all the wind instruments when she made land-fall. However, estimates at the coast were near 200mph. Even 75 miles inland, sustained winds of 120mph were reported. Six offshore oil drilling platforms recorded a maximum significant wave height of 14.5m (47.6ft), a value not expected to be exceeded within a century. When Camille landed at Pass Christian, Mississippi, the storm surge reached 24 feet. The hurricane dumped 10 inches of rain on the coast and a total of 30 inches in Virginia, with catastrophic flooding. With over a billion dollars of property damage and 259 deaths, Camille devastated the Gulf Coast with an impact that was not exceeded until Katrina.
For input to their hindcast the WAMDI group could use only partial wind observations before and during the storm. But they could compare their predictions with measurements of wave heights by a string of buoys off the Louisiana coast. The agreement was excellent right up to the peak of the storm, when the buoys were torn from their moorings and observations ceased.
The 3GWAM model also performed well for Hurricanes Anita and Frederick and even better for the six storms in the North Atlantic. The only question was whether accurate predictions could be made, say, 6 hours in advance. During a real storm, forecasters would be limited by the rapid changes in and accuracy of wind data, and by the power of their computers. Nevertheless, these excellent results motivated several nations to adopt third-generation forecasting models like 3GWAM and to provide nearly continuous forecasts.
Between 1988 and 2007 major improvements were made in forecasting models and in the availability of accurate wind observations by satellite radar. The 3GWAM model, for example, now had several variants, including one for relatively shallow coastal areas and another with an additional limit on the final spectrum. The Canadian program OWI was now in its third revision. These models were also tested by hindcasting some extreme weather conditions. R. Jensen and colleagues hindcasted six hurricanes, including some of the most notorious: Camille, Lili, Ivan, Dennis, Katrina, and Rita. Again, the matches with observations were very impressive.
How well do the different national weather centers predict wave heights in comparison with each other and for how long in advance? Do they agree and are they accurate? To find out, J.-R. Bidlot and M. W. Holt of the ECMWF carried out a massive “validation” exercise in 2006. They compared the predictions of wave heights from February 1 to March 31, 2004, by six national centers who shared the same inputs of wind speed and direction. The predictions were compared with observations made by a fleet of 79 buoys off both coasts of the United States and surrounding the British Isles. In one example they compared predictions made one day in advance by the U.S. National Centers for Environmental Prediction (using WAVEWATCH III) and by the U.K. Meteorological Office (using the Automated Tropical Cyclone Forecast). The ATCF (a second-generation model) performed just as well as the third-generation model but nonetheless was replaced by WAVE-WATCH III in 2008.
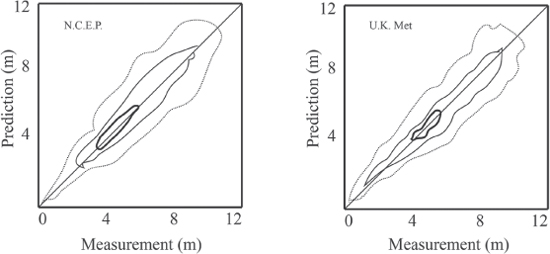
In figure 6.1 we see predictions of wave height by two different models one day in advance. The contours show the scatter of measurements. The 45-degree line going from the lower left to the upper right represents 100% correlation between measurements and predictions. As can be seen, the correlations are not quite perfect: for the scattered dots above the line, the predicted wave heights were slightly higher than the measured wave heights, and vice versa. Also the predictions are somewhat less accurate the higher the wave. But overall, the correlations are still quite close for both models. That was a general conclusion: these third-generation forecasts are reasonably accurate one day in advance.
Perhaps the best way to evaluate the progress forecasters have made is to ask how well they can predict wave heights as much as three days in advance. Bidlot and Holt found that the error in predictions increases from 0.5m one day in advance to about 0.8m at three days in advance. Not too bad!
Fig. 6.1 Predictions and measurements of wave heights by two forecast centers, February 1–March 31, 2004. (Drawn by author from J.-R. Bidlot et al., “Intercomparison of Forecast Systems with Buoy Data,” Journal of the American Meteorology Society, Apr. 2002, p. 287.)
Peter Janssen, a scientist at the ECMWF, carried out a similar study in 2007. He compared predictions of the continually upgraded 3GWAM model with buoy observations for the 14 hurricane seasons between 1992 and 2006. He found that the mean error in the predicted significant wave height increases, as one might expect, the more in advance the prediction is made. One day in advance, the mean error was always around 0.5m; ten days in advance the error was still only 1.5m. That’s impressive.
Forecasting maximum wave heights at sea during a hurricane is difficult, but estimating the storm surge at the moment a hurricane touches land is even more demanding. Storm surge is the hill of water pushed ashore by hurricane winds. The height of the surge at any point on land depends not only on the meteorological properties of the hurricane but also on the shape of the coastline it approaches. Gradually ascending coastlines (small slopes underwater close to shore) have the tendency to pile up more water onshore, leading to higher storm surges. Coastlines shaped like funnels tend to concentrate the waters, increasing their heights and their destructive potential.
At least five factors influence the formation of a storm surge. First, there is the low atmospheric pressure under the hurricane, which tends to suck up the surface of the sea, particularly under the eye of the storm. A 1-millibar drop in atmospheric pressure causes a 1-cm rise of the sea. With normal atmospheric pressure set at 1,013 millibars and hurricane eyes down to 909 millibars (Camille), that calculates out to over 100cm, or 1m, in surge height.
Second, the horizontal force of hurricane wind scoops up even more water and drives currents in the water. The currents tend to veer away from the direction of the wind because of the Coriolis effect. These unpredictable currents, turning to the right in the Northern Hemisphere and to the left in the Southern Hemisphere, greatly complicate the forecaster’s task.
A third factor are the powerful wind-driven waves riding on top of the surge. Like all wind-driven waves, they don’t actually move much water toward the shore, but when they break as surf, they carry considerable momentum. Their water can ride up the beach to a height above the mean water level equal to twice the height of the wave before it breaks.
As noted above, the shape of the coastline and the offshore bottom also influence the behavior of the surge. A steep shore, like that in southeastern Florida, produces a weaker surge but more powerful battering waves as they rise sharply up the beach. A shallow shore, like that in the Gulf of Mexico, produces a higher surge and relatively weaker waves.
Finally, if the hurricane reaches the shore near the lunar high tide for the area, the storm surge will be that much higher.
With all these factors acting simultaneously in a rapidly changing storm, forecasters have a daunting task to meet their responsibilities. Specialized models such as SWAN (Simulating Waves Nearshore) and SLOSH (Sea, Lake, and Overland Surge from Hurricanes) have been developed to meet the need for models of storms that impact coastal areas. SWAN was created by a team at the Technical University of Delft; SLOSH was developed at the U.S. National Ocean and Atmosphere Agency (NOAA) to model surges from hurricanes.
SWAN is a typical third-generation model that predicts the evolution of the two-dimensional wave spectrum by solving the energy equation, taking into account energy gains, losses, and transfers. In addition, it can be adapted to incorporate the shoaling, refraction, and diffraction that will occur at a specific location like the coast of Louisiana or Mississippi. It can even deal with the reflection and transmission of waves by breakwaters and cliffs.
The real-time performance of SWAN was tested in relatively mild conditions in 2003. In that year, the National Science Foundation and the Office of Naval Research sponsored the Nearshore Canyon Experiment (NCEX) near La Jolla, California. This shore is marked by two deep submarine canyons which greatly modify incoming swells from the Pacific. The goal of the experiment was to match real-time predictions of the onshore waves with buoy observations.
During the experiment, a 17-second swell approached the shore at an angle. The SWAN model predicted the variation of wave heights along the shore very well, as well as the offshore currents, but its predictions of wave heights were too low: a mere meter at best. In another NCEX exercise in the Santa Barbara Channel, real-time SWAN predictions of wave heights were too low again. Hindcasts showed that the presence of the Channel Islands upset the predictions.
SLOSH was developed at the National Hurricane Center in Miami, Florida. It too is a third-generation computer model that takes into account the pressure, forward speed, size, track, and winds of a hurricane. Hindcasts show its predictions of surge heights to be accurate to within ±20%, not bad for such a complex model.
As an example of the use of SLOSH, the following forecast was issued by the Hurricane Center on August 27, 2005, a day and a half before Hurricane Katrina made landfall: “Coastal storm surge flooding of 15 to 20 feet (4.5–6.0m) above normal tide levels . . . locally as high as 25 feet (7.5m) along with large and dangerous battering waves . . . can be expected near and to the east of where the center makes landfall.” Compare this forecast with the surges that Katrina actually produced: a maximum storm surge of more than 25 feet (8m) at Waveland, Bay St. Louis, and Diamondhead. The surge at Pass Christian in Mississippi was one of the highest ever seen, with a height of 27.8 feet (8.5m).
Because of the uncertainty in track forecasts, the SLOSH storm surge model is run for a wide variety of possible storm tracks. These possibilities are reduced to families of storm tracks, each representing one of the generalized directions of approach (west, north-by-northwest, north, northeast, etc.) that a hurricane would logically follow in a given area. These forecasts clearly improve in accuracy as the hurricane approaches the coast.
In a hurricane on the Gulf Coast, the highest surges occur on the right (east) side of the storm, where the winds are highest owing to their counterclockwise rotation. This side is often called the “dirty side” of the storm. This does not mean that the lower winds and surges on the left side of the storm are not dangerous: they may still cause massive destruction of the kind witnessed in New Orleans, which took the hit from the “clean side” of Hurricane Katrina.
If you log onto the Internet at the NOAA WAVEWATCH III page of the National Weather Service’s Environmental Modeling Center (as of this writing, http://polar.ncep.noaa.gov/waves/index2.shtml), you can see daily maps of wave heights and winds in all the world’s oceans. You can also see forecasts as animated maps that change in steps of 3 hours, starting from when you sign on, to 180 hours in the future. This kind of information, freely available to the public, has been available only since about 2000. It has become possible because of two parallel developments: the improvement in forecasting models such as WAVEWATCH III and 3GWAM, and the advent of radar-equipped satellites. Each development stimulated improvements in the other.
Since about 1980, earth-orbiting satellites have revolutionized meteorology, oceanography, environmental science, and geology. Researchers are now able to observe the entire globe, in many wavelengths and in all weather, with minimum delay. Weather satellites enable us to observe hurricanes in all their fury and provide the raw data to allow us to predict the weather for the coming week. Ocean-monitoring satellites measure surface winds, currents, and wave heights in near real time. Some satellites measure the long-term variations of sea levels to within millimeters. Environmental satellites track deforestation in the Amazon basin, the temperature of the seas, and the melting of glaciers. We are far richer in our knowledge of our planet than we were only a couple of decades ago.
Satellite observation of the oceans began with SEASAT in 1978. This satellite was equipped with several radar devices to image the sea. At that time many scientists doubted that radar could yield sharp images because of the random motions of the waves. But SEASAT proved them wrong. Postprocessing of its data yielded the first radar images of waves longer than about 30m in a 10 × 15km area. Unfortunately, SEASAT’s electronics were crippled after 3 months by a short circuit, and the satellite was abandoned.
At present four satellites are monitoring the oceans, sending down a flood of data. Several nations have banded together to build and operate these satellites and share their data. The European Space Agency launched ERS-1 in 1991, ERS-2 in 1995, and ENVISAT in 2002. The United States and France collaborate to operate JASON-1 (launched in 2001) and JASON-2 (2002).
ERS-1 and ERS-2 are equipped with several types of radar altimeters as well as instruments to measure ocean temperature and atmospheric ozone. They have collected a wealth of data on the earth’s land surfaces, oceans, and polar caps and have been used to monitor natural disasters such as severe flooding or earthquakes. ENVISAT is an improved and updated version of ERS-2.
JASON-1 and -2 are more specialized, being dedicated to observations of the oceans. They carry a suite of radar altimeters to measure wave heights and surface winds. In addition, JASON-2 measures variations of sea level as small as a millimeter over a year, information that can be used to follow the impact of climate change on the oceans. This precision allows the hills and valleys in the ocean surface to be mapped; from these data, the ocean currents can be predicted. JASON-2 also monitors the El Niño effect and the large-scale eddies in the ocean. Both versions of JASON continue the pioneering observations of Topex/Poseidon, which operated between 1992 and 2006.
Each of these four ocean-monitoring satellites orbits the earth in about 100 minutes, passing from pole to pole. Moreover, their orbits are sun-synchronous, meaning that the plane of each orbit always faces the sun by continuously turning around the earth at the same rate as the earth revolves in its orbit around the sun. That ensures that a given point on the earth is observed at the same local time every day. That is useful, for example, in measuring sea temperatures.
The satellites map the sea in strips that are spaced apart in longitude, so that it takes several days for a satellite to pass over the same point on the earth again (for example, ENVISAT takes about 3 days to do so). A global network of tracking stations continually monitors the satellites, so that their positions in space are known within centimeters. The stations also download data from the satellites periodically.
Data analysis and archiving takes place at multiple forecast centers. In the United States and the United Kingdom, the active agencies are NOAA and the Meteorological Office, respectively, both of which use the WAVEWATCH III forecasting model. The European Union’s ECMWF uses the 3GWAM model.
Each ocean-monitoring satellite is equipped with three radar instruments: a scanning radar altimeter to measure wind speed and direction and wave heights; a scatterometer to measure wind speed near the ocean surface; and a synthetic aperture radar to measure directional wave spectra. These radars use microwave radiation to measure the distance of the satellite from the tops of the waves, accurate to within a few centimeters.
As you probably know, radar (the word originated as an acronym for “radio detection and ranging”) was invented during the Second World War in a collaboration between British and American scientists; it is generally credited with saving the British from invasion by Nazi Germany. The radar altimeter, which is the principal instrument on board the ocean satellites, was actually invented way back in 1924 by Lloyd Espinschied, an engineer at Bell Telephone Laboratories. He took a number of years to make it practical for aircraft, however. It wasn’t until 1938 that it became standard equipment on commercial planes. SEASAT carried the first set of satellite radar altimeters in 1978. To appreciate how radar altimetry produces useful observations of the sea we need to get into the weeds a bit.
The basic idea behind radar is simple. A radar antenna emits a burst of short pulses of microwave radiation. (By “short,” I mean measured in nanoseconds, or billionths of a second; by “microwave,” I mean radiation with wavelengths of a few centimeters.) The same antenna that emits the pulse receives the echo of that pulse from the target after a time delay that depends on the distance to the target. The distance is equal to the delay multiplied by the constant speed of light, 300,000km/s.
Let’s say the antenna is pointing straight down from the satellite. Then the radar performs as a simple altimeter, recording the present distance of the satellite from the sea. But unlike an aircraft altimeter, which converts the measurements into heights from the ground up, a satellite altimeter converts the measurements into distances from the satellite down. This is possible and desirable, because the present height of the satellite (say, above mean sea level) is known independently to within a few centimeters from the tracking stations that monitor the satellite in its orbit. That means that the radar distances to the sea can resolve the heights of waves above mean sea level.
In practice it is the shape of the return pulse that indicates the mean heights of the waves. If the sea were perfectly flat, it would act as a mirror and the leading edge of the return pulse would rise very sharply to its peak intensity. If, on the other hand, the sea were rough, the slope of the leading edge would be gradual, as waves of different heights reflect the incident pulse.
With some modifications an altimeter becomes a scatterometer, which measures the wind speed at the sea surface. It is based on two empirical relationships: (a) wave heights increase with increasing wind speed; and (b) the taller the wave, the more it scatters microwave radiation. Here is how it works: When the sea is rough, the incident pulse is scattered in many directions by the random faces of the waves. Therefore, the return pulse is somewhat weaker than if the sea were flat and were acting as a mirror to reflect all the incident radiation. This decrease in the intensity of the return pulse, beyond that expected for a flat surface, can be calibrated to yield the speed of the wind.
A simple altimeter on a satellite yields wave heights along a line in the sea. A side-scanning altimeter sweeps a pencil beam back and forth in the direction perpendicular to the satellite’s path, like a blind man sweeping his cane back and forth as he works his way down a sidewalk. These sweeps build up a two-dimensional image whose spatial resolution (100–300m) is determined by the width of the radar beam.
Synthetic aperture radar (or SAR) also sweeps out a two-dimensional strip of the ocean but with spatial resolution much better in its forward direction than is possible with a scanning altimeter. For example, the European ocean satellite ERS-1 delivered a radar map of the waves in a 5 × 10km area at intervals of 200km along the satellite’s path. It achieved a resolution of 30m in the forward direction and 100km in the transverse direction. The reason it can achieve this higher resolution is that it illuminates each patch in the target area repeatedly at many different angles of incidence, with pulses of a fixed microwave frequency. Each return pulse from the patch is Doppler-shifted in frequency because of the changing angles of incidence. The Doppler shifts change predictably as the satellite passes over the patch, so these shifts effectively label the patch’s location in the target area. The satellite’s electronics use the label to add together the intensities of all the echoes from that patch, producing a crisp, high-resolution image.
Figure 6.2 illustrates the principle of SAR. Imagine a satellite moving in a precise orbit that serves as a reference frame from which distances to the sea can be measured. The straight line labeled V (for velocity) is the satellite’s path in the figure. At regular intervals along the path (marked by the dots), the satellite emits a radar pulse at a fixed radio frequency—say, at 13 gigahertz (GHz) (2.3-cm wavelength). For our purposes we can say that the radar beam has the shape of a pyramid, whose base is a rectangular footprint on the sea. Each pulse travels to the sea, where the beam strikes the surface, illuminates the waves there, and is reflected.
Each ocean wave in the rectangular footprint of the beam reflects a part of the return pulse, and its part is Doppler-shifted in frequency, relative to the incident frequency of 13 GHz. The Doppler shift depends on the location of the wave in the footprint. The shift is proportional to the component of the satellite velocity along the line of sight from the satellite to the wave. So for example, the shift is zero for a wave directly under the satellite; it is negative (blue-shifted) for waves further toward the front edge of the rectangular footprint and positive (red-shifted) for waves toward the rear edge. In this way the position of every wave in the footprint is labeled with a unique Doppler shift.
As the satellite moves from position 1 to position 2, each wave in the footprint is illuminated repeatedly, and each time its distinctive Doppler shift changes in a predictable fashion. The satellite electronics use the Doppler label to collect and add the intensities of all the echoes from a given wave in the footprint. In addition, the electronics process all the distance measurements to this wave to determine the height of its crest. In practice, many thousands of echoes are collected for each wave in the footprint.
Fig. 6.2 Illustration of the principle of synthetic aperture radar on a satellite moving from point 1 to point 2. V, satellite’s path; D, length of beam’s footprint on the sea. (Drawn by author from S. W. McCandless, Jr., and C. R. Jackson, chap. 1 of NOAA, Synthetic Aperture Radar Marine User Manual, 2004.)
The result is a high-resolution three-dimensional microwave image of the sea along the path of the satellite. Figure 6.3 shows an example, an image of San Francisco Bay and its famous bridge. It was made by the Jet Propulsion Laboratory’s experimental aircraft, with novel radar that uses polarized beams for higher spatial resolution. (I have enhanced the waves for greater clarity.) Individual waves longer than about 30m show up with a brightness that depends on the wave’s height.
This image now has to be processed to obtain the spectrum of wave heights from which the significant wave height can be determined. It is this wave height that appears in the forecasts for the region. It can be compared with the significant wave height that is calculated with, say, the WAVE-WATCH program, given the local wind as input.
Fig. 6.3 A microwave image of San Francisco Bay in the vicinity of the famous bridge. (Courtesy of Yijun He et al., Journal of Atmospheric and Oceanic Technology 23 [2006]: 1768, used with permission of the American Meteorological Society.)
SAR works because the radar pulse travels at the speed of light, which is much faster than the satellite’s speed or, for that matter, faster than any changes in wave shapes. I have skipped over the nasty complications involved in processing such SAR data using sophisticated Fourier-based algorithms. For example, I have assumed that the Doppler shifts are precisely correlated with a wave’s position within the footprint. But the waves are moving randomly, and these motions introduce random Doppler shifts (noise) in the coding of the waves as the thousands of radar transmissions are sent and received. The result is a slightly fuzzier image than would be produced if the waves were absolutely stationary.
Radar has been honed into a superb tool for imaging the ocean. Much thought has gone into extracting useful information from SAR data. Once again, Klaus Hasselmann and his close associates (including Sophia, his wife) were the leaders in this effort. The technique applies not only to surface waves but also to interior waves and the topography of the bottom, as well as the temperature of the sea and the direction and strength of surface winds. These modeling tools and satellite measuring techniques have been critical in understanding the different types of waves that we’ll cover in the next chapters.