“It’s got us, boys!” Ernest Shackleton screamed. He and five crewmen were in a 20-foot lifeboat in the midst of an Antarctic gale, on a desperate 800-mile voyage. Now they were in mortal danger, tossed in mountainous seas and freezing in the icy Antarctic storm.
In 1915 Shackleton had led a 23-man crew on an expedition to be the first to reach the South Pole for the glory of England. But their ship, Endurance, had been locked in the sea ice and slowly crushed to matchsticks. Shackleton and his crew had no choice but to risk a perilous attempt to escape in two small boats. With luck, courage, and skill they managed to reach rocky Elephant Island, home to hundreds of elephant and fur seals. But they were still 800 miles from South Georgia, where lay a large whaling station. Shackleton decided to sail on to South Georgia with a small crew to seek help. Now in this horrendous storm, the end seemed near.
Shackleton later wrote:
At midnight I was at the tiller and suddenly noticed a line of clear sky between the south and southwest. I called to the other men that the sky was clearing and then a moment later I realized that what I had seen was not a rift in the clouds but the white crest of an enormous wave. During twenty-six years’ experience of the ocean in all its moods I had not encountered a wave so gigantic. It was a mighty upheaval of the ocean, a thing quite apart from the big white-capped seas that had been our tireless companions for many days. I shouted “For God’s sake hold on! It’s got us!” Then came a moment of suspense that seemed to be drawn out into hours. White surged the foam of the breaking sea around us. We felt our boat being lifted and flung forward like a cork in breaking surf. We were in a seething chaos of tortured water; but somehow the boat lived through it, half filled with water, sagging to the dead weight and shuddering under the blow. We bailed with the energy of men fighting for life, flinging the water over the sides with every receptacle that came to our hands, and after ten minutes of uncertainty we felt the boat renew her life beneath us. She floated again and ceased to lurch drunkenly as though dazed by the attack of the sea. Earnestly we hoped that never again would we encounter such a wave. (Sir Ernest Shackle-ton, South: The “Endurance” Expedition, 1919)
Shackleton did make it to South Georgia and was able to rescue all of his men. Their epic voyage made maritime history—and that gigantic wave is part of that history.
Stories like this have abounded in the folklore of the sea for hundreds of years. Sailors have often told of moments of absolute terror when rogue waves taller than their ship’s mast rose without warning, barreling toward them like some monster in a nightmare. Sometimes these waves appeared suddenly out of a calm ocean; more often, they arose in a violent gale. And sometimes they came in groups of three, named the notorious Three Sisters: just when the petrified sailors thought they had survived the monster, two more giant waves would crash down on their lumbering boat in rapid succession.
Many of these accounts were probably exaggerated by the sailors’ horror and maybe embellished for effect, but the sheer weight of eyewitness testimony lends some credibility to them. Paul C. Liu, a scientist at NOAA’s Great Lakes Laboratory, listed several dozen of the most notable in the journal Geofizika in 2007 (vol. 24). Most of these occurrences are based on eyewitness reports and rough estimates of wave heights, but they do not lack for drama. For example, in 1896 Joshua Slocum was sailing around the world single-handedly in his 40-foot sloop Spray. He wrote this account of his experience much later, in his book Sailing Alone around the World: “One day, well off the coast of Patagonia, while the sloop was reaching under short sail, a tremendous wave, the culmination it seemed of many waves, rolled down upon her in a storm, roaring as it came. I had only a moment to get all sail down and myself up on the peak halyards, out of danger when I saw the mighty crest towering masthead-high above me. The mountain of water submerged my vessel. She shook in every timber and reeled under the weight of the sea, but rose quickly out of it and rode grandly over the rollers that followed. It may have been a minute that from my hold in the rigging I could see no part of the Spray’s hull.”
Small boats are by no means the only craft that have been threatened by giant waves. The luxury ocean liner Queen Mary encountered one in 1942. In December of that year, while carrying 16,000 troops from New York to Great Britain to fight in the war, this 82,000-ton ship was pounded by a storm in the North Atlantic. Some 700 miles west of Scotland she was hit broadside by a powerful wave that rolled her by an angle estimated later at 52 degrees. Another 3 degrees and she might have capsized. But she slowly righted herself and pressed on to her destination. Walter Ford Carter, whose father was aboard at the time, estimated that the wave was 92 feet (28m) high. Another account placed it at 70 feet (21m), but there was no damage to the ship that could support either number.
The wreck of the oil tanker World Glory provides dramatic evidence of another giant wave. On June 13, 1968, the 45,000-ton ship was fighting her way through heavy seas along the southeast coast of Africa, the scene of many a shipwreck. She was riding southward on the infamous Agulhas Current and facing into a fierce gale that was blowing against the current. The waves were 50 feet (15m) high, very steep, and more than half the length of the 737-foot ship. Captain Androutsopoulos reduced speed to the minimum required to point the bow directly into the oncoming rollers. Nevertheless, the ship was swept with green water for hours.
Then suddenly, an extraordinary wave, estimated at 70 feet (21m), rolled under the ship, lifted her high up, and let her hang for a moment. The captain heard an ominous crack and saw the bow tilt down at a frightening angle: the ship had snapped in half under its own weight. Within a few moments the two halves began to drift apart, still battered by high waves. Only a few survived to tell their tale at the inquiry.
There is no doubt that many, many ships have been crushed in giant seas in the midst of a brutal storm. What is at issue is the size of the largest waves, how frequently they appear, and what the state of the sea was. Waves 30, 40, even 50 feet high are sometimes seen in the North Atlantic during winter or in the “Furious Fifties” of the Southern Sea. But until recently, many oceanographers believed that sailors were exaggerating and that waves higher than, say, 50 feet were mere fantasy. There are some early incidents that give one pause, however. Consider, for example, the following.
In February 1933 the U.S. Navy’s oil tanker Ramapo was trapped in a massive storm that stretched from Asia to the U.S. Pacific coast. The ship had delivered 70,000 barrels of fuel oil to the Naval Station in Manila and now was returning home to San Diego. Sixty-knot winds had been blowing from the west for seven days, across thousands of miles of ocean. Now the waves were huge—50 feet (15m) from crest to trough. They rolled forward at 45 knots, driving the ship before them. In this following sea, the ship was pitching wildly, with its bow pointing skyward every 15 seconds.
At three o’clock on the night of February 7, the officer on the bridge happened to look back to the stern and saw a monster wave overtaking the ship. At that instant, the ship’s stern was in a trough and the bow was tipped up at a sharp angle. In one brief look, the officer saw he could line up the crest of the wave behind him with the crow’s nest on the mast amidships. As he watched, the enormous wave lifted the stern, broke over the ship in a thundering mass of water, and drove it forward into a deep trough.
Incredibly, the ship survived, with only minor damage to the structures on deck. And thanks to the brief, almost unconscious observation of the officer, it was possible to estimate the height of the monster wave from the length of the ship (148m) and the position of the crow’s nest. The shocking result was a crest-to-trough height of 34m, or 112 feet! It was the largest wave ever reported.
The crew of the Ramapo was lucky. If the ship had been longer than the 340-m wavelength of the wave, it might have been lifted amidships and cracked in half just like the World Glory. But as it was only about half a wavelength long, the ship rode the waves reasonably well. This eyewitness report has the support of a measurement, however imperfect it might have been in the moment of crisis.
Still more credible evidence emerged from the voyage of another luxury liner. In September 1995, the 70,000-ton Queen Elizabeth II was crossing from Cherbourg to New York. To avoid Hurricane Luis, the ship sailed south of its normal track. Nevertheless, the waves were topping 18m. On September 11 at four in the morning, the windows of the Grand Lounge, at a height of 22m (73ft), were smashed in.
Eleven minutes later an enormous wave loomed out of the darkness. (See the preface for a photo of a similar wave.) Captain R. W. Warwick said: “It looked as though the ship was heading straight for the white cliffs of Dover. The wave seemed to take ages to arrive but it was probably less than a minute before it broke with tremendous force over the bow. An incredible shudder went through the ship, followed a few minutes later by two smaller shudders. There seemed to be two waves in succession as the ship fell into the ‘hole’ behind the first one. The second wave of 28–29m whilst breaking, crashed over the foredeck, carrying away the forward whistle mast.”
Warwick recalled later that he saw that the crest of the second wave was directly in the horizontal line of sight from the bridge, at a height of 29m (96ft). In addition, a Canadian buoy in the area registered a wave of 30m (98ft) sometime during that storm.
Broken windows are convincing evidence for the heights of waves. Take the example of the Caledonian Star, a cruise ship that was returning from a visit to Antarctica in March 2001. A fierce gale had been blowing for several days off Cape Horn, the tip of South America. On March 2 the ship was struck by a wave that smashed the inch-thick windows of the bridge, 98 feet above the sea. The officer at the helm said later that the wave was solitary and twice as tall as the average.
These enormous rogue waves are still taking lives despite new technologies and ship safety systems: in April 2012, the headlines in San Francisco read, “Search for four missing sailors called off after fatal rogue wave hit yacht during race” (Associated Press, April 15, 2012).
The most famous wave in maritime history was recorded by instruments on the Draupner oil rig in the North Sea off Norway on January 1, 1995. This wave is notable not only for its size but also for the fact that for the first time an objective instrument made the measurement.
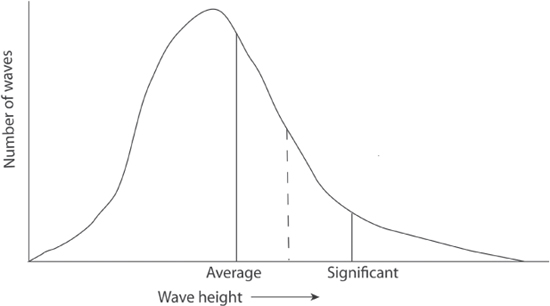
A severe storm had been raging for several days. A down-pointing laser wave gauge, mounted at one of the corners of the platform of the oil rig, was recording continuously during 20 minutes out of every hour during the storm. The time series shows that the significant wave heights—the mean wave height, trough to crest, of the highest third of the waves—were generally around 11–12m during the entire afternoon of January 1. From standard statistical arguments one could expect the maximum wave height (crest to trough) would be about 20m.
Then at 3:30 p.m. a single wave spiked in the records with a maximum height (crest to trough) close to 26m—about 85 feet! Not the biggest ever reported, but the source was unassailable, and the fact of being single makes this wave unique. Moreover, one would not expect a wave this tall to appear in a sea of 11-m waves very often. At the time, Paul Taylor, a scientist at Oxford University, estimated the chance of a recurrence was 1 out of 200,000 waves, or one wave in 10,000 years.
The Draupner wave caused quite a bit of excitement among ocean engineers and oceanographers. It established without question that extraordinarily high waves do exist and supported visual estimates of their sizes. A search for more examples revealed that sensors on the North Sea oil rig Goma recorded 466 waves over 70 feet high in 12 years, or nearly one a week, thus refuting the oceanographers’ disbelief of sailors’ extreme wave stories. But were these waves abnormal rogues, or might they have been unusually tall waves resulting from violent storms?
In any case, giant waves were far more numerous than previously thought. And one search of marine casualty records showed that at least 20 supertankers and container ships (more than 200m long) had been lost between 1969 and 1994 (Douglas Falkner, quoted in Graham Lawton, “Monsters of the Deep,” New Scientist 170, June 30, 2001). Could rogue waves have caused any of these expensive wrecks? A thorough scientific study of the phenomenon was urgently needed.
First, it was critical to distinguish between a rogue wave and “normal” tall waves. In fact, a rogue wave is not necessarily very tall, although great height makes great headlines. A rogue is just unexpectedly tall, considering the state of the sea. A good engineering definition is a wave whose height is twice the significant wave height. So in a sea with 3-m waves, a single 6-m wave would still qualify as a rogue by this definition. It probably would appear suddenly and disappear without doing much damage to a ship. The key point is that nobody knew why and how these rogue waves developed, whereas “normal” tall waves were obviously created by violent storms.
Therefore, in December 2000 the European Union funded a three-year investigation of shipping accidents and their possible connection to rogue waves. The project, called MAXWAVE, was headed by Wolfgang Rosenthal and Susanne Lehner, senior scientists at the GKSS Research Center at Geesthacht, Germany. Eleven meteorological and oceanographic institutions in Europe joined the effort.
Rosenthal and Lehner outlined four major goals for the project: to confirm the existence of rogue waves and estimate the risk of encounters, to apply new knowledge of rogues to ship design, to develop forecasting methods for rogues, and to disseminate the information to the marine community. The final goal of this project, they wrote, was “to improve the understanding of the physical processes responsible for the generation of extreme waves and to identify geophysical conditions in which such waves are most likely to occur” (Journal of Offshore Mechanics and Arctic Engineering 130 [2008]: 21006). The project would exploit, for the first time, the archives of satellite SAR observations to develop reliable statistics and make detailed studies of individual events. As Rosenthal and Lehner explained, the ESA satellites ERS-1 and ERS-2 produce radar images of waves in a 5 × 10km area every 200km, with 30-m resolution. These images are normally used to generate wave spectra that indicate the average conditions in the scanned “box.” But the raw SAR images contain more detailed information which could be analyzed for the possible appearance of rogue waves.
Rosenthal and Lehner’s team (one of seven) obtained 34,000 images, evenly distributed around the globe, for a 27-day period from April to May 2001. The images were processed and automatically searched for individual extreme waves with a specially designed technique. Despite the relatively small size of this data sample, the team discovered 10 extreme waves of 25-m height. One wave had a height of 28m (92ft) from crest to trough.
In another study a 27-day series of ERS-1 images obtained during August and September 1996 was processed to reveal maximum wave heights in 3 × 3 degree areas (about 180 miles square) over the whole globe. The resulting map showed a belt of tall waves (18–20m high) in the Furious Fifties latitudes of the Southern Ocean and in the track of Hurricane Fran in the western North Atlantic. No waves higher than 8m were seen anywhere else.
These were useful results, but how extreme were these waves? More precisely, how often does a single exceptionally tall wave—say, one 20 or 25m high—appear, and what is the significant wave height at the time? Are these waves to be expected as rare eruptions in a very violent sea? Or are special physics needed to explain them?
To find out, the team examined the nearly continuous records of wave heights obtained at the Draupner and Ekofisk oil rigs in the North Sea and off the Belgian coast. The observations were made by down-pointing laser instruments and floating buoys and had been collected over two decades. Their great advantage, in addition to their continuity, is that they could reveal the profile of each wave. From the data the team could determine the significant wave heights in a stormy or quiet sea, as well as the maximum heights of individual waves.
The oil rig records showed that individual rogue waves like the one recorded from the Draupner have a steep front; a sharp, pointy peak; and long, flat trough. The whole Draupner event, from the preceding trough to the following trough, lasted a mere 10 seconds. So we can see how difficult it is to find and measure individual rogues.
The team was surprised to find that the frequency of waves twice the significant wave heights was not unusual. The distribution of wave heights was exactly what is expected for a randomly varying sea surface. A few exceptions were found, such as the famous Draupner wave, but on the whole the frequencies of wave heights, even very large heights, are normal. Very tall waves, the researchers concluded, are just rather rare. We shall see that this conclusion has been contested up to the present time.
Do rogue waves occur preferentially at particular locations? At a news conference on July 21, 2004, Rosenthal and Lehner claimed they do. Their study of three weeks of ERS SAR data suggested that rogues arise where waves meet currents, such as the Agulhas off the east coast of South Africa or the Gulf Stream. But they admitted that rogues can also appear far from currents, where weather fronts are moving. “We know some of the reasons for the rogue waves, but we do not know them all,” Rosenthal concluded.
Another MAXWAVE team tried to find wind or wave conditions that would be likely to produce a rogue wave. They compiled a database of over 650 ship accidents in heavy weather between 1995 and 1999, using the Lloyd’s Marine Insurance files. The data were pared down to 245 accidents for which locations and times were known. Then hindcasts were calculated to obtain wave spectra, significant wave heights, wave steepness, and several other parameters.
The study failed to find a smoking gun—that is, a reliable predictor for a rogue wave. In particular, the significant wave height on the day before or during these accidents was surprisingly low, about 1–5m. So even if the tallest wave was 10m, it still didn’t follow that it caused the accident. Many accidents were, however, associated with steep waves, and some were associated with a cross-sea, in which a swell was crossing the wind direction at a large angle.
A map of the locations of the 245 accidents showed that they were concentrated in four areas of heavy shipping: the U.S. East Coast, the North Sea, the Mediterranean Sea, and the coast of China. This result led to the suggestion that ocean currents such as the Gulf Stream and Kirushiro Current could be generating rogue waves. The Agulhas Current, on the southeast coast of Africa, had previously been suspected because of its long history of shipwrecks. But no wrecks in the Agulhas were found in this study. Actually, the Cape of Good Hope, where the Agulhas meets the prevailing west wind, seemed a better candidate for producing rogues.
Although the findings of the MAXWAVE project proved inconclusive on the causes of rogue waves, researchers were able to summarize the observed properties of these extreme waves. They are at least twice the significant height in size, so they are statistically unexpected. They are very steep and peaked and follow an unusually deep trough. These waves can arise singly or in small groups, in calm seas or violent storms, in shallow or deep water, in coastal currents or far out at sea. They are fast and sweep by in at most a few tens of seconds.
At the end of the MAXWAVE project, a team of theorists proposed three classes of rogue waves, based on what they looked like and their profiles in space and time, along with possible mechanisms for their generation.
1. A single extreme wave—a wave tower—might arise from the interaction between a wave train and a current. When a wind-driven train encounters a current flowing in the opposite direction, the waves can pile up to an extreme height. The Agulhas Current was still considered a candidate for this type.
2. Rogue waves can occur in groups of three or more high peaks—the three sisters effect. Sister waves are thought to receive energy from the atmosphere by a line of thunderstorms preceding a cold front and traveling in the propagation direction of the group.
3. Two wave trains with similar wavelengths but crossing each other in different directions (a cross-sea) can produce an interference pattern that produces unusually tall waves. This condition is called a white wall and is probably what the Queen Elizabeth II encountered.
The MAXWAVE project was most successful in exploring the frequency of rogues and in devising techniques to locate them in SAR images. But much work remained to apply these techniques to the mountains of available SAR images. Therefore, Lehner and Rosenthal organized a follow-on program called WaveAtlas, which aims at producing global maps of individual rogue waves. As of mid-2011, a million SAR images from 1998 to 2000 had been processed. Each covers a small area, 5 × 10 degrees (about 300 × 600 miles). Several new hotspots for rogue waves have already been identified: the southwest coast of Greenland, the North Pacific in winter, the southwest coast of Australia, and Cape Horn, at the southern tip of South America. The analysis continues.
With all the current excitement about rogue waves, we need to be reminded that some very tall waves are not necessarily rogues. Tall waves can be expected in a particularly violent storm. Take, for example, the experience of a British research team in February 2000. This group boarded the 295-foot ship Discovery on February 6 and sailed west from Southampton. They planned to measure the wind speeds and wave heights at the peak of a powerful storm. The team had done this sort of thing before and expected no great difficulties. They were in for some surprises.
By February 8 the ship was 250km west of Scotland, near the small island of Rockall. The wind was howling at a steady 72km/h (45mph). The captain of the ship headed straight into the wind, but nevertheless the ship rolled badly. During the next 12 hours the wind rose to 83km/h, and the sea went mad. The team was measuring waves with a significant height of 18.5m (60ft), and these waves were setting a record. But the best—or worst—was yet to come.
Past midnight on February 8 the ship was battered by waves of 20, 25, and an astounding 29.5m (96.8ft), the largest ever measured with scientific instruments. Windows broke. The ship almost collided with a trawler. A lifeboat came loose and was banging against the starboard side. People suffered bruises and broken ribs.
As tall as these waves were, they were not rogues: they could be expected with such record-breaking significant wave heights. However, these monster waves did pose a problem: they continued to arrive regularly for 12 hours, long after the peak winds had subsided. So evidently these huge waves were not wind-driven; they were waves in a swell. The team is still struggling to find an explanation for them.
After the MAXWAVE project published its results in 2002, rogue waves were accepted as real, with a much higher occurrence probability than 1 in 10,000 years, as Paul Taylor had posited. It was also clear that they were responsible for some shipwrecks. The next logical scientific step was to understand them in physical terms. Could scientists learn enough about their origins to be able to predict them?
Theorists have picked up the challenge enthusiastically. Indeed, modeling rogue waves has become a hot topic in the past decade. The first question that has to be settled is whether rogue waves are just very rare examples of a random wave or are the result of some special kind of physics.
What do scientists mean by a “random” wave? They think of the tossing sea surface as an interference pattern among many weak Stokes waves that move in different directions (see chapter 4 for Stokes waves). When several waves overlap constructively, they create a taller wave. But because they move independently, their meeting at one place and time is a random event, seemingly unpredictable. Most of the sea surface is covered with such random waves.
Random doesn’t mean chaotic, however. There is method to the madness of waves because they obey the laws of chance. The most familiar example of a random process is the tossing of coins. If you toss a coin 10 times, you expect to get 5 heads and 5 tails, more or less, because the chance (probability) of getting either a head or a tail in each toss is the same—50%. But if you repeated this 10-toss game a thousand times, there is a good chance that at least once you would get 10 heads and no tails. That’s an “extreme” event that is due entirely to chance. If you plot the difference between the numbers of heads and tails in a long series of tosses, you get a bell-shaped curve, the so-called Gaussian, or “normal,” distribution. The peak of the curve corresponds to equal numbers of heads and tails which you would get most of the time, and the wings of the curve correspond to rare (“extreme”) events where there were far more heads than tails, or vice versa.
In the same way, 10 ocean waves might overlap and interfere constructively to build a towering wave 10 times higher than any of the original waves. This would be a rogue event, due entirely to chance.
Way back in 1880, John William Strutt (later known as Lord Rayleigh), of Cambridge University, gave a mathematical description of random waves. This was a relatively minor accomplishment in his vast output. He made important contributions to all the fields of physics, including optics, electro-magnetism, and sound. He was also the first to provide a scientific answer to the age-old child’s question “Why is the sky blue?” (The answer was molecular scattering of the sun’s light waves.) He was above all a theorist, but in 1904 he shared a Nobel Prize with William Ramsay for the discovery of a new element, argon.
Fig. 8.1 Rayleigh distribution of wave heights in a random sea. The highest third of waves are found in the tail, up to the dashed line.
But getting back to his contribution to the understanding of ocean waves, he viewed the sea surface as made up of many overlapping sinusoidal waves. He also assumed that their frequencies and amplitudes were distributed according to a bell-shaped curve and had propagation directions and phases distributed uniformly. The waves could interfere with one another and produce a fluctuating sea surface. His was a theory of linear waves which are intrinsically weak but may combine to create tall waves.
Rayleigh derived a simple formula for the distribution of wave heights graphed in figure 8.1. The higher the wave, the more infrequent it is. The highest waves appear in the long, thin tail of the distribution. Rayleigh’s predictions of wave heights agreed reasonably well with the observations of his day. But that was before rogue waves were accepted as real.
Rayleigh’s theory of wave heights has been extended to include a broader range of frequencies; to deal with wave groups instead of infinitely long trains; and to treat nonsinusoidal waves with cusps and deep troughs. The question today is whether a Rayleigh-type distribution can account for the estimated frequency of rogues. Several tests suggest that it can.
For example, in 1998 marine scientist Michel Olagnon examined buoy measurements of 2 million waves and found no exceptions to the Rayleigh distribution. In 2000, he repeated the comparison with 3 million waves and confirmed his earlier conclusion. Then in 2008, five years of buoy measurements off the Mediterranean coast of Spain were analyzed by Leo Holthuijsen and colleagues. They had 10 million waves to work with, and found waves with heights as large as 2.8 times the significant wave height, but still the Raleigh distribution fitted the data nicely.
The North Sea is a proven breeding ground for extreme waves because of the frequency of powerful storms and the possible influence of a shallow bottom, less than 100m deep in places. Oil rigs there, like Norway’s Ekofisk, have been recording wave profiles continuously for as long as a decade. Therefore, Harald Krogstadt and friends decided to look for rogues in 100,000 samples of Ekofisk records. In 2008 they confirmed that the highest waves (rogues) are actually members of a normal population of random waves—although way out in the tail. A Raleigh distribution, modified to account for the cusps and deep troughs of big waves, fitted the data to a tee. Like the MAXWAVE team, these Norwegian researchers could not find any criterion, such as significant wave height, that might forecast a series of extreme waves. Therefore, forecasting rogue waves, just like trying to predict when a string of 10 heads might appear in repeated 10-toss games, remains a distant goal.
The latest statistics of rogue waves were compiled by Burkard Baschek (UCLA) and his colleague Jennifer Imai (California State University, Long Beach). In 2011 they examined buoy measurements on the U.S. west coast made over 81 years. They found over 7,100 rogues, with the tallest at 19m high (62ft). From these data they could estimate the likelihood of a rogue in the open sea (101 per year) and in coastal waters (63 per year). Along the world’s major shipping lanes the chance is about 1% per day for a wave at least 11m tall, but it need not qualify as a rogue. Of course, their estimates don’t take into account special circumstances such as currents or a rough bottom topography, but they are interesting nevertheless.
We can use the following example to illustrate the statistics of random rogue waves. In 2005 an extreme wave in the open sea almost destroyed a ship. The 510-foot research ship Explorer was on route between Vancouver and Japan, carrying more than 680 students and 120 faculty and staff. On January 27 the ship was located 650 miles south of Alaska, plowing through heavy seas. Suddenly a 50-foot wave leaped out of the sea and flooded the bridge, knocking out the controls. Three of the four engines were disabled by the shock, and the crew could barely keep the bow of the ship headed into the high seas. It was at risk of turning broadside to the waves and capsizing. Fortunately, the crew did manage to use emergency steering methods to save the ship, and it limped back to port with only two injured crew members.
If we assume that this random 50-foot wave was a rogue and that the significant height was 25 feet, we can calculate that a wave of this height would arise only once every 3,000 waves. So if the average wave period was, say, 10 seconds, a random rogue would be expected every 8 hours. The Explorer was actually quite lucky not to be hit more than once.
Some scientists are not convinced that rogue waves are just the tails of a Rayleigh distribution. They think that special circumstances and special physics are required to produce at least some of them. They point to a probable connection between currents (such as the Agulhas) and rogues. Likewise, the high incidence of rogues in the shallow North Sea points to the influence of the sea floor topography. And they say that encountering three rogues in succession (the Three Sisters) would be impossibly improbable if rogues were truly random events. How is it possible that a rogue wave can arise from a calm sea, they ask. Finally, being told that a rogue is completely unpredictable and “just happens” leaves a scientist feeling quite unsatisfied.
For these reasons theorists began to explore other mechanisms that could explain rogue waves, with the hope of being able to predict them. Two classes of models have been thoroughly investigated in the past decade.
First are models that involve the focusing of wave energy. Focusing can occur in several ways: because of the different wave speeds within a group (dispersion), through the interaction of a group with a current, or by the crossing of wind-driven waves and swells (a cross-sea). All of these mechanisms are examples of constructive interference, a familiar “linear” process. Second, there are models that involve “nonlinear” processes, such as the intrinsic instability of a wave group or the interaction of a wave with itself. Somehow nonlinearity allows waves within a group to steal energy from their neighbors and grow to extreme heights. Below, I discuss both kinds of models, beginning with some linear models.
The simplest way to generate a single rogue wave in a random sea is to invoke a gust of wind. Imagine a mild or moderate sea made up of many weak sinusoidal waves of different wavelengths that are running in random directions. Now imagine that a gust of wind slaps the surface and launches a group of waves in the wind’s direction. Such a group will have short waves in front and longer waves in back (as we saw in chapter 2). Within a few moments the longer and faster waves overtake the shorter and slower waves and overlap them. This process creates a high crest in the group.
If, in addition, the crest happens to coincide with a momentary crest in the random sea, a rogue wave can be formed. Remember, a rogue needs to be only twice the height of the significant wave height, not necessarily a very tall wave or a long-lived wave. This mechanism was described in great mathematical detail in a 2009 scholarly book by C. Kharif, E. Pelinovsky, and A. Slunyaev, Rogue Waves in the Ocean; and it was simulated by Efim Pelinovsky and his Russian colleagues in 2011. Kharif and colleagues claimed that this process would work even in a rough sea. They also estimated that such a rogue event would only last two minutes before the overlapping waves would again disperse.
This way of focusing wave energy, using the variation of wave speed with wavelength, has also been demonstrated in wave tank experiments. The scheme works well if the wave is restricted to travel in only one dimension, but other tank experiments show that a rogue is not generated if the wave is allowed to spread in several directions.
Another possible focusing mechanism involves strong currents such as the Agulhas or the Gulf Stream. The Agulhas Current is well known for generating big waves. Seasoned mariners tell of the “Cape rollers” that the southwestern gales drive northeast against this current. Swells 10 to 13m high are not unusual. It is easy to picture a swell moving in the opposite direction to a current. When the swell meets the current, it slows down, shortening its wavelengths and rising abruptly in height. It might even be stopped dead and reflected backwards by the current.
The British ship Waratah probably met such conditions on her voyage from Melbourne, Australia, to London, with a stop at Durban, South Africa. She left Durban for Cape Town on July 26, 1909, with 211 passengers and crew aboard. Late in the day the wind picked up sharply, gusting to 50 knots (93km/h) and raising waves 10m high. The ship was seen battling the waves by observers on other ships, the last time 180 miles from Durban. The 465-foot Waratah never made it to Cape Town. She vanished without a trace. No one survived. It seems most likely that a rogue wave engulfed the ship, but without hard evidence it is impossible to say. Several attempts have been made to find the wreck but to no avail. Plans are afoot to use a submersible to search the bottom within a 50-mile radius of where she was last seen.
Let’s return to the physics. Two British scientists—M. Longuet-Higgins and R. Stewart—were the first to describe the focusing of wave energy by a current. In 1961, long before rogue waves were recognized, they imagined a train of single-wavelength waves riding into a current. The current could either oppose or assist the wave. In their model, the volume of the current was steady, but its speed varied along its length, as would occur if the current were spreading out. They learned that if the current and the wave were moving in the same direction, the wave would lose energy to the current. But when the current opposed the wave, the wave would gain energy from the current. Basically, the current pushes back on the wave, exerting a steady force through a distance of several wavelengths. And that amounts to doing work on the wave. The wave rises in height as a consequence.
The effect depends on the relative speeds of current and wave. If, for example, the opposing current’s speed was a quarter of the wave’s initial speed, the wave’s height would grow by a factor of 3. But the average speed of the Agulhas Current is only a few percent of the speed of wind-driven waves, so applying this analysis does not appear realistic.
In reality, however, a current like the Agulhas may have pockets of higher and lower speeds because of the rough bottom in this shallow area. Benjamin White and Bengt Fornberg examined the effects of such speed variations on a wave train in 1998. They postulated that the current has random fluctuations of speed in time and space, and they looked for any effects from these fluctuations on an oncoming wave.
In one of their numerical simulations, a plane wave front enters an opposing current that has pockets of fast and slow speeds. As different parts of the wave front encounter different water speeds, they are refracted, so that they bend in new directions. Each part of the front follows its own curving trajectory or ray. Where the rays cross, they interfere constructively to form what are called caustics (sunlight refracted through ripples onto the bottom of a shallow pond illustrates this effect), and the local amplitude rises. These are the places where a rogue wave might be formed. And as pockets of current speed change, the whole pattern of rays and rogues may change within a few moments.
This scenario works well only if the incident wave does not spread laterally (according to K. B. Dysthe). If it does spread, the caustics smear out, and the chance of forming a rogue is reduced. But because we’re not absolutely sure of the frequency with which rogues appear, this reduction may not be fatal to the idea.
Much of the recent research on rogue waves invokes nonlinear processes. Only these, it is thought, can explain rogues that are too tall or too frequent to be explained by the simpler linear theories. Nonlinearity also is interesting in itself because of the unexpected effects it reveals.
We need to be clear about the meaning of nonlinearity. It refers to a change in a system that depends on the present state of the system. It usually involves a positive feedback loop, so that the system interacts with itself. As an example, consider compound interest. Part of the growth in your savings account comes from the interest you earned this year on the principle. That is the linear part of the growth. But you also gained from the interest on last year’s interest; interest on interest. That is the nonlinear part, a kind of feedback loop. This nonlinear growth produces an exponential rise in wealth (if you don’t spend the profit).
In a group of ocean waves, as we shall see, long waves can steal energy from shorter waves. That is a nonlinear process that wouldn’t happen otherwise. In chapter 4, I briefly discussed the Stokes wave, which is the simplest example of a nonlinear wave. It interacts with itself to produce a sharper cusp and a flatter trough than a sinusoidal wave has. Waves in a swell resemble Stokes waves.
For a long time, it was thought that Stokes waves could propagate indefinitely without change of shape. Then in 1967, two British physicists discovered by accident that a train of Stokes waves can become unstable after traveling some distance in a wave tank. T. Brooke Benjamin was a brilliant English mathematical physicist and mathematician at Oxford University and a highly respected expert in fluid mechanics. Jim E. Feir was his student. This important discovery became known as the Benjamin-Feir Instability.
The two researchers intended to generate a train of waves with constant frequency and amplitude, but unexpectedly, their wave generator imposed a slow variation of amplitude along the length of the train. The wave train moved down the tank without incident until suddenly two new wave frequencies (“sidebands”) appeared in the train. One frequency was slightly higher than the primary wave’s frequency; the other was slightly lower. These sidebands grew exponentially in height at the expense of the primary wave, which eventually disintegrated. After eliminating all possible sources of equipment vibrations and imprecision, Benjamin and Feir determined that this nonlinear phenomenon was indeed real: the slight amplitude deviation was reinforced nonlinearly, leading to this sideband instability. Nobody had ever seen or expected the likes of this before.
Could this Benjamin-Feir instability produce a rogue wave? Many scientists thought so. To test the idea, they had to investigate the later stages of the instability, when the sidebands waves would grow to impressive heights. And to do that they employed a strange wave equation, the nonlinear Schrödinger equation. (We talked briefly about the origin of this equation in chapter 4.) Let’s look at a recent example of its predictions. This numerical simulation was performed by Christian Kharif and Efim Pelinovsky in 2003.
In figure 8.2A we see the original wave. It has a constant wavelength and a slightly varying amplitude. After a certain time, the instability occurs and a single wave group is formed (fig. 8.2B). Its central wave has a crest-to-trough height almost three times the significant wave height. Here indeed is a rogue wave! A study of the instability showed that the wave group had extracted energy from the original wave in order to form the high central peak. In the later stages of the event (fig. 8.2C), both the original wave group and the tall central peak have disappeared and have been replaced by a chain of wave groups, each with a central peak twice as high as the average. Finally, assuming no dissipation in the model, the groups return their energy to the primary wave, which recovers almost completely (fig. 8.2D).
Other theorists have pursued variations of this attractive scenario. They discovered that if the whole chain of events repeats, then the wave groups pulsate periodically: they become “breathers.” These early numerical simulations were highly artificial and were intended to show how well the Benjamin-Feir instability might work under ideal conditions. In particular, theorists wanted to learn how to model nonlinear waves with various exotic wave equations, such as the nonlinear Schrödinger, Dysthe, or Zakharov equations. The results were highly encouraging.
Fig. 8.2 The Benjamin Feir instability can generate a rogue at the center of a group of waves. The diagrams show the stages of the event: A, the original wave; B, single wave group formed after instability; C, subsequent chain of wave groups with a high central peak; D, return to original wave. (Drawn after C. Kharif and E. Pelinovsky, European Journal of Mechanics, B: Fluids 22 [2003]: 603.)
Several limiting factors for this scenario were discovered later, however. First, a wave train is unstable only if it spreads away from the wind direction by less than 35 degrees. In other words, a rogue forms only in a nearly unidirectional wave train. Secondly, the instability is less likely when the frequency spectrum of the initial wave train is broad. And finally, tank experiments suggest that even small amounts of dissipation—say, by wave breaking—may suppress the Benjamin-Feir instability entirely.
Perhaps the critical question is whether the Benjamin-Feir instability could arise at all in a random sea. And if it could, would a rogue wave break up before it reaches its maximum theoretical height? A. R. Osborne, M. Onerato, and M. Serio of the University of Torino tackled this difficult question in 2005. They asked under what conditions the Benjamin-Feir instability would increase the probability of a rogue wave in a random sea.
They began by calculating many examples of wave groups in a random sea. To do that, they selected one of the JONSWAP energy spectra and varied the phases of waves randomly. Then they calculated the evolution of each wave group for nine hours, using the nonlinear Schrödinger equation. That interval allowed different wavelengths to exchange energy. Finally, they calculated the distribution of wave heights in each group and averaged the results.
They learned that large-amplitude waves can appear from a random sea with a higher probability than the Rayleigh distribution forecasts, but only if the sea is very stormy—that is, only when the JONSWAP spectrum has a very high, narrow peak with most of the energy in a limited set of frequencies. Under those circumstances, very long wave groups are more likely, and the Benjamin-Feir instability also becomes more likely.
An international conference on rogue waves is held every few years. One was held in Brest in November 2000, another in Hawaii in January 2005, and another in Edinburgh in December 2005. Clearly, the experts are learning a lot about nonlinear water waves. The theory and simulations are becoming very esoteric, although tank experiments are helping to guide the theory. Some scientists are combining linear and nonlinear effects, such as the instabilities caused by crossing seas. Others are showing that even slight dissipation or damping of waves can mitigate the instabilities and can therefore prevent the generation of rogue waves. So the search and research goes on.
But the prospects of predicting rogue waves, or their precursors, seem as remote as ever. And yet that is what the operators of oil rigs and captains of container ships most desire. They now know what locations are best to avoid, if they can. But it’s difficult to avoid a rogue in the open sea, far from a coast. Perhaps a major experiment at sea, like JONSWAP, is needed to clarify the science.