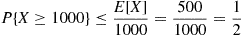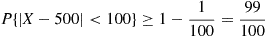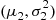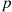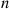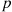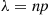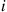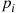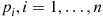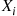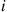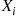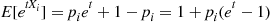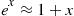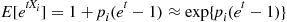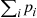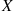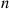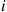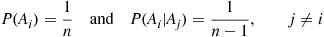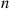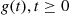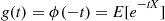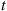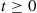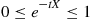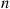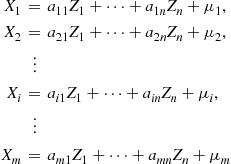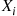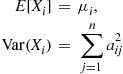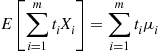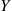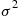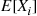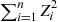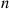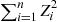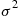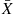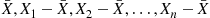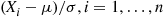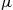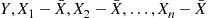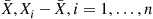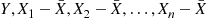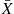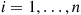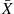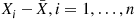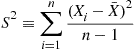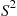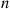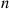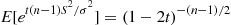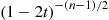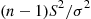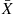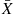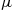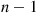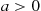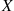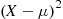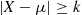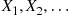Solution:
ϕX+Y(t)=ϕX(t)ϕY(t)=eλ1(et-1)eλ2(et-1)=e(λ1+λ2)(et-1)
Hence, X+Y is Poisson distributed with mean λ1+λ2
is Poisson distributed with mean λ1+λ2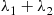 , verifying the result given in Example 2.37. ■
, verifying the result given in Example 2.37. ■
Solution:
ϕX+Y(t)=ϕX(t)ϕY(t)=expσ12t22+μ1texpσ22t22+μ2t=exp(σ12+σ22)t22+(μ1+μ2)t
which is the moment generating function of a normal random variable with mean μ1+μ2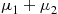 and variance σ12+σ22
and variance σ12+σ22 . Hence, the result follows since the moment generating function uniquely determines the distribution. ■
. Hence, the result follows since the moment generating function uniquely determines the distribution. ■
Example 2.47
The Poisson Paradigm
We showed in Section 2.2.4 that the number of successes that occur in n independent trials, each of which results in a success with probability p
independent trials, each of which results in a success with probability p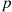 is, when n
is, when n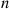 is large and p
is large and p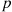 small, approximately a Poisson random variable with parameter λ=np
small, approximately a Poisson random variable with parameter λ=np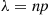 . This result, however, can be substantially strengthened. First it is not necessary that the trials have the same success probability, only that all the success probabilities are small. To see that this is the case, suppose that the trials are independent, with trial i
. This result, however, can be substantially strengthened. First it is not necessary that the trials have the same success probability, only that all the success probabilities are small. To see that this is the case, suppose that the trials are independent, with trial i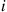 resulting in a success with probability pi
resulting in a success with probability pi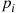 , where all the pi,i=1,…,n
, where all the pi,i=1,…,n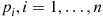 are small. Letting Xi
are small. Letting Xi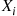 equal 1 if trial i
equal 1 if trial i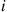 is a success, and 0 otherwise, it follows that the number of successes, call it X
is a success, and 0 otherwise, it follows that the number of successes, call it X , can be expressed as
, can be expressed as
X=∑i=1nXi
Using that Xi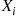 is a Bernoulli (or binary) random variable, its moment generating function is
is a Bernoulli (or binary) random variable, its moment generating function is
E[etXi]=piet+1-pi=1+pi(et-1)
Now, using the result that, for ∣x∣ small,
small,
ex≈1+x
it follows, because pi(et-1) is small when pi
is small when pi is small, that
is small, that
E[etXi]=1+pi(et-1)≈exp{pi(et-1)}
Because the moment generating function of a sum of independent random variables is the product of their moment generating functions, the preceding implies that
E[etX]≈∏i=1nexp{pi(et-1)}=exp∑ipi(et-1)
But the right side of the preceding is the moment generating function of a Poisson random variable with mean ∑ipi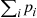 , thus arguing that this is approximately the distribution of X
, thus arguing that this is approximately the distribution of X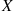 .
.
Not only is it not necessary for the trials to have the same success probability for the number of successes to approximately have a Poisson distribution, they need not even be independent, provided that their dependence is weak. For instance, recall the matching problem (Example 2.31) where n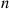 people randomly select hats from a set consisting of one hat from each person. By regarding the random selections of hats as constituting n
people randomly select hats from a set consisting of one hat from each person. By regarding the random selections of hats as constituting n trials, where we say that trial i
trials, where we say that trial i is a success if person i
is a success if person i chooses his or her own hat, it follows that, with Ai
chooses his or her own hat, it follows that, with Ai being the event that trial i
being the event that trial i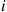 is a success,
is a success,
P(Ai)=1nandP(Ai∣Aj)=1n-1,j≠i
Hence, whereas the trials are not independent, their dependence appears, for large n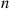 , to be weak. Because of this weak dependence, and the small trial success probabilities, it would seem that the number of matches should approximately have a Poisson distribution with mean 1 when n
, to be weak. Because of this weak dependence, and the small trial success probabilities, it would seem that the number of matches should approximately have a Poisson distribution with mean 1 when n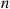 is large, and this is shown to be the case in Example 3.23.
is large, and this is shown to be the case in Example 3.23.
The statement that “the number of successes in n trials that are either independent or at most weakly dependent is, when the trial success probabilities are all small, approximately a Poisson random variable” is known as the Poisson paradigm. ■
trials that are either independent or at most weakly dependent is, when the trial success probabilities are all small, approximately a Poisson random variable” is known as the Poisson paradigm. ■
Remark
For a nonnegative random variable X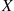 , it is often convenient to define its Laplace transform g(t),t≥0
, it is often convenient to define its Laplace transform g(t),t≥0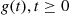 , by
, by
g(t)=ϕ(-t)=E[e-tX]
That is, the Laplace transform evaluated at t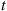 is just the moment generating function evaluated at -t
is just the moment generating function evaluated at -t . The advantage of dealing with the Laplace transform, rather than the moment generating function, when the random variable is nonnegative is that if X≥0
. The advantage of dealing with the Laplace transform, rather than the moment generating function, when the random variable is nonnegative is that if X≥0 and t≥0
and t≥0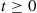 , then
, then
0≤e-tX≤1
That is, the Laplace transform is always between 0 and 1. As in the case of moment generating functions, it remains true that nonnegative random variables that have the same Laplace transform must also have the same distribution. ■
It is also possible to define the joint moment generating function of two or more random variables. This is done as follows. For any n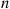 random variables X1,…,Xn
random variables X1,…,Xn , the joint moment generating function, ϕ(t1,…,tn)
, the joint moment generating function, ϕ(t1,…,tn) , is defined for all real values of t1,…,tn
, is defined for all real values of t1,…,tn by
by
ϕ(t1,…,tn)=E[e(t1X1+⋯+tnXn)]
It can be shown that ϕ(t1,…,tn) uniquely determines the joint distribution of X1,…,Xn
uniquely determines the joint distribution of X1,…,Xn .
.
Example 2.48
The Multivariate Normal Distribution
Let Z1,…,Zn be a set of n
be a set of n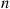 independent standard normal random variables. If, for some constants aij
independent standard normal random variables. If, for some constants aij , 1≤i≤m,1≤j≤n
, 1≤i≤m,1≤j≤n , and μi,1≤i≤m
, and μi,1≤i≤m ,
,
X1=a11Z1+⋯+a1nZn+μ1,X2=a21Z1+⋯+a2nZn+μ2,⋮Xi=ai1Z1+⋯+ainZn+μi,⋮Xm=am1Z1+⋯+amnZn+μm
then the random variables X1,…,Xm are said to have a multivariate normal distribution.
are said to have a multivariate normal distribution.
It follows from the fact that the sum of independent normal random variables is itself a normal random variable that each Xi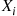 is a normal random variable with mean and variance given by
is a normal random variable with mean and variance given by
E[Xi]=μi,Var(Xi)=∑j=1naij2
Let us now determine
ϕ(t1,…,tm)=E[exp{t1X1+⋯+tmXm}]
the joint moment generating function of X1,…,Xm . The first thing to note is that since ∑i=1mtiXi
. The first thing to note is that since ∑i=1mtiXi is itself a linear combination of the independent normal random variables Z1,…,Zn
is itself a linear combination of the independent normal random variables Z1,…,Zn , it is also normally distributed. Its mean and variance are respectively
, it is also normally distributed. Its mean and variance are respectively
E∑i=1mtiXi=∑i=1mtiμi
and
Var∑i=1mtiXi=Cov∑i=1mtiXi,∑j=1mtjXj=∑i=1m∑j=1mtitjCov(Xi,Xj)
Now, if Y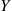 is a normal random variable with mean μ
is a normal random variable with mean μ and variance σ2
and variance σ2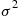 , then
, then
E[eY]=ϕY(t)∣t=1=eμ+σ2/2
Thus, we see that
ϕ(t1,…,tm)=exp∑i=1mtiμi+12∑i=1m∑j=1mtitjCov(Xi,Xj)
which shows that the joint distribution of X1,…,Xm is completely determined from a knowledge of the values of E[Xi]
is completely determined from a knowledge of the values of E[Xi]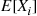 and Cov(Xi,Xj
and Cov(Xi,Xj ), i,j=1,…,m
), i,j=1,…,m . ■
. ■
2.6.1 The Joint Distribution of the Sample Mean and Sample Variance from a Normal Population
Let X1,…,Xn be independent and identically distributed random variables, each with mean μ
be independent and identically distributed random variables, each with mean μ and variance σ2
and variance σ2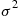 . The random variable S2
. The random variable S2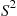 defined by
defined by
S2=∑i=1n(Xi-X¯)2n-1
is called the sample variance of these data. To compute E[S2]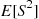 we use the identity
we use the identity
∑i=1n(Xi-X¯)2=∑i=1n(Xi-μ)2-n(X¯-μ)2 (2.21)
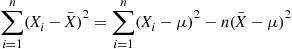 (2.21)
(2.21)which is proven as follows:
∑i=1n(Xi-X¯)=∑i=1n(Xi-μ+μ-X¯)2=∑i=1n(Xi-μ)2+n(μ-X¯)2+2(μ-X¯)∑i=1n(Xi-μ)=∑i=1n(Xi-μ)2+n(μ-X¯)2+2(μ-X¯)(nX¯-nμ)=∑i=1n(Xi-μ)2+n(μ-X¯)2-2n(μ-X¯)2
and Identity (2.21) follows.
Using Identity (2.21) gives
E[(n-1)S2]=∑i=1nE[(Xi-μ)2]-nE[(X¯-μ)2]=nσ2-nVar(X¯)=(n-1)σ2from Proposition 2.4(b)
Thus, we obtain from the preceding that
E[S2]=σ2
We will now determine the joint distribution of the sample mean X¯=∑i=1nXi/n and the sample variance S2
and the sample variance S2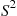 when the Xi
when the Xi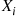 have a normal distribution. To begin we need the concept of a chi-squared random variable.
have a normal distribution. To begin we need the concept of a chi-squared random variable.
Definition 2.2
If Z1,…,Zn are independent standard normal random variables, then the random variable ∑i=1nZi2
are independent standard normal random variables, then the random variable ∑i=1nZi2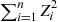 is said to be a chi-squared random variable with n
is said to be a chi-squared random variable with n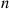 degrees of freedom.
degrees of freedom.
We shall now compute the moment generating function of ∑i=1nZi2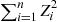 . To begin, note that
. To begin, note that
E[exp{tZi2}]=12π∫-∞∞etx2e-x2/2dx=12π∫-∞∞e-x2/2σ2dxwhereσ2=(1-2t)-1=σ=(1-2t)-1/2
Hence,
Eexpt∑i=1nZi2=∏i=1nE[exp{tZi2}]=(1-2t)-n/2
Now, let X1,…,Xn be independent normal random variables, each with mean μ
be independent normal random variables, each with mean μ and variance σ2
and variance σ2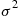 , and let X¯=∑i=1nXi/n
, and let X¯=∑i=1nXi/n and S2
and S2 denote their sample mean and sample variance. Since the sum of independent normal random variables is also a normal random variable, it follows that X¯
denote their sample mean and sample variance. Since the sum of independent normal random variables is also a normal random variable, it follows that X¯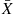 is a normal random variable with expected value μ
is a normal random variable with expected value μ and variance σ2/n
and variance σ2/n . In addition, from Proposition 2.4,
. In addition, from Proposition 2.4,
Cov(X¯,Xi-X¯)=0,i=1,…,n (2.22)
 (2.22)
(2.22)Also, since X¯,X1-X¯,X2-X¯,…,Xn-X¯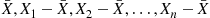 are all linear combinations of the independent standard normal random variables (Xi-μ)/σ,i=1,…,n
are all linear combinations of the independent standard normal random variables (Xi-μ)/σ,i=1,…,n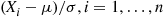 , it follows that the random variables X¯,X1-X¯,X2-X¯,…,Xn-X¯
, it follows that the random variables X¯,X1-X¯,X2-X¯,…,Xn-X¯ have a joint distribution that is multivariate normal. However, if we let Y
have a joint distribution that is multivariate normal. However, if we let Y be a normal random variable with mean μ
be a normal random variable with mean μ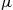 and variance σ2/n
and variance σ2/n that is independent of X1,…,Xn
that is independent of X1,…,Xn , then the random variables Y,X1-X¯,X2-X¯,…,Xn-X¯
, then the random variables Y,X1-X¯,X2-X¯,…,Xn-X¯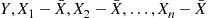 also have a multivariate normal distribution, and by Equation (2.22), they have the same expected values and covariances as the random variables X¯,Xi-X¯,i=1,…,n
also have a multivariate normal distribution, and by Equation (2.22), they have the same expected values and covariances as the random variables X¯,Xi-X¯,i=1,…,n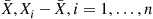 . Thus, since a multivariate normal distribution is completely determined by its expected values and covariances, we can conclude that the random vectors Y,X1-X¯,X2-X¯,…,Xn-X¯
. Thus, since a multivariate normal distribution is completely determined by its expected values and covariances, we can conclude that the random vectors Y,X1-X¯,X2-X¯,…,Xn-X¯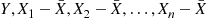 and X¯,X1-X¯,X2-X¯,…,Xn-X¯
and X¯,X1-X¯,X2-X¯,…,Xn-X¯ have the same joint distribution; thus showing that X¯
have the same joint distribution; thus showing that X¯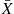 is independent of the sequence of deviations Xi-X¯
is independent of the sequence of deviations Xi-X¯ , i=1,…,n
, i=1,…,n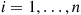 .
.
Since X¯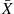 is independent of the sequence of deviations Xi-X¯,i=1,…,n
is independent of the sequence of deviations Xi-X¯,i=1,…,n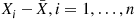 , it follows that it is also independent of the sample variance
, it follows that it is also independent of the sample variance
S2≡∑i=1n(Xi-X¯)2n-1
To determine the distribution of S2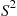 , use Identity (2.21) to obtain
, use Identity (2.21) to obtain
(n-1)S2=∑i=1n(Xi-μ)2-n(X¯-μ)2
Dividing both sides of this equation by σ2 yields
yields
(n-1)S2σ2+X¯-μσ/n2=∑i=1n(Xi-μ)2σ2 (2.23)
 (2.23)
(2.23)Now, ∑i=1n(Xi-μ)2/σ2 is the sum of the squares of n
is the sum of the squares of n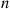 independent standard normal random variables, and so is a chi-squared random variable with n
independent standard normal random variables, and so is a chi-squared random variable with n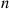 degrees of freedom; it thus has moment generating function (1-2t)-n/2
degrees of freedom; it thus has moment generating function (1-2t)-n/2 . Also [(X¯-μ)/(σ/n)]2
. Also [(X¯-μ)/(σ/n)]2 is the square of a standard normal random variable and so is a chi-squared random variable with one degree of freedom; it thus has moment generating function (1-2t)-1/2
is the square of a standard normal random variable and so is a chi-squared random variable with one degree of freedom; it thus has moment generating function (1-2t)-1/2 . In addition, we have previously seen that the two random variables on the left side of Equation (2.23) are independent. Therefore, because the moment generating function of the sum of independent random variables is equal to the product of their individual moment generating functions, we obtain that
. In addition, we have previously seen that the two random variables on the left side of Equation (2.23) are independent. Therefore, because the moment generating function of the sum of independent random variables is equal to the product of their individual moment generating functions, we obtain that
E[et(n-1)S2/σ2](1-2t)-1/2=(1-2t)-n/2
or
E[et(n-1)S2/σ2]=(1-2t)-(n-1)/2
But because (1-2t)-(n-1)/2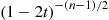 is the moment generating function of a chi-squared random variable with n-1
is the moment generating function of a chi-squared random variable with n-1 degrees of freedom, we can conclude, since the moment generating function uniquely determines the distribution of the random variable, that this is the distribution of (n-1)S2/σ2
degrees of freedom, we can conclude, since the moment generating function uniquely determines the distribution of the random variable, that this is the distribution of (n-1)S2/σ2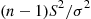 .
.
Summing up, we have shown the following.
2.7 The Distribution of the Number of Events that Occur
Consider arbitrary events A1,…,An , and let X
, and let X denote the number of these events that occur. We will determine the probability mass function of X
denote the number of these events that occur. We will determine the probability mass function of X . To begin, for 1≤k≤n
. To begin, for 1≤k≤n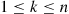 , let
, let
Sk=∑i1<…<ikP(Ai1…Aik)
equal the sum of the probabilities of all the nk intersections of k
intersections of k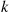 distinct events, and note that the inclusion-exclusion identity states that
distinct events, and note that the inclusion-exclusion identity states that
P(X>0)=P(∪i=1nAi)=S1-S2+S3-⋯+(-1)n+1Sn
Now, fix k of the n
of the n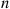 events — say Ai1,…,Aik
events — say Ai1,…,Aik — and let
— and let
A=∩j=1kAij
be the event that all k of these events occur. Also, let
of these events occur. Also, let
B=∩j∉{i1,…,ik}Ajc
be the event that none of the other n-k events occur. Consequently, AB
events occur. Consequently, AB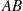 is the event that Ai1,…,Aik
is the event that Ai1,…,Aik are the only events to occur. Because
are the only events to occur. Because
A=AB∪ABc
we have
P(A)=P(AB)+P(ABc)
or, equivalently,
P(AB)=P(A)-P(ABc)
Because Bc occurs if at least one of the events Aj,j∉{i1,…,ik}
occurs if at least one of the events Aj,j∉{i1,…,ik}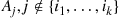 , occur, we see that
, occur, we see that
Bc=∪j∉{i1,…,ik}Aj
Thus,
P(ABc)=P(A∪j∉{i1,…,ik}Aj)=P(∪j∉{i1,…,ik}AAj)
Applying the inclusion-exclusion identity gives
P(ABc)=∑j∉{i1,…,ik}P(AAj)-∑j1<j2∉{i1,…,ik}P(AAj1Aj2)+∑j1<j2<j3∉{i1,…,ik}P(AAj1Aj2Aj3)-…
Using that A=∩j=1kAij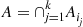 , the preceding shows that the probability that the k
, the preceding shows that the probability that the k events Ai1,…,Aik
events Ai1,…,Aik are the only events to occur is
are the only events to occur is
P(A)-P(ABc)=P(Ai1…Aik)-∑j∉{i1,…,ik}P(Ai1…AikAj)+∑j1<j2∉{i1,…,ik}P(Ai1…AikAj1Aj2)-∑j1<j2<j3∉{i1,…,ik}P(Ai1…AikAj1Aj2Aj3)+⋯
Summing the preceding over all sets of k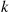 distinct indices yields
distinct indices yields
P(X=k)=∑i1<…<ikP(Ai1…Aik)-∑i1<…<ik∑j∉{i1,…,ik}P(Ai1…AikAj)+∑i1<…<ik∑j1<j2∉{i1,…,ik}P(Ai1⋯AikAj1Aj2)-⋯ (2.24)
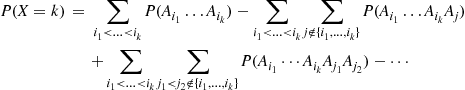 (2.24)
(2.24)First, note that
∑i1<…<ikP(Ai1…Aik)=Sk
Now, consider
∑i1<…<ik∑j∉{i1,…,ik}P(Ai1…AikAj)
The probability of every intersection of k+1 distinct events Am1,…,Amk+1
distinct events Am1,…,Amk+1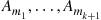 will appear k+1k
will appear k+1k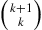 times in this multiple summation. This is so because each choice of k
times in this multiple summation. This is so because each choice of k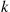 of its indices to play the role of i1,…,ik
of its indices to play the role of i1,…,ik and the other to play the role of j
and the other to play the role of j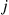 results in the addition of the term P(Am1…Amk+1)
results in the addition of the term P(Am1…Amk+1) . Hence,
. Hence,
∑i1<…<ik∑j∉{i1,…,ik}P(Ai1…AikAj)=k+1k∑m1<…<mk+1P(Am1…Amk+1)=k+1kSk+1
Similarly, because the probability of every intersection of k+2 distinct events Am1,…,Amk+2
distinct events Am1,…,Amk+2 will appear k+2k
will appear k+2k times in ∑i1<…<ik∑j1<j2∉{i1,…,ik}P(Ai1…AikAj1Aj2)
times in ∑i1<…<ik∑j1<j2∉{i1,…,ik}P(Ai1…AikAj1Aj2)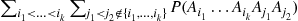 , it follows that
, it follows that
∑i1<…<ik∑j1<j2∉{i1,…,ik}P(Ai1…AikAj1Aj2)=k+2kSk+2
Repeating this argument for the rest of the multiple summations in (2.24) yields the result
P(X=k)=Sk-k+1kSk+1+k+2kSk+2-⋯+(-1)n-knkSn
The preceding can be written as
P(X=k)=∑j=kn(-1)k+jjkSj
Using this we will now prove that
P(X≥k)=∑j=kn(-1)k+jj-1k-1Sj
The proof uses a backwards mathematical induction that starts with k=n . Now, when k=n
. Now, when k=n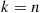 the preceding identity states that
the preceding identity states that
P(X=n)=Sn
which is true. So assume that
P(X≥k+1)=∑j=k+1n(-1)k+1+jj-1kSj
But then
P(X≥k)=P(X=k)+P(X≥k+1)=∑j=kn(-1)k+jjkSj+∑j=k+1n(-1)k+1+jj-1kSj=Sk+∑j=k+1n(-1)k+jjk-j-1kSj=Sk+∑j=k+1n(-1)k+jj-1k-1Sj=∑j=kn(-1)k+jj-1k-1Sj
which completes the proof.
2.8 Limit Theorems
We start this section by proving a result known as Markov’s inequality.
Proposition 2.6
Markov’s Inequality
If X is a random variable that takes only nonnegative values, then for any value a>0
is a random variable that takes only nonnegative values, then for any value a>0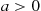
P{X≥a}≤E[X]a
Proof
We give a proof for the case where X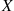 is continuous with density f
is continuous with density f .
.
E[X]=∫0∞xf(x)dx=∫0axf(x)dx+∫a∞xf(x)dx≥∫a∞xf(x)dx≥∫a∞af(x)dx=a∫a∞f(x)dx=aP{X≥a}
and the result is proven.
As a corollary, we obtain the following.
Proposition 2.7
Chebyshev’s Inequality
If X is a random variable with mean μ
is a random variable with mean μ and variance σ2
and variance σ2 , then, for any value k>0
, then, for any value k>0 ,
,
P{∣X-μ∣≥k}≤σ2k2
Proof
Since (X-μ)2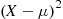 is a nonnegative random variable, we can apply Markov’s inequality (with a=k2
is a nonnegative random variable, we can apply Markov’s inequality (with a=k2 ) to obtain
) to obtain
P{(X-μ)2≥k2}≤E[(X-μ)2]k2
But since (X-μ)2≥k2 if and only if ∣X-μ∣≥k
if and only if ∣X-μ∣≥k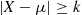 , the preceding is equivalent to
, the preceding is equivalent to
P{∣X-μ∣≥k}≤E[(X-μ)2]k2=σ2k2
and the proof is complete.
The importance of Markov’s and Chebyshev’s inequalities is that they enable us to derive bounds on probabilities when only the mean, or both the mean and the variance, of the probability distribution are known. Of course, if the actual distribution were known, then the desired probabilities could be exactly computed, and we would not need to resort to bounds.
Example 2.49
Suppose we know that the number of items produced in a factory during a week is a random variable with mean 500.
(a) What can be said about the probability that this week’s production will be at least 1000?
(b) If the variance of a week’s production is known to equal 100, then what can be said about the probability that this week’s production will be between 400 and 600?
Solution: Let X be the number of items that will be produced in a week.
be the number of items that will be produced in a week.
(a) By Markov’s inequality,
P{X≥1000}≤E[X]1000=5001000=12
(b) By Chebyshev’s inequality,
P{∣X-500∣≥100}≤σ2(100)2=1100
Hence,
P{∣X-500∣<100}≥1-1100=99100
and so the probability that this week’s production will be between 400 and 600 is at least 0.99. ■
The following theorem, known as the strong law of large numbers, is probably the most well-known result in probability theory. It states that the average of a sequence of independent random variables having the same distribution will, with probability 1, converge to the mean of that distribution.
Theorem 2.1
Strong Law of Large Numbers
Let X1,X2,…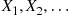 be a sequence of independent random variables having a common distribution, and let E[Xi]=μ
be a sequence of independent random variables having a common distribution, and let E[Xi]=μ . Then, with probability 1,
. Then, with probability 1,
X1+X2+⋯+Xnn→μasn→∞
 is given by
is given by
 is just the moment generating function of a binomial random variable having parameters
is just the moment generating function of a binomial random variable having parameters  and
and  . Thus, this must be the distribution of
. Thus, this must be the distribution of  . ■
. ■
 is Poisson distributed with mean
is Poisson distributed with mean 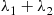 , verifying the result given in Example 2.37. ■
, verifying the result given in Example 2.37. ■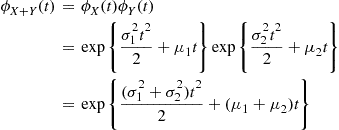
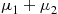 and variance
and variance  . Hence, the result follows since the moment generating function uniquely determines the distribution. ■
. Hence, the result follows since the moment generating function uniquely determines the distribution. ■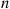 random variables
random variables  , the joint moment generating function,
, the joint moment generating function,  , is defined for all real values of
, is defined for all real values of  by
by
 uniquely determines the joint distribution of
uniquely determines the joint distribution of  .
. be independent and identically distributed random variables, each with mean
be independent and identically distributed random variables, each with mean  and variance
and variance 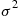 . The random variable
. The random variable 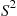 defined by
defined by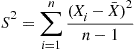
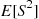 we use the identity
we use the identity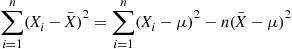 (2.21)
(2.21)

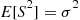
 and the sample variance
and the sample variance 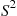 when the
when the 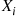 have a normal distribution. To begin we need the concept of a chi-squared random variable.
have a normal distribution. To begin we need the concept of a chi-squared random variable. , and let
, and let  denote the number of these events that occur. We will determine the probability mass function of
denote the number of these events that occur. We will determine the probability mass function of  . To begin, for
. To begin, for 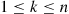 , let
, let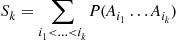
 intersections of
intersections of 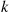 distinct events, and note that the inclusion-exclusion identity states that
distinct events, and note that the inclusion-exclusion identity states that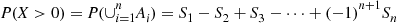
 of the
of the 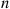 events — say
events — say  — and let
— and let
 of these events occur. Also, let
of these events occur. Also, let
 events occur. Consequently,
events occur. Consequently, 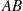 is the event that
is the event that  are the only events to occur. Because
are the only events to occur. Because

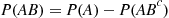
 occurs if at least one of the events
occurs if at least one of the events 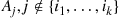 , occur, we see that
, occur, we see that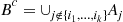
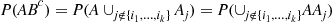

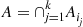 , the preceding shows that the probability that the
, the preceding shows that the probability that the  events
events  are the only events to occur is
are the only events to occur is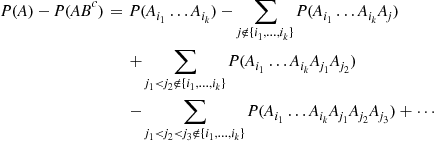
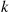 distinct indices yields
distinct indices yields (2.24)
(2.24)

 distinct events
distinct events 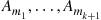 will appear
will appear 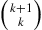 times in this multiple summation. This is so because each choice of
times in this multiple summation. This is so because each choice of 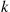 of its indices to play the role of
of its indices to play the role of  and the other to play the role of
and the other to play the role of 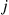 results in the addition of the term
results in the addition of the term  . Hence,
. Hence,
 distinct events
distinct events  will appear
will appear  times in
times in 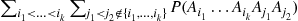 , it follows that
, it follows that
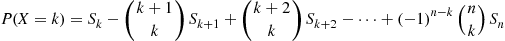


 . Now, when
. Now, when 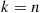 the preceding identity states that
the preceding identity states that
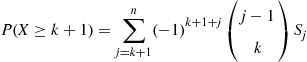

 be the number of items that will be produced in a week.
be the number of items that will be produced in a week.