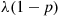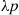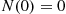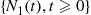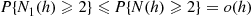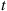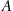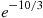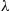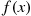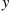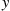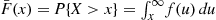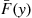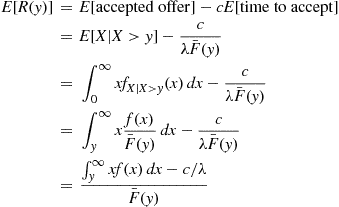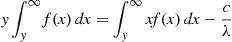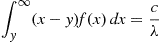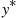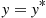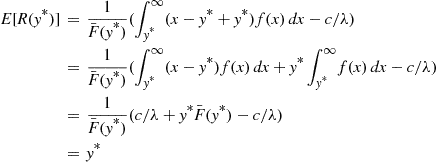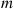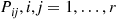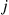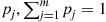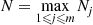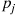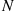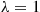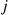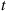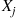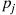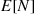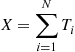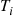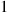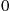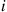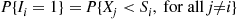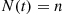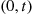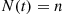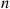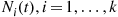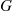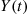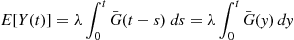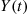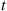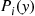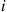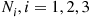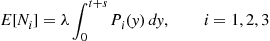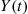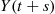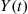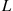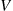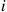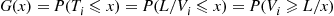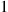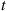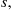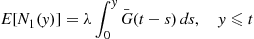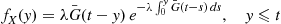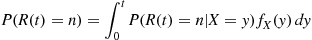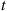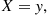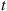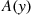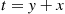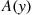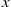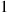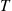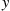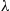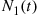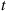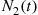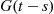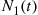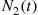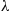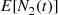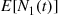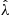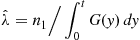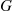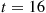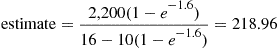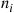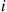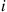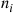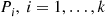5.3.4 Further Properties of Poisson Processes
Consider a Poisson process {N(t),t⩾0} having rate λ
having rate λ , and suppose that each time an event occurs it is classified as either a type I or a type II event. Suppose further that each event is classified as a type I event with probability p
, and suppose that each time an event occurs it is classified as either a type I or a type II event. Suppose further that each event is classified as a type I event with probability p or a type II event with probability 1-p
or a type II event with probability 1-p , independently of all other events. For example, suppose that customers arrive at a store in accordance with a Poisson process having rate λ
, independently of all other events. For example, suppose that customers arrive at a store in accordance with a Poisson process having rate λ ; and suppose that each arrival is male with probability 12
; and suppose that each arrival is male with probability 12 and female with probability 12
and female with probability 12 . Then a type I event would correspond to a male arrival and a type II event to a female arrival.
. Then a type I event would correspond to a male arrival and a type II event to a female arrival.
Let N1(t) and N2(t)
and N2(t)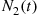 denote respectively the number of type I and type II events occurring in [0,t]
denote respectively the number of type I and type II events occurring in [0,t] . Note that N(t)=N1(t)+N2(t)
. Note that N(t)=N1(t)+N2(t) .
.
Proof
It is easy to verify that {N1(t),t⩾0} is a Poisson process with rate λp
is a Poisson process with rate λp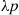 by verifying that it satisfies Definition 5.3.
by verifying that it satisfies Definition 5.3.
• N1(0)=0 follows from the fact that N(0)=0
follows from the fact that N(0)=0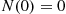 .
.
• It is easy to see that {N1(t),t⩾0}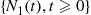 inherits the stationary and independent increment properties of the process {N(t),t⩾0}
inherits the stationary and independent increment properties of the process {N(t),t⩾0} . This is true because the distribution of the number of type I events in an interval can be obtained by conditioning on the number of events in that interval, and the distribution of this latter quantity depends only on the length of the interval and is independent of what has occurred in any nonoverlapping interval.
. This is true because the distribution of the number of type I events in an interval can be obtained by conditioning on the number of events in that interval, and the distribution of this latter quantity depends only on the length of the interval and is independent of what has occurred in any nonoverlapping interval.
• P{N1(h)=1}=P{N1(h)=1∣N(h)=1}P{N(h)=1}
+P{N1(h)=1∣N(h)⩾2}P{N(h)⩾2}=p(λh+o(h))+o(h)=λph+o(h)
• P{N1(h)⩾2}⩽P{N(h)⩾2}=o(h)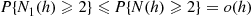
Thus we see that {N1(t),t⩾0} is a Poisson process with rate λp
is a Poisson process with rate λp and, by a similar argument, that {N2(t),t⩾0}
and, by a similar argument, that {N2(t),t⩾0} is a Poisson process with rate λ(1-p)
is a Poisson process with rate λ(1-p) . Because the probability of a type I event in the interval from t
. Because the probability of a type I event in the interval from t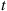 to t+h
to t+h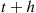 is independent of all that occurs in intervals that do not overlap (t,t+h)
is independent of all that occurs in intervals that do not overlap (t,t+h)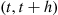 , it is independent of knowledge of when type II events occur, showing that the two Poisson processes are independent. (For another way of proving independence, see Example 3.23.) ■
, it is independent of knowledge of when type II events occur, showing that the two Poisson processes are independent. (For another way of proving independence, see Example 3.23.) ■
Example 5.14
If immigrants to area A arrive at a Poisson rate of ten per week, and if each immigrant is of English descent with probability 112
arrive at a Poisson rate of ten per week, and if each immigrant is of English descent with probability 112 , then what is the probability that no people of English descent will emigrate to area A
, then what is the probability that no people of English descent will emigrate to area A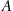 during the month of February?
during the month of February?
Example 5.15
Suppose nonnegative offers to buy an item that you want to sell arrive according to a Poisson process with rate λ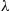 . Assume that each offer is the value of a continuous random variable having density function f(x)
. Assume that each offer is the value of a continuous random variable having density function f(x)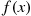 . Once the offer is presented to you, you must either accept it or reject it and wait for the next offer. We suppose that you incur costs at a rate c
. Once the offer is presented to you, you must either accept it or reject it and wait for the next offer. We suppose that you incur costs at a rate c per unit time until the item is sold, and that your objective is to maximize your expected total return, where the total return is equal to the amount received minus the total cost incurred. Suppose you employ the policy of accepting the first offer that is greater than some specified value y
per unit time until the item is sold, and that your objective is to maximize your expected total return, where the total return is equal to the amount received minus the total cost incurred. Suppose you employ the policy of accepting the first offer that is greater than some specified value y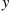 . (Such a type of policy, which we call a y
. (Such a type of policy, which we call a y -policy, can be shown to be optimal.) What is the best value of y
-policy, can be shown to be optimal.) What is the best value of y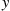 ? What is the maximal expected net return?
? What is the maximal expected net return?
Solution: Let us compute the expected total return when you use the y -policy, and then choose the value of y
-policy, and then choose the value of y that maximizes this quantity. Let X
that maximizes this quantity. Let X denote the value of a random offer, and let F¯(x)=P{X>x}=∫x∞f(u)du
denote the value of a random offer, and let F¯(x)=P{X>x}=∫x∞f(u)du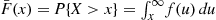 be its tail distribution function. Because each offer will be greater than y
be its tail distribution function. Because each offer will be greater than y with probability F¯(y)
with probability F¯(y)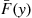 , it follows that such offers occur according to a Poisson process with rate λF¯(y)
, it follows that such offers occur according to a Poisson process with rate λF¯(y) . Hence, the time until an offer is accepted is an exponential random variable with rate λF¯(y)
. Hence, the time until an offer is accepted is an exponential random variable with rate λF¯(y) . Letting R(y)
. Letting R(y) denote the total return from the policy that accepts the first offer that is greater than y
denote the total return from the policy that accepts the first offer that is greater than y , we have
, we have
E[R(y)]=E[acceptedoffer]-cE[timetoaccept]=E[X∣X>y]-cλF¯(y)=∫0∞xfX∣X>y(x)dx-cλF¯(y)=∫y∞xf(x)F¯(y)dx-cλF¯(y)=∫y∞xf(x)dx-c/λF¯(y) (5.14)
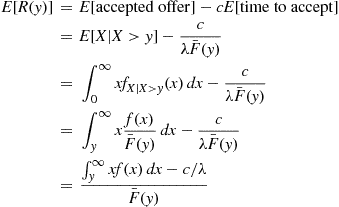 (5.14)
(5.14)
Differentiation yields
ddyE[R(y)]=0⇔-F¯(y)yf(y)+∫y∞xf(x)dx-cλf(y)=0
Therefore, the optimal value of y satisfies
satisfies
yF¯(y)=∫y∞xf(x)dx-cλ
or
y∫y∞f(x)dx=∫y∞xf(x)dx-cλ
or
∫y∞(x-y)f(x)dx=cλ
It is not difficult to show that there is a unique value of y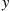 that satisfies the preceding. Hence, the optimal policy is the one that accepts the first offer that is greater than y∗
that satisfies the preceding. Hence, the optimal policy is the one that accepts the first offer that is greater than y∗ , where y∗
, where y∗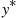 is such that
is such that
∫y∗∞(x-y∗)f(x)dx=c/λ
Putting y=y∗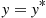 in Equation (5.14) shows that the maximal expected net return is
in Equation (5.14) shows that the maximal expected net return is
E[R(y∗)]=1F¯(y∗)(∫y∗∞(x-y∗+y∗)f(x)dx-c/λ)=1F¯(y∗)(∫y∗∞(x-y∗)f(x)dx+y∗∫y∗∞f(x)dx-c/λ)=1F¯(y∗)(c/λ+y∗F¯(y∗)-c/λ)=y∗
Thus, the optimal critical value is also the maximal expected net return. To understand why this is so, let m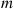 be the maximal expected net return, and note that when an offer is rejected the problem basically starts anew and so the maximal expected additional net return from then on is m
be the maximal expected net return, and note that when an offer is rejected the problem basically starts anew and so the maximal expected additional net return from then on is m . But this implies that it is optimal to accept an offer if and only if it is at least as large as m
. But this implies that it is optimal to accept an offer if and only if it is at least as large as m , showing that m
, showing that m is the optimal critical value. ■
is the optimal critical value. ■
It follows from Proposition 5.2 that if each of a Poisson number of individuals is independently classified into one of two possible groups with respective probabilities p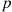 and 1-p
and 1-p , then the number of individuals in each of the two groups will be independent Poisson random variables. Because this result easily generalizes to the case where the classification is into any one of r
, then the number of individuals in each of the two groups will be independent Poisson random variables. Because this result easily generalizes to the case where the classification is into any one of r possible groups, we have the following application to a model of employees moving about in an organization.
possible groups, we have the following application to a model of employees moving about in an organization.
Example 5.16
Consider a system in which individuals at any time are classified as being in one of r possible states, and assume that an individual changes states in accordance with a Markov chain having transition probabilities Pij,i,j=1,…,r
possible states, and assume that an individual changes states in accordance with a Markov chain having transition probabilities Pij,i,j=1,…,r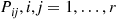 . That is, if an individual is in state i
. That is, if an individual is in state i during a time period then, independently of its previous states, it will be in state j
during a time period then, independently of its previous states, it will be in state j during the next time period with probability Pij
during the next time period with probability Pij . The individuals are assumed to move through the system independently of each other. Suppose that the numbers of people initially in states 1,2,…,r
. The individuals are assumed to move through the system independently of each other. Suppose that the numbers of people initially in states 1,2,…,r are independent Poisson random variables with respective means λ1,λ2,…,λr
are independent Poisson random variables with respective means λ1,λ2,…,λr . We are interested in determining the joint distribution of the numbers of individuals in states 1,2,…,r
. We are interested in determining the joint distribution of the numbers of individuals in states 1,2,…,r at some time n
at some time n .
.
Solution: For fixed i , let Nj(i),j=1,…,r
, let Nj(i),j=1,…,r denote the number of those individuals, initially in state i
denote the number of those individuals, initially in state i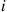 , that are in state j
, that are in state j at time n
at time n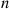 . Now each of the (Poisson distributed) number of people initially in state i
. Now each of the (Poisson distributed) number of people initially in state i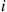 will, independently of each other, be in state j
will, independently of each other, be in state j at time n
at time n with probability Pijn
with probability Pijn , where Pijn
, where Pijn is the n
is the n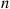 -stage transition probability for the Markov chain having transition probabilities Pij
-stage transition probability for the Markov chain having transition probabilities Pij . Hence, the Nj(i),j=1,…,r
. Hence, the Nj(i),j=1,…,r will be independent Poisson random variables with respective means λiPijn
will be independent Poisson random variables with respective means λiPijn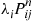 , j=1,…,r
, j=1,…,r . Because the sum of independent Poisson random variables is itself a Poisson random variable, it follows that the number of individuals in state j
. Because the sum of independent Poisson random variables is itself a Poisson random variable, it follows that the number of individuals in state j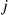 at time n
at time n —namely ∑i=1rNj(i)
—namely ∑i=1rNj(i) —will be independent Poisson random variables with respective means ∑iλiPijn
—will be independent Poisson random variables with respective means ∑iλiPijn , for j=1,…,r
, for j=1,…,r . ■
. ■
Example 5.17
The Coupon Collecting Problem
There are m different types of coupons. Each time a person collects a coupon it is, independently of ones previously obtained, a type j
different types of coupons. Each time a person collects a coupon it is, independently of ones previously obtained, a type j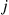 coupon with probability pj,∑j=1mpj=1
coupon with probability pj,∑j=1mpj=1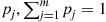 . Let N
. Let N denote the number of coupons one needs to collect in order to have a complete collection of at least one of each type. Find E[N]
denote the number of coupons one needs to collect in order to have a complete collection of at least one of each type. Find E[N] .
.
Solution: If we let Nj denote the number one must collect to obtain a type j
denote the number one must collect to obtain a type j coupon, then we can express N
coupon, then we can express N as
as
N=max1⩽j⩽mNj
However, even though each Nj is geometric with parameter pj
is geometric with parameter pj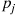 , the foregoing representation of N
, the foregoing representation of N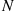 is not that useful, because the random variables Nj
is not that useful, because the random variables Nj are not independent.
are not independent.
We can, however, transform the problem into one of determining the expected value of the maximum of independent random variables. To do so, suppose that coupons are collected at times chosen according to a Poisson process with rate λ=1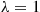 . Say that an event of this Poisson process is of type j,1⩽j⩽m
. Say that an event of this Poisson process is of type j,1⩽j⩽m , if the coupon obtained at that time is a type j
, if the coupon obtained at that time is a type j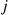 coupon. If we now let Nj(t)
coupon. If we now let Nj(t) denote the number of type j
denote the number of type j coupons collected by time t
coupons collected by time t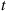 , then it follows from Proposition 5.2 that {Nj(t),t⩾0},j=1,…,m
, then it follows from Proposition 5.2 that {Nj(t),t⩾0},j=1,…,m are independent Poisson processes with respective rates λpj=pj
are independent Poisson processes with respective rates λpj=pj . Let Xj
. Let Xj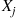 denote the time of the first event of the j
denote the time of the first event of the j th process, and let
th process, and let
X=max1⩽j⩽mXj
denote the time at which a complete collection is amassed. Since the Xj are independent exponential random variables with respective rates pj
are independent exponential random variables with respective rates pj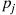 , it follows that
, it follows that
P{X<t}=P{max1⩽j⩽mXj<t}=P{Xj<t,forj=1,…,m}=∏j=1m(1-e-pjt)
Therefore,
E[X]=∫0∞P{X>t}dt=∫0∞1-∏j=1m(1-e-pjt)dt (5.15)
 (5.15)
(5.15)
It remains to relate E[X] , the expected time until one has a complete set, to E[N]
, the expected time until one has a complete set, to E[N]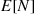 , the expected number of coupons it takes. This can be done by letting Ti
, the expected number of coupons it takes. This can be done by letting Ti denote the i
denote the i th interarrival time of the Poisson process that counts the number of coupons obtained. Then it is easy to see that
th interarrival time of the Poisson process that counts the number of coupons obtained. Then it is easy to see that
X=∑i=1NTi
Since the Ti are independent exponentials with rate 1, and N
are independent exponentials with rate 1, and N is independent of the Ti
is independent of the Ti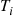 , we see that
, we see that
E[X∣N]=NE[Ti]=N
Therefore,
E[X]=E[N]
and so E[N] is as given in Equation (5.15).
is as given in Equation (5.15).
Let us now compute the expected number of types that appear only once in the complete collection. Letting Ii equal 1
equal 1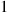 if there is only a single type i
if there is only a single type i coupon in the final set, and letting it equal 0
coupon in the final set, and letting it equal 0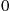 otherwise, we thus want
otherwise, we thus want
E∑i=1mIi=∑i=1mE[Ii]=∑i=1mP{Ii=1}
Now there will be a single type i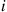 coupon in the final set if a coupon of each type has appeared before the second coupon of type i
coupon in the final set if a coupon of each type has appeared before the second coupon of type i is obtained. Thus, letting Si
is obtained. Thus, letting Si denote the time at which the second type i
denote the time at which the second type i coupon is obtained, we have
coupon is obtained, we have
P{Ii=1}=P{Xj<Si,forallj≠i}
Using that Si has a gamma distribution with parameters (2,pi)
has a gamma distribution with parameters (2,pi) , this yields
, this yields
P{Ii=1}=∫0∞P{Xj<Siforallj≠i∣Si=x}pie-pixpixdx=∫0∞P{Xj<x,forallj≠i}pi2xe-pixdx=∫0∞∏j≠i(1-e-pjx)pi2xe-pixdx
Therefore, we have the result
E∑i=1mIi=∫0∞∑i=1m∏j≠i(1-e-pjx)pi2xe-pixdx=∫0∞x∏j=1m(1-e-pjx)∑i=1mpi2e-pix1-e-pixdx■
The next probability calculation related to Poisson processes that we shall determine is the probability that n events occur in one Poisson process before m
events occur in one Poisson process before m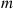 events have occurred in a second and independent Poisson process. More formally let {N1(t),t⩾0}
events have occurred in a second and independent Poisson process. More formally let {N1(t),t⩾0} and {N2(t),t⩾0}
and {N2(t),t⩾0} be two independent Poisson processes having respective rates λ1
be two independent Poisson processes having respective rates λ1 and λ2
and λ2 . Also, let Sn1
. Also, let Sn1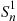 denote the time of the n
denote the time of the n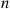 th event of the first process, and Sm2
th event of the first process, and Sm2 the time of the m
the time of the m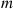 th event of the second process. We seek
th event of the second process. We seek
PSn1<Sm2
Before attempting to calculate this for general n and m
and m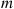 , let us consider the special case n=m=1
, let us consider the special case n=m=1 . Since S11
. Since S11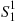 , the time of the first event of the N1(t)
, the time of the first event of the N1(t)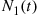 process, and S12
process, and S12 , the time of the first event of the N2(t)
, the time of the first event of the N2(t)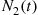 process, are both exponentially distributed random variables (by Proposition 5.1) with respective means 1/λ1
process, are both exponentially distributed random variables (by Proposition 5.1) with respective means 1/λ1 and 1/λ2
and 1/λ2 , it follows from Section 5.2.3 that
, it follows from Section 5.2.3 that
PS11<S12=λ1λ1+λ2 (5.16)
 (5.16)
(5.16)
Let us now consider the probability that two events occur in the N1(t)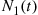 process before a single event has occurred in the N2(t)
process before a single event has occurred in the N2(t)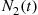 process. That is, P{S21<S12}
process. That is, P{S21<S12} . To calculate this we reason as follows: In order for the N1(t)
. To calculate this we reason as follows: In order for the N1(t) process to have two events before a single event occurs in the N2(t)
process to have two events before a single event occurs in the N2(t) process, it is first necessary for the initial event that occurs to be an event of the N1(t)
process, it is first necessary for the initial event that occurs to be an event of the N1(t)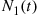 process (and this occurs, by Equation (5.16), with probability λ1/(λ1+λ2)
process (and this occurs, by Equation (5.16), with probability λ1/(λ1+λ2)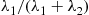 ). Now, given that the initial event is from the N1(t)
). Now, given that the initial event is from the N1(t) process, the next thing that must occur for S21
process, the next thing that must occur for S21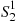 to be less than S12
to be less than S12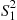 is for the second event also to be an event of the N1(t)
is for the second event also to be an event of the N1(t) process. However, when the first event occurs both processes start all over again (by the memoryless property of Poisson processes) and hence this conditional probability is also λ1/(λ1+λ2)
process. However, when the first event occurs both processes start all over again (by the memoryless property of Poisson processes) and hence this conditional probability is also λ1/(λ1+λ2) ; thus, the desired probability is given by
; thus, the desired probability is given by
PS21<S12=λ1λ1+λ22
In fact, this reasoning shows that each event that occurs is going to be an event of the N1(t) process with probability λ1/(λ1+λ2)
process with probability λ1/(λ1+λ2)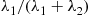 or an event of the N2(t)
or an event of the N2(t)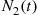 process with probability λ2/(λ1+λ2)
process with probability λ2/(λ1+λ2) , independent of all that has previously occurred. In other words, the probability that the N1(t)
, independent of all that has previously occurred. In other words, the probability that the N1(t) process reaches n
process reaches n before the N2(t)
before the N2(t) process reaches m
process reaches m is just the probability that n
is just the probability that n heads will appear before m
heads will appear before m tails if one flips a coin having probability p=λ1/(λ1+λ2)
tails if one flips a coin having probability p=λ1/(λ1+λ2) of a head appearing. But by noting that this event will occur if and only if the first n+m-1
of a head appearing. But by noting that this event will occur if and only if the first n+m-1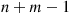 tosses result in n
tosses result in n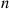 or more heads, we see that our desired probability is given by
or more heads, we see that our desired probability is given by
PSn1<Sm2=∑k=nn+m-1n+m-1kλ1λ1+λ2kλ2λ1+λ2n+m-1-k
5.3.5 Conditional Distribution of the Arrival Times
Suppose we are told that exactly one event of a Poisson process has taken place by time t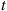 , and we are asked to determine the distribution of the time at which the event occurred. Now, since a Poisson process possesses stationary and independent increments it seems reasonable that each interval in [0,t]
, and we are asked to determine the distribution of the time at which the event occurred. Now, since a Poisson process possesses stationary and independent increments it seems reasonable that each interval in [0,t] of equal length should have the same probability of containing the event. In other words, the time of the event should be uniformly distributed over [0,t]
of equal length should have the same probability of containing the event. In other words, the time of the event should be uniformly distributed over [0,t] . This is easily checked since, for s⩽t
. This is easily checked since, for s⩽t ,
,
P{T1<s∣N(t)=1}=P{T1<s,N(t)=1}P{N(t)=1}=P{1eventin[0,s),0eventsin[s,t]}P{N(t)=1}=P{1eventin[0,s)}P{0eventsin[s,t]}P{N(t)=1}=λse-λse-λ(t-s)λte-λt=st
This result may be generalized, but before doing so we need to introduce the concept of order statistics.
Let Y1,Y2,…,Yn be n
be n random variables. We say that Y(1),Y(2),…,Y(n)
random variables. We say that Y(1),Y(2),…,Y(n) are the order statistics corresponding to Y1,Y2,…,Yn
are the order statistics corresponding to Y1,Y2,…,Yn if Y(k)
if Y(k) is the k
is the k th smallest value among Y1,…,Yn
th smallest value among Y1,…,Yn , k=1,2,…,n
, k=1,2,…,n . For instance, if n=3
. For instance, if n=3 and Y1=4
and Y1=4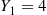 , Y2=5
, Y2=5 , Y3=1
, Y3=1 then Y(1)=1,Y(2)=4
then Y(1)=1,Y(2)=4 , Y(3)=5
, Y(3)=5 . If the Yi,i=1,…,n
. If the Yi,i=1,…,n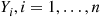 , are independent identically distributed continuous random variables with probability density f
, are independent identically distributed continuous random variables with probability density f , then the joint density of the order statistics Y(1),Y(2),…,Y(n)
, then the joint density of the order statistics Y(1),Y(2),…,Y(n)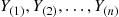 is given by
is given by
f(y1,y2,…,yn)=n!∏i=1nf(yi),y1<y2<⋯<yn
The preceding follows since
(i) (Y(1),Y(2),…,Y(n)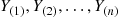 ) will equal (y1,y2,…,yn
) will equal (y1,y2,…,yn ) if (Y1,Y2,…,Yn
) if (Y1,Y2,…,Yn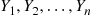 ) is equal to any of the n
) is equal to any of the n ! permutations of (y1,y2,…,yn
! permutations of (y1,y2,…,yn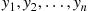 );
);
and
(ii) the probability density that (Y1,Y2,…,Yn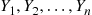 ) is equal to yi1,…,yin
) is equal to yi1,…,yin is ∏j=1nf(yij)=∏j=1nf(yj)
is ∏j=1nf(yij)=∏j=1nf(yj)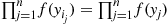 when i1,…,in
when i1,…,in is a permutation of 1,2,…,n
is a permutation of 1,2,…,n .
.
If the Yi,i=1,…,n , are uniformly distributed over (0,t)
, are uniformly distributed over (0,t) , then we obtain from the preceding that the joint density function of the order statistics Y(1),Y(2),…,Y(n)
, then we obtain from the preceding that the joint density function of the order statistics Y(1),Y(2),…,Y(n) is
is
f(y1,y2,…,yn)=n!tn,0<y1<y2<⋯<yn<t
We are now ready for the following useful theorem.
Proof
To obtain the conditional density of S1,…,Sn given that N(t)=n
given that N(t)=n note that for 0<s1<⋯<sn<t
note that for 0<s1<⋯<sn<t the event that S1=s1,S2=s2,…,Sn=sn,N(t)=n
the event that S1=s1,S2=s2,…,Sn=sn,N(t)=n is equivalent to the event that the first n+1
is equivalent to the event that the first n+1 interarrival times satisfy T1=s1,T2=s2-s1,…,Tn=sn-sn-1,Tn+1>t-sn
interarrival times satisfy T1=s1,T2=s2-s1,…,Tn=sn-sn-1,Tn+1>t-sn . Hence, using Proposition 5.1, we have that the conditional joint density of S1,…,Sn
. Hence, using Proposition 5.1, we have that the conditional joint density of S1,…,Sn given that N(t)=n
given that N(t)=n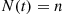 is as follows:
is as follows:
f(s1,…,sn∣n)=f(s1,…,sn,n)P{N(t)=n}=λe-λs1λe-λ(s2-s1)⋯λe-λ(sn-sn-1)e-λ(t-sn)e-λt(λt)n/n!=n!tn,0<s1<⋯<sn<t
which proves the result. ■
Application of Theorem 5.2 (Sampling a Poisson Process)
In Proposition 5.2 we showed that if each event of a Poisson process is independently classified as a type I event with probability p and as a type II event with probability 1-p
and as a type II event with probability 1-p then the counting processes of type I and type II events are independent Poisson processes with respective rates λp
then the counting processes of type I and type II events are independent Poisson processes with respective rates λp and λ(1-p)
and λ(1-p) . Suppose now, however, that there are k
. Suppose now, however, that there are k possible types of events and that the probability that an event is classified as a type i
possible types of events and that the probability that an event is classified as a type i event, i=1,…,k
event, i=1,…,k , depends on the time the event occurs. Specifically, suppose that if an event occurs at time y
, depends on the time the event occurs. Specifically, suppose that if an event occurs at time y then it will be classified as a type i
then it will be classified as a type i event, independently of anything that has previously occurred, with probability Pi(y),i=1,…,k
event, independently of anything that has previously occurred, with probability Pi(y),i=1,…,k where ∑i=1kPi(y)=1
where ∑i=1kPi(y)=1 . Upon using Theorem 5.2 we can prove the following useful proposition.
. Upon using Theorem 5.2 we can prove the following useful proposition.
Proposition 5.3
If Ni(t),i=1,…,k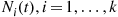 , represents the number of type i
, represents the number of type i events occurring by time t
events occurring by time t then Ni(t),i=1,…,k
then Ni(t),i=1,…,k , are independent Poisson random variables having means
, are independent Poisson random variables having means
E[Ni(t)]=λ∫0tPi(s)ds
Before proving this proposition, let us first illustrate its use.
Example 5.18
An Infinite Server Queue
Suppose that customers arrive at a service station in accordance with a Poisson process with rate λ . Upon arrival the customer is immediately served by one of an infinite number of possible servers, and the service times are assumed to be independent with a common distribution G
. Upon arrival the customer is immediately served by one of an infinite number of possible servers, and the service times are assumed to be independent with a common distribution G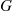 . What is the distribution of X(t)
. What is the distribution of X(t) , the number of customers that have completed service by time t
, the number of customers that have completed service by time t ? What is the distribution of Y(t)
? What is the distribution of Y(t)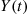 , the number of customers that are being served at time t
, the number of customers that are being served at time t ?
?
To answer the preceding questions let us agree to call an entering customer a type I customer if he completes his service by time t and a type II customer if he does not complete his service by time t
and a type II customer if he does not complete his service by time t . Now, if the customer enters at time s,s⩽t
. Now, if the customer enters at time s,s⩽t , then he will be a type I customer if his service time is less than t-s
, then he will be a type I customer if his service time is less than t-s . Since the service time distribution is G
. Since the service time distribution is G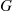 , the probability of this will be G(t-s)
, the probability of this will be G(t-s) . Similarly, a customer entering at time s,s⩽t
. Similarly, a customer entering at time s,s⩽t , will be a type II customer with probability G¯(t-s)=1-G(t-s)
, will be a type II customer with probability G¯(t-s)=1-G(t-s) . Hence, from Proposition 5.3 we obtain that the distribution of X(t)
. Hence, from Proposition 5.3 we obtain that the distribution of X(t) , the number of customers that have completed service by time t
, the number of customers that have completed service by time t , is Poisson distributed with mean
, is Poisson distributed with mean
E[X(t)]=λ∫0tG(t-s)ds=λ∫0tG(y)dy (5.17)
 (5.17)
(5.17)
Similarly, the distribution of Y(t) , the number of customers being served at time t
, the number of customers being served at time t is Poisson with mean
is Poisson with mean
E[Y(t)]=λ∫0tG¯(t-s)ds=λ∫0tG¯(y)dy (5.18)
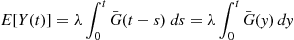 (5.18)
(5.18)
Furthermore, X(t) and Y(t)
and Y(t) are independent.
are independent.
Suppose now that we are interested in computing the joint distribution of Y(t)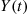 and Y(t+s)
and Y(t+s) —that is, the joint distribution of the number in the system at time t
—that is, the joint distribution of the number in the system at time t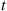 and at time t+s
and at time t+s . To accomplish this, say that an arrival is
. To accomplish this, say that an arrival is
Hence, an arrival at time y will be type i
will be type i with probability Pi(y)
with probability Pi(y)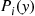 given by
given by
P1(y)=G(t+s-y)-G(t-y),ify<t0,otherwiseP2(y)=G¯(t+s-y),ify<t0,otherwiseP3(y)=G¯(t+s-y),ift<y<t+s0,otherwiseP4(y)=1-P1(y)-P2(y)-P3(y)
Thus, if Ni=Ni(s+t),i=1,2,3 , denotes the number of type i
, denotes the number of type i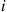 events that occur, then from Proposition 5.3, Ni,i=1,2,3
events that occur, then from Proposition 5.3, Ni,i=1,2,3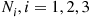 , are independent Poisson random variables with respective means
, are independent Poisson random variables with respective means
E[Ni]=λ∫0t+sPi(y)dy,i=1,2,3
Because
Y(t)=N1+N2,Y(t+s)=N2+N3
it is now an easy matter to compute the joint distribution of Y(t)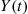 and Y(t+s)
and Y(t+s)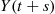 . For instance,
. For instance,
Cov[Y(t),Y(t+s)]=Cov(N1+N2,N2+N3)=Cov(N2,N2)byindependenceofN1,N2,N3=Var(N2)=λ∫0tG¯(t+s-y)dy=λ∫0tG¯(u+s)du
where the last equality follows since the variance of a Poisson random variable equals its mean, and from the substitution u=t-y . Also, the joint distribution of Y(t)
. Also, the joint distribution of Y(t)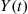 and Y(t+s)
and Y(t+s) is as follows:
is as follows:
P{Y(t)=i,Y(t+s)=j}=P{N1+N2=i,N2+N3=j}=∑l=0min(i,j)P{N2=l,N1=i-l,N3=j-l}=∑l=0min(i,j)P{N2=l}P{N1=i-l}P{N3=j-l}■
Example 5.19
A One Lane Road with No Overtaking
Consider a one lane road with a single entrance and a single exit point which are of distance L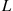 from each other (See Figure 5.2). Suppose that cars enter this road according to a Poisson process with rate λ
from each other (See Figure 5.2). Suppose that cars enter this road according to a Poisson process with rate λ , and that each entering car has an attached random value V
, and that each entering car has an attached random value V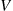 which represents the velocity at which the car will travel, with the proviso that whenever the car encounters a slower moving car it must decrease its speed to that of the slower moving car. Let Vi
which represents the velocity at which the car will travel, with the proviso that whenever the car encounters a slower moving car it must decrease its speed to that of the slower moving car. Let Vi denote the velocity value of the i
denote the velocity value of the i th car to enter the road, and suppose that Vi,i⩾1
th car to enter the road, and suppose that Vi,i⩾1 are independent and identically distributed and, in addition, are independent of the counting process of cars entering the road. Assuming that the road is empty at time 0
are independent and identically distributed and, in addition, are independent of the counting process of cars entering the road. Assuming that the road is empty at time 0 , we are interested in determining
, we are interested in determining
(a) the probability mass function of R(t), the number of cars on the road at time t
the number of cars on the road at time t ; and
; and
(b) the distribution of the road traversal time of a car that enters the road at time y .
.
Solution: Let Ti=L/Vi denote the time it would take car i
denote the time it would take car i to travel the road if it were empty when car i
to travel the road if it were empty when car i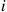 arrived. Call Ti
arrived. Call Ti the free travel time of car i
the free travel time of car i , and note that T1,T2,…
, and note that T1,T2,… are independent with distribution function
are independent with distribution function
G(x)=P(Ti⩽x)=P(L/Vi⩽x)=P(Vi⩾L/x)
Let us say that an event occurs each time that a car enters the road. Also, let t be a fixed value, and say that an event that occurs at time s
be a fixed value, and say that an event that occurs at time s is a type 1
is a type 1 event if both s⩽t
event if both s⩽t and the free travel time of the car entering the road at time s
and the free travel time of the car entering the road at time s exceeds t-s
exceeds t-s . In other words, a car entering the road is a type 1
. In other words, a car entering the road is a type 1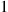 event if the car would be on the road at time t
event if the car would be on the road at time t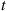 even if the road were empty when it entered. Note that, independent of all that occurred prior to time s,
even if the road were empty when it entered. Note that, independent of all that occurred prior to time s,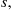 an event occurring at time s
an event occurring at time s is a type 1
is a type 1 event with probability
event with probability
P(s)=G¯(t-s),ifs⩽t0,ifs>t
Letting N1(y) denote the number of type 1
denote the number of type 1 events that occur by time y
events that occur by time y , it follows from Proposition 5.3 that N1(y)
, it follows from Proposition 5.3 that N1(y) is, for y⩽t,
is, for y⩽t, a Poisson random variable with mean
a Poisson random variable with mean
E[N1(y)]=λ∫0yG¯(t-s)ds,y⩽t
Because there will be no cars on the road at time t if and only if N1(t)=0,
if and only if N1(t)=0,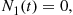 it follows that
it follows that
P(R(t)=0)=P(N1(t)=0)=e-λ∫0tG¯(t-s)ds=e-λ∫0tG¯(u)du
To determine P(R(t)=n)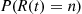 for n>0
for n>0 we will condition on when the first type 1
we will condition on when the first type 1 event occurs. With X
event occurs. With X equal to the time of the first type 1
equal to the time of the first type 1 event (or to ∞
event (or to ∞ if there are no type 1
if there are no type 1 events), its distribution function is obtained by noting that
events), its distribution function is obtained by noting that
X⩽y⇔N1(y)>0
thus showing that
FX(y)=P(X⩽y)=P(N1(y)>0)=1-e-λ∫0yG¯(t-s)ds,y⩽t
Differentiating gives the density function of X :
:
fX(y)=λG¯(t-y)e-λ∫0yG¯(t-s)ds,y⩽t
To use the identity
P(R(t)=n)=∫0tP(R(t)=n∣X=y)fX(y)dy (5.19)
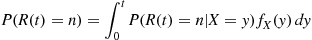 (5.19)
(5.19)
note that if X=y⩽t then the leading car that is on the road at time t
then the leading car that is on the road at time t entered at time y.
entered at time y. Because all other cars that arrive between y
Because all other cars that arrive between y and t
and t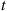 will also be on the road at time t
will also be on the road at time t , it follows that, conditional on X=y,
, it follows that, conditional on X=y,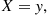 the number of cars on the road at time t
the number of cars on the road at time t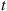 will be distributed as 1
will be distributed as 1 plus a Poisson random variable with mean λ(t-y).
plus a Poisson random variable with mean λ(t-y). Therefore, for n>0
Therefore, for n>0
P(R(t)=n∣X=y)=e-λ(t-y)(λ(t-y))n-1(n-1)!,ify⩽t0,ify=∞
Substituting this into Equation (5.19) yields
P(R(t)=n)=∫0te-λ(t-y)(λ(t-y))n-1(n-1)!λG¯(t-y)e-λ∫0yG¯(t-s)dsdy
(b) Let T be the free travel time of the car that enters the road at time y,
be the free travel time of the car that enters the road at time y, and let A(y)
and let A(y)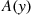 be its actual travel time. To determine P(A(y)<x),
be its actual travel time. To determine P(A(y)<x), let t=y+x
let t=y+x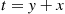 and note that A(y)
and note that A(y)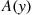 will be less than x
will be less than x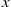 if and only if both T<x
if and only if both T<x and there have been no type 1
and there have been no type 1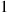 events (using t=y+x
events (using t=y+x ) before time y
) before time y . That is,
. That is,
A(y)<x⇔T<x,N1(y)=0
Because T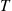 is independent of what has occurred prior to time y
is independent of what has occurred prior to time y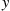 , the preceding gives
, the preceding gives
P(A(y)<x)=P(T<x)P(N1(y)=0)=G(x)e-λ∫0yG¯(y+x-s)ds=G(x)e-λ∫xy+xG¯(u)du■
Example 5.20
Tracking the Number of HIV Infections
There is a relatively long incubation period from the time when an individual becomes infected with the HIV virus, which causes AIDS, until the symptoms of the disease appear. As a result, it is difficult for public health officials to be certain of the number of members of the population that are infected at any given time. We will now present a first approximation model for this phenomenon, which can be used to obtain a rough estimate of the number of infected individuals.
Let us suppose that individuals contract the HIV virus in accordance with a Poisson process whose rate λ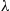 is unknown. Suppose that the time from when an individual becomes infected until symptoms of the disease appear is a random variable having a known distribution G
is unknown. Suppose that the time from when an individual becomes infected until symptoms of the disease appear is a random variable having a known distribution G . Suppose also that the incubation times of different infected individuals are independent.
. Suppose also that the incubation times of different infected individuals are independent.
Let N1(t)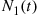 denote the number of individuals who have shown symptoms of the disease by time t
denote the number of individuals who have shown symptoms of the disease by time t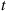 . Also, let N2(t)
. Also, let N2(t)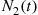 denote the number who are HIV positive but have not yet shown any symptoms by time t
denote the number who are HIV positive but have not yet shown any symptoms by time t . Now, since an individual who contracts the virus at time s
. Now, since an individual who contracts the virus at time s will have symptoms by time t
will have symptoms by time t with probability G(t-s)
with probability G(t-s)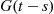 and will not with probability G¯(t-s)
and will not with probability G¯(t-s) , it follows from Proposition 5.3 that N1(t)
, it follows from Proposition 5.3 that N1(t)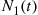 and N2(t)
and N2(t)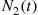 are independent Poisson random variables with respective means
are independent Poisson random variables with respective means
E[N1(t)]=λ∫0tG(t-s)ds=λ∫0tG(y)dy
and
E[N2(t)]=λ∫0tG¯(t-s)ds=λ∫0tG¯(y)dy
Now, if we knew λ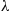 , then we could use it to estimate N2(t)
, then we could use it to estimate N2(t) , the number of individuals infected but without any outward symptoms at time t
, the number of individuals infected but without any outward symptoms at time t , by its mean value E[N2(t)]
, by its mean value E[N2(t)]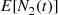 . However, since λ
. However, since λ is unknown, we must first estimate it. Now, we will presumably know the value of N1(t)
is unknown, we must first estimate it. Now, we will presumably know the value of N1(t) , and so we can use its known value as an estimate of its mean E[N1(t)]
, and so we can use its known value as an estimate of its mean E[N1(t)]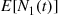 . That is, if the number of individuals who have exhibited symptoms by time t
. That is, if the number of individuals who have exhibited symptoms by time t is n1
is n1 , then we can estimate that
, then we can estimate that
n1≈E[N1(t)]=λ∫0tG(y)dy
Therefore, we can estimate λ by the quantity λˆ
by the quantity λˆ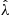 given by
given by
λˆ=n1/∫0tG(y)dy
Using this estimate of λ , we can estimate the number of infected but symptomless individuals at time t
, we can estimate the number of infected but symptomless individuals at time t by
by
estimateofN2(t)=λˆ∫0tG¯(y)dy=n1∫0tG¯(y)dy∫0tG(y)dy
For example, suppose that G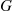 is exponential with mean μ
is exponential with mean μ . Then G¯(y)=e-y/μ
. Then G¯(y)=e-y/μ , and a simple integration gives that
, and a simple integration gives that
estimateofN2(t)=n1μ(1-e-t/μ)t-μ(1-e-t/μ)
If we suppose that t=16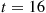 years, μ=10
years, μ=10 years, and n1=220
years, and n1=220 thousand, then the estimate of the number of infected but symptomless individuals at time 16 is
thousand, then the estimate of the number of infected but symptomless individuals at time 16 is
estimate=2,200(1-e-1.6)16-10(1-e-1.6)=218.96
That is, if we suppose that the foregoing model is approximately correct (and we should be aware that the assumption of a constant infection rate λ that is unchanging over time is almost certainly a weak point of the model), then if the incubation period is exponential with mean 10 years and if the total number of individuals who have exhibited AIDS symptoms during the first 16 years of the epidemic is 220 thousand, then we can expect that approximately 219 thousand individuals are HIV positive though symptomless at time 16. ■
that is unchanging over time is almost certainly a weak point of the model), then if the incubation period is exponential with mean 10 years and if the total number of individuals who have exhibited AIDS symptoms during the first 16 years of the epidemic is 220 thousand, then we can expect that approximately 219 thousand individuals are HIV positive though symptomless at time 16. ■
Proof of Proposition 5.3
Let us compute the joint probability P{Ni(t)=ni,i=1,…,k} . To do so note first that in order for there to have been ni
. To do so note first that in order for there to have been ni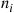 type i
type i events for i=1,…,k
events for i=1,…,k there must have been a total of ∑i=1kni
there must have been a total of ∑i=1kni events. Hence, conditioning on N(t)
events. Hence, conditioning on N(t) yields
yields
P{N1(t)=n1,…,Nk(t)=nk}=PN1(t)=n1,…,Nk(t)=nkN(t)=∑i=1kni×PN(t)=∑i=1kni
Now consider an arbitrary event that occurred in the interval [0,t] . If it had occurred at time s
. If it had occurred at time s , then the probability that it would be a type i
, then the probability that it would be a type i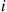 event would be Pi(s)
event would be Pi(s) . Hence, since by Theorem 5.2 this event will have occurred at some time uniformly distributed on [0,t]
. Hence, since by Theorem 5.2 this event will have occurred at some time uniformly distributed on [0,t] , it follows that the probability that this event will be a type i
, it follows that the probability that this event will be a type i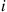 event is
event is
Pi=1t∫0tPi(s)ds
independently of the other events. Hence,
PNi(t)=ni,i=1,…,kN(t)=∑i=1kni
will just equal the multinomial probability of ni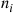 type i
type i outcomes for i=1,…,k
outcomes for i=1,…,k when each of ∑i=1kni
when each of ∑i=1kni independent trials results in outcome i
independent trials results in outcome i with probability Pi,i=1,…,k
with probability Pi,i=1,…,k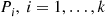 . That is,
. That is,
PN1(t)=n1,…,Nk(t)=nkN(t)=∑i=1kni=∑i=1kni!n1!⋯nk!P1n1⋯Pknk
Consequently,
P{N1(t)=n1,…,Nk(t)=nk}=(∑ini)!n1!⋯nk!P1n1⋯Pknke-λt(λt)∑ini(∑ini)!=∏i=1ke-λtPi(λtPi)ni/ni!
and the proof is complete. ■
 having rate
having rate  , and suppose that each time an event occurs it is classified as either a type I or a type II event. Suppose further that each event is classified as a type I event with probability
, and suppose that each time an event occurs it is classified as either a type I or a type II event. Suppose further that each event is classified as a type I event with probability  or a type II event with probability
or a type II event with probability  , independently of all other events. For example, suppose that customers arrive at a store in accordance with a Poisson process having rate
, independently of all other events. For example, suppose that customers arrive at a store in accordance with a Poisson process having rate  ; and suppose that each arrival is male with probability
; and suppose that each arrival is male with probability  and female with probability
and female with probability  . Then a type I event would correspond to a male arrival and a type II event to a female arrival.
. Then a type I event would correspond to a male arrival and a type II event to a female arrival. and
and 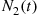 denote respectively the number of type I and type II events occurring in
denote respectively the number of type I and type II events occurring in  . Note that
. Note that  .
.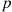 and
and  , then the number of individuals in each of the two groups will be independent Poisson random variables. Because this result easily generalizes to the case where the classification is into any one of
, then the number of individuals in each of the two groups will be independent Poisson random variables. Because this result easily generalizes to the case where the classification is into any one of  possible groups, we have the following application to a model of employees moving about in an organization.
possible groups, we have the following application to a model of employees moving about in an organization. , let
, let  denote the number of those individuals, initially in state
denote the number of those individuals, initially in state 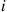 , that are in state
, that are in state  at time
at time 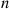 . Now each of the (Poisson distributed) number of people initially in state
. Now each of the (Poisson distributed) number of people initially in state 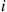 will, independently of each other, be in state
will, independently of each other, be in state  at time
at time  with probability
with probability  , where
, where  is the
is the 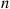 -stage transition probability for the Markov chain having transition probabilities
-stage transition probability for the Markov chain having transition probabilities  . Hence, the
. Hence, the  will be independent Poisson random variables with respective means
will be independent Poisson random variables with respective means 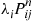 ,
,  . Because the sum of independent Poisson random variables is itself a Poisson random variable, it follows that the number of individuals in state
. Because the sum of independent Poisson random variables is itself a Poisson random variable, it follows that the number of individuals in state 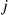 at time
at time  —namely
—namely  —will be independent Poisson random variables with respective means
—will be independent Poisson random variables with respective means  , for
, for  .
. 
 events occur in one Poisson process before
events occur in one Poisson process before 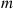 events have occurred in a second and independent Poisson process. More formally let
events have occurred in a second and independent Poisson process. More formally let  and
and  be two independent Poisson processes having respective rates
be two independent Poisson processes having respective rates  and
and  . Also, let
. Also, let 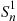 denote the time of the
denote the time of the 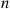 th event of the first process, and
th event of the first process, and  the time of the
the time of the 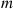 th event of the second process. We seek
th event of the second process. We seek
 and
and 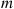 , let us consider the special case
, let us consider the special case  . Since
. Since 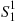 , the time of the first event of the
, the time of the first event of the 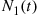 process, and
process, and  , the time of the first event of the
, the time of the first event of the 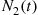 process, are both exponentially distributed random variables (by Proposition 5.1) with respective means
process, are both exponentially distributed random variables (by Proposition 5.1) with respective means  and
and  , it follows from Section 5.2.3 that
, it follows from Section 5.2.3 that (5.16)
(5.16)
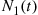 process before a single event has occurred in the
process before a single event has occurred in the 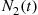 process. That is,
process. That is,  . To calculate this we reason as follows: In order for the
. To calculate this we reason as follows: In order for the  process to have two events before a single event occurs in the
process to have two events before a single event occurs in the  process, it is first necessary for the initial event that occurs to be an event of the
process, it is first necessary for the initial event that occurs to be an event of the 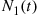 process (and this occurs, by Equation (5.16), with probability
process (and this occurs, by Equation (5.16), with probability 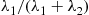 ). Now, given that the initial event is from the
). Now, given that the initial event is from the  process, the next thing that must occur for
process, the next thing that must occur for 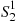 to be less than
to be less than 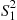 is for the second event also to be an event of the
is for the second event also to be an event of the  process. However, when the first event occurs both processes start all over again (by the memoryless property of Poisson processes) and hence this conditional probability is also
process. However, when the first event occurs both processes start all over again (by the memoryless property of Poisson processes) and hence this conditional probability is also  ; thus, the desired probability is given by
; thus, the desired probability is given by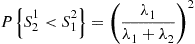
 process with probability
process with probability 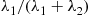 or an event of the
or an event of the 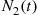 process with probability
process with probability  , independent of all that has previously occurred. In other words, the probability that the
, independent of all that has previously occurred. In other words, the probability that the  process reaches
process reaches  before the
before the  process reaches
process reaches  is just the probability that
is just the probability that  heads will appear before
heads will appear before  tails if one flips a coin having probability
tails if one flips a coin having probability  of a head appearing. But by noting that this event will occur if and only if the first
of a head appearing. But by noting that this event will occur if and only if the first 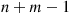 tosses result in
tosses result in 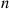 or more heads, we see that our desired probability is given by
or more heads, we see that our desired probability is given by
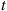 , and we are asked to determine the distribution of the time at which the event occurred. Now, since a Poisson process possesses stationary and independent increments it seems reasonable that each interval in
, and we are asked to determine the distribution of the time at which the event occurred. Now, since a Poisson process possesses stationary and independent increments it seems reasonable that each interval in  of equal length should have the same probability of containing the event. In other words, the time of the event should be uniformly distributed over
of equal length should have the same probability of containing the event. In other words, the time of the event should be uniformly distributed over  . This is easily checked since, for
. This is easily checked since, for  ,
,
 be
be  random variables. We say that
random variables. We say that  are the order statistics corresponding to
are the order statistics corresponding to  if
if  is the
is the  th smallest value among
th smallest value among  ,
,  . For instance, if
. For instance, if  and
and 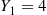 ,
,  ,
,  then
then  ,
,  . If the
. If the 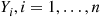 , are independent identically distributed continuous random variables with probability density
, are independent identically distributed continuous random variables with probability density  , then the joint density of the order statistics
, then the joint density of the order statistics 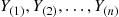 is given by
is given by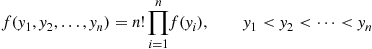
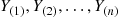 ) will equal (
) will equal ( ) if (
) if (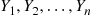 ) is equal to any of the
) is equal to any of the  ! permutations of (
! permutations of (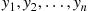 );
);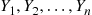 ) is equal to
) is equal to  is
is 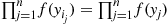 when
when  is a permutation of
is a permutation of  .
. , are uniformly distributed over
, are uniformly distributed over  , then we obtain from the preceding that the joint density function of the order statistics
, then we obtain from the preceding that the joint density function of the order statistics  is
is