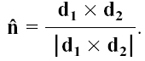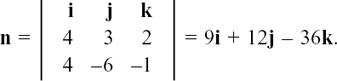11
Working with vectors
In the last chapter, we used both magnitude and direction to represent complex numbers in Argand diagrams. Now, we shall extend this idea to discover how we can handle physical quantities which have both magnitude and direction, working in both two and three dimensions.
The chapter is divided into the following sections.
11.A Basic rules for handling vectors
(a) What are vectors?
(b) Adding vectors and what this can mean physically,
(c) Using components to describe vectors,
(d) Vector components in three-dimensional space,
(e) Finding the magnitude of a three-dimensional vector,
Finding unit vectors
11.B Multiplying vectors
(a) Defining the scalar or dot product of two vectors,
(b) Working out the dot product of two vectors,
(c) Defining the vector or cross product of two vectors,
(d) Working out the cross product of two vectors,
(e) Can we multiply three vectors together by using dot or cross products?
(f) The vector triple product,
(g) The scalar triple product and what it means geometrically
11.C Finding equations for lines and planes
(a) Finding a vector equation for a line,
(b) Dealing with lines in two dimensions,
(c) Dealing with lines in three dimensions,
(d) Finding the Cartesian equation of a line in three dimensions,
(e) Another form for the vector equation of a line,
(f) Finding vector equations for planes,
(g) Finding equations of planes using normal vectors,
(h) Finding the perpendicular distance from the origin to a plane,
(i) The Cartesian form of the equation of a plane,
(j) Finding where a line intersects a plane,
(k) Finding the line of intersection of two planes
11.D Finding angles and distances involving lines and planes
(a) Finding the angle between two lines,
(b) Finding the angle between two planes,
(c) Finding the acute angle between a line and a plane,
(d) Finding the shortest distance from a point to a line,
(e) Finding the shortest distance from a point to a plane,
(f) Finding the shortest distance between two skew lines
11.A Basic rules for handling vectors
11.A.(a) What are vectors?
Some physical properties, such as temperature or area, are given completely by their magnitude and so only need a single number to represent them. Such quantities are called scalars. But there are other physical quantities, such as force, velocity or acceleration, for which we must know direction as well as size or magnitude in order to work with them. It is often very helpful to represent such quantities by directed lines. Such directed lines are called vectors. Because vectors carry the physical information of both magnitude and direction, using them gives us a very neat way of handling these quantities.
It is important to avoid any confusion between vectors and scalars so we must make the distinction clear when we write them. Scalars are written with no special marking so we write 3 or 16 or k, say. If a vector runs from O to A, we can write it as 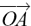 or print it as a single boldface letter, say a. Since we can’t do boldface in handwriting, we would show that this is a vector by underlining it and writing it as a. I have done this in my diagrams.
or print it as a single boldface letter, say a. Since we can’t do boldface in handwriting, we would show that this is a vector by underlining it and writing it as a. I have done this in my diagrams.
Figure 11.A.1 illustrates some properties of vectors.
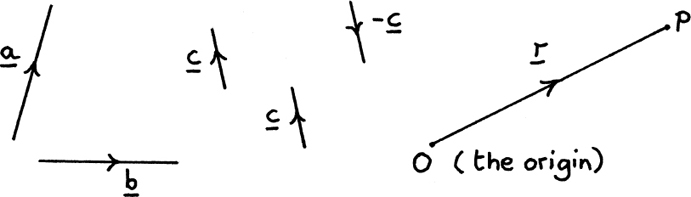
Figure 11.A.l (the origin)
• Two vectors are equal if and only if they are equal in both magnitude and direction. So although a and b are the same length they are not equal because they are in different directions. However, the two vectors marked c are defined to be equal although we need a shift to move the directed lines exactly on top of each other.
• Multiplying a vector by a positive number or scalar just has the effect of changing its scale or magnitude. So, for example, the vector 2a would be twice as long as a but in the same direction as a.
• Multiplying a vector by a negative number reverses its direction as well. I have shown –1 × c = –c in my diagram.
• The zero vector is the vector which has zero magnitude. Therefore it has no direction and so there is only one zero vector.
• The vector r in the drawing above is called the position vector of the point P from the fixed origin O, and describes the displacement of P from O.
11.A.(b) Adding vectors and what this can mean physically
Vectors can have different directions from each other so how can we make sense of adding them? Since we can think of vectors as displacements or journeys, to add two vectors we just need to find the single displacement which gives the same result as doing the two displacements separately. The left-hand drawing in Figure 11.A.2 shows that the single vector of p + q is given by doing p followed by q and also by doing q followed by p. Each of the two joined together triangles shows what is called the triangle law of addition.
So, for example, if a boat sets a course to move with velocity p in water flowing with velocity q, then it will actually have a resultant velocity of p + q. The third side of the triangle gives the speed and direction in which it will move.
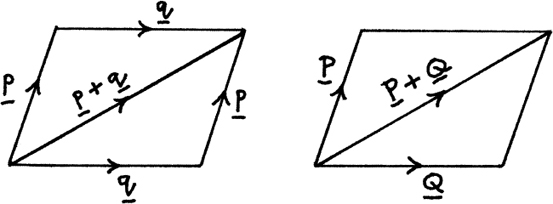
Figure 11.A.2
The right-hand drawing could represent two forces P and Q acting on a particle. Their joint resultant effect is given by the vector P + Q which is the diagonal of the parallelogram. This picture shows what is called the parallelogram law for the addition of forces which is simply another way of looking at the triangle law of addition.
Figure 11.A.3 shows another useful result.

Figure 11.A.3
We have the two points P and Q whose position vectors from the origin, O, are p and q. The vector 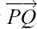 gives the displacement from P to Q but we can also move from P to Q by doing
gives the displacement from P to Q but we can also move from P to Q by doing 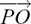 followed by
followed by  This gives us the result
This gives us the result
 = –p + q.
= –p + q.
We can show the addition of any number of vectors by putting them nose to tail and seeing what the final displacement is. Figure 11.A.4 shows that the successive displacements of a, b, c, d and e are equivalent to the single displacement of r. It demonstrates the vector sum a + b + c + d + e = r.

Figure 11.A.4
The addition works in exactly the same way if the vectors shown are being placed nose to tail in three dimensions. You can add the vectors in any order you choose. The result is the same. If the vectors join up so that there is no gap between the tail of the first vector and the head of the last one then their vector sum is zero. So, for example, if the vectors a, b, c, d, e and –r were representing forces acting on a particle then there would be no net force acting on it.
We now know how to add vectors but how would we subtract them? If we have the vector c then –c is defined to be the vector having the same magnitude but the reverse direction to c. Subtracting c is the same as adding –c.
Here are three examples in which we use the rule for adding vectors.
EXAMPLE (1)
Figure 11.A.5
Figure 11.A.5 shows how the swimming speed in still water and the current need to combine to give the required resultant velocity. It would not work for the swimmer to strike out directly for the opposite bank as the current would push him downstream. If v stands for the speed at which he is swimming, then using Pythagoras’ Theorem on the triangle, we have 1 = 0.25 + v 2 so v = 0.866 to 3 s.f. His angle θ with the near bank is given by θ = cos–1 (1/2) = 60°. The time taken for him to swim across the river is (25/0.866) = 28.9 s to 1 d.p.
EXAMPLE (2)

Figure 11.A.6

EXAMPLE (3)

Figure 11.A.7

If the point K divides the line PQ internally in the ratio l: m and the position vectors of P, Q and K with respect to O are p, q and k, then
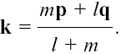
EXERCISE 11.A.1
(1) A particle is in equilibrium under the action of three forces of 7N, 10N and 13N. What is the angle between the lines of action of the two largest forces?
(2) In triangle ABC, the sides of the triangle are given as vectors by 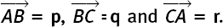 D, E and F are the midpoints of BC, CA and AB respectively. A straight line joining the vertex of a triangle to the midpoint of the opposite side is called a median. The medians of this triangle, also given as vectors, are
D, E and F are the midpoints of BC, CA and AB respectively. A straight line joining the vertex of a triangle to the midpoint of the opposite side is called a median. The medians of this triangle, also given as vectors, are 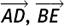 and
and 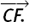 Find
Find  in terms of p, q and r and simplify your answer as far as possible.
in terms of p, q and r and simplify your answer as far as possible.
(3) The position vectors from the origin of A, B and C in triangle ABC are a, b and c respectively. BM is a median of the triangle. Find the position vector g of the point G which is 2/3 of the way down BM from B. What does your answer tell you about the three medians of the triangle?
(4) Just before this exercise, we found a formula for the position vector of a point which divides a line internally in the ratio l : m. Now suppose that instead the point K divides the line PQ so that PK/KM = l/m with K lying on the other side of Q from P. We say in this case that K divides the line PQ externally. Since we are changing direction as we move from P to K and back from K to Q, we say that the ratio is l : –m. Show that, with this adjustment in sign, the formula for the position vector of K is unchanged.
It would be very complicated if any problem involving vectors could only be solved by drawing a diagram and then working out its geometry. We now make vectors much easier to handle by finding out how to write them in component form.
11.A(c) Using components to describe vectors
We want a non-visual way of working with vectors so we don’t have to draw them to work with them. We’ll first think how we could do this if all the vectors lie in the same plane so that we are in two-dimensional space. If we could describe each of these vectors in terms of some chosen reference vectors, then we could work out how they affect each other by using algebra. For example, in Figure 11.A.8, I have chosen g and h as my two reference vectors. Using them, we can build up a grid which makes it possible to describe the position vectors with respect to the origin of any points in the plane as multiples of g and h.
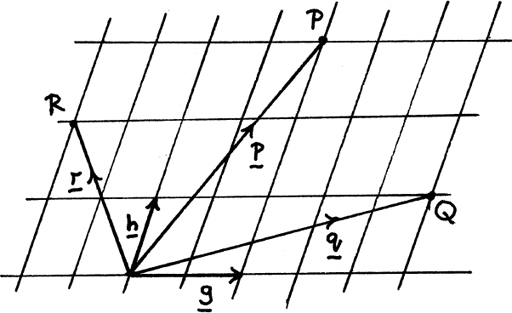
Figure 11.A.8
You can see that the position vectors from O to the points P, Q and R are described by
p = g + 3h, q = (5/2)g + h and r = –g + 2h.
As an example of working with these vectors, we have
q + r = [(5/2)g + h)] + (– g + 2h) = (3/2)g + 3h.
Check that this will work geometrically on the grid.
We can describe any point in the plane using multiples of g and h. In other words, if we choose any point P with position vector r then we can write r = ag + bh where a and b are numbers whose value depends on the particular position of P. This includes the possibility of irrational numbers so, for example, we could have 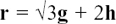 .
.
You can choose any pair of vectors to describe the positions of all the points in this plane in this way just so long as your two chosen vectors aren’t parallel to each other. Because neither g nor h can be written in terms of the other, mathematicians call them linearly independent. Any two non-parallel vectors in the plane will be linearly independent.
In practice, there is a huge advantage in choosing two vectors that are perpendicular to each other, and making each of them one unit in length. (Vectors with unit length are called unit vectors.) We call these i and j, with i running along the x-axis and j running up the y-axis.
Then we can write the position vector r of any point P as r = ai + bj. The particular numerical values given to a and b describe where P is.
So, for example, in Figure 11.A.9 we have p = 3i + 2j, q = 2i – j and r = – i – j.
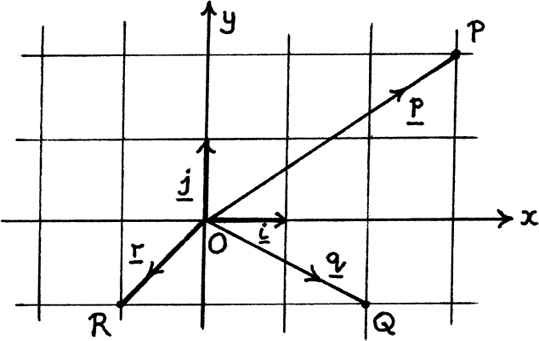
Figure 11.A.9
Sometimes it is useful in physical problems to be able to split a vector up into two components. For example, we might want to split a force into its horizontal and vertical components. Or, given a velocity V with known magnitude and direction, you might be asked to find X and Y where X and Y are the components of V due east and due north respectively. I have shown this in Figure 11.A. 10.

Figure 11.A.10
We have V = X + Y as a vector sum. V, the magnitude or numerical size of V, is represented by the length of the hypotenuse of the triangle.
If we know V and the size of the angle θ, how can we use these to find X and Y, the magnitudes of X and Y?
To do this, we use the trigonometry of right-angled triangles. (See Section 4.A.(a) if necessary.)
We have sin θ = Y/V so Y = V sin θ and cos θ = X/V so V cos θ = X.
If we know both V and θ, we can now find X and Y.
Similarly, if we are asked this question the other way round, so that we need to find the magnitude and direction of V from its components X and Y, we can do this in two steps.
Firstly, we can find the magnitude V of V by using the known magnitudes X of X and Y of Y.
Now, by Pythagoras’ Theorem, we have V2 = X2 + Y2 so 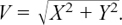 This tells us V, the magnitude of V. This magnitude can also be written as |V|.
This tells us V, the magnitude of V. This magnitude can also be written as |V|.
Secondly, we can say that tan θ = Y/X so θ = tan–1 Y/X and this gives us the direction of V.
Try these questions now.
EXERCISE 11.A.2
(1) A ship is sailing on a course of N 62° E at a speed of 42 knots. (Because we know the direction as well as the magnitude of its speed, we know its velocity.) What is the component of its velocity due east? What is the component of its velocity due north? Draw a sketch showing the course of the ship and its vector components.
(2) A particle is acted upon by the three forces P = 2i – 3j, Q = 4i + j and S = –3i + 2j. What is the resultant force R which acts on the particle? Draw a sketch showing P, Q, S and R.
(3) If f = 2i + j and g = i + 4j and h = 4i + 2j, is it possible to find multiples of the pairs of vectors (a) f and g, (b) g and h, and (c) f and h to write down the position vector relative to the origin of any point in two-dimensional space? If it is possible, describe in each case how you would combine that pair of vectors to write the vector r = 4i + 9j. If it is not possible, why is this?
11.A.(d) Vector components in three-dimensional space
We saw in the previous section how we could use two vectors to form a two-dimensional grid and then find a combination of multiples of these two vectors to describe the position vector of any point relative to the origin. Similarly, if we are working in three dimensions, we start by choosing any three vectors which can be rearranged to form a three-dimensional grid. We can then describe the position vector of any point from the origin by taking a combination of multiples of these three vectors.
For working in two dimensions, we found it most convenient to use the pair of unit vectors i and j running along the x- and y-axes respectively. When we move into three dimensions, we add a third unit vector k which runs along a z-axis which is perpendicular to both the x- and y-axes. It is usually most convenient to have the z-axis running vertically upwards. I show this in Figure 11.A. 11
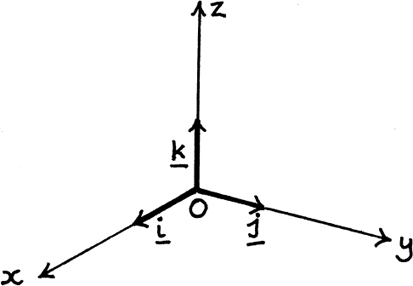
Figure 11.A.11
Now we can write the position vector r of any point P in space in the form r = ai + bj + ck with particular numerical values of a, b and c for each chosen r.

We could have drawn the z-axis in two ways to make it be perpendicular to the x- and y-axes. In physical applications, we always choose the direction of the z-axis so that x, y and z fit to the thumb, first finger and second finger of the right hand. We then get what’s called a right-handed coordinate system. You’ll see that my axes fit this rule and that your left hand would give a mirror image.
Each of these axes can be extended in its negative direction also, so that we can represent vectors such as r = –3i – 2j or r = 2i – j – 5k.
Adding vectors is extremely easy if you know their components. All you have to do is to find the total for each separate component.
For example, suppose you have two forces P and Q with P = 3i + j –4k and Q = 2i –4j + 2k. Then their resultant R = P + Q = 5i –3j – 2k.
11.A.(e) Finding the magnitude of a three-dimensional vector
If we have a vector in component form, we may need to find its length or magnitude. Figure 11.A. 12 shows you how we would do this for the vector 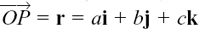 . We again write the length or magnitude of r as |r|.
. We again write the length or magnitude of r as |r|.

Figure 11.A.12
Now, working with the lengths OA, OB and OC we have OA = a, OB = b and OC = c. Also, PQ = OC so PQ = c.
In the right-angled triangle OQA, we have OQ2 = a2 + b2 and, in the right-angled triangle OPQ, we have OP2 = OQ2 + PQ2. So OP2 = a2 + b2 + c2. The formula for the length OP or |r| is the three-dimensional form of Pythagoras’ Theorem.
If r= ai+ bj+ ck then |r| = 
The direction of OP is given by the three angles which OP makes with the x-, y- and z-axes. We’ll call these three angles α β and γ.
OP makes ∠POA = α with the x-axis and we have
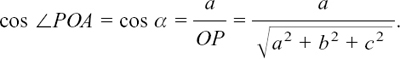
Similarly, we have
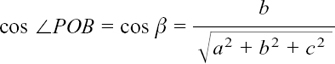
and

These are called the direction cosines of OP.
Notice that the vector cos α i + cos β j + cos γ k is in the same direction as the vector 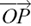 , but scaled down by a factor of the length of OP. Therefore it is a unit vector in the direction of p and we write it as
, but scaled down by a factor of the length of OP. Therefore it is a unit vector in the direction of p and we write it as 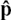 .
.
Here’s a practical application which uses components and magnitude.
If a body is acted on by three forces P, Q and S, find the resultant force R, and its magnitude |R| if P = 3i – 5j + 2k, Q = –2i + 4j + 4k and S = 3i – 3j – 4k.
We have
P + Q + S = R = (3 – 2 + 3)i + (– 5 + 4 – 3)j + (2 + 4 – 4)k = 4i – 4j + 2k
and
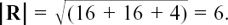
It is sometimes convenient to write vectors in column vector form. So, for example, we would write i, j and k in the form

More rarely, we use the row vector form. This would give us
i = (1, 0, 0), j = (0, 1, 0) and k = (0, 0, 1).
11.A.(f) Finding unit vectors
Sometimes, such as when we work with planes in Section 11.C.(h), we need to find a unit vector in the same direction as a given vector, u. We call this unit vector û.
Here is a numerical example of how the working out goes. Suppose you need the unit vector in the same direction as u = 2i – j + 2k.
The length or magnitude of u is given by 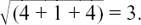 Also, the required vector must be parallel to u. So we can get the vector we want by just scaling down u by a factor of 3. It is û =
Also, the required vector must be parallel to u. So we can get the vector we want by just scaling down u by a factor of 3. It is û = 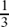 (2i – j + 2k).
(2i – j + 2k).
Remember that each of the vectors i, j and k has unit length and so they are unit vectors.
Now try these questions yourself.
EXERCISE 11.A.3
(1) What is the magnitude of the vector v = 4i + 3j? Find a unit vector 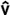 which is in the same direction as v. Repeat this question for w = 8i – 15j.
which is in the same direction as v. Repeat this question for w = 8i – 15j.
(2) Find the length of the vector p = 4i + 3j + 12k. Draw a little sketch like Figure 11.A.12 so that you can see the three-dimensional Pythagoras’ Theorem working in this case. Write down a unit vector in the same direction as p.
(3) If the three forces P = 4i + 3j + 7k, Q = 2i + 9j – 7k and R = 4i – 7j + k act on a particle, what fourth force is required so that the particle is in equilibrium? What is its magnitude?
(4) Working in two dimensions, write down two non-zero vectors p and q whose sum is zero. What is the physical meaning of p + q if p and q are (a) displacements (b) forces?
(5) Find and write down three non-parallel vectors p, q and r in three dimensions whose vector sum is zero. Could you use combinations of your three chosen vectors to write down the position vector of any point in three-dimensional space? If not, why not?
11.B Multiplying vectors
In the previous section we found out how we could add vectors by thinking of their sum as the single displacement which is equivalent to putting together their successive displacements. Can we define a way to multiply two vectors together so that we get a useful result while taking account of the directions of the vectors as well as their magnitudes? It turns out that there are two different ways of doing this and this section describes them both.
11.B.(a) Defining the scalar or dot product of two vectors
This method for multiplying vectors is called the dot product because we write the two vectors with a dot between them. Figure 11.B.1 shows how we define the product a • b of the two vectors a and b and also gives a very neat practical application.

Figure 11.B.1
The man is pulling the block with a constant force a so that it moves along the horizontal ground. The work done in moving the block through a distance b is then given by the distance moved multiplied by the magnitude of the component of the force in the direction of motion.
This is |a||b| cos θ so we define the scalar or dot product as
where θ is the angle between a and b when they are placed tail to tail.
To use the least possible force, we would need to pull horizontally, so that we are pulling in the same direction as we want the object to move. Then we would have θ = 0 and cos θ = 1 so that the work done = a • b = |a||b| = the magnitude of the force multiplied by the distance moved in the direction of the force.

Each of the magnitudes |a| and |b| is a number and cos θ is a number, so a • b is not a vector but a number or scalar. This is why it’s called the scalar product. When writing down two vectors multiplied in this way, you must include the dot between them. Writing ab is meaningless.
11.B.(b) Working out the dot product of two vectors
We’ll start by looking at the simplest cases. What will happen when we multiply pairs of the unit vectors i, j and k together, using the dot product rule? Work out for yourself what the answers are to i • i, i • j and i • k.
If you have done this you will see that the complete set of results is as follows:
i • i = j • j = k • k = 1
and
i • j = j • i = i • k = k • i = j • k = k • j = 0.
This is because i, j and k are all one unit in length and are mutually perpendicular. We are also using cos 0° = 1 and cos 90° = 0.
There is a neat way of working out the dot product of any two vectors when they are given in component form. To do this we shall need to use the following result.
(a + b) • c = a • c + b • c for any three vectors a, b and c.
This is what mathematicians call the distributive law. They have shown that, for this kind of multiplication, it doesn’t matter whether we do the adding or the multiplying first.
Now suppose we have two vectors a = a1 i + a2 j + a3 k and b = b1 i + b2 j + b3 k.
Then a • b = (a1 i + a2j + a3k) • (b1i + b2j + b3k).
Working out all the nine separate little dot products that we get from multiplying these two brackets together and using the results above, gives us the following rule.
If a = a1i + a2j + a3k and b = b1i + b2j + b3k then
a • b = |a||b| cos θ = a1b1 + a2b2 + a3b3.
Here are some examples of applications of the dot product.
EXAMPLE (1)
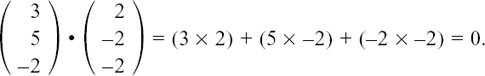
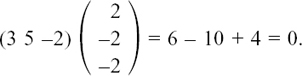
EXAMPLE (2)
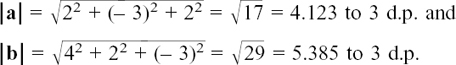
 If you need to find the angle between two vectors, it’s always worth checking first whether the vectors are parallel before working out the dot product. For example, if you had been given a = 2i + j –3k and b = 6i + 3j – 9k then b = 3a showing that the vectors are parallel and in the same direction, so the angle between them is 0°. If we’d had b = –6i – 3j + 9k, so that b = –3a, again the vectors are parallel but in opposite directions so the angle between them is 180°.
If you need to find the angle between two vectors, it’s always worth checking first whether the vectors are parallel before working out the dot product. For example, if you had been given a = 2i + j –3k and b = 6i + 3j – 9k then b = 3a showing that the vectors are parallel and in the same direction, so the angle between them is 0°. If we’d had b = –6i – 3j + 9k, so that b = –3a, again the vectors are parallel but in opposite directions so the angle between them is 180°.
EXAMPLE (3)
 Students quite often make the mistake of thinking that a, b and c are the sides of the triangle ABC but they are the position vectors of A, B and C from the origin.
Students quite often make the mistake of thinking that a, b and c are the sides of the triangle ABC but they are the position vectors of A, B and C from the origin.
I’ve shown this in Figure 11.B.2.
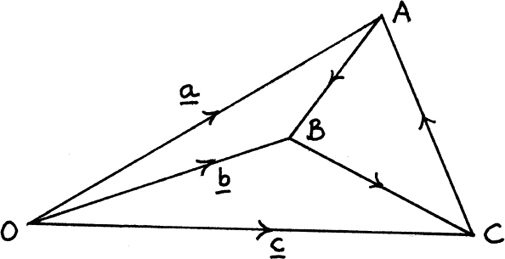
Figure 11.B.2
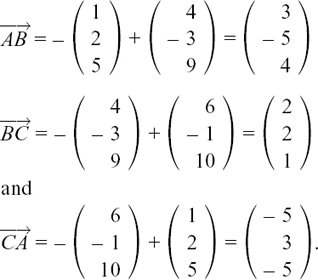
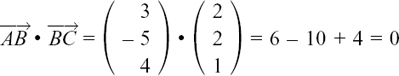
EXAMPLE (4)
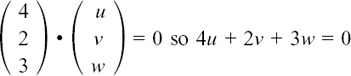

Now try these questions.
EXERCISE 11.B.1
(1) Find the angles between the following pairs of vectors, giving your answers in degrees to 1 d.p. if they aren’t exact.
(a) a = 2i – 3j – k and b = 5i + j + 2k
(b) a = 2i – 7j + 3k and b = 6i – 21j + 9k
(c) a = 4i – 6j + 5k and b = –3i + 3j + 6k
(d) a = 3i – 5j + 2k and b = i + j – 3k
(e) a = 2i – j + 3k and b = –8i + 4j – 12k
(2) The position vectors of the points A, B and C with respect to the origin O are a = 8i – j + 8k, b = i + 4j + 5k and c = 4i – 3j + 6k respectively.
Show that the triangle ABC is right-angled and find its area. Try to answer this question without looking at Example (3) above. Read it through again before you start if you want to.
(3) Find unit vectors which are perpendicular to the following pairs of vectors:
(a) a = 4j + 3k and b = 6i + 4j + 7k
(b) a = –i + 4j and b = 2i – 4j – 3k
(c) a = 3i + 2j and b = 3j + 4k
11.B.(c) Defining the vector or cross product of two vectors
Is it possible to find a way to multiply two vectors together so that we get a vector result? The problem is that, working from the two directions of our starting vectors, we have to find some way of using these to give us the single direction of the resulting vector. This problem makes it impossible to define this kind of vector multiplication in two dimensions but there is a very neat way of solving it in three dimensions. It works like this.
We first slide the two vectors together, if necessary, so that their tails meet. Now they both lie in one particular flat surface or plane. We can use the direction perpendicular to this plane to give us the direction of our vector product. We only have to decide which of the two possible perpendicular directions to choose.
Figure 11.B.3 shows how we do this to find the vector product of the two vectors a and b. I’ve drawn b both in its original position and also shifted so that the tails of a and b meet.

Figure 11.B.3
We define the vector product of a and b as

where 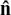 is a unit vector perpendicular to the plane in which a and b lie.
is a unit vector perpendicular to the plane in which a and b lie.
We choose the direction of  so that a, b and
so that a, b and  can fit along the thumb, first finger and second finger of your right hand. (Check this with your hand and my drawing.) Notice that this means that the direction of b × a is given by
can fit along the thumb, first finger and second finger of your right hand. (Check this with your hand and my drawing.) Notice that this means that the direction of b × a is given by  so a × b = –(b x a). Notice, also, that the definition means that a × a = the zero vector 0i + 0j + 0k since sin 0° = 0.
so a × b = –(b x a). Notice, also, that the definition means that a × a = the zero vector 0i + 0j + 0k since sin 0° = 0.
The multiplication sign used to show the vector product is called ‘cross’. It is also sometimes written using a little upside down v so a ∧ b is the same as a × b.
The cross product has the following three very useful practical applications.
Application (1) area
We’ll look at how cross products give the areas of parallelograms and triangles.
The area of a parallelogram is equal to its base multiplied by its perpendicular height.
In Figure 11.B.4 we have a parallelogram whose base is |b| and whose perpendicular height h is given by h = | a| sin θ where | a| is the length of the slant side.
But a x b = |a||b| sin θ 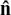 where
where 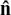 is the unit vector perpendicular to a and b.
is the unit vector perpendicular to a and b.
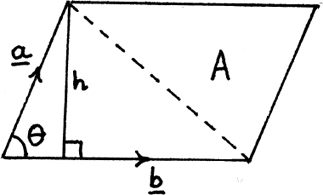
Figure 11.B.4
Therefore its area A is given by the magnitude of a × b or A = |a × b|. From this result, we see that the area of a triangle with base of length |b| and slant side |a| is given by  The cross product of any two vector sides of a triangle can be used to find its area.
The cross product of any two vector sides of a triangle can be used to find its area.
Application (2) torque
The vector product gives us a way to define the torque or moment of a force about a point. Figure 11.B.5 shows how this works.

Figure 11.B.5
If we have a force F acting through a point P with position vector r with respect to O, then F and r lie in a plane through O. I have drawn  as a unit vector perpendicular to this plane and I have also redrawn the force vector F shifted so that its tail is at O. The dashed line shows the line of action of the force F.
as a unit vector perpendicular to this plane and I have also redrawn the force vector F shifted so that its tail is at O. The dashed line shows the line of action of the force F.
The torque or moment of F about an axis through O perpendicular to this plane is given by
torque 
You can think of |T|, the magnitude of T, in two ways. We have |T| = |F| multiplied by the perpendicular distance of O from the line of action of F or we also have |T| = |r| multiplied by the component of F perpendicular to r. I’ve shown both these interpretations on my diagram.
Torque measures the turning effect of F about the axis through O perpendicular to the plane in which r and F lie. It is independent of the position of P on the line of action of F. You can see that this must be so from Figure 11.B.6, looking down at the plane containing the line of action of F and the origin and showing the position vectors of three different choices of point on this line of action. (Again I’ve shown the line of action of F as a dashed line.)
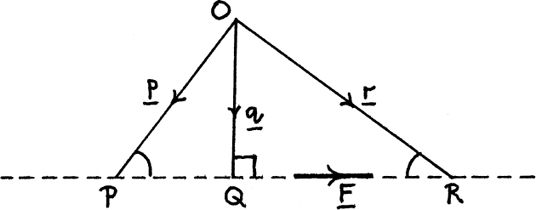
Figure 11.B.6
We have |p| sin P = |q| = |r| sin R, so the torque of F about the perpendicular axis through O is independent of the point chosen on the line of action of the force.
You can also see that the value of sin θ does indeed give the various practical possibilities, such as when a person applies torque using a spanner to turn a nut. You get maximum turn if you pull it at a right angle with θ = 90° and sin θ = 1. If you pull along the line of the spanner then θ = 0° and sin θ = 0 and you get no turn at all.
Application (3) angular momentum
The vector product also gives us a way to define angular momentum. In Figure 11.B.7, I’ve shown a particle of mass m with position vector r relative to an origin O. If this particle has velocity v then its momentum p is given by p = mv.
The angular momentum or moment of momentum of the particle is defined as


Figure 11.B.7
I’ve drawn  as a unit normal vector to the plane in which r and v lie. We have r × p = m(r × v) = m|r||v| sin θ
as a unit normal vector to the plane in which r and v lie. We have r × p = m(r × v) = m|r||v| sin θ 
These three applications show that not only does this definition of vector multiplication make sense mathematically but it also has extremely useful physical meanings.
11.B.(d) Working out the cross product of two vectors
Again we’ll start by looking at the simplest cases. What answers do we get if we work out the cross products for the different possible pairs we can choose from the unit vectors, i, j and k? Work out for yourself what i × i, i × j and j × i give.
If you have done this, you will see that the complete set of results will be as follows:
i × i = j × j = k × k = the zero vector.
(Remember that the zero vector is the vector 0i + 0j + 0k.)
Also, i × j = k and j × k = i and k × i = j
while j × i = –k and k × j = –i and i × k = –j.
This is because sin 0° = 0 and sin 90° = 1 and each vector is of unit length. You can see how the various plus and minus signs come by using the right-hand rule for each product.
Next we see how we can work out the cross product of two vectors by using their components. Fortunately, mathematicians have shown that the distributive law is true for the cross product. That is, if we have three vectors a, b and c, then (a × c) + (b × c) = (a + b) × c.
Now suppose we have a = a1i + a2j + a3k and b = b1i + b2j + b3k so that a × b = (a1i + a2j + a3k) × (b1i + b2j + b3k). Working out all the nine separate little cross products that we get from multiplying these two brackets together and using the distributive law from above gives us the following rule.
If we have two vectors a = a1 i + a2 j + a3 k and b = b1 i + b2 j + b3 k
then their vector or cross product is given by
a × b = (a2b3 – a3b2)i + (a3b1 – a1b3)j + (a1b2 – a2b1)k.
It can be helpful when working out a vector product to set out the two vectors in the form of what is called a determinant. To do this we write

The rule for multiplying out this determinant is that we start from the top row and multiply down, taking an element from each row in all possible ways except that no element is allowed to be directly underneath another. The sign of each multiplication depends on the order in which the components are chosen. I’ve shown how the working out goes by writing the determinant in a double form in Figure 11.B.8.
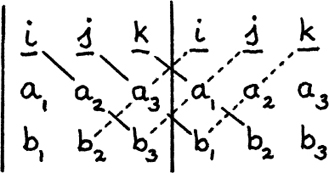
Figure 11.B.8
We put together all the diagonal multiplications with the forwards slanting ones being positive and the backwards slanting ones, shown with dashed lines, being negative. This gives us the answer
which, tidied up, is
as we found before.
EXERCISE 11.B.2
Work out the cross product a × b for each of the following pairs of vectors a and b.
(1) a = i + j and b = j + k
(2) a = 3i + j + 2k and b = 51 + k
(3) a = 2i – 7j + 3k and b = i – 2j – k
(4) a = i – 2j – k and b = 2i –7j + 3k
(5) a = 5i – 2k and b = 3i + 4k
Here are two more examples which make use of the cross product.
EXAMPLE
EXAMPLE
EXERCISE 11.B.3
(1) Find unit vectors which are perpendicular to each of the following pairs of vectors.
(a) a = 4j + 3k and b = 6i + 4j + 7k
(b) a = –i + 4j and b = 2i – 4j – 3k
(c) a = 3i + 2j and b = 3j + 4k
(d) a = 3i + 2j + 2k and b = –3i + j + 4k
(e) a = 2i + 2k and b = 2j + 4j – 5k
(f) a = 4i+ 3j + 2k and b = –4i + 3j
(2) The three forces F1, F2 and F3 all act on a rigid body.
(3) If a = xi + yj + zk, b = 2i – j + k and c = i – 3j – 5k and a × b = c can you find the values of x, y and z?
(4) Starting with the vector u = 2i – j – 2k, find three mutually perpendicular unit vectors, with one of them in the direction of u. (Hint: think what is happening geometrically here. There are an infinite number of vectors perpendicular to u and any of these will do for your second vector. Also it’s easier to find the mutually perpendicular vectors first and then convert them into unit vectors. Perpendicular vectors are also called orthogonal vectors.)
11.B.(e) Can we multiply three vectors together by using dot or cross products?
Our options are limited because the result of the first multiplication must be a vector otherwise the second multiplication isn’t defined. So, for example, we can’t work out (a • b) • c or c × (a • b). (The brackets tell us which pair to multiply first.) Therefore the first multiplication which we do must be a cross product. The second multiplication can then be either a cross product or a dot product. We’ll look at these two possibilities separately.
11.B.(f) The vector triple product
The multiplication (a × b) × c is an example of what is called the vector triple product. You might think that (a × b) × c = a × (b × c) but, in general, this is not so. You can understand this if you imagine the vectors a and b lying in the plane of a table. Then d = a × b has a direction perpendicular to this table. Since d × c is perpendicular to d, working out d × c puts you back in the table again. Similarly, the vector a × (b × c) lies in the same plane as b and c. In general, this won’t be the same as the plane in which a and b lie.
Here’s a numerical example to show how this works. If a = i + k and b = 2j + 3k and c = 2i + j + k, then working out u = (a × b) × c gives us u = –5i + 6j + 4k. You can see that u lies in the plane of a and b because it can be written as a linear combination of a and b. Check for yourself that u = –5a + 3b. (You might need to look back at Section 11.A.(d) here.)
Similarly, working out v = a × (b × c) gives v = –6i + 3j + 6k and v lies in the plane of b and c because v = 3b – 3c.
EXERCISE 11.B.4
(1) Try working out a similar example for yourself.
(2) For any three vectors a, b and c, it can be proved that a × (b × c) = (a • c)b – (a • b)c. Check that this formula works both for my numerical example before this exercise and for your answer to the first question of this exercise.
11.B.(g) The scalar triple product and what it means geometrically
Now we look at multiplications in which we first find a cross product and then find the dot product of this with some third vector. So, for example, we might find (a × b) • c. Multiplications like this are called scalar triple products. The working out will always result in a scalar or number.
The scalar triple product has a useful geometrical interpretation. To show you how this works, we’ll take the numerical example of V = (2i × 3j) • 4k. This particular scalar triple product gives the volume of a rectangular box. Now we will see why this is so.
First, we work out the cross product of 2i × 3j = 6k. Figure 11.B.9 shows you that this 6k gives the size of the area of the base of the left-hand box, but as a vector in the k direction.

Figure 11.B.9
Next we work out the dot product of 6k • 4k = 24, which gives us the actual volume of the left-hand box.
Similarly, (3j × 4k) • 2i gives the volume of the right-hand box. This is the same size but we are starting with the left-hand face to find its volume. We have
In general, given three vectors a, b and c, we can always find the scalar triple product of (a × b) • c and the answer will be a number, not a vector.
Also, (a × b) • c = a • (b × c). Both of these multiplications give the volume of the slant-sided box made by sliding the three vectors a, b and c together so that their tails meet. (This box is called a parallelepiped.)
I show how this works in Figure 11.B. 10. The volume of this box is given by the area of its base multiplied by its perpendicular height. I’ve shown the base separately on the right-hand side of the diagram.

Figure 11.B.10
We have a × b = |a||b| sin R  where
where  is a unit vector perpendicular to the parallelogram with sides given by a and b, A is its area and R is the angle between a and b.
is a unit vector perpendicular to the parallelogram with sides given by a and b, A is its area and R is the angle between a and b.
So  where S is the angle between c and
where S is the angle between c and  .
.
But 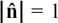 and |c| cos S = h which is the perpendicular height of the box.
and |c| cos S = h which is the perpendicular height of the box.
Therefore (a x b) •c =Ah which is the volume of the box whose edges are the vectors a, b and c. Equally, (b × c) • a and (c × a) • b give the volume of the same box, so we have
The last three are the same as the first three since the order in which we work out a dot product leaves the answer unchanged. However, if we interchange the order of the vectors in the cross product, the answer will change in sign since a × b = –(b × a).
EXERCISE 11.B.5
If a = 3i – j + 2k and b = i – 2j + 2k and c = 2i + 4j – k, work out each of the following:
(1) (a × b) • c
(2) a • (b × c)
(3) b • (a × c)
(4) The three vectors a, b and c all lie in the same plane. What happens when you work out (a) (a × b) × c? (b) (a × b) • c?
11.C Finding equations for lines and planes
The results we have found in the previous two sections mean that we shall now be able to find vector equations for straight lines and planes. We start by considering lines.
11.C.(a) Finding a vector equation for a line
Using vectors gives us a very neat way of writing down an equation which gives the position vector of any point on a given straight line. This method works equally well in two or three dimensions.
Suppose we’ve got a straight line like the one I show in Figure 11.C.1. (You have to imagine that it extends infinitely far in either direction.) O is the origin and A is a known point on the line. P is any general point on the line.
Figure 11.C.1
In order to write down the vector equation of this line, we need to know two things.
• We have to know the position vector of some point which lies on the line. On my diagram, we know that  .
.
• We have to know a vector which gives the direction of the line, like d in my diagram. This is called a direction vector.
Then the position vector r of any general point P on the line is given by the equation
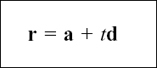
where t tells us how much of d we need to take in order to get from A to P. (t = 2 for the particular P I have shown in my drawing.)

Notice that writing r = ta + d would give you a completely different line!
It’s important to realise that there are many possible ways of writing the vector equation of any given line. So, in my example above, any point A on the line would work equally well provided we knew its position vector, and any vector lying parallel to d would work equally well as a direction vector. For example, I could have used 3d or –d.
11.C.(b) Dealing with lines in two dimensions
If we are working in two dimensions we can think of any line as lying in a plane containing the origin where all the vectors can be described in terms of just i and j. It is as though we are looking at the line in an infinitely large piece of graph paper.
Suppose that we have a line L with the equation r = a + td with a = 2i + j and d = i – j.
Letting t = 0, 1 and –2 in turn, we find that the points with position vectors r = 2i + j, r = 3i and r = 3j all lie on this line. I show a sketch of it in Figure 11.C.2.
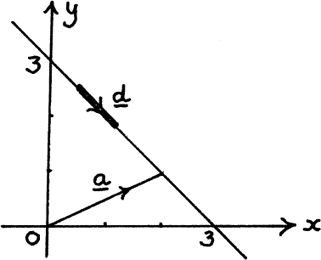
Figure 11.C.2
Writing any general point on the line as r = xi + yj, and using column vectors, we have
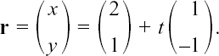
Vectors are only equal if their components are equal so we must have x = 2 + t and y = 1 – t.
Adding these equations to get rid of t, we find that x + y = 3. This is the Cartesian form of the equation of this line. It’s now in the form described in Section 2.B.(f).
We can also work backwards to get a vector equation of a line from its Cartesian equation.
Suppose we have the line 2y = x + 4. First, we find a possible a, the position vector of a known point on the line. Any such point will do, so I’ll choose the point (2, 3) with position vector a = 2i + 3j.
Now we need a direction vector for the line. Its gradient, working as in Section 2.B.(d), is 1/2 so its direction is given by the vector d = 2i + j.
Therefore we can write its vector equation as r = 2i + 3j + t(2i + j).
Notice that we have a huge choice as to how we write a vector equation for this line. It would have worked equally well with a = –2i + j and d = –2i – j. I’ve shown both possibilities in Figure 11.C.3, the first using solid lines for a and d and the second using dashed lines.

Figure 11.C.3
We can see that the point I’ve marked P, with p = 4i + 4j, lies on this line. If we use r = 2i + 3j + t(2i + j) then we put t = 1 to get r = p. If we use r = –2i + j + t(– 2i – j) then we put t = –3 to get r = p. Looking at the graph you can see that the vectors do actually work like this.
EXERCISE 11.C.1
(1) Find a cartesian equation for each of the following lines:
(a) r = 2i – 3j + t(i + 2j)
(b) r = i – 2j + t(4j)
(2) Find a vector equation for each of the following lines:
(a) y = 3x + 5
(b) 2y = 5x – 3
If we have two straight lines in two dimensions then they must either be parallel, in which case their two direction vectors must be parallel, or they must cut each other at some point.
Here’s an example. Suppose we have three lines L1, L2 and L3 and we need to find the relationship of L1 with each of L2 and L3.
The letters s and m work in exactly the same way for their lines as t does for line L1. Lines L1 and L2 are parallel because their direction vectors are parallel since 2i – 4j = –2(– i + 2j).
Lines L1 and L3 aren’t parallel so now we’ll find where they meet. Suppose that they meet at the point P with position vector p. Then, working with column vectors, we have
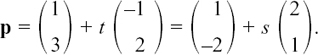
Vectors are equal if their components are equal so we have the following two equations.

From (1) we have t = –2s. Substituting this in (2) gives 3 – 4s = –2 + s so s = 1. Therefore t = –2. The two lines meet at the point with position vector p = 3i – j.
Notice that you can either substitute t = –2 in L1 or s = 1 in L3 to get this result.
If we tried to find where the parallel lines L1 and L2 meet using this method, we wouldn’t be able to solve the equations for t and m. See for yourself!
Try these two questions.
EXERCISE 11.C.2
(1) Find the point of intersection of the lines r = i + j + s(3i – 2j) and r = 6i + t(2i + j).
(2) The line L1 has the vector equation r = i + 3j + t(2i + 3j). Find the vector equation of the line L2 which is perpendicular to L1 and which passes through the point whose position vector from the origin is r = 3i + 4j.
ll.C.(c) Dealing with lines in three dimensions
The general equation for a straight line of r = a + td is unchanged but now both a and d are three-dimensional vectors. Here are some examples of equations of particular lines so we can look in more detail at how they actually work.
Suppose that Line L1 has the equation r = i + 3k + t(2i + j + k) so that the vector a in Figure 11.C.1 is i + 3k and the vector d is 2i + j + k.
Different values of t give the position vectors of different points on this line.
Suppose there are two more lines L2 and L3 so that now we have the following three lines.
The letters s and m work in exactly the same way for their lines as t does for line L1. Both the lines L2 and L3 have special relationships with line L1. Can you spot what they are?

Comparing lines L1 and L2 with the general form of the equation for a straight line of r = a + td, we see that both lines have the same position vector of a = i + 3k but they have different direction vectors. Therefore they cut each other at the point with position vector r = i + 3k.
Line L3 has the same direction as line L1 since its direction vector is just scaled up by a factor of 2. So either lines L1 and L3 are parallel or they are really the same line.
Putting t = 0 for line L1 gives r = i + 3k but there is no value we can give to m in line L3 which would make r = i + 3k. Therefore L1 and L3 are distinct parallel lines.
Now we’ll consider two more lines.
They are not parallel since their direction vectors aren’t parallel but do they cut each other? If not, they are what are called skew lines.
If they do cut each other then the point P where they cut must lie on both lines. We’ll call its position vector from the origin p.
The point P can only exist if there are values of s and t so that
The working is easier if we write this equation using column vectors. Doing this gives us
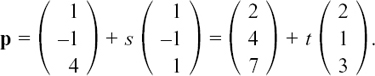
For this equation to have a solution, each of the three components of the vectors must be equal, so we get

Is this possible? If we add (1) and (2) we get 0 = 6 + 3t so t = –2. Substituting this value in (1) gives s = –3.
The next step is very important. The lines only meet if these values of s and t also fit equation (3).
Substituting s = –3 and t = –2 in 4 + s = 7 + 3t gives the LHS = 4 – 3 = 1 and the RHS = 7 – 6 = 1. Therefore the three equations are consistent (that is, there is a solution which fits all three of them) and the lines do cut each other.
Now, putting s = –3 we find that the position vector p of the point of intersection P is p = –2i + 2j + k. You will see that putting t = –2 gives exactly the same result.
Try some for yourself now.
EXERCISE 11.C.3
Find whether the following pairs of lines are (a) parallel, (b) non–parallel and intersecting, or (c) non–parallel and non–intersecting and therefore skew.
(1) r = i + 2j – k + s(2i – j + 3k) and r = 5i – j + t(6i – 3j + 9k)
(2) r = –i – j + 5k + s(2i – 3k) and r = 4i – 4j + 2k + t(i – j)
(3) r = 2i + k + s(i+ 3j + 4k) and r = i + 3j + t(2j + k)
(4) r = i + 3j + 2k + s(i – j + 2k) and r = 2i + 6j + 4k + t(i – 3j + 2k)
(5) r = i – 2j + k + s( – j + 2k) and r = 3i – 6j + 3k + t (2i + 2j – k)
ll.C(d) Finding the Cartesian equation of a line in three dimensions
We know that an equation like 3x + 4y = 12 describes a line in two–dimensional space. Will it also describe a line in three–dimensional space? In Example (2) of Section ll.C.(i) we shall show that it actually describes a plane. So, how would we write the equation of a line in three dimensions in terms of x, y and z?
To show you how the working goes, I’ll take the particular example of the line whose vector equation is r = 2i + 3j – 4k + t(3i – j + 2k).
Since r is standing for the position vector from O of any point on the line, we’ll write r = xi + yj + zk. The values of x, y and z vary as the point P moves on the line. So now we can say
r = xi + yj + zk = 2i + 3j – 4k + t(3i – j + 2k).
The working is easier if we write this equation using column vectors. This gives
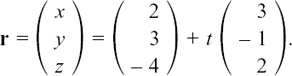
This equation can only be satisfied if it is true for each separate component. We have

Rearranging each equation for t gives us
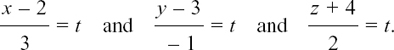
Therefore we can say
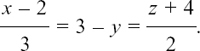
This is the equation of the line in terms of x, y and z (also called its cartesian equation). So, if x = 5 for example, we would have 1 = 3–y so y = 2 and z + 4 = 2 so z = –2 which means that the point with position vector r = 5i + 2j – 2k lies on this line. Looking back at the equation of the line written in column vectors above, we can see that t = 1 gives this point.
Working in exactly the same way, we get this general rule.
If a = a1i + a2j + a3k and d = d1i + d2j + d3k
then the equation of the line r = a + td can also be written as
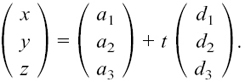
This rearranges to give the Cartesian equation of the line as

Notice how the components of the position vector a and the direction vector d appear in the Cartesian equation.
If we are finding the Cartesian equation of the line r = a + td, and either a or d or both have components equal to zero, the working can be a little tricky.
EXAMPLE (1)
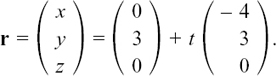
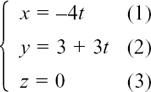


Next we have two examples showing the reverse process of converting the Cartesian equation of a line into its vector equation.
EXAMPLE (2) Suppose we have the line with the equation

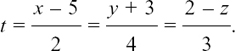
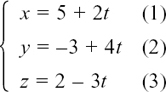
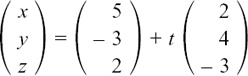
EXAMPLE (3) Suppose we have the line with the equation


Now try these questions yourself.
EXERCISE 11.C.4
(1) Find the Cartesian equation for each of the following lines.
(a) r = i – 2j + 5k + t(3i + 2j – 7k)
(b) r = 3i + 5k + t(2i – j + k)
(c) r = 2j – 3k + t(i – k)
(2) Find the vector equation for each of the following lines.
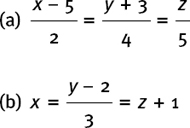
(c) 3X = 5 – y and z = 0
(3) A straight line in three-dimensional space passes through the points A and B with position vectors relative to the origin of a = 4i and b = 3j.
(a) Find its vector equation.
(b) Find its Cartesian equation.
11.C.(e) Another form for the vector equation of a line
We can use the cross product to write the vector equation of a straight line in the following way. From Figure 11.C.4 (which is the same drawing that I used in Section 11.C.(a)) we have  and d is in the same direction as
and d is in the same direction as 
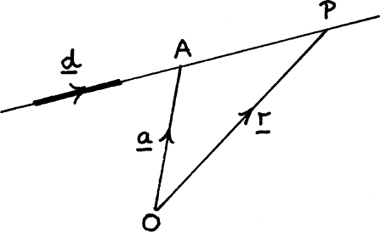
Figure 11.C.4
Therefore, 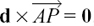 , the zero vector. This gives us the alternative form for the equation of a straight line of (r – a) × d = 0 = 0i + 0j + 0k.
, the zero vector. This gives us the alternative form for the equation of a straight line of (r – a) × d = 0 = 0i + 0j + 0k.
11.C.(f) Finding vector equations for planes
One possible way of doing this is to use a very similar method to the one we used in Section 11.C.(a) to find the vector equation of a line. The difference is that now we want an equation which gives the position vector of any point in a flat surface or plane. We’ll start with the case where the origin lies in the plane. Figure 11.C.5 shows part of a plane like this.
We’ve now got a very similar situation to the one described in Section 11.A.(c) except that this plane is a two–dimensional space embedded in a three-dimensional space. To find the position vector of any point P, we have to know two non-parallel vectors which lie in the plane. I have called these d and e. It is then possible to get to P by adding together suitable multiples of d and e. This gives us the equation of the plane as r = sd + te where the values of the numbers s and t can be chosen to give us the position vector of any point in the plane. In Figure 11.C.5, r is given by s = 1.4 and t = 1.1 approximately.

Figure 11.C.5
Now suppose we have a plane which doesn’t pass through the origin. Figure 11.C.6 shows part of a plane like this. Again, d and e are known vectors which lie in the plane. But now we also need a way of getting to the plane from the origin, so we have to know the position vector of some particular point in the plane. In Figure 11.C.6, this point is A with position vector a.
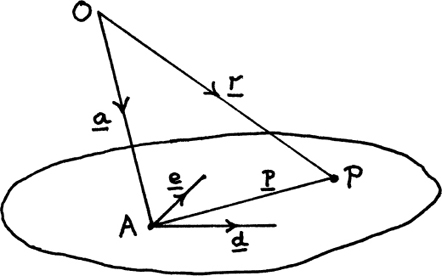
Figure 11.C.6
Once we have reached the plane, we can find the position of any general point P relative to A in the same way that we did above by saying that p = sd + te. (For my particular P, s = 1.2 and t = 1.) Now we can get the equation of the plane in terms of the known vectors a, d and e.
We have r = a + p but p = sd + te, so r = a + sd + te.
In the special case where the plane passes through the origin, we can leave out the a because we can choose O to be the known point in the plane. If two planes are parallel, then the same d and e can be used for both of them, since we can move these vectors so that they lie in either plane. The equations of the planes are different because each one must also include a position vector from the origin to a known point in that particular plane.
Writing the equation of a plane in this way has one big disadvantage. There are infinitely many directions which vectors lying in the plane can have. Therefore there are infinitely many pairs like d and e to choose from. It would be much nicer if we could use a direction which is unique to the plane. There is a direction which has exactly this property. Can you think what it is? The next section explains how we use it.
11.C.(g) Finding equations of planes using normal vectors
The direction perpendicular to a plane is unique to that plane (and any plane parallel to it). To see how we can use this to give us another form of the equation of a plane, we’ll again start with the case where the plane passes through the origin. I’ve shown part of such a plane in Figure 11.C.7.

Figure 11.C.7
Suppose we know a vector n which is perpendicular to the plane. This means that n is perpendicular to the position vector r of any point in the plane relative to the origin. Therefore the dot product of the perpendicular vectors n and r is zero and we can write the vector equation of the plane as n • r = 0. The vector n is called a normal vector to the plane. Any vector parallel to the n I have drawn will also be a normal vector to this plane and will work equally well. In particular, we could have used –n. Provided we know two non-parallel vectors which lie in the plane, say d and e, then we can always find a vector n by working out the cross product of d and e. (See Section 11.B.(d) if necessary.)
Now we extend this method to find the equation of a plane which doesn’t pass through the origin. I’ve shown part of such a plane in Figure 11.C.8. This time, we have to be able to get to the plane first from the origin, so we must know the position vector of some particular point in the plane from the origin. In Figure 11.C.8, this point is A with position vector a.
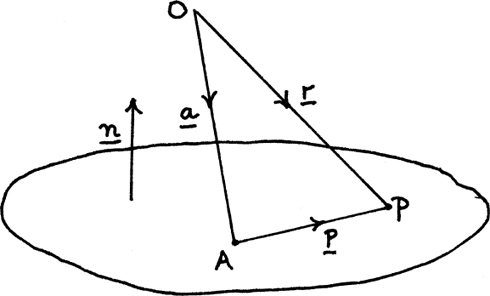
Figure 11.C.8
If P is any general point in the plane, so that the vector  = p, then n and p are perpendicular to each other. Therefore n • p = 0 but p = r – a.
= p, then n and p are perpendicular to each other. Therefore n • p = 0 but p = r – a.
This gives us the vector equation of the plane as
n • (r – a) = 0 or n • r = n • a = C
where C is the number we get from working out the dot product of the two known vectors n and a.
Again, if we know two non-parallel vectors d and e which lie in the plane then we can use their cross product, d × e, to find a vector n which is perpendicular or normal to this plane.
11.C.(h) Finding the perpendicular distance from the origin to a plane
We can obtain a particularly useful form of the equation of a plane by finding a normal vector to it which has unit length. I’ll call this unit normal vector  . You can see why it is useful by looking at Figure 11.C.9.
. You can see why it is useful by looking at Figure 11.C.9.
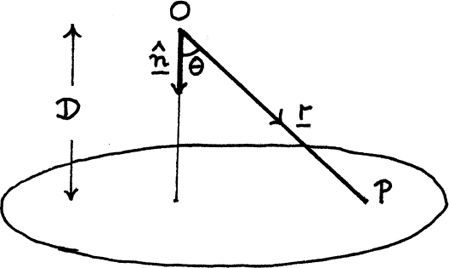
Figure 11.C.9
Since  , we have
, we have 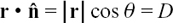 where |D| is the perpendicular distance from the origin to the plane. We write the distance as |D| because distances are always taken as positive. If
where |D| is the perpendicular distance from the origin to the plane. We write the distance as |D| because distances are always taken as positive. If  was pointing upwards in Figure 11.C.8, the calculated D from
was pointing upwards in Figure 11.C.8, the calculated D from  would be negative since θ, the angle between
would be negative since θ, the angle between  and r, would now be obtuse.
and r, would now be obtuse.
Knowing how to find this distance will make it easier to find some shortest distances in Sections 11.D.(e) and (f). It also has applications in computer graphics.
As a numerical example, we’ll find the perpendicular distance from the origin to the plane with equation r = 3i + k + s(2i – 4j + 5k) + t(i – k).
Comparing this with the general form r = a + sd + te, we have d = 2i – 4j + 5k and e = i – k.
Working out d × e will give us a normal vector, n, to the plane. We have

From this we have  and the unit vector
and the unit vector 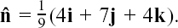 .
.
Now, 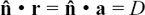 where |D| is the perpendicular distance from the origin to the plane, and a = 3i + k. Working with column vectors, we have
where |D| is the perpendicular distance from the origin to the plane, and a = 3i + k. Working with column vectors, we have
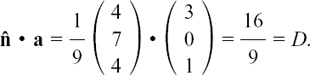
The perpendicular distance from the origin to this plane is 16/9 units.
EXERCISE 11.C.5
Find the equations of the following planes in the form  and hence find the perpendicular distance from the origin to the plane in each case.
and hence find the perpendicular distance from the origin to the plane in each case.
(1) r = 4i + j + s(2i – 4j – 3k) + t(–i + 4j)
(2) r = 2i – 3j – k + s(3j + 4k) + t(3i + 2j)
(3) r = 3j + 6k + s(3i + 2j + 2k) + t(–3i + j + 4k)
Can you explain why you get a rather surprising result for (3)?
11.C.(i) The Cartesian form of the equation of a plane
Starting with the vector equation of a plane in the form n • r = n • a = C it is very easy to find the Cartesian equation of the plane. We let r = xi + yj + zk, remembering that r is the position vector of any general point in the plane. We let n = ai + bj + ck where, for any particular plane, we know the values of a, b and c. Then, using column vectors, we have
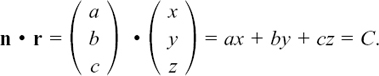
The Cartesian form of the equation of a plane is ax + by + cz = C. Here are two numerical examples.
EXAMPLE (1)

EXAMPLE (2)

Figure 11.C.10
EXERCISE 11.C.6
Try these questions yourself now.
(1) Find the perpendicular distance from the origin to each of the following planes.
(a) 3x + 2y – 6z = 6
(b) 8x – 15z = 12
(c) 2x – y + 2z = 7
(d) 4x – 7y – 4Z = 18
(2) The plane Π contains the three points P, Q and R with p = –i + 3j, q = i + 2j + 6k and r = i + 12k. Find its cartesian equation.
11.C.(j) Finding where a line intersects a plane
Suppose we have the line L with equation r = 4i – j + 2k + t(i + 2k) and the plane Π with equation 3x–2y + 5z=11. We want to find the point P where the line L cuts the plane Π.
First, we check that the line and the plane aren’t parallel. The direction vector for the line is d = i + 2k. The normal vector to the plane is n = 3i – 2j + 5k. Working out the dot product of d and n gives us 13 so d and n aren’t perpendicular to each other. Therefore the line and the plane aren’t parallel.
Suppose that line L cuts the plane Π at the point P with position vector p and p = xi + yj + zk.
P lies on the line so, working with column vectors, we have
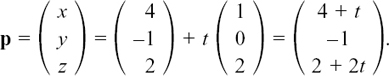
But P also lies in the plane, so these values for x, y and z must also satisfy the equation of the plane. Therefore we can say
3(4 + t) – 2(–1) + 5(2 + 2t) = 11.
Solving this equation gives us t = –1 so the point of intersection of the line and the plane has the position vector p = 3i – j.
EXERCISE 11.C.7
(1) Line L with the equation r = –2i + 5j + k + t(3i – j + k) and plane Π with the equation 2x + 3y – 4z = 3
(2) Line L with the equation r = 3i – 5j + 4k + t(2i + 3j – 4k) and plane Π with the equation 2x + 3y – 4z = 4
(3) Line L with the equation r = i – 4k + t(2i – 3j + k) and plane Π with the equation 4x – 5y + z = 12
(4) Line L with the equation r = i + 2j – 5k + t(2i – 3j + k) and plane Π with the equation 2x + 5y – 3z = 6
11.C.(k) Finding the line of intersection of two planes
Any two planes will intersect in a straight line unless they are parallel. If they are parallel then their normal vectors will also be parallel. It’s always wise to check this before looking for a line of intersection.
Suppose that plane Π1 has the equation x – 2y + 3z = 6 and plane Π2, has the equation 2x + 3y – 5z = 5.
Do these two planes intersect each other? If so, what is the equation of their line of intersection?
Π1 has the normal vector n1 = i – 2j + 3k and Π2 has the normal vector n2 = 2i + 3j – 5k. Since n1 and n2 aren’t parallel, the planes do intersect.
Let the equation of the line of intersection be r = a + td. Since this line lies in both planes it must be perpendicular to both n1 and n2. Therefore the cross product of n1 and n2 will give us a direction vector d for this line.
Working this out, we get n1 × n2 = d = i + 1lj + 7k. Check this for yourself.
To find a, we need to find the position vector of a point which lies on both planes and therefore on their line of intersection. Any such point will do. One way to find such a point is to put z = 0 in the equations for both planes, and then solve the two resulting simultaneous equations for x and y. This gives us

The solution of these two simultaneous equations is x = 4 and y = –1. (See Section 2.C.(b) if necessary.)
Therefore the points A with coordinates (4, – 1, 0) lies on both planes. Its position vector from the origin is a = 4i – j. We can now write the equation of the line of intersection of Π1 and Π2 as
To find a, I could equally well have chosen to put x = 0 or y = 0 instead of z = 0. I chose z because, in this case, it made the equations easier to solve. You can check for yourself that if you put x = 0 you get the different point A with a = –45j – 28k.
Now we have the equation of the line of intersection of Π1 and Π2 as r = –45j – 28k + s(i + 11j + 7k). Although the equation looks different, it gives the same line as r = 4i –j + t(i + 11j + 7k). For example, the point with position vector r = 7i + 32j + 21k lies on the line. To get it, we put t = 3 or s = 7.
Since two non-parallel planes intersect in a straight line, we can say that, in general, any pair of equations ax + by + cz = d and fx + gy + hz = m will represent a line provided the vectors ai + bj + ck and fi + gj + hk are not parallel.
EXERCISE 11.C.8
(1) Plane Π1 with the equation 2x – 5y + z = 4 and plane Π2 with the equation x + 2y – z = 5
(2) Plane Π3 with the equation x – 3y + 5z = 4 and plane Π4 with the equation –3x + 9y – 15z = 8
(3) Plane Π5 with the equation 4x – y + z = 9 and plane Π6 with the equation 2x + 3y – 7z = 8
11.D Finding angles and distances involving lines and planes
Because vectors carry the physical information of both magnitude and direction, using them gives us a powerful method for calculating angles and distances in three dimensions.
11.D.(a) Finding the angle between two lines
Suppose we have two lines with the equations r = a1 + sd1 and r = a2 + td2. The angle between the two lines is given by the angle between their two direction vectors d1 and d2. I show this in Figure 11 .D. 1.
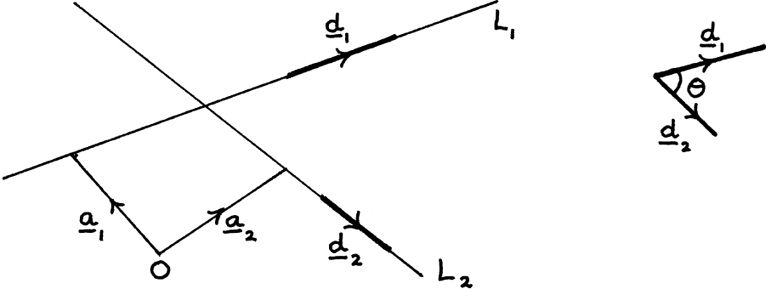
Figure 11.D.1
If the lines don’t cut each other, the angle between them is defined to be the angle we would get by sliding the two direction vectors towards each other until their tails meet while keeping their directions unchanged. We can find this angle using the dot product since d1 • d2 = |d1||d2| cos θ where θ is the angle between d1 and d2.
Here is a numerical example showing how the working out goes.
Suppose we have the two lines L1 and L2 with these equations.

We find the angle between them by calculating the dot product of their two direction vectors. Working in column vectors, we have

This gives 2 + 12 – 6 = 8 = 21 cos θ so θ = cos–l) (8/21)= 67.6° to 1 d.p.
It may happen that the angle θ will be obtuse. For example, if we reverse the direction of d2 in Figure 11.D.1, then θ will be obtuse. In this case, working out n • d will give a negative answer and cos–1 θ will be an obtuse angle. We can then find the acute angle between the lines by subtracting θ from 180°. Or we can avoid this problem by using the absolute value of d1 • d2, which we write as |d1 • d2|, when we find θ. This gives us the following general rule.

EXERCISE 11.D.1
(1) One pair of lines given below is parallel and one pair is perpendicular. Which are they in each case? What is special about the other two pairs?
(a) r = 2i – j + 4k + s(2i – 3j + k) and r = i + 6j + k + t(3i + 4j + k)
(b) r = i – 2j + 4k + s(3i – 2j + k) and r = 2i + j + 5k + t(–6i + 4j – 2k)
(c) r = i + 3j – 2k + s(i – 3j + 4k) and r = –2i – 6j + 4k + t(2i +7j + k)
(d) r = 2i + j – 3k + s(5i – 2j + 3k) and r = 4i + 3j + k + t(3i + 6j – k)
(2) Find the acute angle between each of the following pairs of lines giving your answers correct to 1 d.p.
(a) r = 2i – 5j + k + s(4i –7j – 4k) and r = 3i –7j + 2k + t(3i – 4j + 12k)
(b) r = i – 7j + 2k + s(3i – j + 4k) and r = 2i + 5j + k + t(2i +7j + k)
11.D.(b) Finding the angle between two planes
It is important to choose the correct angle here. It is defined as the angle between two lines, one in each plane, so that they are at right angles to the line of intersection of the two planes, like the angle between the tops of the pages of an open book. Figure 11.D.2 shows part of two planes and the angle θ between them.

Figure 11.D.2
Now this angle is the same as the angle between the normal vectors to the two planes. If these vectors are n1 and n2 then, using the dot product as in the last section, we have 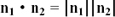 cos θ where θ is the angle between n1 and n2.
cos θ where θ is the angle between n1 and n2.
Here is a numerical example of this.
Suppose we have the two planes Π1 and Π2 with these equations.

We find the angle between them by calculating the dot product of their two normal vectors, 3i – j – 2k and 4i + 2j – 5k. Working in column vectors, we have
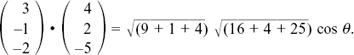
This gives  cos θ giving θ = 37.2° to 1 d.p.
cos θ giving θ = 37.2° to 1 d.p.
If one of the normal vectors to the two planes points upwards and one points downwards, then the angle between them will be obtuse. For example, in Figure 11.D.2, if n2 had been pointing in the opposite direction, then the angle between n1 and n2 would have been (180° – θ) and we would have found the obtuse angle between the two planes. The acute angle is then found by subtracting this from 180°.
Once again, we can avoid this problem by using 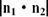 rather than n1 • n2. This gives us the following general rule.
rather than n1 • n2. This gives us the following general rule.
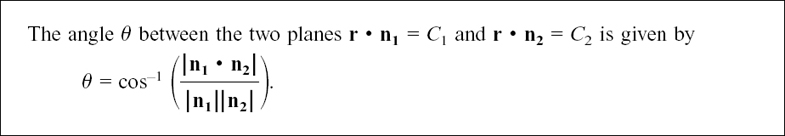
EXERCISE 11.D.2
(1) 3x – 5y + z = 4 and 5x + 2y – z = 5
(2) 4x – 5y + 2z = 6 and 2x + 2y + z = 3
(3) x – 7y + 3Z = 8 and 4x – y – 5z = 6
11.D.(c) Finding the acute angle between a line and a plane
Again the neatest method is to use a normal vector to the plane. I show how this works in Figure 11.D.3 with (a) showing the case where n and d are both pointing out from the same side of the plane and (b) showing them pointing out from opposite sides.

Figure 11.D.3
In both cases, the vector n is normal to plane Π and the vector d gives the direction of line L. We slide n until its tail is at the point of intersection of the line L with the plane Π Then n and L together lie in a plane which is perpendicular to plane H. The angle which the line L makes with the plane Π is defined to be angle θ.
To find θ we first find φ which is the angle between n and d. We’ll consider cases (a) and (b) separately.
(a) Here, we have ϕ = 90° – θ and n • d = |n||d| cos ϕ = |n||d| cos (90° – θ) = |n||d| sin θ using a result from Section 4.A.(h).
(b) This time, we have φ = 90° + θ.
It is more convenient to have just one rule which will work for both (a) and (b). We can get this by taking the absolute value of n • d which we write as |n • d|. Now |n • d| is positive, whatever the sign of n • d and we can now write down this single rule.
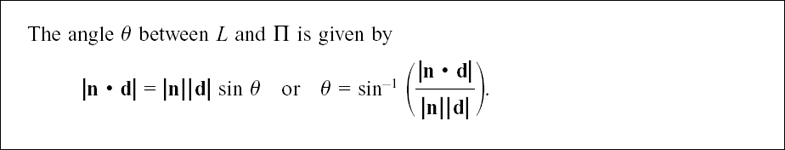
Here is a numerical example of this.
Suppose we are asked to find the angle between line L and plane Π with these equations respectively.

We have n = 3i – 5j + k and d = 2i – 3j – 5k. Using |n • d| = |n||d| sin θ and working with column vectors, we have
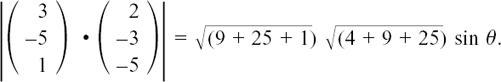
This gives us 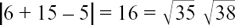 sin θ giving θ = 26.0° to 1 d.p. The angle between line L and plane Π is 26.0° to 1 d.p.
sin θ giving θ = 26.0° to 1 d.p. The angle between line L and plane Π is 26.0° to 1 d.p.
If n • d gives a negative answer, and you need to avoid complications in further calculations, you could always reverse the direction of either n or d.
EXERCISE 11.D.3
Find the acute angle between each of the following pairs of lines and planes giving your answers correct to 1 d.p.
(1) r = 2i – 7j + k + s(3i – 2j + k) and 5x – 2y + z = 8
(2) r = 4i – j + s(i – 7j + 3k) and 2x – 5z = 3
(3) r = i + j + 2k + s(–5i + 7j + 11k) and 3x – y + 2z = 5
11.D.(d) Finding the shortest distance from a point to a line
If we know the position vector p of a point P relative to the origin O, and the equation of a line L, how can we find the shortest distance from P to L?
I shall use a numerical example to answer this question since I can then explain both the principles and how the working out goes. Suppose we are given the following point P and line L.

The shortest distance of P from line L is given by the length of the perpendicular from P to L. Suppose this perpendicular meets L at H. Then we want to find the length of PH. I show this in Figure 11.D.4.
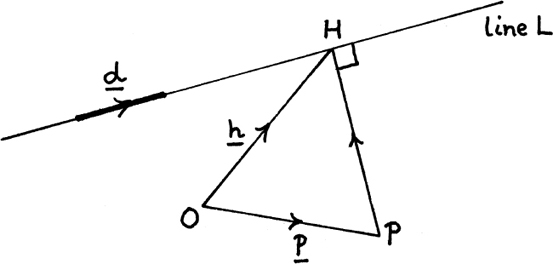
Figure 11.D.4
Since H lies on L, 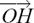 must satisfy the equation of L. Working with column vectors, this gives us
must satisfy the equation of L. Working with column vectors, this gives us

for some value of t which we need to find.
Also, 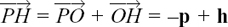 so we have
so we have

But the vector 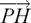 is perpendicular to the direction vector d of line L. So the dot product of
is perpendicular to the direction vector d of line L. So the dot product of  and 3i + j + 4k must be zero. This gives us
and 3i + j + 4k must be zero. This gives us
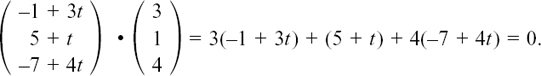
From this, we get 26t = 26 so t = 1. Therefore 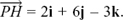
The length of 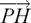 is given by
is given by
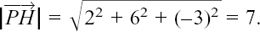
The shortest distance of the point P from the line L is 7 units.
EXERCISE 11.D.4
Find the shortest distances between the following pairs of points and lines, giving your answers correct to 1 d.p. if they aren’t exact. For each pair, I have let p be the position vector of the point P and called the line L.
(1) p = 2i – j + 2k and L is r = –i + 7k + t(4i + j – 2k)
(2) p = i – j + 5k and L is r = 2i – 11j – 8k + t(i + 4j + 3k)
(3) p = –3i – 2j + 6k and L is r = i + 4k + t(2i + j – k)
(This one is a bit sneaky and has a fast answer if you can spot it.)
11.D.(e) Finding the shortest distance from a point to a plane
There is a neat way to tackle this problem. I’ll explain how this works by taking a numerical example and then I’ll summarise the method in a general rule.
We’ll find the shortest distance of the point A with 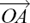 = a = 3i – 2j + 5k from the plane Π with equation 2x + 6y – 3z = 28. This distance is given by the length of AH where AH is perpendicular to Π and H lies in Π. To find it, we split the problem into two parts.
= a = 3i – 2j + 5k from the plane Π with equation 2x + 6y – 3z = 28. This distance is given by the length of AH where AH is perpendicular to Π and H lies in Π. To find it, we split the problem into two parts.
First, we find the perpendicular distance from the origin to the plane. Its equation is 2x + 6y – 3z = 28 which we can rewrite in the form r • n = 28 with n, the normal vector to the plane, given by n = 2i + 6j – 3k.
We have  Therefore
Therefore 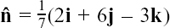 gives us a unit normal vector to the plane.
gives us a unit normal vector to the plane.
Now we have 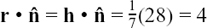 so the perpendicular distance of the plane Π from the origin is 4 units as discussed in Section 11.C.(h).
so the perpendicular distance of the plane Π from the origin is 4 units as discussed in Section 11.C.(h).
Next, we find the distance of the point A from the origin in the direction of  by working out
by working out 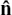 • a. Using column vectors, this is
• a. Using column vectors, this is
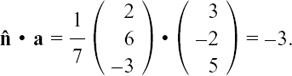
We need to keep the negative sign here because it indicates that A and Π lie on opposite sides of the origin. We see that the total perpendicular distance from A to Π is 7 units. You can see how the distances work out in this particular example in Figure 11.D.5. I have shown the direction of  so that it agrees with the
so that it agrees with the  we found above, with
we found above, with  being positive. Notice that this means that
being positive. Notice that this means that  will give a negative answer since the angle between
will give a negative answer since the angle between  and a is obtuse.
and a is obtuse.

Figure 11.D.5
We can now write down a general rule for finding the shortest distance of a point A with position vector a relative to the origin from a plane Π with the equation n • r = ax + by + cz = C.

Writing the rule in this way takes care of all the different possibilities for the relative positions of A and Π with respect to the origin. In the numerical example we worked out above, we have  units.
units.
Now try these questions yourself.
EXERCISE 11.D.5
(1) Find the shortest distance of the point A from the plane Π in the following two cases.
(a) The equation of Π is 2x – y + 2z = 11and 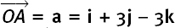
(b) The equation of Π is 3x + 12y – 4z = 79 and 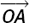 = a = 2i + 7j + 3k
= a = 2i + 7j + 3k
(2) The following question comes from a problem which sometimes faces computer graphics programmers when they want to put highlights on surfaces to add realism.

Figure 11.D.6
The angle of incidence of the ray with the plane is equal to the angle of reflection so the angles which AM and BM make with the normal vector n are equal.
You want to trace the path of the ray by finding the position vector 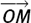 =m of the point M and the size of the equal angles which the ray makes with the plane Π.
=m of the point M and the size of the equal angles which the ray makes with the plane Π.
In order to do this, answer the following questions.
(a) Find the position vector I of L from O. (Hint: L lies on the line AL which is parallel to n and has the known point A lying on it.)
(b) Find the position vector s of S from O. Use this answer to find the length of BS.
(c) From the two triangles ALM and BMS, what can you say about AL/BS and LM/MS? Use this, and the ratio theorem (see Example (3) in Section 11.A.(b) if necessary) to find 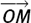 = m.
= m.
(d) Finally, find the angle which the ray AM makes with the plane Π. The reflected ray MB will, of course, make an equal angle with this plane.
11.D.(f) Finding the shortest distance between two skew lines
Skew lines are lines which are not parallel and which do not intersect each other. To find the shortest distance between a pair of skew lines, we shall again make use of the equation of a plane in the form 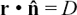 described in Section 11.C.(h). In this equation, r is the position vector from the origin of any general point in the plane,
described in Section 11.C.(h). In this equation, r is the position vector from the origin of any general point in the plane,  is a unit normal vector to the plane, and |D| is the perpendicular distance from the origin to the plane.
is a unit normal vector to the plane, and |D| is the perpendicular distance from the origin to the plane.
First, I’ll describe the general method for finding the shortest distance between two skew lines and then I’ll take a particular example to show how the working out goes.
Suppose that the two lines are L1 and L2 with these equations.

The direction vector of line L1 is d1, and a1 is the position vector of a known point A 1 on this line.
Similarly, the direction vector of line L2 is d2, and a2 is the position vector of a known point A2 on this line.
Now, imagine sliding a copy of line L2 up towards line L1 until it intersects with it at Al. It doesn’t matter what path you take so long as you keep the direction of L2 unchanged. Then line L1 and the shifted line L2 will lie in a plane, Π1, and the point A1 with position vector a1 lies on this plane. Also, we can find a normal vector for Πl by working out the cross product of d1 and d2 since d1 and the shifted d2 both lie in Π1. The normal vector can then be adjusted to give a unit normal vector for plane Πl which I’ll call  .
.
We can now write the vector equation of Π1 in the form 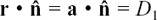 where |D1| is the perpendicular distance of plane Π1 from the origin taken as positive regardless of the calculated sign of D1.
where |D1| is the perpendicular distance of plane Π1 from the origin taken as positive regardless of the calculated sign of D1.
Similarly, we can shift a copy of line L1 until it intersects with line L2 at A2. The shifted line L1 and line L2 lie in a second plane Π2 with the point A2 lying in it. The planes Π1 and Π2 are parallel to each other since the  already found is a unit normal vector to Π2 as well. This is because d2 and the shifted d1 both lie in Π2, so their cross product also gives a normal vector to Π2. So the vector equation of plane Π2 can be written in the form
already found is a unit normal vector to Π2 as well. This is because d2 and the shifted d1 both lie in Π2, so their cross product also gives a normal vector to Π2. So the vector equation of plane Π2 can be written in the form 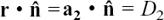 where |D2| is the perpendicular distance of plane Π2 from the origin.
where |D2| is the perpendicular distance of plane Π2 from the origin.
The shortest distance between the two skew lines L1 and L2 is now given by |D1 – D2|. We must use D1 and D2 here, including their signs, because this takes care of whether the two planes are on the same side or opposite sides of the origin. (We had to do something similar when we wrote down the rule at the end of the previous section.) Notice also that 
This gives us the following general rule.
The shortest distance between the two skew lines r = a1 + sd1 and r = a2 + td2
is given by  where
where 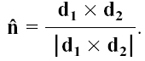
Here is a numerical example. We shall find the shortest distance between the two skew lines L1 and L2 with these equations.

The point A1 with position vector a1 = i + 2j + 2k lies on L1. Shifting a copy of L2 until it intersects with L1 at A1 gives plane Π1 with the point A1 lying in it.
The point A2 with position vector a2 = i – 3k lies on L2. Shifting a copy of L1 until it intersects with L2 at A2 gives plane Π2 with the point A2 lying in it.
The cross product of the two direction vectors, 4i + 3j + 2k and 4i – 6j – k gives a common normal vector n to both planes. Working this out gives
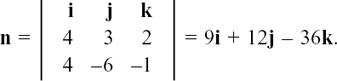
We have  gives a unit normal vector to both planes.
gives a unit normal vector to both planes.
Now, working with column vectors, we have

and

So the shortest distance between the two skew lines L1 and L2 is given by
 units.
units.
The different signs of D1 and D2 show that these two planes lie on opposite sides of the origin. I’ve shown a sketch of this in Figure 11.D.7.
Figure 11.D.7
EXERCISE 11.D.6
Now try these for yourself.
Find the shortest distance between each of the following pairs of skew lines.
(1) L1 is given by r = 3i + j + 7k + s(j + 2k) and L2 is given by r = –i + 3j + 2k + t(3i + 3j + 4k)
(2) L1 is given by r = 3i + 2j – 5k + s(2i + 4j – 5k) and L2 is given by r = i – 3j – 5k + t(i + k)
(3) L1 is given by r = 4i – j – 2k + s(4i + 4j + 3k) and L2 is given by r = –i + 2j + 3k + t(4i – 3j + 3k)

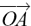 or print it as a single boldface letter, say a. Since we can’t do boldface in handwriting, we would show that this is a vector by underlining it and writing it as a. I have done this in my diagrams.
or print it as a single boldface letter, say a. Since we can’t do boldface in handwriting, we would show that this is a vector by underlining it and writing it as a. I have done this in my diagrams.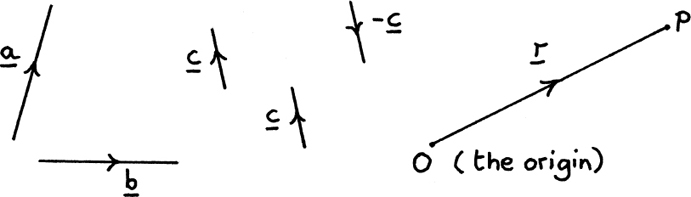


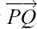
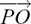 followed by
followed by  This gives us the result
This gives us the result






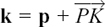
 = l/(l + m)
= l/(l + m)  = –p + q. So
= –p + q. So
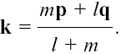

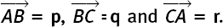
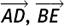 and
and 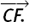 Find
Find  in terms of p, q and r and simplify your answer as far as possible.
in terms of p, q and r and simplify your answer as far as possible.
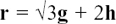


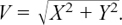


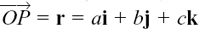


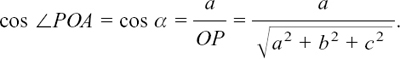
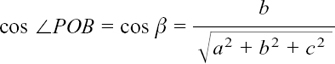

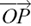
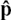 .
.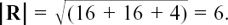

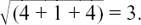
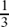 (2i – j + 2k).
(2i – j + 2k).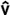 which is in the same direction as v. Repeat this question for w = 8i – 15j.
which is in the same direction as v. Repeat this question for w = 8i – 15j.

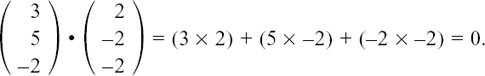
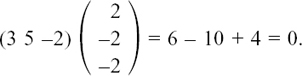
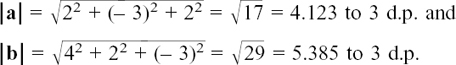




 I will use column vectors for the working in this example. We have
I will use column vectors for the working in this example. We have 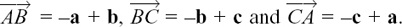 This gives
This gives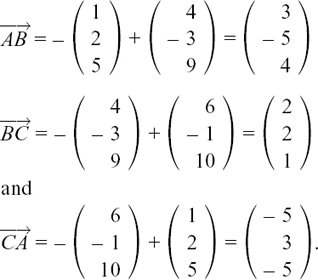

 Check this for yourself.
Check this for yourself.
 . We get
. We get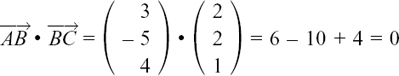
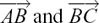
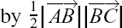

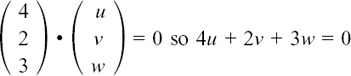

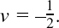
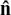
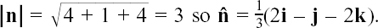
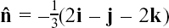



 can fit along the thumb, first finger and second finger of your right hand. (Check this with your hand and my drawing.) Notice that this means that the direction of b × a is given by
can fit along the thumb, first finger and second finger of your right hand. (Check this with your hand and my drawing.) Notice that this means that the direction of b × a is given by  so a × b = –(b x a). Notice, also, that the definition means that a × a = the zero vector 0i + 0j + 0k since sin 0° = 0.
so a × b = –(b x a). Notice, also, that the definition means that a × a = the zero vector 0i + 0j + 0k since sin 0° = 0.







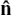
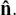


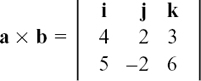
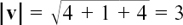
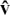 = 1/3(2i – j – 2k). This method is easier than when we used the dot product in Example (4) in Section 11.B.(b) to find this same vector. We shall need to find unit vectors which are mutually perpendicular to two given vectors when we work with equations of planes in Section 11.C.(h).
= 1/3(2i – j – 2k). This method is easier than when we used the dot product in Example (4) in Section 11.B.(b) to find this same vector. We shall need to find unit vectors which are mutually perpendicular to two given vectors when we work with equations of planes in Section 11.C.(h).


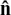 is a unit vector perpendicular to the parallelogram with sides given by a and b, A is its area and R is the angle between a and b.
is a unit vector perpendicular to the parallelogram with sides given by a and b, A is its area and R is the angle between a and b.
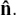 .
.


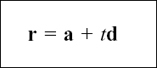


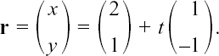

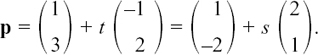


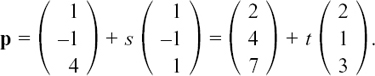

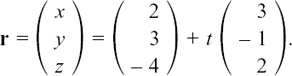

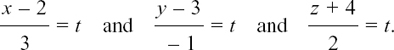
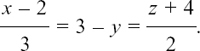
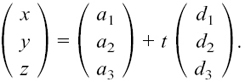

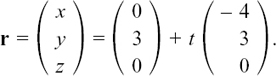
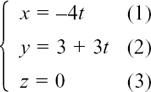



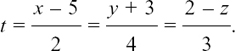
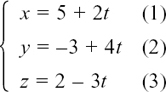
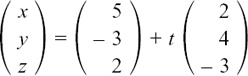



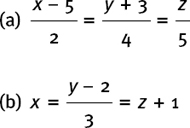



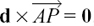




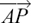
 . You can see why it is useful by looking at
. You can see why it is useful by looking at 

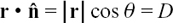 where |D| is the perpendicular distance from the origin to the plane. We write the distance as |D| because distances are always taken as positive. If
where |D| is the perpendicular distance from the origin to the plane. We write the distance as |D| because distances are always taken as positive. If  would be negative since θ, the angle between
would be negative since θ, the angle between 

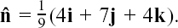 .
.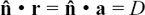
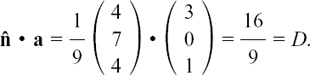

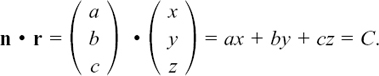


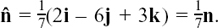 Since
Since  and r • n = 19, we have
and r • n = 19, we have 
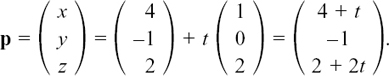






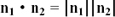

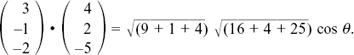

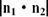
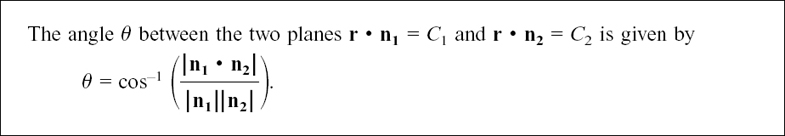

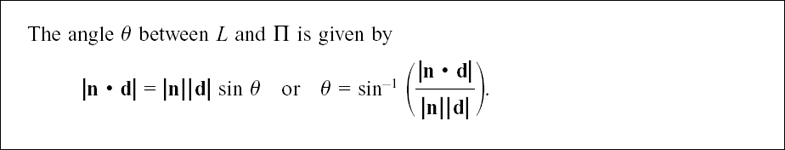

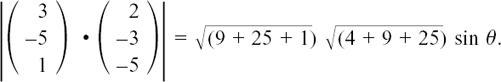
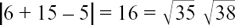


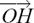

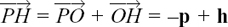

 and 3i + j + 4k must be zero. This gives us
and 3i + j + 4k must be zero. This gives us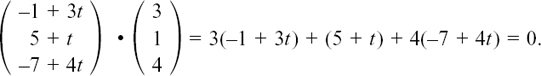
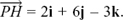
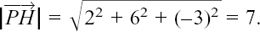

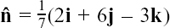 gives us a unit normal vector to the plane.
gives us a unit normal vector to the plane.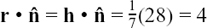

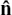 • a. Using column vectors, this is
• a. Using column vectors, this is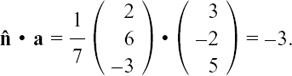
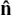
 we found above, with
we found above, with  being positive. Notice that this means that
being positive. Notice that this means that  will give a negative answer since the angle between
will give a negative answer since the angle between  and a is obtuse.
and a is obtuse.


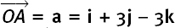
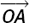
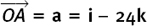
 . I show a sketch of the ray’s path marked with double arrows in
. I show a sketch of the ray’s path marked with double arrows in 
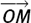
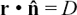


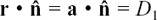

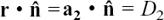 where |D2| is the perpendicular distance of plane Π2 from the origin.
where |D2| is the perpendicular distance of plane Π2 from the origin.