
(a) 8a + b + 3c (1b is written as just b.)
(b) 5ab + 5a + 3b (since ab = ba.)
(c) 5p + 5pq + 8q
(d) 2x + 5y + 3xy
(a) 23 = 8
(b) 5a2 = 5 × 22 = 20
(c) (5a)2 = 102 = 100
(d) 12 = 1
(e) 8 + 3 = 11
(a) 6xy
(b) 15x3y
(c) 6a + 9b
(d) 6a2 + 10ab
(e) 6p3 + 4p2q + 2pq2
(f) 6x3 + 4x3y + 2x2y2
(a) ab + cd = 2 × 3 + 4 × 5 = 6 + 20 = 26
(b) ab2e = 2 × 32 × 0 = 0!
(c) ab2d = 2 × 32 × 5 = 2 × 9 × 5 = 90
(d) (abd)2 = (2 × 3 × 5)2 = 302 = 900
(e) a(b + cd) = 2(3 + 4 × 5) = 2(3 + 20) = 46
(f) ab2d + c3 = 2 × 32 × 5 + 43 = 90 + 64 = 154
(g) ab + d – c = 2 × 3 + 5 – 4 = 6 + 5 – 4 = 7
(h) a(b + d) – c = 2(3 + 5) – 4 = 2 × 8 – 4 = 16 – 4 = 12
(a) 3x(2x + 3y) + 4y(x + 7y) = 6x2 + 9xy + 4xy + 28y2 = 6x2 + 13xy + 28y2
(b) 5p2 (2p + 3q) + q2 (3p + 5q) + pq(p + 2q) = 10p3 + 15p2q + 3pq2 + 5q3 + p2q + 2pq2 = 10p3 + 16p2q + 5pq2 + 5q3
(a) a2 = 32 = 3 × 3 = 9 (b) 3b2 = 3 × 42 = 3 × 16 = 48 (c) (3b)2 = (12)2 = 144
Notice this last pair! Students quite often confuse (b) and (c). In (b), only the b is squared.
(d) c2 = 12 = 1 × 1 = 1 (not 2!)
(e) ab + c = 3 × 4 + 1 = 12 + 1 = 13
(f) bd – ac = 4 × 5 – 3 × 1 = 20 – 3 = 17
(g) b(d – ac) = 4(5 – 3 × 1) = 4(2) = 8
(h) d2 – b2 = 52 – 42 = 25 – 16 = 9
(i) (d – b) (d + b) = (5 – 4) (5 + 4) = 9
(j) d2 + b2 = 52 + 42 = 25 + 16 = 41
(k) (d + b)(d + b) = (5 + 4)(5 + 4) = 9 × 9 = 81
(l) a2 + c2d = 32 × 4 + 12 × 5 = 9 × 4 + 1 × 5 = 36 + 5 = 41
(m) 5e(a2 – 3b2) = 0 since it is all multiplied by 0
(n) ab + da = 34 + 53 = 81 + 125 = 206
(a) 3a(2b + 3c) + 2a(b + 5c) = 6ab + 9ac + 2ab + 10ac = 8ab + 19ac
(b) 2xy(3x2 + 2xy + y2) = 6x3y + 4x2y2 + 2xy3
(c) 5p(2p + 3q) + 2q(3p + q) = 10p2 + 15pq + 6pq + 2q2 = 10p2 + 21pq + 2q2
(d) 2c2(3c + 2d) + 5d2 (2c + d) = 6c3 + 4c2d + 10cd2 + 5d3
(1) 2x – (x – 2y) + 5y = 2x – x + 2y + 5y = x + 7y
(2) 4(3a – 2b) – 6(2a – b) = 12a – 8b – 12a + 6b = –2b
(3) 6(2c + d) – 2(3c – d) + 5 = 12c + 6d – 6c + 2d + 5 = 6c + 8d + 5
(4) 6a – 2(3a – 5b) – (a + 4b) = 6a – 6a + 10b – a – 4b = – a + 6b
(5) 3x(2x – 3y + 2z) – 4x(2x + 5y – 3z) = 6x2 – 9xy + 6xz – 8x2 – 20xy + 12xz = –2x2 – 29xy + 18xz
(6) 2xy(3x – 4 y) – 5xy(2x – y) = 6x2y – 8xy2 – 10x2y + 5xy2 = – 4x2y – 3xy2
(7) 2a2(3a – 2ab) – 5ab(2a2 – 4ab) = 6a3 – 4a3b – 10a3b + 20a2b2 = 6a3 – 14a3b + 20a2b2
(8) –3p – p – q + 2pq – 6q = – 4p – 7q + 2pq
(1) 5(a + 2b)
(2) a(3a + 2b)
(3) 3a(a – 2b)
(4) x(5y + 8z)
(5) 5x(y–2z)
(6) ab(a + 3b)
(7) 2pq(2q–3p)
(8) x2y2 (3y + 5x)
(9) 2pq(2p + q – 3pq)
(10) a2b2(2b + 3a – 6)
(1) (x + 2)(x + 3) = x2 + 2x + 3x + 6 = x2 + 5x + 6
(2) (a + 3)(a – 4) = a2 + 3a – 4a – 12 = a2 – a – 12
(3) (x – 2)(x – 3) = x2 – 2x – 3x + 6 = x2 – 5x + 6
(4) (p + 3)(2p + 1) = 2p2 + 6p + p + 3 = 2p2 + 7p + 3
(5) (3x – 2)(3x + 2) = 9x2 – 6x + 6x – 4 = 9x2 – 4
(6) (2x – 3y)(x + 2y) = 2x2 – 3xy + 4xy – 6y2 = 2x2 + xy – 6y2
(7) (3a – 2b)(2a – 5b) = 6a2 – 4ab – 15ab + 10b2 = 6a2 – 19ab + 10b2
(8) (3x + 4y)2= (3x + 4y)(3x + 4y) = 9x2 + 12xy + 12xy + 16y2 = 9x2 + 24xy + 16y2
(9) (3x – 4y)2= (3x – 4y) (3x – 4y) = 9x2 – 12xy – 12xy + 16y2 = 9x2 – 24xy + 16y2
(10) (3x + 4y) (3x – 4y) = 9x2 + 12xy – 12xy – 16y2 = 9x2 – 16y2
(11) (2p2 + 3pq)(5p + 3q) = 10p3 + 15p2q + 6p2q + 9pq2 = 10p3 + 21p2q + 9pq2
(12) (2ab – b2) (a2 – 3ab) = 2a3b – a2b2 – 6a2b2 + 3ab3 = 2a3b – 7a2b2 + 3ab3
(13) (a + b) (a2 – ab + b2) = a3 – a2b + ab2 + a2b – ab2 + b3 = a3 + b3
(14) (a – b) (a2 + ab + b2) = a3 + a2b + ab2 – a2b – ab2 – b3 = a3 – b3
These last two often have useful applications so I have separated them out.
(15) The answer to (b) comes out as 1 less than the answer to (a) each time.
Using n we have the starting number plus 1 is n + 1 and the starting number minus 1 is n–1.
These two, multiplied together, give (n + 1) (n – 1) which is n2 – 1.
This is 1 less than the starting number squared, and therefore the answer to (b) will always be 1 less than the answer to (a).
(1) (x + 7)(x + 1)
(2) (p + 5)(p + 1)
(3) (x + 6)(x + 1)
(4) (x + 2)(x + 3)
(5) (y + 3)(y + 3) or (y + 3)2
(6) (x + 2)(x + 4)
(7) (a + 2)(a + 5)
(8) (x + 4)(x + 5)
(9) (x + 4)(x + 9)
(1) (3x + 5)(x + 1)
(2) (2y + 1)(y + 7)
(3) (3a + 2)(a + 3)
(4) (3x + 1)(x + 6)
(5) (5p + 3)(p + 4)
(6) (5x + 6)(x + 2)
(1) (x – 3)(x – 8)
(2) (y – 3)(y – 6)
(3) (x – 2)(x – 9)
(4) (p –3)(p + 8)
(5) (x – 2)(x + 6)
(6) (2q + 1)(q – 3)
(7) (3x +2)(x – 4)
(8) (2a – 5)(a + 1)
(9) (2x + 3)(x – 4)
(10) (3b – 2)(b – 6)
(11) (3x – 5y)(3x + 5y)
(12) (4x2 – 9y2)(4x2 + 9y2) = (2x – 3y)(2x + 3y) (4x2 + 9y2)
The 4x2 + 9y2 won’t factorise any further.
(a) They are all equivalent except for  and
and 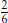 .
.
(b) They are all equivalent.
(c) The middle one is the odd one out.
(d) The first two are equivalent because the z cancels, but it isn’t possible to cancel the p in the last one.
(d) No simplification is possible.
(g) No simplification is possible.
(Notice, there was a common factor of 3 on the bottom.)
(4) There is a common factor of (2x – y) on the bottom. So you should have

(5) There is a common factor of x on the bottom, so we can say
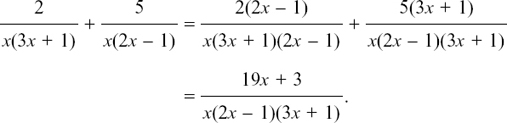
(6) There is a hidden common factor of (x + y) so we get

or you can write this as

I shall put in all the brackets from the start in these answers.
(1) The x underneath is a common factor, so
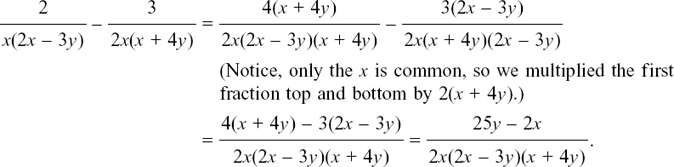
When the two fractions are combined, the top has two chunks which are subtracted. This has been tidied up by multiplying out the brackets, and then putting together as much as possible. The bottom, with the brackets multiplied, is already in a neat factorised form, and so we generally leave it this way.
(2) First, we put in the brackets and get

 dividing top and bottom by 3b.
dividing top and bottom by 3b.
dividing top and bottom by xyz.
It is quicker to do the cancelling before the multiplying (which you can show by crossing through the same factors above and below, if you like).
Then you can leave out the second step of the above working.
But you must remember that only factors of the whole of the top and bottom can be cancelled.
Don’t be tempted to cancel the 5s!
Exercise 1.D.1
Exercise 1.F.1
(1) 10111 = 1 + 1(21) + 1(22) + 0(23) + 1(24) = 1 + 2 + 4 + 16 = 23
(2) 1111 = 1 + 1(21) + 1(22) + 1(23) = 1 + 2 + 4 + 8 = 15
(3) 111011 = 1 + 1(21) + 0(22) + 1(23) + 1(24) + 1(25) = 1 + 2 + 8 + 16 + 32 = 59

During this working we have used the fact that 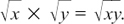 An example of this is
An example of this is  which is the same as 2 × 3 = 6.
which is the same as 2 × 3 = 6.
|
|
(1) x + 8 = 5 so x = 5 – 8 = –3.
(2) 5y = 40 so  = 8.
= 8.
(3) 2y = 7 so 
(4) 7 + 2x = 5 – x so 2x + x = 5 – 7 so 
(5) 4 + 2b = 5b + 9 so 4 – 9 = 5b – 2b so –5 = 3b and 
(6) 3(x – 3) = 6 so 3x – 9 = 6 so 3x = 15 and x = 5.
(7) 3(y – 2) = 2(y – 1) so 3y – 6 = 2y – 2 so 3y – 2y = –2 + 6 so y = 4.
(8) 2(3a – 1) = 3(4a + 3) so 6a – 2 = 12a + 9 so – 2 – 9 = 12a – 6a so – 11 = 6a and 
(9) 3x – 1 = 2(2x – 1) + 3 so 3x – 1 = 4x – 2 + 3 so – 1 – 1 = 4x – 3x so x = –2.
(10) 2(p + 2) = 6p – 3(p – 4) so 2p + 4 = 6p – 3p + 12 so 4 – 12 = 3p – 2p and p = –8.
 so, multiplying by 3, 15 + 3x = 2x and x = –15.
so, multiplying by 3, 15 + 3x = 2x and x = –15.
(3) Multiplying both sides of 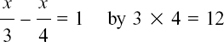 gives
gives
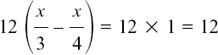 so 4x – 3x = 12 and x = 12.
so 4x – 3x = 12 and x = 12.
(4) Start by putting in the two brackets, so you have 
Multiply by 30 to get rid of fractions (notice you don’t need to use 90).
Then 10y – 6(3y – 7) = 5(y – 2) so 10y – 18y + 42 = 5y – 10 so 52 = 13y and y = 4.
(5) First, put in brackets to give 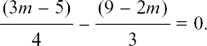
Then multiply by 12 to give 3(3m – 5) – 4(9 – 2m) = 0 (not = 12!) so 9m – 15 – 36 + 8m = 0 so 17m = 51 and m = 3.
 Putting in brackets and multiplying both sides by 6 gives
Putting in brackets and multiplying both sides by 6 gives
 so 3(x – 1) – 2(x –2) = 6
so 3(x – 1) – 2(x –2) = 6
so 3x – 3 – 2x + 4 = 6 and x = 5.
 Multiplying both sides by 4(p – 1), and cancelling, gives
Multiplying both sides by 4(p – 1), and cancelling, gives
4(p + 1) = 3(p – 1) so 4p + 4 = 3p – 3 and p = –7.
 Multiplying both sides by y(y + 1), and cancelling, gives
Multiplying both sides by y(y + 1), and cancelling, gives
2(y + 1) = 3y so 2y + 2 = 3y and y = 2.
 Multiplying both sides by (2x + 3) (x – 2), and cancelling, gives
Multiplying both sides by (2x + 3) (x – 2), and cancelling, gives
4(x – 2) = 3(2x + 3) so 4x – 8 = 6x + 9 so -17 = 2x and x = –y.
 To get rid of fractions, we must multiply by (x + 2)(x + 5).
To get rid of fractions, we must multiply by (x + 2)(x + 5).
Then, cancelling, we get
2x(x + 5) = 3x(x + 2) – (x + 2) (x + 5).
(Notice that the –1 has also been multiplied by (x + 2)(x + 5).)
So 2x2 + 10x = 3x2 + 6x – (x2 + 7x + 10) = 3x2 + 6x – x2 – 7x – 10
so 11x = –10 and 
We get rid of the fractions first by multiplying both sides by 3 × 2 × 7 = 42.
We have
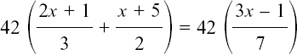
so
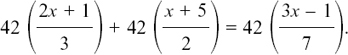
Notice that each separate chunk of the equation is getting multiplied by the 42.
We then cancel down each fraction in turn to obtain
14(2x + 1) + 21(x + 5) = 6(3x – 1)
28x + 14 + 21x + 105 = 18x – 6
28x + 21x – 18x = –14 – 105 – 6
so 31x = –125 giving 
 Putting in brackets and multiplying by 20 gives
Putting in brackets and multiplying by 20 gives

so 5(x + 3) –4(x – 1) = 2(2x – 1) so 21 = 3x giving x = 7.
(1)  so
so 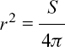 and
and 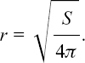
(b) V = πr2h so  and
and 
(c) S = 2πr2 + 2πrh so S – 2πr2 = 2πrh and 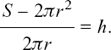
(a) v2 = u2 + 2as so v2 – u2 = 2as and 
(b) v2 = u2 + 2as so v2 – 2as = u2 and 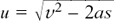
Multiplying by R R1 R2 to get rid of the fractions, we get
R1 R2 –RR2 = RR1 so R2(R1 – R) = RR1 and 
If R1 = 3 and R = 2 we have R2 = 6. We should use a resistance R2 of 6Ω.
Exercise 2.B.1
(1) m = –5
(2)  so
so 
(3) 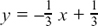 so
so 
(4)  so
so 
(1) Sketch (c)
(2) Sketch (b): y + 4x = 4 so y =–4x + 4.
(3) Sketch (a): 4y = x + 4 so 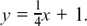
(4) Sketch (e)
(5) Sketch (h)
(6) Sketch (g)
(7) Sketch (d)
(8) Sketch (f): y + 2x =–2 so y = –2x – 2.
Notice that appearances can be deceptive. For example, (c), (d) and (h) all look the same until you take account of the different scales marked on the axes. Exercise 2.B.4, 2.B.5 and 2.B.6 all have answers given after Self-test 4.
(1) The coordinates are  = (3,10).
= (3,10).
(2) The coordinates are 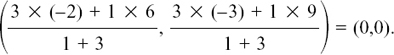
Multiplying (2) by 2 gives |
||
|
Adding (1) and (3) gives lla = 88 so a = 8. Substituting in (1) gives 40 – 2b = 68 so b = –14. Check in (2): LHS = 24 – 14 = 10 = RHS. |
|
Multiplying (1) by 5 and (2) by 2 gives |
||
|
Adding (3) and (4) gives 29p = 29 so p = 1. Substituting in (1) gives 5 –2q = 9 so q = –2. Check in (2): LHS = 2 –10 = –8 = RHS. |
|
First, get rid of fractions by writing 8 × (1)and 3 × (2). |
||
|
This gives |
|
|
Multiplying (4) by 8 gives |
|
|
Adding (3) and (5) gives 73x = 292 so x = 4. |
|
|
Substituting in (2) gives 12 + y/3 = 13 so y/3 = 1 and y = 3. |
|
|
Check in (1): LHS = |
|
Use the same trick which we met earlier of letting |
||
|
Then we have: |
|
|
Multiplying (4) by 2 we have |
|
|
Adding these two gives 7X = 14 so X = 2. |
|
|
Substituting in (3) gives 6 + 4Y = 0 so |
|
|
Check in (1): LHS = |
(1) x2 + 9x + 14 = (x + 2)(x + 7) = 0 so x = –2 or x = –7.
(2) x2 + 4x – 12 = (x – 2)(x + 6) = 0 so x = 2 or x = –6.
(3) x2 – 11x + 18 = (x – 2)(x – 9) = 0 so x = 2 or x = 9.
(4) x2 – x – 20 = (x + 4) (x – 5) = 0 so x = –4 or x = 5.
(5) 2x2 + 13x + 6 = (2x + 1)(x + 6) = 0 so x = –1 2 or x = –6.
(6) 3x2 – 7x – 6 = (3x + 2)(x – 3) = 0 so x = –2 3 or x = 3.
(1) x = ±3
(3) x – 3 = ±2 so x = + 1 or x = +5
(4) 2x – 3 = ±5 so x = 4 or x = –1.
(5) 3x – 2 = ±6 so 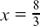 or x =
or x = 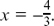
(1) x2 + 4x = 21 so (x + 2)2 – 4 = 21 so (x + 2)2 = 25 so x + 2 = ±5 and x = 3 or x = –7.
(2) x2 – 6x + 8 = 0 so x2 – 6x = – 8 so (x – 3)2 – 9 = – 8 so (x – 3)2 = 1 so x – 3 = ±1 and x = 4 or x = 2.
(3) x2 – 3x – 10 = 0 so x2 – 3x = 10 so 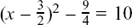 so
so 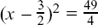 so
so  and x = 5 or x = –2.
and x = 5 or x = –2.
(1) y = x2 – 4x + 3 = (x – 2)2 – 1 so the least value of y is –1 which is when x = 2, that is, the lowest point on the curve is at (2, –1).
The y-intercept is (0,3).
When y = 0, (x – 2)2 – 1 = 0 so x – 2 = ±1 and x = 3 or 1.
Therefore the equation x2 – 4x + 3 = 0 has the two roots x = 1 and x = 3, so the curve y = x2 – 4x + 3 cuts the x-axis at (0.1) and (0,3).
Curve (b) is just curve (a) turned upside down by being reflected in the x-axis, since the sign for y is just the opposite way round.
The sketch for this question is shown beside the one for question (2) below.
(2) y= x2 + 2x – 8 = (x+ 1)2 – 1 – 8 so the least value of y is –9 when x = –1. The lowest point on the curve is at (–1, –9). The y-intercept is (0, –8). When y= 0, (x + 1)2– 9 = 0 so (x+ 1)2= 9 and x + 1 = ±3. The roots of x2+ 2x– 8 = 0 are x = 2 and x = –4, and the curve y = x2+ 2x – 8 cuts the x-axis at (–4, 0) and (2, 0). Again, curve (b) is just curve (a) turned upside down.

(a) 2x2 + 7x + 3 = 0 so (2x + 1)(x + 3) = 0 and  or –3.
or –3.
(b) 3x2 + 4x + 1 = 0 so (3x + 1)(x + 1) = 0 and  or x = –1.
or x = –1.
(c) 2x2 + x – 4 = 0 gives ‘b2 – 4ac’ = 1 – 4 × 2 × –4 = 33
so there is no whole number factorisation.
Using the formula, we have  or –1.686 to 3 d.p.
or –1.686 to 3 d.p.
(d) 6x2 – 7x + 2 = 0 so (2x – 1)(3x – 2) = 0 and  or
or 
(e) x2 – 5x + 3 = 0 gives ‘b2 – 4ac’ = 25 – 12 = 13
so there is no whole number factorisation.
Using the formula, we have 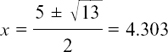 or 0.697 to 3.d.p.
or 0.697 to 3.d.p.
(f) 6x2 + 5x – 6 = 0 so (3x – 2)(2x + 3) = 0 and 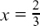 or
or 
(g) x2 – 81 = 0 so (x – 9)(x + 9) = 0 and x = 9 or x = –9.
Or, you could say, x2 = 81 so x = ±9.
(h) 6x2 – x – 12 = 0 so (3x + 4)(2x – 3) = 0 and  or
or 
(i) x2 – 2 = 0 so x2 = 2 and  = ±1.414 to 3.d.p.
= ±1.414 to 3.d.p.
Or, you could say  , factorising, which gives the same pair of answers as above.
, factorising, which gives the same pair of answers as above.
(j) Factorising x2 – 5x = 0 we have x(x – 5) = 0 so x = 0 or x = 5.
|
Don’t be tempted to divide x2 – 5x = 0 through by x. If you do this, you lose the possible answer of x = 0. When x = 0, this division is actually impossible because we cannot divide by zero. |
In all the questions above, where I have used factorisation, it is equally acceptable if you got your answers by using the formula.
Getting rid of fractions by multiplying by (2x + 3)(x + 1), we have
(2x – 3)(x + 1) = (2x + 3)(x – 1) so 2x2 – x – 3 = 2x2 + x – 3
so 0 = 2x so x = 0.
Getting rid of fractions by multiplying by y(y + 1)(y – 1), we have:
2y(y – 1) + y(y + 1) = 3(y + 1)(y – 1) so 2y2 – 2y + y2 + y = 3y2 – 3
so y = 3.
Getting rid of fractions by multiplying by (x + 1) (2x – 1), we have:
4x2 + 6x – 4 = x2 – 7x – 8 so 3x2 + 13x + 4 = 0
so (3x + 1) (x + 4) = 0 so x = – 3 or x = –4.
The sketches fit to the given equations as follows.
(1) Sketch (e)
(4) Sketch (d)
(6) Sketch (c)
(7) Sketch (b)
(8) Sketch (f)
(10) Sketch (a)
The sketches for equations (2), (3), (5) and (9) are shown below.
Exercise 2.E.1
(1) y = f(x) = 3x3 + 2x2 – 3x – 2
Guessing and substitution show that f (1) = 0 so (x – 1) is a factor, and f (–1) = 0 so (x + 1) is a factor.
Matching up the two sides, we have
f (x) = 3x3 + 2x2 – 3x – 2 = (x – 1)(x + 1)(3x + 2).
The roots of f(x) = 0 are 1, –1 and  . The y intercept is at (0, –2).
. The y intercept is at (0, –2).
The coefficient of x3 is positive, so we have graph 1 below.

(2) y = f (x) = 2 + 3x – 3x2 – 2x3
Guessing and substitution show that f(1) and f(–2) = 0 so (x – 1) and (x + 2) are both factors.
Matching up the two sides, we have
f(x) = 2 + 3x – 3x2 – 2x3 = (x – 1) (x + 2)(–2x – 1) = –(2x + 1)(x – 1)(x + 2)
taking out a factor of –1.
The roots of f(x) = 0 are 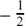 , 1 and –2, and the y intercept is at (0, 2).
, 1 and –2, and the y intercept is at (0, 2).
The coefficient of x3 is negative so we have graph 2 on the previous page.
(3) y = f(x) = 4x3 – 15x2 + 12x + 4
Guessing and substitution give f(2) = 0 so (x – 2) is a factor. There is no obvious second root so matching up the two sides, we have
f(x) = 4x3 – 15x2 + 12x + 4 = (x – 2)(4x2 + px – 2).
Matching the terms in x2 gives –15x2 = –8x2 + px2, so p = –7.
Checking, using the terms in x, gives 12x = –2px – 2x, so p = –7 is correct.
Therefore
f (x) = (x – 2) (4x2 – 7x – 2) = (x – 2)(x – 2)(4x + 1),
factorising the second bracket.
We see that f (x) = 0 has the root 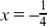 and the double repeated root of x = 2. Just as we found with quadratic equations, this means that the curve of y = f(x) touches the x-axis when x = 2.
and the double repeated root of x = 2. Just as we found with quadratic equations, this means that the curve of y = f(x) touches the x-axis when x = 2.
The y intercept is at (0,4) and the coefficient of x3 is positive, so we get graph 3 below.

(4) y = f(x) = x3 – 3x2 + 3x – 1
Guessing and substituting shows that f(1) = 0, so (x – 1) is a factor, and there is no obvious second root.
Matching up the two sides gives
x3 – 3x2 + 3x – 1 = (x – 1)(x2 + px + 1).
Matching up the terms in x2 gives
–3x2 = –x2 + px2, so p = -2.
Checking, using the terms in x, gives 3x = x – px, so p = –2 is correct. Therefore,
y = f(x) = (x – 1)(x2 – 2x + 1) = (x – 1)(x – 1)2 = (x – 1)3.
This time, we have a single triply repeated root at x = 1. The y intercept is at (0, – 1).
The coefficient of x3 is positive, so we get graph 4 above.
If you look at this on a graph-sketching calculator, or plot values close to x = 1 for yourself, you will see that the curve flattens near x = 1 where the three roots are all bunched together.
(1) f(x) = x3 + 2x2 – 5x – 6 so f(2) = 8 + 8 – 10 – 6 = 0.
Therefore (x – 2) is a factor and we have x3 + 2x2 – 5x – 6 = (x – 2)(x2 + px + 3).
Matching the term in x2 gives 2x2 = –2x2 + px2, so p = 4.
Checking, using the term in x gives –5x = –2px + 3x, so p = 4 is correct.
So f(x) = (x – 2)(x2 + 4x + 3) = (x – 2)(x + 1)(x + 3), factorising the second bracket.
(2) f(x) = 2x3 – 3x2 – 8x – 3 so f (3) = 54 – 27 – 24 – 3 = 0, so (x – 3) is a factor.
We have 2x3 – 3x2 – 8x – 3 = (x – 3)(2x2 + px + 1).
Matching up the terms in x2 gives –3x2 = –6x2 + px2, so p = 3.
Checking with the term in x gives – 8x = –3px + x, so p = 3 is correct.
So f(x) = (x – 3)(2x2 + 3x + 1) = (x – 3)(2x + l)(x + 1), factorising the second bracket.
(3) f(x) = 3x3 + x2 – 12x – 4
Testing some values for x, we find that f(2) = 24 + 4 – 24 – 4 = 0, so (x – 2) is a factor. We have 3x3 + x2 – 12x – 4 = (x – 2)(3x2 + px + 2).
Matching up the terms in x2 gives x2 = –6x2 + px2, so p = 7.
Checking, using the term in x, gives –12x = –2px + 2x, so p = 7 is correct.
So f(x) = (x – 2)(3x2 + 7x + 2) = (x – 2)(3x + 1)(x + 2), factorising the second bracket.
Therefore the solutions of f(x) = 0 are x = 2,  and x = –2.
and x = –2.
(4) f(x) = 2x3 + 7x2 + 2x – 3
Testing some values, we find f(–1) = –2 + 7 – 2 – 3 = 0, so (x + 1) is a factor. We have 2x3 + 7x2 + 2x – 3 = (x + 1)(2x2 + px – 3).
Matching up the terms in x2 gives 7x2 = 2x2 + px2, so p = 5
Checking, using the terms in x, gives 2x = px – 3x, so p = 5 is correct.
So f(x) = (x + 1)(2x2 + 5x – 3) = (x + l)(2x – l)(x + 3), factorising the second bracket.
Therefore the solutions of f(x) = 0 are x = –1, and x = –3.
and x = –3.
(5) x4 – 29x2 + 100 = 0.
We have a quadratic equation in a beard and dark glasses.
Putting y = x2, we have y2 – 29y + 100 = 0 so (y – 25)(y – 4) = 0.
So y = 25 which means that x2 = 25, so x = ±5, or y = 4 which means that x2 = 4, so x = ±2.
(6) We have f(x) = 5x3 + ax2 + bx – 6. (x – 3) is a factor, so f(3) = 0.
This gives 135 + 9a + 3b – 6 = 0. Therefore
9a + 3b = – 129 so 3a + b = –43. |
(1) |
Also,
f(–2) = –40 so –40 + 4a – 2b – 6 = –40 so 2a – b = 3. |
(2) |
(1) added to (2) gives 5a = –40 so a = –8.
Substituting in (1) gives –24 + b = –43 so b = –19.
So 5x3 – 8x2 – 19x – 6 = (x – 3) (5x2 + px + 2).
Matching terms in x2 gives –8x2 = – 15x2 + px2, so p = 1.
Checking with the term in x gives –19x = –3px + 2x, so p = 7 is correct.
5x2 + 7x + 2 = (5x + 2)(x + 1) therefore f(x) = (x – 3)(5x + 2)(x + 1).
(7) The working for the long division is shown below.

Since the division process leaves no remainder, (3x – 2) is a factor of 12x3 + 4x2 – 17x + 6.
Alternatively, substituting 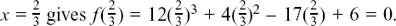
(8) The working for the long division is shown below.

Alternatively, putting 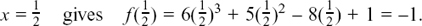
Exercise 3.A.1
(1) In (a), the volumes are directly proportional to the heights, therefore
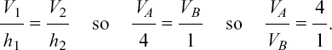
We can see that the volume of A is 4 times the volume of B.
In (b), the volumes are directly proportional to the (radius)2, therefore
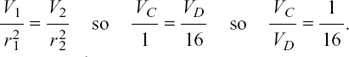
Cylinder C has  of the volume of cylinder D.
of the volume of cylinder D.
(2) The kinetic energy is directly proportional to the (speed)2, therefore

(3) The volume is directly proportional to the (radius)3, therefore
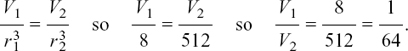
(4) The time of the swing is directly proportional to the square root of the length, therefore

The time of swing of the first pendulum is  of the time of swing of the second pendulum.
of the time of swing of the second pendulum.
Here are the functions which you should have found.
(b) shows f(x) + 2. |
(c) shows f(x) – 2. |
|
(b) shows g(x + 2). |
(c) shows g(x – 2). |
Because we know a = 2, it must be a sideways shift which is happening in these two diagrams.
(b) shows 2h(x). |
(c) shows h(2x). |
|
(b) shows p(x) + 2. |
(c) shows p(x + 2). |
Exercise 3.B.2
(a) f (g(x)) = f(2x) = 3(2x) – 5 = 6x – 5 (b) g(f(x)) = g(3x – 5) = 2(3x – 5) = 6x – 10
(a) f (g(x)) = f (4 – x) = (4 – x)2 (b) g(f(x)) = g(x2) = 4 – x2
(a) f (g(x)) = f (x – 4) 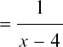 , x ≠ 4 (b) g(f(x)) = g(1/x) = 1/x – 4, x ≠ 0
, x ≠ 4 (b) g(f(x)) = g(1/x) = 1/x – 4, x ≠ 0
If you are in doubt about any of these, replace x by ‘lump’ in the definition of the function to see what is happening. Notice that, in (3), we have to exclude the two values of x which would result in trying to divide by zero.
(1) f–1 (x) = 
(2) f–1 (x) = x + 9
(3) y = 5x – 9 so y + 9 = 5x and  so f– 1 (x) =
so f– 1 (x) = 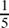 (x + 9).
(x + 9).
(4) f(x) is self-inverse so f– 1 (x) = 8 – x.
(5) f– 1 (x) = 4x
(6) f(x) is self-inverse so f–1 (x) = 4/x
(7) y = 3 – 2x so 2x = 3 – y and 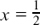 (3 – y) so f– 1 (x) =
(3 – y) so f– 1 (x) = 
(8) Let  so xy + 2y = x – 3 so 3 + 2y = x – xy = x(1 – y).
so xy + 2y = x – 3 so 3 + 2y = x – xy = x(1 – y).
Notice the cunning choice of sides here to avoid lots of minuses. This gives

 so xy – 2y = 2x + 3 so xy – 2x = 2y + 3
so xy – 2y = 2x + 3 so xy – 2x = 2y + 3
so x(y – 2) = 2y + 3 so 
We see that this particular f(x) is self-inverse.
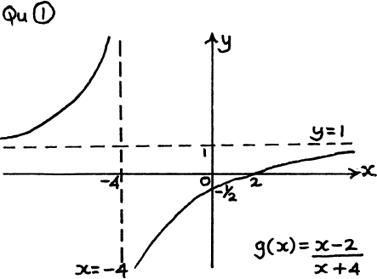
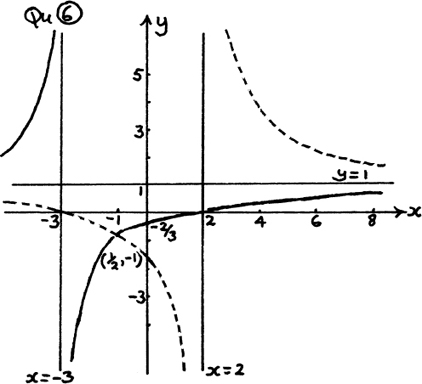
(1) The facts we need for the graph sketch are as follows:
(a) g(x) = 0 when x = 2. (b) When x = 0, 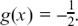
(c) The value of g(x) is very large and positive if x is just less than –4.
The value of g(x) is very large and negative if x is just greater than –4.
so, as x becomes large, the value of g(x) approaches 1, since both 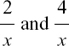
become smaller and smaller.
The sketch is given in graph 1 below.
The working for the inverse function goes as follows.

(2) The facts we need for the graph sketch are as follows:
(a) h(x) = 0 when  (b) When x = 0, h(x) = –5.
(b) When x = 0, h(x) = –5.
(c) The value of h(x) is very large and positive if x is just less than –1.
The value of h(x) is very large and negative if x is just greater than –1.
(d) As x becomes large, the value of h(x) approaches 2, because
 and both 5/2x and 1/x become very small.
and both 5/2x and 1/x become very small.
The sketch is shown in graph 2 below.

The working for the inverse function is as follows.
 so xy + y = 2x – 5 so y + 5 = 2x – xy = x(2 – y)
so xy + y = 2x – 5 so y + 5 = 2x – xy = x(2 – y)
so 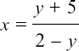 and
and 
Check: and
and 
(3) I show the sketch for  below.
below.
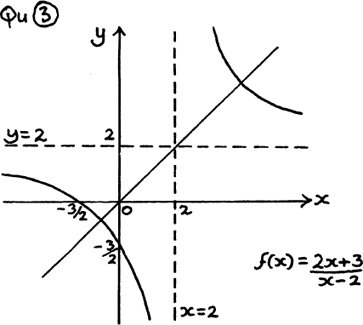
You can see that it is self-inverse because it is symmetrical about the line y = x.
(a) 4 = 22 so log2 4 = 2.
(b) 8 = 23 so log2 8 = 3.
(c) 2 = 21 so log2 2 = 1.
(d) 1 = 2° so log2 1 = 0.
(a) 9 = 32 so log3 9 = 2.
(b) 81 = 34 so log3 (81) = 4.
(e) 1 = 3° so log3 1 = 0.
(f) 3 = 31 so log3 3 = 1.
(h) 27 = 23 so log3 (27) = 3.
(a) 100 = 102 so log10 (100) = 2.
(b) 1000 = 103 so log10 (1000) = 3.
(c) 10 = 101 so log10 (10) = 1.
(d) 1 = 10° so log10 (1) = 0.
(f) 0.01 = 10–2 so log10 (0.01) = –2.
(a) log3 3x = log3 3 + log3 x = 1 + log3 x.
(b) log3 27x2 = log3 27 + log3 x2 = log3 33 + log3 x2 = 3 + 2 log3x.
(c) log3 (x/y) = log3 x – log3 y.
(d) log3 (x2/a2) = log3 x2 – log3 a2 = 2 log3x – 2 log3 a.
(e) log3 (axn) = log3a + log3 (xn) = log3 a + n log3 x.
(f) log3 (9ax) = log3 9 + log3 (ax) = log3 32 + x log3 a = 2 + x log3 a.
(g) There is no possible change here.
(a) log10 x + log10 (x – 1) = log10 (x2 – x).
(b) 2 log10 x – log10 y = log10 (x2) – log10 y = log10 (x2/y).
(c) log10 (x + 1) – log10 (x – 1) = log10 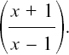
(d) 3 log10 x + 2 log10 y = log10 (x3) + log10 (y2) = log10 (x3 y2).
Exercise 4.A.1
The following are the answers to part (A).
 so x = 8 sin34° = 4.47 cm to 2 d.p.
so x = 8 sin34° = 4.47 cm to 2 d.p.
(2) tan 38° =  so y = 5 tan 38° = 3.91 cm to 2 d.p.
so y = 5 tan 38° = 3.91 cm to 2 d.p.
(3) cos 72° =  so x = 15 cos 72° = 4.64 cm to 2 d.p.
so x = 15 cos 72° = 4.64 cm to 2 d.p.
(4) tan 54° =  so x =
so x =  = 4.36 cm to 2 d.p.
= 4.36 cm to 2 d.p.
(5) cos 48° =  so x =
so x =  = 4.48 cm to 2 d.p.
= 4.48 cm to 2 d.p.
(6) sin 28° =  so y =
so y = 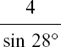 = 8.52 cm to 2 d.p.
= 8.52 cm to 2 d.p.
These are the answers to part (B).
(1) tan a = so a = 60.3° to 1 d.p.
so a = 60.3° to 1 d.p.
(2) sin b = – so b = 38.7° to 1 d.p.4
– so b = 38.7° to 1 d.p.4
(3) cosc = so c = 48.2° to 1 d.p.
so c = 48.2° to 1 d.p.
(4) sin d =  so d = 53.1° to 1 d.p.
so d = 53.1° to 1 d.p.
Calling the length of the unknown side x in each case, the answers are as follows:
(1) x2 = 42 + 72 = 16 + 49 = 65 so x = 8.06 to 2 d.p.
(2) 82 = 52 + x2 so x2 = 64 – 25 = 39 and x = 6.24 to 2 d.p.
(3) 92 = x2 + 62 so x2 = 81 – 36 = 45 and x = 6.71 to 2 d.p.
(4) 102 = 82 + d2 so d2 = 100 – 64 = 36 and d = 6.
Exercise 4.B.1
(1) First, show the information on a sketch like the one below.

Then ∠C = 180° − 78° − 65° = 37°.
Also  so
so  = 8.13 cm. to 2 d.p.
= 8.13 cm. to 2 d.p.
And  so
so  = 7.53 cm. to 2 d.p.
= 7.53 cm. to 2 d.p.
(2) First, we draw a sketch, which I’ve done below.
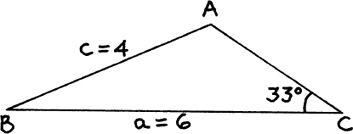
Now we can say
 so sin A
so sin A  so A = 54.7(8)° = 54.8° to 1 d.p.
so A = 54.7(8)° = 54.8° to 1 d.p.
The only problem is that this looks wildly improbable from the sketch above, but the sketch does seem to fit the known facts quite well. What has gone wrong?
In fact, as you may already have realised, the known facts fit two possible triangles. Can you draw them both?

I’ve drawn sketches for both of them below in (a) and (b).
(I cheated by only giving one of them in my solution above; you may either have spotted the snag, or have sketched (b), or sketched (a) as I did.)
In (b), I have drawn a dotted line showing where the side AB of (a) would come, so you can see how it has been swung round from B to give the other possible position.

Now you have the right-hand sketch, you can see that the other possible answer for ∠A is 180° – 54.78° = 125.2° to 1 d.p. and this is the value for triangle (a).
Your calculator will give you identical values for the sin of 54.8° and 125.2°.
How it is actually possible to have the sin of an angle greater than 90° will be explained later, in Section 5.A.(c).
Next, we find the other measurements for each triangle in turn.
In ΔABC (a), ∠B = 180° − 33° − 125.22° = 21.78° = 21.8° to 1 d.p.
and  so b = 2.73 cm to 2 d.p.
so b = 2.73 cm to 2 d.p.
(working with 2 d.p. to avoid rounding errors in the answer).
In ΔABC (b), ∠B = 180° − 33° − 54.78° = 92.22° = 92.2° to 1 d.p.
and 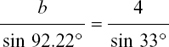 so b = 7.34 cm to 2 d.p.
so b = 7.34 cm to 2 d.p.
The two sets of answers now fit the two drawings in believable ways.
We met just this same situation of ambiguous information giving us two possible triangles in case (4) of Section 4.A.(e) on congruent triangles.
(3) First we draw a sketch like the one below.

This time, there is only one possible diagram because if we swing AB around B it only cuts AC again the other side of C. Now
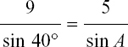 so sin A
so sin A  so A = 20.9(2)° to 1 d.p.
so A = 20.9(2)° to 1 d.p.
making a note of the second decimal place for use in further calculations. Therefore B = 180° – 40° – 20.92° = 119.08° = 119.1° to 1 d.p.
Assuming from question (2) that it’s all right to use sin 119.08° from your calculator to find b, you get
 so b =
so b = 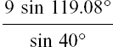 = 12.24 cm to 2 d.p.
= 12.24 cm to 2 d.p.
Exercise 4.B.2
(b) a2 = b2 + c2 − 2bc cos A = 25 + 64 − 80 cos 72° so a = 8.02 units to 2 d.p.
(iii) ∠C = 180° − 123.20° − 40.60° = 16.2° to 1 d.p.
(b) ∠QPR = 120°

so cos 120° = −  = − cos 60°
= − cos 60°
so sin 120° =  = sin 60°
= sin 60°
Exercise 4.C.1
(1) The centre is at (1, –2) and the radius is 4 units.
(2) x2 – 2x + y2 – 4y = 0 = (x – 1)2 – 1 + (y – 2)2 – 4 so (x – 1)2 + (y – 2)2 = 5.
The centre is at (1,2) and the radius is  units.
units.
(3) x2 – 8x + y2 + 7 = 0 = (x – 4)2 – 16 + y2 + 7 so (x – 4)2 + y2 = 9.
The centre is at (4,0) and the radius is 3 units.
(4) x2 – 6x + y2 + 2y – 6 = 0 = (x – 3)2 – 9 + (y + 1)2 – 1 – 6 so (x – 3)2 + (y + 1)2 = 16.
The centre is at (3, – 1) and the radius is 4 units.
The centre is at  and the radius is
and the radius is  units.
units.
(6) x2 + 3x + y2 + 2y + 1 = 0
so 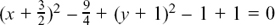 so
so 
The centre is at  and the radius is
and the radius is  units.
units.
(7) The circle x2 + y2 + 2x – 4y = 0 can be rewritten as (x + 1)2 + (y – 2)2 = 5 so its centre is at the point (–1, 2).
This is also the centre of the new circle, but the radius of the new circle is 5 units. Therefore its equation is (x + 1)2 + (y – 2)2 = 52 or x2 + 2x + y2 – 4y = 20.
(8) The equation of the circle is x2 – 2ax + y2 – 2by + c = 0.
It passes through the point (0,0), therefore putting x = 0 and y = 0 must satisfy its equation. Doing this gives us c = 0.
The point (3,0) also lies on the circle. Putting x = 3 and y = 0 gives 9 – 6a = 0 so  .
.
The point (0,4) also lies on the circle. Putting x = 0 and y = 4 gives 16 – 8b = 0 so b = 2. Therefore the equation of the circle is x2 – 3x + y2 – 4y = 0.
Rewriting the equation as  by completing the squares, gives its centre as the point
by completing the squares, gives its centre as the point 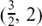 and its radius as
and its radius as  units.
units.
There is also a neat geometrical way to do this question.
The sketch below shows the three points A, O and B which the circle must pass through. Now, ∠AOB = 90° so it is an angle in a semicircle (Section 4.C.(c)) so AB is a diameter of the circle. Therefore, the centre C must be the point 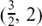 and the radius must be
and the radius must be  units, since the length of AB is 5 units by Pythagoras’ Theorem.
units, since the length of AB is 5 units by Pythagoras’ Theorem.
This then gives us the same equation as the method using algebra.

Putting x = 3y + 5 in the equation of the circle gives
(3y + 5)2 – 6(3y + 5) + y2 – 2y + 5 = 0
so 9y2 + 30y + 25– 18y – 30 + y2 – 2y + 5 = 0.
Therefore 10y2 + 10y = 0 so y2 + y = 0 so y(y + 1) = 0 so y = 0 or y = –1.
|
Remember not to divide through by y in the equation above of y2 + y = 0. If you do this, you lose the answer of y = 0 (for which this division would have been impossible). |
If y = 0 then x = 5 and if y = –1 then x = 2 so the line 3y = x – 5 cuts the given circle at the two points (5, 0) and (2, –1).
(b) Substituting x = 2y – 4 in the equation of the circle gives
(2y – 4)2 – 6(2y – 4) + y2 – 2y + 5 = 0
So 4y2 – 16y + 16 – 12y + 24 + y2 – 2y + 5 = 0 so 5y2 – 30y + 45 = 0
so y2 – 6y + 9 = 0 so (y – 3)2 = 0.
The repeated root of y = 3 shows that the line 2y = x + 4 is a tangent to the circle. When y = 3, x = 2 so its point of contact is (2, 3).
(c) Substituting y = 2x + 3 in the equation of the circle gives
x2 – 6x + (2x + 3)2 – 2(2x + 3) + 5 = 0
so x2 – 6x + 4x2 + 12x + 9 – 4x – 6 + 5 = 0 so 5x2 + 2x + 8 = 0.
Putting a = 5 and b = 2 and c = 8 and using the quadratic equation formula gives b2 – 4ac = 22 – 160 = –156.
Therefore this equation has no real roots and the line y = 2x + 3 does not cut this circle at all.
For the sketch, we write x2 – 6x + y2 – 2y + 5 = 0 as (x – 3)2 + (y – 1)2 = 5 so the centre of the circle is at the point (3, 1) and its radius is  units. I show the sketch of this circle and the three lines below.
units. I show the sketch of this circle and the three lines below.

x2 + 16x + y2 – 4y – 101 = 0 can be written as
(x + 8)2 – 64 + (y – 2)2 – 4 – 101 =0 or (x + 8)2 + (y – 2)2 = 169
so its centre is at the point (–8, 2) and its radius is 13 units. This makes it possible to draw the sketch on the next page.
(a) The radius which joins (–8, 2) to (4, –3) has a gradient of 12
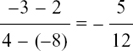 so the gradient of tangent (a) is
so the gradient of tangent (a) is 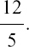
It passes through (4, –3) so its equation is y + 3 = 
or 5y + 15 = 12x – 48 or 5y = 12x – 63.
(b) The radius which joins (–8, 2) to (–3, 14) has a gradient of
 so the gradient of tangent (b) is
so the gradient of tangent (b) is 
It passes through (–3, 14) so its equation is y – 14 = 
or 12y – 168 = –5x – 15 or 12y + 5x = 153.
(c) The radius which joins (–8, 2) to (–21, 2) has a gradient of

From the sketch we see that this radius has zero gradient because it is horizontal. Therefore tangent (c) is vertical and has the equation x = –21.
(d) The radius which joins (–8, 2) to (–8, –11) has a gradient of
 so it is a fraction which is undefined.
so it is a fraction which is undefined.
Looking at the sketch shows us that this radius is vertical, so tangent (d) is horizontal and its equation is y = –11.
Exercise 4.D.1
The missing measurements are as follows:
30°, 45°,  120°,
120°, 
 π, 210°,
π, 210°, 
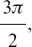 315°, 2π.
315°, 2π.
(a) The arc length = rθ = 5 × π/6 = 2.62 cm to 2 d.p.
(b) The area of  sin θ =
sin θ =  × 25 × sin (π/6) = 6.25 cm2.
× 25 × sin (π/6) = 6.25 cm2.
|
Remember that you must set your calculator in radian mode before you find the sin of the angle. |
(c) To find the area of the segment, we first find the area of the sector. This is  So the area of the segment is 6.545 – 6.25 = 0.30 cm2 to 2 d.p.
So the area of the segment is 6.545 – 6.25 = 0.30 cm2 to 2 d.p.
(2) I will follow my own recommendation here and work in radians. If you don’t, you must use the formula for the area of a sector given in Section 4.D.(d).
I start by saying that 60° is the same as π/3 radians.
The area of the whole circle is π(32) = 28.274m2.
The area of the minor sector 
So the area of the shaded part of the circle is 28.274 – 4.712 = 23.56 m2 to 2 d.p.
The answer to the thinking point is 90° or π/2.
The reason for this is that the area of the triangle is given by  sin θ. The radius r is a fixed length, so the maximum area is obtained when sin θ has its greatest value of one when θ = π/2. The largest area the triangle can have is
sin θ. The radius r is a fixed length, so the maximum area is obtained when sin θ has its greatest value of one when θ = π/2. The largest area the triangle can have is 
Exercise 5.B.1
Here is the sketch of y = cosec x drawn using the graph of y = sin x.
The two graphs touch each other whenever sin x = ±1, and the graph shows that cosec x becomes very large whenever sin x approaches zero. The vertical lines are called asymptotes. The curve becomes very close to them near its jumps or discontinuities.

Here is the sketch of y = cot x drawn using the graph of y = tan x. I have shown y = tan x with a dashed line so that you can see y = cot x more easily.
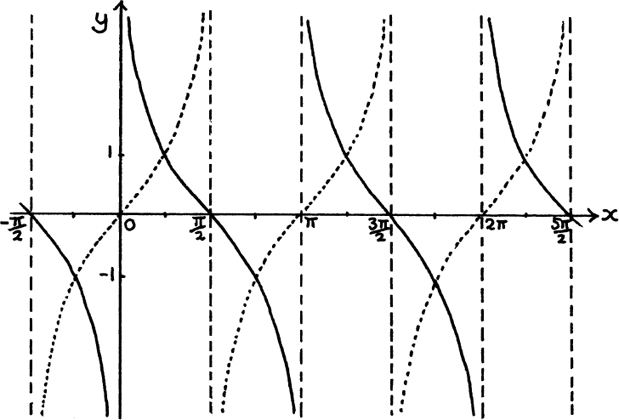
It is a kind of mirror image of y = tan x since it behaves in exactly the opposite way; going off to infinity when tan x = 0, and itself equalling zero when tan x goes off towards infinity. (These last two properties are always true for reciprocal graphs, which helps when sketching them.) However, if you look at the graph of y = tan x in a mirror, you will see that you also have to slide the mirror image to the right (or left!) by π/2 in order to get the graph of y = cot x.
Here are the sketches which you should have.
The original graphs are shown with dashed lines and the reciprocal graphs are shown with solid lines.

Notice what a difference the two zeros for y =f(x) make to the reciprocal graph in (2).
In (3), using the rules for sketching reciprocal graphs gives us the graph we already know the shape of from Section 3.B.(g).

In (5), y = 1/ex = e–x.
In (6), the two graphs cross each other where 
Therefore (x + 3)2 = (x – 2)2 so x2 + 6x + 9 = x2 – 4x + 4 so 10x = –5 and 
Substituting  in either f(x) or 1/f(x) gives y = –1, so the two graphs cut at the point
in either f(x) or 1/f(x) gives y = –1, so the two graphs cut at the point 
It’s worth comparing the graph for this reciprocal function with the graph which we sketched in Section 3.B.(i) of the inverse function of f(x).
I show below the sketches you should have. Each sketch gives the answers to the individual questions for that function.
In (4), because the curve has been shifted up by one unit, it is no longer odd. It no longer fits onto itself if it is rotated through a half turn about the origin.
In (6), sin (t + π/3) gets to every value faster by π/3. The sin curve has been shifted π/3 to the left. We say that the two curves are out of phase by π/3.

Here are the eight sketches which you should have drawn. Each sketch shows the position of P after time t and the corresponding length of x which I have drawn using a heavy black line. I have also shown the starting position of P when t = 0 on each sketch.
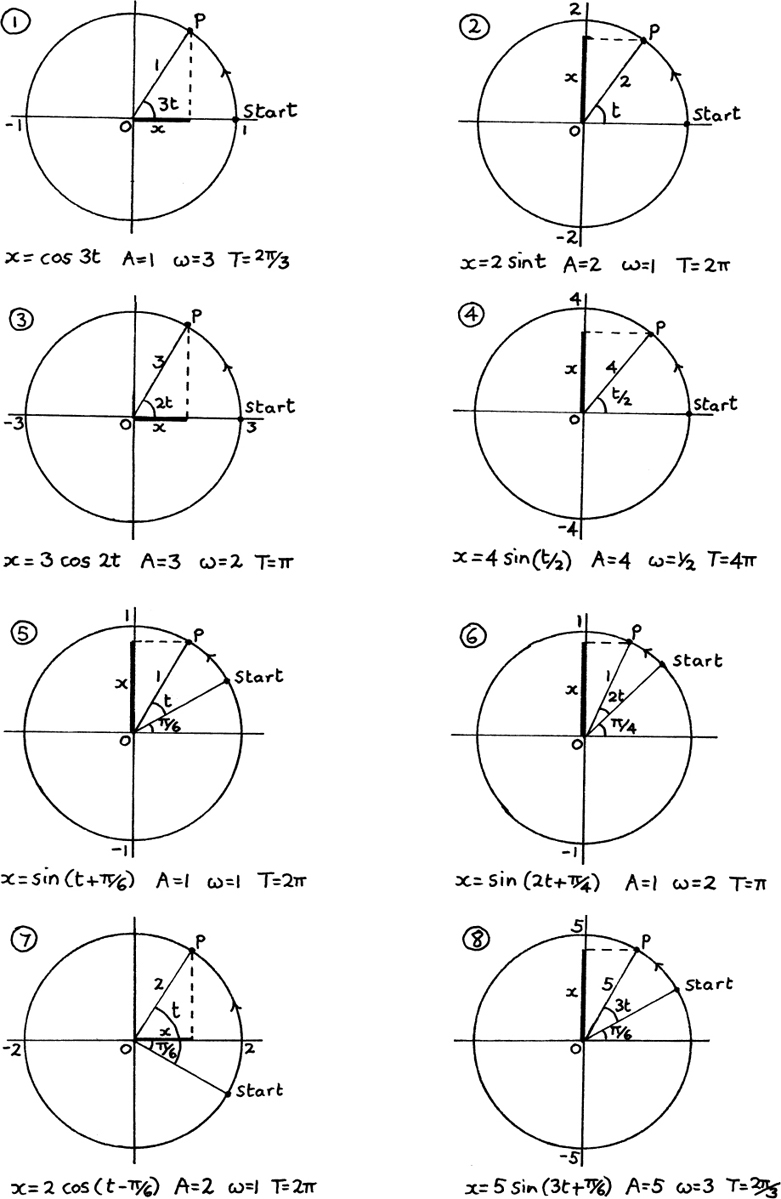
(1)  cos t – sin t = R cos (t + α) = R cos t cos α – R sin t sin α so
cos t – sin t = R cos (t + α) = R cos t cos α – R sin t sin α so 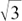 = R cos α and 1 = R sin α so R = 2 and tan α =
= R cos α and 1 = R sin α so R = 2 and tan α =  giving α = π/6.
giving α = π/6.
Therefore x =  cos t – sin t can be written as x = 2 cos (t + π/6).
cos t – sin t can be written as x = 2 cos (t + π/6).
We have A = 2, ω = 1 and T = 2π.
(2) 5 cos t + 12 sin t = R cos (t – α) = R cos t cos α + R sin t sin α so 5 = Rcos α and 12 = R sin α so R = 13 and α = tan–1  = 1.176.
= 1.176.
Therefore x = 5 cos t + 12 sin t can be written as x = 13 cos (t – 1.176).

We have A = 13, ω = 1 and T = 2π.
(3) 15 cos t – 8 sin t = R cos (t + α) = R cos t cos α – R sin t sin α so 15 = R cos α and 8 = R sin α so R = 17 and α = tan–1  = 0.490.
= 0.490.
Therefore x = 15 cos t – 8 sin t can be written in the form x = 17 cos (t + 0.490).

We have A = 17, ω = 1 and T = 2π.
(4) 2 cos t – 3 sin t = R cos (t + α) = R cos t cos α – R sin t sin α so 2 = R cos α and 3 = R sin α so 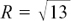 and α =
and α =  = 0.983.
= 0.983.
Therefore x = 2 cos t – 3 sin t can be written as  cos (t + 0.983).
cos (t + 0.983).

We have  ω = 1 and T = 2π.
ω = 1 and T = 2π.
(5) cos 4t – sin 4t = R cos (4t + α) = R cos 4t cos α – R sin 4t sin α so 1 = R cos α and 1 = R sin α so  and α = tan–1 1 = π/4.
and α = tan–1 1 = π/4.
Therefore x = cos 4t – sin 4t can be written as  cos (4t + π/4).
cos (4t + π/4).

We have  ω = 4 and T = 2π/4 = π/2.
ω = 4 and T = 2π/4 = π/2.
(6)  sin 3t – cos 3t = R sin (3t – α) = R sin 3t cos α – R cos 3t sin α so
sin 3t – cos 3t = R sin (3t – α) = R sin 3t cos α – R cos 3t sin α so  = R cos α and 1 = R sin α so R = 2 and α = tan–1
= R cos α and 1 = R sin α so R = 2 and α = tan–1  = π/6.
= π/6.
Therefore x =  sin 3t – cos 3t can be written as x = 2 sin (3t – π/6).
sin 3t – cos 3t can be written as x = 2 sin (3t – π/6).
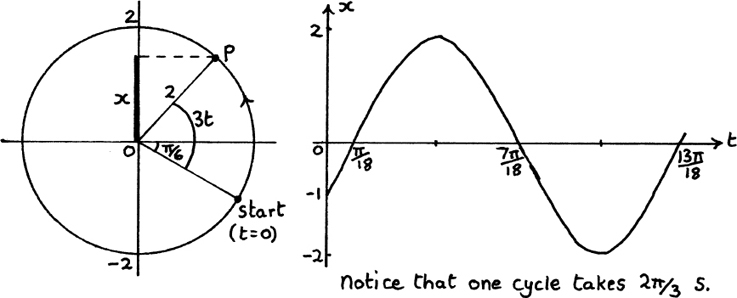
We have A = 2, ω = 3 and T = 2π/3.
This is checked by calculator.
We have 2 cos2 x + 3 cos x + 1 = 0 so (2 cos x + 1)(cos x + 1) = 0.
(a) Either  so the principal value is 120°, or cos x = –1 so the principal value is 180°.
so the principal value is 120°, or cos x = –1 so the principal value is 180°.
(b) The solutions between 0° and 360° are 120° and 360° – 120° = 240°, and 180°.
(Notice that there are only three solutions here in the given range!)
(c) The general solution is x = 360° n ± 120° and x = 360° n ± 180°.
All the answers given by 360°n ± 180° are included if we just write 360° n + 180°.
If you sketch the graph of y = cos x with the line y = –1, you will see that the line y = –1 is a tangent to the curve of cos x and so it is only giving us single points of intersection on each cycle.
Using tan2 x + 1 = sec2 x gives us tan2 x + 2 tan x – 3 = 0, so (tan x – 1) (tan x + 3) = 0.
(a) Either tan x = 1 giving the principal value of x = 45°, or tan x = –3 giving the principal value of x = –71.57° = –71.6° to 1 d.p.
(b) The solutions between 0° and 360° are 45°, 180° + 45°, 180° + (–71.57°) and 360° + (–71.57°) giving 45°, 225°, 108.4° and 288.4° to 1 d.p.
(c) The general solution to 1 d.p. for all possible angles is given by x = 180°n + 45° and x =180°n + (–71.6°) = 180°n – 71.6°.
We have cos2 x + 2 sin x = 1 so (1 – sin2 x) + 2 sin x = 1 so 0 = sin2 x – 2 sin x.
|
Don’t divide through by sin x here, so giving yourself 0 = sin x – 2. If you do this, you have ignored the possibility that sin x = 0. Instead, we factorise, getting 0 = sin x (sin x – 2) so either sin x = 0, or sin x = 2 which is impossible. |
(a) sin x = 0 gives a principal value of 0 radians.
(b) The solutions from 0 to 2π are 0, π and 2π.
(c) The general solution is x = nπ radians where n is any whole number.
(c) 360°n ± 48.2° (to get (b), put n = 0 or 1)
(a) 78.7°
(b) 78.7° and 258.7°
(c) 180°n + 78.7°
(a) 2π/3
(b) 2π/3 and 4π/3
(c) 2πn ± 2π/3
(a) –π/4
(b) 3π/4 and 7π/4
(c) nπ + (–π/4) = nπ – π/4
(a) 23.6°
(b) 23.6° and 156.4°
(c) 180°n + (–1)n 23.6°
In the following questions, I’ve used PV to stand for ‘principal value’.
(6) Using sin2 x + cos2 x = 1 gives 6(1 – cos2 x) + 5 cos x = 7
so 6 cos2 x – 5 cos x + 1 = 0 so (3 cos x – 1)(2 cos x – 1) = 0.

(b) The solutions between 0 and 2π are 1.23 and 5.05 and π/3 and 5π/3.
(c) The general solution is x = 2nπ ± 1.23 and x = 2nπ ± π/3.
(7) tan2 x = tan x so tan2 x – tan x = 0 so tan x (tan x – 1) = 0.
Either tan x = 0 giving a PV of 0 so that the general solution is x = nπ.
This gives the solutions 0, π or 2π if 0 ≤ x ≤ 2π.
Or tan x = 1 giving a PV of π/4 so the general solution is x = nπ + π/4. This gives the solutions π/4 and 5π/4 if 0 ≤ x ≤ 2π.
(8) Using the identity tan2 x + 1 = sec2 x we get 2 tan2 x = 1 so 
If tan  , the PV is 35.3° and if
, the PV is 35.3° and if  , the PV is –35.3°.
, the PV is –35.3°.
The general solution is x = 180°n ± 35.3°. (This puts together both the principal values which we have found.)
The solutions between 0° and 360° are 35.3°, 144.7°, 215.3° and 324.7°.
(9) Using sin 2x = 2 sin x cos x gives 2 sin x cos x – 3 cos x = 0 so cos x (2 sin x – 3) = 0.
Either  which has no solution, or cos x = 0 giving a PV of x = π/2.
which has no solution, or cos x = 0 giving a PV of x = π/2.
This gives a general solution x = 2nπ ± π/2 so x = π/2 or 3π/2 if 0 ≤ x ≤ 2π.
(10) Using Section 5.D.(h) gives sin 5x + sin x = 2 sin 3x cos 2x = 0.
So either sin 3x = 0 or cos 2x = 0.
If sin 3x = 0 the PV of 3x = 0° so the PV of x = 0°
The general solution is 3x = 180n° or x = 60n°.
The solutions between 0° and 360° are 0°, 60°, 120°, 180°, 240°, 300° and 360°.
If cos 2x = 0, the PV of 2x = 90° so the PV of x = 45°.
The general solution is 2x = 360n° ± 90° or x = 180n° ± 45°.
The solutions between 0° and 360° are 45°, 135°, 225° and 315°.
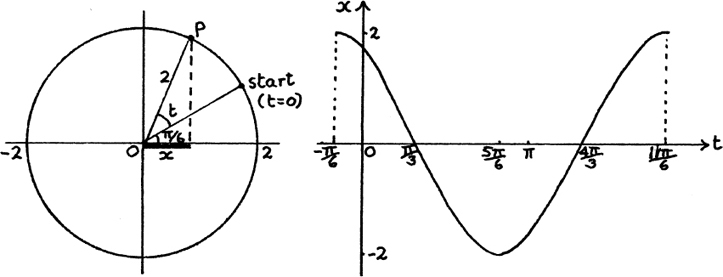
(1) Notice that we are working in radians here.
In Section 5.D. (g) I showed that 3 cos t – 2 sin t =  where a = 0.588 radians to 3 d.p.
where a = 0.588 radians to 3 d.p.
(a) This has no solutions since we can’t have cos t > 1.
(b) This equation gives cos (t + α) = 1 so the principal value is t + α = 0.
This gives the general solution that t + α = 2nπ so t = 2nπ – α, with α = 0.588.
If 0 ≤ t ≤ 2π, we get t = 5.70 to 2 d.p.
(c) The equation gives  cos (t + α) = 1 so cos (t + α) =
cos (t + α) = 1 so cos (t + α) = 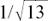 which gives the principal value for (t + α) of 1.290 radians to 3 d.p.
which gives the principal value for (t + α) of 1.290 radians to 3 d.p.
The general solution for (t + α) is given by t + α = 2nπ ± 1.290.
Putting in α = 0.588, the solutions between 0 and 2π are given by putting n = 0 and n = 1.
These solutions are t = 0.70 and t = 4.41 to 2 d.p.
I show all these answers in the sketch below. 
(2) In Section 5.D.(g) we showed that 3 sin 2t + cos 2t = 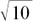 sin (2t + α) where α = tan–1
sin (2t + α) where α = tan–1  = 18.43° to 2 d.p.
= 18.43° to 2 d.p.
We have  sin (2t + α) = 2 so the principal value for (2t + α) is 39.23°.
sin (2t + α) = 2 so the principal value for (2t + α) is 39.23°.
The general solution for 2t + α is 180°n + (– 1)n (39.23°), so
2t = 180°n+ (–1)n (39.23°) – 18.43°
giving
t = 90°n + (–1)n (19.62°) – 9.22°.
Putting n = 0, n = 1, n = 2 and n = 3 gives the solutions between 0° and 360° of t = 10.4°, 61.2°, 190.4° and 241.2° to 1 d.p.
Exercise 6.B.1
(ii) 107 = a + (n – 1)d = 2 + 7 (n – 1), so 7n = 112 and n = 16.
(iii) S16 = 16/2 (2 + 107) = 872.
(b) 100 + 95 + 90 + . . . + 15
(i) a = 100 and d = –5.
(ii) 15 = a + (n – 1)d = 100 + (n – 1)(–5) so 5n = 105 – 15, and n = 18.
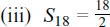 (100 + 15) = 1035.
(100 + 15) = 1035.
(i) a = 6 and d = 
 so
so 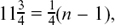 and 47 = n – 1, therefore n = 48.
and 47 = n – 1, therefore n = 48.
(iii) S48 = 48/2 (6 + 71/4) = 24 × 6 + 6 × 71 = 570.
(2)
(a) 1 + 2 + 3 + . . . + 100
a = 1 and d = 1 and n = 100.
 = 5050.
= 5050.
(b) 2 + 4 + 6 + . . . + 100
a = 2 and d = 2 and n = 50.
 = 2550.
= 2550.
(c) The sum of the odd numbers up to 100 is 5050 – 2550 = 2500.
a = 1 and l = n and the number of terms is n so 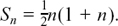
This is an often-used rule and it often appears in formula books.
(3) a = 11 and S18 = 1269 so we have 1269 = 9(22 + 17d). This gives 1269 = 198 + 153d so d = 7.
(4) a = 7 and d = 4. Let Sn = 1375. We have to find what n is. We can say
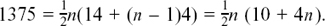
Tidying up gives us
2n2 + 5n − 1375 = 0.
So 
Since the number of terms of a series must be a positive whole number, the answer is 25.
(5) The third term is twice the first term, so a + 2d = 2a giving d =  Also
Also

This gives
39 = 13a/2 so a = 78/13 = 6 and d = 3.
(5) Let F = 0.7777 . . . Then 10F = 7.7777 . . . Subtracting, we have 9F = 7 so 
(6) Let F = 0.292929. . . Then 100F = 29.292929. . . Subtracting, we have 99F = 29 so 
(7) Let F = 2.5343434. .. Then 100F = 253.4343434.. . Subtracting, we have 99F = 250.9 so 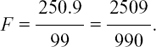
(8) If  then, multiplying by 1000, we have
then, multiplying by 1000, we have
1000F = 40210.6106106106. . .
F= 40.2106106106. . .
Subtracting, we get 999F = 40170.4 so 
(9) If  then multiplying by 1 000 000, we have
then multiplying by 1 000 000, we have
1 000 000F = 142 857.142857 . . .
F = 0.142857. . .
Subtracting, we get 999 999F = 142 857, so  rather amazingly.
rather amazingly.
The digits of the decimal forms of  , etc. make interesting patterns. You might like to look at these for yourself.
, etc. make interesting patterns. You might like to look at these for yourself.
(4) We want the terms to alternate in sign, with the odd terms being negative and the even terms positive. We can make this happen by multiplying each term by something which flips sign in this way. (–l)r will fit our requirements exactly. (This is what we used when we wrote down the general solution for a sin in Section 5.E.(d).) So we write

(1) The first four terms are 5 + 7 + 9 + 11 = 32. (An AP!)
The nth term is 2n + 3, and the (n + 1)th term is 2(n + 1) + 3 = 2n + 5.
(2) The first four terms are  giving a GP this time. (Remember that
giving a GP this time. (Remember that  from Section 1.D.(b).)
from Section 1.D.(b).)
The nth term is  The (n + l)th term is
The (n + l)th term is 
(3) The first four terms added are 
The nth term is 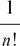 and the (n + 1)th term is
and the (n + 1)th term is
(I gave the meaning of n! at the end of Section 6.A.(a).)
(4) The first four terms added are 
The nth term is  and the (n + 1)th term is
and the (n + 1)th term is  replacing n by n + 1 in the previous formula.
replacing n by n + 1 in the previous formula.
(5) The first four terms are 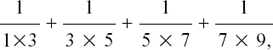 that is,
that is, 
The nth term is 
The (n + l)th term is 

 using (S3) and (S 1).
using (S3) and (S 1).
Factorising, we get

Check: If n = 3
LHS = 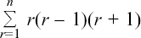 = 1(0)(2) + 2(1)(3) + 3(2)(4) = 30.
= 1(0)(2) + 2(1)(3) + 3(2)(4) = 30.
Putting n = 3 in the RHS gives  (3)(4)(9 + 3 – 2) = 30.
(3)(4)(9 + 3 – 2) = 30.
These checks are useful not only to be confident that your working is correct, but also because they give you good practice in handling series, and seeing the terms building up into the sums.
so 4 ≡ A(x + 3) + B(x + 2).
Putting x = –3, we get 4 = –B, so B = –4.
Putting x = –2, we get 4 = A.
Check with x = 0: LHS = 4 and RHS = 12 – 8 = 4.
So 
so 6 ≡ A(2y + 1) + B(2y – 1).
Putting  , we get 6 = 2A, so A = 3.
, we get 6 = 2A, so A = 3.
Putting  we get 6 = –2B, so B = –3.
we get 6 = –2B, so B = –3.
Check with y = 0: LHS = 6; RHS = 3 + 3 = 6.
So 
so 10 ≡ A(x – 1)(x + 4) + Bx(x + 4) + Cx(x – 1).
Putting x = 1, we get 10 = 5B, so B = 2.
Putting x = –4, we get 10 = 20C, so 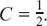
Putting x = 0, we get 10 = –4A, so 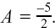
Check with x = 2, say. (We can’t use x = 0 as we’ve used it already.)
We get LHS = 10 and RHS = 
So 

When you use partial fractions for integrating, it is usually better to keep A, B and C as fractions on top of the original fractions, so I shall leave my answers in the form
 rather than
rather than 
so 5 ≡ A(x + 3)2 + B(x – 2)(x + 3) + C (x – 2).
Putting x = –3, we get 5 = C(–5) so C = –1.
Putting x = 2, we get 5 = A(52) so 
Comparing the terms in x2, we have 0 = Ax2 + Bx2 so B = 
Checking with x = 0, we get the LHS = 5 and the RHS = 
So 
so 2 = Ay(y – 1) + B(y – 1) + Cy2.
(y2 works just like any other repeated factor.)
Putting y = 0, we get 2 = –B so B = –2.
Putting y = 1, we get 2 = C.
Comparing the terms in y2, we have 0 = Ay2 + Cy2 so A = –C so A = –2.
Checking with y = 2, we get the LHS = 2 and the RHS = (–2)(2) + (–2)(1) + (2)(4) = 2.
So 
so 14 ≡ (Ax + B)(x + 2) + C(x2 + 3).
Putting x = –2, we get 14 = 7C so C = 2.
Putting x = 0, we get 14 = 2B + 3C so 2B = 8 and B = 4.
Comparing the terms in x2, we have 0 = Ax2 + Cx2 so A = –C = –2.
Checking with x = 1, the LHS = 14, and the RHS = (–2 + 4)(3) + 2(4) = 14.
so  .
.
The second form looks a bit tidier.
so 4 ≡ A(y2 + 1) + (By + C)y.
Putting y = 0, we have 4 = A.
Comparing the terms in y2, we have 0 = Ay2 + By2 so B = –A = –4.
Putting y = 1, we get 4 = 4(2) + (–4 + C)(l), so 4 = 8 – 4 + C so C = 0.
Checking with y = 2, we get the LHS = 4, and the RHS = 4(5) + (–8)(2) = 20 – 16 = 4.
So 
(I haven’t filled in all the very straight forward parts of these questions.)
so 4 ≡ A(x – 1)2 + B(x – 1)(x + 3) + C(x + 3).
Putting x = 1, we get 4 = 4C so C = 1.
Putting x = –3, we get 4 = 16A so 
Matching the terms in x2, we get 0 = Ax2 + Bx2 so 
Checking with x = 0 gives the LHS = 4, and the RHS =
So 
so 3p + 1 ≡ A(p + 2)2 + B(2p – 1)(p + 2) + C(2p – 1).
Putting p = –2, we get –5 = –5C so C = 1.
Putting 
Matching the terms in p2, we get 0 = Ap2 + 2Bp2 so 2B = –A so 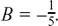
Checking with p = 0 gives the LHS = 1, and the RHS = 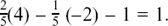
So 
 so 4x – 5 ≡ A(x – 3)2 + B(2x + 1)(x – 3) + C(2x + 1). Working in a similar way to (2), you should get
so 4x – 5 ≡ A(x – 3)2 + B(2x + 1)(x – 3) + C(2x + 1). Working in a similar way to (2), you should get

so 10y ≡ A(y2 + 9) + (By + C)(y – 1).
Putting y = 1, we get 10 = 10A so A = 1.
Matching the terms in y2, we get 0 = Ay2 + By2, so B = –A = –1.
Matching the terms in y we get 10y = Cy – By so C = 10 + B = 9.
Checking with y = 0, the LHS = 0, and the RHS = +1(9) + (9)(–1) = 0.
So 
Notice particularly here the rewriting of the second fraction with the minus sign outside, using the line of the fraction as a bracket.
which gives 
(6) This one is top-heavy, so we rewrite it as
(7) This is also top-heavy, so we write it as

Did you spot how the x4 – 1 could be factorised? It uses the difference of two squares twice. We can say x4 – 1 = (x2 – l)(x2 + 1) = (x – 1) (x + l)(x2 + 1).
So 
so 2 ≡ A(x + 1)(x2 + 1) + B(x – 1)(x2 + 1) + (Cx + D)(x – l)(x + 1).
Putting x = –1 gives 2 = –4B so B = 
Putting x = 1 gives 2 = 4A so A = 
Matching the terms in x3 gives 0 = A + B + C so C = 0.
Putting x = 0 gives 2 = A – B – D so D = –1.
Putting x = 2 gives the LHS = 2 and the RHS 
The final answer is 

Students sometimes leave out the first of these fractions, forgetting that u2 is a repeated factor of u times u.
Now we have, getting rid of fractions,
u2 – 1 ≡ Au(2u + 1) + B(2u + 1) + Cu2.
Putting u = 0 we get –1 = B.
Putting u = – we get
we get  C so 1 – 4 = C and C = –3.
C so 1 – 4 = C and C = –3.
Matching the terms in u2 gives us u2 = 2Au2 + Cu2 so 1 = 2A + C so A = 2.
Putting u = 1 gives the LHS = 0 and the RHS = 2(1) (3) – 1(3) – 3(1) = 0.
so 
This one is also top-heavy and the rearranging is a bit tricky. You may prefer to use long division. If not, it can be rearranged this way:

Notice that the line of the fraction is acting as a bracket, again.
The partial fractions for 
So 
Notice the signs!
(a) The first four terms of  are
are  and
and 
(b) 4r2 – 1 = (2r – 1)(2r + 1) (the difference of two squares again!)
The second bracket has just been slid along one space, so we get 
The sum to infinity of this series is 1.
(1) The sixth row of Pascal’s Triangle is:
1 6 15 20 15 6 1 (P6)
so the expansion of (x – 2y)6 is given by
x6 + 6(x5)(–2y)1 + 15(x4)(–2y)2 + 20(x3)(–2y)3 + 15(x2)(–2y)4 + 6(x)(–2y)5 + (–2y)6.
= x6 – 12x5y + 60x4 y2 – 160x3y3 + 240x2 y4 – 192xy5 + 64y6.
(2) The fifth row of Pascal’s Triangle is given by:
1 5 10 10 5 1 (P5)
so the expansion of (2x2 –y2)5 is
(2x2)5 + 5(2x2)4 (–y2) + 10(2x2)3 (–y2)2 + 10(2x2)2 (–y2)3 + 5(2x2) (–y2)4 + (– y2)5
= 32x10 – 80 x8y2 + 80x6 y4 – 40x4 y6 + 10x2y8 – y10.
(3) The fourth row of Pascal’s Triangle is:
14 6 4 1 (P4)
so the expansion of  is
is

(4) The third row of Pascal’s Triangle is
1 3 3 1 (P3)
so the expansion of 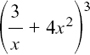 is
is


It is very easy to make mistakes with complicated terms like we have in these questions. It is safest always to put in the working step as I have done, rather than trying to do it in your head.
(which you can see must be the case since you are choosing all as). The term is a16. We define 0! to be equal to 1 to make the formula work in this case.
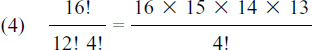 = 1820. The term is 1820a12b4.
= 1820. The term is 1820a12b4.
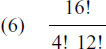 .= 1820. The term is1820a4b12.
.= 1820. The term is1820a4b12.
(9) This works in exactly the same way as the others.
r is just standing for whichever power of a we might be interested in.
We get  and the term is
and the term is 
Notice the symmetry of the pairs (1) and (8), (3) and (7), and (4) and (6). This is the same symmetry which we saw in Pascal’s Triangle.
(1) The first four terms of (2x – y)12.
Using (B1), with ‘a’ = 2x and ‘b’ = –y and n = 12, we get

= 4096x12 – 24576x11 y + 67584xl0y2 – 112640x9y3.
(2) The first four terms of (1 – 2x)18.
Using (B 2) with ‘x’ = –2x and n = 18, we get

(3) The first four terms in the expansion of (1 + x2)10. Using (B 2) with ‘x’ = x2 and n = 10, we get

(4) The first four terms in the expansion of  Using (B 1) with ‘a’ = x/2 and ‘b’ = 3y and n = 16 we get
Using (B 1) with ‘a’ = x/2 and ‘b’ = 3y and n = 16 we get

Then (a) + (b) =

This rearrangement is possible because it does not matter which order we multiply the numbers in.
The answer that (a) + (b) = (c) is another way of saying that 84 + 126 in (P 9) gives 210 in (P 10).
(b) is 
(c) is 
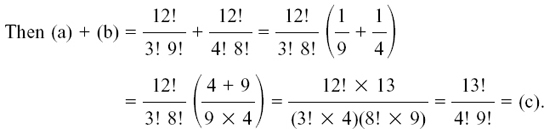
This answer corresponds to 220 + 495 in (P 12) giving 715 in (P 13).
(3) This last question looks horrible because it has letters instead of numbers, but it works in just the same way as (1) and (2).

k + 1 – r is the same as k – r + 1. The numbers are just being put together in a different order. Having this result will make it very easy for us to prove the binomial theorem by induction in Section 7.D.(b).
(a) The term in x6 in the expansion of (2 – 3x)11 is

(b) The term in x6 in the expansion of (2x – y)8 is

(c) The term in x6 in the expansion of (y2 – 2x2)10 is

(a) The constant term in the expansion of
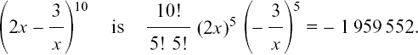
(b) The constant term in the expansion of

(c) The constant term in the expansion of
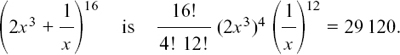
(3) The term in x10 in the expansion of (1 + x)7 (2 – 3x)5 comes from x7 × x3 and x6 × x4 and x5 × x5. So it is:

(1) Most people try to spread the numbers much too evenly when they do this. To show you by example that such an even spread isn’t to be expected, I have written out for you two lists of numbers below. The first list gives ten sets of six numbers chosen by using the random number generator on my calculator and taking the first two digits, discarding anything over 49. The second list gives the results of the draws from ten consecutive weeks in a lottery similar to the one I described before this exercise.

You can see from these lists that two consecutive numbers have come up surprisingly often, in fact ten times altogether. Also, runs of the same number occur, with 10 coming up in four consecutive lottery draws, for example. There are also corridors with no numbers in. For example, there are no 42, 43 or 44 in the ten consecutive lottery draws. You can see the uneven spread of the numbers even more clearly if you show these lists on squared paper also.
(2) Exactly the same rules of probability apply to each set of numbers, so each of them have an equal chance of

of being the correct choice.
(3) You would be wiser to pick the third choice. The reason for this is that many people think that ‘random’ means more or less evenly spread. This is not so. ‘Random’ means just that; the choices can happen anywhere, and therefore there will sometimes be bunching, and sometimes large gaps, as you can see in the two lists above. The behaviour of such random distributions of numbers is explained mathematically in courses on statistics. These mathematical descriptions can then be used to answer questions such as how much concern should be felt about clusters of cases of particular illnesses such as childhood leukaemia; is there a local cause or are such clusters to be expected anyway?
Since most people would probably think that 44, 45, 46, 47, 48, 49, would be very unlikely, if these numbers did come up, you would be less likely to have to share your winnings! The choice of 1, 2, 3, 4, 5, 6 would be less satisfactory since many people have favourite ‘lucky’ numbers which they choose, and such numbers are usually small. Other people are likely to choose birthdays, so they will be restricted to 31 or less. It is also likely that many people would be very doubtful about choosing even two numbers together, never mind the whole six. In fact, in a situation like this, the probability of getting at least one pair of consecutive numbers is about one half; much higher than you would probably guess.
(4) On any particular draw of this lottery, there will be 43 numbers which are not chosen. The number of different possibilities if six numbers are chosen from these 43 numbers and the order of choice doesn’t matter, is given by
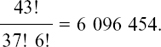
We know already that the total number of ways of picking 6 numbers from 49 numbers is 13 983 816.
This means that there are 13 983 816 – 6 096 454 = 7 887 362 ways of choosing at least one number correctly. Therefore the probability of doing this is

We see that you should expect to have at least one number correct more often than not, which makes it not quite as encouraging for future prize-winning as it might seem.
The expansion is valid if 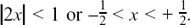
This is just the same as the first expansion in this section except that x has been replaced by –3x, so it tidies up particularly nicely.

It’s worth remembering that
 and
and  where
where  stands for whatever we have in this position in the bracket, and
stands for whatever we have in this position in the bracket, and  < 1.
< 1.
Here,  so we must have |3x| < 1 or
so we must have |3x| < 1 or 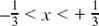 for the expansion to be valid.
for the expansion to be valid.
For the expansion to be valid, we must have 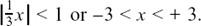
(a) Here,  For the expansion to be valid, we must have
For the expansion to be valid, we must have  , so |3x| < 1, so
, so |3x| < 1, so 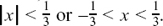 (Remember that |–3x| = |3x|.) Then:
(Remember that |–3x| = |3x|.) Then:

= 1 – x – x2 – 3x3, giving the first four terms.
(b) Here,  , so we must have
, so we must have  that is |x| < 2 or –2 < x < 2. Then:
that is |x| < 2 or –2 < x < 2. Then:

 giving the first four terms.
giving the first four terms.
(c) This time, we must rearrange to get the  form.
form.

Here, , so we must have
, so we must have 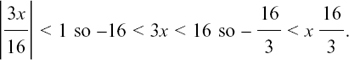
(d) Rearranging again, we have

Here,  , so we require
, so we require  < 1, so –4 < x < 4.
< 1, so –4 < x < 4.
(e) Again, rearranging is necessary.
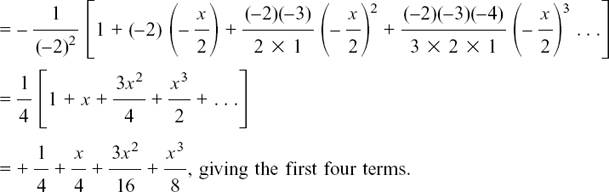
Here,  , so we require
, so we require  < 1 so
< 1 so  so –2 < x < 2.
so –2 < x < 2.
(f) Rearranging yet again, we have

The first four terms are given by

 See Section 1.D.(b) if you need help with this).
See Section 1.D.(b) if you need help with this).

This time,  so require
so require 
(2) METHOD (1) 
Now we take just the multiplications giving the terms up to x2, giving

METHOD (2) Writing  in partial fractions, we get
in partial fractions, we get
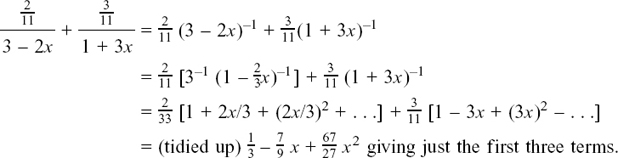
In order for the first expansion to be valid, we require that  so
so 
For the second expansion to be valid, we must have |3x| < 1 so 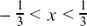 .
.
Therefore, in order to fit both requirements simultaneously, we must take the tighter of the two restrictions which is that 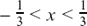 .
.
(1) We want to show that 1 + 2 + 3 + 4 + . . . + n =  .
.
First, check that the statement is true when n = 1.
LHS = 1. RHS =  , so, yes, St[1] is true.
, so, yes, St[1] is true.
Then, suppose that the statement is true for n = a particular value, k, so
 St[k]
St[k]
Now we must show that this means that it is also true for n = k + 1. That is, we must show that
 St[k + 1]
St[k + 1]
(The extra term has been added on to the LHS and k has been replaced by k + 1 in the formula on the RHS.)
Now, the whole bunch of 1 + 2 + 3 + . . . + k on the LHS of St[k + 1] can be replaced by  using St[k]. So we have that the LHS of St[k + 1] =
using St[k]. So we have that the LHS of St[k + 1] = 
But, factorising this, we have
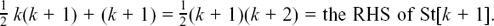
We have taken out the factor of (k + 1), and also the  because we know we want it at the front. This means that we must have the 2 in the second bracket to make the whole thing multiply out correctly.
because we know we want it at the front. This means that we must have the 2 in the second bracket to make the whole thing multiply out correctly.
So, if the statement is true when n = k, then it is also true when n = k + 1.
But it is true when n = 1, so therefore it is true when n = 2, and so on through all the counting numbers.
So it looks as if the sum of n odd numbers is n2.
Suppose this statement is true when n = a particular value, k. Then
1 + 3 + 5 + . . . + (2k – 1) = k2. St[k]
Nasty pitfall. The nth odd number isn’t n, but 2n – 1. (For instance, the third odd number isn’t 3 but 5.)
We must now show that if St[k] is true, then St[k + 1] is also true, so
1 + 3 + 5 + . . . + (2k – 1) + (2k + 1) = (k + 1)2. St[k + 1]
Using St[k], the LHS of St[k + 1] = k2 + (2k + 1) = (k + 1)2 = RHS of St[k + 1].
But the statement is true when n = 1, so therefore it is true through all the counting numbers.
(3) We have to show that
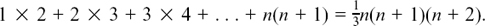
First, we check that this formula is true when n = 1.
The LHS is 1 × 2 = 2 and the RHS is 1/3(1)(2)(3) = 2, so St[1] is true.
Then we suppose the statement is true for n = a particular value, k, so that
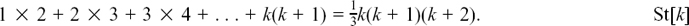
We must then show that St[k + 1] is true, that is, that
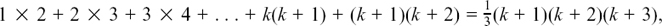
adding the extra term to the LHS and putting n = k + 1 on the RHS.
Using St[k], the LHS of St[k + 1] is
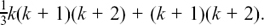
Now, we factorise by taking out  . We get
. We get

which is the RHS of St[k + 1]. (Check by multiplying out this last bracket if you are unsure about this step.)
So, if St[k] is true, then St[k + 1] is true.
But St[1] is true, and so St[2] is true, and so on through all the counting numbers.
(1) dy/dx = 14x + 12x3
(2) dx/dt = 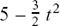
(3) y = 3– 2x–3 so dy/dx = 0 + 6x–4 = 6/x4.
(a) If x is increased by a small amount δx, so that y gets increased by a correspondingly small amount δy, we have
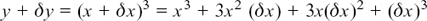
But y=x3
so  so
so 
Now, when we let δx → 0, we can ignore the terms 3x(δx) and (δx)2, so the limit of δy/δx as δx → 0 is dy/dx = 3x2.
(b) Here, we are taking the particular case of x = 2 and δx = 0.001 so we have
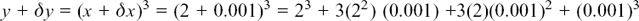
But y = 23 so

and since δx = 0.001, we have
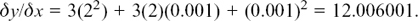
If we make δx even smaller, δy/δx will approach even more closely to the value of 3(22) = 12 given by dy/dx = 3x2 when x = 2.
(1) We have y = sin t so dy/dt = cos t and d2y/dx2 = – sin t = –y
so we do get the same kind of link between the acceleration and the distance of Y from O. The point Y is also moving in SHM, but it is starting from the central position on its path whereas X started from its most extreme positive position.
(When t = 0 we have y = 0 too, but if x = cos t, then x = 1 when t = 0.)
(2) For this new object, x = 3 cos t + 4 sin t.
dx/dt = –3 sin t + 4 cos t and d2y/dt2 = –3 cos t –4 sin t = –x.
So this object is also moving in SHM. This equation describes a motion which starts from an intermediate point when the time t = 0.
We know from Section 5.D.(f) that if x = 3 cos t + 4 sin t then the two most extreme values of x are x = +5 and x = –5. When t = 0, x = 3.
Here are the answers you should have. To help you, I have shown the two separate bits in square brackets, before tidying up, and also put what I chose for X at the side of each answer.
(1) dy/dx = [4(2x2 + 3)3] [4x] = 16x(2x2 + 3)3 with X = 2x2 + 3.
(2) dx/dt = [5(t3 + 2)4] [3t2] = 15t2(t3 + 2)4 with X = t3 + 2.
(3) dy/dx = [4(3x2 – 2x)3] [6x – 2] = 8(3x – 1) (3x2 – 2x)3 with X = 3x2 – 2x.
(4) dx/dt =  with X = 3t + 4.
with X = 3t + 4.
(5) dy/dx = [3e4x] [4] = 12e4x with X= 4x.
(6) dx/dt =  with X= t2 + 1.
with X= t2 + 1.
(7) dy/dx =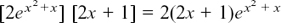 with X = x2 + x.
with X = x2 + x.
(8) dx/dt = [–sin (4t + π/3)] [4] = –4sin (4t + π/3) with X = 4t + π/3.
(9) dx/dt =cost+ [cos 2t] [2] = cos t + 2 cos 2t with X = 2t.
(10) dy/dx = [cos (x2)] [2x] = 2x cos (x2) with X = x2.
(11) dy/dx = [2 sin x] [cos x] = 2 sin x cos x with X = sin x.
(12) dy/dx = [3 cos2 x] [– sin x] = –3 sin x cos2 x with X = cos x.

Students often give the answer of 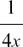 for this one!
for this one!
These are the answers you should have for dy/dx in each case.
(1) 5e5x
(2) –2e–2x
(7) 7 cos 7x
(8) –4 sin x cos3 x
(9) 2 cos (2x + Π)
(10) –3 sin (3x + 4).
I have used the square brackets again to make the working clear for you.
(1) dy/dx = [5 cos4 2x] [–2 sin 2x] = –10 sin 2x cos4 2x.
(2) dy/dx = [3 sin2 (4x + 1)] [4 cos (4x + 1)] = 12 cos (4x + 1) sin2 (4x + 1).
(4) dx/dθ = [3 (2 cos 2θ + 5)2] [–4 sin 2θ] = –12 sin 2θ (2 cos 2θ + 5)2.
(8)dy/dx = [cos (cos 4x)] [–4 sin 4x] = –4 sin 4x cos (cos 4x).
(10) Using the third law of logs to make this question easier,we have

Again, I have sometimes used square brackets to show the way in which the answers build up more clearly.
(1) u = 7x2 and v = cos 3x so

(2) u = e3x and v = sin 2x so
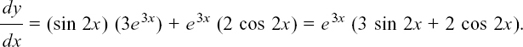
(3) u = 4x5 and v = (x2 + 3)3 so

(4) u = e2t + 1 and v = cos (2t + 1) so
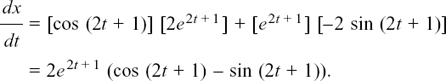
(5) u = 7t2 and v = ln (2t – 1) so
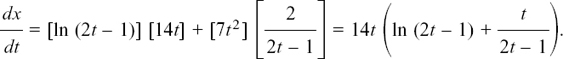
(6) u = (t2 + 1)1/2 and v = sin (2t + θ) so

(7) y = [(x2 + 1)5] [e3x cos 2x] so u = (x2 + 1)5 and v = e3x cos 2x.
First, using the Product Rule to find dv/dx, we have
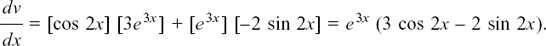
Now, using the Product Rule again to find dy/dx, we have

(8) x = (2 + t)e3t so dx/dt = (e3t)(1) + (2 + t)(3e3t) = (7 + 3t)e3t.
Using the Product Rule again, we get

(9) x = ekt so dx/dt = k ekt and d2xldt2 = k2ekt.

Therefore ekt(k2 – 2k – 3) = 0 but ekt is never equal to zero. So we have
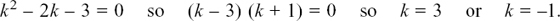
(10) We know from the last question that both e3t and e–t fit this equation. Multiplying them by constant numbers will make no difference to this fit.
Therefore x = Ae3t + Be–t is a solution to this equation.
(In fact, it is the solution to this equation which covers all possible situations.)
Using the Product Rule gives
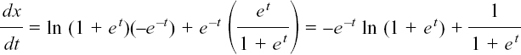
because (et) (e–t) = e0 = 1.
Therefore 
These last two questions show how you can use either the Product Rule or the Quotient Rule to answer them.
(5) If y = ln (sec x + tan x) then we know from Example (1) in Section 8.C.(e) that d/dx (tan x) = sec2 x and from question (2) above that d/dx (sec x) = sec x tan x. Therefore

taking out sec x as a factor on the top of this fraction and then cancelling.
(remembering that ex × e–x = ex–x = e0 = 1 and d/dx(e–x)= –e–x).
 using the second law of logs, so
using the second law of logs, so

(8) Here, we need to use the Product Rule to differentiate the ‘u’ of x2 sin x on the top. Doing this first gives
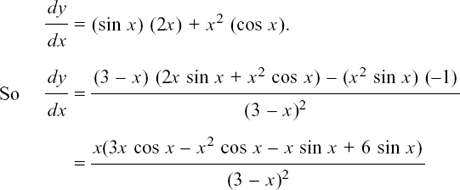
(Notice that this time we have found that the gradient of the curve is always positive, except when  , when the curve itself is undefined.)
, when the curve itself is undefined.)
The bottom of this fraction is always positive, and ad – bc is a constant number itself since it is made up of constant numbers.
Therefore, dy/dx will remain always either positive or negative depending on the particular values of a, b, c, and d, unless x = –d/c, when the function y itself is undefined.
The only exception to this is the special case when ad – bc = 0 when
 everywhere, so
everywhere, so  must be totally flat.
must be totally flat.
If we put a = 6, d = 1, b = 3 and c = 2, we would have an example of this. We then get

It is totally flat!

See if you can show for yourself that, if ad – bc = 0, then
must simplify down to the form y = a constant, so giving a horizontal line with a gradient of zero.
Hint: if ad – bc = 0 then ad = bc. Put ad = bc = k and substitute for d and c in the equation for y. Then tidy this up.
(1) If ex = 2 then e–x = 
Using the definitions for sinh x, cosh x and tanh x gives us

(2) e0 = 1 so sinh x = 0 and cosh x = 1. This gives tanh x = 0/1 = 0.
(a) 2 sinh 2x
(b) 3 cosh (3x + 5)
(c) Using the Product Rule, we get

(1) dy/dx = cosh x and cosh(0) = 1, so the gradient of the curve y = sinh x at the origin is 1.
(2) The line y = x is the tangent to the curve y = sinh x when it passes through the origin, since this line also passes through the origin and has a gradient of 1.
(3) Since y = sinh x and y = sinh–1 x are symmetrically placed either side of y = x, this line is also the tangent to y = sinh–1 x at the origin, and the gradient of sinh–1 x here must also be 1.




I’ll include more details for the last three questions, by putting X = ‘lump’, as these are slightly more complicated.

The first thing to do here is to use the second rule of logs to write y more simply. (This saves a huge amount of work.) This gives us
so 
(4) We can solve 8 sinh x = 3 sech x in two ways.
METHOD (1) Do it in the same way you would solve a trig equation.
8 sinh x = 3/cosh x so 8 sinh x cosh x = 3 so 4 sinh 2x = 3
using the rule of Section 8.D.(d) that sinh 2x = 2 sinh x cosh x.
We now have sinh  and
and 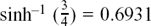 so x = 0.347 to 3 d.p.
so x = 0.347 to 3 d.p.
Notice that you don’t have the infinite numbers of solutions that you get with trig equations to worry about here! This is one way in which sinh and cosh don’t behave like sin and cos.
I show a sketch of what’s happening graphically here below.
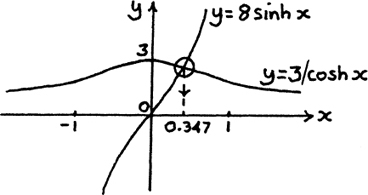
METHOD (2) Write everything in terms of ex. This gives

since e2x is always positive. This gives 2x = ln 2 so x = 0.347 as before.
(a) We solve 2 sinh2 x – 5 cosh x – 1 = 0 in a very similar way to the trig equations in Section 5.E.(b).
sinh2 x = cosh2 x – 1 so 2(cosh2 x – 1) – 5 cosh x – 1 = 0 so 2 cosh2 x – 5 cosh x – 3 = 0 so (2 cosh x + 1)(cosh x – 3) = 0
so cosh  (which is impossible as you can see from the graph in Figure 8.D.5) or cosh x = 3. This gives x = cosh–1 (3) = 1.763 to 3 d.p.
(which is impossible as you can see from the graph in Figure 8.D.5) or cosh x = 3. This gives x = cosh–1 (3) = 1.763 to 3 d.p.
(x could also be –1.763 from the symmetry of the cosh graph. Excellent, if you also got this answer!)
(b) 3 sech2 x + 8 tanh x – 7 = 0 so, using 1 – tanh2 x = sech2 x, we have
3(1– tanh2 x) + 8 tanh x–7 = 0 so 0 = (3 tanh x – 2)(tanh x – 2)
so tanh  giving x = 0.805 to 3 d.p. or tanh x = 2 which is impossible since the values of tanh x lie between –1 and +1 as you can see in Figure 8.D.7.
giving x = 0.805 to 3 d.p. or tanh x = 2 which is impossible since the values of tanh x lie between –1 and +1 as you can see in Figure 8.D.7.
(1) y = ex so dy/dx = ex.
(a) x = 0 so dy/dx = e0 = 1 so the gradient of the tangent at (0, 1) is 1.
The equation of this tangent is y – 1 = 1(x – 0) so y = x + 1.
(b) x = 1 so dy/dx = e1 = e.
The equation of the tangent at (1, e) is y – e = e(x – 1) so y = ex.
Notice that this particular tangent passes through the origin, and has a gradient of e. The lines y = x and y = 3x also pass through the origin. Since 1 < e, y = x doesn’t cut the curve of y = ex at all – there are no solutions to the equation x = ex. However, the line y = 3x cuts the curve y = ex twice, because 3 > e. This means that the equation 3x = ex has two solutions.
(c) x = 2 so dy/dx = e2.
The equation of the tangent at (2, e2) is y – e2 = e2 (x – 2) so y = e2 x – e2, so it cuts the y-axis at about –7.4.
(2) y = tan x so dy/dx = sec2 x. (I showed this result in Section 8.C.(e).)
(a) x = 0 so dy/dx = 1.
When x = 0, y = 0 also, so the equation of the tangent at (0,0) is y = x.
(b) If x = π/4, then y = 1 and

The equation of the tangent at (π/4, 1) is y – 1 = 2(x – π/4) so y = 2x + (1 – π/2).
This tangent cuts the y-axis at about –0.57.
(3) Tangent (a) in (2) actually crosses the curve at the origin. It is behaving just like the tangents at the origin to y = sinh x and y = tanh x which we found in the last section. Each of these tangents happens to be the line y = x, but other tangents can also cross their curves. An example of this is tangent (c) to y = cos x at x = π/2, just before this exercise.
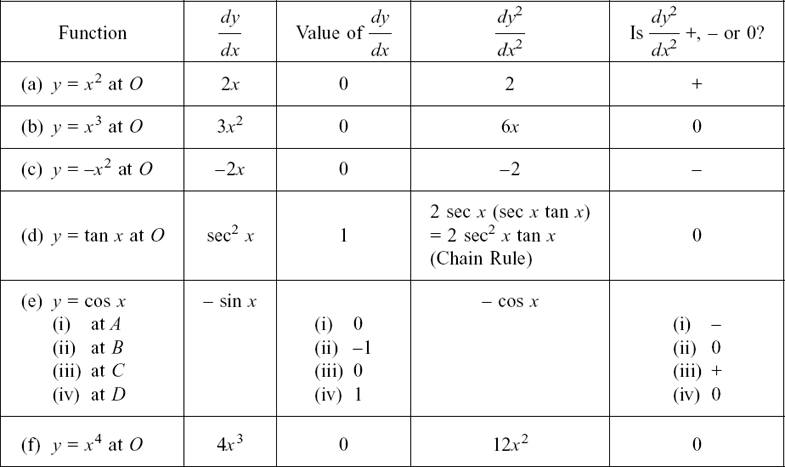
 so y = f(x) cuts the y-axis at
so y = f(x) cuts the y-axis at  .
.
(2) f(x) = 0 when x = 1 so y =f(x) cuts the x-axis at (1, 0).
(3) We cannot divide by zero so we must exclude the values x = –2 and x = +2.
The straight lines x = –2 and x = +2 are vertical asymptotes for y = f(x).
The value of f(x) is large and negative if x is just less than –2.
The value of f(x) is large and positive if x is just greater than –2.
The value of f(x) is large and negative if x is just less than +2.
The value of f(x) is large and positive if x is just greater than +2.
 dividing top and bottom by x2.
dividing top and bottom by x2.
1/x, 1/x2 and 4/x2 all tend to zero when x becomes large, so f(x) → 0/1 = 0 for both large positive and negative values of x. This means that y = 0 is a horizontal asymptote.
There is no value of x on the x-axis which fits this equation since ‘b2 – 4ac’ = –12.
In other words, this equation has no real roots.
Therefore, there are no turning points. This curve never has a horizontal tangent.
I show a sketch of it at the end of the answers to this exercise.
(1) g(0) = 0 so y = g(x) cuts the x-axis at (0, 0). This answers (2) as well.
(3) 1 + x2 is always positive so no value of x has to be excluded.
 dividing top and bottom by x2.
dividing top and bottom by x2.
1/x and 1/x2 both tend to zero when x becomes large, so again y = 0 is a horizontal asymptote.
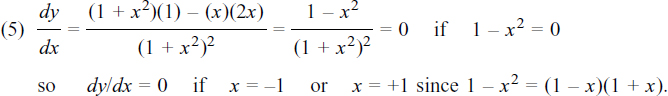
Passing through x = –1, the sequence of values of dy/dx goes – 0 + so there is a local maximum of g(–1) =  the point
the point 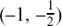 .
.
Passing through x = +1, the sequence of values of dy/dx goes + 0 – so there is a local maximum of g(+1) =  at the point
at the point  .
.
I show a sketch of this curve at the end of the answers to this exercise.
It is another example of an odd function. If you turn the page upside down, the curve looks unchanged. It has its one moment of glory near the origin, and then sinks back to the x-axis.
(1) h(0) is undefined. There is a vertical asymptote of x = 0.
(2) h(x) = 0 if x + 4/x = 0 or x2 = 4.
There are no values of x on the x-axis which fit this equation, so h(x) never cuts the x-axis.
(3) We have already decided in (1) that we must exclude x = 0.
(4) As x → ∞ we have 4/x → 0 so h(x) gets closer and closer to the line y = x.
The same thing is true if x → – ∞, so y = x is an asymptote of y = h(x).
(5) dy/dx = h′(x) = 1 – 4/x2 so h′(x) = 0 if x = –2 or x = +2.
d2y/dx2 = 8/x3 so if x = –2, d2y/dx2 is negative.
Therefore, there is a local maximum of h(–2) = –4 at the point (–2, –4).
If x = +2, d2y/dx2 is positive so there is a local minimum of h(2) = 4 at the point (2,4).
Notice that the local minimum value is larger than the local maximum value! This is possible because the function h(x) has a discontinuity at x = 0. The curve does a jump there.
I show a sketch of this curve at the end of the answers to this exercise.
This looks quite like (c) but the change in sign makes an enormous difference to the behaviour of the function and the shape of its curve.
(1) p(0) is undefined, There is a vertical asymptote of x = 0.
(2) p(x) = 0 if x – (9/x) = 0 so x = 9/x so x2 – 9 = 0 so x = –3 or x = +3.
The curve cuts the x-axis at (–3, 0) and (+3, 0).
(3) We have already decided that we must exclude x = 0.
(4) As x → ∞, p(x) → x just like example (c) above.
(5) dy/dx =p′(x) = 1 + 9/x2 = 0 if 9/x2 = –1 or x2 = –9.
There are no values of x on the x-axis which fit this equation therefore this curve has no turning points.
I show a sketch of it at the end of the answers to this exercise.
Both (c) and (d) are also odd functions. Try turning the page upside down.
(e) y =f(x) = x2 ex
(1) f(0) = 0 so the curve passes through the origin. In fact, it has the repeated root x = 0 there, so it just touches the x-axis.
(2) has been answered by (1). There are no other solutions of f(x) = 0 since ex is never equal to zero.
(3) There are no values of x which must be excluded.
(4) x2ex becomes very large, as x becomes very large and positive.
When x becomes large and negative, ex gets smaller faster than x2 gets larger, so x2ex becomes very small.
(5) dy/dx = ex(2x + x2) = 0 if x = 0 or x = –2.
d2y/dx2 = (2x + x2)ex + ex (2 + 2x) = ex(x2 + 4x + 2).
If x = 0, d2y/dx2 is positive, so y = 0 is a local minimum.
If x = – 2, d2y/dx2 is negative, so y = 4/e2 is a local maximum.
This gives the sketch which I show below.
(1) I show a drawing for this question in diagram (1) below.

The volume of the box is given by V = (10 – 2x)(10 – 2x)x = l00x – 40x2 + 4x3.
dV/dx = 100 – 80x + 12x2 so dV/dx = 0 if 3x2 – 20x + 25 = 0
or (3x – 5)(x – 5) = 0. The solutions to this equation are x = 5 or  .
.
Clearly, x = 5 gives the minimum value. After removing these squares there would be no cardboard left!
Checking for absolute certain that  does give a maximum value for V, we have
does give a maximum value for V, we have  which is negative if
which is negative if 
So the maximum volume of the box is  to 1 d.p.
to 1 d.p.
(2) I show a cross-section along the axis of the cylinder in diagram (2) above.
If V is the volume of the cylinder, then V = πr2h.
We now need to use the physical relationship of the cylinder to the sphere to find r in terms of h and R.
We can do this by using Pythagoras’ Theorem in triangle AOB. This gives us

It is easier this time to substitute for r than h, so we have

Differentiating V with respect to h we get

Differentiating again, we get  which is negative since h is positive, so this value of h does give us the maximum volume of the cylinder.
which is negative since h is positive, so this value of h does give us the maximum volume of the cylinder.
Also,  we have
we have  . This gives
. This gives
The volume of the cylinder 
The volume of the sphere is  so the largest cylinder fills
so the largest cylinder fills 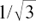 of the hollow inside the sphere.
of the hollow inside the sphere.  is 0.577 to 3 d.p. so it does fill more than half of it.
is 0.577 to 3 d.p. so it does fill more than half of it.
(3) In Section 5.D.(f) we showed that 4 sin t + 3 cos t = 5 sin(t + 0.6435).
The maximum value for a sin is one, so the maximum distance of the particle from the origin is 5 units.
(1) We want to solve 2x3 – 3x2 + 6x + 1 = 0, so we need to have some idea of the shape of f(x) = 2x3 – 3x2 + 6x + 1. We can see that f(0) = 1 and f′(x) = 6x2 – 6x + 6. Try using this to look for turning points if you got stuck finding the roots of this equation.

f’(x) is never equal to zero because its ‘b2 – 4ac’ is negative. Also, since the coefficient of x2 is positive, f’(x) is always positive, meaning that f(x) always has a positive gradient. It must look something like graph (1) below, and it only has one root.
f(–1) = –10, so this single root lies between x = 0 and x = –1 since f(x) is continuous, and it is closer to x = 0.
Using the Newton–Raphson rule starting with x1 = 0 gives us
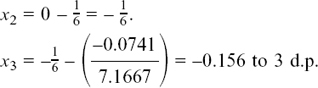
Repeating the process gives x = –0.156 to 3 d.p. again, so this is the required solution.
(2) The sketch of ex = 3 – x, in graph (2) below, shows the single solution.
We have to solve ex – 3 + x = 0, so we put f(x) = ex – 3 + x, giving f′(x) = ex + 1.
f(1) = e – 2 = 0.718 and f(0.5) = –0.851 so the solution lies between these two values since f(x) is continuous.

Repeating the process confirms this answer to 3 d.p.
(3) We can see from sketch (3) below that (i) has just the single solution of x = 0 while (ii) has three solutions symmetrically placed. (y = x is a tangent here, just like it was to y = tanh x.)
Let f(x) = sinh x – 2x so f’(x) = cosh x – 2.
Using a calculator, f(1) = –0.825, f(2) = –0.373 and f(3) = 4.018 so there is a solution between x = 2 and x = 3 since f(x) is continuous.
Starting with x1 = 2 gives 
Repeating the process three more times confirms the answer as x = 2.177 to 3 d.p.



In these answers, I shall use the shorthand ‘w.r.t’ to mean ‘with respect to’. (This is quite commonly done in maths.)
(1) Differentiating x2 y2 = 25 implicitly w.r.t. x gives

The gradient of x2y2 = 25 at (1, 5) is –5.
The equation of the tangent here is y – 5 = –5(x – 1) or y + 5x = 10.
(2) Differentiating x2 + 3xy – y2 = 2 implicitly w.r.t x gives
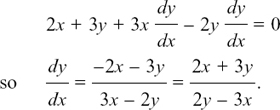
The gradient of the curve at (1, 2) is 
The equation of the tangent here is y – 2 = 8(x – 1) or y = 8x – 6.
(3) Differentiating 1/y + 2/x = 1 implicitly w.r.t. x gives

The gradient of the curve at (4, 2) is 
The equation of the tangent here is  or 2y + x = 8.
or 2y + x = 8.
Alternatively, multiplying the original equation by xy gives x + 2y = xy.
Differentiating this implicitly w.r.t. x gives
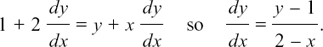
This looks alarmingly different from the first answer, but substituting x = 4 and y = 2 gives  as before, and therefore, of course, the equation of the tangent is the same.
as before, and therefore, of course, the equation of the tangent is the same.
Because x and y are related by fitting the equation of the given curve,  will give the same answer for any particular point, using either form.
will give the same answer for any particular point, using either form.
(a) Putting X = 2x – 5 and y = sin–1 X, we have

We must have –1 < 2x – 5 < 1 so 4 < 2x < 6 or 2 < x < 3.
(b) Putting X = 3x + 1 and y = cosh–1 X, we have

We must have 3x + 1 > 1 so x > 0.
(5) y = tanh–1 x so tanh y = x and differentiating implicitly w.r.t. x gives

(This working uses results from Section 8.D.(c).)
The answer we have found agrees with the answer to question (3) of Exercise 8.D.3 where we used
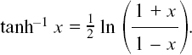
From Figure 8.D.8 we see that –1 < x < 1, and y = tanh–1 x has a positive gradient.
(6) (a) If y = xx then 1n y = 1n (xx) = x 1n x so 1/y dy/dx = In x + x (1/x) = In x + 1
Therefore dy/dx = y(ln x + 1) = (1n x + 1) xx.
(b) If y = 3x(x + 2) then In y = In (3x(x + 2)) = In 3 + In (x(x + 2)) = In 3 + (x + 2) In x.
(The splitting up is a bit tricky here! It uses both the first and third rules of logs.) Differentiating implicitly w.r.t. x gives
(c) y = (3x)(x + 2) so ln y = ln ((3x)(x + 2)) = (x + 2) ln 3x.
(This is what you also get for (b) if you aren’t careful!) Differentiating implicitly w.r.t. x gives

(1) Putting ‘t’ = 2t, we get 
Putting ‘t’ = –t, we get 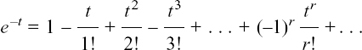
which is what we expect from the shape of its graph in Section 5.A.(a).
(3) f(t) = cos t, f′(t) = –sin t,f″(t) =– cos t and f‴ (t) = sin t.
Differentiating again brings us back to where we started.
We have f(0) = l, f′(0) = 0, f″(0) = – 1 and f‴(0) = 0, giving us the series

starting the count with r = 0. It’s a good idea to check that you’ve written down the rth term correctly by putting r = 0, 1 and 2 and checking that you do actually get the first three terms of the series. Then you can do any necessary tweakings to make it right.
(a) Putting ‘t’ =2t in the series above, we get

 .
.
as we expect it to be, from the shape of the graph in Section 5.A.(a).
(c) Similarly, putting ‘t’ = nt gives us

(4) f(t) = sinh t so f′(t) = cosh t and f″(t) = sinh t and so on.
From this, we have f(0) = 0, f′(0) = 1 and f″(0) = 0, and so on. This gives
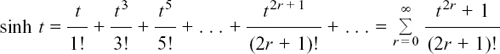
Adding the series gives 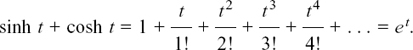
(1) If f′(x) = ex then y =f(x) = ex + C. Putting y = 2 and x = 0 gives 2 = e° + C=l + C so C = 1, giving us y = ex + 1.
(2) If g′(x) = sinh x then y = g(x) = cosh x + C. (See Sections 8.D.(a) and (b) if necessary.) Putting y = x = 0 gives 0 = cosh (0) + C = 1 + C so C = –1 giving y = cosh x – 1.
(3) If h’(x) = 3x2 then y = h(x) = x3 + C. Putting y = 2 and x = 1 gives 2 = 1 + C so C = 1 giving y = x3 + 1.
The three curves look like my drawings below.


(1) If x = 5t3 + 3t2 then (a) v = dx/dt = 15t2 + 6t and (b)
(2) If v = 3t2 + 2t then
(a) x = t3 + t2 + 5 since x = 5 when t = 0.
(b) a = dv/dt = 6t + 2.
(3) If a = d2 x/dt2 = 2t+1 then
(a) v = dx/dt = t2 + t + 5 since v = 5 when t = 0.
(b) 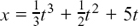 since x = 0 when t = 0.
since x = 0 when t = 0.
(a) x = 2e2t – 1 since x = 1 when t = 0 and e0 = 1.
(b) a = dv/dt = 8 e2t.
(5) If v = dx/dt = – sin t then
(a) x = cos t since x = 1 when t = 0.
(b) a = dv/dt = d2x/dt2 = – cos t so we have d2x/dt2 = – x.
The acceleration is towards the origin and equal to the distance from the origin so this is an example of SHM. (For more information on SHM see Sections 5.C.(b) and 8.A.(e).)
(6) v = dx/dt = cos (t + π/6) so
(a) x = sin (t + π/6) since x =  when t = 0.
when t = 0.
(b) a = dv/dt = d2x/dt2 = – sin (t + π/6) so, again, d2x/dt2 = – x giving another example of SHM.
The values of the sin, cos and tan of certain particular angles are often useful in integration. You will find these special values in Section 4.A.(g). Also, if you have trouble remembering which way the signs go when you differentiate and integrate sin and cos, remember the rule ‘Solve Damn Problem or Sin Differentiates Plus’. The other three are then easy to get.
The sketches for questions (3), (4), (5) and (6) are shown below.

The effect of the 2 is just to double the integral so doubling the area, as you can see above. It can be taken outside as a factor, giving 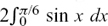 if we want.
if we want.
See the sketch above. Notice that this isn’t twice (3)! If you had any trouble with these sketches, you should go back to Section 5.C.(a).
using a calculator to evaluate sinh(1). The sketch is on the previous page. If you need help with this, go back to Sections 8 D.(a) and (b).
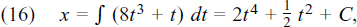 but x = 2 when t = 0 so C = 2.
but x = 2 when t = 0 so C = 2.
Thinking point after Exercise 9.A.3
In graph (c), a = 0 when  At this instant, the particle’s acceleration is zero. It changes from negative (the particle was under some kind of decreasing drag) to positive. (The particle is now receiving some kind of increasing forwards push.)
At this instant, the particle’s acceleration is zero. It changes from negative (the particle was under some kind of decreasing drag) to positive. (The particle is now receiving some kind of increasing forwards push.)
This is reflected in graph (b). We see the particle’s velocity decreasing up to 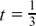 and then increasing again. The curve has a negative slope up to
and then increasing again. The curve has a negative slope up to 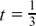 (dv/dt is negative), zero slope at
(dv/dt is negative), zero slope at  (dv/dt = 0), and a positive slope when
(dv/dt = 0), and a positive slope when 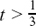 (dv/dt is positive.)
(dv/dt is positive.)
Graph (a) shows how this affects the distance travelled.
We have d2x/dt2 = dv/dt = a = 0 at  . The graph shows how the distance is being covered increasingly slowly as the time gets closer to
. The graph shows how the distance is being covered increasingly slowly as the time gets closer to  , and then faster again as the velocity picks up afterwards. The flattening in the graph (which gives the point of inflection where the tangent crosses the curve), shows that the change in the change of distance (that is, d/dt (dx/dt)), is happening increasingly slowly up to
, and then faster again as the velocity picks up afterwards. The flattening in the graph (which gives the point of inflection where the tangent crosses the curve), shows that the change in the change of distance (that is, d/dt (dx/dt)), is happening increasingly slowly up to  . It is zero at
. It is zero at 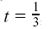 and then becomes positive afterwards. (Remember that d2x/dt2 is the same thing as dv/dt)
and then becomes positive afterwards. (Remember that d2x/dt2 is the same thing as dv/dt)
You could imagine that the particle puts its brakes on at t = 0, gradually raising the pedal until 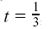 , when both its feet are instantaneously off the pedals. After
, when both its feet are instantaneously off the pedals. After 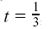 , it gradually increases its pressure on the accelerator, and vrooms off along the positive x-axis.
, it gradually increases its pressure on the accelerator, and vrooms off along the positive x-axis.
If we know what both x and v are when t = 0, we can move both forwards (differentiating), and backwards (integrating), between these particular curves. If we don’t have this specific knowledge then moving backwards from (c) would give v = 3t2 – 2t + C and x = t3 – t2 + Ct + K where C and K are constants representing the unknown amount of shift from the horizontal axis in both (b) and (a).
(1) ln |x + 3| + C
(2) 2ln |t –4| + C
(5) –4 In |3 – t| + C
(8) This one can’t be done because  (which gives a zero on the bottom of the fraction) lies between the limits of 1 and 3.
(which gives a zero on the bottom of the fraction) lies between the limits of 1 and 3.
(1) 8t
(3) 2e2t
(4) 5e5x+2
(5) –3e–3t

(10) 3 cos 3t
(11) –sin (x+π/3)
(12) 2 cos (2x+π/6)
(13) 2 sinh (2t+5)
(14) –5 cosh (8–5x)
(15) 3 sin2 x cos x
(16) sec2 x

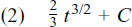

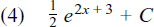
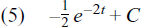

(7) ln |x+2|+C

(9) -ln |1-x|+C

(11) sin (x + π/6) + C

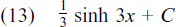
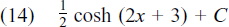
(15) sin 4 x + C




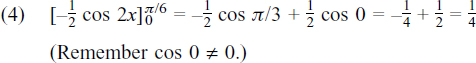
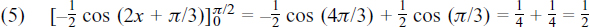



(You can see it will be this from Section 8.D.(a) and Section 9.A.(d).)


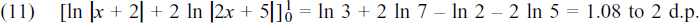
I’ll give you the answers to each of the thinking point integrals when we look at the technique for that particular one.
(1) Let t = 2x2 – 3 so dt/dx = 4x so we can replace 2x dx by  . Then
. Then

(2) Let t = 2x3 + 9 so dt/dx = 6x2.
Also, if x = 0 then t = 9 and if x = 2 then t = 25. So

(3) Let t = x – 4 so dt/dx = 1 and x = t + 4.
Also, if x = 4 then t = 0 and if x = 5 then t = 1. So

(1) I = In |x2 + 3x + 9| + C
(2) I = In |3x2 + 2x + 7| + C
(3) I = 2 In |x2 + 4x + 7| + C
(4) Let u = 3x2 + 4 so du/dx = 6x. Then

(5) Let u = x3 – 1 so du/dx = 3x2. Then
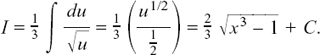
(6) Let u = 1 – 4x2 so du/dx = –8x. Then

(7) Let u = 1 – x2 so du/dx = –2x. Then

(8) Let u = x + x2 so du/dx = 1 + 2x. Then
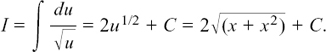
(9) Let u = 2x – 7 so du/dx = 2. Then

(4) Let u = cos 3x so du/dx = –3 sin 3x and  . Then
. Then

(5) Let u = 1 + sin x so du/dx = cos x. Then

(6) Let u = sin x so du/dx = cos x. Then
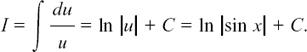
(8) cos 6x = 1 – 2 sin2 3x (using cos 2A = 1 – 2 sin2 A) so  , therefore
, therefore


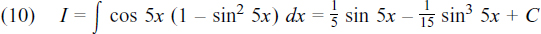
using cosh 2x = cosh2 x + sinh2 x = 2 cosh2 x – 1 from Section 8.D.(d).
(13) If t = sin x then dt/dx = cos x.
If x = π/6 then  and if x = 0 then t = 0, so
and if x = 0 then t = 0, so

so we have  to 3 d.p.
to 3 d.p.
(14) If t = cosh x then dt/dx = sinh x, so

(15) If x = 2 sin t then dx/dt = 2 cos t.
If x = 1 then  . If x = 0 then sin t = 0 so t = 0.
. If x = 0 then sin t = 0 so t = 0.

(16) If x = sin t then dx/dt = cos t.
If  then t = π/6 and if x = 0 then t = 0.
then t = π/6 and if x = 0 then t = 0.

(17) Let t = 4 + sin x so dt/dx = cos x.
If x = π/2 then t = 5 and if x = 0 then t = 4.

(18) If x = 2 cos t then dx/dt = –2 sin t.
If 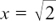 then t = π/4 and if x = 1 then t = π/3.
then t = π/4 and if x = 1 then t = π/3.
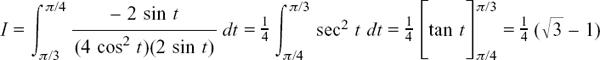
(1) ‘a’ = 5 so I = 3 sinh–1 (x/5) + C.
(2) ‘a’ = 3 so I=2 sin–1 (x/3) + C.
(3) ‘a’ = 4 so 
 so ‘x’ = x + 3 and ‘a’ = 1, giving tan–1 (x + 3) + C.
so ‘x’ = x + 3 and ‘a’ = 1, giving tan–1 (x + 3) + C.
= 2 ln |t2 + 8t + 17|– 13 tan–1 (t + 4) + C
 so ‘x’ = 3u + 4 and ‘a’ = 1 so dx/du = 3.
so ‘x’ = 3u + 4 and ‘a’ = 1 so dx/du = 3.
This gives 
(9) I will do this one using the second method I gave you where we put up with the fractions in order to use the tan–1 rule directly. We have
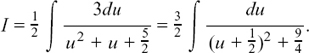
Now we put 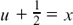 and
and  which gives us
which gives us
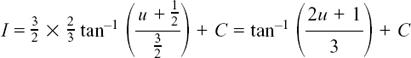
You might like to look at questions (8) and (9) being worked out the opposite way round in (2)(d) and (2)(i) of Exercise 8.D.3.
(3) This one often causes problems although it looks so simple. The important thing to notice about it is that it counts as top heavy, so we say
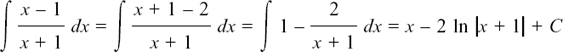


Don’t forget the 1 when you rewrite the integral after finding the partial fractions.
(10) First, factorise y3 –y2 as y2(y – 1). Then you will find

(12) Let t = ex so that dt/dx = ex. Remembering that e2x = (ex)2, we can then rewrite I in the form

Now we can combine this answer into a single log, and we must also replace t by ex. Doing this gives

If you had any difficulties finding any of these partial fractions, you will find that all of them come in the answers to the exercises of Section 6.E.
(Watch out for this one! The usual mistake is to say it is l/2x.)
Let u = 2t so du/dt = 2 and dv/dt = sin 3t so 
This gives 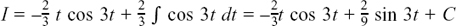 .
.
Let u = x so du/dx = 1 and dv/dx = ex so v = ex.
This gives 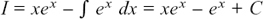
Let u = x2 so du/dx = 2x and dv/dx = sin x so v = –cos x.
This gives 
For  , we let u = x so du/dx = 1 and dv/dx = cos x so v = sin x.
, we let u = x so du/dx = 1 and dv/dx = cos x so v = sin x.
This gives 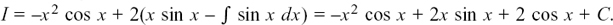 .
.

Let u = ln x so du/dx = 1/x and dv/dx = x2 so  .
.
This gives  .
.

Let u = ln x so du/dx = 1/x and dv/dx = 1/x so v = In x. Doing this gives

This one can also be done by substitution.
If we let ln x = t then dt/dx = 1/x and  as before.
as before.

Putting u = (ln x)2 and dv/dx = x2 gives du/dx = 2/x ln x and 
This then gives

from (a), given  .
.
Let u = tan–1 x so  and dv/dx = x2 so
and dv/dx = x2 so 
This gives 
This fraction is top-heavy so we cunningly rewrite the top as x(1 + x2) – x. This then gives us

If we let u = e–x and dv/dx = sin x, we have du/dx = –e–x and v = – cos x. This then gives us

Using integration by parts again on this second integral gives

I’ll let u = e–t so du/dt = –e–t and dv/dx = cosh 2t so 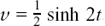 .
.
This gives 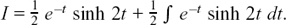
Now I integrate  by parts, and I must have u = e–t and dv/dt= sinh 2t so du/dt = –e–t and
by parts, and I must have u = e–t and dv/dt= sinh 2t so du/dt = –e–t and 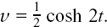 This then gives me
This then gives me 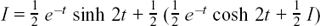 so
so 
I’ve swapped the order here to avoid minus signs. I can do this because the multiplication is the same either way round. This then gives me

using 
(1) 
Let u = cosn–1 x so du/dx = –(n – 1) cosn–2 x sin x and dv/dx = cos x so ν = sin x. Using integration by parts gives

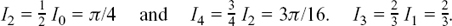
(c) The answers are the same as Example (1) because the curves for y = sinn x and y = cosn x from 0 to Π/2 are mirror images of each other in the line x = Π/4. I show this for the sin x/cos x and sin2 x/cos2 x pairs in the graphs below.

because cos(–nΠ) = cos nΠ since the cos graph is even.


(See Example (4) in Section 9.B.(c) for the method here.)
(see Example (8) in Section 9.B.(f) for the method here.)

because cos (n + m)x = cos [–(n + m)x], and the same for (n – m).
(d) (ii) If n = m, we have

This uses sin 2A = 2 sin A cos A from Section 5.D.(d).
(3) Let 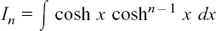 because we can easily integrate cosh x.
because we can easily integrate cosh x.
Now put u = coshn–1 x so du/dx = (n – 1) coshn – 2 x sinh x, and dv/dx = cosh x so v = sinh x. This gives
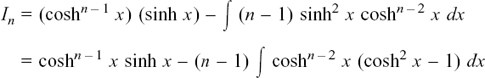
using cosh2 x – sinh2 x = 1 from Section 8.D.(a), so

and, rearranging, we have 
(4) We say

splitting the integral in a similar way to Example (3). But this time we do use integration by parts.
We let dv/dx = sec2 x so v = tan x and u = secn – 2 x. Then

because d/dx (sec x) = sec x tan x (Section 8.C.(e)). This gives us
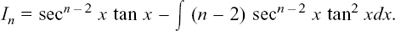
Now we use the identity tan2 x + 1 = sec2 x to get the integral all back in terms of sec x. This gives us

Now,

so, tidied up, we have

Finally, tan(Π/4) = 1 and tan 0 = 0 and sec(π = /4) and sec 0 = 1, so we have
and sec 0 = 1, so we have

In these answers, I shall quote the results we have just found in this section. You might need to show these yourself for exam purposes.
(1) This becomes 
(using t = tan π/4 = if x = π/2, and t = 0 if x = 0)

(2) This becomes 
(3) This becomes 

Exercise 9.C.1
Putting y = 1 when x = Π/6 gives C = 0 so we have y2 = 2 sin x.
If we let C = ln A, we get In |x/A|= 3t so x/A = e3t and x = Ae3t.
Putting x = 1 when t = 0 gives A = 1 so x = e3t.
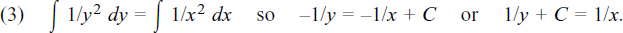 .
.
Putting  and x = 1 gives C = –1.
and x = 1 gives C = –1.
Putting y = 2 when x = 1 gives K = 7.
From this, y2 + 1 = Ax. Putting y = 0 and x = 1 gives A = 1 so y2 = x – 1
Putting y = 2 when x = 4 gives A = 2.
Putting y =π/ 2 when 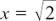 gives C = –1.
gives C = –1.
Putting r = 2 when θ = 0 gives In 2A = 0 so 2A = 1 and 
(9)You need to be a bit crafty here,and say
ex + y = ex ey so 
Using integration by parts gives

Putting y = 0 when x = 0 gives C = 2.
Putting y = 0 when x = 0 gives C = 0.
where A is a constant. c = c0 when t = t0 so A = l/c0.
 to find partial fractions.
to find partial fractions.
so 1= P(b – x) + Q(a – x).
Putting x = b gives  and putting x = a gives
and putting x = a gives 
so 
Now we can say that

so 
(We know physically that a > x and b > x.)
Using the second law of logs gives
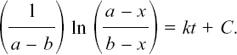
x = 0 when t = 0 so  so we have
so we have
 ,
,
which takes some getting through but it’s all right if you do it slowly and steadily!
(2) We start with dv/dt = a so 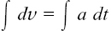 so v = at + C.
so v = at + C.
We know that v = u when t = 0 so C = u and we now have (a) v = u + at.
(The integration here is so straightforward that you don’t have to write in the step with the integral signs unless you want to.)
Now, 
Since s = 0 when t = 0, we have K = 0 and this gives us (b)  .
.
From (a) we have 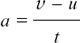 . Substituting this in (b) gives
. Substituting this in (b) gives

To get equation (d), you can substitute for t in (c) using (a). This gives
 .
.
You can also get (d) by using the Chain Rule to say dv/dt = dv/ds ds/dt = v dv/ds. From this,
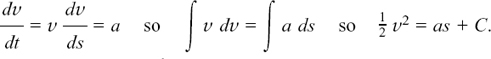
v = u when s = 0 so  and we get (d) v2 = u2 + 2as.
and we get (d) v2 = u2 + 2as.
It is quite likely that these four equations of motion will be very familiar to you. They describe the simplest case of what happens if a particle is accelerating, which is when this acceleration is constant.

They are only true if the acceleration is constant!
We’ve now done enough other examples for you to know that, if the amount of acceleration depends, for example, on the length of time you have been travelling, then you will get very different equations for the velocity and distance after a time of t.
One reason why the four equations above are physically useful is that they describe the motion of a body which is falling freely to the ground because of gravity, provided that we think that air resistance will have too slight an effect to matter. Whether this is true will depend on the type of object falling; a feather is designed to behave differently from a stone. (If they were falling in a vacuum, their behaviour would be identical; physics will tell you why this amazing thing is so.) I used the second of these equations of motion in the example of the ball thrown up in the air in Section 2.D.(g). In this particular case, a = –g because we are taking the upwards direction as positive, so the acceleration due to gravity is negative since it is downwards.
If the acceleration is constant, we can see particularly nicely how the gradients and areas relate to each other when we compare the graphs of velocity against time and distance against time.
I show these two graphs below.

In (a), you can see that the acceleration (which is the rate of change of velocity with time) is given by the gradient of the line. This means that
 .
.
The area under the line in graph (a) is given by adding the rectangle and the triangle, so it is  which is the same as the distance s.
which is the same as the distance s.
The gradient of the curve of the distance-time graph shown in (b) gives us the rate of change of distance with time, that is, the velocity v at any time t. We have 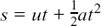 so ds/dt = u + at = v.
so ds/dt = u + at = v.
These two graphs have the same backwards and forwards links between them as the two graphs I used in Section 9.A.(c) to show you how differentiation and integration are the reverse processes of each other.
v = 0 when t = 0 so  and we have ln g – ln |g – kv\ = kt
and we have ln g – ln |g – kv\ = kt
so 
This gives v = g/k (1 – e –kt).
Since e–kt gets closer and closer to zero as t increases, v gets closer and closer to what is called its terminal value of g/k.
(4) We have 
so –1(2k) ln |g – kv2| = gx + C. Now, v = 0 when x = 0 so C = –1f(2k) ln g
so 
We’ll show in the second part of the question that g is always greater than kv2, so we can use ordinary brackets for this log since the expression inside the brackets is always positive.
The second part of this question starts by asking us to write v in terms of x. We have just shown that

This means that
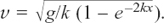
As x increases, e–2kx gets closer and closer to zero, so v gets closer and closer to the terminal velocity of  It never actually becomes equal to it (this is the limiting value), so it certainly never becomes greater than it, and this justifies the use of ordinary brackets for the log in the answer to the first part of this question.
It never actually becomes equal to it (this is the limiting value), so it certainly never becomes greater than it, and this justifies the use of ordinary brackets for the log in the answer to the first part of this question.
Notice that the two terminal velocities which we have found for v in the last two questions mean that such a drag force is physically possible. If v had been able to become any larger in either case, the net force on the particle would be pushing it back upwards. This would mean that the second force acting on the particle couldn’t be due to air resistance or viscosity because physically these forces can only slow down motion.


(1) (a) |3| = 3 and arg 3 = 0
(b) |–2| = 2 and arg (–2) = π
(c) |2j| = 2 and arg (2j) = π/2
(d) |–5j| = 5 and arg (–5j) = –π/2
(2) All four roots have a modulus of 1.
arg root (a) = 0, arg root (b) = π/2, arg root (c) = π, and arg root (d) = –π/2.
(3) For equation (1), z1 = 1 + j and z2 = 1 –j, so 
arg z1 = tan–1(1) = π/4 radians and arg z2 = –π/4 radians, by symmetry.
For equation (2), z1 = 2 + 3j and z2 = 2 – 3j so 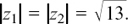
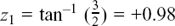 radians, so arg z2 = –0.98 radians by symmetry.
radians, so arg z2 = –0.98 radians by symmetry.
For equation (3), z1 = –2 + j and z2 = –2 –j so 
 radians, so arg z2 = –2.68 radians by symmetry.
radians, so arg z2 = –2.68 radians by symmetry.
For equation (4),  and
and  so
so 
 radians, so arg z2 = –1.99 radians by symmetry.
radians, so arg z2 = –1.99 radians by symmetry.
(1) 1 + 7j
(2) –6 + 5j
(3) 5 + 4j
(b) 7j
(c) 1
(d) 6 + 23j
(2) (a) You should have (i) w = 3 + 4j and |w| = 5, (ii) w = 15 + 8j and |w| = 17 and (iii) w = 7 + 24j and |w| = 25.
These give the three right-angled triangles with sides of lengths 3, 4 and 5 units, 8, 15 and 17 units, and 7, 24 and 25 units respectively.
(b) w = z2 = (x + jy)2 = x2 –y2 + 2xyj so u = x2 – y2 and v = 2xy.
If x and y are whole numbers, then |w|, u and v must also be whole numbers. (In case (iii), |z| is also a whole number.)
(c) You should find that drawing the Argand diagram for w gives you a triangle with sides of 119, 120 and 169 units, which is almost isosceles.
Drawing the Argand diagram for W gives you a remarkably long thin triangle with sides of 239, 28 560 and 28 561 units.
Both triangles have sides given by whole numbers and, of course, fit Pythagoras’ Theorem.
(3) You will know if you have the right answers for this question since you are just checking what you have already done.
I will go through one as an example in case you have any problems.
The roots of z2 + 2z + 6 = 0 from question (4) of Exercise 10.A.1 are 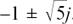 Putting
Putting  back into the equation gives
back into the equation gives

The other root checks similarly.
For this equation, a = 1, b = 2 and c = 6.
The sum of the roots is

The product of the roots is
 .
.
(4) The three roots are symmetrically placed so they will look like the ones in my drawing below.

Each root has a modulus of one and the arguments are 0, 2π/3 and – 2π/3. From this, root (1) = 1,

(These results use the sin and cos of π/3 from Section 4.A.(g) and the symmetry of the figure.)
If root (2) = ω, then |ω × ω| = 1 since |ω| = 1, and arg(ω × ω) = 2 argω = 4π/3.
The principal value of this argument is –2π/3, SO we see that ω × ω = ω2 or multiplying root (2) by itself gives root (3).
Equally, we could say that

Similarly, we can show that ω2 × ω2 = ω, using either of the above methods.
The thinking point at the end of Exercise 10.B.2 is answered in Section 10.D.(a).
The conjugates are all shown drawn in on this diagram. They are all reflections of each other in the real axis. Notice that this means that z5 is its own conjugate.
The working for the first four questions is exactly the same as in the example given just before the exercise. For each one, you just multiply the top and the bottom by the conjugate of the bottom and then tidy up.
The answers you should have are as follows.
(3) j
Notice that the answer to question (3) is the same as the result which we got by using the mod/arg form in Section 10.B.(c).
(5) Multiplying out the bottom gives  . Simplifying this gives
. Simplifying this gives  .
.
Adding these gives 
(See Section l.C.(c) if necessary.)
(1) The working for each of these is the same as in the example which I have already given, so I shall just give you the three pairs of answers here.
(a) 2 +j and –2 –j
(b) 4 +j and –4 –j
(c) – 3 + 2j and 3 – 2j.
Each pair of roots forms a straight line on its Argand diagram.
(2) The four Argand diagrams are shown below.
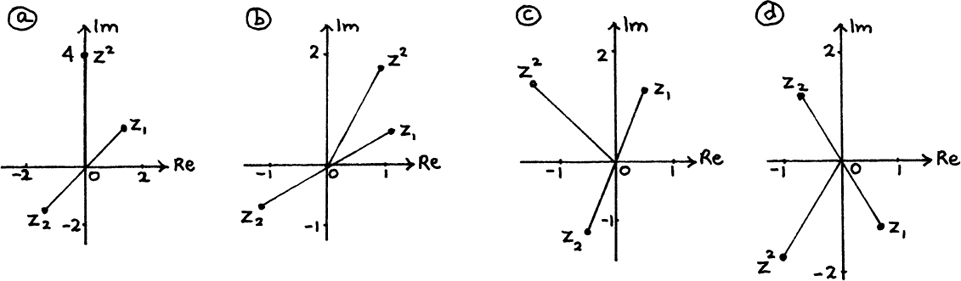
The working for each part goes as follows.
(a) z2 = 4j = [4, π/2] in mod/arg form, so z1 = [2, π/4] and z2 = [2, – 3π/4].
(1) cos 3θ +j sin 3θ = (cos θ+7 sin θ)3
= cos3 θ + 3 cos2 θ (j sin θ) + 3 cos θ (j sin θ)2 + (j sin θ)3
(a) Equating the real parts gives
cos 3θ = cos3 θ – 3cos θ sin2 θ = cos3 θ – 3 cos θ (1 – cos2 θ) = 4 cos3 θ – 3 cos θ.
(b) Equating the imaginary parts gives
sin 3θ = 3 cos2 θ sin θ – sin3 θ = 3sin θ – 4sin3 θ.
(2) cos 7θ +j sin 7θ = (cos θ + jsin θ)7
= cos7 θ + 7 cos6 θ (j sin θ) + 21 cos5 θ (j sin θ)2 + 35 cos4 θ (j sin θ)3 + 35 cos3 θ (j sin θ)3 + 21 cos2 θ (j sin θ)5 + 7 cos θ (j sin θ)7
Equating the real parts gives
cos 7θ = cos7 θ –21 cos5 θ sin2 θ + 35 cos3 θ sin4 θ – 7 cos θ sin6 θ
= cos7 θ –21 cos5 θ (1 – cos2 θ) + 35 cos3 θ (1– cos2 θ)2 – 7 cos θ (1 – cos2 θ)3 = cos7 θ –21 cos5 θ + 21 cos7 θ + 35 cos3 θ – 70cos5 θ + 35 cos7 θ – 7cos θ (1–3 cos2 θ + 3 cos4 θ – cos6 θ)
= 64cos7 θ –112 cos5 θ + 56 cos3 θ – 7 cos θ.
I have used the general rule for finding roots for these answers, but your answers will be equally good if you have used the geometry of your sketches. In either case, these sketches make a check on your arithmetic because you can quickly get a good idea of whether your calculated roots fit with what you have drawn.
(1) Let w = z3 = 27j so |w| = 27 and arg w = π/2 + 2kπ. Then

giving the three distinct solutions of 3ej(π/6) 3ej(5π/6) and 3e–j(π/2)
(2) Let w = z4 = 1 + j so  and arg w = π/4. This gives us
and arg w = π/4. This gives us

giving the four solutions 21/8 exp [j (π/16)], 21/8 exp [j (9π/16)], 21/8 exp [j(–7π/16)] and 21/8 exp [j (– 15π/16)].
(3) Let  so
so  and
and  radians to 3 d.p.
radians to 3 d.p.
So |z| = 1 and 
giving exp (–0.309j), exp (1.785j) and exp (2.403j).
The three roots in a + bj form to 2 d.p. are
cos (–0.309) +j sin (–0.309) = 0.95 – 0.30j,
cos (1.785) +j sin (1.785) = –0.21 + 0.98j,
cos (–2.403) +jsin (–2.403) = –0.74 – 0.67j.
(4) Let w = z5 = –4 + 4j so  so and arg w = 3π/4, giving us
so and arg w = 3π/4, giving us  , so that
, so that

giving 

(5) Let  so
so  and arg w = –2π/3 SO |Z| = 81/6 = 21/2,giving
and arg w = –2π/3 SO |Z| = 81/6 = 21/2,giving

with k = 0, –1, –2, 1, 2 and 3 to give the six distinct answers.
Now we know from the beginning of this section that w4 = –1 has the four roots of ejπ/4, ej(3π/4), ej(–π/4) and ej(–3π/4).
w4 = –4 will have the same four roots except that each one will be multiplied by  . Writing the first of these in a + bj form gives
. Writing the first of these in a + bj form gives  Similarly, the other three roots are –1 + j, 1 —j and –1 –j. Now, using the first root, we have
Similarly, the other three roots are –1 + j, 1 —j and –1 –j. Now, using the first root, we have

multiplying top and bottom by –j.
z–1 = (z + 1)(–1 +j) = –z + zj–1 +j so z(2–j)=j
giving

In a similar way, the other two roots come out as –1 –2j and  . You could save the extra working here by noticing that, if you had started by multiplying out, you would have got an equation for z with real coefficients. This means that its roots must come in conjugate pairs, which you will see these roots do indeed do.
. You could save the extra working here by noticing that, if you had started by multiplying out, you would have got an equation for z with real coefficients. This means that its roots must come in conjugate pairs, which you will see these roots do indeed do.
If you are at all doubtful about any of your sketches, use my solutions to draw yourself a new one so that you can check your own version.
(1) a = 1, b = –(3 – 2j) and c = –(1 + 3j) so

(2) a = 1, b = 3 – 4j and c = –(22 + 6j) so

(3) a=1,b = 2 + j and c = –(3 + j) so
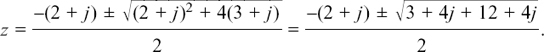
From (l)(b) from Exercise 10.C.1 we know that the square roots of 15 + 8j are 4 +j and –4 –j so we have
 or –3 –j.
or –3 –j.

We know that the square roots of 3 + 4j are ±(2 +j) from (1)(a) from Exercise 10.C.1 so

(5) a = 1, b = –1 and c = –1 + 3j so
 or –1 + j
or –1 + j
using (1)(c) from Exercise 10.C.1.
(6) a = 1, b = –2(1 +j) and c = 5(1 – 2j) so

Using the methods of Section l0.C.(a), the square roots of–5 + 12j are ±(2 + 3j), or you could also get these from multiplying the two roots of 5 – 12j from the previous answer by j. This gives
z = (l+j)±(2 + 3j) = 3+4j or –1–2j.
(7) If we put w = z2, we have w2 – (1 + j)w +j = 0. Using the formula gives
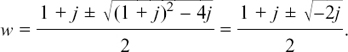
The square roots of–2j are 1 –j and –1 +j, either from using the methods of Section l0.C.(a) or drawing a little picture as I have below.

This gives  so z2 = 1 or j so
so z2 = 1 or j so 
(1) z = 1 + 2j is also a root of f(z) = z4 – 3z3 + az2 + bz – 30 = 0.
Therefore (z – (1 – 2j)) (z – (1 + 2j)) is a factor of f(z).
Multiplied together, this gives (z2 – 2z + 5) is a factor, so now we have
z4 – 3z3 + az2 + bz– 30 = (z2 – 2z + 5) (z2 + pz – 6).
Matching the terms in z3 gives us –3z3 = pz3 – 2z3 so p = –1. Therefore
z4 – 3z3 + az2 + bz–30 = (z2 – 2z + 5)(z2 – z – 6).
Matching the terms in z2 gives us az2 = 5z2 – 6z2 + 2z2 so a = 1.
Matching the terms in z gives us bz = 12z – 5z so b = 7.
The other two roots come from z2 – z – 6 = (z – 3)(z + 2) = 0 so they are z = 3 and z = –2.
(2) –j is also a root so (z –j) (z – (–j)) is a factor of the equation.
Multiplying these gives us
z4 + az3 + bz2 – 4z + 13 = (z2 + 1) (z2 + pz + 13).
Matching terms in z gives –4z = pz so p = –4. We now have
z4 + az3 + bz2 – 4z + 13 = (z2 + 1) (z2 – 4z + 13).
Matching terms in z3 gives az3 = –4z3 so a = –4.
Matching terms in z2 gives bz2 = z2 + 13z2 so b = 14.
The other two roots come from the solution of z2 – 4z + 13 = 0.
Using the formula (see Section 10.D.(b) if necessary) gives us the conjugate pair of z = 2 ± 3j
(3) z=1+j is also a root of the equation f(z) = 0 so (z – (1 –j)) (z – (1 + j)) = z2 – 2z + 2 is a factor of f(z).
This gives us

Matching terms in z gives 0 = –z + 2pz so 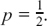
We now have

Matching the terms in z3 gives 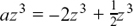 so
so 
Matching the terms in z2 gives  so
so 
For the remaining two roots, we solve  or 2z2 + z + 1 = 0.
or 2z2 + z + 1 = 0.
Using the formula gives the conjugate pair of 
Exercise 10.E.1
I show the sketch for each question below.

I show the sketches for each of the answers below.
(5) is the impossible question. You can’t have a length of –2 units!

(1) (a) Putting z = x + jy gives
|(x – 1) + jy| = |(x + 1) +jy|
so 
so (x – 1)2 + y2 = (x + 1)2 + y2 so 0 = 4x or x = 0.
This means that Re (z) = 0 so z may lie anywhere on the imaginary axis.
You can also think of this geometrically as all the points of intersection of lots of pairs of circles, each pair having the same radius but with centres at (1,0) and (– 1,0). This means that these points of intersection are all on the imaginary axis.
 = 1 so |z + 1| = |2z –j| so |(x + 1) +jy| = |2x +j (2y –1)
= 1 so |z + 1| = |2z –j| so |(x + 1) +jy| = |2x +j (2y –1)
so  so (x + 1)2 + y2 = 4x2 + (2y – 1)2.
so (x + 1)2 + y2 = 4x2 + (2y – 1)2.
Tidying up gives
3x2 – 2x + 3y2 – 4y = 0 so 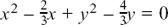
so 
so the path of z is a circle whose centre is at  and whose radius is
and whose radius is  units.
units.
(2) (a) |z| ≤ |z –j| so |x +jy| ≤ |x +j(y – 1)|
so  so
so  .
.
This means that 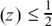 so z can lie anywhere in the region below the horizontal line
so z can lie anywhere in the region below the horizontal line 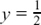 .
.
so  so x2 + y2 ≤ 2(x2 + (y – 1)2)
so x2 + y2 ≤ 2(x2 + (y – 1)2)
which tidied up gives 0 ≤ x2 + y2 – 4y + 2 or x2 + (y – 2)2 ≥ 2
so z can be anywhere outside or on the boundary of the circle with its centre at 2j and a radius of  units.
units.
(c) 2|z| ≤ |2z–j| so 2|x +jy| ≤ |2x +j(2y – 1)|
so  so 4(x2+y2) ≤ 4x2 + (2y– 1)2 so
so 4(x2+y2) ≤ 4x2 + (2y– 1)2 so 
We have  so z can lie anywhere on or below the horizontal line
so z can lie anywhere on or below the horizontal line  .
.
(3) We have 
This means that x must be equal to zero since the LHS of this equation is real. So we can say
 putting x = 0.
putting x = 0.
Tidying this fraction up by multiplying the top and bottom by the conjugate of the bottom gives
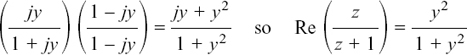
and we have
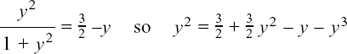
y = 1 is a solution, so we get (y – 1) (2y2 + y + 3) = 0.
Now 2y2 + y + 3 = 0 has no real roots. Therefore, since y is real, there is just the one solution to the given equation of z =j
(1) We can’t have z = 1 as this would give a zero underneath the fraction.
(2) (a) If z = 2 then w = 2+j
(b) If z = 1 –j then 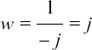 multiplying top and bottom by j
multiplying top and bottom by j
Simplifying the fraction by multiplying it top and bottom by (x – 1) – jy gives

(4) If u = v it must be true that x2–x+y2+y=x–y–1.
Therefore the path of z is given by the equation x2 – 2x + y2 + 2y + 1 = 0.
This is the same as (x – 1)2 + (y + 1)2 = 1 so, if u = v then z must lie on the circle whose centre is at 1 –j and whose radius is 1.
(5) I show the two Argand diagrams below. Again the little circle at z = 1 is to show that we have to exclude this point.

(6) (a) If z1=–j then w1 = 0.

I have shown all these pairs of points marked on the two Argand diagrams above. It looks as though the part of the z–circle which turns anticlockwise or positively from (0, –1) to the point which we aren’t allowed of (1,0) is giving the positive values on u = v, and the part which turns clockwise or negatively between these two points is giving the negative values on u = v.
It also looks as if the points are coming in the same order when they transfer from u = v to the circle of z, but we can see that equal distances apart on u = v don’t mean that we get equal distances apart on the z–circle. The circle is made up of a kind of variegated elastic.
You might like to see for yourself where points like w7 = 10 + 10j or w8 = –10 – 10j will go. (If you do this by first writing z in terms of w, you will find that this particular relationship has a rather special property.)
(7) If v = 0 then from (3) we get x – y – 1 = 0 so z lies on the line y = x –1.
We just have to exclude the point (1,0) where z = 1.
(8) If u = – v then from (3) we get
x2 – x + y2 + y = –x + y + 1 or x2 + y2 = 1.
This means that z lies on the unit circle about the origin, again excluding the point (1,0) where z = 1.
(9) You have sufficient information above to check your two sketches.
(10) Although the shapes of the paths of w and z are different, you will see from your two sketches that the angles at which these paths cut each other are unchanged. This is an example of an important general property of transformations like this.
All the questions which you have answered here are just on the edge of a whole new area of maths. You will learn the general theory of what is happening here if you do a course on complex variables.
(1) Since the particle is in equilibrium, the vector sum of the three forces acting on it is zero. Therefore they can be represented by the three sides of a triangle. I have drawn a sketch of this. You should always draw a sketch for this type of question.
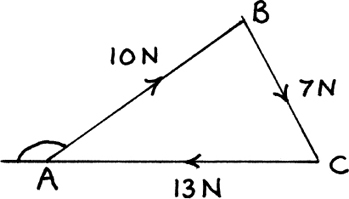
Notice that the arrows follow each other round, so giving zero displacement as the sum. It doesn’t matter that the directions shown in the sketch may not be the true directions of the forces since the sizes of the angles between the directions will be correct. The orientation of the triangle doesn’t affect these.
We are asked for the angle between the lines of action of the two largest forces. This is the obtuse angle at A We find this by first finding 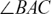 using the Cosine Rule. (See Section 4.B.(c) if necessary.) This gives us cos .A= (100 + 169 – 49)/260 so .A = 32.2° to 1 d.p. and the required angle is 180° – 32.2° = 147.8°.
using the Cosine Rule. (See Section 4.B.(c) if necessary.) This gives us cos .A= (100 + 169 – 49)/260 so .A = 32.2° to 1 d.p. and the required angle is 180° – 32.2° = 147.8°.
(2) Again, I have drawn a sketch. The three medians do all meet in a common point though we shall not need to use this result for this solution.

We have 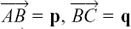 and
and  . Also
. Also  and
and  . So
. So 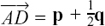 and
and  and
and 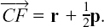
Therefore  which is the zero vector since the sum p + q + r gives zero displacement. Notice that this means that
which is the zero vector since the sum p + q + r gives zero displacement. Notice that this means that 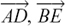 and
and 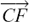 will also fit together to make a triangle!
will also fit together to make a triangle!
(3)Again, I have drawn a sketch. Remember that a, b and c are not the vectors giving the sides of the triangle ABC but the position vectors of A, B and C from the origin, O.

Let 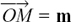 . Since M is the midpoint of AC, we have
. Since M is the midpoint of AC, we have  using the ratio theorem.
using the ratio theorem.
We_are told that G divides BM in the ratio 2 : 1 so, again using the ratio theorem, we have 
Since this answer is symmetrical in a, b and c, the position vectors of the points 2/3 of the way down the other two medians will also work out to the same result of 1/3 (a + b + c). Therefore the three medians of the triangle must intersect each other at the point G which lies 2/3 of the way down each of them from the corresponding vertex of the triangle.
G is called the centroid or centre of mass of triangle ABC. It is useful to remember that its position vector from the origin is given by  where a, b and c are the position vectors from the origin of A, B and C Notice that a, b and c are not the sides of the triangle.
where a, b and c are the position vectors from the origin of A, B and C Notice that a, b and c are not the sides of the triangle.
(4) Again, I have drawn a sketch.

From this, we have  but
but 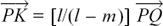 and
and  so
so

We now replace m by –m in this result to take account of KQ being in the opposite direction to PK and so PK : KQ = l : –m. Doing this gives us the same formula for k as we found for the internal division of PQ in Example (3). We now have
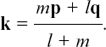
Exercise 11.A.2
(1) First we draw the sketch as I show below.

X, the magnitude of the component X of the velocity due east, is given by
X = 42 cos 28° = 37.1 knots to 1 d.p.
Y, the magnitude of the component Y of the velocity due north, is given by
Y= 42 sin 28° = 19.7 knots to 1 d.p.
(2) R = P + Q + S = (2i – 3j) + (4i + j) + (– 3i + 2j) = 3i. I show a sketch below.
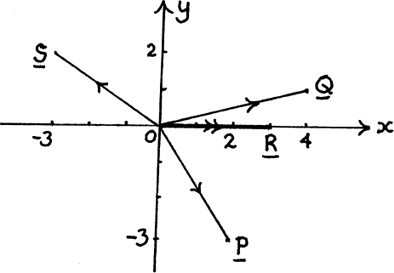
This vector addition works in exactly the same way as adding the complex numbers 2 – 3j, 4 +j and –3 + 2j, so getting 3, and then showing this result on an Argand diagram as in Section l0.B.(a).
(3) (a) We can write down the position vector from the origin of any point in two-dimensional space using multiples of f and g.
In particular, r = 4i + 9j = (2i + j) + 2(i + 4j) = f + 2g.
(b) Using multiples of g = i + 4j and h = 4i + 2j, it is again possible to find the position vector from the origin of any point in two-dimensional space.
In particular,  .
.
If you can’t spot this combination, you could find it in the following way.
Let r = 4i + 9j = a (i + 4j) + b (4i + 2j) where a and b are numbers which we have to find.
Matching up the i components gives us 4 = a + 4b.
Matching up the j components gives us 9 = 4a + 2b.
Solving these two simultaneous equations as in Section 2.C gives us a = 2 and b = 1/2.
Therefore 
(c) It is not possible to find the position vector of any point in two-dimensional space by using multiples of f = 2i + j and h = 4i + 2j because f and h are parallel to each other, with h = 2f. Only vectors which are also parallel to them can be described. In particular, since r is not parallel, it can’t be described in terms of f and h.
It is impossible to find numbers a and b such that 4i + 9j = a (2i + j) + b (4i + 2j) because the equations 2a + 4b = 4 and a + 2b = 9 have no solutions.
The two pairs of f and g and g and h are both linearly independent but the pair f and h are linearly dependent since h = 2f.
(1) If v = 4i + 3j then 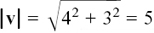 , and
, and  .
.
If w = 8i – 15j then  , and
, and  .
.
(2) Your sketch should be similar to my Figure 11.A.12 but with a = 4, b = 3 and c = 12. Then  . The unit vector is
. The unit vector is  .
.
(3) The resultant force F of P, Q and R is given by
F = P + Q + R = (4i + 3j + 7k) + (2i + 9j – 7k) + (4i – 7j + k) = l0i + 5j + k.
For the particle to be in equilibrium, we need to have an extra force of -F acting on it, so we need a fourth force of –l0i – 5j – k.
(4) We want the sum of p and q to be zero, with neither p nor q themselves equal to zero. An example of this is p = 2i–3j and q = –2i + 3j. We just need any pair such that p = –q.
If p and q are displacements, then making the displacement p followed by the displacement q brings you back to where you started.
If p and q are forces, they are equal and opposite so, if they both act on a particle, they will have no net effect. If they act on a larger body, and their lines of action are parallel rather than identical, then they will have a turning effect on the body and form what is called a couple.
(5) There is an infinite number of possibilities here!
One example is p = 2i + 3j–k, q = –3i – j + 4k and r = i – 2j–3k.
Since p, q and r have a vector sum of zero, we can say that r = –p –q. Therefore r can be described in terms of p and q and so these three vectors are not linearly independent. Geometrically, they form the sides of a triangle, since put together they give zero displacement. This means that they lie in a flat surface, a two-dimensional space inside our three-dimensional space. We can’t describe all points in three-dimensional space in terms of them because we can’t escape from this flat surface.

so
(b) Here b = 3a so the two vectors are parallel and the angle between them is zero. (The working out of a • b gives cos t = 1 so t = 0°.)
so cos t = 0 and t = 90°, so a and b are perpendicular.
so 
(e) Here b = –4a so the two vectors are parallel and in opposite directions so the angle between them is 180°. (The working out of a • b would give cos t = –1.)
(2) We have  and
and  and
and 
The dot product of  and
and  is (3 x 4) + (– 7 x 2) + (1 x 2) = 0 so the sides BC and CA are perpendicular. Since the triangle is right-angled, its area .A is given by
is (3 x 4) + (– 7 x 2) + (1 x 2) = 0 so the sides BC and CA are perpendicular. Since the triangle is right-angled, its area .A is given by  . We have
. We have 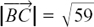 and
and  so A = 18.8 square units to 1 d.p.
so A = 18.8 square units to 1 d.p.
(3) (a) Working as in Example (4) we have
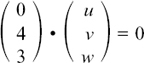 so
so and
and 
If we let v = 9 then w = –12 and u = 8. (These are the smallest whole number solutions.)
This gives n = 8i + 9j –12k and 
Therefore  or, equally good,
or, equally good,  .
.
(b) We have
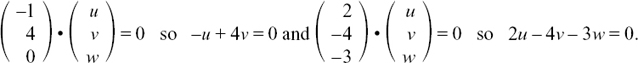
If we let u = 12 then v = 3 and w = 4. (These are the smallest whole number solutions.)
This gives n = 12i + 3j + 4k and 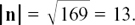 .
.
Therefore 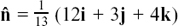 or, equally good,
or, equally good,  .
.
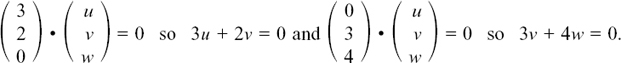
If we let u = 8 then v = –12 and w = 9.
This gives n = 8i – 12j + 9k and 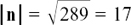
Therefore  with
with  an equally good solution.
an equally good solution.
Since both a and b here lie in the x–z plane, their cross product is parallel to the y-axis.
It's worth comparing your solutions to l(a), (b) and (c) below with those for 3 (a), (b) and (c) in Exercise 11.B.1. The questions are identical but the methods of solution are different.
(1) (a) A vector perpendicular to a and b is given by

From this we have  so the unit vector
so the unit vector  .
.
(b) A vector perpendicular to a and b is given by

From this we have  so the unit vector
so the unit vector  or
or  .
.
(c) A vector perpendicular to a and b is given by

From this we have 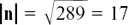 so the unit vector
so the unit vector 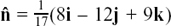 .
.
(d) A vector perpendicular to a and b is given by
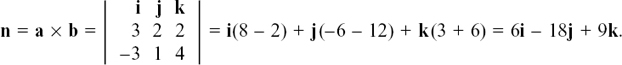
From this we have  so the unit vector
so the unit vector 
(e) A vector perpendicular to a and b is given by
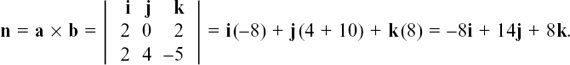
From this we have  so the unit vector
so the unit vector 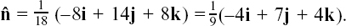
(f) A vector perpendicular to a and b is given by
From this we have  so the unit vector
so the unit vector 
(2) R = F1 + F2 + F3 = 6i + j + k.
Since F1 acts through the origin, its moment M1 about the origin is zero. M2, the moment of F2 about the origin, is given by

M3, the moment of F3 about the origin, is given by
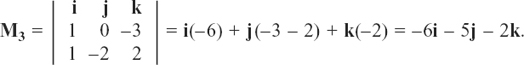
The total moment of the three forces about the origin is given by M1 + M2 + M3 = –18i + 2j –4k.
(3) We have a × b = c which gives us

For the vectors to be equal, the separate components must be equal, so this gives us the three equations

Now (2) + (3) gives 2z + 2y = 2 which is the same as (1) so there is more than one set of possible solutions to these equations. For example, x = 1, y = 2 and z = –1 will fit, giving a1 = i + 2j–k, and so also will x = 3, y = 1 and z = 0, giving a2 = 3i + j. There is no unique solution for a.
We can see why this is by looking at a physical example. Suppose that b is a force. Then c = a × b is the equation which gives the moment c of b about the origin with a being the position vector of any point on its line of action. So we see that there are an infinite number of possibilities for a.
If you draw a little sketch, you will see that the direction of the line of action of b is given by a2 – a1 = 2i – j + k. All the possible solutions for a are given by substituting different values for t in the equation a = i + 2j–k + t(2i – j + k). Notice that putting t = 0 gives a1 and putting t = 1 gives a2. We look at equations of lines in more detail in Section ll.C.(a).
(4) One possible vector which is perpendicular to u = 2i – j – 2k is v = 3i + 4j + k. Then a vector w which is mutually perpendicular to u and v is given by

Now 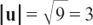 and
and  and
and  so the three mutually perpendicular unit vectors are given by
so the three mutually perpendicular unit vectors are given by  and
and  and
and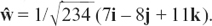
(1) Here is the working for u = (a × b) × c. We have

Now u = 3i + 2j + 4k = 3(i + 2j) + 4(–j + k) = 3a + 4b so u lies in the plane of a and b.
Next we find a × (b × c). Working out b × c first, we have

Now v = 4i – 2j = 4(–j + k) + 2(2i + j – 2k) = 4b + 2c so v lies in the plane of b and c.
(2) I will show the working out only for the answer to (1) given above.
We have found that a × (b × c) = 4i – 2j. Now, working with column vectors, we have

So (a • c) b – (a • b) c = 4b + 2c = 4(–j + k) + 2(2i + j – 2k) = 4i – 2j = a × (b × c). The working using the results from my numerical example is exactly similar.
(1) We work out a x b first and then use this to find (a × b) • c.

(2) We work out b x c first and then use this to find a • (b × c).
 .
.
(3) We work out a x e first and then use this to find b • (a× c).

The answer to (3) has the opposite sign to the answers to (1) and (2) because of the flip of a and c. The letters no longer follow each other round in the order abcabc . . .
(4) (a) a × b = d, say, where d is perpendicular to the plane in which a, b and c lie. So d × c lies in the plane, in a direction perpendicular to c.
(b) (a × b) • c = 0 since d is perpendicular to the plane but c lies in it, and so d • c = 0 The three vectors form a squashed box which has zero volume.
Exercise ll.C.l
(1) (a) Working with column vectors, we have

The components of the vectors are equal so x = 2 + t and y = –3 + 2t. From this we have t = x – 2 and so y = –3 + 2(x – 2) = 2x –7. The Cartesian equation of this line is y = 2x –7.
(b) Working with column vectors, we have

The components of the vectors are equal so x = 1 and y = –2 + 4t. The Cartesian equation of this line is x = 1. Since its direction vector is 4j, it is parallel to the y-axis. Each value of t gives a different point on the line. For example, putting t = 2 gives the point (1, 6).
(2) (a) The general vector equation of a line is r = a + td. There are lots of possible ways for writing the equation of the line asked for here depending on which points A you choose on the line to give a and how you choose the direction vector d.
We have y = 3x + 5. I will choose (0, 5) to be A so a = 5j. The gradient of the line is 3 so I'll let d = i + 3j.
This gives the vector equation of the line as r = 5j + t(i + 3j).
(b) This line has the Cartesian equation of 2y = 5x – 3. I will choose the point (1, 1) to be A giving a = i + j. The gradient of the line is 5/2 so I'll take d = 2i + 5j. This gives the vector equation of the line as r = i + j + t(2i + 5j).
(1) Let the point of intersection of the two lines be r = p. Working with column vectors, this gives us

The separate components of the vectors are equal so we have
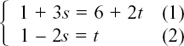
Using (2) to substitute in (1) gives 1 + 3s = 6 + 2(1 – 2s) so s =1 so t = –1. This gives P = 4i – j.
(2) L1 is given by r = i + 3j + t(2i + 3j). Let L2 be r = a + td. We know L2 passes through r = 3i + 4j so we can choose a = 3i + 4j.
Also, the lines are perpendicular so d • (2i + 3j) = 0. Therefore, a possible choice for d is –3i + 2j. (Or you could have 3i – 2j.)
The vector equation of L2 can be written as r = 3i + 4j + t(–3i + 2j).
(1) This pair of lines is parallel because their direction vectors are parallel.
(2) If this pair of lines meet at P with position vector p then we would have

For this equation to have a solution, each of the three components of the vectors must be equal, so we get

From (2) we have t = –3 and from (3) we have s = 1.
Now we must check whether these values fit (1). Substituting, we have the LHS = 1 and the
RHS = 1 so therefore the two lines do meet at the point with p = i – j + 2k.
(3) If this pair of lines meet at P with position vector p then we would have
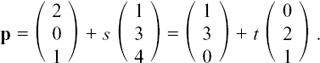
For this equation to have a solution, each of the three components of the vectors must be equal, so we get

From (1) we have s = –1 which gives t = –3 from (2).
Now we must check whether these values fit (3). Substituting, we have the LHS = –3 and the RHS = –3 so therefore the two lines do meet at the point with p = i – 3j – 3k.
(4) The two lines aren’t parallel since their direction vectors aren’t parallel. If this pair of lines meet at P with position vector p then we would have

For this equation to have a solution, each of the three components of the vectors must be equal, so we get
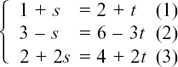
(1) + (2) gives 4 = 8 – 2t so t = 2. Substituting this in (2) gives s = 3. (It's important to stay with the same two equations to find a solution for s)
Now we check whether these values also satisfy (3). Substituting gives the LHS = 8 and the RHS = 8 so therefore the two lines do meet at the point with p = 4i + 8k.
(5) If this pair of lines meet at P with position vector p then we would have
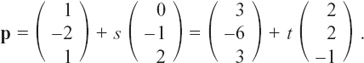
For this equation to have a solution, each of the three components of the vectors must be equal, so we get

From (1) we have t = –1. Substituting this value in (2) gives s = 6.
Now we check whether these values fit (3). Substituting, we have the LHS = 13 and the RHS = 4. Therefore these equations have no solution and this pair of lines does not meet. Since they are not parallel either, they are skew lines.
(1) (a) Letting r = xi + yj + zk we have

This gives us the three equations
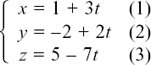
and rearranging each of these in the form t = . . . gives us the Cartesian equation

(b) Letting r = xi + yj + zk we have
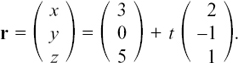
This gives us the three equations

and rearranging each of these in the form t = . . . gives us the Cartesian equation

(c) Letting r = xi + yj + zk we have
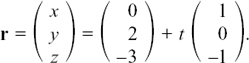
This gives us the three equations

and rearranging (1) and (3) in the form t = . . . and putting y = 2 gives us the Cartesian equation

(2) (a) We start by putting all three expressions equal to t. This gives us
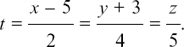
Working with t, and each of the x, y and z expressions in turn, gives us the three equations below for x, y and z.

Writing these equations as components in column vector form gives us

which is the vector equation of the line.
(b) Again we start by putting all three expressions equal to t. This gives us

Working with t, and each of the x, y and z expressions in turn, gives us the three equations below for x, y and z.

Writing these equations as components in column vector form gives us

which is the vector equation of the line.
(c) This time we put the first two expressions equal to t but, since z = 0, we must deal with it separately. We have
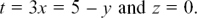
This gives us the three equations below for x, y and z.

Writing these equations as components in column vector form gives us

We could write this vector equation more neatly as

with  .
.
(3) (a)  gives us a direction vector for this line. Since A lies on it, we can write its vector equation as r = 4i + t(–4i + 3j).
gives us a direction vector for this line. Since A lies on it, we can write its vector equation as r = 4i + t(–4i + 3j).
(b) For the Cartesian equation of this line, working in column vectors, we have

This gives us the three equations

Rearranging these gives us the Cartesian equation
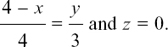
For each of these solutions, I shall use the vector equation of a plane in the form r = a + sd + te for reference.
(1) We have d = 2i – 4j – 3k and e = – i + 4j.
Now d × e gives n, a normal vector to the plane.
This gives us n = d × e = 12i + 3j + 4k. (The working is similar to Exercise 1l.B.3(l)(b).) Since |n| = 13 we have 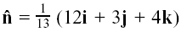 .
.
Also, for this plane we have a = 4i + j, so using 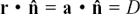 gives us
gives us

The perpendicular distance from the origin to this plane is 51/13 units.
(2) We have d = 3j + 4k and e = 3i + 2j.
Now d × e gives n, a normal vector to the plane.
This gives us n = d × e = –8i + 12j – 9k. (The working is similar to Exercise 11.B.3(l)(c).) Since |n| = 17 we have  .
.
Also, for this plane we have a = 2i – 3j – k, so using  gives us
gives us

So |D|, the perpendicular distance from the origin to this plane, is 43/17 units.
(3) We have d = 3i + 2j + 2k and e = –3i + j + 4k.
Now d × e gives n, a normal vector to the plane.
This gives us d × e = 6i – 18j + 9k. (The working is the same as Exercise 11.B.3(1)(d).) Since |n| = 21 we have 
Also, for this plane we have a = 3j + 6k, so using  gives us
gives us

We have found that the origin actually lies in this plane. You can see that this will be so because, for this plane, a = d + e, meaning that the vector a itself lies in the plane.
(1) (a) We have n = 3i + 2j – 6k so  and
and  . Therefore, to write the equation of the plane in terms of
. Therefore, to write the equation of the plane in terms of  , we must divide by 7.
, we must divide by 7.
This then gives us  The perpendicular distance from the origin to this plane is 6/7 units.
The perpendicular distance from the origin to this plane is 6/7 units.
(b) We have n = 8i – 15k so 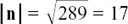 and
and 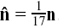 . Therefore, to write the equation of the plane in terms of
. Therefore, to write the equation of the plane in terms of  , we must divide by 17.
, we must divide by 17.
This then gives us 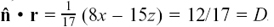 .The perpendicular distance from the origin to this plane is 12/17 units.
.The perpendicular distance from the origin to this plane is 12/17 units.
(c) We have n = 2i – j + 2k so 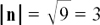 and
and 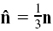 .Therefore, to write the equation of the plane in terms of
.Therefore, to write the equation of the plane in terms of 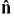 , we must divide by 3.
, we must divide by 3.
This then gives us  The perpendicular distance from the origin to this plane is 7/3 units.
The perpendicular distance from the origin to this plane is 7/3 units.
(d) We have n = 4i – 7j – 4k so 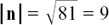 and
and  . Therefore, to write the equation of the plane in terms of
. Therefore, to write the equation of the plane in terms of  , we must divide by 9.
, we must divide by 9.
This then gives us 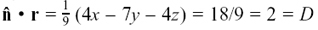 . The perpendicular distance from the origin to this plane is 2 units.
. The perpendicular distance from the origin to this plane is 2 units.
(2) The vectors  and
and  lie in the plane.
lie in the plane.  and
and 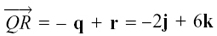 . A normal vector to the plane is given by
. A normal vector to the plane is given by

So we could most conveniently take n as  .
.
Now we use the equation for the plane of n • r = n • a. Here, we know that P, Q and R all lie in the plane, so any of p, q or r could be used for a.
I'll choose p. This gives

so the Cartesian equation of this plane is 3x – 6y – 2z = –21. Check for yourself that you get the same answer if you use q or r for a.
(1) Suppose L and Π meet at P with position vector p from the origin. Then p = xi + yj + zk must satisfy the equation of the line. So
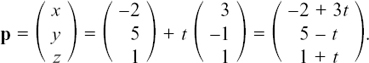
But p also satisfies the equation of the plane so we have

which gives t = 4. Therefore p = 10i + j + 5k.
(2) This time we have

But p also satisfies the equation of the plane so we have

which gives t = 1. Therefore p = 5i – 2j.
(3) This time we have

But p also satisfies the equation of the plane so we have

Which gives t = 1/2. Therefore 
(4) This time we have

But p also satisfies the equation of the plane so we have

which gives t = 3/2. Therefore 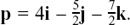
(1) The normal vectors to the two planes are given by n1 =2i – 5j + k and n2 = i + 2j – k.
Now, working out n1 × n2 gives 3i + 3j + 9k but it is neater to take d as i + j + 3k. The equations of the two planes are 2x – 5y + z = 4 and x + 2y – z = 5. Putting y = 0 in each of these gives

Adding (1) and (2) gives x = 3 so z = –2. Therefore the point with position vector 3i – 2k lies on both planes. We can now write the equation of the line of intersection as r = 3i – 2k + t(i + j + 3k).
(2) This time the two normal vectors are parallel since n2 = –3n1 so the two planes are parallel. (We can check that they aren’t in fact the same plane by multiplying the equation for Π3 by –3.) There is no line of intersection.
(3) The normal vectors to the two planes are given by n1 = 4i – j + k and n2 = 2i + 3j – 7k.
Now, working out n1 × n2 gives 4i + 30j + 14k but it is neater to take d as 2i + 15j + 7k.
The equations of the two planes are 4x – y + z = 9 and 2x + 3y – 7z = 8. Putting z = 0 in each of these gives

Adding (1) and –2 × (2) gives –7y = –7 so y = 1 so x = 5/2. Therefore the point with position vector (5/2) i + j lies on both planes. It is important to note here that we can’t double up this vector to make it look nicer because it is a position vector and we mustn’t alter its length. We can now write the equation of the line of intersection as r = (5/2) i + j + t (2i + 15j + 7k).
In this exercise, I'll refer to each pair of lines using r = a1 + sd1 and r = a2 + td2.
(1) For the two lines given in 1(b), we have d2 = –2d1 so the lines are parallel.
For the two lines given in 1(d), we have d1 • d2 = 0, so these two lines are perpendicular.
For the two lines given in 1(a), we have a1 • a2 = 0 so the position vectors from the origin to the known points on each line are perpendicular to each other. The lines themselves are skew.
For the two lines given in 1(c), we have a2 = –2a1 so the position vectors from the origin to the known points on each line lie on a straight line through the origin. The lines themselves are skew.
(2) Suppose the acute angle between the two lines is θ.
(a) We have
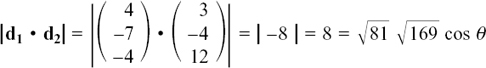
so cos θ = 8/117 and θ = 86.1° to 1 d.p.
(b) This time we have
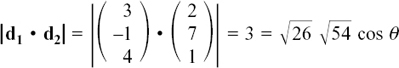
so  and θ = 85.4° to 1 d.p.
and θ = 85.4° to 1 d.p.
In my solutions, I'll refer to the normal vectors to each of the two planes as n1 and n2.
(1) To find θ, the acute angle between the planes, we have

so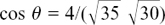 and θ = 82.9° to 1 d.p.
and θ = 82.9° to 1 d.p.
(2) This time we have

so the two planes are perpendicular.
(3) Now we have
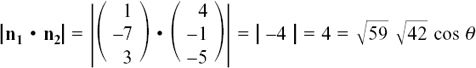
so  and θ = 85.4° to 1 d.p.
and θ = 85.4° to 1 d.p.
In each solution, I am using the rule |n • d| = |n||d| sin θ.
(1) We have n = 5i – 2j + k and d = 3i – 2j + k so

so to 1 d.p.
to 1 d.p.
(2) We have n = 2i – 5k and d = i – 7j + 3k so
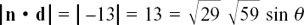 so
so to 1 d.p.
to 1 d.p.
(3) We have n = 3i – j + 2k and d = –5i + 7j + 11k. This time, we have |n • d| = 0 so sin θ = 0 so θ = 0. Either this line lies in the plane or it is parallel to it. We know that the point with position vector i + j + 2k lies on the line. Substituting x = 1, y = 1 and z = 2 in the equation 3x –y + 2z = 5 of the plane gives the LHS = 6, so this point does not lie in the plane. Therefore the line is parallel to the plane.
In all my solutions, I have let H be the foot of the perpendicular from P to line L with  In each case we have to find
In each case we have to find  .
.
(1) Since H lies on L we can say
 for some value of t.
for some value of t.
Therefore

Now 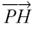 is perpendicular to 4i + j – 2k so we have
is perpendicular to 4i + j – 2k so we have
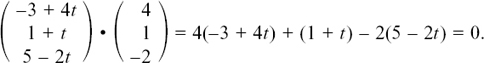
This gives t = 1 so 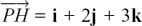 and
and  units to 2 d.p.
units to 2 d.p.
(2) This time we have
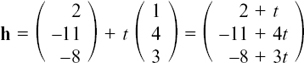 for some value of t.
for some value of t.

Now 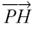 is perpendicular to i + 4j + 3k so we have
is perpendicular to i + 4j + 3k so we have

This gives t = 3 so  and
and  units.
units.
(3) Working as before, we have
 for some value of t
for some value of t

Now  is perpendicular to 2i + j – k so we have
is perpendicular to 2i + j – k so we have

This gives t = –2 so  is, in fact, the zero vector. P actually lies on line L so its distance from L is zero. The fast way to spot this answer was to notice that putting t = –2 in the equation of L gives the position vector of P so P lies on L.
is, in fact, the zero vector. P actually lies on line L so its distance from L is zero. The fast way to spot this answer was to notice that putting t = –2 in the equation of L gives the position vector of P so P lies on L.
(1) In both (a) and (b) we find the shortest distance of A from Π by working out 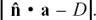
(a) Working as in the example I have given in the text, the equation of Π is 2x – y + 2z = 11 so n = 2i – j + 2k and |n| = 3.
Therefore  and
and 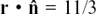 so D = 11/3 units.
so D = 11/3 units.
Next, the distance of A from O in the direction of 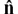 is given by
is given by  .
.
Working with column vectors, we have

Therefore the shortest distance of .4 from Π is |(–7/3) – (11/3)| = 6 units.
(b) The equation of Π is 3x + 12y – 4z = 79 so n = 3i + 12j – 4k and  . Therefore
. Therefore and
and  so D = 79/13 units. Next, the distance of A from O in the direction of
so D = 79/13 units. Next, the distance of A from O in the direction of  is given by
is given by  . Working with column vectors, we have
. Working with column vectors, we have
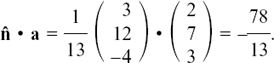
Therefore the shortest distance of A from Π is |(78/13) – (79/13)| = 1/13 units.
(2) (a) We can write the equation of the line AL as r = i – 24k + t(2i –2j + k). So, working with column vectors, we can say

The line intersects the plane where r = l.
There we have a value of t such that 2(1 + 2t) – 2(–2t) + (–24 + t) = 5 since l must also satisfy the equation of the plane.
This gives t = 3 so l = 7i – 6j – 21k and  .
.
Since 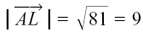 , the perpendicular distance from A to Π is 9 units.
, the perpendicular distance from A to Π is 9 units.
(This method provides an alternative way to find the shortest distance from a point to a plane. It also gives the position vector of the foot of the perpendicular from the point to the plane.)
(b) We can write the equation of the line BS as r = i + 4j + 2k + t(2i – 2j + k).
So, working with column vectors, we can say

The line intersects the plane where r = s.
There we have a value of t such that 2(1 + 2t) – 2(4 –2t) + (2 + t) = 5 since s must also satisfy the equation of the plane.
This gives t = 1 so s = 3i + 2j + 3k and 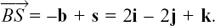
Since  , the perpendicular distance from B to Π is 3 units.
, the perpendicular distance from B to Π is 3 units.
Notice that  meaning that A and B are both on the same side of Π and therefore it is physically possible to have a ray reflected from A to B by striking plane Π.
meaning that A and B are both on the same side of Π and therefore it is physically possible to have a ray reflected from A to B by striking plane Π.
(c) The two triangles ALM and BMS are similar because both triangles are right-angled and the angles at M are equal. Therefore AL/BS = LM/MS but AL/BS = 9/3 = 3/1.
Since M divides LS in the ratio 3 : 1, we have

(d) We want to_find  . We can do this using the dot product of
. We can do this using the dot product of  and
and  . We have
. We have 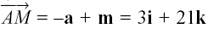 and
and  .
.

So  to 1 d.p.
to 1 d.p.
(1) Working as in the example I have given in the text, we have a1 = 3i + j + 7k and d1 = j + 2k for line L1.
For line L2, we have a2 = –i + 3j + 2k and d2 = 3i + 3j + 4k.
Plane Π1 has L1 and a shifted copy of L2 lying in it. This plane has a normal vector of n = d1 × d2. Working this out gives

Now  so
so .
.
Π1 has the equation  .
.
Plane Π2 has L2 and a shifted copy of L1 lying in it and has the same unit normal vector  .
.
Its equation is  .
.
The shortest distance between the two skew lines is |D1–D2| = |–3–2| = 5 units.
(2) Working as in the example I have given in the text, we have a1 = 3i + 2j – 5k and d1 = 2i + 4j – 5k for line L1.
For line L2, we have a2 = i – 3j – 5k and d2 = i + k.
Plane Π1 has L1 and a shifted copy of L2 lying in it. This plane has a normal vector of n = d1 × d2. Working this out gives

Now  so
so 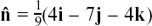 .
.
Plane Π2 has L2 and a shifted copy of L1 lying in it and has the same unit normal vector  .
.
Its equation is 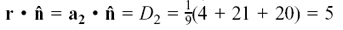 .
.
The shortest distance between the two skew lines is |D1 – D2| = |2 – 5| = 3 units.
(3) Working as in the example I have given in the text, we have a1 = 4i – j – 2k and d1 = 4i + 4j + 3k for line L1.
For line L2, we have a2 = –i + 2j + 3k and d2 = 4i – 3j + 3k.
Plane Π1 has L1 and a shifted copy of L2 lying in it. This plane has a normal vector of n = d1×d2. Working this out gives

Now 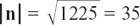 so
so 
Π1 has the equation 
Plane Π2 has L2 and a shifted copy of L1 lying in it and has the same unit normal vector  .
.
Its equation is  .
.
The shortest distance between the two skew lines is |D1 – D2| = |4 – (–3)| = 7 units.

Each of the problems in this exercise can also be solved by substituting directly into the general rule which I gave on p. 516. In each case, the shortest distance is found by calculating  .
.
