In many areas of science and engineering, information can be made clearer and more helpful if it is thought of in a mathematical way. Because this is so, algebra is extremely important since it gives you a powerful and concise way of handling information to solve problems. This means that you need to be confident and comfortable with the various techniques for handling expressions and equations.
The chapter is divided up into the following sections.
1.A Handling unknown quantities
(a) Where do you start? Self-test 1
(d) Working out in the right order
(f) Putting into brackets, or factorising
1.B Multiplications and factorising: the next stage
(b) Multiplying out two brackets,
(c) More factorisation: putting things back into brackets
(a) Equivalent fractions and cancelling down
(b) Tidying up more complicated fractions
(c) Adding fractions in arithmetic and algebra
(d) Repeated factors in adding fractions
1.D The three rules for working with powers
(a) Handling powers which are whole numbers
1.E The different kinds of numbers
(a) The counting numbers and zero
(b) Including negative numbers: the set of integers
(c) Including fractions: the set of rational numbers
(d) Including everything on the number line: the set of real numbers
(e) Complex numbers: a very brief forwards look
1.F Working with different kinds of number: some examples
(a) Other number bases: the binary system
(c) A useful application – simplifying square roots
(d) Simplifying fractions with √ signs underneath
All the maths in this book which is directly concerned with your courses depends on a foundation of basic algebra. In case you need some extra help with this, I have included two revision sections at the beginning of this first chapter. Each of these sections starts with a short self-test so that you can find out if you need to work through it.
It’s important to try these if you are in any doubt about your algebra. You have to build on a firm base if you are to proceed happily; otherwise it is like climbing a ladder which has some rungs missing, or, more dangerously, rungs which appear to be in place until you tread on them.
Answer each of the following short questions.
(A) Find the value of each of the following expressions if a = 3, b = 1, c = 0 and d = 2.
(1) a2
(2) b2
(3) ab + d
(4) a(b + d)
(5) 2c + 3d
(6) 2a2
(7) (2a)2
(8) 4ab + 3bd
(9) a + bc
(10) d3
(B) Find the values of each of the following expressions if x = 2, y = –3, u = 1, v = –2, w = 4 and z = –1.
(1) 3xy
(2) 5vy
(3) 2x + 3y + 2v
(4) v2
(5) 3z2
(6) w + vy
(7) 2x – 5vw
(8) 2y – 3v + 2z – w
(9) 2y2
(10) z3
(C) Simplify (that is, write in the shortest possible form).
(1) 3p – 2q + p + q
(2) 3p2 + 2pq – q2 – 7pq
(3) 5p – 7q – 2p – 3q + 3pq
(D) Multiply out the following expressions.
(1) 5(2g + 3h)
(2) g(3g – 2h)
(3) 3k2 (2k – 5m + 2n)
(4) 3k – (2m + 3n – 5k)
(E) Factorise the following expressions.
(1) 3x2 + 2xy
(2) 3pq + 6q2
(3) 5x2y – 7xy2
Here are the answers. (Give yourself one point for each correct answer, which gives a maximum possible score of 30.)
(A)(1) 9(2) 1(3) 5(4) 9(5) 6(6) 18(7) 36(8) 18(9) 3 (10) 8
(B)(1) –18(2) 30(3) –9(4) 4(5) 3(6) 10(7) 44(8) –6(9) 18 (10) –1
(C)(1) 4p – q(2) 3p2 – 5pq – q2 (3) 3p – 10q + 3pq
(D)(1) 10g + 15h(2) 3g2 – 2gh(3) 6k3 – 15k2m + 6k2n (4) 8k – 2m – 3n
(E)(1) x(3x + 2y)(2) 3q(p + 2q)(3) xy(5x – 7y)
If you scored anything less than 25 points then I would advise you to work through Section 1.A. If you made just the odd mistake, and realised what it was when you saw the answer, then go ahead to Section 1.B. If you are in any doubt, it is best to go through Section 1.A. now; these are your tools and you need to feel happy with them.
Much of what was tested above can be shown in the handling of the following. Try it for yourself. (You may have met this apparently mysterious kind of mind-reading before.)
(1) Think of a number between 1 and 10. (A small number is easier to use.)
(2) Add 3 to it.
(3) Double the number you have now.
(4) Add the number you first thought of.
(5) Divide the number you have now by 3.
(6) Take away the number you first thought of.
(7) The number you are thinking of now is . . . 2!
How can we lay bare the bones of what is happening here, so that we can see how it is possible for me to know your final answer even though I don’t know what number you were thinking of at the start?
It is easier for me to keep track of what is happening, and so be able to arrange for it to go the way I want, if I label this number with a letter. So suppose I call it x. Suppose also that your number was 7 and we can then keep a parallel track of what goes on.
|
You |
Me |
(1) |
7 |
x |
(2) |
10 |
x + 3 (My unknown number plus 3.) |
(3) |
20 |
2(x + 3) = 2x + 6 (Each of these show the doubling.) |
(4) |
27 |
2x + 6 + x = 3x + 6 (I add in the unknown number.) |
(5) |
9 |
|
(6) |
2 |
2 (The x has been taken away.) |
Both your 7 and my x have been got rid of as a result of this list of instructions.
My list uses algebra to make the handling of an unknown quantity easier by tagging it with a letter. It also shows some of the ways in which this handling is done.
There are certain rules which need to be followed in handling letters which are standing for numbers. Here I remind you of these.
Adding
a + b means quantity a added to quantity b.
a + a + b + b + b = 2a + 3b. Here, we have twice the first quantity and three times the second quantity added together. There is no shorter way of writing 2a + 3b unless we know what the letters are standing for.
We could equally have said b + a for a + b, and 3b + 2a for 2a + 3b. It doesn’t matter what order we do the adding in.
Multiplying
ab means a × b (that is, the two quantities multiplied together) and the letters are usually, but not always, written in alphabetical order.
In particular, a × 1 = a, and a × 0 = 0.
5ab would mean 5 × a × b.
It doesn’t matter what order we do the multiplying in, for example 3 × 5 = 5 × 3.
Working out powers
If numbers are multiplied by themselves, we use a special shorthand to show that this is happening.
a2 means a × a and is called a squared.
a3 means a × a × a and is called a cubed.
an means a multiplied by itself with n lots of a and is called a to the power n.
Little raised numbers, like the 2, 3 and n above, are called powers or indices. Using these little numbers makes it much easier to keep a track of what is happening when we multiply. (It was a major breakthrough when they were first used.) You can see why this is in the following example.
Then a2 = a × a and a3 = a × a × a so a2 × a3 = a × a × a × a × a = a5.
The powers are added. (For example, 22 × 23 = 4 × 8 = 32 = 25.)
We can write this as a general rule.
an × am = an+m
where a stands for any number except 0 and n and m can stand for any numbers.
In this section, n and m will only be standing for positive whole numbers, so we can see that they would work in the same way as the example above.
To make the rule work, we need to think of a as being the same as a1. Then, for example, a × a2 = a1 × a2 = a3 which fits with what we know is true, for example 2 × 22 = 23 or 2 × 4 = 8.
Also, this rule for adding the powers when multiplying only works if we have powers of the same number, so 22 × 23 = 25 and 72 × 73 = 75 but 22 × 73 cannot be combined as a single power.
If we have numbers and different letters, we just deal with each bit separately, so for example 3a2b × 2ab3 = 6a3b4.
Working out mixtures – using brackets
a + bc means quantity a added to the result of multiplying b and c. The multiplication of b and c must be done before a is added.
If a = 2 and b = 3 and c = 4 then a + bc = 2 + 3 × 4 = 2 + 12 = 14.
If we want a and b to be added first, and the result to be multiplied by c, we use a bracket and write (a + b)c or c(a + b), as the order of the multiplication does not matter. This gives a result of 5 × 4 = 4 × 5 = 20.
A bracket collects together a whole lot of terms so that the same thing can be done to all of them, like corralling a lot of sheep, and then dipping them. So a(b + c) means ab + ac. The a multiplies every separate item in the bracket.
Similarly, 2x(x + y + 3xy) = 2x2 + 2xy + 6x2y. The brackets show that everything inside them is to be multiplied by the 2x. It is important to put in brackets if you want the same thing to happen to a whole collection of stuff, both because it tells you that that is what you are doing, and also because it tells anyone else reading your working that that is what you meant. Many mistakes come from left-out brackets.
Here is another example of how you need brackets to show that you want different results.
If a = 2 then 3a2 = 3 × 2 × 2 = 12 but (3a)2 = 62 = 36. The brackets are necessary to show that it is the whole of 3a which is to be squared.
Try these questions yourself now.
(1) Put the following together as much as possible.
(a) 3a + 2b + 5a + 7c – b – 4c
(b) 3ab + b + 5a + 2b + 2ba
(c) 7p + 3pq – 2p + 2pq + 8q
(d) 5x + 2y – 3x + xy + 3y + 2xy
(2) If a = 2 and b = 1, find
(a) a3
(b) 5a2
(c) (5a)2
(d) b2
(e) 2a2 + 3b2
(3) Multiply the following together.
(a) (2x)(3y)
(b) (3x2 )(5xy)
(c) 3(2a + 3b)
(d) 2a(3a + 5b)
(e) 2p(3p2 + 2pq + q2)
If you are replacing letters by numbers, then you must stick to the following rules to work out the answer from these numbers.
(1) In general, we work from left to right.
(2) Any working inside a bracket must be done first.
(3) When doing the working out, first find any powers, then do any multiplying and dividing, and finally do any adding and subtracting.
Here are two examples.
Example (1)
If a = 2, b = 3, c = 4 and d = 6, find 3a(2d + bc) – 4c.
Example (2)
If x = 2, y = 3, z = 4 and w = 6, work out the value of x(2y2 – z) + 3w2.
We start by working out the inside of the bracket.
Now try the following yourself.
(1) If a = 2, b = 3, c = 4, d = 5 and e = 0 find the values of:
(a) ab + cd
(b) ab2e
(c) ab2d
(d) (abd)2
(e) a(b + cd)
(f) ab2d + c3
(g) ab + d – c
(h) a(b + d) – c
(2) Multiply out the following, tidying up the answers by putting together as much as possible.
(a) 3x(2x + 3y) + 4y(x + 7y)
(b) 5p2(2p + 3q) + q2(3p + 5q) + pq(p + 2q)
Check your answers to these two questions, before going on.
Questions (3) and (4) are very similar to (1) and (2) and will give you some more practice if you need it.
(3) If a = 3, b = 4, c = 1, d = 5 and e = 0 find the values of:
(a) a2
(b) 3b2
(c) (3b)2
(d) c2
(e) ab + c
(f) bd – ac
(g) b(d – ac)
(h) d2 – b2
(i) (d – b) (d + b)
(j) d2 + b2
(k) (d + b) (d + b)
(l) a2b + c2d
(m) 5e(a2 – 3b2 )
(n) ab + da
(4) Multiply out and collect like terms together if possible:
(a) 3a(2b + 3c) + 2a(b + 5c)
(b) 2xy(3x2 + 2xy + y2 )
(c) 5p(2p + 3q) + 2q(3p + q)
(d) 2c2 (3c + 2d) + 5d2 (2c + d)
We shall need to be able to do more complicated things with minus signs than we have met so far, so here is a reminder about dealing with signed numbers.
Ordinary numbers, such as 6, are written as +6 in order to show that they are different from negative numbers such as –5. If the sign in front of a number is +, then it can sometimes be left out. (We don’t speak of having +2 apples, for example.) A negative sign can never be left out, in any working combination of numbers.
One way of understanding how signed numbers work is to think of them in terms of money. Then +2 represents having £2, and –3 represents owing £3, etc.
So using brackets to keep each number and its sign conveniently connected, we have for example:
| (+2) + (+5) = (+7) | Ordinary addition. |
| (–3) + (–7) = (–10) | Adding two debts. |
| (+4) + (–9) = (–5) | You still have a debt. |
| (+3) – (–7) = (+10) | Taking away a debt means you gain. |
The same idea carries through to multiplication (which can be thought of as repeated addition, so 3 × 2 means 3 lots of 2, or adding 2 to itself three times).
Some examples are:
| (+2) × (–3) = (–6) | Doubling a debt! |
| (–3) × (+5) = (–15) | Taking away 3 lots of 5. |
| (–3) × (–7) = (+21) | Taking away a debt of 7 three times. |
The rule for multiplying signed numbers
Two signs which are the same give plus and two different signs give minus.
Here are two examples of this in action.
(1) 3a – 2(b – 2a) + 7b = 3a – 2b + 4a + 7b = 7a + 5b.
(2) 2p – (p + 2q – m).
Here, you can think of the minus sign outside the bracket as meaning –1, so that when the bracket is multiplied by it, all the signs inside it will change.
We get 2p – p – 2q + m = p – 2q + m.
Now try the following questions.
Multiply out the following, tidying up the answers as much as possible.
(1) 2x – (x – 2y) + 5y
(2) 4(3a – 2b) – 6(2a – b)
(3) 6(2c + d) – 2(3c – d) + 5
(4) 6a – 2(3a – 5b) – (a + 4b)
(5) 3x(2x – 3y + 2z) – 4x(2x + 5y – 3z)
(6) 2xy(3x – 4y) – 5xy(2x – y)
(7) 2a2 (3a – 2ab) – 5ab(2a2 – 4ab)
(8) –3p – (p + q) + 2q(p – 3)
The process described in the previous section can be done in reverse, so, for example, xy + xz = x(y + z).
This reverse process is called factorisation and x is called a factor of the expression, that is, something you multiply by to get the whole answer, just as 2, 3, 4, 6 are all factors of 12. We can say 12 = 3 × 4 = 2 × 6. Each factor divides into 12 exactly.
Here are three examples showing this process happening.
(1) 3a2 + 2ab = a(3a + 2b). This is as far as we can go.
(2) 3p2q + 4pq2 = pq (3p + 4q) factorising as much as possible.
(3) 4a2b3 – 6a3b2 = 2a2b2(2b – 3a) factorising as far as possible.
xy + x = x(y + 1) not x(y + 0) because x × 1 = x but x × 0 = 0.
It is useful to remember that factorisation is just the reverse process to multiplying out. If you are at all doubtful that you have factorised correctly, you can check by multiplying out your answer that you do get back to what you started with originally.
Here’s an example.
If you factorise 3c2 + 2cd + c, which of the following gives the right answer?
(1) 3c(c + 2d + 1)
(2) c(3c + 2d)
(3) c(3c + 2d + 1).
Multiplying out gives (1) 3c2 + 6cd + 3c (2) 3c2 + 2cd and (3) 3c2 + 2cd + c so (3) is the correct one.
Factorise the following yourself, taking out as many factors as you can.
(1) 5a + 10b
(2) 3a2 + 2ab
(3) 3a 2 – 6ab
(4) 5xy + 8xz
(5) 5xy –10xz
(6) a2 b + 3ab2
(7) 4pq2 – 6p2 q
(8) 3x2 y3 + 5x3y2
(9) 4p2q + 2pq2 – 6p2q2
(10) 2a2b3 + 3a3b2 – 6a2b2
This section also starts with a self-test. It is sensible to do it even if you think you don’t have any problems with these because it won’t take you very long to check that you are in this happy state. It’s a good idea to cover my answers until you’ve done yours.
(A) Multiply out the following
(1) (2x + 3y) (x + 5y)
(2) (3a – 5b)(2a – b)
(3) (3x + 2)2
(4) (2y – 5)2
(5) (2p2 + 3pq)(q2 – 2pq)
(B)
(1) x2 + 9x + 14
(2) y2 + 8y + 12
(3) x2 + 8x + 16
(4) p2 + 13p + 22
(C)
(1) 2x2 + 7x + 3
(2) 3a2 + 16a + 5
(3) 3b2 + 10b + 7
(4) 5x2 + 8x + 3
(D)
(1) x2 + x – 2
(2) 2a2 + a – 15
(3) 2x2 + 5x – 12
(4) p2 – q2
(5) 6y2 – 19y + 10
(6) 4x2 – 81y2
(7) 6x2 – 19x + 10
(8) 4x2 – 12x + 9
As in the first test, give yourself one point for each correct answer so that the highest total score is 21. Again, if you got 16 or less, work through this following section.
If you are in any doubt, it is much better to get it sorted out now, because lots of later work will depend on it.
These are the answers that you should have.
(A)
(1) 2x2 + 13xy + 15y2
(2) 6a2 – 13ab + 5b2
(3) 9x2 + 12x + 4
(4) 4y2 – 20y + 25
(5) 3pq3 – 4p3 q – 4p2q2
(B)
(1) (x + 2)(x + 7)
(2) (y + 2)(y + 6)
(3) (x + 4)2
(4) (p + 2)(p + 11)
(C)
(1) (2x + 1)(x + 3)
(2) (3a + 1)(a + 5)
(3) (3b + 7)(b + 7)
(4) (5x + 3)(x + 1)
(D)
(1) (x + 2)(x - 1)
(2) (2a - 5)(a + 3)
(3) (2x - 3)(x + 4)
(4) (p - q)(p + q)
(5) (3y - 2)(2y - 5)
(6) (2x - 9y)(2x + 9y)
(7) (3x - 2)(2x - 5)
(8) (2x - 3)2
To multiply out two brackets, each bit of the first bracket must be multiplied by each bit of the second bracket, so
(a + b)(c + d) = ac + bd + ad + bc.
The ac + bd + ad + bc can be written in any order.
You could also think of this process, if you like, as
(a + b)(c + d) = a(c + d) + b(c + d) = ac + ad + bc + bd.
You can see this working numerically by putting a = 1, b = 2, c = 3 and d = 4.
(a + b)(c + d) = (1 + 2)(3 + 4) = 3 × 7 = 21
and
ac + ad + bc + bd = 3 + 4 + 6 + 8 = 21.
Also, you can see that the order of doing the multiplying doesn’t matter, since
ac + bd + bc + ad = 3 + 8 + 6 + 4 = 21 too.
Figure 1.B.1 shows this process happening with areas. (a + b)(c + d) gives the total area of the rectangle.
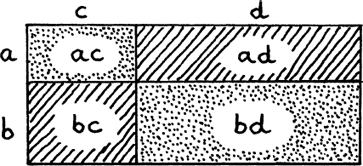
Figure 1.B.1
Exactly the same system is used to work out (a + b)2. We have
(a + b)2 = (a + b)(a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2
We can see this working in Figure 1.B.2.
Figure 1.B.2
We can see the two squares and the two same-shaped rectangles.
Don’t forget the middle bit of 2ab.
The diagram shows that (a + b)2 is not the same thing as a2 + b2. In a similar way, we have
(a – b)2 = (a – b)(a – b) = a2 – 2ab + b2.
What happens if the signs are opposite ways round, so we have (a + b)(a – b)?
We get
(a + b)(a – b) = a2 – b2
because the middle bits cancel out.
This result is called the difference of two squares.
You need to be good at spotting examples of this because it is of very great importance in simplifying and factorising in many different situations.
To help you to get good at this, here are some further examples.
Put back into two brackets (1) x2 – 9y2,(2) 49a2 – 64b2.
The answers are (1) (x + 3y)(x – 3y) and (2) (7a + 8b)(7a – 8b).
Check these are true by multiplying them back out, and then try the following ones for yourself.
(1) x2 – y2
(2) 4a2 – 9b2
(3) 16p2 – 9q2
(4) 16a2 – 25b2
(5) 36p2 – 100q2
These are the answers that you should have.
(1) (x + y)(x – y)
(2) (2a + 3b)(2a – 3b)
(3) (4p + 3q)(4p – 3q)
(4) (4a + 5b)(4a – 5b)
(5) (6p + 10q)(6p – 10q)
In each case, the brackets can equally well be written the other way round since the letters are standing for numbers.
Here is a more complicated example of multiplication of brackets.
(3x + xy)(xy + y2 ) = 3x2y + x2y2 + 3xy2 + xy3
Again, the basic strategy is the same. Each bit or chunk of the first bracket is multiplied by each bit or chunk of the second one.
(This can be checked by putting x = 2 and y = 3. Each side should come to 180.)
Multiply out the following pairs of brackets.
(1) (x + 2)(x + 3)
(2) (a + 3)(a – 4)
(3) (x – 2)(x – 3)
(4) (p + 3)(2p + 1)
(5) (3x – 2)(3x + 2)
(6) (2x – 3y)(x + 2y)
(7) (3a – 2b)(2a – 5b)
(8) (3x + 4y)2
(9) (3x – 4y)2
(10) (3x + 4y)(3x – 4y)
(11) (2p2 + 3pq)(5p + 3q)
(12) (2ab – b2)(a2 – 3ab)
(13) (a + b)(a2 – ab + b2)
(14) (a – b)(a2 + ab + b2)
(15) Try working through the following steps.
(a) Think of a positive whole number, and write down its square.
(b) Add 1 to your original whole number, and multiply the result by the original number with 1 taken away from it.
(c) Repeat this process twice more.
(d) Describe in words what seems to be happening.
(e) Must this always happen whatever your starting number is?
Show that it must by taking a starting number of n so that you can see exactly what must happen every time.
Again, the reverse process to multiplying out two brackets is called factorisation. Very often it is important to be able to replace a more complicated expression by two simpler expressions multiplied together.
We have already done some examples of this, when we were working with the difference of two squares in the previous section.
What happens, though, if there is a middle bit to be sorted out?
For example, suppose we have x2 + 7x + 12.
Can we replace this expression by two multiplied brackets?
We would have x2 + 7x + 12 = (something) (something), and we have to find out what the somethings must be.
We can see that we will need to have x at the beginning of each of the brackets.
Both signs in the brackets are positive since the left-hand side is all positive, so at the ends we need two numbers which when multiplied give +12 and which when added give +7. What two numbers will do this?
+3 and +4 will do what we want, so we can say x2 + 7x + 12 = (x + 3) (x + 4), giving us an alternative way of writing this expression.
Equally, x2 + 7x + 12 = (x + 4)(x + 3).
The order of the brackets is not important because multiplication of numbers gives the same answer either way on. For example, 2 × 3 = 3 × 2 = 6.
In all the questions which follow, your answer will be equally correct if you have your brackets in the opposite order from mine.
Try putting the following into brackets yourself.
(1) x2 + 8x + 7
(2) p2 + 6p + 5
(3) x2 + 7x + 6
(4) x2 + 5x + 6
(5) y2 + 6y + 9
(6) x2 + 6x + 8
(7) a2 + 7a + 10
(8) x2 + 9x + 20
Now, a step further! Suppose we have 2x2 + 7x + 3 = (something) (something). This time we need 2x and x at the fronts of the brackets to give the 2x2. If it is possible to factorise this with whole numbers then the ends will need 1 and 3 to give 1 × 3 = 3.
Do we need (2x + 3)(x + 1) or (2x + 1)(x + 3)?
Multiplying out, we see that
(2x + 3)(x + 1) = 2x 2 + 5x + 3 which is wrong,
(2x + 1)(x + 3) = 2x 2 + 7x + 3 so this is the one we need.
Try factorising these for yourself now.
(1) 3x2 + 8x + 5
(2) 2y2 + 15y + 7
(3) 3a2 + 11a + 6
(4) 3x2 + 19x + 6
(5) 5p2 + 23p + 12
(6) 5x2 + 16x + 12
The system is exactly the same if the expression involves minus signs. Here are two examples showing what can happen.
Example (1)
Factorise x2 – 10x + 16.
Here we require two numbers which when multiplied give +16, and which when put together give –10. Can you see what they will be?
Both the numbers must be negative, and we see that –2 and –8 will fit the requirements. This gives us x2 – 10x + 16 = (x – 2)(x – 8) = (x – 8)(x – 2).
Example (2)
Factorise x2 – 3x – 10.
Now we require two numbers which when multiplied give –10 and which when put together give –3. Can you see what we will need?
This time, to give the –10, they need to be of different signs.
We see that –5 and +2 will do what we want, so we have
x2 – 3x – 10 = (x – 5)(x + 2) = (x + 2)(x – 5).
Remember that it makes no difference which way round you write the brackets.
Now try factorising the following yourself.
(1) x2 – 11x + 24
(2) y2 – 9y + 18
(3) x2 –11x + 18
(4) p2 + 5p – 24
(5) x2 + 4x – 12
(6) 2q2–sq–3
(7) 3x2 – 10x – 8
(8) 2a2–3a–5
(9) 2x2 – 5x – 12
(10) 3b2 – 20b + 12
(11) 9x2–25y2
(12) 16x4 – 81y4, a sneaky one!
Very many students find handling fractions in algebra quite difficult, but it is important to be able to simplify these fractions as far as possible. This is because they often come into longer pieces of working and, if you do not simplify as you go along, the whole thing will become hideously complicated. It is only too likely then that you will make mistakes.
This section is designed to save you from this. You will find that if you understand how arithmetical fractions work then using fractions in algebra will be easy. If you have been using a calculator to do fractions, it’s likely that you will have forgotten how they actually work, so I’ve drawn some little pictures of what is happening to help you.
If you think that you can already work well with fractions, try some of each exercise to be sure that there are no problems before you move on to the next section.
Because we are looking here at what we can and can’t do with fractions, we shall need to use the sign ≠.
The sign ≠ means ‘is not equal to’.
means a divided by b.
a is called the numerator and b is called the denominator.
In dividing, the order that the letters are written in matters, unlike a × b, which is the same as b × a.
The order also matters with subtraction; a – b is, not the same as b – a unless both a and b are zero. But a + b = b + a always.
For example, 2 × 3 = 3 × 2 and 2 + 3 = 3 + 2, but 
and 2 – 3 ≠ 3 – 2.
Also,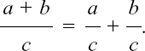 
For example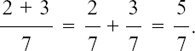
The whole of a + b is divided by c, and so we can get the same result by splitting this up into two separate divisions. The line in the fraction is effectively working as a bracket.
In fact, it is safer to write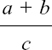 
as 
if it is part of some working.
In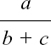 
, the number a is divided by the whole of the number (b + c).
From this, we see that
You can check this by putting a = 4, b = 2, c = 3, say.
Dividing by c is the same as multiplying by 1/c so
For example, if a = 6, b = 4, and c = 2 then
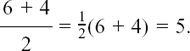
If you find half of 10, it is the same as dividing 10 by 2.
Fractions always keep the same value if they are multiplied or divided top and bottom by the same number, so
These are shown in the drawings in Figure l.C.l.
These four equal fractions are said to be equivalent to each other. The process of dividing the top and bottom of a fraction by the same number is called cancellation or cancelling down.
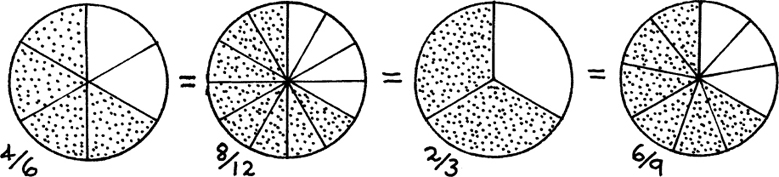
Figure 1.C.1
For example,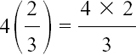 
not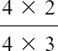 
which is still 
.
In words, four lots of two thirds is eight thirds.
This works in exactly the same way with fractions in algebra.
So, for example:
(dividing top and bottom by a)
(dividing top and bottom by w)
and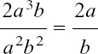 
(dividing top and bottom by a2b).
Check these three results by giving your own values to the letters.
When doing this, it is important to avoid values which would involve you in trying to divide by zero, because this cannot be done.
You can use a calculator to investigate this by dividing 4, say, by a very small number, say 0.00001.
Now repeat the process, dividing 4 by an even smaller number.
The closer the number you divide by gets to zero, the larger the answer becomes. In fact, by choosing a sufficiently small number, you can make the answer as large as you please.
If you try to divide by zero itself, you get an ERROR message.
Cancel down the following fractions yourself as far as possible.
Sometimes, the process of factorising will be very important in simplifying fractions. Here are some examples of possible simplifications, and some warnings of what can’t be done. If you have always found this sort of thing difficult, it may help you here to highlight the matching parts which are cancelling with each other in the same colour.
dividing top and bottom by x.
(2) 
dividing top and bottom by the whole chunk of (b + c).
(3) 
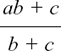can’t be simplified.
We can’t cancel the (b + c) here because a only multiplies b.
(4) 
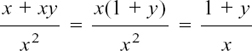
dividing top and bottom by x.
(5) 
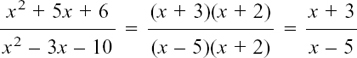
dividing top and bottom by (x + 2).
(6) 
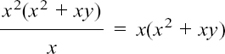
dividing top and bottom by x.
It is not true that 
This wrong answer comes from cancelling the x twice on the top of the fraction, but only once underneath.
It is like saying 
(4)(6) = (2)(3) = 6 but really (4)(6) = (24) = 12.
You can halve either the 4 or the 6 but not both!
(7) 
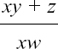is not the same as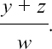 
We cannot cancel the x here because x is only a factor of part of the top. You can check this by putting x = 2, y = 3, z = 4, and w = 5. Then
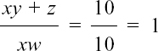and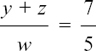
If we had put x = 1, the difference would not have shown up, since both answers would have been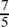 
.
This is because multiplying by 1 actually leaves numbers unchanged.
This example shows that checking with numbers is only a check, and never a proof that something is true.
Try these questions yourself now.
(1) Which of the following fractions are the same as each other (equivalent)?
(2) Factorise and cancel down the following fractions if possible,
It is particularly easy to add fractions which have the same number underneath.
For example, 
I’ve drawn this one in Figure 1.C.2 below.
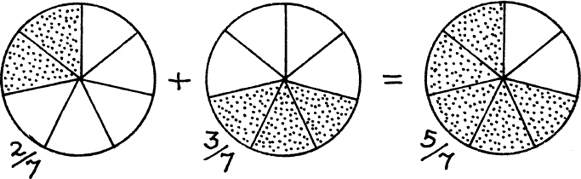
Figure 1.C.2
If the fractions which we want to add don’t have the same denominator then we have to first rewrite them as equivalent fractions which do share the same denominator.
For example, to find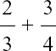 
we use 
and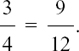 
The two fractions have both been written as parts of 12. The number 12 is called the common denominator. It’s now very easy to add them, and we have
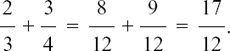
The answer of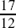 
can also be written as 
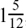, but in general, for scientific and engineering purposes, it is better to leave such arithmetical fractions in their top-heavy state.
You should be safe now from the most usual mistake made when adding fractions, which is to add the tops and add the bottoms.
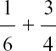(for example) is not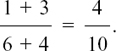
We can see that this must be wrong from Figure l.C.3.
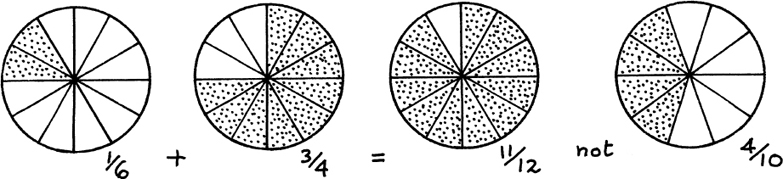
Figure 1.C.3
Since the process in arithmetic is exactly the same as the process we use to add fractions in algebra, it is worth practising adding some numerical fractions yourself without using a calculator, before we move on to this.
Try adding these three.
The letters work in exactly the same way as the numbers. We can say
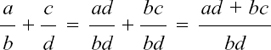
where a, b, c and d are standing for unknown numbers, and neither b nor d are zero. We have written both fractions as parts of bd to make it easy to add them.
Indeed, we can say
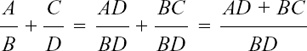
where A, B, C and D are standing for whole lumps or chunks of letters and numbers.
As an example of this, we will find
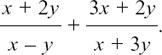
Here, A = x + 2y, B = x – y, C = 3x + 2y and D = x + 3y. So we have:
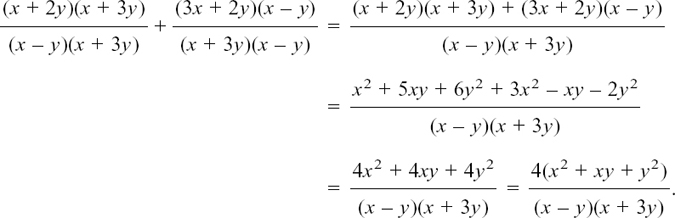
We don’t usually multiply out the brackets on the bottom, because then we might miss a possible cancellation. (This saves you some work.)
Try combining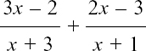 
into a single fraction, yourself.
The working should go as follows:
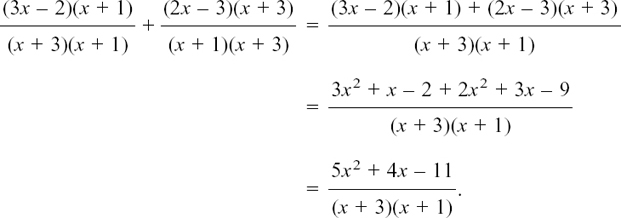
(Remember that the order in which we multiply the brackets doesn’t matter.)
Sometimes, the addition is a little easier because there is a repeated factor. Here’s a numerical example of this.
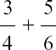has a repeated factor of 2 underneath.
So, instead of saying
We can say more directly
The number 12, which is the smallest number which both 4 and 6 will divide into, is called the lowest common denominator or l.c.d. for short.
This same simplification applies to fractions in algebra.
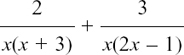
There is a repeated factor of x underneath, so we say
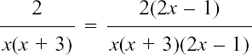
and
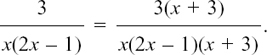
So
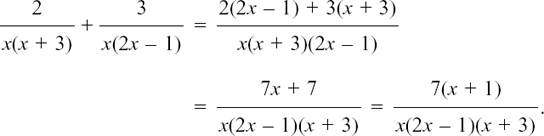
You can follow through this example experimentally, converting it into arithmetical fractions by putting in some value of your choice for x.
Be careful though! There are three values which you mustn’t choose. Can you see what they are?
You can’t have x = 0 or x = –3 or x = because each of these values would involve trying to divide by zero, which is impossible as we saw at the end of Section l.C.(a).
In this example, it would not have been wrong to put everything over the common denominator of x(x + 3)x(2x – 1) or x2 (x + 3)(2x – 1). It would just have taken longer to work out.
EXAMPLE (2)
Here, (3x – 2y) is a repeated factor underneath, so the expression is equal to
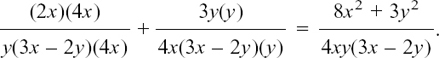
Check this example by putting x = 4, y = 2 and z = 5.
You should get
Try these for yourself.
Subtraction works in exactly the same kind of way as addition, so, for example
In just the same way,
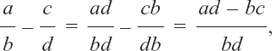
where a, b, c and d are standing for numbers such as the 2,3,5 and 8 we had in the first example.
Equally, just as in adding fractions, we can say that
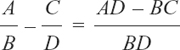
where A, B, C and D stand for any chunks of letters and numbers.
The line in a fraction works in the same way as a bracket. If we are adding fractions this won’t affect what happens, but if we are subtracting them we have to be careful. For example, suppose we have
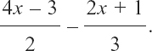
The minus sign in the middle is affecting the whole right-hand chunk. We can show this most safely by rewriting using brackets. Then we have:
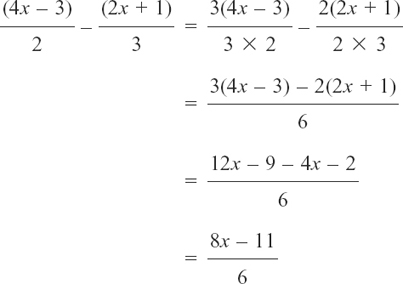
The safest strategy is always to put the brackets in, because then they will be there on the occasions when their presence is vital.
Try these mixed additions and subtractions yourself.
This is very straightforward. (It is much easier than adding!) We simply say
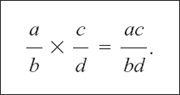
That is, we multiply the tops, and multiply the bottoms.
We can take 
as a numerical example of what’s happening. If you take two thirds of three quarters, you get one half. I show this happening in Figure 1.C.4.
Figure 1.C.4
If A, B, C and D are standing for any chunks of letters and numbers, then we can say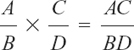 
.
It may then be possible to cancel down, for example
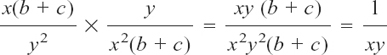
dividing top and bottom by xy(b + c). You should always cancel down the answer like this if it is possible. The reason for this is that often fractions like this come in as part of the working out of a larger problem, and it pays to simplify them as much as possible before going on to the next step, to make that next step as easy as possible for yourself.
You can also do the cancelling before you do the multiplying if you want; I show the working done this way in Figure 1.C.5. Cancellations are usually shown by diagonal lines. Notice that, when everything on the top cancels, we finish up with 1 not 0.
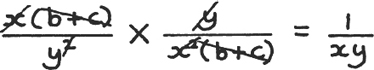
Figure 1.C.5
The rule for dividing fractions is to turn the second fraction upside down and then multiply.
We can see that this works by taking the numerical example of one and one half divided by one half. We get
(that is, there are three halves in 1).
Now try these questions, cancelling down your answers where possible.
(c)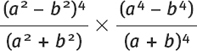
Be cunning!
It will be useful for us now to spend some time looking in more detail at how numbers written as powers of other numbers can be combined with each other. (We have already looked briefly at the rules for multiplying such numbers in Section 1.A.(c).)
We’ll use the four numbers 8 = 23, 32 = 25, 9 = 32 and 81 = 34 as examples.
We could combine these numbers in many ways, some of which I have written down here.
(1) 32 × 8
(2) 9 × 81
(3) 32 ÷ 8
(4) 8 ÷ 9
(5) 8 × 9
(6) 81 ÷ 32
(7) 82
If we rewrite the numbers as powers, we get the following results.
(1) 32 × 8 = 25 × 23 = (2 × 2 × 2 × 2 × 2) × (2 × 2 × 2) = 25 +3 = 28 = 256.
The answer to the multiplication can be obtained by adding the powers.
(2) Similarly, 9×81 = 32 × 34 = (3 × 3) × (3 × 3 × 3 × 3) = 32+4 = 36 = 729.
Again, the result can be obtained by adding the powers.
(3) 
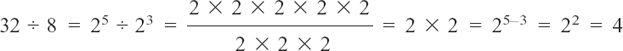This time, the answer has been obtained by subtracting the powers.
(4) Similarly,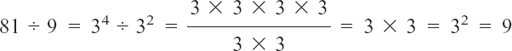 
and again the result is obtained by subtracting the powers.
(5) 8 × 9 = 23 × 32. This time, the calculation is made no easier by writing the numbers in this form. As they are powers of different numbers, we cannot use the same system as we did in (1) and (2).
Returning to the original form, 8×9 = 72.
(6) Similarly, there is no advantage to be gained by writing 81 ÷ 32 as 34 ÷ 25.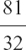 
can be left like this, or written in decimal form as 2.53125.
(7) 82 = (2 × 2 × 2)2 = (2 × 2 × 2) × (2 × 2 × 2) = 26 and 82 = (23)2 = 26.
The answer comes from multiplying the two powers.
Any powers which are whole numbers will work in the same kind of way, so we will now write down the three rules or laws for working with powers.
The three rules for powers
Rule (1) |
am × an = am+n |
|
Example: a2 × a3 =(a × a) × (a × a × a) = a5. |
Rule (2) |
am ÷ an = am–n |
|
Example: |
Rule (3) |
(am)n = amn |
|
Example: (a2)3 = (a × a) × (a × a) (a × a) = a6. |
We saw from the numerical examples that we must have powers of the same number for these rules to work. There, we used either 2 or 3, and for the rules above I have used a. The number a is called the base that we are working with.
It can be shown that the three rules above are true for any values of m and n, provided that a ≠ 0, but it is not possible for us to prove this yet. However, by using powers which are whole numbers we can see how some particular cases will have to go.
(1) 
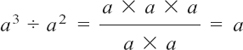and, by Rule (2), a3 ÷ a2 = a3–2 = a1.
So we must have
a1 = a.
(2) 
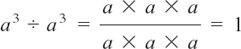and, by Rule (2), a3 ÷ a3 = a3–3 = a0.
So we must have
a0 = 1.
(3) 
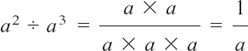and, by Rule (2), a2 ÷ a3 = a2–3 = a–1.
So we must have
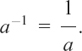
In fact, more generally,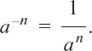 
(4) a1/2 × a1/2 = a1 by Rule (1), and a1 = a.
So a1/2 is the number which multiplied by itself gives a.
a1/2 means the square root of a.
Similarly, a1/3 × a1/3 × a1/3 = a1 by Rule (1).
So a1/3 means the cube root of a, or 
.
and a1/n means the nth root of a or a1/n =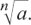 
Here are four examples.
What are
(1) 41/2
(2) 81/3
(3) 272/3
(4) 161/4?
(1) 41/2 means the square root of 4, so it means the number which multiplied by itself gives 4. There are two numbers which do this. What are they?
They are + 2 and –2. So 41/2 = +2 or –2.
We can write this as 41/2 = ±2. (The symbol ± means + or –.)
(2) 81/3 means the cube root of 8 so it means finding a number a so that a × a × a = 8. What can a be?
There is only one possible value for a in ordinary numbers, which is +2.
(I say ‘ordinary numbers’ here because it is possible to extend the number system so that other possibilities open up. In fact, as we shall see in Chapter 10, we then rather pleasingly get three cube roots. But for the present, we are only interested in solutions in ordinary numbers.)
(3) 272/3 = (271/3)2 by Rule (3). But 271/3 = 3 so (271/3)2 = 32 = 9.
(4) 161/4 means the fourth root of 16. What are the possibilities here?
There are two possibilities using ordinary numbers.
We have 2 × 2 × 2 × 2 = 16 and –2 × –2 × –2 × –2 = 16 so 161/4 = ±2.
In general we can say that each even root of a positive number has two possible solutions, and each odd root of either a positive or a negative number has just one solution.
At present, we cannot find any even roots of negative numbers, although in Chapter 10 we will find out how it is possible to extend the number system so that we can have roots for these numbers too. Have a guess at how many fourth roots of 16 we shall then have.
Yes, it is most satisfyingly four.
It is very useful to get a feeling for what these powers do, so that you can quickly recognise alternative ways of writing them, or possible simplifications.
Try these numerical examples without a calculator to help you develop this feel.
Then go through, checking all your answers on your calculator. If you have a mismatch, try to spot which one has gone wrong. Maybe the answers are the same but just in a different form? (Your calculator will only give you positive values for roots; you have to add possible alternative negative answers yourself.) Make sure that you know how powers work on your calculator; read its little instruction book if necessary!
(1) 3–1
(2) 16l/2
(3) 93/2
(4) 27–1/3
(5) 40
(6) 71
(7) 7–2
(8) 4–1/2
(9) 321/5
(10) 16–3/4
(11) 253/2
(12) 49–1/2
The number system has been invented and extended as people needed ways to describe ever more complicated situations and transactions. This procedure took thousands of years, so I have to compress it somewhat in this brief description.
By inventing names, with symbols for those names, it became possible to count how many distinct objects there were when they were collected together. It was also then possible to count the totals when collections were combined together, provided enough names or symbols had been invented.
Having a symbol for zero was a great advance. The oldest written record with a symbol for zero dates from the ninth century in a Hindu manuscript.
We don’t very often have to say that we have none of something. So why is having a symbol for zero so important?
It makes it possible to put in all the necessary place values in our system for writing numbers, for example 301. Having a place value system means that once the symbols for 1 to 9 are learnt, a number of any size can be written. This use of the symbol for zero was ridiculed by some people when it was first adopted. How could it be possible to write a large number, they said, by using lots of symbols which each individually stand for nothing?
The fact that it took two centuries before this symbol for zero was invented shows what a subtle development it was.
The first important extension to the system of counting numbers for a collection of objects is having some arrangement to represent what happens if we want to take away more than we have, so that we owe.
If we include the negative numbers we can do this.
We now have the number system of integers given by
... –4, –3, –2, –1, 0, 1, 2, 3, 4, ...
The German mathematician Kronecker said of these numbers: ‘God made the whole numbers; everything else is the work of man.’
Also now we have a nice symmetry.
For every number there is another number so that put together they make zero, so each number has its matching pair. These pairs of numbers are reflections of each other around zero. What are the pairs of (a) +7, (b) –9, and (c) 0?
(a) +7 has the pair –7.
(b) –9 has the pair +9.
(c) 0 is its own pair.
Putting together any two numbers in this system gives us another number in the system. It has a nice completeness about it.
The next major extension to the number system results from the requirement of being able to divide quantities up. To do this, we have to include fractions, that is, numbers which can be written in the form a/b where a and b are integers or whole numbers, excluding the case when b = 0. These numbers are called the rational numbers. Then the integers themselves come from the special case in which b = 1, so they are included in this description.
We can now divide quantities into smaller amounts, even if the numbers involved mean that the result of the division is not a whole number (provided of course that the quantity concerned is physically divisible into non-integer amounts).
We have a second nice symmetry here, this time about 1.
For every number except zero, there is now another number so that multiplied together we get 1. For example, 
has the pair 
.
What are the pairs of (a)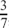
, (b)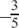 
and (c) 1?
(a) 
has the pair 
.
(b) 
has the pair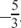 
.
(c) 1 is its own pair.
Putting together any two numbers in this system by multiplying them together gives us another number in the system, so we have exactly the same sort of completeness that we had above with adding. The two systems have the same underlying structure of each number having its own individual partner so that each pair together gives a special number, zero in the case of adding and 1 in the case of multiplying.
If we put little tiny points for the value of each possible fraction on a number line how close will these points be together? Will there be any gaps?
Suppose we have two fractions F1 and F2 which are very close together, say F1 =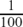 
and F2 = 
.
Then, there must be at least one fraction which lies between these two. Can you think of one?
There are lots of possibilities for this. In particular, we could take (F1 + F2)/2.
This is exactly midway between F1 and F2. Here, it would be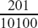 
.
This system of insertion can be infinitely repeated, so we see that there can’t be any spaces between these fractions.
If the fractions are packed infinitely closely together, where is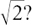 
Is it a fraction? Trying a few possibilities doesn’t look very promising, but maybe we just haven’t got the right numbers.
Suppose that it is possible, and we have found a and b so that
and therefore
a2 = 2b2.
We’ll also suppose that any possible cancelling down of the fraction a/b has already been done, so it is tidied up as much as possible.
What kind of number must 2b2 be?
It must be even, so a2 must be even as well.
What happens if you square (a) even numbers (b) odd numbers?
An even number squared gives another even number and an odd number squared gives an odd number. We can show this by writing even numbers as 2n(with n standing for any whole number) and odd numbers as 2n + 1.
Then (2n)2 = 4n2 and (2n + 1)2 = 4n2 + 4n + 1.
Because of this, we see that the number a must be even. We could call it 2a1 to show this. Then
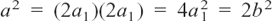which means that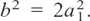 
Now, by the same argument as before, b must also be even, so a and b could have been cancelled down.
But if we cancel them, we can use exactly the same argument to show that they would cancel down again, and so on for ever.
So there is no fraction which is exactly equal to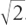 
.
This argument is due to the Pythagoreans of Ancient Greece. They were disconcerted and alarmed by such numbers, which they called ‘incommensurable’. There is a story that the first Pythagorean to show their existence was thrown into the sea for his pains.
In fact,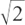 
is somewhere between 
and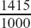 
. So although the fractions are packed infinitely closely, there are still gaps where the numbers like , 
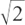, etc. are.
(This is one of the mysteries of maths and is because infinite numbers of things behave in very peculiar ways.)
These numbers, together with π and similar numbers, are called irrational numbers. The rational and irrational numbers together are called the set of real numbers.
Here’s another example of how infinite quantities of things behave in unexpected ways.
If we have two collections or sets of objects and we can tally off each object in the first set with a corresponding object in the second set and vice versa, like knives and forks in place settings, then the two sets must have an equal number of objects in them.
Or must they?
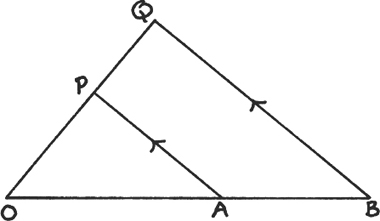
Figure 1.E.1
Suppose we start with the two lines meeting at O which I have drawn above in Figure 1.E. 1, and we then draw parallel lines like AP and BQ so that point A is matched with point P and point B is matched with point Q. All the points on the two lines can be paired off in this way, so the two lines must be equal in length. But clearly they are not! We can no longer say that the sets are equal because now there are an infinite number of objects involved and the usual rules no longer apply.
Finally, to make the list complete, we will jump ahead of ourselves briefly. We know that 2×2 = 4 and –2 × –2 = 4. So the square root of 4 is +2 or –2. But we have no number for the square root of–4.
In Chapter 10, we shall find out how it is possible to extend the number system even further so that we can have an answer for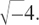 
In fact, even better, we get two answers, just like 
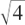has two answers.
We get this extension by including the so-called imaginary numbers. The real and imaginary numbers together form the set of complex numbers.
We have to use ten symbols for writing numbers because our counting system is based on 10. Our whole system is therefore called the decimal system, although in ordinary speech we use ‘decimals’ for just the fractions written in this system.
However, other bases can be used. One of the most important of these is the system based on 2, the binary system. This involves counting in place values given by powers of 2 instead of powers of 10.
So, for example,
324 in the decimal system |
= 4(100) + 2(101) + 3(10)2 = 4 + 2(10) + 3(100). |
11001 in the binary system |
= 1(20) + 0(21) + 0(22) + 1(23) + 1(24) |
|
= 1 + 0(2) + 0(4) + 1(8) + 1(16) |
|
= 1 + 8 + 16 = 25 in the decimal system. |
Notice that, in each case, we have processed the number from right to left, instead of from left to right.
In each case, we wrote down the number of units, the number of ‘tens’, the number of ‘hundreds’, etc., where the ‘ten’ or 10 of the binary system is 2, the ‘hundred’ or 100 of the binary system is 22 or 4, and so on.
Counting in binary goes 1, 10, 11, 100, 101, 110, 111, 1000, etc. instead of the decimal 1, 2, 3, 4, 5, 6, 7, 8, etc.
The binary system only requires two symbols to write, those for one and zero, which is why it is so important. The separate digits of numbers written in this system can be represented by electric current either flowing or not flowing in a circuit, and therefore numbers can be handled in this form by computers.
Try converting these three binary numbers into decimal numbers for yourself.
How can we go the other way, and convert decimal numbers into binary numbers?
If we have the number 109, say, we could do it just by splitting it up into powers of two.
109 |
= 64 + 45 = 64 + 32 + 13 = 64 + 32 + 8 + 5 |
|
= 64 + 32 + 8 + 4+1 = 26 + 25 + 23 + 22 + 1 |
|
= 1101101 in binary or base 2. |
(A useful way of showing that this number is in base 2 is to write the 2 as a little subscript, so we write the number as 11011012.)
This is good for seeing what is happening, but not so good as a standard method of conversion.
What we have actually done here is to split the number up into progressively higher powers of 2, which we can do equally well by repeatedly dividing it by 2, recording the remainder at each stage so we get the smaller powers as they shed off.
I show the working for this below.
Try converting these three decimal numbers to binary numbers for yourself.
If you have the use of a computer and know a programming language, you could write a program to do this, since the process of dividing by 2 is a repeated loop until the number being divided is itself less than 2. You just have to record the remainders so that you can display or print out your binary conversion at the end.
This system works equally well in other number bases.
For example, in base 8, we have a ‘ten’ of 8 and a ‘hundred’ of 82, etc.
So 2378 = 7 + 3(81) + 2(82) = 7 + 24 + 128 = 15910.
Working the other way round is done by repeated division by 8.
So, for example, to convert 39710 into base 8, you would do the working shown below.
39710 =6158.
Check: 6158 |
=5 + 1 × 8 + 6 × 82 |
|
= 39710. |
In this section, we look briefly at how the different numbers are built up.
Many numbers can be written as products (i.e. multiplications) of smaller numbers or factors in quite a few different ways, for example
12 = 2 × 6 = 2 × 3 × 2 = 3 × 4= 12 × 1.
Numbers which have no factors other than themselves and one are called prime numbers. No smaller number (except for 1) will divide into them exactly. 7, 11 and 19 are all examples of prime numbers.
Are there any even prime numbers?
Every even number can be divided exactly by 2, so there is just one even prime number, which is 2 itself.
Every number can be written as a product of its prime factors, so for example
15 = 3 × 5 and 12 = 22 × 3.
Mathematicians have shown that every number can only be broken down into a product of prime factors in one way, so, if we split 126 as 2 × 32 × 7, we don’t have to worry that maybe it could also be split so that it has some completely different prime factors.
Is there a pattern for how prime numbers slot into the other numbers? Figure 1.F.1 shows all the prime numbers between 1 and 50, as shaded squares.
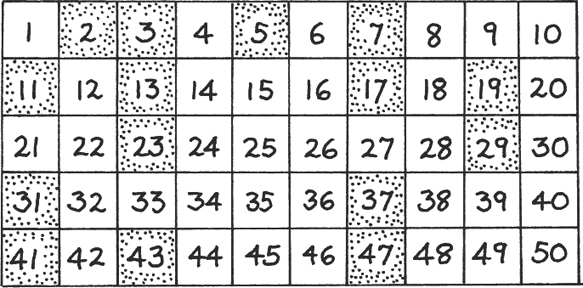
Figure 1.F.1
It doesn’t look as though there is a pattern, although we do notice that many of them seem to come in pairs with just one number in between. We also see that, as we go down through the numbers, we are getting more and more possible prime factors for the numbers which we haven’t yet reached. Does this mean that after a while we will have collected all the building blocks that we need to make future numbers, so that there will no longer be any new prime numbers?
The answer to this question is that we will never have enough building blocks to make all the possible future numbers. Given any prime number, however large, it is always possible to find at least one larger one.
We can show that this is true in the following neat way.
We start by taking a numerical example, because it is easier then to explain how the argument goes.
Suppose we think that 23 might be the largest prime number. (I have deliberately chosen quite a small number here. It is, in fact, easy to find larger prime numbers than 23, but it will do very nicely to show how the general argument goes.) First, we list all the prime numbers up to 23. (We don’t normally include the number 1 in these – 1 is its own special unique case of a number.) Doing this gives us 2, 3, 5, 7, 11, 13, 17, 19 and 23 itself.
Next, we use all these prime numbers to write down a new number. This new number is
(2 × 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23) + 1.
What kind of number is this? None of the prime numbers up to 23 will divide into it exactly, because each of these divisions would leave a remainder of 1. So either it is itself a prime number, or it has prime factors which are larger than 23.
Either way round, we have shown that there must be at least one prime number which is larger than 23, and we could use this argument in exactly the same way to show that if we start with any prime number N, then there must be at least one prime number larger than N.
This very nice ingenious method is due to Euclid, a mathematician from Ancient Greece.
We can often use a number’s prime factors to simplify its square root.
For example,
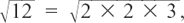but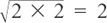 
, so we can say 
.
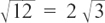Here is another example.
.
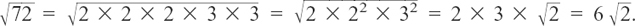When square roots appear as part of a long calculation, it often makes things much easier if you rewrite them like this. Using a calculator to find them is often not very helpful in mid–calculation because it frequently gives you a string of decimals which is very awkward to handle.
Try some for yourself now. Simplify these numbers in the same way.
signs underneathIn Section l.E.(d), I showed that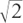 
is irrational. Most square roots are irrational, the exceptions being numbers such as 
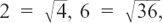etc. Numbers such as 4 and 36 are called perfect squares.
If we have a number made up of two separate bits, one of which is rational and one of which is irrational, like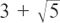 
, then the combined number will be irrational.
But the matching pair of numbers of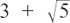 
and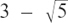 
have two rather nice properties.
We can see the first of these by adding them.
This gives us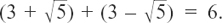 
(We have lost the irrational part.)
Can you see what other good possibility we have?
Multiplying them together also works very nicely.
We get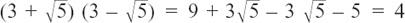 
.
This is another application of the ubiquitous difference of two squares. (We have also used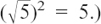 
Fractions such as 
are particularly unwelcome because they involve dividing by a number which is partly rational and partly irrational. We can get round this problem in the following way.
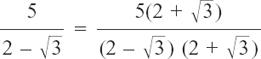
multiplying top and bottom of the fraction by 
. This gives
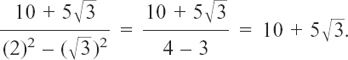
We have cleverly got the 
signs the on the bottom to cancel out, by multiplying the fraction top and bottom by 
Then we use the fact that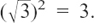 
As another example, we will simplify 
The denominator (or underneath number) is particularly unpleasant this time.
Can you see what we could multiply by to get rid of the 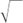signs on the bottom? Look again at the previous example if necessary.
We multiply the top and the bottom by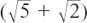 
and get:
It may help you to recognise references to this process if you know that this process of removing the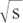 
on the bottom is called rationalising the denominator. Numbers like 
are called surds.
We shall use exactly this process in Chapter 10 to simplify complex numbers.
Try simplifying these three for yourself.
