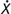 , etc.,
, etc.,In this chapter we look at how it is possible to describe relationships which are changing and how we can find out the rate of this change.
The chapter is split up into the following sections.
8.A Some problems answered and difficulties solved
(a) How can we find a speed from knowing the distance travelled?
(b) How does y = xn change as x changes?
(c) Different ways of writing differentiation: dx/dt, f’(t), 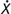 , etc.,
, etc.,
(d) Some special cases of y = axn,
(e) Differentiating x = cos t answers another thinking point,
(f) Can we always differentiate? If not, why not?
8.B Natural growth and decay – the number e
(a) Even more money – compound interest and exponential growth,
(b) What is the equation of this smooth growth curve?
(c) Getting numerical results from the natural growth law of x = et,
(d) Relating ln x to the log of x using other bases,
(e) What do we get if we differentiate ln t?
8.C Differentiating more complicated functions
(b) Writing the Chain Rule as F’(x) = f’(g(x))g’(x),
(c) Differentiating functions with angles in degrees or logs to base 10,
(d) The Product Rule, or ‘uν’ Rule,
(e) The Quotient Rule, or ‘u/ν’ Rule
8.D The hyperbolic functions of sinh x and cosh x
(a) Getting symmetries from ex and e-x,
(b) Differentiating sinh x and cosh x,
(c) Using sinh x and cosh x to get other hyperbolic functions,
(d) Comparing other hyperbolic and trig formulas – Osborn’s Rule,
(e) Finding the inverse function for sinh x,
(f) Can we find an inverse function for cosh x?
(g) tanh x and its inverse function tanh–1 x,
(h) What’s in a name? Why ‘hyperbolic’ functions?
(i) Differentiating inverse trig and hyperbolic functions,
8.E Some uses for differentiation
(a) Finding the equations of tangents to particular curves,
(b) Finding turning points and points of inflection,
(c) General rules for sketching curves
(d) Some practical uses of turning points,
(e) A clever use for tangents – the Newton–Raphson Rule
(a) How implicit differentiation works, using circles as examples,
(b) Using implicit differentiation with more complicated relationships,
(c) Differentiating inverse functions implicitly,
(d) Differentiating exponential functions like x = 2t,
(e) A practical application of implicit differentiation,
8.G Writing functions in an alternative form using series
What kinds of things can differentiation tell us? I find that sometimes students know some rules but don’t really know what use these rules are. We start this chapter by looking at some examples based on earlier thinking points. In these, we wanted to find answers to what is happening in particular physical situations.
If you see how we can use differentiation to help us here, you will understand better what kinds of things it can do for you.
Suppose somebody is walking at a steady speed of 3 miles per hour (m.p.h.). Then the distance travelled for different lengths of time can be shown on a graph sketch like the one in Figure 8.A.1.

Figure 8.A.1
Since equal distances are covered in equal intervals of time, the speed is represented by the gradient of the line, and this can be found by using any of the triangles I have drawn in; the size does not matter.
Any two points (x1, y1) and (x2, y2) on the line will give its gradient, using the formula
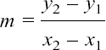 from Section 2.B(d)
from Section 2.B(d)
Each of these triangles will give a gradient of 3. This represents the constant rate of change of distance travelled, or steady speed, of 3 m.p.h.
But how can we find the speed if the rate at which the distance is covered is continually changing?
This question first came up at the end of the thinking point of Section 2.D.(g), in which we looked at how the motion of a ball thrown up in the air changes as time passes.
Look at this again so that we can use it together now.
Because of the pull of gravity, the speed of the ball is changing all the while. It is moving fastest when it leaves the thrower’s hands and when it returns to them; and slowest when it comes instantaneously to rest at the highest point of its motion. (We can say that it does this because there is an instant in its motion when, rather like the Grand Old Duke of York, it is neither moving up nor down.) Between these two extremes, its speed is changing smoothly, so that the graph of the distance travelled against the time that this has taken is a curve.
The last question I asked you in this thinking point was whether you could think of a way of estimating the ball’s speed one second after it has been thrown up in the air. Surely since we can find how far it has travelled at any instant we should be able to do this?
We used the equation 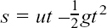 to give us the distance s in metres (m), travelled by the ball after a time of t seconds (s), if it is thrown up at a speed of u metres per second (ms–1).
to give us the distance s in metres (m), travelled by the ball after a time of t seconds (s), if it is thrown up at a speed of u metres per second (ms–1).
In our example, the ball was thrown up at a speed of 14 ms–1, and we took g, the acceleration due to gravity, as 9.8 metres per second per second (ms–2).
This then gave us the equation of s = 14t – 4.9t2 for the curve.
I have drawn a new sketch graph, in Figure 8.A.2.(a), showing how the height of the ball changes with time over the first 1.4 seconds of the motion.

Figure 8.A.2
I have drawn in the separate changes in height for each 0.2 second interval on this graph, to give a picture of how the speed is changing. You can see the inaccuracy in this by drawing in the slant sides of the triangles yourself. The slopes or gradients of these slant sides are giving the average speeds over each 0.2 second interval, but they only give an approximation to the actual shape of the curve. It seems reasonable to think that, at any point where two adjacent triangles touch it, the steepness of the curve will be somewhere between the steepness of the slant sides of these two triangles.
Taking the equation of the curve as s = 14t – 4.9t2, we can make the table (a) below for the different values of s.

We now use the triangles either side of t = 1 to get estimates of the speed when t = 1.
I will call the change in height Δs and the corresponding change in time Δt.
(Δ is the Greek capital D, pronounced ‘delta’. It is often used to mean ‘the change in’. We have used it this way already in Section 3.A.(b).)
The left-hand triangle gives
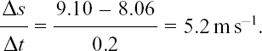
The right-hand triangle gives

From Figure 8.A.2(a), we believe that 5.2 ms–1 is an over-estimate and 3.2 ms–1 is an under-estimate of the speed when t = 1.
Next, we try taking smaller time intervals either side of t = 1. I have done this in table (b), and I show the separate changes in height on this small section of curve in Figure 8.A.2(b). Again, you should draw in the slant sides yourself.
Taking the two triangles on either side of t = 1 again, the left-hand triangle gives
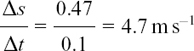
and the right-hand triangle gives

We see that we are getting closer to an agreement between the estimates.
Infilling again in the same kind of way gives us the table below.
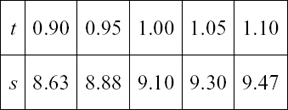
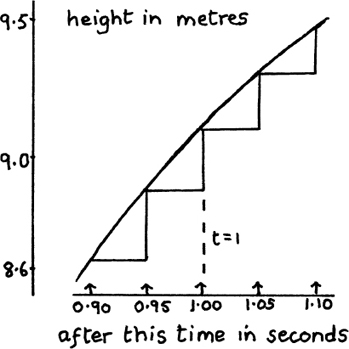
Figure 8.A.3
I have shown again, in Figure 8.A.3, a magnified picture of the small part of the curve which we are considering here. If you now draw in the slant sides of the triangles, you will find that they are almost indistinguishable from the curve itself.
Since the differences are now becoming very small, it seems a good idea to show this by labelling them in a slightly different way. I shall use δ, which is the small Greek letter d, and call the changes δs and δt. δ is very commonly used in maths to mean ‘a small change in’.
Now, looking at the two small triangles either side of t = 1 shown in Figure 8.A.3, the left-hand triangle gives

and the right-hand triangle gives

So, coming from the left and from the right, we have two sets of approximations which are getting closer and closer to the speed at the instant when t = 1. We have
5.2 → 4.7 → 4.4 and 4 ← 3.7 ← 3.2
This system looks very promising. We can see that the smaller the differences are the better the approximation is, so perhaps we should focus on making the differences extremely small and see what happens?
We don’t want to specify exactly how small since, for any given interval, we know we could always halve that and so get a better approximation.
So what we will do is to look at what happens to δs/δt, just making the proviso that we are letting δt become smaller and smaller. We are snuggling the little triangles in closer and closer to t = 1 from both sides.
Also, it would be much nicer if we could get a rule for finding the speed which works for different initial speeds, u, and for the slightly different possible values of g as we travel over the earth’s surface, so that we don’t have to recalculate every time these are different. So, instead of taking particular values, we will work with u and g.
We start with 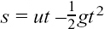 and then see what happens to this equation at the nearby time of t + δt.
and then see what happens to this equation at the nearby time of t + δt.
If the time has changed by a small amount δt then the distance s will also have changed by a correspondingly small amount δs. So we will have
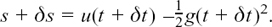
Now,
(t +δt)2 = t2 +2t(δt) + (δt)2.
So
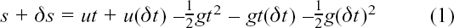
But, at time t,

Subtracting (2) from (1) gives
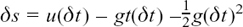
so

But, if we now let δt get closer and closer to zero, it will become so small that we can ignore the 
Because δs is also becoming very small, the fraction δs/δt continues to give the slope of the slant side of the little triangle. The smaller this triangle becomes, the closer this slope gets to the slope of the curve itself at the point (t, s).
As δt gets smaller and smaller, ds/dt will become closer and closer in size to u – gt.
We write this mathematically by saying that the limit of δs/δt as δt → 0 is u – gt.
The limit 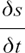 as δt → 0 is called
as δt → 0 is called 
In this particular example, we have ds/dt = u – gt. We now have a rule to tell us the speed at any point on the path of the ball.
The value of ds/dt tells us the rate of change of s with respect to t for any chosen value of t while the ball is still in motion.
The line with gradient ds/dt which touches the curve at this particular value of t, showing its steepness there, is called the tangent to the curve at this point.
Returning to the particular case of u = 14 and g = 9.8, we can now work out the speed of the ball one second after it has been thrown into the air.
It is given by u = ds/dt = u – gt = 14 – 9.8 = 4.2, so the speed is 4.2 ms–1. I show this on Figure 8.A.4(a). I also show again, in Figure 8.A.4(b), the little sketch of the actual path of the ball, which is straight up and straight down. The graph of Figure 8.A.4(a) shows how its distance from the ground changes with time.
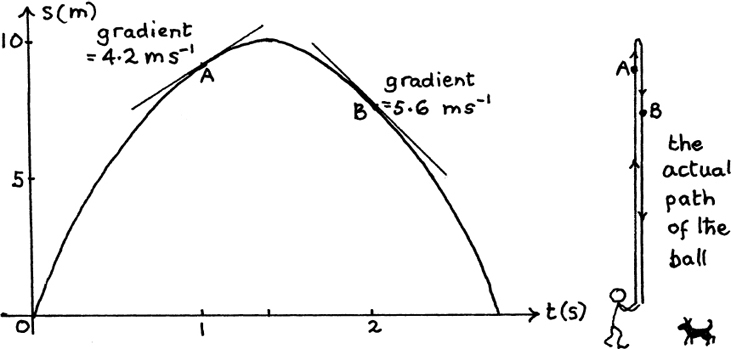
Figure 8.A.4
The gradient of the curve at A, that is, of its tangent there, is 4.2. The speed of the ball after half a second is 4.2 ms–1 vertically upwards.
Similarly, if t = 2, ds/dt = –5.6. The gradient of the curve, given by the gradient of its tangent at B, is negative. The speed of the ball is 5.6 ms–1 vertically downwards.
Taking the vertically upwards direction as positive, we can say that the velocity of the ball (which describes the direction of its motion as well as its speed) is 4.2 ms–1 at A and –5.6ms–1 at B.

When you first looked at this thinking point, because the acceleration is constant, you may have used the formula ν = u + at to find the speed when t = 1, putting u = 14 and a = –9.8. This also gives ν = 4.2. This method works very well in this particular example, but the method we have just been looking at above is enormously more powerful because it can cope with situations of non-constant acceleration (and much else besides).
We can now answer this question provided that n is a positive whole number.
(I am putting in just enough examples here of where these formulas come from to show you how they link back to past work, and to justify using them in their hundreds of applications.)
We will look at what kind of small change, δy, we will get in y if we change x by the small amount δx. We have
y = xn so y + δy = (x + δx)n.
Now, we can expand (x + δx)n using Rule (B1) from Section 7.A.(e). This gives us
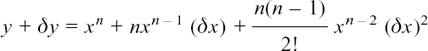
+ terms with higher powers of δx.
Putting y = xn, and tidying up, gives us
 other terms with higher powers of δx
other terms with higher powers of δx
so
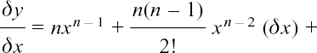 other terms with higher powers of δx.
other terms with higher powers of δx.
If we now let δx → 0, everything except nxn – 1 becomes so small that we can ignore it, and we have
The limit of 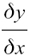 as δx → 0 is nxn – 1.
as δx → 0 is nxn – 1.
If y = xn then 
We know that this result is true if n is a positive whole number because we showed that the Binomial Theorem is true in this case.
Mathematicians have shown that this result is still true if n is any real number, and we will use this widened version.
Multiplying by a constant, a, will just have the effect of multiplying the answer by a. This gives us the following general rule.
If y = axn then 
Doing this process is called differentiating (with respect to x if the function is in terms of x, or with respect to t if it is in terms of t etc.).
If we have a string of terms similar to this which are added or subtracted, we can go through differentiating term by term in order to find the total rate of change, so, for example, if y = 3x2 + 2x, then dy/dx = 6x + 2.
 , etc.
, etc.There is another way of writing dy/dx, dx/dt, etc. which emphasises more that we are doing the process of differentiation to functions.
In Chapter 3, we used f(x), g(x), f(t) and so on to talk about functions of x and t.
If we have y = f(x), then  is also sometimes written as f’(x).
is also sometimes written as f’(x).
If we have x = f(t), then 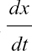 can also be written as f’(t).
can also be written as f’(t).
Writing x = f(t) stresses that x is a function of the variable t.
The dash in f’(t) means that the function f(t) has been differentiated with respect to this variable.
In the particular circumstances when x = f(t) is a function of time, sometimes the dot notation is used.
In this notation dx/dt is written as 
If x = f(t) then 
Historically, the ideas of calculus were developed separately but in parallel by eminent (but rivalrous) mathematicians.
The notation dx/dt was used by the German mathematician Leibnitz.
The notation 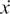 was used by the English mathematician and physicist Newton.
was used by the English mathematician and physicist Newton.
Here are some examples, using the two most usual notations.
(1) If y = f(x) = 3x4 + 2x3 then 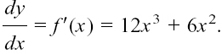
(2) If 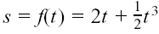 then
then 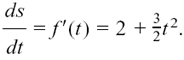
(3) If x = f(t) = 5t +4t1/2 then 
(4) If  then
then 
(If you are unsure about the use of powers here, see Section 1.D.)
Try these for yourself. Differentiate with respect to whatever letter the function is written in on the right-hand side.
(1) y = 7x2 + 3x4
(3) y = 3 – 2/x3
(4) x = 2t1/2 + 3t–1/2.
(a) Show, by thinking about what happens when x is increased by a small amount δx, that if y = x3 then dy/dx = 3x2.
(b) Check what happens at each stage of your working numerically by taking the particular case of x = 2 and δx = 0.001.
Students sometimes have difficulty linking the rule for differentiating y =axn back to these two particular cases, so I have put in two examples here to show how this works.
For example, if y = 3x then, using the rule above, we get dy/dx = 3x0 = 3 since x0 = 1. (This is also in Section 1.D.(b).)
The result of using the rule agrees entirely with what we know to be the gradient of the line. (See Figure 8.A.5(a).)
For example, if y = 4 then we can say y = 4x0.
Now using the rule gives us dy/dx = 0 X 4x–1 = 0.
Again, this fits in with what we can see to be true in Figure 8.A.5(b).
The line y = 4 is horizontal and its gradient is zero.
Figure 8.A.5
Two special cases
If y = ax then 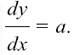
If y = a then 
(a stands for any constant number.)
In Section 5.A.(d), we looked at how the point X moves on the line AB as P moves round a circle of unit radius at 1 rad/s. You should go back to this now, and answer the questions there, if you haven’t already done so. Because this particular kind of motion is of enormous importance in physics and engineering applications, I will use it as a last example of how we can find a rate of change by considering what happens over smaller and smaller time intervals. After this, we will use these results as we need them without specifically proving any further ones.
I show the diagram again here in Figure 8.A.6. The final question of this thinking point was to find the speed of X after a time interval of t seconds, knowing that the distance OX is given by OX = x = cos t.

Figure 8.A.6
We would also like the answer to tell us whether X is moving from left to right, in which case x is increasing and the motion is in the positive direction; or from right to left, in which case x is decreasing and the direction of the motion is negative.
If we can find the speed with its attached + or – sign then we will have found the velocity of the point X. I have shown the graph of the distance x moved by X as P goes round its circle in Figure 8.A.7.

Figure 8.A.7
We know x = cos t.
How does x change as t changes?
We saw in the thinking point that X moves fastest as it passes through O and instantaneously comes to rest every time it gets to either A or B because then it turns back on itself.
Also, when t = 0, it starts by moving in the negative direction towards O. Its velocity will be negative for the first Π seconds of its motion. Also, its velocity changes regularly with time just like its distance from O does.
Do you have any idea how you could write this velocity in terms of t?

Could it be that the rate of change of X’s distance from O with time, that is dx/dt, is equal to – sin t? To answer this question, we shall look how x changes if we change t by a small amount δt.
We are again looking at the gradients of the slanted sides of the little triangles as they tuck in closer and closer to any particular point Q on the curve x = cos t. I show a possible pair in Figure 8.A.8.
To find dx/dt, we have to find the limiting value of δx/δt as δt → 0.
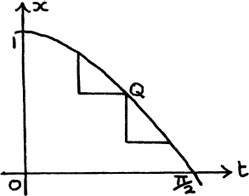
Figure 8.A.8
If the time changes by a small amount δt, so that the distance changes by a correspondingly small amount δx, we have x + δx = cos(t + δt). Which of the formulas from Chapter 5 can we use here on the RHS?

We can use cos(A + B) = cos A cos B – sin A sin B (Section 5.D.(b)). So then we have
x + δx = cos t cos(δt) – sin t sin(δt).
Now comes the step which only works because we are measuring the angle turned through by P in radians.
In Section 4.D.(e), we looked at some special properties of very small angles measured in radians. (Have another look at this section now.)
We found there that, for a very small angle θ, cos θ → 1 as θ → 0, and sin θ → θ as θ → 0. So here, cos(δt) → 1 and sin (δt) → δt as δt → 0. Therefore
as δt → 0, x + δx → cos t – (δt) sin t
but
x = cos t so δx → − (δt) sin t so 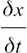 → − sin t as δ t → 0.
→ − sin t as δ t → 0.
Therefore we have the following result.
If x = cost t then 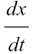 = − sin t.
= − sin t.
So the velocity of the point X after time t is – sin t.
If the radius of the circle is 1 metre then, when X passes through O on its way to B, it has a velocity of – sin π/2 = –1 ms–1.
The corresponding result for the curve y = sin t can be shown in a very similar way. Try doing this for yourself. This is what you should get.
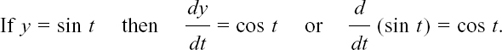
We are now able to get a very interesting result for the motion of X.
The rate of change of velocity with time is acceleration. But

So the acceleration of the point X is always towards O and equal in magnitude to the distance of X from O.
This means that, if X is a particle of unit mass, then the force on X which would make it move in this way is also equal in size to the distance of X from O, and always acts towards O.
These last two results will be unchanged for a larger circle but, if the speed of P is different, the relationship will be altered by some constant factor depending on the new speed.
The point X is moving in what is called simple harmonic motion (SHM).
A physical example of this is the motion of the bob of a simple pendulum.
The joint effects of the force of gravity and the tension in the string on the bob produce a force on it which gives it an acceleration of the kind we have described.
We said above that acceleration is the rate of change of velocity with time.
Also, velocity is the rate of change of distance with time.
So acceleration is the rate of change of a quantity which is itself a rate of change.
If we call the velocity ν and the acceleration a, then
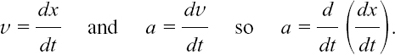
This is written as
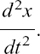
So, here, we can say that

This is an example of what is called a differential equation. A differential equation is an equation which includes terms like dx/dt or d2x/dt2.
We know the solution of this particular example of this equation, which is that x = cos t. We’ll look at some more equations like this in section 9.C.(c).
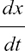 is called the first derivative of x with respect to t.
is called the first derivative of x with respect to t.
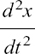 is called the second derivative of x with respect to t.
is called the second derivative of x with respect to t.
This is what happens with the other notations.
If x = f(t) then 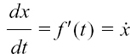 and
and 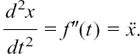
(1) Do we get the same kind of results if we look at the motion of the point Y on the vertical axis described near the end of Section 5.C.(b)?
The distance OY is given by y = sin t.
Find for yourself the velocity dy/dt and the acceleration d2y/dt2 of Y.
Can you link up d2y/dt2 and y by an equation?
(2) What happens if we have an object moving so that its distance from the origin can be described as a combination of sin t and cos t?
For example, what would happen if we had x = 3 cos t + 4 sin t?
Find dx/dt and d2x/dt2, and see if you can find a linking equation between x and d2x/dt2.
In all the examples which we have looked at, we have been using the same process of tucking the little triangles in closer and closer to the point we are considering on the curve, to get better and better approximations to its steepness and so to its rate of change at that point.
Is it always possible to do this?
If we have some relationship giving y in terms of x, can we always go ahead and find dy/dx?
What kinds of thing might happen which would mean that we could not differentiate y with respect to x?
The graph sketches in Figure 8.A.9 may suggest some potential problems to you.
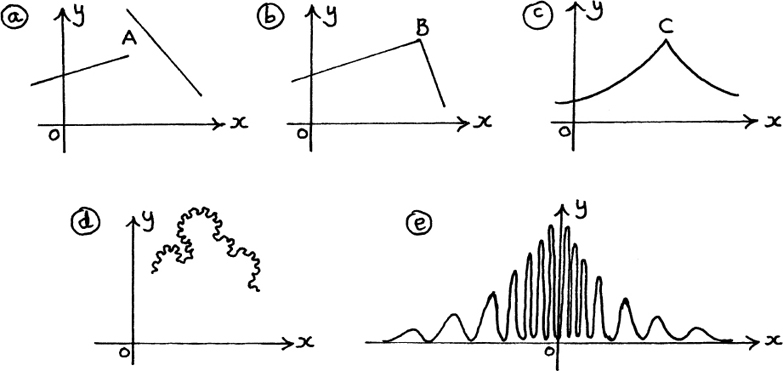
Figure 8.A.9
Also, suppose we can no longer draw the small triangles near some point on a graph because tiny differences in x give rise to huge differences in y? Can you think of such an example on any of the graphs which we have already sketched in this book?
Make a list for yourself of all the circumstances which you think will spell trouble for the process of differentiating.

I hope that you will have thought of some of these possibilities.
In order to differentiate successfully, we must have the following conditions.
There is no meaning to the slope at the point where the break is.
For example, we can’t find dy/dx at the points B and C in Figure 8.A.9(b) and (c).
Any graph which has some value of x for which the function is undefined because it is impossible to divide by zero will give a discontinuity like this.
Another example is the function f(x) = (x + 3)/(x – 2) which we drew in Figure 3.B.16 in Section 3.B.(i). It has a discontinuity like this when x = 2. dy/dx does not exist for this value of x.
Unfortunately, it isn’t possible to produce watertight definitions of the problems just by using pictures.
For example, in Figure 8.A.9(b), would we be all right if we rounded off the sharp point? How rounded off is the balance point of a see-saw?
How close to the origin can we get in Figure 8.A.9(e) before the wiggles become so violent it is impossible to find the slope?
Suppose we severely squash the horizontal scale on an ordinary sin graph. It will then become very wiggly. If we squash it far enough can we make it impossible to find the slope? But surely that would be ridiculous? How could differentiation depend on the personal scale we have chosen?
The study of how continuity and differentiability can be defined rigorously to make clear just what is possible is what mathematicians call analysis.
I have tried here to give you enough of an insight into what is happening so that you will have a feel of when there might be a problem, and be suitably cautious.
I have found that many students regard e as something of a mystery – something that obviously matters a lot in calculus because it is always being used, but why? You will know, if you are studying science or engineering, that e is involved in many of the equations which describe the physical relationships which are important in your subject. This next section sets out to give you at least some of the reasons why e is so important. If you are in a hurry, you can leave the reading of it until later, but you should go through highlighting all the boxes of important results, both so that you can use them now and also to pinpoint them for yourself if you want to do more investigation later on.
I have already described some relationships of natural growth in Section 3.C. If you want to understand how e works, you should start by having another look at this before going on.
In Section 6.C.(h) we looked at how it is possible to make invested money grow faster by using a system of compound interest so that the new interest is calculated as a percentage not only of the original amount of money invested, but also of the interest which has so far been accumulated.
I said there that this updating of interest is usually done either yearly or six-monthly. Would the shorter time interval make very much difference? We would expect it to make some difference because there will be some interest at the end of six months. At the end of the year, you would receive interest on this interest as well as the interest on the original amount of money which you invested.
If this case, how much better would it be to have an even shorter time interval, say three monthly?
This is an important question to answer because rates of growth which depend on how much of a quantity is present at any particular time are very important in many real-life physical situations.
Rather than returning to the situation of Section 6.C.(h), we will look at a slightly different picture. It turns out to be particularly interesting to start from the special case of what happens when the extra amount or interest received at the end of a unit time interval is equal to the amount originally saved.
Unfortunately, this is an unlikely arrangement for a bank to make, so we shall look at the following example instead.
Suppose there is a group of cousins who each receive £100 from their wealthy uncle one Christmas. So strongly does he feel about the virtues of prudence and thrift that he says he will arrange things so that their savings increase at an equal rate to the amount saved, so that if the £100 is saved until the following Christmas, he will then add a further £100 to it.
All five cousins decide that they will save their £100.
The first cousin is happy to look forward to receiving the extra £100 the next Christmas, which will then give him a total of £200.
The second cousin decides to capitalise on her uncle’s offer by suggesting that he increase her savings by a system of compound interest. She will split the year into two halves. Her uncle will give her £50 at the end of the first half-year, so she will have £150.
Since she will then be saving £150 instead of £100, at the end of the second half-year she will get an extra £75 instead of just £50, so giving her a total of £225 at the end of the year.
Her uncle agrees, so we can write this in the same form which we used with compound interest in Section 6.C.(h).
We have

which tidies up as

The two steps in her savings are given by the second and third terms of a geometric progression (GP) which has a first term of £100 and a common ratio of 
The third cousin, seeing this calculation, considers that having the interest updated quarterly would be even more beneficial.
The pattern for her quarterly updates will go
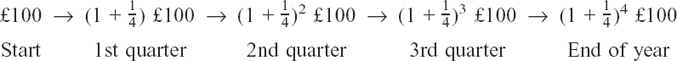
giving her a total at the next Christmas of £244.14 to the nearest penny.
Again, the four steps in the savings are given by a GP, wth a common ratio this time of 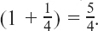
How much would the fourth cousin (who negotiates monthly updates) get by the end of the year?

He would get 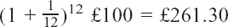 to the nearest penny.
to the nearest penny.
This time, the twelve steps of the savings are given by a GP which has a common ratio of 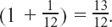
The fifth and youngest cousin is keen to see how much she can negotiate to get.
Try estimating for yourself how much you think she might get. What do you think her best arrangement would be?

She decides to go for the most extreme position and says
‘If I am saving as you want, could we not consider that, over the year, the money that you will give me becomes more and more mine, and so it can really be considered as feeding in continuously to become part of my savings as the year goes by. And then I shall be getting a rate of increase equal to the total amount I have saved all the while. Since we are reckoning here on infinitely small time intervals, I shall do infinitely better than any of my other cousins!’
Is she right?
If we look at what happens as the time intervals become shorter, we find the following:
Weekly updates would give her a final total of 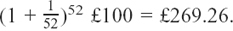
Daily updates would give her a final total of 
Hourly updates would give her 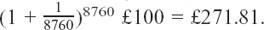
See for yourself what happens if the interest is updated every minute.
The amounts are increasing, but more and more slowly.
Now we know that the increases for the first four cousins are all coming in definite steps, and we saw that each scheme was described by a different GP.
The increases given by updates every minute are still described by a GP, this time with 525 600 steps, and a common ratio of
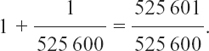
The steps are now exceedingly tiny, but they are still there. This GP would give a grand total at the end of the year of £271.82 to the nearest penny.
When the youngest cousin gets what she wants, the steps will have been smoothed out to give a continuous growth curve. We know that her £100 will have been multiplied by a factor of about 2.7182 by the end of the year.
What is this number which is equal to about 2.7182?
To find the answer to this, we’ll now look at the pattern of her increases as the time intervals get shorter and shorter. These go
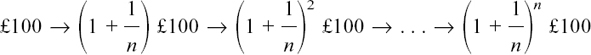
where n is as large a number as we care to think of, as she is breaking her year into infinitely short time intervals. So she finishes up with
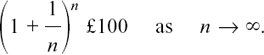
Now, we can do a binomial expansion on

We use the formula (B2), from Section 7.A.(e), which starts

We have to put x = 1/n, where n is a positive whole number, but a very large one indeed. We get
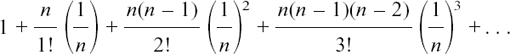
and, as n becomes larger and larger, n – 1, n – 2, etc. are all relatively close to n.
We are getting nearer and nearer to the series

as the amount by which we must multiply the £100 to find her total savings.
As we go further and further in summing this series, we find that the running sum gets closer and closer to a value of about 2.71828, so she gets £271.83 to the nearest penny, doing the best of the cousins, but not dramatically better than her next cousin.
This number, to which the pretty series
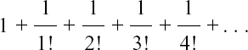
converges is extremely important mathematically, and is indeed the famous e.
You can see its value to as many places as your calculator will allow, by putting in 1 and then pressing ex.
We now have this important result.
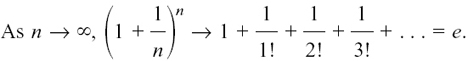
We have found in this section that, when the interest is updated at the end of equal time intervals, so that the total amount of money is increasing in separate jumps, then these increasing amounts of money form the terms of a GP (with a different GP for each set of equal time intervals).
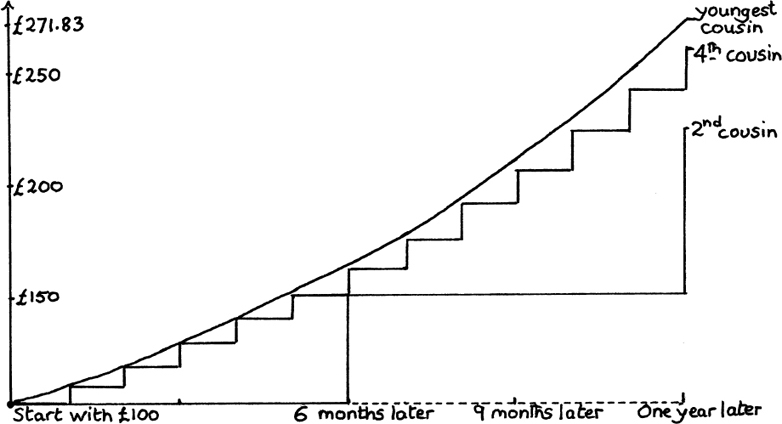
Figure 8.B.1
However, when the interest is updated continuously, so that the amount of money saved is increasing smoothly all the while, the result is no longer described by the steps of a GP but by a smooth growth curve.
You can see these differences in Figure 8.B.1 where I show the growth in the savings of the second, fourth and youngest cousin.
In order to be able to apply the mechanism of this smooth growth curve to other situations, we need to know what its equation is.
It becomes easier to see what this must be if we look at how the differences between the graphs are building up at an intermediate point.
For example, after six months we have the following totals.
The first cousin still has £100.
The second cousin has 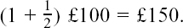
The third cousin has 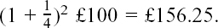
The fourth cousin has 
We can emphasise that we are considering a half-yearly interval here by writing
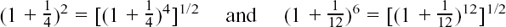
so, for example, the fourth cousin has
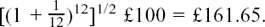
It then seems reasonable to say that, at the end of the half-year, the fifth cousin would have
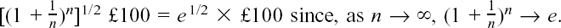
Now, the accumulating totals for the first four cousins increase in definite jumps, but the total for the fifth cousin is increasing smoothly, so it would seem reasonable to say that, after a time interval of any length t, where t is measured in years, she would have a total of et × £100.
Her smooth growth curve has the equation x = 100 et where t represents the time interval along the horizontal axis and x represents her total savings in £ s.
Because the rate of increase of et is equal to et itself for any value of t, it must be true that
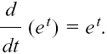
This property of et that its rate of change is always equal to et itself makes it very special.
If you tried drawing the sketch in the thinking point of Section 3.C.(e), you should have found that the gradient of the tangent when x = 1.5 was about the same as the height of the curve for that value of x.
I have taken the simplest possible form of the natural growth law here, leaving out the 100 which we included for the £100 earlier, to make this section simpler.
Starting from x = et, see if you can answer the following questions.
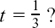
To help you, I have shown these questions in Figure 8.B.2. (You will need to use your calculator to get the answers.)
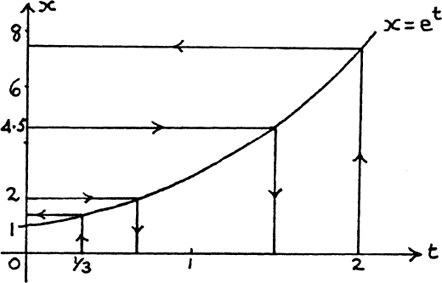
Figure 8.B.2

(1) This is straightforward. Using x = et, we have
(a) x = e2 so x = 7.3891 to 4 d.p. using a calculator
(b) x = e1/3 so x = 1.3956 to 4 d.p.
The first answer corresponds to the amount of money, measured in units of £100, which the fifth cousin would have after two years (if her uncle leaves the system of growth unchanged). This would be £738.91. The second answer corresponds to the amount she would have after 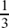 of a year or 4 months. This is £139.56.
of a year or 4 months. This is £139.56.
(2) This question is a bit more tricky because we want to go back the other way. We need to use the inverse function which will take us back from x to t.
Because of the way it was obtained, the growth curve is smooth and has no gaps, so there will be a value of x for any particular value of t.
We define the inverse function by introducing the natural log and saying
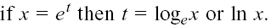
(Natural logs, that is logs to the base e, are usually written as In rather than loge.) This now gives us the answer for question (2)(a) that t = ln 1 = 0 so 1 = e0 which agrees with the meaning we gave to the power 0 in Section 1.D.(b).
It also agrees with the starting amount of money of 1 × £100 when t = 0.
The answer for question (2)(b) is t = In 2 = 0.693 to 3 d.p. using a calculator.
The fifth cousin would have £200 after 0.693 × 12 = 8.3 months approximately.
Question (2)(c) has the answer of ln(4.5) = 1.504 to 3 d.p., giving the fifth cousin £450 after approximately  years.
years.
If we have a function x = f(t), then we write its inverse function (if it exists) in the form x = f–1(t).
Here, we have f(t) = et and f–1 (t) = ln t.
Since doing the function followed by doing the inverse function brings you back to where you started, we have
For the particular functions of f(t) = et and f–1 (t) = ln t, this gives us

These equations are extremely useful and are worth surrounding in bright colour.
I have sketched x = f(t) = et and x = f–1(t) = ln t in Figure 8.B.3.
Notice the following points here.
• The sketch includes negative values of t. If t represents time, then these represent times before we started doing the measuring.
• The value of et is always greater than zero although, for large negative values of t, it gets infinitely close to zero.
• We can only find the natural log of a positive quantity. (This is true for any log.) This agrees with 2–3, say, being 1/23 = 1/8.
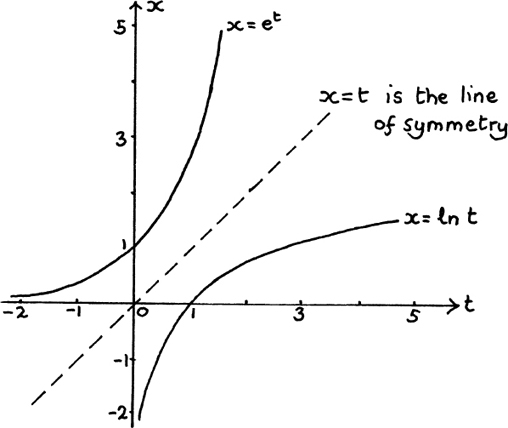
Figure 8.B.3
Starting from a similar situation in Section 3.C.(b), we defined the inverse function of f(x)=2x as f–1(x) = log2 x.
It will now be of great practical importance to us to find a rule which will tell us how to write logs to other bases (in particular, base 10) in terms of logs to base e (or natural logs).
To find this rule, we will start with some number a and suppose that log10 a = y and ln a = loge a = x. (In this section on changing bases, I will write the natural logs as loge rather than In to emphasise that these are logs to the base e.)
If log10 a = y then a = 10y and if loge a = x then a = ex. (This is what ‘base 10’ and ‘base e’ mean.)
But it must also be possible to write 10 itself as a power of e.
Let’s say that 10 = ec. This means that we can say that c = loge 10.
(Using my calculator gives me c = 2.302 585 093 but this is only an approximation to nine decimal places. Any further rounding off will make it even more inexact so we’ll carry on calling it c for short.)
Now we say that a = 10y = (ec)y = ecy.
But also a = ex so now we have ex = ecy so x = cy.
Putting back what x, y and c are in terms of logs gives us
loge a = (loge 10) (log10 a) or lna = (ln 10)(log10 a).
It is also worth surrounding this in bright colour.
We now have a rule which makes it possible for us to change a log to base 10 into a log to base e. (One way of remembering it is to think of it as sort of ‘cancelling’ the 10.) Try choosing some particular values for a and than check on your calculator that the rule does work.
Being able to write logs to base 10 in terms of logs to base e (that is, natural logs) will be very important when we want to find the rates of change of functions of logs to base 10. We shall see how to do this in Section 8.C.(c).
The rule above can be extended to cover any change of base, say from m to n.
logn a = (logn m) (logm a).
This rule gives us a special case which is sometimes quite useful. If we put n = a and m = b, we get
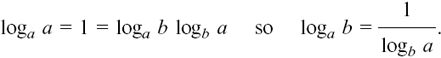
We have now seen how logs to other bases can be converted into natural logs. It is possible to define all other logs and powers in terms of logs and powers of e, and this is done in the rigorous approach of mathematical analysis. It is then possible to give a meaning to such unnerving quantities as 2π, for example. Doing this properly is a slow and careful process. In this book I try to give you enough examples of places where you need to be careful, to help you to understand why this detailed analysis is done.
What is the rate of change of x = ln t with respect to t?
That is, what is dx/dt?
If x = ln t then t = ex so 
But it seems reasonable in general to say that

since we can say that the fraction

Provided that none of the problems talked about in Section 8.A.(f) is present, then when δt→ 0, δx → 0 also, so this step is justified. Now here we have

This gives us the enormously important result that

This is another box worth surrounding with bright colour.
I should point out here that the letters we use are not important in themselves; they are just names or tags.
So it is equally true, for example, that
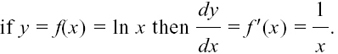
Before we start looking at ways of how we can do this, I will collect together in a box all the functions we can now differentiate. Remember that the letters of the variables can be changed as you wish. (I have used y, x, t and θ for mine.)
Rates of change we already know
(1)If y = f(x) = axn then dy/dx = f'(x) = naxn–1. So if y = ax then dy/dx = a and if y = a then dy/dx = 0 (a stands for any constant number).
(2)If x = f(t) = sin t then dx/dt = f'(t) = cos t.
(3)If x = f(t) = cos t then dx/dt = f'(t) = –sin t.
(4)If x = f(t) = et then dx/dt =f'(t) = et.
(5)If x = f(t) = ln t then dx/dt = f'(t) = 1/t.
I have used the letter f for a function here, all through, but of course you can use other letters if you want.

Students sometimes mix up the minus sign in (2) and (3). There are two ways you can use to remember that the minus sign comes when you differentiate a cos.
• Remember the shape of the first bit of the sin and cos graphs.The cos graph is going downhill here, so d/dt (cos t) must be – sin t.
• Sin Differentiates Plus so Solve Damn Problem.
It is often necessary to be able to find the rate of change of functions which have been built up from simpler ones. For example, we might have x = f(t) = sin 3t or y = f(x) = (3x2 + 2)5 or y = f(θ) = sin3 2θ etc. The Chain Rule gives us a way of dealing with all of these.
I will explain how this works by showing you the following four examples.
(1) y = (3x2 + 5)5
(2) x = sin(3t + π/2)
(3) 
(4) y = ln(2t2 + 3t)
Each of these is built up from functions which we can easily differentiate.
We can show this in the following way.
(1) y = (3x2 + 5)5 becomes y = X5 if we put X = 3x2 + 5.
(2) x = sin(3t + π/2) becomes y = sin X if we put X = 3t + π/2.
(3)  becomes y = eX if we put X = x2 + 2.
becomes y = eX if we put X = x2 + 2.
(4) y = ln(2t2 + 3t) becomes y = ln X if we put X = 2t2 + 3t.
In each of these, X stands for a whole lump or chunk which makes a second function.
Taking example (1), we have y as a function not just of x but also of this X which is itself a function of x.
It is for this reason that the Chain Rule is also known as ‘function of a function’.
Being able to write y in this way makes the finding of dy/dx very much simpler because we can split it into two easy steps.
We justify this by going back to the stage of the very small changes, and saying
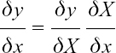 just using the ordinary rules of fractions.
just using the ordinary rules of fractions.
Now, provided none of the potential difficulties which we talked about in Section 8.A.(f) are present at any of the points we are interested in, so that as δx gets very small we also have δX getting very small, we can say that

This gives us the following result.
The Chain Rule
If y is a function of X, and X is a function of x, then 
Using this now in each of the four examples which we had above, and changing the letters when necessary, we get the following results.
(1) 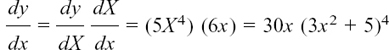
Notice that I have given the final answer in terms of the original x. You should always do this.
(2) 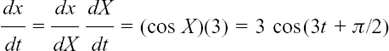

Remember here that π/2 is a constant, and so gives zero when it is differentiated.
(3) 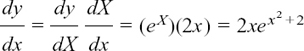
Using the Chain Rule also gives us the result that d/dt(e–t) = –e–t. This describes a process of decay where the rate of change of the substance present at time t is equal to minus the amount of the substance present at that time. The minus sign shows that this rate of change is negative, and the amount of the substance present is decreasing.

You will avoid a lot of mistakes if you remember that if eX is differentiated with respect to X then the answer is eX.
So if you have esomething complicated, then ethe same something complicated must be part of your answer when you differentiate.
(4) 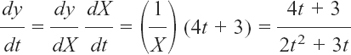
Try these questions for yourself now.
It is very important to be able to do these differentiations quickly and reliably because they will be the basic step of many further processes. (In particular, when you come to use partial differentiation, which involves having functions of more than one variable, you need to be able to do this process without any worries.)
For this reason, I start off with easy questions and build them up gradually so that you can get really confident with them.
I think you will find that quite quickly you can work with the X in your head, just writing down the two multiplied bits and then tidying them up for the final answer.
Differentiate each of these functions with respect to the letter used in their description.
(1) y = (2x2 + 3)4
(2) x = (t3 + 2)5
(3) y = (3x2 – 2x)4
(4) x = (3t + 4)1/2
(5) y = 3e4x
(6) x = et2 + 1
(7) y = 2ex2 + x
(8) x = cos(4t + π/3)
(9) x = sin t + sin 2t
(10) y = sin(x2)
(11) y = sin2x, which means (sinx)2. Hint: let X = sin x .
(12) y = cos3 x
(13) y = In 4x
(14) y = In(3x + 1)
(15) x = In(2t2 + 1)
(16) y = cos(5x2 + π)
(17) x = sin(2t2 + 3)
(18) y = In(sin x)
The next step is to be able to use the Chain Rule more than once in the same question. With practice on the easy ones (which are then often built into more complicated ones), you will find this no problem.
Try these ten quickies now, doing the X part in your head.
Differentiate each of the following with respect to x.
(1) y = e5x
(2) y = e–2x
(4) y = ln(2x + 3)
(5) y = ln(1 + x)
(6) y = ln(1 – x)
(7) y = sin 7x
(8) y = 4 x
(9) y = sin (2x + π)
(10) y = cos(3x + 4)
Now we are ready to do the functions of functions of functions. (In fact, you can chain together as many as you like, with them all folded inside each other like a set of Russian dollies.)
EXAMPLE (1) Find dy/dx for y = sin3 (4x) (which means, of course, y = (sin(4x))3.
We think of this first as y = X3, with X = sin 4x, and write dy/dx = (3X2)(4 cos 4x) = 12 cos 4x sin2 4x.
The second use of the Chain Rule, on the sin 4x, has become so automatic that you hardly notice that you are doing it.
EXAMPLE (2) Find dy/dt if y = ln(sin 3t).
Thinking of this as ln X, with X = sin 3t, we can write
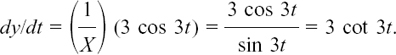
Try these now for yourself. Differentiate each function with respect to the letter used in their description.
(1) y = cos5 2x
(2) y = sin3 (4x + 1)
(3) x = ln(sin(2t + 3))
(4) x = (2 cos 2θ + 5)3
(5) y = ln(1 + cos x)
(6) x = In(3t + sin2 3t)
(8) y = sin(cos 4x)
(9) y = (1 + sin2 t)1/2
(10) y = ln[(1 + sin2t)1/2)] (This is easier than it looks. Think!)
You may come across the Chain Rule written in the dash notation for functions as above. It means exactly the same thing as what you have just been doing. I will show you how this is so by taking an example.
Suppose we want to differentiate y = (3x2 + 2)4 with respect to x.
Because we are using function notation, we need to label the three functions involved here with different letters.
I shall let y = F(x) = (3x2 + 2)4.
Now y is also a function of (3x2 + 2). (This is what we have been calling X.)
I shall let X = 3x2 + 2 = g(x), to show that it also is a function of x.
Since y is a function of X, we can also write y =f(X) =f(g(x)). (In this particular example, y =f(3x2 + 2).)
Next, it is important to be sure what the dash notation means for a function.
f′(x) means the function f(x) differentiated with respect to x,
f′(t) means the function f(t)differentiated with respect to t.
f'(X) means the function f(X) differentiated with respect to X, even though X is itself a function of x, so f'(g(x)) means the function f(g(x)) differentiated with respect to g(x).
It corresponds to what we have called dy/dX.
So, in this particular example, g'(x) = 6x and f'(g(x)) = 4(3x2 + 2)3. So we have

Use whichever notation you prefer.
When we showed that
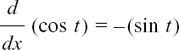
in Section 8.A.(e) everything ran smoothly because the angle t was in radians.
How could we find the slope of the graph of x = cos θ if θ is in degrees? (We know that we can draw the graph of x = cos θ. The only difference is that the horizontal scale will be in degrees instead of radians.)
In order to find dx/dθ from x = cos θ we shall first have to convert θ to radians.
From Section 4.D.(a) we have

with the angle now in radians.
We also know from the Chain Rule that, if a is some constant number, and x = cos(aθ), then dx/dθ = – a sin θ.
Exactly the same principle works here with a = π/180.

writing the angle again in degrees.
The π/180 is the gearing mechanism or scale factor which lets us have the horizontal scale in degrees instead of radians.
We can use a similar process to differentiate a function in terms of logs to base ten (or any other base, but ten is the one you are most likely to want to use).
To do this, we go back to the relationship between logs to base e and logs to base 10 which we found in Section 8.B.(d). This says that
ln a = (ln 10)(log10 a).
So, for example, if we want to find dy/dx for the function y = log10 x, we rewrite this as
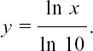
Now 1/ln 10 is just a number, so we have
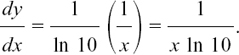
Here, the l/(ln 10) is acting as a gearing mechanism or scaling factor which makes the differentiation work in the slightly altered circumstances of a different base.
We now have the following two rules.
To differentiate functions involving degrees, convert first to radians.
To differentiate functions involving other logs, convert first to natural logs.
The Product Rule moves us a further step on in being able to differentiate functions which are built up from simpler functions. It is therefore another technique we will need for practical applications.
As its name suggests, it gives us a way of dealing with two functions which are multiplied together to give a third function.
For example, suppose we have y = f(x) = 3x2 sin 2x.
The function f(x) is made up of two functions, u(x) = 3x2 and v(x) = sin 2x, which are multiplied together. So we can say y = uv.
If we alter x by a small amount δx then y will also alter by a small amount δy. Also the two components, u and v, of y will each alter by small amounts since they are also functions of x. (We are assuming here that none of the complications of Section 8.A.(f) is present.) So we can say that u alters by the small amount δu and v alters by the small amount δv.
This gives us
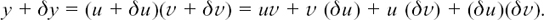
But y = uv, so
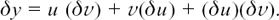
Dividing all through by δx gives
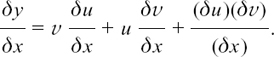
Now, if we make δx become smaller and smaller, so δx → 0, then δu and δv will also become very small.
This means that,

Two very small things multiplied together and then divided by one very small thing give a very small result. This result will become closer and closer to zero as δx itself becomes closer and closer to zero, so we now get the result that
the limit of 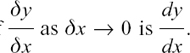
This gives us the following.
The Product Rule

In the particular example that we started with, du/dx = 6x and dv/dx = 2 cos 2x so we have
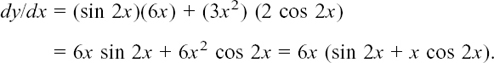
The Product Rule can also be written in function notation as
if y = uv then y’ = vu’ + uv’.
This covers the case of y, u and v all being functions of x, or all being functions of any other letter which it might be convenient to work with.
Try these for yourself, tidying up all the answers as far as possible. Find dy/dx for each of the following.
(1) y = 7x2 cos 3x
(2) y = e3x sin 2x
(3) y = 4x5 (x2 + 3)3
Find dx/dt for each of the following.
(4) x = e2t + 1 cos (2t + 1)
(5) x = 7t2 ln (2t – 1)
(6) x = (t2 + 1)1/2 sin (2t +π)
(7) Find dy/dx if y = (x2 + 1)5 e3x cos 2x.
If you have three functions multiplied together like this, there is no special new Product Rule which you should use. You just bunch any two of the functions together and then use the Product Rule twice.
Here, you could say y = [(x2 + 1)5] [e3x cos 2x] and go on from there.
In the following questions, you will need to remember that

so to find d2x/dt2 you differentiate twice.
These questions are included here not just as practice in differentiating but because, if you have seen them working this way round, they will then be easier for you to solve when you come to do the opposite process in real-life physical applications. There you will be starting with the differential equation (that is the equation which has the terms in d2x/dt2 and dx/dt) and finding a solution which fits it.
(8) If x = (2 + t)e3t find (a)  and (b)
and (b) 
Show that 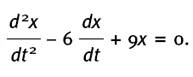
(9) If x = ekt where k stands for some constant number, find (a) dx/dt and (b) d2x/dt2.
If 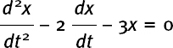 find the two possible values of k.
find the two possible values of k.
(10) If x = Ae3t + Be–t, where A and B are standing for constant numbers, show that
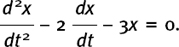
(There is a very quick way to do this one; look at your answer to the previous question.)
(11)If x = e–t ln (1 + et) show that 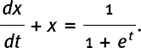
This rule gives us a good way of differentiating a function which is made up of two simpler functions written as a fraction.
We start with a function y =f(x) = u/v where u and v are both themselves functions of x.
The following result can then be shown by a very similar argument to the one we used for the Product Rule in Section 8.C.(d).

Notice the minus sign in the middle of the Quotient Rule. Because of this it matters what order the top two bits are written in. This is why I wrote the Product Rule in the same order. Then ‘ν comes virst’ for both.

Because the Quotient Rule automatically tidies up the answer by putting it over a common denominator, I think that it is easier to use it for a function like y =f(x) = 2x/(3x – 1), rather than writing this as 2x(3x – 1)–1 and then using the Product Rule.
Here are two examples of using the Quotient Rule.
EXAMPLE (1) We can use it to find out what the answer is if we differentiate y = tan x with respect to x. We write
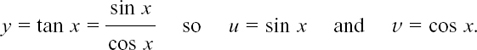
So

But

Therefore, we have

EXAMPLE (2) We will use the Quotient Rule to find dy/dx if 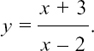
u = x + 3 and v = x – 2 so we get
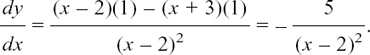
This is undefined when x = 2, but otherwise it will always be negative since (x – 2)2 must be positive.
The value of dy/dx at any particular point of a curve is telling us the slope of the curve at that point. You can see how it tallies with the shape of the curve for this particular function because we sketched it in Section 3.B.(i). We thought there, from the information that we then had, that this curve should always have a negative slope except where x = 2 when y itself was undefined. Now we see that this is indeed true!
Knowing dy/dx gives us a rule for finding the slope at any particular point of the curve. We can see this here by taking a couple of examples of points on this curve, say A, (3,6), and B, 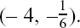
We get at A and at B
and at B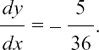
These gradients agree well with the sketch; we can see that the tangent at B would be much less steep than the tangent at A.
The Quotient Rule can also be written in function notation like this.
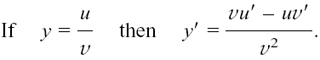
Try these questions yourself now.
(1) By writing 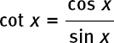 show that
show that 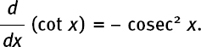
(2) By writing  show that
show that 
(3) Show similarly that 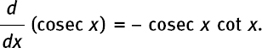
(4) Find 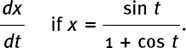
(5) Show that 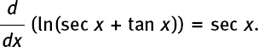
(6) Find 
(7) Find 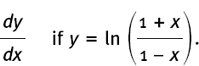
(Think how you can make this one simpler to do!)
(8) Find 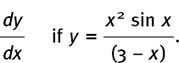
(9) Find 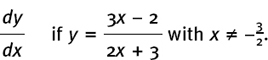
(10) Find 
where a, b, c and d are all constant numbers, and x ≠ – d/c. Are there any values of x which make dy/dx = 0?
Here is a summary of the new useful results we now have. (We also have the box of results at the beginning of Section 8.C.)
More rates of change we now know
• If y = tan x then dy/dx = sec2 x.
• If y = cot x then dy/dx = – cosec2 x.
• If y = sec x then dy/dx = sec x tan x.
• If y = cosec x then dy/dx = – cosec x cot x.
• If y = ln(sec x + tan x) then dy/dx = sec x.
It is worth highlighting this box because, when you come to do the process of differentiation the opposite way round in the next chapter, being able to spot these will be very helpful to you.

Now that we know the Chain, Product and Quotient Rules for differentiation we are able to look at an interesting extension of the two graphs of y = ex and y = e–x.
The graph of y = ex is not symmetrical and neither is the graph of y = e–x, and yet the two graphs shown together have a striking mutual symmetry which is clear from Figure 8.D.1. This is because each is the mirror image of the other in the y-axis.
Can we exploit this?
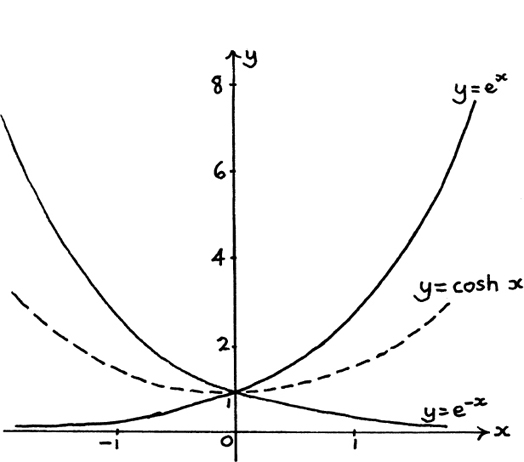
Figure 8.D.1
If we create a new function by taking the average value of ex and e–x for each value of x, we shall get the function which I have shown by the dashed line in the sketch. It is called y = cosh x. The reason for this is that it behaves in many ways like cos x, curious though this may seem at first sight. Its equation is given by
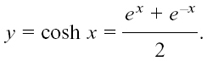
This function is even, that is, cosh(–x) = cosh x for any particular value of x.
It describes the curve in which a heavy uniform chain hangs under its own weight. It also describes the sag in a metal tape measure when it is extended, and was used to correct for this before the invention of electronic measuring devices.
If 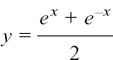 gives an interesting result, what about
gives an interesting result, what about 
We can think of this as finding the average value of ex and – e–x for each value of x.
This gives us the curve shown as a dashed line in Figure 8.D.2.
This function is called sinh x and it is odd. That is, sinh x = – sinh(–x) for any particular value of x.
We now have the pair of definitions
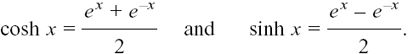

Figure 8.D.2
Remembering from the rules for powers that
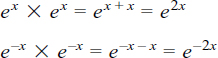
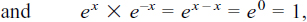
we have
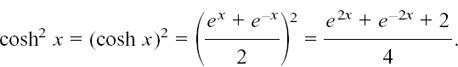

cosh2 x is the way in which mathematicians write (cosh x)2. It does not mean cosh x2, which is more safely written as cosh(x2). In fact
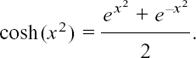
It is just the same as cosh x except that the x is replaced by x2.
We also have
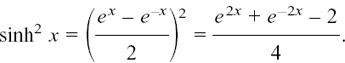
So
cosh2 x – sinh2 x = 1.
This is true whatever value we choose for x on the x-axis, so it is an example of an identity. I described some examples of identities in Section 2.D.(h).
Try showing for yourself that cosh2 x – sinh2 x = 1, without looking at my working, to make sure you can do it.
We begin to see now just why cosh x and sinh x have been named in this way. The above relationship is curiously like the trig identity of cos2 x + sin2 x = 1.
We know that d/dx (ex) = ex and d/dx (e–x) = – e–x.
What do we get if we differentiate (a) y = sinh x and (b) y = cosh x with respect to x? Have a go at doing this for yourself.

This is what you should have.
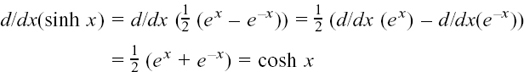
and, similarly,
d/dx(cosh x) = sinh x.
Again we see that sinh x and cosh x are behaving very similarly to sin x and cos x, though not quite identically since d/dx(sin x) = cos x but d/dx(cos x) = – sin x.
This seems very strange just now, because we have completely different graphs for these two pairs of functions. The mystery of this curious set of links becomes solved later on, in Section 10.C.(b).
Also, just as we did with sin and cos, we can use the Chain Rule to differentiate slightly more complicated functions involving sinh and cosh. For example,
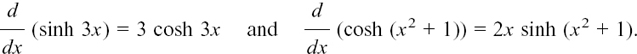
Because of the similarities which we have already seen, it makes sense to define further hyperbolic functions to correspond to the other trig functions, so we say
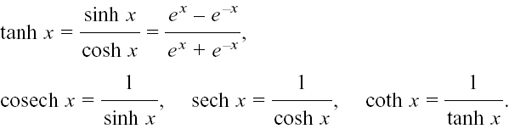
Dividing cosh2 x – sinh2 x = 1 by cosh2 x gives us
1 – tanh2 x = sech2 x
and dividing cosh2 x – sinh2 x = 1 by sinh2 x gives us
coth2 x – 1 = cosech2 x
again similar but not identical results to the two trig rules of
tan2 x + 1 = sec2 x and cot2 x + 1 = cosec2 x.
We can now use the Quotient Rule to find d/dx (tanh x). Writing
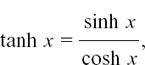
we get

(You can get this same result by working directly with tanh x written in terms of ex and e–x but this is longer. It was question (6) in Exercise 8.C.5.)
Show for yourself that the following three rules are true.
(1) 
(2) 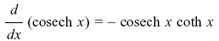
(3) 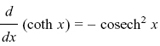
(The working for these is very similar to the working for the corresponding trig functions which came in Exercise 8.C.5.)
(1) If ex = 2, find the values of (a) sinh x, (b) cosh x and (c) tanh x by using their definitions in terms of ex and e–x.
(2) If x = 0, find the values of (a) sinh x and (b) cosh x. Check that your answers are believable by looking at the graph sketches of these two functions. What is tanh x when x = 0?
(3) Differentiate the following with respect to x.
(a) y = cosh 2x
(b) y = sinh (3x + 5)
(c) y = e2x sinh 3x
(d) y = tanh 5x
(e) y = ln (cosh x)
(f) y = cosh2 3x
In this section, we look at whether some other rules which are true for trig functions are also true for hyperbolic functions.
(1) In Section 5.D.(d), we showed that sin 2A = 2 sin A cos A. Is it true that sinh 2x = 2 sinh x cosh x?
We look at the more complicated side first and see whether it will simplify to give the other side. Doing this gives us
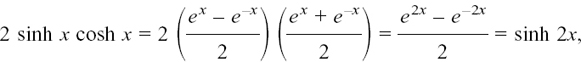
so this is another rule which transfers exactly.
(2) Investigate for yourself whether the trig rule of cos 2A = cos2 A – sin2 A has the corresponding rule for hyperbolic functions of cosh 2x = cosh2 2x – sinh2 2x. Indeed, could this be so?

I hope you will have seen straight away that it couldn’t be so since we know that cosh2 x – sinh2 x = 1. Try finding for yourself what cosh2 x + sinh2 x is equal to.

You should have
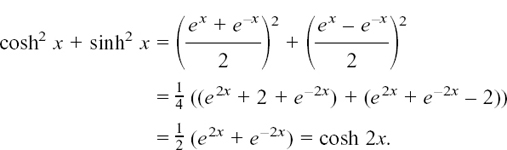
This time we have the two rules

The different results of (1) and (2) are examples of Osborn’s Rule which says that the trig rules match the corresponding hyperbolic rules exactly, unless the working somewhere involves two sins or two sinhs multiplied together. In this case, there is a sign change there.
We look now at the function y = sinh x to see whether we can find a function that will take us back the other way. We’ll start by considering a numerical example so that we can see what is happening here.
Suppose we know that sinh x = 2. What value of x would give this result?
I show this question pictorially in Figure 8.D.3.
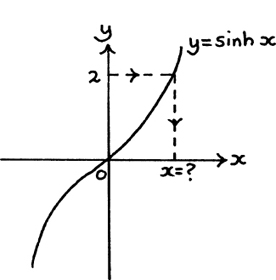
Figure 8.D.3
We say that x = sinh–1 2 meaning that x is the number whose sinh is equal to 2.

Sinh–1 x does not mean 1/sinh x. This would be written as (sinh x)–1 .
Using a sequence like INV-HYP-SIN on your calculator should give you the answer of x = 1.44 to 2 d.p. but how can we show this process actually happening? We have
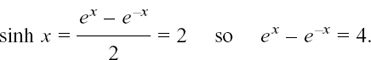
Multiplying through by ex gives e2x – 1 = 4ex so e2x – 4ex –1 = 0.
This is actually a quadratic equation in ex, which we can see by putting ex = m.
This gives us m2 – 4m –1 = 0. We now use the formula to get
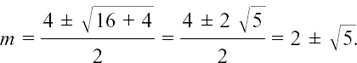
Now, 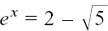 is not a possible solution, because ex is always positive.
is not a possible solution, because ex is always positive.
Therefore we have 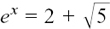 so
so 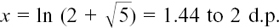
Having seen what happens with this particular example, we will now see how we can find a general rule for y = sinh–1 x.
We use exactly the same method that we did with the numerical example. We start with
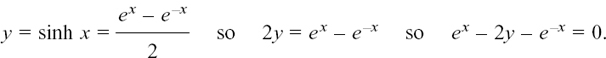
Multiplying through by ex gives
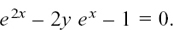
Again, this is a quadratic equation. We see this very nicely by putting m = ex.
Then we have m2 – 2y m – 1 = 0, and using the formula gives

Replacing m by ex gives us
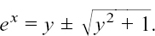
Now, ex is always positive for every x which we can choose on the x-axis. However, 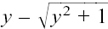 is always negative since
is always negative since 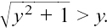
Therefore we cannot have 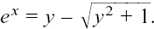
This gives us just the single possibility of  .
.
Taking natural logs of both sides of this equation, we get

We now have the rule for finding the original x if we know what y is, but it is giving us x as a function of y. We can see this from the direction of the arrows in Figure 8.D.4(a) which shows sinh x = 1 giving x = 0.88, and sinh x = 3 giving x = 1.82 to 2 d.p.
We want a rule which will give us y as a function of x so we interchange x and y.
This gives us the inverse function of

Try feeding in x = 1 and x = 3 to this, so that you can see it actually working.
I show a sketch of this function in Figure 8.D.4(b).
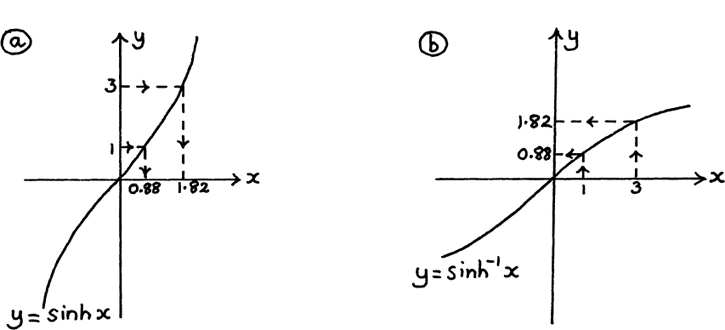
Figure 8.D.4
The interchanging of x and y means that, as for every function and its inverse, the graphs of y = sinh x and y = sinh–1 x are symmetrical about the line y = x.
If you draw your own sketch, showing both y = sinh x and y = sinh–1 x together, you can see this symmetry.
We can also see graphically in Figure 8.D.4(a) that y = sinh–1 x must be a function because there is only one value of x which can give a particular value of sinh x, so there will be no ambiguity when we want to go back the other way.
To extract as much information as possible from the two graphs above, and from Section 8.D.(b), try answering the following questions yourself.
(1) What is the gradient of the curve y = sinh x at the origin?
(2) From your answer to (1), what special property does the line y = x have?
(3) From the symmetry of the two graphs, what is the gradient of the curve y = sinh–1 x at the origin?
Again we start by looking at a numerical example.
If cosh x = 2, what value of x could have given this result?
We see immediately from Figure 8.D.5 that there will be two possible values of x. This is because cosh(x) = cosh(–x) for all values of x.
Doing the working in exactly the same way as we did for sinh x = 2 in Section 8.D.(e), we find that  (Do this for yourself.)
(Do this for yourself.)
Both these possibilities are positive so they are both possible solutions.
If we take 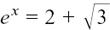 we get
we get 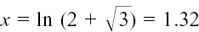 to 2 d.p.
to 2 d.p.
If we take 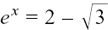 we get
we get 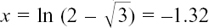 to 2 d.p.
to 2 d.p.

Figure 8.D.5
Looking at the numbers in these two logs, it may seem surprising to you that they do give a matching pair of plus and minus answers. We shall see why this is so when we find a general rule for y = cosh–1 x.
You will find that your calculator only gives you the answer of x = 1.32 to 2 d.p. for cosh–1 2.
The reason for this is that, just as we saw with the inverse trig functions in Section 5.A.(g), it is much more convenient to arrange things so that we have a single-valued answer and therefore a function. We can do this here by restricting ourselves to the right-hand side of the graph so that x ≥ 0. We then get only one possible answer for x from each value of cosh x.
Now we look for the general rule for cosh–1 x
The procedure is very similar to what we did for sinh–1 x in the last section.
See how far you can get by yourself.

You should have
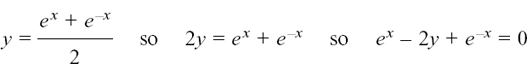
so
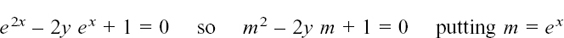
so
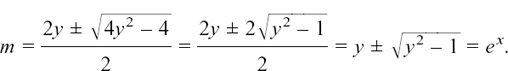
Both of these possibilities are positive, so we find that we are getting two possible solutions. We have

so, taking natural logs,
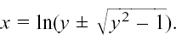
It is a nuisance having a general formula with this ± in the middle of the log where we can’t easily get at it, so now we use a cunning trick involving the difference of two squares to put it somewhere better.
It goes like this:
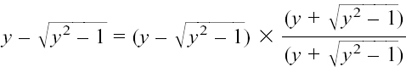
(multiplying top and bottom by the same thing leaves the value unchanged)
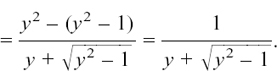
Why is this any better?
It is because, if we have ln(1/a), this is the same as ln 1 – ln a, using the second rule of logs. These rules are listed in Section 3.C.(d).
But ln 1 = 0 because e0 = 1. You can see that this agrees with Figure 8.D.1. So
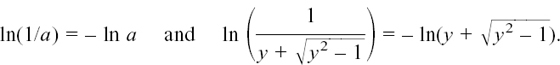
This gives us the two solutions that 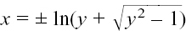 and we see now why ln
and we see now why ln  in the numerical example earlier.
in the numerical example earlier.
We now have the two possible values for x from a given y value.
Interchanging x and y so that we can write this as a relation for y in terms of x, we have
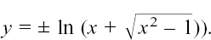
If we restrict the x values by saying x ≥ 0, we have the inverse function of

This is called the principal inverse function for cosh.
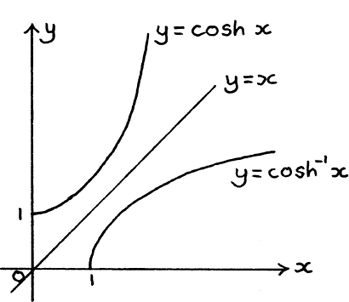
Figure 8.D.6
I show the two functions, y = cosh x and y = cosh–1 x for x ≥ 0 in Figure 8.D.6. Just as with any inverse pair of functions, they are symmetrical about the line y = x.
What will the graph of y = tanh x look like? It is not possible to get this one quite so simply from the graphs of y = ex and y = e–x. We have
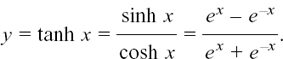
Try answering the following questions yourself.
(1) What is tanh (0)?
(2) Can you work out the connection between tanh (–x) and tanh (x)?
What will this mean for the graph sketch?
(3) Multiply the top and bottom of the fraction (ex – e–x)/(ex + e–x) by e–x.
From your answer to this, can you see what happens to the values of tanh x when x takes very large positive values?
Now try multiplying the top and bottom of the original fraction by ex. Can you see what will happen to the value of tanh x when x takes large negative values?
(You could check that your ideas are right by choosing some particular large positive and negative values for x and using your calculator.)
(4) What is the gradient of the curve y = tanh x at the origin?
(You may need to look at Section 8.D.(c) to answer this question.)
(5) See if you can use all the information from your answers to the previous questions to draw a sketch of the graph for y = tanh x.

You should have the following answers.
(1) tanh (0) = 0 because sinh (0) = 0.
(2) Replacing x by –x gives
so the left-hand side of the graph will be given by reflecting the right-hand side of the graph in the y-axis and then turning it upside down. y = tanh x is an odd function, just like y = tan x. (We drew this in Section 5.A.(e).)
(3) You should get

The value of tanh x will become closer and closer to one as the value of x increases because e–2x becomes extremely small when x takes large positive values.
Similarly, multiplying the top and bottom of the fraction by ex shows that tanh x gets closer and closer to –1 when x takes large negative values, since e2x then becomes extremely small.
(4) d/dx (tanh x) = sech2 x, so the gradient of y = tanh x when x = 0 is 1, because sech(0) = 1. Also, since sech2 x is positive, the gradient of y = tanh x is always positive.
(5) Putting all this information together gives us the graph sketch shown in Figure 8.D.7.
The lines y = 1 and y = –1 are horizontal asymptotes for this graph.
I have also drawn on the graph a line showing how we could find the value of x when tanh 
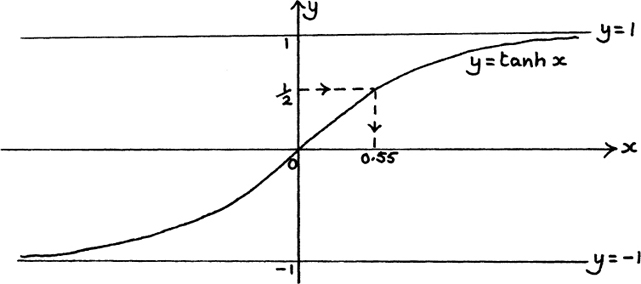
Figure 8.D.7
If you use your calculator to find 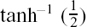 , you will get x = 0.55 to 2 d.p.
, you will get x = 0.55 to 2 d.p.
We can see from the shape of the graph that each value of tanh x can only come from one possible value of x, so therefore the function y = tanh x will have an inverse function. Now we’ll find the rule that gives us this. We have
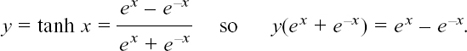
Multiplying all through by ex gives y(e2x + 1) = e2x – 1, so

Therefore
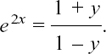
Taking logs both sides, we have
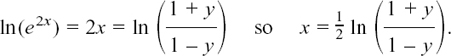
We now have the rule to get back to the original x if we know y. Use it to check that, if you put 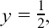 you do get x = 0.55 to 2 d.p.
you do get x = 0.55 to 2 d.p.
Interchanging x and y as before, so that we have this rule as a function of x, we get the inverse function of
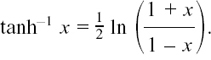
To give the log of a positive quantity, the possible values of x will have to lie between –1 and +1.
We can see that this is where the values of x must lie from looking at the graph sketch of y = tanh–1 x which I have drawn with y = tanh x in Figure 8.D.8.
Figure 8.D.8
I have used the line of symmetry y = x to draw this sketch. I have also used the answer to Question (4) which was that the gradient of y = tanh x when x = 0 is 1. This means that y = x is a tangent to both y = tanh x and y = tanh–1 x. It is a very interesting tangent because it crosses both of the curves, which sort of flex themselves when x = 0. The line y = x does exactly the same thing with y = sinh x and y = sinh–1 x at the origin, as you’ll see if you draw it in on Figure 8.D.4(a) and (b). We shall look at points of inflection like this in more detail in Section 8.E.(b).
You may find it helpful here to emphasise the separateness of the two curves by using two colours on them. Be careful to put the colour correctly on the two separate halves of each graph! (The tanh graph is a flattened S shape.)
We were able to see from the graph that y = tanh x must have an inverse function, but suppose we didn’t know what the graph looked like? Can we still show that the inverse relation will be a function?
To do this, we have to show that it isn’t possible to get the same value for tanh x from two different values for x, so that, when we go back the other way, there is only one possible answer.
In other words, we have to show that the only way that tanh a = tanh b is for a and b to be themselves equal.
We put tanh a = tanh b so
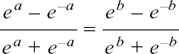
and see what happens. Try tidying this up for yourself, and see if you can show that a and b must be equal.

Multiplying by (ea + e –a(eb + e–b) to get rid of fractions, we get
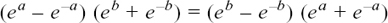
so
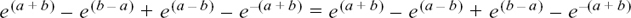
so
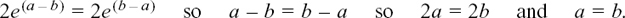
We’ve now shown that the inverse function does exist, without reference to the graph.

Remember that it is not true that ea × eb = eab. We must add the powers.
The mystery of why sinh x and cosh x are called hyperbolic functions has not yet been explained. This section tells you why this is so.
Suppose we let x = cosh θ and y = sinh θ and then plot the points that we get for different values of θ on a graph. For example, if θ = 0, we have x = cosh θ = 1 and y = sinh θ = 0, so one point on this graph will be (1,0).
Since cosh2 θ – sinh2 θ = 1, we know that the equation of this graph will be x2 – y2 = 1. This is the equation of the hyperbola which I show below in Figure 8.D.9.
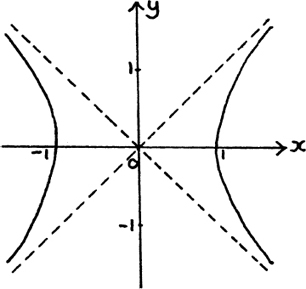
Figure 8.D.9
This graph may look a more familiar shape if you turn it through 45° anticlockwise. The two dashed lines make this resemblance easier to see.
Actually, only the right-hand side of it is given by x = cosh θ and y = sinh θ. Can you see why this is? Can you think of a way that we could get the whole graph?

cosh θ can’t be negative, and the points on the left-hand side of the graph have negative values for x.
We could get the whole graph by putting x = sec θ and y = tan θ.
Since sec2 θ – tan2 θ = 1, we still have x2 – y2 = 1, and we have the left-hand side of the graph too, since sec θ can take negative values.
In a similar way, x = cos θ and y = sin θ are linked to the circle x2 +y2 = 1. Indeed, it was this circle which we used to define the sin and cos of angles greater than 90° in Section 5.A.(c).
The variable θ which we have used for this hyperbola and circle is called a parameter. We can get other curves of the same type by subtly adjusting how we use it. For example, x = 2 cosh θ and y = 3 sinh θ gives the hyperbola (x/2)2 – (y/3)2 = 1 and x = 5 cos θ with y = 5 sin θ gives x2 + y2 = 25, the circle with centre (0,0) and radius 5 units.
Unbalancing them to give x = 4 cos θ and y = 3 sin θ, say, gives a squashed circle, or ellipse, with the equation (x/4)2 + (y/3)2 = 1. This is centred at the origin and cuts the axes at (4, 0), (0, 3), (–4, 0) and (0, –3).
There isn’t space to go into this in more detail just now, but you will find that this use of parameters to describe particular curves is often of great practical use in extracting further information from relationships between physical quantities.
Finally, you may be thinking that the name ‘hyperbolic’ isn’t the only strange thing about these functions. Why is there this curious link between them and the trig functions? I’ll show you the reason for this in Section 10.C.(b).
This is something which students quite often find difficult, but if you have worked through the earlier parts of this section so that you are now happy with what these inverse functions do, you should find it quite straightforward. We’ll look at two examples of differentiation, and then see how using the Chain Rule makes it possible to get lots of other similar results very easily.
EXAMPLE (1) How can we find dy/dx if y = sinh–1 x?
We could set about doing this in two ways.
METHOD (1) Let y = sinh–1 x. Then x = sinh y because this is what the inverse function of sinh–1 means. Therefore dx/dy = cosh y.
Now we use the argument of Section 8.B.(e) to say
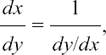
excluding any values of x for which dy/dx = 0.
(It is also possible to do this by implicit differentiation. I show you this method in Section 8.F.(c).)
Therefore
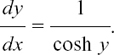
But cosh2 y = sinh2 y + 1, so

But we know that the gradient of y = sinh x is always positive. (How do we know this? What is d/dx (sinh x)?)

It is cosh x and cosh x is always positive. Therefore
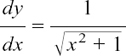
and we have the result that
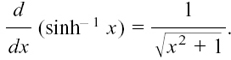
METHOD (2) This uses the result which we found in Section 8.D.(e) that 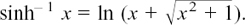
Therefore we can say
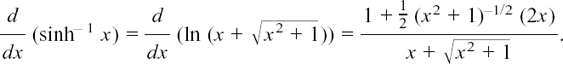
This doesn’t look too good, but it is tidied up amazingly by multiplying the top and bottom by  . We then get
. We then get
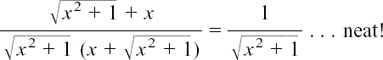
EXAMPLE (2) This time, we differentiate an inverse trig function.
We will find dy/dx if y = tan–1 x (or arctan x as it is also known).
Remember that y = tan–1 x means that y is the angle between –π/2 and π/2 whose tan is x. I explained this in Section 5.A.(i).

Then we use the identity tan2 y + 1 = sec2 y to get sec2 y = x2 + 1, so

giving us the result

EXAMPLE (3) This example shows how we can apply the above result.
Suppose we need to find
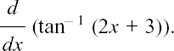
We don’t need to do all the previous working again because 2x + 3 is itself a function of x. Therefore we can just use the Chain Rule, putting X = 2x + 3, and remembering that dy/dx = (dy/dX) (dX/dx). (See Section 8.C.(a) if necessary.)
Here, we have

so
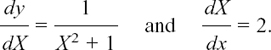
Therefore
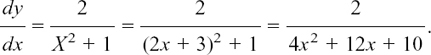
In general, we can say that if y = tan–1 (lump), and the lump is a function of x, then
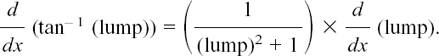
If you think of it this way, you will probably be able to write the answers down straight away.
We get a particularly useful version of this if we put (lump) = x/a where a is a constant. This gives us
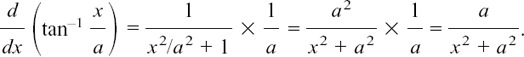
This result is very useful for finding some particular kinds of integral, as we shall see in Section 9.B.(d).
Exactly the same system can be used to differentiate inverse functions of other more complicated functions.
So, for example, if we have sinh–1 (lump), then
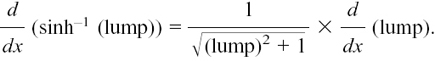
In particular, if (lump) = x/a, we have
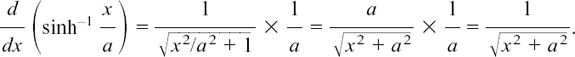
I have tidied up the first fraction by multiplying it top and bottom by a, remembering that a put inside a square root must be written a2.
(1) By choosing suitable values for a, and using the pair of results

differentiate the following with respect to x.
(2) Use the Chain Rule to differentiate the following with respect to x.
(4) Solve the equation 8 sinh x = 3 sech x.
(5) Find all the possible solutions of the following equations.
(a) 2 sinh2 x – 5 cosh x – 1 = 0
(b) 3 sech2 x + 8 tanh x – 7 = 0
In Section 8.C.(e), we found the gradient of two of the tangents to the curve
y = (x + 3)/(x – 2)
by using the Quotient Rule to find dy/dx for this curve.
Since dy/dx tells us the steepness or gradient of a curve at any given point on it, it makes it possible for us to find the equation of the tangent to the curve at any point on it, provided that this is a point where the curve has a tangent, and none of the problems of Section 8.A.(f) exist.
Here are two examples of doing this.
EXAMPLE (1) Find the equations of the tangents to the curve y = x2 – 4x + 3 at the two points (a) (5,8) and (b) (2, –1).
To find the gradients of the tangents we differentiate y = x2 – 4x + 3 with respect to x giving dy/dx = 2x – 4.

This gives us the rule to find the gradient of the tangent for any value of x. It is not the equation of the tangent.
(a) When x = 5, dy/dx = 10 – 4 = 6 so m = 6 for the tangent at (5,8).
Using y – y1 = m(x – x1) for the equation of the tangent, from Section 2.B.(f), we have y – 8 = 6(x – 5), so y = 6x – 22 is the equation of tangent (a).
(b) When x = 2, dy/dx = 0.
What is happening here? Try drawing your own sketch to show how this makes sense.

If dy/dx = 0, the tangent is horizontal. This tangent is at the lowest point of the curve y = x2 – 4x + 3, and its equation is y = –1.
I show a sketch of the curve and these two tangents in Figure 8.E.1.

Figure 8.E.1
EXAMPLE (2) Find the equations of the tangents to the curve y = cos x when
(a) x = π/2, (b) x = π/6 and (c) x = π.
If y = cos x then dy/dx = – sin x so the gradient of tangent (a) is – sin π/2 = – 1. It touches the curve y = cos x at the point (π/2, 0) and its equation is y = –1(x – π/2) or y + x = π/2.
The gradient of tangent (b) is 
(We found the sin, cos and tan of π/6, π/4, and π/3 (that is, 30°, 45° and 60°), in Section 4.A.(g).)
Tangent (b) touches the curve  and its equation is
and its equation is 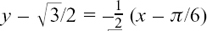 or
or  or
or 
This looks a little unfriendly, but it is not surprising that the equation of a tangent to a cos curve should involve numbers like π and  . The value of
. The value of  is 1.13 to 2 d.p. and this agrees with the look of the y intercept of tangent (b) on the graph sketch which I have drawn below.
is 1.13 to 2 d.p. and this agrees with the look of the y intercept of tangent (b) on the graph sketch which I have drawn below.
The gradient of tangent (c) is – sin π = 0 so this tangent is horizontal. Its equation is y = –1.
All three tangents are shown here in Figure 8.E.2.
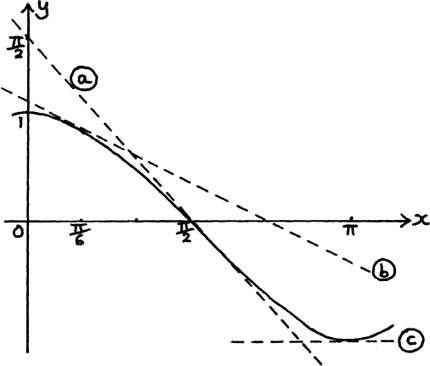
Figure 8.E.2
Find the equations of the tangents to the curves
(1) y = ex at
(a) x = o
(b) x = 1 and
(c) x = 2.
(2) y = tan x at
Draw sketches in each case to show these tangents.
Use one of the results which you have found in (1) to decide how many solutions there are to the equations (i) x = ex and (ii) 3x = ex.
(3) There is something special about one of the tangents in Example (2) above and one of the tangents to the curve y = tan x in question (2) in this exercise.Can you spot what this special property is? There were examples of tangents with this same property in the previous section, too.
A turning point on a curve with the equation y = f(x) is a point at which dy/dx = 0, or f′(x) = 0, writing the same thing in function notation. Turning points are also sometimes called stationary points, and the values of f(x) where f′(x) = 0 are called stationary values.
From the examples which we have just looked at in the previous section we can see that it will be useful when sketching curves if we can find where the horizontal tangents are, that is the points where dy/dx = 0. Finding the answer to this will not only help us to draw graph sketches, but also to extract useful information about physical relationships. (For example, in Section 2.D.(g), the horizontal tangent is at the point of the curve corresponding to the highest point reached by the ball, so ds/dt = 0 at this point.)
Sometimes it is also helpful to know what the value of d2y/dx2 is for particular values of x. d2y/dx2 means d/dx (dy/dx), so it tells us the rate of change of the rate of change with respect to x. We used it, but with a different letter, in Section 8.A.(e) when we found d2x/dt2 for x = cos t.
To help you to understand the different possibilities, I have drawn sketches showing interesting points on the curves of some simple functions in Figure 8.E.3. You should fill in your own answers to the questions I have asked you in the table below the drawings.
Figure 8.E.3
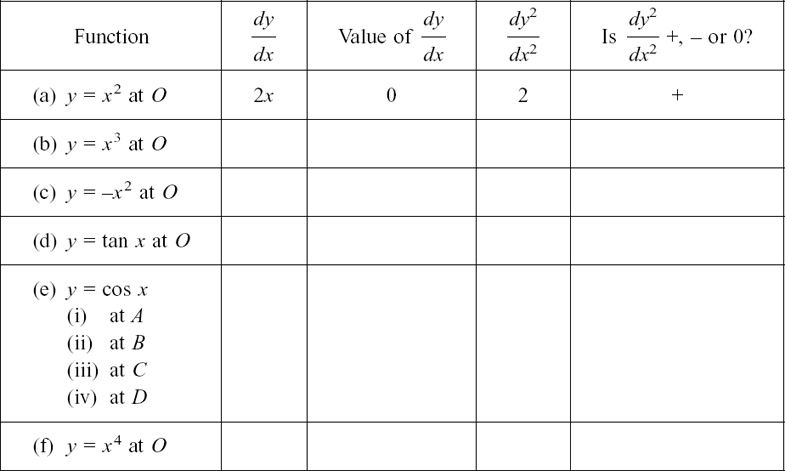
Now check your answers to this table. These are given at the back of the book as Table 8.E.2 after the answers to Exercise 8.E. 1.
Next, go back to the curves in Figure 8.E.3 and look at what is happening to the steepness of the curve either side of the marked point in each case, and try answering the following questions.
(1) Is the slope positive or negative?
(2) Does this sign change as you move through the marked point?
(3) Is the steepness increasing or decreasing as you move through the marked point?
(4) What happens to the sense of turn of the curve either side of the marked point? (I have shown this with curved arrows.)
You may find that it helps you to think about what is happening here if you sketch in some of your own tangents to the curves in my diagrams. (I’d suggest using pencil for this, then you can do it more experimentally.)
It’s important for your understanding here that you do try to answer these questions yourself. Don’t just skip to the next bit to get them answered for you.

Now, we’ll look together at what the answers to the four questions above tell us.
We find that the points marked with letters (including the various points at the origin, marked O in each diagram) fit into three different categories. These are as follows:
(1) At O in diagrams (a) and (f), and at C in (e), we have what is called a local minimum (‘local’ because sometimes curves may dip down below this value somewhere else). At these points, the value of dy/dx is zero because the tangent to the curve is horizontal. As we pass through these points, the slope of the tangents changes from negative to positive as the value of x increases. The sense of turn remains anticlockwise through these points.
(2) At O in diagram (c), and at A in (e) we have what is called a local maximum. Again, the value of dy/dx is zero at these points. As we pass through these points, the slope of the tangents changes from positive to negative as the value of x increases. The sense of turn remains clockwise through these points.
(1) and (2) give the result that
 at any local maximum or minimum.
at any local maximum or minimum.
(3) At O in diagrams (b) and (d), and at B and D in diagram (e), we have points where the curve flexes itself. These are called points of inflection. The tangent to each curve at these points crosses the curve there, and the sense of turn changes. At O in (b) and (d), and at B in (e), it changes from clockwise to anticlockwise, and at D in (e) it changes from anticlockwise to clockwise.
O in (b) is the only one of these points where we also have dy/dx = 0.
Either side of each of these points the slope of the tangents remains either positive or negative. In the first three cases, the slopes of the tangents first become flatter as we approach the point and then steeper again once we are through it. This means that the slope itself has a local minimum at the point concerned. In other words, d/dx (dy/dx) = d2y/dx2 = 0 at each of these points.
In the fourth case, of curve (e) at D, the slope becomes steeper as we approach D, and then less steep once we have passed D, so this slope has a local maximum at D. Again, d2y/dx2 = 0.
If you find d2y/dx2 for the other examples we have met of tangents crossing curves, you’ll see that it is also zero at these points. (You could check for yourself with y = sin x, y = sinh x and y = tanh x, all at the origin.)
 at any point of inflection
at any point of inflection
We have seen that d2y/dx2 = 0 at any point of inflection.
What will happen to the value of d2y/dx2 at a local maximum or minimum?
At each of the local maximum points from (c) and (e), the slope of the curve goes from positive to negative, so the change in the slope is negative.
In both cases, d2y/dx2 is negative at the maximum point.
At the two local minimum points of (a) and (e), the slope of the curve goes from negative to positive, so the change in the slope is positive.
In both cases, d2y/dx2 is positive at the minimum point.
The case of the local minimum in (f) works out a little differently. The slope of the curve goes from negative to positive, and its rate of change is positive except at the point O itself.
We have d2y/dx2 = 12x2 = 0 at the point O, although it is positive either side of O. At O itself, the curve is very blunt because it has its four roots of x = 0 all bunched together here. This has the effect of making the rate of change of dy/dx at this point (that is, d2y/dx2) equal to zero. This effect, which will happen whenever a curve is blunt like this, makes the rules for testing for maximum and minimum points slightly more complicated, because it is only sometimes possible to use the sign of d2y/dx2 to test which we’ve got.

Here is a summary of the above results, so that we can use them to find out how particular curves will behave.
Finding and classifying turning points and points of inflection
For a point to be a local maximum, dy/dx must be equal to zero. Then use either
Test (1): the gradients of the tangents move through the point in the sequence + 0 –, so test the value of dy/dx either side of this point,
or
Test (2): if the value of d2y/dx2 is negative at this point, then it is a local maximum, but if d2y/dx2 = 0 then Test (1) must be used.
For a point to be a local minimum, dy/dx must be equal to zero. Then use either
Test (1): the gradients of the tangents move through the point in the sequence – 0 +, so test the value of dy/dx either side of this point,
or
Test (2): if the value of d2y/dx2 is positive at this point, then it is a local minimum, but if d2y/dx2 = 0 then Test (1) must be used.
For a point of inflection,
(1) the value of dy/dx does not change sign as it moves through the point (it may or may not be equal to zero at the point itself),
and
(2) the value of d2y/dx2 at the point must be equal to zero.
The tests outlined in this previous section give us useful extra information which we can use for sketching graphs.
I have already listed informally the other questions which we need to answer in order to draw a graph sketch in Section 3.B.(i) where we sketched y = (x + 3)/(x – 2). You should look back at how we built up this sketch before going on.
Now that we can include finding the turning points, I can give you a complete summary of the questions which you need to answer in order to sketch a curve.
For convenience, I will call this curve y = f(x) but, of course, other letters can be used.
Questions to answer in order to draw a graph sketch
(1) Does the curve cut the y-axis? If so, where? (Try putting x = 0.)
(2) Does the curve cut the x-axis? If so where?
(This is the same as asking if the equation f(x) = 0 has any roots on the x-axis.)
(3) Are there any values of x which have to be excluded because they would mean trying to divide by zero?
If so, what are they? (Such values of x will give you vertical asymptotes. An asymptote is a line which the curve of the graph of the function becomes closer and closer to.)
What happens to the values of f(x) for values of x just either side of the forbidden values?
(4) What happens to the values of f(x) when x takes very large positive or negative values?
(If it gets closer and closer to some fixed limit then this will give you a horizontal asymptote.)
(5) Are there any turning points? (That is, are there any values of x for which f’(x) or dy/dx = 0?) If so, what are they?
You will need to find the value of f(x) (the stationary value) for each of these values of x.
Test each turning point to find whether it is a local maximum, local minimum or point of inflection. (The tests for this are at the end of the previous section.) You don’t usually need to find points of inflection where dy/dx ≠ 0 unless you are specifically asked to do so.
An example to show these tests in action
We’ll draw a sketch of

so we go through answering each of the questions in the list above in turn.
(1) Putting x = 0 gives  so the curve y =f (x) cuts the y-axis at the point (0,
so the curve y =f (x) cuts the y-axis at the point (0,  ).
).
(2) f(x) = 0 if x – 5 = 0 so if x = 5.
The curve y =f(x) cuts the x-axis at (5,0).
(3) Any value of x which makes x2 – 9 = 0 must be excluded.
x2 – 9 = (x + 3) (x – 3) so we can’t have x = –3 or x = 3.
The lines x = –3 and x = 3 are vertical asympotes of y =f(x).
Testing with nearby values of x, using a calculator, gives:
The value of f(x) is large and negative if x is just less than –3.
The value of f(x) is large and positive if x is just greater than –3.
The value of f(x) is large and positive if x is just less than +3.
The value of f(x) is large and negative if x is just greater than +3.
(4) The easiest way to see what will happen to y =f(x) = (x – 5)/(x2 – 9) if x takes very large positive values, is to divide the top and bottom of the fraction by x2. This gives us
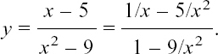
Now, as x becomes very large, each of 1/x, –5/x2 and –9/x2 becomes very small.
We can say that, as x → ∞, each of 1/x, –5/x2, and –9/x2→ 0.
So we will have  or 0 as x →∞.
or 0 as x →∞.
Exactly the same thing happens for large negative values of x, so the line y = 0 (which is the x-axis – be careful here!) is also an asymptote.
Check with some large values of x on your calculator that the value of y really is getting close to zero.
You could also look at what is happening entirely experimentally by using your calculator, but you might then be left with a sneaky feeling that perhaps the curve does some strange unforeseen wiggle which your calculator hasn’t revealed. Remember that you can’t ever prove what a curve will do by testing with numerical values, but you can certainly prove that it won’t do something. It is always wise to check your ideas of what it does do.
A mistake which students quite often make when graph-sketching is to work out exact values for some very boring bit of the curve which is almost a straight line. Then they think that the whole thing is probably a straight line, so getting a total disaster. The method I have given you here shows you how to find all the interesting bits.
(5) Differentiating y = f(x), using the Quotient Rule, we get
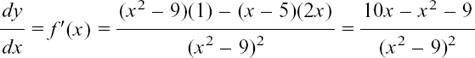
so 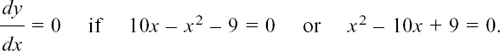
Factorising gives (x – 1) (x – 9) = 0 so x = 1 or x = 9 for the stationary values.
(You could also find these by using the quadratic formula to solve the equation.) The two stationary values are 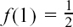 and
and  , so the turning points are
, so the turning points are  and
and 

Remember that these turning points are points on the original curve, so that to find them you must substitute the two values of x which give them into the equation of the original curve.
Now we want to know whether there are local maximum or minimum points on the curve.
Finding d2y/dx2 is not a pleasant prospect here, so we look at the values of dy/dx or f′(x) either side of x = 1 and x = 9.
Passing through x = 1, the sequence goes – 0 + giving a local minimum of 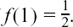 You can show this here by choosing, say, x = 0 and x = 2 and substituting these values into the expression which we have found for dy/dx. These particular values give
You can show this here by choosing, say, x = 0 and x = 2 and substituting these values into the expression which we have found for dy/dx. These particular values give  and
and  , confirming the sequence of – 0 +.
, confirming the sequence of – 0 +.
Similarly, passing through x = 9, the sequence goes + 0 – giving a local maximum of 
Notice that the value of the local minimum is actually greater than the value of the local maximum for this curve.
We now have all the information we need to draw the graph sketch. I show this in Figure 8.E.4.
Figure 8.E.4
Now try sketching the graphs of the following functions yourself.
Students often find graph-sketching difficult, but if you answer all the questions in my list for each curve, you should find that you can draw the sketches successfully. You will also understand why the curve behaves as it does, which won’t be the case if you just use a graph-sketching calculator.
Being able to find the turning points of a function can have much wider implications than just making it easier to sketch its graph. In particular, it gives us a method of answering many practical questions.
Since most of the examples we shall look at together in this section involve the volumes and surface areas of solid shapes, I am putting in a table here to give some of these.
A summary of volumes and surface areas of the commonest solids
The four solids are shown in Figure 8.E.5.
Figure 8.E.5
In each formula, V stands for volume and A stands for surface area.
(1) For a closed rectangular box, V = lbh and A = 2lb + 2bh + 2lh.
(2) For a closed cylinder, V = πr2h and A = 2πr2 + 2πrh.
(3) For a cone, including its base,  and A = πrl + πr2.
and A = πrl + πr2.
(4) For a sphere, 

A volume must always involve three lengths multiplied together. A surface area must always involve two lengths multiplied together. If you find that you have an equation for which this isn’t true, go back and recheck! Something has gone wrong somewhere.
EXAMPLE (1) This is typical of the sort of problem which we can now solve. It comes in two parts.
(a) A manufacturer wishes to construct a metal can to hold a given volume of liquid. If the can is made entirely of the same thickness of metal, what is the best ratio of the height of the can to its radius so that the least amount of metal is used?
(b) To make the construction more rigid, it is decided that it will be necessary to use a double thickness of metal for the top and bottom of the can. In order to keep the cost of production to a minimum, what dimensions should the can now have? Give the answer again in the form of the best ratio of its height to its radius.
(a) We start by drawing a sketch of the can (which I have done in Figure 8.E.6, giving it a height of h and a radius of r).
Next, we label the other quantities we shall need to deal with.
Let the volume be V, the area be A, and the ratio of h/r be x.
Figure 8.E.6
Since the can is being made to hold a given quantity of liquid, we know that V is a fixed quantity. We have V = πr2h, and h/r = x, so
The surface area, A, is made up of the two circular ends of the can and its curved surface, which would unroll to give a rectangle.
This gives us A = 2πr2 + 2πrh.
At present, we only know how to differentiate functions with one variable, but the expression which we have for A involves the two variables, r and h.
However, we know that the fixed quantity V = πr2h, so h = V/πr2.
Substituting this for h gives us
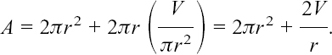
We’ve now got A described entirely in terms of the one variable, r.
Since we want a minimum value of A, what should we do next?

We should find dA/dr, and look for values of r which make it equal to zero. We get:
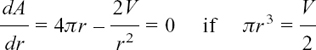
so the ratio
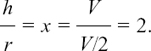
(Remember when you differentiate that both π and V are constants.)
Now we check for certain that this gives a minimum value for A. We get
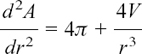
which is positive since the value for r which we have found is positive. Therefore, we have found the ratio which gives a minimum value for A.
We have found that the surface area is smallest when the radius of the cylinder is half its height. This means that the vertical cross-section through the central axis will be a square.
(b) Now that the two ends of the can are to be made from a double thickness of metal, it seems likely that we should make the can taller and thinner in order to minimise the amount of metal we use. We will assume that a double thickness costs twice as much, and take the cost per unit area of the curved sides of the can to be c. Then the metal in the two ends will cost 2c per unit area, and we will call the total cost of the can C.
V and x will have the same equations as before but we will now have
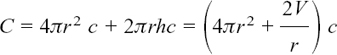
so
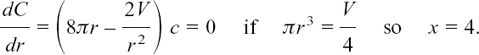
In the same way as before, this gives a minimum for the cost, so we have found that the height should now be four times the radius.
We can see how this pair of answers might work out numerically by taking the particular case of a half-litre can. This makes V = 500 cubic centimetres.
Then, in case (a) where h = 2r we have 500 = 2πr3 so r = 4.30 cm to 2 d.p. and h = 8.60 cm to 2 d.p.
In case (b) where h = 4r we have 500 = 4πr3 so r = 3.41 cm to 2 d.p. and h = 13.66 cm to 2 d.p.
EXAMPLE (2) What is the volume of the largest cylinder which can be placed inside a cone of fixed height H and radius R so that it just touches it inside, as I show in Figure 8.E.7(a)? Is it possible to fill in more than half the space inside this cone with such a cylinder?
We can see that the possible shape of the cylinder can vary between a sort of thin pencil to a flat biscuit. The largest possible size will occur somewhere between these two extremes.
I will call the height of the cylinder h and its radius r.
Then its volume V is given by V = πr2h and we have to find the largest possible value of V (which will be in terms of R and H, the radius and height of the cone), as r and h vary.
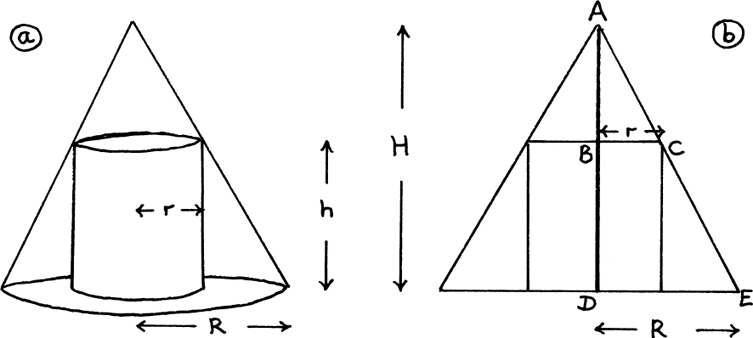
Figure 8.E.7
Since, at present, we can only differentiate functions with one variable, we must somehow use the physical relationship of the cone to the cylinder to find h in terms of r. To see how we can do this, we take a vertical cross-section along the joint axis of the cone and cylinder which gives us Figure 8.E.7(b).
We can now use the two similar triangles, ABC and ADE. These triangles nest into each other, so their sides are in the same proportion. Therefore
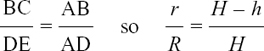
so rH = RH –Rh and Rh = RH – rH = H(R – r).
Therefore
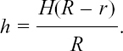
Substituting this for h in the equation V = πr2h we get
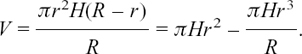
We can now find dV/dr (remembering that π, H and R are all constants). We get
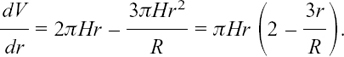
To find the maximum V, we put dV/dr = 0. Now
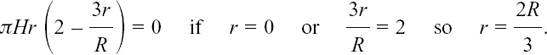
We can see physically that r = 0 gives us the minimum value of zero for V.
Also, d2V/dr2 is negative if r = 2R/3. (Check this for yourself.) Therefore, this value of r gives us the maximum volume.
How high will this cylinder be? We have
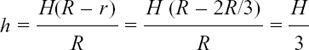
so it is one third of the height of the cone.
The volume of this cylinder is
The volume of the cone is  H so the proportion of it which is filled by this largest possible cylinder is
H so the proportion of it which is filled by this largest possible cylinder is , that is, less than half of it.
, that is, less than half of it.
Try these for yourself.
(1) What is the maximum volume of a square-based open box made by cutting squares from the corners of a square piece of cardboard with sides 10 cm long, and then bending up the sides. I’m assuming here that the sides will then be taped together – you don’t have to make allowances for overlap.
(2) What are the dimensions of the largest cylinder which can be placed inside a sphere of fixed radius R so that its two ends just touch the sphere? Is it possible to fill more than half of the interior of the sphere this way?
(3) What is the maximum distance from the origin of a particle moving on the x-axis so that its distance from O is given by the equation x = 3 cos t + 4 sin t?
Before rushing into differentiating here, have a think about how else you could write 3 cos t + 4 sin t. (Look back at Section 5.D.(f) if necessary.)
This is an ingenious application of the properties of tangents which makes it possible to find closer and closer approximations to the roots of equations which are too difficult to solve exactly. (In the United States, the credit for this method is usually given entirely to Isaac Newton and it is called Newton’s method.)
First, I’ll explain graphically how it works.
Suppose you have some equation f(x) = 0 which you want to solve, so you want to find as accurately as possible the point where the curve y = f(x) crosses the x-axis. It may, of course, do this more than once, but we will look at just one crossing point, where x = a, say.
In order to start the Newton–Raphson process, we need to have some idea of where a is. Suppose that by some ingenious method we have been able to find that x = x1 is a value close to a. Figure 8.E.8(a) shows the curve of f(x) near a and x1.

Figure 8.E.8
Then, if the curve really looks like my drawing, the tangent to the curve at x = x1 will cut the x-axis at a point x2 which is closer to the true root a than x1 was.
How can we find out what x2 is, from knowing what y = f(x) and x1 are?
The point P has coordinates (x1, y1), or (x1, f(x1)), so we do know some measurements.
From Figure 8.E.8(b) we can say that the gradient of the tangent at P is f(x1)/(x1 – x2). But the gradient of any tangent is also given by dy/dx or f′(x) at the point concerned. This means that we know that the gradient of this particular tangent is f′(x1). (Using f′ here instead of dy/dx is very hand y as it makes it easier for us to talk about particular gradients.) We can now say that
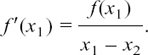
Next, we need to rearrange this to give us a rule for finding x2. We get
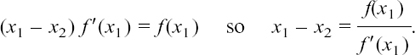
This gives us
The Newton–Raphson Rule
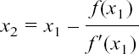
(One of my students gave me a handy way of remembering which way round the last bit goes. She said ‘dashed goes down’.)
If x1 is close to the root x = a, and if the curve is not too wiggly or behaving in other unexpected ways, then x2 will be closer to a than x1 was. (Sorting out these ‘ifs’ is what the subject of mathematical analysis does. It makes it possible to get results like this by analysing just what properties the curve must have near x = a for the method to work. For example, we certainly won’t want any of the complications described in Section 8.A.(f).)
Having found x2, we can then repeat the process to get an even better approximation of x3 to a, and so on, until we have as many decimal places of accuracy as we require.
Next, we will look at how this process works taking some particular examples.
EXAMPLE (1) For my first example, I will take an equation that we can solve exactly, so that you will be able to see how this process actually gives the right answer.
Suppose f(x) = x3 + x2 – 9x – 9 = (x – 3) (x + 1) (x + 3) so f’(x) = 3x2 + 2x – 9.
I show a picture of f(x) in Figure 8.E.9.
We can see from the factorisation that one of the roots of f(x) = 0 is x = 3.
We’ll take x = 4 as a starting value, and see if the Newton–Raphson process takes us towards the true root of x = 3. We have
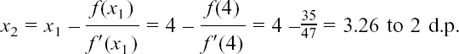
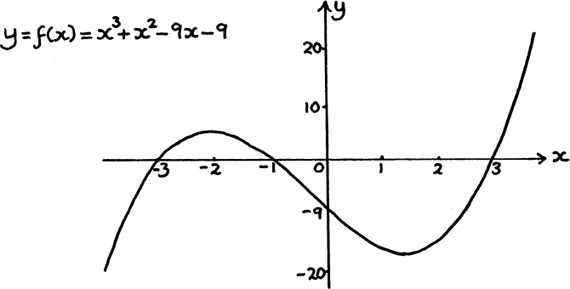
Figure 8.E.9
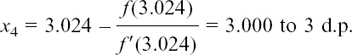 Check this one, too.
Check this one, too.
In this particular example, the process is working beautifully, and you can see the successive answers homing in on x = 3.
If we hadn’t known where the roots were, we could have used the changes in sign of f(x) to show us where to look.
Working out some values gives us f(4) = 35, f(2) = – 15, f(0) = – 9, f(–2) = 5 and f(–4) = –21.
Looking at the picture of Figure 8.E.9, you can see the sign changing either side of each root, as the curve crosses the x-axis.
Have we made a brilliant discovery here?
Will we always be able to use this system to find an interval in which a root must lie? Try deciding for yourself whether the following two statements are true.
STATEMENT (1) If f(x) = 5x3 + 6x2 – 23x + 12 then f(0) = 12 and f(2) = 30
. Therefore there is no root between x = 0 and x = 2.
STATEMENT (2) If 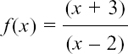 then f(1) = – 4 and f(3) = 6.
then f(1) = – 4 and f(3) = 6.
Therefore f(x) has a root between x = 1 and x = 3.
If you don’t agree with these statements, see if you can work out what is really happening.
Everything you need to be able to do this has already come in this book.

We can see what is really happening in the first case by using the methods of Section 2.E.(a).
We have f(x) = 5x3 + 6x2 – 23x +12, and f(1) = 0, so immediately we know that statement (1) is false.
What is actually going on?
Since f(1) = 0, we know that (x – 1) is a factor of f(x).
Matching up the end terms gives us
5x3 + 6x2 – 23x + 12 = (x – 1) (5x2 + px – 12).
Matching the terms in x2 gives us
6x2 = –5x2 + px2 so p = 11.
Now we have
f(x) = (x – 1) (5x2 + 11x – 12) = (x – 1) (5x – 4)(x + 3).
This means that the roots of f(x) = 0 are x = 1, x = 5 and x = –3.
There are two roots in the interval from x = 0 to x = 2. I show a sketch of y = f(x) in Figure 8.E.10.

Figure 8.E.10
We would only see the sign change for the roots 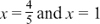 by taking a value between them. Check for yourself that choosing such a value does make f(x) come out negative.
by taking a value between them. Check for yourself that choosing such a value does make f(x) come out negative.
Statement (2) is wrong for quite a different reason. We drew a picture of this function in Section 3.B.(i). The sign change here doesn’t mean that f(x) has crossed the x-axis between x = 1 and x = 3. The curve has a jump or discontinuity when x = 2 and gets to the other side of the x-axis this way.
The two examples above give us two useful rules to remember when looking for roots.
Rules for using a sign change when looking for roots
(1) If f(x1) and f(x2) have different signs, there must be at least one root between x1 and x2 provided that f(x) is continuous from x1 to x2.
(2) If f(x) is continuous, then a sign-change tells us that there is an odd number of roots in the interval.
You can think of ‘continuous’ here as meaning that f(x) can be drawn with a continuous straight line. The subtle mathematical non-pictorial meaning of this word is described in courses on mathematical analysis.
Obviously too, in order to be able to use the Newton–Raphson method, we must be able to differentiate f(x). It mustn’t have any of the problems which were described in Section 8.A.(f), in the part where we are working.
EXAMPLE (2)
Next, we’ll use the Newton–Raphson method to find all the roots of
(a) tanh x = 2x and
(b) tanh  .
.
How many will there be? Will it be the same number for both (a) and (b)?
Try sketching what you think will happen, using Section 8.D.(g) if you need to.

We found in Section 8.D.(g) that y = x is the tangent to y = tanh x at the origin because d/dx (tanh x) = sech2 x and sech2 (0) = 1.
We can see from this, and from the shape of y = tanh x, that y = 2x will cut y = tanh x only once, at the origin, so x = 0 is the only solution of (a). I show a picture of this in Figure 8.E. 11.

Figure 8.E.11
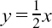 will cut y = tanh x three times, once at the origin and also at two other points symmetrically placed either side of the origin because y = tanh x is odd. (Turn it upside down and it looks the same.) So we just have one solution to find.
will cut y = tanh x three times, once at the origin and also at two other points symmetrically placed either side of the origin because y = tanh x is odd. (Turn it upside down and it looks the same.) So we just have one solution to find.
We want the value of x on the right-hand side of the graph for which
tanh  so tanh
so tanh 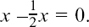
We let f(x) = tanh 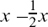 and look for the solution here of f(x) = 0
and look for the solution here of f(x) = 0
From the sketch we can see that if x < a then x > 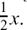 . It looks as though a may be quite close to 2.
. It looks as though a may be quite close to 2.
f(2) = – 0.036 to 3 d.p. so the root is to the left of this.
f(1.9) = 0.006 to 3 d.p. The change in sign confirms that the root lies between 1.9 and 2, since f(x) is continuous.
Since f(1.9) is closer to zero, we’ll start with x1 = 1.9.
We have 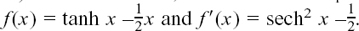 . This gives us
. This gives us 
The three solutions of 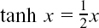 are x = –1.915, x = 0 and x = 1.915, correct to 3 d.p.
are x = –1.915, x = 0 and x = 1.915, correct to 3 d.p.
EXAMPLE (3)
Show, by drawing a sketch, that sin x = 3 – 2x has just one solution. Find this solution correct to 3 d.p.
See how far you can get with this one yourself before you look at my solution.

We want to solve sin x = 3 – 2x which is the same as sin x – 3 + 2x = 0.
We let f(x) = sin x–3 + 2x so f’(x) = cos x + 2.
We can see from the sketch of Figure 8.E.12 that the root is less than  It also looks as though it could be greater than 1.
It also looks as though it could be greater than 1.
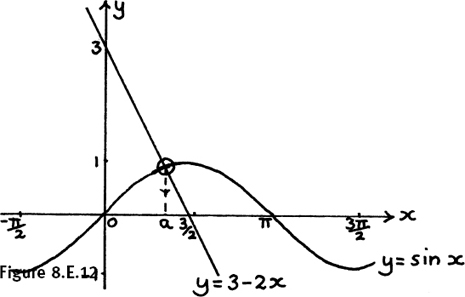
Figure 8.E.12
f(1) = –0.159 and f(1.5) = 0.997 so there is a root between x = 1 and x = 1.5 since f(x) is continuous.
Since f(1) is closer to zero, we’ll start with x1 = 1. This gives us

so the solution is x = 1.063 radians correct to 3 d.p.
For each of the following, draw a sketch to help you decide where the roots of the following equations might lie, and then use the Newton–Raphson process to find these roots correct to 3 d.p.
(1) 2x3 – 3X2 + 6x + 1 = 0
(2) ex = 3 – x,
(3) (a) 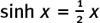
(b) sinh x = 2x
How could we find the rate of change of y with respect to x if we have a relation between them which does not give y described in terms of x? Let’s look at two examples.
EXAMPLE (1)
Suppose we are given the equation x2 + y2 = 25.
This is the equation of the circle whose centre is at the origin and whose radius is five units. (See Section 4.C.(d) if necessary.)
The relationship here between x and y is called implicit, because we don’t have it in the form of y given as some expression in x.
We can easily draw a sketch of this circle, and we can see how steep the curve looks at any point on it by sketching the tangent at that point. (Indeed, we can actually find this slope, using the property of the tangent being perpendicular to the radius, as we did in Section 4.C.(f).)
But how can we find dy/dx for this circle? Developing a technique to do this will make it possible for us to find dy/dx for other curves where we have no alternative method of finding the gradient.
One possibility would be to start by rearranging its equation so that we have y2 = 25 – x2.
What is y? Can you see a possible complication here?

We have  .This is not a function because there are two possible values of y for each possible value of x. These possible values of x lie between –5 and +5 inclusive.
.This is not a function because there are two possible values of y for each possible value of x. These possible values of x lie between –5 and +5 inclusive.
We can see exactly what is happening in Figure 8.F. 1.

Figure 8.F.1
The equation  gives the top half of the circle.
gives the top half of the circle.
The equation  gives the bottom half of the circle, and each of these are functions.
gives the bottom half of the circle, and each of these are functions.
Differentiating these square roots would not be very pleasant. We therefore argue that it would seem reasonable to go through the equation x2 +y2 = 25 differentiating it term by term with respect to x in just the same way that we differentiated the equation y = x2 – 4x + 3 term by term to give dy/dx = 2x – 4 in Section 8.E.(a).
(The equation y = x2 – 4x + 3 gives y explicitly in terms of x.)
The problem that we have with this new equation is that we shall need to differentiate y2 with respect to x.
We can do this by using the Chain Rule. We know that y2 differentiated with respect to y is 2y, and we then multiply this answer by dy/dx.
We are saying that

Now, differentiating x2 + y2 = 25 term by term with respect to x gives us

How does this result fit in with the particular examples shown on Figure 8.F.1?
At the point (4,3), 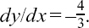
This agrees with what we know the gradient of the tangent here must be, because the gradient of the radius to this point is 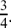 The tangent is perpendicular to the radius so its gradient is
The tangent is perpendicular to the radius so its gradient is  (Thisusesm1 m2 =–1 from Section 2.B.(h).)
(Thisusesm1 m2 =–1 from Section 2.B.(h).)
In fact, at any point on this circle with coordinates (x,y), the gradient of the radius is y/x and the gradient of the tangent is –x/y. We can see here that geometry and calculus both give us the same result.
This extends to special cases like the gradient at the point (0, –5) which is zero, and the gradient at the point (–5, 0) where dy/dx is undefined. Clearly from the diagram this must be so, because the tangent here is vertical.
EXAMPLE (2)
Suppose this time that we want to find dy/dx for the implicit equation
x2 –6x + y2 –4y= 12.
What kind of curve does this give?

This equation can be written in the form (x – 3)2 + (y – 2)2 = 25.
It describes the circle whose centre is at (3,2) and whose radius is 5 units.
We drew this particular circle in Section 4.C.(f) and found the gradients and equations of some of its tangents. This will help us now to see what is happening geometrically, and so to be able to make sense of some of the answers which we get by calculus.
To find dy/dx for this circle we again differentiate its equation term by term, remembering that y differentiated with repect to x is simply dy/dx. We get
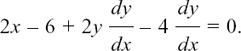

Remember that differentiating a number gives zero, so d/dx (12) = 0. It doesn’t change so its rate of change is zero.
Tidying up gives

dividing top and bottom of this fraction by 2. Always simplify when you can.
We can now see how this ties in with the gradients of the four tangents
which we already found for this particular circle in Section 4.C.(f).
The points of contact of these tangents are (7,5), (–1,–1), (3,7) and (8,2).
Try using dy/dx yourself here to find the gradients of these four tangents. Use Figure 4.C. 11 in Section 4.C.(f) to sort out what is happening if some of your results seem rather curious.
Substituting in these pairs of values for x and y in turn, we get
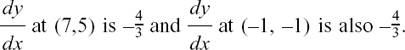
(We can see that this is right on Figure 4.C. 11. The gradients of the two radii to the points of contact are both 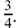 )
)
dy/dx at (3,7) is zero and the tangent there is horizontal.

When you find that the gradient of the tangent at the point (8,2) is dy/dx =–5/0, don’t be tempted to cross your fingers and say that this is zero as many students do! dy/dx at (8,2) is undefined because the tangent is vertical.
Using Figure 4. C. 11 we have seen geometrically that the answers which we have found by differentiating do make sense.
Also, from this same diagram, we can see that the gradient of the radius to the point (x,y) on this circle is (y – 2)/(x – 3).
Therefore, using m1m2 =–1, the gradient of the tangent at this point is
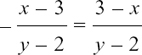
which is exactly what we get by differentiating.
Find dy/dx for the circle whose equation is
x2 + 16x + y2 – 4y – 101 = 0.
Use this result to find the gradient of the tangents to this circle at the four points with coordinates (4, –3), (–3, 14), (–8, –11) and (–21, 2).
Draw a sketch of this circle showing these four tangents.
Check your results with the answers to Exercise 4.C.3 which find these same gradients without differentiating.
What will we do if we have a curve whose equation has a term with x and y multiplied together? Let’s look at an example.
EXAMPLE (1)
Suppose we have the equation 2x2 + xy – y2 = 5.
In order to differentiate xy with respect to x we use the Product Rule because we have the two variables x and y multiplied together. (See Section 8.C.(d) if necessary.)
This gives us
So differentiating 2x2 + xy – y2 = 5 with respect to x gives
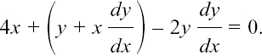
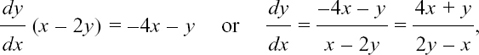
multiplying top and bottom of the fraction by –1 to make it easier to handle.
At the point (2,3) on this curve, (check that it is!), we have  giving the slope of the tangent here, and therefore the gradient of the curve at this point.
giving the slope of the tangent here, and therefore the gradient of the curve at this point.
We can find the equation of this tangent using y – y1 = m(x – x1) from Section 2.B.(f). It is  or 4y = 11x – 10.
or 4y = 11x – 10.
As students sometimes find this process slightly tricky, I shall give you another example which needs the use of the Product Rule.
EXAMPLE (2)
Find dy/dx for the equation 2x3 – 3x2y + 5xy2 + 2y3 = 6 and hence find the gradient of the tangent at the point (1,1).
I think it is easier if you take the numbers outside as factors for the terms involving the Product Rule, particularly if they are negative, as it is easy to lose one of the minus signs otherwise.
I shall start by showing the equation split up in a working sort of way as follows:
2x3 – 3([x2] [y]) + 5 ([x] [y2]) + 2y3 = 6.
Now, differentiating all through with respect to x we get
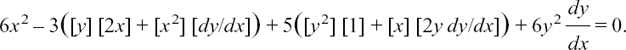
Tidying up, we get

so
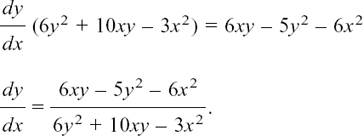
The slope of the tangent at the point (1,1), i.e. the gradient of the curve at that point, is given by
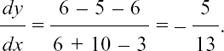
Try this similar example for yourself now.
EXAM PLE (3)
Find dy/dx for the curve given by the equation 3x3 + 7x2y – 3xy2 + 2y3 = 21. Hence find the gradient of the tangent at the point (1, 2) on this curve.


Make sure that you haven’t started off your answer with ‘dy/dx =’ because this is not at all what you mean.
What you are doing here is differentiating the whole expression with respect to x, so your answer should only start with ‘dy/dx =’ if the original equation starts in the form ‘y =’.
Setting out the given equation in a working sort of way as I did in the last example gives
3x3 + 7([x2][y]) – 3 ([x][y2]) + 2y3 = 21.
(You don’t have to do this step, but if you are at all unsure about keeping track of where you are then I think it will help you.)
Differentiating this expression term by term with respect to x gives
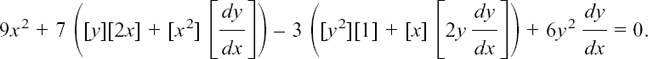
Again I have used square brackets so I can show you how the Product Rule is working on each bit. Tidying this up gives

so
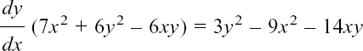
therefore 
At the point (1,2) on the curve, the slope of the tangent is dy/dx = –25/19.
In Section 8.D.(i), we differentiated inverse trig and hyperbolic functions using dy/dx = 1/(dx/dy). This seems reasonable if we take these as the limiting cases of δy/δx and 1/(δx/δy) respectively. For this rule to work, we have to be sure that dy/dx is not equal to zero for any particular value of x which we might want to consider.
It is also possible to differentiate these inverse functions implicitly.
I’ll show you how you can do this by taking the example of y = f(x) = sin–1 (x/a).
We know from Section 5.A.(h) that y must lie between – π/2 and + π/2 inclusive. The function itself looks like the sketch in Figure 8.F.2.

Figure 8.F.2
Notice that for this function we must have –a ≤ x ≤ a.
We have y =f(x) = sin–1 x/a, so therefore x/a = sin y because this is an inverse function, and there is only the one possible value for y from a given value of x/a.
Differentiating x/a = sin y implicitly with respect to x gives
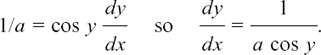
But
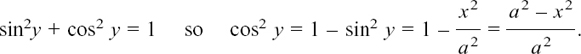
We can see from Figure 8.F.2 that the gradient of y = sin–1 (x/a) is positive, and therefore we can say
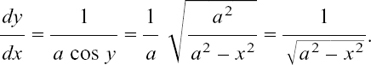
(The √ means that we are taking the positive square root here.) We know that for this function to work we must have –a ≤ x ≤ a. Now, we must also exclude x = a and x = –a. Why do we have to do this?

The answer is: because when x = a or x = –a the tangent to y = sin–1 (x/a) is vertical. The fraction 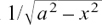 is undefined. We’ve now seen what happens when dy/dx = 1/0, and why we must exclude this possibility.
is undefined. We’ve now seen what happens when dy/dx = 1/0, and why we must exclude this possibility.
This gives us the following result.
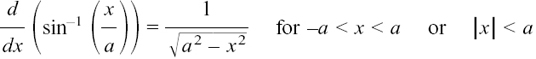
In Section 8.D.(f) we showed that 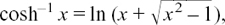 , and that, to have this inverse function for y = cosh x, we needed to restrict the possible values of x by saying that x ≥ 0, so that we were taking the cosh of a positive quantity.
, and that, to have this inverse function for y = cosh x, we needed to restrict the possible values of x by saying that x ≥ 0, so that we were taking the cosh of a positive quantity.
We’ll now differentiate f(x) = cosh–1 (x/a) implicitly. In Figure 8.F.3 I show a sketch of y = a cosh x and y = cosh–1 (x/a). It is very similar to Figure 8.D.6 except that 1 is replaced by a.

Figure 8.F.3
We can see from this sketch that, if y = cosh–1 (x/a), then we must have x ≥ a. Try finding d/dx (cosh–1 (x/a)) for yourself by using implicit differentiation.

The method is very similar to what we just did for y = sin–1 (x/a). We have y =f(x) = cosh–1 (x/a) so x/a = cosh y. Differentiating implicitly with respect to x gives
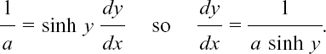
Using cosh2 y – sinh2 y = 1 gives us
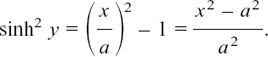
We can also see that the gradient of y = cosh–1 (x/a) is positive, so we can say that

Also, like last time, we can’t have x = a because this is where the tangent to y = cosh–1 (x/a) is vertical, and we would have the undefined fraction of  We now have the result that
We now have the result that
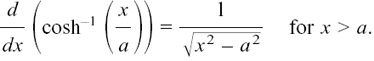
We can use the Chain Rule with these results to differentiate more fancy functions in exactly the same way that we used it in Section 8.D.(i) for fancy inverse functions of sinh and tanh.
I’ll show you how to find d/dx (sin–1 (x2 – 1)) as an example.
We have just shown that if y = sin–1 X then
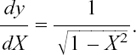
In this particular example, X = x2 – 1 so dX/dx = 2x. Using the Chain Rule of dy/dx = (dy/dX) (dX/dx) we have

For this to work, we would need to have 0 ≤ x2 < 2 so 
In general, we can say that
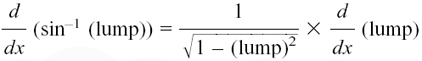
with the requirement that –1 (lump) < 1.
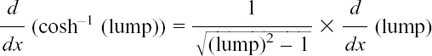
with the requirement that (lump) > 1.
You may be given the formula below as a rule for differentiating inverse functions.

This has exactly the same meaning as what we have been doing above. The only difference is that it is written in function notation.
I think that you might need reminding just how this works.
• f′ (x) means f(x) differentiated with respect to x.
• f′ (X) means f′ (X) differentiated with respect to X.
• f′ (f(x)) means f(f(x)) differentiated with respect to f(x).
In general, we can say that
f′ (lump) means f(lump) differentiated with respect to (lump).
I can now show you where this formula comes from.
Suppose we have an inverse function y =f–1 (x).
Then x =f(y) because this is what an inverse function means.
Differentiating implicitly with respect to x, using the Chain Rule, gives
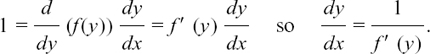
But y = f–1(x)and f–1 (x) is also a function of x. Suppose we call it F(x). Then we can say
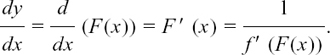
This particular function is the one which we used in Section 3.C.(a) to describe an example of cell growth. We said in Section 3.C.(e) that the rate of increase at any time t is equal to some constant, k, multiplied by the number of cells present at that time, but we couldn’t then find the value of k.
It’s now easy for us to do this. We have x = 2t so, taking natural logs both sides of this equation, ln x = ln (2t) = t ln 2 using the third rule of logs of Section 3.C.(d).
Differentiating ln x = t ln 2 implicitly with respect to t, we get

We now know that the value of k is ln 2. (I said it would be this in Section 3.C.(e).)
We can also write this answer in terms of t if we want to. We have
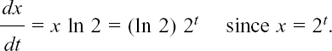
The ln 2 is the scaling factor which gives us the difference between the rate of increase of x = 2t and x = et. If x = et, the scaling factor, k, is equal to 1.
The rate of increase at any given time is the same as the quantity of the substance present at that time.
Here is a second rather nastier-looking example. (Although it looks nasty, it is actually quite simple to do.)
If 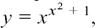 what is dy/dx?
what is dy/dx?
Again we take natural logs both sides of the equation. This gives us

Differentiating implicitly with respect to x, using the Product Rule, gives us
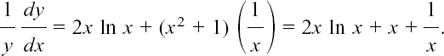
Therefore
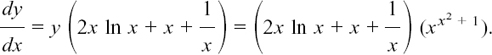
I shall finish this section on implicit differentiation by giving you an example of a practical use for it.
The volume of metal in a hollow sphere remains constant. If the inner radius is increasing at the rate of 3 cm s–1 find the rate of increase of the outer radius when the two radii are 2 cm and 4 cm respectively.
The volume of a sphere of radius r is  I show a drawing of a cross-section through the centre of the hollow sphere in Figure 8.F.4.
I show a drawing of a cross-section through the centre of the hollow sphere in Figure 8.F.4.
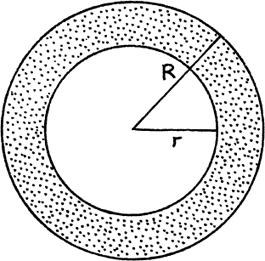
Figure 8.F.4
The volume of metal, V, is given by

V, R and r are functions of time, t, so differentiating implicitly with respect to t gives

The volume V remains constant so dV/dt = 0.
Therefore we have
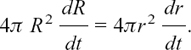
At the instant we are interested in, R = 4, r = 2 and dr/dt = 3. Therefore, 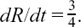
At this instant, the outer radius is increasing at a rate of 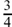 cm s–1.
cm s–1.
In the first three questions, differentiate the given equation implicitly, rearranging in each case to find an expression for dy/dx. Then use this answer to find
(a) the gradient of each curve at the point whose coordinates are given in the question, and
(b) the equation of the tangent to the curve at this point.
(1) x2 y2 = 25. The point is (1,5).
(2) x2 + 3xy – y2 = 2. The point is (1,2).
(3) 1/y + 2/x = 1
Do this one by differentiating the equation given above. Then do it a second time by differentiating the equation you get if you multiply all through by xy to get rid of the fractions.
In each case, use your expression for dy/dx to find the gradient of the curve at the point (4,2), and the equation of the tangent there.
(4) Use the Chain Rule to differentiate the following two functions with respect to x
(a) sin–1 (2x – 5)
(b) cosh–1 (3x + 1)
In both cases, say what restrictions you must put on x for the answer to work.
(6) Differentiate the following three functions with respect to x
We know already that we can write
1 + x + x2 + x3 + x4 + . . . as 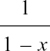 provided that |x| < 1,
provided that |x| < 1,
using the rule for the sum to infinity of a GP, from Section 6.C.(c).
We also found in Section 7.C.(a) that if we did a binomial expansion on (1 –x)–1, keeping our fingers crossed that it would work with n = –1, we did in fact get the same series.
Might it be possible to find a way of writing other functions in the alternative form of series?
The answer to this question is a qualified ‘yes’. When calculus is approached entirely through proofs and arguments based on taking mathematical limits, one of the most powerful results to come out of this is Taylor’s Theorem. This gives a proof that such series expansions do indeed exist if certain conditions are met. (We saw some reasons why such a formal approach is necessary to lay mathematically firm foundations for calculus in Section 8.A.(f).) This rigorous approach is beyond my scope here because to do it properly takes a great deal of space and a dedicated book. My purpose is to give you a working knowledge that you can use in other areas together with an intuitive feel and understanding for what is happening, which will then make a pathway to lead you into whatever depth you later need to go. It is, however, possible for me to show you what some of the results of this approach will be, so that you can see why they are important.
Taylor’s Theorem gives a way of approximating to functions by considering their rates of change, and the rates of their rates of change, and so on. In other words, if we have a function x = f(t), then the theorem makes it possible (with certain qualifications concerning how this function behaves) to write the function in terms of dx/dt, d2x/dt2 and so on, or, in function notation, in terms of f′(t), f″(t) and so on. There is a very good description of how this works in Louis Lyons’ book All you wanted to know about mathematics but were afraid to ask (Cambridge University Press 1995).
Because these series are so important we will look at some straightforward cases together now. We will only consider functions like et or sin t or cos t where we know that we can continue differentiating for ever if we want to. Also, we will only look at functions for which we know that there is no problem differentiating when t = 0.
Let us suppose that it is possible to write such a function as a series expansion so that we have

a0, a1, etc. are coefficients which will depend upon the particular function f(t) which we are considering.
If we put t = 0 in (1) above, we get f(0) = a0 because everything else disappears.
Also, if the series of (1) is truly representing the function f(t), we would expect that differentiating it term by term should give the same result as differentiating the function itself. (This isn’t obvious – we have seen in Section 6.F that infinite series can behave in very odd ways indeed. It can in fact be shown that it does work for all the examples which we shall look at here.)
If we differentiate (1) with respect to t, we get
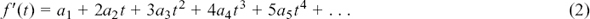
Putting t = 0 now gives us f′(0) = a1 because all the further terms disappear. This system is beginning to look promising. Similarly
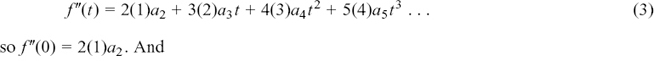
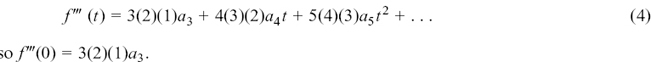
Writing all these dashes for the successive differentiations is beginning to be a little clumsy, so I will replace them from now on with a number which stands for the number of times that f(t) has been differentiated.
Do the next differentiation yourself, so finding f4 (0).

You should have f4 (0) = 4(3)(2)(1)a4.
We can see that these are building up using factorials and we can write the results so far as
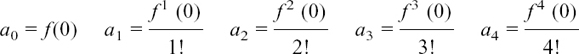
Since we are only considering functions here which can be differentiated as often as we like, we could say that ar= fr (0)/r! where ar is the rth coefficient. (We started the count with r = 0).
This gives us the following result.
Provided that certain conditions are met, it is possible to say
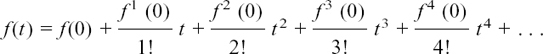

The little superscript numbers in the above expression refer to how many times f(t) has been differentiated; they are not powers.
Series like this, which are a special case of Taylor series, are called Maclaurin series after the Scots mathematician Colin Maclaurin.
We can now use these results to write down some particular examples.
EXAMPLE (1) f(t) = et.
We have already found in Section 8.B.(a) that we can write e in the form of the infinite series
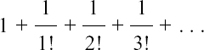
Will we get a similar series for f(t) = et if we use the above process on it?
We know that f(t) = et remains unchanged when it is differentiated with respect to t, so we have f(t) =f′(t) =f"(t) = fr(t) = et for all values of r. Also e0 = 1, so we get
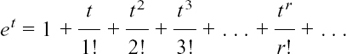
which agrees with our previous series if we put t = 1 so that we start with e.
This series can also be written in the Σ form which we described in Section 6.D.
We would have
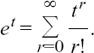
Notice that we are starting the count with r = 0.
EXAMPLE (2) f(t) = Sin t.
If f(t) = sin t then f′(t) = cos t,f″(t) = – sin t,f‴(t) = – cos t and f ″″ (t) = sin t.
At this point, we have come back to the beginning of the cycle again. Now, sin(0) = 0 and cos (0) = 1 so we have
 and so on.
and so on.
So
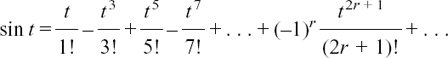
starting the count with r = 0.
Notice the flip of the signs given by the (–1)r. If r is even, the term is positive, but if r is odd then the term is negative.
This series can be written in the Σ form as

We have already found experimentally and geometrically in Section 4.D.(e) that the first term of this series gives us a very good approximation for sin t if t is small.

For the same reason as then, it is essential that t is measured in radians for any trig series.

How far do you need to go with summing this series for sin t in the case of t = π/6 to get a good approximation to the exact answer of 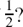 (Let’s say ‘good’ means to 4 d.p.) It works amazingly quickly. Try t = π/2 too.
(Let’s say ‘good’ means to 4 d.p.) It works amazingly quickly. Try t = π/2 too.
For this process to work at all, we are assuming that adding the terms of the various series that we get will bring us closer and closer to some definite sum the further we go, that is, we are assuming that these series are convergent. (I describe the meaning of ‘convergent’ in Sections 6.C.(c) and (d), through the various possibilities of what can happen when we sum GPs.) If any of these series isn’t convergent, we would find as we did there with the geometric series 2, 6, 18, ... and its non-existent sum to infinity, that we were writing nonsense.
This time, the answers repeat in pairs when we differentiate. We have f′(t) = sinh t and f"(t) = cosh t and so on. Also,
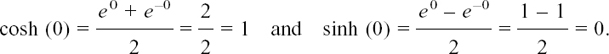
This gives us
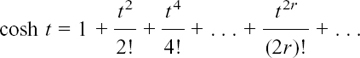
Writing this in ∑ form gives us
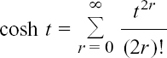
again starting the sum with r = 0.
Now, suppose instead that we had wanted the series for f(t) = cosh (2t).
We could do this in two ways, of which the easiest is simply to replace the ‘t’ in the series above by 2t. This then gives us
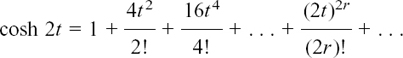
Alternatively, we could have successively differentiated f(t) = cosh(2t) with respect to t to find the coefficients.
Each time that f(t) = cosh(2t) is differentiated with respect to t, it gets multiplied by 2 because of the Chain Rule, so the answer comes out exactly the same.
EXAMPLE(4) f(t) = ln(l + t)
(Why couldn’t we find a series for ln t?)
(Because ln 0 is undefined and so we immediately run into an impossible situation.)
If f(t) = ln (1+t) then 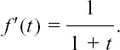
To find f"(t), it is easiest to write this as (1 + t) –1. Then differentiating again, we get

Find f3(t),f4(t) and f5(t) for yourself.

You should have the following answers.

This gives us f(0) = ln 1 = 0, f1 (0) = l,f2 (0) = – l,f3(0) = 2!,f4 (0) = –3!, and f5(0) = 4!.
If this pattern continues, what will we have for fr(0)?

We would get (–1)r–1 (r – 1)!.
Putting all this information together gives us the series

Cancelling as much as possible, we get the series

We can write this in the ∑ form as
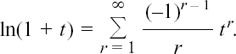
Notice that this time we are starting the count with r = 1.
Try putting t = 1, and see if you can find a good approximation to ln 2 from summing the first few terms of the series above.
You have In 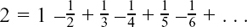
This is the series which we met briefly at the end of Section 6.F when we said that it is convergent, unlike the frog down the well, or harmonic series of  which isn’t.
which isn’t.
As you feed in each successive term, you will see the sums flipping from one side to the other of the actual value of ln 2. Unfortunately, although they are getting closer to ln 2, this is happening extremely slowly.
A much faster way of finding ln 2 by means of a series comes from using
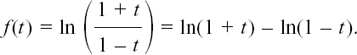
We know that 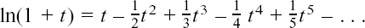
Putting ‘t’ = –t gives 
So 
assuming that we can do this tricky move.
What value of t would you have to use to find ln 2 from
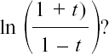

Putting  gives 1 + t = 2 – 2t so 3t = 1 and
gives 1 + t = 2 – 2t so 3t = 1 and 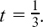
Try substituting 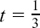 in the series above and see how you now get on with finding a value for ln 2. You will see that this series converges much more rapidly.
in the series above and see how you now get on with finding a value for ln 2. You will see that this series converges much more rapidly.
There is an important question that we need to ask here.
Do all of these series work for any value of t?
For example, we already know from Section 6.C.(c) that the GP of 1+x + x2+x3 + ... is only convergent if |x| <1.
It seems quite possible that the series which we have been looking at here only converge to their functions for a restricted set of values for t.
In fact, it can be shown that the series for et, sin t, cos t, sinh t, and cosh t are convergent for all values of t. However, the series for ln(1 + t) is only convergent if –1 < t ≤ 1.
EXERCISE 8.G.1 Now try the following questions yourself.
(1) Use the series expansion for et which we found in the first example to write down the series expansions of (a) e2t and (b) e–t.
(2) Use the series expansion which we found for sin t in the second example to write down the series expansions for (a) sin 2t and (b) sin(–t).
(3) Find the series expansion for f(t) = cos t and then use this to write down expansions for (a) cos 2t (b) cos(– t) and (c) cos (nt) where n is standing for a positive whole number.
(4) Find the series expansion for f(t) = sinh t.
Now check that you’ve got the right answer by adding your series together and using  from Section 8.D.(a).
from Section 8.D.(a).
Now that we have a way of writing et, cosh t, sinh t, cos t and sin t in the form of series, the curious similarities which we have been finding in the behaviour of the trig functions cos t and sin t and the hyperbolic functions cosh t and sinh t no longer seem quite so surprising.
We know that et = cosh t + sinh t.
It looks as though, with a bit of cunning juggling, we ought to be able to link et, cos t and sin t. Can you see any way of doing this? Maybe if we put ‘t’ = –t? Or if we subtracted the series?

Whatever we do, we cannot quite make it work – yet. We shall find out in Section 10.C.(b) that these series do all slot together most beautifully.