9.1 Galloping horse. This example of palaeolithic cave painting, from Lascaux (Dordogne, France), dates to approximately 15000 BC. Photo: AKG London.
Realities of art
The key to perception—to art and science, indeed to civilization—is representing. How concerned are artists with representing objects in two dimensions as though in the space of the three-dimensional world?
From the beginning, art seems to have been associated with magic and with religious, not only physical, views of the world. Cave paintings seem to have had significance in terms of what we would call sympathetic magic. Perhaps pictures were regarded as talismans; as charms for good or evil, capable of evoking thoughts and moods not only in men but also in Gods: for they are found on cave walls almost inaccessible to human view. Sometimes they were painted in succession, one upon another, as though the place of the paintings took on a special quality. Something of this magic quality of art is associated with all religious paintings, including the Christian, and is with us still.
In our society pictures are valued in monetary terms far beyond ‘reason’. An original painting may cost hundreds even thousands of times more than a virtually indistinguishable copy. A painting’s value depends greatly on the artist and whether it is identified as genuine. It is something of a sacred object even when its subject is profane. Evidently paintings are regarded as more than surrogate retinal images: they can be valued more highly than sight itself.
In religious paintings, the subject was of first importance, for they were used for conveying and unifying belief among largely illiterate people. But what is portrayed is not always important. A bunch of grapes or a dead hare are not in themselves interesting or valuable, and yet a picture of such worthless objects can command more than a man earns in a lifetime. But is this conceivable if paintings are no more than representations of the shapes and colours of objects? It is, indeed, just because a painting is not simply a spatial record that it can have a value and an interest far greater than the objects it portrays.
9.1 Galloping horse. This example of palaeolithic cave painting, from Lascaux (Dordogne, France), dates to approximately 15000 BC. Photo: AKG London.
With the recent discovery of the Chauvet caves in the South of France, examples of pictures go back 30 000 years. Upon seeing cave art for the first time, Picasso is supposed to have said: ‘Have we made any progress?’ It would seem that over the millennia art, religion, and science have gradually separated. One might say that art is now primarily evocative—science primarily explanatory. They have grown ever further apart since the Greeks; but each depends in various ways upon the other, finding and giving mutual inspiration. An outstanding mutual contribution is the discovery or invention of rules for showing depth by perspective.
Representations of perspective
It is striking how seldom accurate representation of space is found in art. Indeed some of the most prized paintings appear perfectly flat. Certainly the ability to represent depth is regarded as but one, and a minor, accomplishment, except in special cases. And yet paintings generally include objects which we normally see in depth. So there is a problem: why is strict geometrical perspective rather seldom adopted? After all, the retinal image is in geometrical perspective (every feature halved in size with doubling of distance), so why does the artist seldom reproduce the eye’s image to record depth in pictures? We may say at once that there is a very real difficulty in this. Although the retinal image is in strict perspective, like a photograph, this is not how we see the world—because the image is effectively modified by perceptual scaling (see Chapter 10).
Perspective is a remarkably recent development in Western art. In prehistoric pictures, and in pictures of early and non-Western societies, there was no formally correct perspective. It does not appear until the Italian Renaissance of the sixteenth century. We will consider this after looking at, to us, curious perspectives of Egyptian and oriental pictures.
Egyptian art
In the highly developed formalized painting of the ancient Egyptians, going back 5000 years, human figures are shown as anatomical impossibilities. Hands and feet and breasts are all shown as from the side, the shoulders front view and heads in profile, with an eye at the side, like an ear (Figure 9.2). In Egyptian pictures there is virtually no foreshortening or perspective. The sizes of the figures are determined not by distances but by their relative importance. The Pharaohs and the heads of families are huge compared with the lesser figures, such as conquered people and wives. Instead of an overall picture from a particular viewing point—which is familiar to us—each feature is represented from its most easily recognized view, combined to look paradoxical.
Almost all the stone statues stand or sit with no activity, looking straight ahead, with the head at right angles to the shoulders. This gives them a timeless dignity; but did the sculptors accept these restraints for art’s sake, or because they lacked the artifice to show free natural positions and movements? Was it because massive stone simply did not allow such freedom to the sculptors? Or—very different—was it because the statues were based on drawings? It is known from part-finished colossal statues that they started as drawings on a grid of squares (the size of the statue’s fist being marked on the block to set the scale) continually redrawn as stone was removed. (Wouldn’t it have been possible to project a shadow of a wire grid onto the stone, so it would remain as the surface was cut away?) The many small figures of servants, made of wood or clay, placed in tombs to serve in the after life, are very different: far more naturalistic, free of the restraints of the formal reliefs and impressive stone statues. Is this because for making these small informal figures, drawings were not used?
9.2 Egyptian figures. The figure has each feature—eyes, shoulders, feet and so on—in characteristic ‘sideways’ positions, without perspective. (Courtesy of Andromeda Oxford Limited.)
Oriental art
Chinese drawings and paintings represent space with rules quite different from the geometry of the retinal image, often from many viewing positions at the same time. Chinese and Japanese paintings often combine a downwards view of buildings with a sideways view of people. Preferred for monumental pictures, was the large hanging scroll, two metres high and sometimes much more, especially from the tenth century. With a series of viewpoints, mountains could be shown at the top without dominating the lower parts of the pictures (Figure 9.3). The aim was to unify nature with man.
Here rectangular objects, such as tables, look odd to us as they have ‘reversed’ perspective—diverging rather than converging with distance. One has to be careful, though, for by a particularly interesting distortion illusion, parallel lines appear to converge when depth is suggested (Figure 10.15). Most of the ‘negative perspective’ in oriental painting is produced in this way—in the eye of the beholder—though sometimes it is exaggerated by the artist.
One might say that the ancient Egyptian combinations of views of parts of figures—profile heads, full-face eyes, sideways breasts, and so on—are much the same as the mixed views of Japanese and Chinese painting, though the ‘units’ are different. For the Egyptians the units are parts of objects; in oriental pictures the figures have a consistent viewpoint, but they are placed in a scene as views from displaced eyes.
9.3 Chinese perspective. This is odd to our eyes, as it is neither geometrical nor as the world appears through constancy scaling of the retinal image. The Chinese adopted elaborate symbolic conventions. What appear as drawn distortions (‘negative perspective’) are often in the observer’s eye and brain as in Figure 10.21.
It is an extraordinary fact that simple geometrical perspective took so long to develop—far longer than fire or the wheel—yet in a way it has always been present for the seeing, as the images in our eyes are perspective projections. Linear geometrical perspective in pictures is the invention of Italian Renaissance artists. It has had profound effects on art and on science.
How to paint a scene in the perspective of the eye’s image was discovered by the Italian artist-engineer Filippo Brunelleschi (1377–1446). While planning the cathedral of Florence, he introduced a painting of his imagination into the existing buildings, to see how it would look when built. This virtual reality was accomplished with a painting with a hole in it and a mirror (Figure 9.4).
The laws and principles of perspective were first clearly described by Leonardo da Vinci (1452–1519) in his Notebooks, where he outlines a course of study for the artist. The problem was not only to present existing objects in perspective but also to create perspective for imaginary objects, when there was nothing to copy. Leonardo called perspective ‘the bridle and rudder of painting’, describing it in the following way:

9.4 The first virtual reality. Brunelleschi introduced a painting of the proposed cathedral into the surrounding buildings, with a mirror. The painting of the proposed cathedral was about 0.5 × 0.5 metres, the mirror being half this size. Looking through a peephole in the painting at a mirror behind which were the existing buildings; the painting appeared as a ‘virtual reality’ of the future. This is worth trying, with a postcard and a mirror.
Perspective is nothing else than the seeing of a plane behind a sheet of glass, smooth and quite transparent, on the surface of which all the things approach the point of the eye in pyramids, and these pyramids are intersected on the glass plane.
Leonardo treated the perspective of drawings as a branch of geometry. He described how perspective could be drawn directly on a sheet of glass (Figure 9.5), a technique used by the Dutch masters and, in a later form, with the camera obscura which employs a lens to form an image of the scene which may be traced directly (page 34).
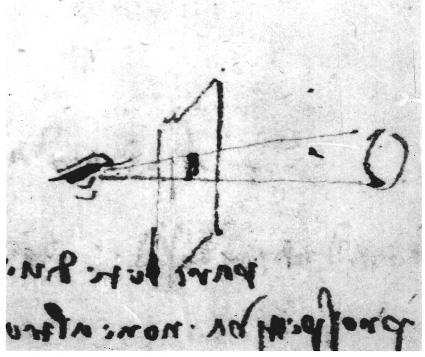
9.5 Leonardo’s sketch showing how three-dimensional objects appear on a plane intersecting the cone of rays from object to eye. It is worth tracing a scene on a window pane.
The projection is determined simply by the geometry of the situation and this constitutes so-called geometrical perspective; but as Leonardo realized more clearly than many later writers, there is more to the matter than pure geometry. Leonardo includes in his account of perspective such effects as increasing haze and blueness with increasing distance, and the importance of shadows and shading in drawings to represent the orientation of objects. These considerations go beyond geometry. Geometrical (or linear) perspective was dominating Western painting by AD 1500 (Figure 9.6), the first artist to use it outside Italy being Albrecht Dürer (1471–1528), from Nuremberg. Spreading to Eastern art it could be incongruous. Later, tracings from the camera obscura were used by the Dutch painter Jan Vermeer (1632–75) for some of his interiors, by the Venetian Antonio Canaletto (1697–1768) (Figure 9.7), and many artists prior to photography, which became available after the middle of the nineteenth century, and is undoubtedly much used by draughtsmen and painters in the present time.
Let’s look at what is going on, in as simple a way as possible. Consider a simple ellipse such as in Figure 9.8. This might represent an elliptical object seen normally or a circular object seen obliquely. This figure does not uniquely indicate any one kind of object; it could be a projection of any of an infinite variety of objects, each seen from a certain angle of view. The art of the draughtsman and painter is in large part to make us accept just one out of the infinite set of possible interpretations of a figure: to make us see a certain shape from a certain point of view. This is where geometry goes out and perception comes in. To limit the ambiguity of perspective, artists must make use of perceptual cues available to a single eye. They are forbidden the binocular distance cues of convergence and disparity, and also motion parallax. Indeed, these cues will work against them. Paintings are generally more compelling for depth when viewed with a single eye with the head kept still—because motion and the second eye show that the picture is flat.
We have to consider a double reality. The painting is itself a physical object, and our eyes may see it as such, flat on the wall; but it can also evoke quite other objects—people, ships, buildings—lying in a different space and, indeed, in a different time. It is the artist’s task to make us reject the first reality while conveying the second—so that we see his world, not mere patches of colour and textures on a surface.
As we have seen from the example of the ellipse, a picture can represent a given object from one viewing position, or any of an infinite set of different objects seen in other orientations, or distances. This means that for the picture to represent something unambiguously we must see what the object really is—what its shape is, and how it lies in space. It is very much easier to represent familiar than unfamiliar objects. When we know what the object is, then we know how it must be lying to give the projection given by the artist. For example, if we know that the ellipse is representing a circular object, then we know that this must be lying at a certain oblique angle, the angle giving the eccentricity drawn on the plane by the artist. We all know that wheels, dinner plates, the pupil of the human eye, and so on, are circular objects, which makes the artist’s task easier. This is clear from the power that very simple line drawings have for indicating form and orientation and distance—when the object is familiar. Consider the drawing of the boy with the hoop in the cartoon (Figure 9.9). It is clear that the ellipse represents a circle at an oblique angle, because we know that it represents a hoop and we know that hoops are circular. The hoop in this figure is, in fact, the same as the ellipse seen ambiguously, without context, in Figure 9.8. But when we know what it is, we know how to see it. It would have been extremely hard for the artist to represent a squashed hoop.
9.7 This Canaletto is a fine example of perspective. Has he painted the perspective as given in the image of the eye (or in a camera obscura, or photographic camera)—or following size–distance modifications by the size constancy of his visual brain? (And of course he has artistic licence to change it as he wishes.)
Look at the amoebic shape of the spilled wine in Figure 9.10: it is seen as lying on a flat surface (the road), though the shape alone could equally well represent an infinity of shapes, lying in various orientations. Suppose we remove the rest of the drawing so that we have no clue as to what it represents (Figure 9.11, showing only the puddle). It could equally well be anything of rather indeterminate shape standing up and facing us, perhaps something like an anvil. (Does it not look slightly higher in the full drawing where it is clearly lying obliquely on the ground, than when it appears alone as an upright shape?) Although the figure is so simple, a wiggly line, it is evoking vast experience of seeing and handling objects (including mis-handling when we drop bottles), and this physical knowledge very much determines how we see the amoeboid shape as a particular object.
We may now take another example, again of an ellipse in a cartoon, but this one illustrates a rather different point (Figure 9.12). This is of some interest, for it is presented without any explicit context and yet it clearly lies on the floor. It is seen as a circle. The boy below (not shown—yet seen!) could be cutting an elliptical hole, but we assume he is cutting a circle. This puts our viewing position at a certain height which is not determined by any other feature in the drawing, but only by our interpretation of the meaning of the shape, based on our knowledge of small boys.

9.11 The same shape as the puddle in the cartoon; but how does it lie in space now, without a context? It could be upright.
9.12 Another ellipse. This time we assume it is a circle and see it as flat, because we know that the invisible boy under the floor (almost seen!) would generally saw a roughly circular hole.
When an artist employs strict geometrical perspective he does not draw what he sees—he represents his retinal image. As we know, these are very different; for what is seen is affected by constancy scaling (see pages 171–172 for more details). A photograph, on the other hand, represents the retinal image but not how the scene appears. By comparing a drawing with a photograph taken from exactly the same position, we could determine just how far the artist adopts perspective and how far he or she draws the world as seen after the retinal images are scaled for constancy. In a photograph distant objects generally look too small. It is a common disappointment that a grand mountain range comes out as a row of pitiful molehills.
The situation here is curious. The camera gives true geometrical perspective; but because we do not see the world as it is projected on the retina, or in a camera, the photograph looks wrong. Indeed it is fortunate that perspective was invented before the photographic camera, or we might have had difficulty accepting photographs as other than weird distortions. As it is, photographs can look quite wrong, particularly when the camera is very close, or not held horizontally. Aiming a camera upwards to take in a tall building gives the impression of the building leaning backwards. Yet this is the true perspective.
Architects recognize that the visual compensation for distance is less efficient when looking upwards, and so have built columns and towers to diverge from bottom to top. The most notable example is the magnificent Campanile at Florence designed by Giotto. Here the artist has applied reversed perspective to reality, to compensate for the inadequate constancy scaling of viewers in this situation. There are examples of this on the horizontal plane, notably the Piazza San Marco in Venice, which is not a true rectangle, but diverges towards the cathedral so that it appears to be rectangular (and even larger) when the cathedral is viewed from across the Piazza. We find similar ‘distortions’ of reality to suit eye and brain in Greek temples; though the Greeks never discovered the projective geometry of perspective. (It is likely that they achieved good compromise results by trials with earlier wooden buildings. In any case, this is a quite different problem from perspective projections of pictures on a plain surface.)
In an important sense, perspective representations of three dimensions are wrong as they do not depict the world as it is seen; but rather, the (idealized) images on the retina. We do not see our retinal images—and we do not see the world according to the sizes or shapes of the retinal images—for these are effectively modified by constancy scaling. Should not the artist ignore perspective and simply draw the world as he sees it?
If the artist ignores perspective altogether, his painting or drawing will look flat, unless other cues to distance are utilized with sufficient force. This seems to be almost impossible; for if the artist did succeed in suggesting depth by other means, this picture would look wrong, for these cues would trigger the constancy scaling system, to expand more distant represented objects. Evidently this means that the artist should use perspective (draw distant objects correspondingly smaller) if the viewer’s constancy scaling is affected by the depth cues. Indeed if all the normal depth cues were present complete perspective should be used, for the viewer would see sizes and distances as though seeing the original scene. But, and this is the important point, in fact, the artist can hardly hope to provide all the depth cues available from reality, so should use a reduced perspective for maximum realism. Something of this is illuminated by the experiments of Adelbert Ames:
The Ames demonstrations
The American psychologist Adelbert Ames II started life as a painter. He went on to create a series of brilliant demonstrations, the most famous being the distorted room and the trapezoid window.
The farther wall of the Ames room is tilted, so that it does not lie normal to the observer. ‘Negative’ perspective makes this oddly shaped room give the same retinal image as a normal rectangular room. There is an infinite set of ‘distortions’ which give the same images as those of a normal room; so there can be an infinite variety of Ames rooms looking like normal rooms, provided their design follows certain quite simple rules. The better it is designed and constructed, the more it looks like a normal rectangular room—ideally being indistinguishable. There is really nothing surprising in this, because the image it gives is the same as for an ordinary room, so it must look the same. But if objects are placed in the room odd things happen, which could not be predicted with certainty.
An object (such as a person) placed at the further back corner looks the same distance and smaller than the same-sized object (or person) at the nearer corner. It looks too small simply because the image is smaller; and the same distance, because there is no visual information that it is at a distance different from the other object. So an adult may be shrunk to appear smaller than a child (Figure 9.13).
Evidently we are so used to rectangular rooms, we accept it as axiomatic that it is the objects inside (the people) which are odd sizes, rather than the room being an odd shape. This is a betting situation; for either could be peculiar. Here the brain makes the wrong bet, as the experimenter has rigged the odds.
An interesting feature of the Ames room is its implication that perception is a matter of making the best bet on the evidence. It has been reported that young wives may not see their husbands as distorted in the room, but see them as normal and the room its true queer shape. Behold the power of love.

9.13 The Ames room—impossible? We accept that the room is rectangular—though in fact it is not—and we see the figures as different sizes though they are the same. We are so used to rooms being rectangular that we bet on this room being normally shaped. Here we are wrong.
To recapitulate: an empty Ames room tells us nothing about perception. If properly constructed it must look like a normal rectangular room, as it gives the same image in the eye. But when objects are added the situation is different. Then the room shows that perception involves betting on odds. Perception goes wrong when common assumptions are not questioned and the true answer is unlikely. This tells us something important about the role of experience and learning, and perhaps inherited knowledge. The visual assumptions can be tested by touching the room’s walls with a stick held in the hands. This gradually reduces its distorting effect on objects in the room, as slowly it comes to look its true peculiar shape (Figure 9.14).
Perhaps the Ames room demonstration is not quite so clear cut. For what happens without the room? If we photograph two people at different distances, from a low eye-level, do they look different sizes or different distances? There is a sort of compromise; the more distant appears both further and smaller (Gregory 1970, page 28). The Room surely adds to the size difference, but this really needs more experiments.
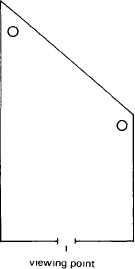
9.14 Geometry of the room. The further wall recedes from the observer (and the camera) to the left. The figure on the left is farther away, but the walls and windows are arranged to give the same retinal images as a normal rectangular room. The figures appear the same distance but different sizes. (The nearer is about half the distance, so is twice as large at the eye.)
9.15 The Ames window. This is its shape, as seen at right angles. It is quite hard to see its true shape in the drawing: one does not quite know whether it is rectangular, and being viewed from the side; or whether it is a perspective-shape—which it is. When slowly rotated it goes through the most amazing transformations. Strictly, perspective is to be found only in pictures and optical images, including the eyes’—not in objects, or ‘reality’. But perspective-shaped objects can upset perception of size and distance.
An equally celebrated Ames demonstration is the trapezoid window. This is a non-rectangular window-like object, made to rotate slowly by means of a motor. It is the shape of a rectangular window but as seen from a highly oblique view (Figure 9.15).
It has shadows painted upon it so that, peculiarly, as it rotates they do not change. What is seen is a complex series of weird phenomena. The direction of rotation is ambiguous, seeming to change spontaneously. This is the ‘windmill’ effect, observed when rotating vanes are seen against the sky, direction of rotation reversing spontaneously as near and far switch, as in the skeleton cube (Figure 10.6). A rod passing through the Ames window will sometimes seem to rotate in the wrong direction. When its movement is seen correctly, though the window’s rotation is perceptually reversed, then the rod seems to pass through the substance of the window, like a ghost.
The window changes in size: a striking effect that is hard to describe. The point is that as the object has a marked oblique perspective shape, the normally reliable assumption of rectangular objects giving such a shape by perspective from an oblique view, misleads eye and brain into a false ‘perceptual hypothesis’. These demonstrations are dramatic and eye-opening, though perhaps too complicated as research tools for measuring what is involved.
Artists make remarkably effective use of many visual cues to depth. In a pencil drawing, shading may be used to indicate the form of an object. The shading is often conventional stippling, or equally spaced lines indicating a flat region, with unequal spacing indicating that the surface is sloping or irregular.
Shading may also indicate cast shadows, which is a different matter from surface texture. Shadows indicate the direction of light falling on objects, and also that something is obstructing the light. Shadows may be caused by overhanging features, as when texture is revealed by small shadows, and then both the texture of the surface and the direction of the illumination are indicated by the form and direction of shadows. This is a matter of surprising significance. Shadows are important not only for highlighting textures for revealing the form of objects: shadow can supplement the single eye, to give something surprisingly close to binocular vision. The light-source, revealed by its shadows, replaces the missing eye of the painter.
Consider a portrait taken full face but with strong side lighting. The profile form of the nose is shown on the cheek (Figure 9.16). The shadow thus gives us a second view of the nose. We get the same effect when looking at the moon through a telescope—indeed until space travel our knowledge of the profiles of crater walls and lunar mountains depended entirely on seeing their shadows cast by oblique sunlight. It is possible to measure the lengths of the shadows and deduce their heights and shapes. For usual object perception the visual system does this continually and it is important: the world looks quite flat when the light is behind us, for then there are no shadows, which makes for flat scenes and dull pictures.

9.16 Two viewing positions from one camera angle. The form of the shadow shows the profile of the nose and eyes.
We have already noted that depth can be reversed by optically interchanging the eyes, each eye receiving the normal view of the other (see Chapter 3). Interestingly enough, similar reversal in depth can be given by the light-source ‘eye’ of cast shadows being shifted from above to below (Figure 9.17). The point is, light normally falls from above. The sun cannot shine from below the horizon and artificial light is generally placed high. When, however, illumination is from below we tend to see reversed depth, much as when our eyes are switched by a pseudoscope (Figure 3.24). This effect was noted by several early writers. David Brewster (1781–1868) records it in his Letters on natural magic, where he describes how, when the direction of light falling upon a medal is changed from above to below, depressions become elevations and elevations depressions: intaglios becomes cameos and vice versa. This was observed at a meeting of the Royal Society in the seventeenth century, of a guinea coin viewed through a microscope. Brewster said of it:
The illusion … is the result of the operation of our own minds, whereby we judge the forms of bodies by the knowledge we have acquired of light and shadow.
He went on to experiment with the effect, finding it more marked in adults than in children. He noted that visual depth may become reversed even when true depth is indicated by touch. This must rank as one of the earliest psychological experiments. But almost all this was known to artists centuries before scientific experiments on how we see.
Apart from perspective, texture gradients (Figure 9.18), the hiding of parts of objects by nearer objects (Figure 9.19), haze associated with distance, and many more ‘cues’ are important for seeing depth and distance in the real world and in pictures.
Powers of various ‘depth cues’ can be measured with the technique described in Chapter 8 [page 234], No features determine depth or form; they can only increase probabilities of seeing in particular ways, yet pictures can have compelling though paradoxical realism.
9.17 Depth-neutral shapes. (a) Illuminated from above. (b) The same lit from below. Depth reverses when the direction of illumination is changed.
9.18 Slope from a perspective gradient. The surface texture is represented by perspective. Texture is the visible surface structure of objects, or of the ground between objects. In this example, the appearance of depth is so powerful that it may seem ‘direct’, not requiring interpretation. But as for any other picture, this is open to alternative interpretations. Indeed, it is actually flat!
Realities of trompe l’oeil
Occasionally, especially in architecture, the artist goes all out to create the most compelling possible illusion of reality. Illusions may fill rooms with statues, or comple missing parts of churches—with the superb technique of trompe l’oeil. With its absence of brush strokes or other surface texture, this tradition goes back to ancient Greek painting—when it was claimed that bees could be fooled by painted flowers. Yet admiration is barbed with criticism that ‘this is not quite art’. Thus, Lucas de Here said of Van Eyck’s almost too realistic pictures: ‘They are mirrors, yes, mirrors, not paintings.’
When depth is shown very realistically, depicted objects rotate—following every movement of the observer. This can be disturbing. Just why this dramatic movement is seen in flat perspective pictures, that lack surface texture is not entirely clear. Easy to achieve by stereoscopic projection, this is an interesting phenomenon which needs more investigation. The seen movement is surprising and perceptually revealing, because it does not depend on changes at the eyes. For if the picture is rotated nothing happens. This is worth trying. The seen motion depends upon the observer’s hypothesis of his or her body movement through space. We know too little about the subtle relations between seeing and doing.
9.19 A cunning trick of occlusion for upsetting depth perception. The two sets of squares, though they appear in the same order, are differently arranged in distance. In the third row of playing cards the Jack is nearer than the six. This works because occlusion is a powerful visual cue; here it is misleading because what should be occluding parts of nearer cards are cut-outs.
No doubt this apparent motion of trompe l’oeil would be too disturbing for seeing pictures in a gallery. Artists gain more by settling for less realism than is technically possible.