
10.1 Newton’s house (at Woolsthorpe, near Grantham in Lincolnshire) with a rainbow. Why is the rainbow an illusion though the house is real?
Illusions
What are illusions?
When a perception departs from the external world, to disagree with physical reality, we say we experience an illusion. So an illusion differs from truth. But how do we know the truth? There are different accounts of truth through the history of science—and these differ from accounts in art, religion, and in the many flavours of mysticism and metaphysics.
There are accepted realities of common sense by which we live from day to day, but when described explicitly these turn out to be riddled with contradictions. Contradictions of common sense and appearances feed philosophy and science, to generate counter-intuitive claims to reality such as quantum physics and relativity, which are now accepted as scientific truth. But these accounts are so different from how things appear that to take them as reference would force us to say that all perceptions are illusion—which is not helpful.
As naïve appearances have supported survival for a long time in a great variety of situations, we should not dismiss them as entirely false. But, for example, it doesn’t matter for survival whether the sun moves or the Earth rotates; but this does matter for whether the appearance is an illusion.
It turns out to be extremely hard to define ‘illusion’. To say that all appearances of objects are illusions is no more helpful than to say that all experience is a dream. Although logically irrefutable, this drains useful meaning from ‘dream’ and from ‘illusion’. (Similarly, there is little point in saying that everything is beautiful or everything ugly: perception and language need contrasts to have meaning.) We think of objects as real. But what is an object?
What is accepted as an object depends largely on use—such as tables for putting things on and chairs for sitting on. A book on a shelf is an object; but when we are reading, each page or word or letter becomes an object. Object classification is highly dependent upon behaviour. This may suggest a useful distinction between ‘illusion’ and ‘reality’. For we might say that illusions are departures from the world accepted as real for behaviour. On this account they are not departures from recondite physics; but rather from behaviourally accepted objects with characteristics such as lengths and angles and curvatures, which are measured very simply. So illusions can be assessed by comparing what is experienced with what is simply measured with rulers, protractors, scales for weight, clocks, and so on. We can use measurements of carpentry and cooking for measuring illusions of perception.
Some phenomenal phenomena, however, cannot be matched against accepted reality or simply measured. For there are perceptual fictions, which have no object counterpart. Others which are hard to match or measure are perceptual paradoxes, which cannot exist as objects. Others flip from one object perception to another as alternative perceptual ambiguities, which only occasionally could match object reality.
The frequently used term ‘optical illusion’ is misleading when the cause is beyond the eyes’ images. Although this is so for most illusions, some can appropriately be called ‘optical’, or more generally ‘physical’ from their cause. Perhaps the most familiar example of an optical illusion is mirror images. Seeing oneself double—with a silent touchless extra-self in a wrong place, through the looking glass—is deeply paradoxical though resulting from quite simple principles of optics. The cause is physical; but it is also due to the visual brain being unable to cope with the situation. Yet this remains perceptually paradoxical though we understand, conceptually, what is going on. If understanding of reflections fed into visual processing, mirror paradoxes might disappear. So though this cause is physical, the appearance depends also on lack of visual cognition. It can be hard to decide which phenomena of illusion are physical and which are psychological, and of course physiology is always active in perception. There are often mixed causes. If we call a mirror paradox ‘physical’, this attributes its primary cause to optics.
When Sir Isaac Newton walked under a rainbow to his house, surprisingly the house got nearer and nearer, until he went through the door; but the rainbow got no nearer (Figure 10.1). Newton could not walk under its arch of colours as he could through the doorway; yet his perceptual apparatus of eye and brain was working fine for both. It is when a rainbow sets up expectations of normal touchable objects that it misleads, to be an illusion.
Sir Isaac Newton and other physicists, including René Descartes, realized hundreds of years ago that rainbows are within physics—and explained by laws of optics (Figure 10.2). They would not be deluded into seeing it as like a normal object, such as a house; so for them perhaps the rainbow is not illusory. This raises tricky issues of what are perceptual and what are conceptual illusions.

10.1 Newton’s house (at Woolsthorpe, near Grantham in Lincolnshire) with a rainbow. Why is the rainbow an illusion though the house is real?
The fact that perceptions can depart from physically accepted realities of objects has philosophical implications and practical consequences. It tells us that our perceptions are not always, and very likely never, directly related to physical reality. In practical terms it shows that we not only ‘take our lives in our hands’; we trust betting on the odds of eye and brain.
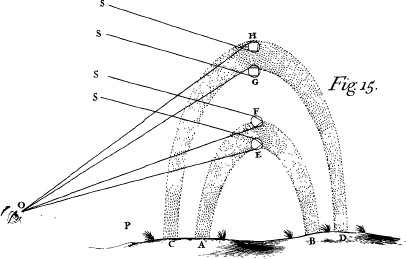
10.2 Newton’s drawing of the optics of a rainbow. Sunlight is reflected once and refracted twice in each drop. From each, a single colour emerges—depending on the height of the drop—many drops at various angles producing the spectral colours spread across the sky. (From Opticks, 1704)
This is unfamiliar country, but for several reasons it is worth taking our journey towards explaining illusions. As for the natural sciences, it turns out to be important to organize the phenomena into categories. This certainly paid off for chemistry and biology, and for kinds of stars. As for these, we need to consider appearances and underlying causes. Phenomenal phenomena are weird experiences, which become even more intriguing as we come to understand them. Here art and science meet—eye to eye.
Some illusions can cross between the senses. Best known is the size–weight illusion: a smaller object feels heavier than a larger object of the same weight. This is worth setting up yourself—to experience literally at first hand (see box).
Although physics and physiology are involved when a weight is lifted, the reason for this powerful illusion is not within the concepts of either: it is a cognitive illusion. For it depends on one’s knowledge of objects—that larger objects are generally heavier than smaller objects of a similar kind. The illusion is surprising. Although it hardly fits physics, it has a rational explanation which tells us a lot about perception.
Seen size affects felt weight
Try filling a small can and a larger one, with, for example, sugar, to the same weight. Pick them up one at a time, or simultaneously with both hands. The smaller will feel considerably heavier. Try it blind-folded. When there is no evidence for the size difference, the size–weight illusion disappears.
The muscles are set for expected weights. As larger objects are usually heavier than smaller objects, the smaller weight calls for less muscle force—so it seems surprisingly heavier than the larger weight.
Perception can go wrong in many ways. Most dramatically, entire inner worlds may be created as seen fictions are mistaken for reality. This can happen in drug-induced states or in mental illness, especially schizophrenia. In addition to hallucinations where experience departs altogether from reality, we all see certain things or patterns as distorted—what are misleadingly called ‘optical illusions’, though the cause is in eye or brain. But let’s start with:
Dreams and hallucinations
Both dreams and hallucinations may be visual or auditory, and may involve any of the other senses, such as smell or touch or pain. When several senses are combined the impression of reality can be overwhelming. Evidently hallucinations can be socially determined, for there are well-attested cases through history of many people together experiencing events which never occurred.
The Canadian brain surgeon Wilder Penfield (1891–1976) triggered memories and produced hallucinations on demand by stimulating the human brain with weak electric currents. Brain tumours may give persistent visual or auditory experiences; the ‘aura’ preceding epileptic seizures may also be associated with hallucinations of various kinds. In these cases, the perceptual system is moved to activity not by the normal signals from sensory receptors, but by brain stimulation. In Penfield’s experiments, these patients undergoing surgery generally experienced something of what was going on in the operating theatre at the time, together with the hallucinations.
Drugs can entirely replace sensed reality with hallucination. It remains somewhat mysterious how hallucinogenic drugs, such as LSD (D-lysergic acid diethylamide) affect vision, but they seem to stimulate regions of brain active in normal perception. These drugs may affect other species in various ways. They disrupt the web spinning of the spider Aranea diamata so that it forms abnormal but characteristic patterns, and monkeys reach out for non-existent objects.
In us, imagery similar to that induced by drugs can occur in half-waking states (hypnagogic dreaming) when the experience can be like a Technicolor film, vivid scenes apparently passing before the eyes although they are shut. In this lucid dreaming the dreamer may have some control. This is more like Virtual Reality than the cinema. Hallucinations have also been found to occur when people are isolated in solitary confinement in prison, or experimentally in isolation chambers, in which the light is diffused with special goggles and nothing happens for hours or days on end. It seems that in the absence of sensory stimulation the brain can run wild to produce fantasies. This is what happens in schizophrenia, when the outside world makes little contact with the individual, so that he or she is effectively isolated. These effects of isolation are interesting not only from the clinical point of view; they offer hazards in normal life. Workers may be effectively isolated for hours with very little to do, in industrial situations where responsibility is taken from the operator by automatic machines needing attention only occasionally. In single-handed sailing and space flights prolonged isolation occurs. The hazards are sufficient reason for sending more than one person on each mission into space.
Throughout history, dreams have been regarded as significant; the Greeks had special houses to be visited for incubating dreams. Dreams have always excited wonder and often more—affecting personal and political decisions, sometimes with terrible results.
For the mystic, dreams and hallucinations are insights into another world. For them the brain is seen as a hindrance to understanding; a filter between us and a supra-physical reality, seen only when the brain’s normal functioning is disturbed by drugs, disease, or starvation. For the more down-to-earth empiricist philosophers the brain is to be trusted only in health. Although interesting and perhaps sometimes suggestive, for science hallucinations are seen as aberrant outputs of the brain, to be mistrusted and even feared, though of course Freud is an exception here. Aldous Huxley (in Doors of perception 1954) describes most vividly the viewpoint of the mystic. But probably all neurologists and most philosophers hold that drugs distort and impair perception and thinking, with a danger of producing long-term effects, without revealing truths from any outside source. The general question is whether there is any extra-sensory perception. This writer, not finding convincing evidence in spite of its universal historical acceptance, takes it to be a sad delusion.
Although there is no evidence, in the author’s opinion, that hallucinations convey new knowledge, no doubt dreams, and other brain activity free of sensory control, may show something of hidden motives and hopes and fears, revealing something of the hidden individual. This, however, is not a main interest here.
If the general view taken here is correct—that perceptions of objects are psychological projections of stimulus patterns, and projections of knowledge and assumptions into assumed reality—the status of perception for knowledge is not as secure as empiricists would like. For perceptions are not essentially different from hallucinations. This is a major reason for transcending individual perceptions with shared observations, and with the controlled experiments of instrument-aided science. How does this fit with truth in art?
Op art—and all that jazz
There are pictures which are extremely disturbing—jazzing and moving, and generating ghostly shapes and colours. These are part of Op-Art, best known in the work of Bridget Riley (Figure 10.3). The cause may be mundane, but does this reduce the significance of the experience?
Some of these remarkable effects are seen in simple patterns of repeated parallel lines or converging rays (Figures 10.4 and 10.5), which were studied by the visual scientist Donald MacKay in the 1950s.
Moiré patterns
If two identical overhead projector transparencies of MacKay’s patterns are sandwiched, and if one is moved slightly across the other, exactly these patterns are seen, projected on the screen. This is evidence that the (single) ray figure is producing moirés—by ‘beating’ with retinal after-images, following small eye movements.
The jazzing occurs in these figures, and in Op-Art, even though the eyes are held as still as possible. It is known that the eyes’ lenses are in continual motion, as they hunt for sharp focus (accommodation), and the lens has some dynamic astigmatism shifting the image very slightly. As the repeated lines must be quite closely spaced, the image may shift from dark to light and back again at each border—stimulating the retina’s on–off receptors, associated with the normal signalling of movement. There are, however, authorities who believe these effects arise directly from movement systems in the brain rather than from the eyes. It should be possible to test between these ideas by stabilizing the image on the retina; or even better, by by-passing fluctuations of the lens—which can be done easily with a flash after-image (see box).

10.3 Fall by Bridget Riley. In this remarkably powerful picture, eye movements and ‘hunting’ of the lens of the eyes shift the retinal image across the receptors, and produce ‘beating’ with each momentary after-image, produced especially when the eyes pause between their sudden jumps (saccades). At least, this is one theory. The physiologist Semir Zeki thinks very differently that movement centres of the brain (in area V) are directly stimulated by these patterns to give experience of motion. So we have a controversy.
10.4 Mackay rays. This jazzes about dramatically, and ghostly chrysanthemum shapes appear. These seem to be moiré patterns, the rays ‘beating’ with their momentary after-images, with small eye movements, or displacements from hunting of the lens for accommodation. Some authorities, however, believe the effects to be directly brain induced, without motion signals from the eyes.
10.5 Closely spaced parallel lines have similar effects to the ray figure. These are the basis of many Op-Art pictures, used by Bridget Riley and other artists to stunning effect.
De-jazzing with an after-image
If the Ray figure is viewed in complete darkness, illuminated for a small fraction of a second with an electronic camera flash, a vivid after-image will be produced, fixed precisely on the retina. Does this show the jazzing and the chrysanthemum patterns normally seen in the Ray figure? If not, a brain-induced explanation is pretty well ruled out, in favour of movement signals from the eyes, due to ‘hunting’ of the lens for accommodation.
For this experiment, it is essential for the eyes to be directed at the centre of the figure, with appropriate accommodation for its distance—but a ‘fixation’ spot of light must not illuminate the figure before or after the flash. The eyes can be accommodated to the correct distance by placing a sheet of glass inclined at 45° and placing a small spot of light to the side, at the same distance as the figure, to reflect from the glass.
What happens?
If you try this experiment, you will see that the jazzing effects disappear. If so, they may be attributed to movement mechanisms stimulated by motion of the repeated lines of these figures.
Classifying phenomenal phenomena
It is important to classify phenomena in science. So we need at least tentative classes of illusions with names to identify them. The classes may depend on appearances and on causes. But as causes of many illusions are unknown, or controversial, and appearances of some can be hard to describe, this is not a simple project and we cannot expect to achieve complete agreement or immediate success.
It is suggestive that errors of language neatly match kinds of visual illusions. So we may start by using the names of language errors to name appearance categories of illusions. We will call them ambiguities, distortions, paradoxes, and fictions.
It may be no accident that these correspond both to errors of language and to errors of perception. Both perception and language give descriptions, and both depend upon how objects and situations are classified for behaviour. It may indeed be that very ancient, prehuman, perceptual classifications are the basis of the structure of languages. Perhaps language developed so fast in humans because it built upon the perceptual experience of many millions of years of classifying objects and actions giving nouns and verbs.
Let’s look at these four kinds of illusions—ambiguities, distortions, paradoxes, fictions—and spell out the differences:
Ambiguities
Any retinal image is infinitely ambiguous. That is: it could correspond to, or represent, an infinity of possibilities of shapes and sizes and distances of objects. This is easily seen with an ellipse: it could be given by a tilted circle, a small near circle (or ellipse), or a farther correspondingly larger circle or ellipse (Figures 9.8, 9.12). The possibilities are endless—yet amazingly, we generally see just one of the infinite range of what might be out there. How this is done remains an only partly solved puzzle of perception.
There are well-known figures which flip between a few possibilities. These are known as ‘ambiguous figures’. They are extremely important for showing the dynamics of perception, the searching for hypotheses of objects that might or might not be in the external world. Here the answer—the perception—is never decided. There are different kinds of flipping ambiguities—between shapes, depths, and different objects. The best known is the Necker cube (Figure 10.6).
Here there is no evidence to indicate which of the large faces is the front or the back. Vision entertains alternative, roughly equally likely hypotheses. So here we see it flip between two equally likely cubes as different depth hypotheses are entertained. What is not clear, is why it is only these depth hypotheses that are entertained and seen. Some well-known change-of-object ambiguities are illustrated in Figures 10.7 and 10.8.
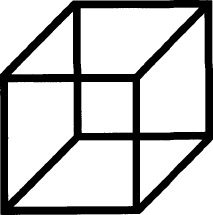
10.6 Necker cube. This flips in depth. Discovered by a Swiss crystallographer, L. A. Necker in 1832, while drawing rhomboid crystals seen with a microscope. Suddenly the drawing (or the crystal) flipped so they looked quite different!
Ambiguities can be extremely useful for perceptual research: as perceptions change though the input to the eyes remains unchanged—so we can see what is going on ‘from the inside’. In particular, visual ambiguities allow us to separate effects of bottom-up signals from the eyes, from top-down knowledge and assumptions (Figure 10.9). This is a very important distinction. There is a wide range of opinions on their relative importance. The more the top-down contribution, the less ‘direct’ is perception. This is bad news for empiricists seeking certainty for seeing, but good news for those who think of perception as intelligently creative—making effective use of limited available data to represent what might be out there.
A beautiful demonstration by the Austrian physicist Ernst Mach, (1838–1916), who was extremely interested in visual perception and made interesting contributions, is the Mach corner (Figure 10.10). This is strong evidence for top-down knowledge and assumption affecting bottom-up signalling of brightness. The general implication is that all ‘raw data’ are cooked!

10.7 Old wife or young mistress? E. G. Boring’s object-ambiguous figure. By looking at different features (ear, neck, nose), this may be flipped at will between the two likely alternatives.
10.8 The duck–rabbit is an even bigger jump between different perceptual object hypotheses–perceptions. (If the figure is rotated by 90°, one will be preferred over the other, as it becomes more likely.)
The hollow face
There is a general rule, or visual assumption, that objects are likely to be convex rather than hollow. Thus, looking into the inside of a box, with one eye, it will generally switch in depth to appear as the outside, though one knows one is looking into the inside. When the box is held in the hand and rotated gently, the effects of reversed movement are bizarre. (Fascinating variations on this theme have been invented by the illusionist Gerry Anders.)
The most dramatic demonstration that probabilities of specific objects are important, is the hollow face. This may be a mask of a normal face on its outside, and hollow on the inside. (These are available in joke shops.) From a metre or so, the inside face will appear as a normal, nose-sticking-out face, though it is hollow. This works, viewed with both eyes in normal lighting. If the mask is slowly rotated it goes through astonishing transformations, reversing direction as the hollow back or the sticking-out front appears, much as for a wire cube when back and front reverse, though more dramatically (Figure 10.11; and see also Plate 3).
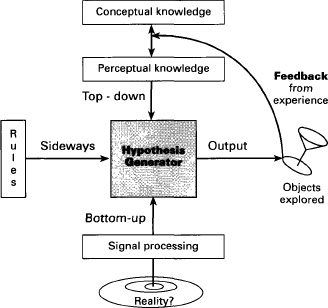
10.9 Ins and outs of vision. Not to be taken too literally, this is a way of relating the notions of bottom-up signals from the eyes, top-down knowledge, and what we are calling sideways rules of perception, such as the Gestalt laws of organization and perspective. This is developed in Chapter 11, ‘Speculations’, with an attempt to classify illusions.
What this demonstrates is important: top-down object knowledge can dominate bottom-up signals.
The more realistic and typical the face, the better it works—remaining apparently normal down to a nearer viewing distance. When upside down, it works less well, as it is now less typical of a face. These simple experiments are well worth trying. They must be seen to be believed.
Distortions
Apparently simple sensations, even brightness, can be distorted. Figure 5.3 is a nice example. Lengths may be distorted, and a straight line may be bent into a curve, so it is difficult to believe it is really straight. Virtually everyone sees these distortions similarly. Many were discovered by physicists and astronomers in the 19th century, when designing hair-lines for eye pieces of optical instruments—to make their measurements more accurate! Several bear the names of distinguished German optical-physicists concerned with avoiding observational errors, but gaining immortality through named illusions.
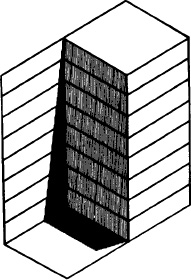
10.10 Mach corner (or card). A shadow (or painted shadow) on a card bent to this shape, changes brightness, or darkness, each time the corner flips in depth. When ‘in’ it is lighter than when ‘out’. This is because when it is seen as a shadow (more likely when ‘in’), it is minimized visually, as shadows are not important objects.
There are several causes of distortions, and it can be hard to establish whether a distortion is physiological or cognitive in origin. One way of finding out is to discover what destroys the illusion. For several reasons we believe the distortion of the café wall illusion to be disturbances of retinal signals of edges—quite simply physiological.
The café wall illusion
This was discovered in Bristol on the tiles of a 19th century café—hence its name. The long illusory wedges seen in Figure 10.12 at first sight contradict the notion that distortion illusions are due to inappropriate size scaling, set by depth cues such as perspective (page 175)—for here there is no perspective, or other depth cues. Is this example evidence against the theory—or is it a different kind of illusion? This shows the importance of classifying phenomena. Without classifications we don’t know how to apply evidence, or assemble evidence for confirming or attacking hypotheses.
10.11 Hollow mask. Though this is a hollow mask, it appears to be a normal nose-sticking-out face—because a hollow face is so unlikely. When rotated, it is seen as turning in the wrong direction. This is because motion parallax is wrongly interpreted. This works with both eyes open, down to a metre or so, when (bottom-up) stereo information beats (top-down) knowledge of faces. It continues to work though one know this face is hollow. (The relative powers of bottom-up signals and top-down knowledge can be assessed by measuring the viewing distance of the change over.)
It turns out that models of the café wall, allowing many variables to be introduced, show that this has a rich lawful set of phenomena.
We should start by noting that the long illusory wedges are not due to errors in the positioning of the ‘tiles’ horizontally (which would be very boring). If alternate rows are slid across, by half a tile width, the direction of the wedges reverses. Nothing else reverses them.
10.12 The café wall illusion. This has large systematic distortions—the long wedges yet here there is no perspective. It has only parallel lines and lines at right angles. So what could cause this massive distortion?
It turns out that this illusion is highly lawful (see box).
Laws of café wall distortion
The wedges reverse when alternate rows of tiles are displaced by half a square (or ‘tile’) width.
The distortion is lost when:
• The ‘mortar’ is brighter than the light ‘tiles’ or darker than the dark ‘tiles’.
• The ‘mortar’ is thick—subtending more than 10′ arc to the eyes.
• The tiles are different colours (for example, red and green) with the same brightnesses (equi-luminance).
The café wall seems to flout a basic feature of symmetry—the Curie principle. The French physicist Pierre Curie (1859–1906), stated that symmetry cannot produce asymmetry. But this figure is symmetrical at the small scale (as any region of displaced tiles is the same as any other region) yet it produces large-scale asymmetry. What is going on?
It turns out that there are two processes. The first is small scale: where there is brightness contrast across the neutral mortar line, half the dark and light tiles move towards each other—forming small scale wedges where there is local asymmetry. The eye integrates these little wedges into the long wedges that are seen.
Perspective illusions
Well-known distortion illusions such as those in Figure 10.13 are very different. They obey completely different laws, and they are destroyed by entirely different conditions. They are all perspective drawings of typical scenes or objects. (Here I have given the game away by calling them ‘perspective’ illusions, but is this the right game?)
Physicists and physiologists, psychologists and philosophers, have tried to explain these distortion illusions for over a hundred years. Current explanations are controversial; but I believe we can develop an explanation for these distortions, which throws light on the nature of object perception. But first, let’s look at various theories that have been proposed. They reflect different views of perception itself, and are remarkably varied.
Theories of ‘perspective’ distortions
The pregnance or ‘good-figure’ theory
The idea of ‘pregnance’ is central to the German school of Gestalt psychologists’ account of perception. The English meaning is similar to the use of the word as in ‘a pregnant sentence’. The illusions are supposed to be due to pregnance exaggerating the distance of features that seem to stand apart, and reducing distances where features seem to belong together.
10.13 Four ‘perspective’ illusions: (a) Hering, (b) Poggendorf, (c) Orbison (two combined), (d) Zöllner.
The status of the notion of pregnance is doubtful. Certainly random or systematic arrangements of dots do tend to be grouped, in various ways, so that some ‘belong’ together while others are rejected or are organized into other patterns (Figure 1.1) but there seems no tendency for the dots to change their positions as a result of such grouping; though surely this should be a prediction of the pregnance theory of distortion.
Empathy theories
It was suggested by Theodore Lipps (based on an idea of the American psychologist R. H. Woodworth) that the observer identifies himself with parts of the figure (or the pillars of a building) and becomes emotionally involved—so that vision is distorted rather as emotion may distort an intellectual judgement. In the Muller–Lyer illusion, (Figure 10.16, page 219) it would be argued that the outgoing ‘arrows’ suggest—emotionally—expansion, which one then sees.
It is true that a very thick column supporting a narrow cornice looks clumsy. And perhaps one does imaginatively stand in the place of the column—as Hercules took the load of the sky off the shoulders of Atlas before turning him to stone. The caryatids of Greek temples (Figure 10.14) embody (quite literally) this idea in architecture. But although of immediate relevance to aesthetics, it can hardly be taken seriously as a theory of the distortion illusions. The Muller–Lyer arrow figures (for example) give distortion whatever one’s mood, and continue to do so when any initial emotional response would surely have died through boredom. There may be perceptual effects of strong emotion, but the illusion figures would seem singularly devoid of emotional content—except to those who try to explain them! More serious: the distortions are virtually the same for all observers though emotions are generally different and change from time to time.
Eye movement theories
These suppose that features producing the distortion make the eyes look in a ‘wrong’ place. In the arrow (Muller–Lyer) illusion, it may be supposed that the eyes are drawn past the lines by the arrow-heads, making the lines look the wrong length. The alternative version is that the eyes are drawn within the lines. But it is clear that neither can be correct. The retinal image can be optically fixed on the retina (Figure 3.17), or more simply (as the reader can easily try) by illuminating the figures with a photographic flash and viewing the after-image, which is stuck on the retinas and moves precisely with the eyes. The result?—the distortions remain unchanged.
10.14 Man enough for the job? Perhaps we identify ourselves with pillars, so that there is a right size in human terms for carrying the load. Is this the basis for distortion illusions? (Caryatids of the Erechtheion, Athens, 421–405 BC, designed by Mnesicles.)
Also, the distortion goes in opposite directions for the pair of arrow figures—but the eyes can’t possibly move in different directions at the same time.
The eye movement theory is sometimes stated in a different form: that it is not actual eye movements, but tendencies to make the eyes move which produce the distortions. But as the eyes can’t move in different directions at the same time, presumably this is also impossible for tendencies or intentions to move the eyes. There is no evidence for the eye movement theories and plenty of evidence against them.
Limited acuity theories
Considering the Muller–Lyer, or arrows illusion: we might well expect the figure with the outgoing fins to look too long and the figure with the ingoing fins to look too short, if the acuity of the eyes was so low that the corners could not be clearly seen—or optically resolved. This may be demonstrated by placing a sheet of tracing paper over the figures, when a slight change of length might appear. The effect is, however, far too small to explain the Muller–Lyer illusion, and does not apply to many of the other figures; so at least in my view this is not a serious candidate. Some authorities do, however, hold similar ideas, generally couched in terms of low spatial-frequency visual filters. These distortions remain, however, when (by careful, clever means) low spatial-frequency components are removed from the figures. I reject this kind of account for these figures; but retinal lateral inhibition is important for some figures depending on brightness differences, such as the café wall illusion (Figure 10.12).
Feature detectors theories
Could it be that these figures upset the orientation detectors (page 77) discovered by Hubel and Wiesel? We may distinguish two kinds of theory along these lines:
1 That orientation detectors exaggerate acute angles, and minimize obtuse angles. This generalization was suggested by Helmholtz, revived since; but there is no physiological evidence for such a physiological cause.
2 That there are interactive effects between orientation (or angle) detectors, perhaps like lateral inhibition interactions in the retinas of the eyes.
It may seem unlikely that the initial stages of pattern detection would be so ‘ill-designed’; though, as Colin Blakemore has pointed out, for retinal interactions, they may be an inevitable side-effect of generally useful lateral inhibition. This is interaction between cone receptor cells such that a strongly stimulated cone cell inhibits the activity of nearby cells, giving a kind of sharpening effect on the signalling of edges where there is blur. Blakemore’s suggestion is that converging lines produce lop-sided lateral inhibition, shifting the neurally signalled peaks, to produce distortions.
Evidence against this as a major effect, is that distortions still occur when the figures have colour contrast but no brightness contrast (isoluminance, or equi-luminance), though it is believed that lateral inhibition only works when there are luminance differences. Also, the distortions still occur when different parts are presented to each eye, by Julesz’s technique (Plate 2) and combined by stereoscopic fusion. Here the lateral inhibition could not be retinal.
Some visual illusions do have their origin in the retina—before brain or mind. The technique invented by Bela Julesz for sharing pictures between the eyes, with patterns of random dots, can be used to see whether a distortion illusion originates in the retinas or further up in the brain, after the signals from the two eyes are combined. If the figure is only visible by the eyes combining their (dotty) signals, and the distortion is seen, it must originate in the brain, not in the eyes.
This does not reject cortical interactions, which remain a possibility. There seem, however, to be better alternatives. This takes us to very different cognitive accounts, including:
Perspective theories
The central idea is that many of the distortion figures suggest depth by perspective, and this produces size changes.
Consider the illusion figures we started with (Figure 10.13). These can be fitted very naturally to typical perspective views of objects lying in three-dimensional space. These figures are flat projections of three dimensions.
Further, it is true of these figures that features represented as distant appear expanded. This is a promising starting point. It immediately suggests that these phenomena are cognitive rather than simply physiological; that they are associated with rules and knowledge of mind rather than to disturbance of physiological function of eye or brain.
10.15 Ponzo illusion. This is a simple perspective figure. The (upper) rectangle, represented as more distant, is expanded.
The phenomena of represented distance producing expansion is clearest in the Ponzo figure (Figure 10.15). The converging lines are typical depth perspective: placing the upper rectangle distant somehow expands it.
The most famous distortion illusion of all is the Muller–Lyer ‘arrows’ (Figure 10.16). These are typical perspective drawings of corners. The outgoing fins are two-dimensional projections, say of the inside corner of a room—the ingoing arrow-heads are perspective drawings of the outside corner of a box or building (Figure 10.17).
These illusion figures are typical perspective views of scenes or of objects in depth. (We may note, however, that in all cases they could be drawings of something quite different, though atypical. This is so, as any retinal image is infinitely ambiguous, though generally but one interpretation is seen.)
Why should perspective depth produce distortion in pictures? The traditional perspective theory simply states that these figures ‘suggest’ depth, and if this suggestion is ‘followed up’, the most distant features appear larger. But how could ‘suggestion of distance’ produce changes of apparent size? Further, why should suggestion of greater distance produce increase in size—though distant objects, giving smaller retinal images, are normally seen somewhat smaller? The traditional perspective theory fails to provide a modus operandi for the distortions, and its predicted size changes are the wrong way round.
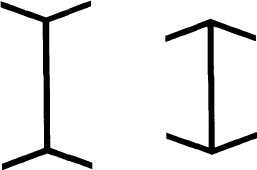
10.16 Muller–Lyer illusion. The line with the outgoing fins looks considerably longer than the equal length line with the ingoing fins. This illusion has received more experimental treatment than any other, perhaps because it is simple, clear-cut, and easy to measure.
Although these predictions of the perspective theory go exactly the wrong way round, this is far better than predictions unrelated to facts. We will try to develop a theory along perspective lines which leads to correct predictions. It is worth devoting some time to this, as by establishing connections between phenomena we gain more general understanding of perception.
There is a perceptual mechanism which is capable of producing such distortions. This is size-constancy scaling. Visual scaling compensates for changes of retinal image sizes, with changes of object distance—so things do not shrink with increasing distance, nearly as much as their images get smaller (Figure 10.18). Consider an audience at a theatre—the faces all look much the same size, yet the retinal images of the further faces are far smaller than the nearer.
This is a most intriguing process, which we can see operating in ourselves. It can go wrong. When it does, instead of keeping the scale of things almost constant in spite of changes of object distance, it can produce a variety of distortions. The box describes a powerful demonstration.
Are your hands the same size?
Look at your two hands, one placed at arm’s length, the other half this distance, at the elbow. They will look almost exactly the same size; yet the image of the further hand will be only half the (linear) size of the nearer. But if the nearer hand is brought to overlap the farther, then they will look very different in sizes. The overlap defeats constancy scaling, showing what perception would be like without it.
This little experiment is well worth carrying out. It may be done also with unknown objects, such as pencils which may be different lengths. Scaling does not depend on knowledge of sizes of the objects.
What we are calling size constancy was described more than three centuries ago by René Descartes (Figure 10.19), in his Dioptrics, of 1637:
I need not, in conclusion, say anything special about the way we see the size and shape of objects; it is completely determined by the way we see the distance and position of their parts. Thus, their size is judged according to our knowledge or opinion as to their distance, in conjunction with the size of the images that they impress on the back of the eye. It is not the absolute size of the images that counts. Clearly they are a hundred times bigger [in area] when the objects are very close to us than when they are ten times farther away; but they do not make us see the objects a hundred times bigger; on the contrary, they seem almost the same size, at any rate so long as we are not deceived by (too great) a distance.
10.18 Constancy scaling. The image of an object halves in size with each doubling of distance of the object. But it does not appear to shrink anything like so much. The brain compensates for the smaller image with increased distance, by size-constancy scaling.
Here is as clear a statement of size constancy as any made later by psychologists; except that Descartes greatly over-states the importance of knowing the sizes or shapes of the objects. He goes on to describe what is now called shape constancy:
Again, our judgements of shape clearly come from our knowledge, or opinion, as to the position of the various parts of the objects and not in accordance with the pictures in the eye; for these pictures normally contain ovals and diamonds when they cause us to see circles and squares.
It is odd that this was not taken up until quite recently, very likely because it did not fit prevailing ideas of physiology or philosophy.
The ability of the perceptual system to compensate for changing distance was investigated in the 1930s by the English psychologist Robert Thouless. Thouless measured size and shape constancy under various conditions for different types of people, using very simple apparatus—rulers and pieces of cardboard. For measuring size constancy, he placed a square of cardboard (which unlike, say, a hand could be of any size), at a given distance from the observer, and also a series of different-sized squares at a nearer position. The subjects were asked to choose the nearer square which appeared the same size as the further square. From the measured sizes the amount of size constancy could be calculated. Thouless’s subjects generally chose a near square of almost the same size as the distant square, though the eyes’ images were very different sizes. Constancy was generally almost perfect for fairly near objects, though it broke down for distant objects, which can look like toys.
10.19 René Descartes (1596–1650), perhaps the most influential of modern philosophers. It is now difficult to escape from his duality of mind and matter, which permeates almost all modern thought in psychology. He clearly described perceptual size and shape constancy, long before they were studied experimentally.
Thouless also measured shape constancy, by cutting out a series of cardboard ellipses, of various eccentricities, which were selected by the subject to match a tilted cardboard circle. Again, it was found that constancy could be nearly perfect—depending on the depth cues available. Thouless’s ‘phenomenal regression to the real object’ might be taken to imply that we have some other knowledge of object reality. This phrase is no longer used. There has been serious confusion over constancy as a process and constancy as the result of visual processes. So the term ‘size scaling’, for the process producing size constancy is useful; and we may also speak of ‘shape constancy’ by scaling.
It is possible to see the mechanism of one’s own size scaling at work with a simple demonstration of what is called Emmert’s law for after-images (see box).
Emmert’s Law
First, obtain a good clear after-image, by looking steadily at a bright light, or preferably a photographic flash. Then look at a distant screen or wall. The after-image will appear to lie on the screen. Then look at a nearer screen. The after-image will now appear correspondingly nearer—and will look smaller. With a hand-held screen (such as a book) moved backwards and forwards, the after-images will expand as the hand moves away and shrink as it approaches the eyes, though of course the retinal after-image remains of constant size. We therefore see the brain’s scaling changing as the distance of the screen changes. The after-image is seen to (nearly) double in size with each doubling in distance of the screen. This is Emmert’s law. It is typical of the psychological projection of retinal images into external space.
Clearly, we are seeing size scaling changes which would normally compensate changes of retinal images with object distance. For any object, there is only one correct perceived size. This is normally given when the distance is correctly perceived. Can scaling be set inappropriately—to produce distortion illusions? Is this the key to an adequate theory of perspective distortion illusions?
Inappropriate constancy-scaling theory
It is one thing to have a theory, quite another to prove it; or at least to show that it is the best of available suggestions. If these distortions are always related to distance, it may indeed seem reasonable to think that perspective sets size scaling—to give errors of perceived size when distance is seen incorrectly. This looks reasonable; but there is a difficulty, which blocked development of a theory along these lines for many years. The difficulty is that the illusion figures generally appear flat. If constancy always follows perceived depth (as in Emmert’s law for after-images), then clearly there is something seriously wrong (or missing) from this account. We shall take the view that the notion is essentially correct, but not complete. Can we complete it?
The reason why the illusion figures appear flat, in spite of their perspective depth features, is not difficult to discover. In the first place, if they are shown on normal textured paper there is visual evidence that they are indeed flat. All perspective pictures have a curious depth paradox: they represent depth, with their perspective and other depth cues; yet as objects the pictures are flat and their textured surfaces provide depth cues showing that they are flat.
We can, however, remove these cues—by making the surface invisible. This can be done for example by painting or drawing with luminous paint. They may be made to glow with soft ultra violet light. Then the illusion figures (or any perspective drawings) appear in dramatic depth. This is well worth trying.
There is strictly only one position from which a perspective picture gives correct perspective to the eye. We have some tolerance for error here; but the illusion figures are often drawn with highly exaggerated perspective—strictly requiring an impossibly small viewing distance. For realistic depth to be given by luminous figures, of for example the Ponzo or Muller–Lyer figures, moderate angles should be used, and they should be viewed from roughly the appropriate distance. (The depth of texture-free luminous figures can be shown to an audience, with striking effect.)
We can get over the difficulty that the distortions occur; though the figures appear flat, by supposing that perspective (or other depth cues) sets constancy scaling directly.
Although there is nothing implausible in this suggestion, it flouts what has, until recently, been assumed about constancy—that it always follows seen depth. This has been held with great authority, as is clear from the following quotation from W. H. Ittleson, who cites support from five other distinguished visual scientists who have worked on this problem. He has this to say: ‘Constancy, it is universally agreed, is dependent upon the proper estimation of distance.’ We suggest that, although scaling can indeed follow perceived distance (as in the Emmert’s law demonstration with after-images), it can also be set directly by depth cues, including perspective. We see this when perceived depth is countermanded by the background texture of pictures. We should then expect distortion illusions to occur when distance is perceived incorrectly—as when there are misleading depth cues. Here we may note that depth cues cannot be appropriate both for the flat surface of the pictures and for the scene or objects they represent. Pictures are inherently paradoxical, suggesting depth yet being flat, so it is hardly surprising that distortions occur.
We suggest, then, there are two kinds of scaling: ‘upwards’ from depth cues and ‘downwards’ from seen depth.
How can we separate effects of ‘upwards’ signals from the eyes, from ‘downwards’ perceptual knowledge or assumptions? We can use phenomena of ambiguity.
Separating bottom-up from top-down by ambiguities
A useful experimental trick is to use perceptual ambiguity for teasing out what is given upwards by cues present in the retinal image, from downwards contributions of knowledge and assumptions. This works because, with ambiguity, perceptions change though the stimulus input remains constant—so top-down effects can be revealed.
Significant phenomena are associated with a flipping Necker cube drawing (Figure 10.6). Much better, is a truly three-dimensional wire cube. (These phenomena are seen most clearly when the cube is coated in luminous paint, to glow in the dark, but this is not essential.)
The skeleton cube will switch in depth, as for the flat figure; but also it will suddenly stand up on one corner, and will rotate with every movement of the observer (at twice the speed), and change shape. These phenomena are worth considerable look-time and think-time, as they can tell us a great deal about how vision is organized: bottom-up and top-down, and as we will suggest, ‘side-ways’.
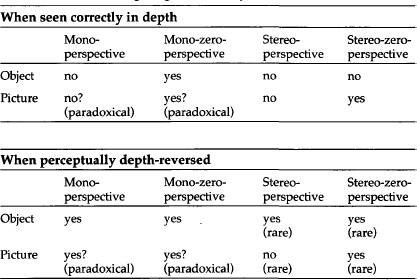
When the wire cube has flipped in depth it moves with instead of, as normally, against every movement of the observer. For as back and front are depth-reversed, motion parallax is attributed wrongly to near and far (see Chapter 6, page 98). What interests us here, though, is the change of shape. Note that when the cube is seen normally, not reversed, its back and front faces appear equal and all the angles right angles. This is quite surprising, for with an isolated skeleton cube there are no depth cues to set size constancy. It shows that here constancy scaling is operating with no bottom-up depth cues. When it flips in depth, the now apparently back face looks too large, and the angles are no longer right angles. It no longer looks like a cube, but a truncated pyramid, with the further face larger than the nearer. This effect is important. It shows that constancy scaling can be set downwards—from depth as seen—rather than signalled (Figure 10.20, Table 10.1).
We have already seen that scaling can be set bottom-up from cues to depth, such as converging perspective lines (Figures 10.13). So scaling can be set upwards from retinal signals, or downwards from knowledge or assumptions. These must be very different processes. They can be isolated by making use of phenomena of ambiguity.
Sometimes both upwards and downwards scaling can be involved. An interesting example is the moon illusion—the moon looking larger than usual when it is low on the horizon. This is so though it always subtends the same angle (0.5°) to the eye of an earth-bound observer.
The moon illusion
The moon also looks larger when high in the sky but seen above mountains. It is not the height, but rather the surroundings that affect its apparent size. The Greek astronomer Ptolomy thought it looks larger because it appears more distant, (what we now call Emmert’s law, page 225) but it looks nearer and larger. This is unlike Emmert’s law.
Table 10.1 Conditions giving distortion (yes) and no distortion (no)
We may liken it to distortions such as in the Ponzo illusion, where perspective, or other depth cues, scale objects as larger when greater distance is signalled, though they do not appear more distant, as the figure lies on a textured background. The moon illusion is not, however, quite the same. For here there is no textured background from the sky to prevent change of apparent distance. What seems to happen is quite complicated: the surrounding depth cues of perspective and so on scale up the size of the moon (bottom-up), so it looks larger. As the sky has no texture—because the moon looks larger, it appears nearer. (This can be demonstrated with luminous disks or balloons in a dark room.) The moon illusion is initiated bottom-up, as for the Ponzo illusion. But this raises a curious question. Why does the moon always appear the same size when high in the sky—and why this particular size? It could be any size and distance, from this retinal image free of context. It seems that the visual system has default assumptions, which are accepted in the absence of scaling information. (This is like a word processor giving a default line length, in the absence of programmed instructions.) We know very little about this for vision. It could be an important principle.
Distortion by absence of perspective
It is important to note that distortion can occur in the absence of perspective—when depth is indicated by other cues, or assumed from knowledge of the object in the picture. In engineering drawings this can be annoying (when perspective is deliberately avoided to show dimensions in isometric projections) for they look weirdly distorted. The effect is seen in this simple perspective-free drawing of a table (Figure 10.21).
We suggest, then, that there are two kinds of scaling: upwards from depth cues and downwards from the prevailing hypothesis of depth.
Measuring distortion and depth
Visual distortions can be measured in various ways including: matching the distorted perception with (an undistorted) ruler (Figure 10.22); nulling, with an equal and opposite distortion; by lengthening or bending or shortening the figure until it appears undistorted.
Measuring visual depth may seem to be impossible. But consider Figure 10.23.
If the figure has perspective, or other depth cues, it is found that the observer places the marker light not at the true distance, but at the apparent distance of this part of the picture, as he or she sees it. For people with normal stereoscopic depth perception this is quite an easy task, giving consistent measures of apparent distances. So, the visual worlds of observers can be plotted in three dimensions in physical space.
This technique shows that the illusion figures are seen in depth according to their perspective features—when depth is not countermanded by texture of the picture plane. It is found that increased distance of features correlates highly with illusory expansion in the perspective illusion figures. So we have objectively related these distortions to perspective depth.

10.21 A top-down distortion. When this is seen as a table lying obliquely in space, the further edge looks too long, and the sides do not look parallel, though this is how they are drawn. This is due to size scaling working downwards from assumed depth.
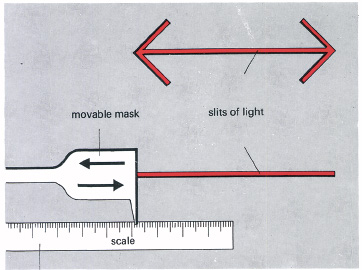
10.22 Measuring length distortion. The observer sees a single Muller–Lyer figure and an adjustable comparison line, set to appear the same length as the distorted line. This gives a direct measure of the distortion. (Back view of the apparatus.)
The finding that apparent depth is closely related to these distortions is suggestive; but it is hardly proof that perspective depth features produce the illusory expansion. Can we think of a more direct test to distinguish between distortions due to errors of the signals of the visual channel and errors due to information (such as perspective) applied inappropriately? We may have this in an experiment carried out by the author with John Harris, in which the distortions were found to vanish when the viewing conditions for the flat figures match the normal conditions for seeing equivalent objects in three-dimensional space.
Illusion-destruction
If the distortions of these figures are due to inappropriate constancy scaling—then the distortions should no longer occur when all the features setting the scaling are appropriate. To make them appropriate, we ensure that the perspective of the figures is exactly the same at the eyes as for viewing an object (such as corners or receding parallel lines) directly. We further ensure that it is seen in its correct depth—as though it were an object, although it is in fact a flat picture. Consider the Muller–Lyer figure (Figure 10.16): this is a flat perspective projection of corners. We make three-dimensional wire model corners, and project them in accurate perspective by casting their shadows on a screen with a small bright light source (Figure 10.24). When this is viewed with the eyes at the same distance as the light source, the perspective of the retinal image is exactly correct—it is the same as when viewing the object directly. But it will still appear flat. To give the correct three-dimensional perception we add a second shadow-casting light, separated horizontally from the first, by the separation of the observer’s eyes. Finally, it is so arranged that one eye sees one of the perspective shadow projections, and the other eye sees only the other projection, by cross polarization. The projections are combined by the brain—to give a three-dimensional perception exactly as though it were a real corner, though it is flat on the screen.
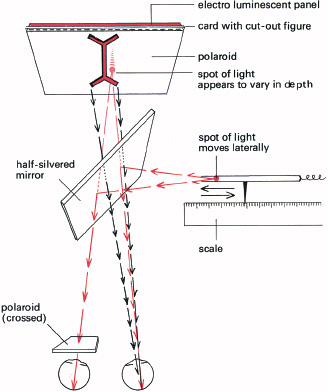
10.23 Measuring apparent depth—‘Pandora’s box’. The flat figure is back-illuminated, to avoid texture and so avoid paradoxical depth. The light from the figure is cross-polarized to one eye, so it is only seen, say, by the right eye. A small adjustable marker light is optically introduced into the figure, by reflection from a part-reflecting glass or perspex sheet. The movable reference light is seen with both eyes. The observer sets it to the apparent distance of any feature of the figure, and its distance is recorded. Thus binocular vision is used to measure monocular depth, for any depth cues. (This can be used with a computer screen).
In this situation, the distortion is entirely absent. It is absent although the visual system is signalling the same angles as in the usual illusion figure, appearing flat and distorted. So how can the illusion be due to distortions of (bottom-up) signals of the visual channel? This seems to be clear evidence that the distortions are produced by depth cues when they are inappropriate to the depth of the object, and when distances are seen incorrectly. The first kind of error is incorrect scaling ‘upwards’ from depth cues; the second is incorrect scaling ‘downwards’ from perceived depth. This is shown in Figures 10.25 and 26.
It turns out that all the perspective illusions are destroyed when presented in appropriate depth. The simplest and easiest example is the Poggendorff illusion.
Distortions similar to those of vision are also found for touch. This presents something of a problem for the theory we have been advocating. John Frisby has provided evidence that people with vivid visual imagery tend to have greater than usual touch illusions. Possibly touch information is interpreted according to visual processing and visual ‘models’ of the world. Somehow the senses interact and combine to give generally consistent perceptions of objects.
Paradoxes
Perhaps the first impossible figure was devised by the Swedish artist Oscar Reutersvärd in 1934. The best known visual paradox is the impossible triangle, designed by the English geneticist Lionel Penrose and his nephew the cosmologist Roger Penrose in 1958. A three-dimensional model which appears impossible was shown in my Royal Institution Christmas Lectures in 1967 (published in The intelligent eye in 1970). This shows that a normal, unpainted object can appear impossible (Figure 10.27). So it does not depend on artificial combinations of visual cues, though the viewing angle is critical.
From another viewing position it does not appear impossible (Figure 10.28).
10.24 3-D shadow projection. A pair of small bright lights (low-voltage halide lamps, in a light-tight box) are horizontally separated by the distance between the eyes. They are cross polarized to the eyes or red–green filters and glasses are used. The illusion figures are made as three-dimensional wire models. With one light their shadow is just the same as the illusion figures—appearing distorted as usual. When the second light is switch on the shadow is immediately seen in the three dimensions of the wire model. The distortion disappears. (This makes a super lecture demonstration. A silver screen should be used to prevent depolarization; or red–green filters and glasses work with any screen.)
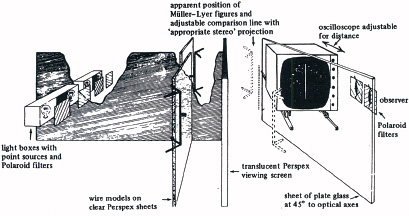
10.25 Muller–Lyer destroyed—apparatus. Horizontally separated small light sources project three-dimensional shadows of wire corners. The separation, giving disparity, and the viewing distance (correct at 40 cm) can be varied.
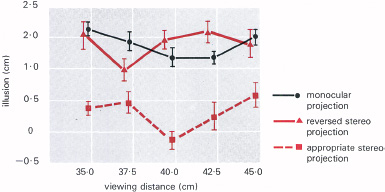
10.26 Muller–Lyer destroyed—results. The Muller–Lyer distortion entirely disappears, when both the perspective and the depth are appropriate. (This is when the viewing distance is 40 cm—the same as the distance of the wire model corners from the point sources—and they are separated by the separation of the eyes (Gregory and Harris, 1975).)
10.27 Impossible object, made of wood. It appears impossible from a critical position, from which the photograph is taken.
The problem arises because of a quite powerful visual rule: that when features or objects are touching they tend to be seen at the same distance. This, though they could well be very different distances. (Binary stars appearing close together may be separated in distance by millions of light years.) It is striking that when any corner of the impossible triangle is hidden, it appears perfectly possible (Figure 10.29).
This illustrates how following a rule, from a false assumption, can generate a paradox. This applies to conceptual and perceptual hypotheses.
10.28 Impossible object—seen as possible. The same wooden model, photographed from different positions. It no longer looks impossible. But although this gives the answer away, Figure 10.29 still cannot be seen as possible!
Fictions
Vision can take off as fiction—illusory contours and surfaces being seen by all observers in normal viewing conditions. The most famous is the Illusory Triangle of the Italian artist-psychologist Gaetano Kanizsa (1974) (Figure 10.30).
An earlier though less impressive ‘fictional’ figure was shown by F. Schumann in 1904 (Figure 10.31).
10.29 The impossible triangle with a hidden corner appears perfectly possible, whichever corner is hidden.
Here another example, using more top-down knowledge, is shown in Figure 10.32. Although shadows are joined to, and so optically are parts of objects, they are perceptually quite distinct and are very seldom confused with objects. Shadows are so powerful as visual cues that they can evoke perception of objects when there are no objects present. This is clear in the typeface of Figure 10.32. Here we see letters as large as life; but in fact, only shadows of imaginary letters are present.
Using a simple figure similar to Kanizsai’s triangle (Figure 10.33), John Harris and the author found that the fictional surfaces are only seen when they are perceptually in front of the inducing figure. When forced behind, by stereopsis, they disappear. This is evidence that they are visual postulates accounting for, and suggested by, the gaps. So occlusion is both an important cue to depth, and is postulated when a nearer occluding object is highly likely even though not present.
10.30 Kanizsa’s ‘fictional’ triangle. The brighter—than background—triangle is not physically present.

10.31 Schumann’s visual ‘fiction’ was shown in 1904—but, curiously, was ignored before Kanizsa’s more dramatic examples.
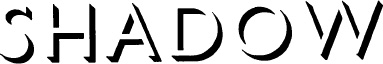
10.32 Letters? These are merely shadows, but we see the objects which would cast these shapes as shadows. The brain invents missing objects on the witness of usually reliable cues.
10.33 Illusory surface destruction—by stereo depth. When seen in a stereoscope, the dots go behind the lines. Then the illusory surface and contours disappear. (They must lie in front to ‘explain’ the gaps).
We see that surprising absence of stimulation can serve as data for perception. Similarly, the illusory letters seen in Figure 10.32 are postulated from the shadows. Even simple perceptions, such as contours and surfaces, can have ‘cognitive’ origins. These are probably not at a very high level of processing. Specific object knowledge does not seem able to create missing parts—such as missing noses—so seems to operate by fairly simple low-level rules.
This account is not universally accepted. Some authorities suppose that these are contrast effects, or are given by neural interactions such as lateral inhibition. The issue is whether these illusory contours are produced directly by stimuli; or far less directly by surprising absence of stimuli, which conveys information.
It is suggestive that fictional contours presented in a stereoscope and combined by the two eyes, can give three-dimensional depth as for true contours or lines. Experiments of this kind are important, to establish what is ‘physiological’ and what is ‘cognitive’. This distinction, though hard to make, runs right through psychology and also through the practice of medicine. Sorting these issues out for clear-cut phenomena of perception may be helpful for thinking about difficult clinical judgements.
This has been a complicated journey. Not everyone will accept the route taken, or the conclusions of the arrival. This is the controversial way science is—and to keep alive and exciting, should be. We will try to bring these difficult issues together in Chapter 11, with speculations at the edge of our understanding of eye and brain, including a tentative classification of the wonderful phenomenal phenomena of illusion.