Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington
Following the work of Ernst Kummer, hopes of finding a proof for the Last Theorem seemed fainter than ever. Furthermore mathematics was beginning to move into different areas of study and there was a risk that the new generation of mathematicians would ignore what seemed an impossible dead-end problem. By the beginning of the twentieth century the problem still held a special place in the hearts of number theorists, but they treated Fermat’s Last Theorem in the same way that chemists treated alchemy. Both were foolish romantic dreams from a past age.
Then in 1908 Paul Wolfskehl, a German industrialist from Darmstadt, gave the problem a new lease of life. The Wolfskehl family were famous for their wealth and their patronage of the arts and sciences, and Paul was no exception. He had studied mathematics at university and, although he devoted most of his life to building the family’s business empire, he maintained contact with professional mathematicians and continued to dabble in number theory. In particular Wolfskehl refused to give up on Fermat’s Last Theorem.
Wolfskehl was by no means a gifted mathematician and he was not destined to make a major contribution to finding a proof of the Last Theorem. Nonetheless, thanks to a curious chain of events, he was to become forever associated with Fermat’s problem, and would inspire thousands of others to take up the challenge.
The story begins with Wolfskehl’s obsession with a beautiful woman, whose identity has never been established. Depressingly for Wolfskehl the mysterious woman rejected him and he was left in such a state of utter despair that he decided to commit suicide. He was a passionate man, but not impetuous, and he planned his death with meticulous detail. He set a date for his suicide and would shoot himself through the head at the stroke of midnight. In the days that remained he settled all his outstanding business affairs, and on the final day he wrote his will and composed letters to all his close friends and family.
Wolfskehl had been so efficient that everything was completed slightly ahead of his midnight deadline, so to while away the hours he went to the library and began browsing through the mathematical publications. It was not long before he found himself staring at Kummer’s classic paper explaining the failure of Cauchy and Lamé. It was one of the great calculations of the age and suitable reading for the final moments of a suicidal mathematician. Wolfskehl worked through the calculation line by line. Suddenly he was startled at what appeared to be a gap in the logic – Kummer had made an assumption and failed to justify a step in his argument. Wolfskehl wondered whether he had uncovered a serious flaw or whether Kummer’s assumption was justified. If the former were true, then there was a chance that proving Fermat’s Last Theorem might be a good deal easier than many had presumed.
He sat down, explored the inadequate segment of the proof, and became engrossed in developing a mini-proof which would either consolidate Kummer’s work or prove that his assumption was wrong, in which case all Kummer’s work would be invalidated. By dawn his work was complete. The bad news, as far as mathematics was concerned, was that Kummer’s proof had been remedied and the Last Theorem remained in the realm of the unattainable. The good news was that the appointed time of the suicide had passed, and Wolfskehl was so proud that he had discovered and corrected a gap in the work of the great Ernst Kummer that his despair and sorrow evaporated. Mathematics had renewed his desire for life.
Wolfskehl tore up his farewell letters and rewrote his will in the light of what had happened that night. Upon his death in 1908 the new will was read out, and the Wolfskehl family were shocked to discover that Paul had bequeathed a large proportion of his fortune as a prize to be awarded to whomsoever could prove Fermat’s Last Theorem. The reward of 100,000 Marks, worth over £1,000,000 in today’s money, was his way of repaying a debt to the conundrum that had saved his life.
The money was put into the charge of the Königliche Gesellschaft der Wissenschaften of Göttingen, which officially announced the competition for the Wolfskehl Prize that same year:
By the power conferred on us, by Dr. Paul Wolfskehl, deceased in Darmstadt, we hereby fund a prize of one hundred thousand Marks, to be given to the person who will be the first to prove the great theorem of Fermat.
The following rules will be followed:
(1) The Königliche Gesellschaft der Wissenschaften in Göttingen will have absolute freedom to decide upon whom the prize should be conferred. It will refuse to accept any manuscript written with the sole aim of entering the competition to obtain the Prize. It will only take into consideration those mathematical memoirs which have appeared in the form of a monograph in the periodicals, or which are for sale in the bookshops. The Society asks the authors of such memoirs to send at least five printed exemplars.
(2) Works which are published in a language which is not understood by the scholarly specialists chosen for the jury will be excluded from the competition. The authors of such works will be allowed to replace them by translations, of guaranteed faithfulness.
(3) The Society declines responsibility for the examination of works not brought to its attention, as well as for the errors which might result from the fact that the author of a work, or part of a work, are unknown to the Society.
(4) The Society retains the right of decision in the case where various persons would have dealt with the solution of the problem, or for the case where the solution is the result of the combined efforts of several scholars, in particular concerning the partition of the Prize.
(5) The award of the Prize by the Society will take place not earlier than two years after the publication of the memoir to be crowned. The interval of time is intended to allow German and foreign mathematicians to voice their opinion about the validity of the solution published.
(6) As soon as the Prize is conferred by the Society, the laureate will be informed by the secretary, in the name of the Society; the result will be published wherever the Prize has been announced during the preceding year. The assignment of the Prize by the Society is not to be the subject of any further discussion.
(7) The payment of the Prize will be made to the laureate, in the next three months after the award, by the Royal Cashier of Göttingen University, or, at the receiver’s own risk, at any other place he may have designated.
(8) The capital may be delivered against receipt, at the Society’s will, either in cash, or by the transfer of financial values. The payment of the Prize will be considered as accomplished by the transmission of these financial values, even though their total value at the day’s end may not attain 100,000 Marks.
(9) If the Prize is not awarded by 13 September 2007, no ulterior claim will be accepted.
The competition for the Wolfskehl Prize is open, as of today, under the above conditions.
Göttingen, 27 June 1908
Die Königliche Gesellschaft der Wissenschaften
It is worth noting that although the Committee would give 100,000 Marks to the first mathematician to prove that Fermat’s Last Theorem is true, they would not award a single pfennig to anybody who might prove that it is false.
The Wolfskehl Prize was announced in all the mathematical journals and news of the competition rapidly spread across Europe. Despite the publicity campaign and the added incentive of an enormous prize the Wolfskehl Committee failed to arouse a great deal of interest among serious mathematicians. The majority of professional mathematicians viewed Fermat’s Last Theorem as a lost cause and decided that they could not afford to waste their careers working on a fool’s errand. However, the prize did succeed in introducing the problem to a whole new audience, a hoard of eager minds who were willing to apply themselves to the ultimate riddle and approach it from a path of complete innocence.
Ever since the Greeks, mathematicians have sought to spice up their textbooks by rephrasing proofs and theorems in the form of solutions to number puzzles. During the latter half of the nineteenth century this playful approach to the subject found its way into the popular press, and number puzzles were to be found alongside crosswords and anagrams. In due course there was a growing audience for mathematical conundrums, as amateurs contemplated everything from the most trivial riddles to profound mathematical problems, including Fermat’s Last Theorem.
Perhaps the most prolific creator of riddles was Henry Dudeney, who wrote for dozens of newspapers and magazines, including the Strand, Cassell’s, the Queen, Tit-Bits, the Weekly Dispatch and Blighty. Another of the great puzzlers of the Victorian Age was the Reverend Charles Dodgson, lecturer in mathematics at Christ Church, Oxford, and better known as the author Lewis Carroll. Dodgson devoted several years to compiling a giant compendium of puzzles entitled Curiosa Mathematica, and although the series was not completed he did write several volumes, including Pillow Problems.
The greatest riddler of them all was the American prodigy Sam Loyd (1841–1911), who as a teenager was making a healthy profit by creating new puzzles and reinventing old ones. He recalls in Sam Loyd and his Puzzles: An Autobiographical Review that some of his early puzzles were created for the circus owner and trickster P.T. Barnum:
Many years ago, when Barnum’s Circus was of a truth ‘the greatest show on earth’, the famous showman got me to prepare for him a series of prize puzzles for advertising purposes. They became widely known as the ‘Questions of the Sphinx’, on account of the large prizes offered to anyone who could master them.
Strangely this autobiography was written in 1928, seventeen years after Loyd’s death. Loyd passed his cunning on to his son, also called Sam, who was the real author of the book, knowing full well that anybody buying it would mistakenly assume that it had been written by the more famous Sam Loyd Senior.
Loyd’s most famous creation was the Victorian equivalent of the Rubik’s Cube, the ‘14–15’ puzzle, which is still found in toyshops today. Fifteen tiles numbered 1 to 15 are arranged in a 4 × 4 grid, and the aim is to slide the tiles and rearrange them into the correct order. Loyd’s offered a significant reward to whoever could complete the puzzle by swapping the ‘ 14’ and ‘15’ into their proper positions via any series of tile slides. Loyd’s son wrote about the fuss generated by this tangible but essentially mathematical puzzle:
A prize of $1,000, offered for the first correct solution to the problem, has never been claimed, although there are thousands of persons who say they performed the required feat. People became infatuated with the puzzle and ludicrous tales are told of shopkeepers who neglected to open their stores; of a distinguished clergyman who stood under a street lamp all through a wintry night trying to recall the way he had performed the feat. The mysterious feature of the puzzle is that none seem to be able to remember the sequence of moves whereby they feel sure they succeeded in solving the puzzle. Pilots are said to have wrecked their ships, and engineers rushed their trains past stations. A famous Baltimore editor tells how he went for his noon lunch and was discovered by his frantic staff long past midnight pushing little pieces of pie around on a plate!
Loyd was always confident that he would never have to pay out the $1,000 because he knew that it is impossible to swap just two pieces without destroying the order elsewhere in the puzzle. In the same way that a mathematician can prove that a particular equation has no solutions, Loyd could prove that his ‘14–15’ puzzle is insoluble.

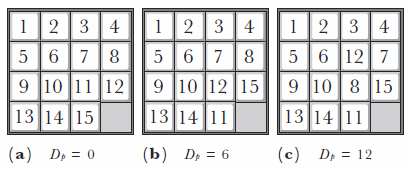
Figure 12. By sliding the tiles it is possible to create various disordered arrangements. For each arrangement it is possible to measure the amount of disorder, via the disorder parameter Dp.
Loyd’s proof began by defining a quantity which measured how disordered a puzzle is, the disorder parameter Dp. The disorder parameter for any given arrangement is the number of tile pairs which arc in the wrong order, so for the correct puzzle, as shown in Figure 12(a), Dp = 0, because no tiles are in the wrong order.
By starting with the ordered puzzle and then sliding the tiles around, it is relatively easy to get to the arrangement shown in Figure 12(b). The tiles are in the correct order until we reach tiles 12 and 11. Obviously the 11 tile should come before the 12 tile and so this pair of tiles is in the wrong order. The complete list of tile pairs which are in the wrong order is as follows: (12,11), (15,13), (15,14), (15,11), (13,11) and (14,11). With six tile pairs in the wrong order in this arrangment, Dp = 6. (Note that tile 10 and tile 12 are next to each other, which is clearly incorrect, but they are not in the wrong order. Therefore this tile pair does not contribute to the disorder parameter.)
After a bit more sliding we get to the arrangement in Figure 12(c). If you compile a list of tile pairs in the wrong order then you will discover that Dp = 12. The important point to notice is that in all these cases, (a), (b) and (c), the value of the disorder parameter is an even number (0, 6 and 12). In fact, if you begin with the correct arrangement and proceed to rearrange it, then this statement is always true. As long as the empty square ends up in the bottom right-hand corner, any amount of tile sliding will always result in an even value for Dp. The even value for the disorder parameter is an integral property of any arrangement derived from the original correct arrangement. In mathematics a property which always holds true no matter what is done to the object is called an invariant.
However, if you examine the arrangement which was being sold by Loyd, in which the 14 and 15 were swapped, then the value of the disorder parameter is one, Dp = 1, i.e. the only pair of tiles out of order are the 14 and 15. For Loyd’s arrangement the disorder parameter has an odd value! Yet we know that any arrangement derived from the correct arrangement has an even value for the disorder parameter. The conclusion is that Loyd’s arrangement cannot be derived from the correct arrangement, and conversely it is impossible to get from Loyd’s arrangement back to the correct one – Loyd’s $1,000 was safe.
Loyd’s puzzle and the disorder parameter demonstrate the power of an invariant. Invariants provide mathematicians with an important strategy to prove that it is impossible to transform one object into another. For example, an area of current excitement concerns the study of knots, and naturally knot theorists are interested in trying to prove whether or not one knot can be transformed into another by twisting and looping but without cutting. In order to answer this question they attempt to find a property of the first knot which cannot be destroyed no matter how much twisting and looping occurs – a knot invariant. They then calculate the same property for the second knot. If the values are different then the conclusion is that it must be impossible to get from the first knot to the second.
Until this technique was invented in the 1920s by Kurt Reidemeister it was impossible to prove that one knot could not be transformed into any other knot. In other words before knot invariants were discovered it was impossible to prove that a granny knot is fundamentally different from a reef knot, an overhand knot or even a simple loop with no knot at all. The concept of an invariant property is central to many other mathematical proofs and, as we shall see in Chapter 5, it would be crucial in bringing Fermat’s Last Theorem back into the mainstream of mathematics.
By the turn of the century, thanks to the likes of Sam Loyd and his ‘14–15’ puzzle, there were millions of amateur problem-solvers throughout Europe and America eagerly looking for new challenges. Once news of Wolfskehl’s legacy filtered down to these budding mathematicians, Fermat’s Last Theorem was once again the world’s most famous problem. The Last Theorem was infinitely more complex than even the hardest of Loyd’s puzzles, but the prize was vastly greater. Amateurs dreamed that they might be able to find a relatively simple trick which had eluded the great professors of the past. The keen twentieth-century amateur was to a large extent on a par with Pierre de Fermat when it came to knowledge of mathematical techniques. The challenge was to match the creativity with which Fermat used his techniques.
Within a few weeks of announcing the Wolfskehl Prize an avalanche of entries poured into the University of Göttingen. Not surprisingly all the proofs were fallacious. Although each entrant was convinced that they had solved this centuries-old problem they had all made subtle, and sometimes not so subtle, errors in their logic. The art of number theory is so abstract that it is frighteningly easy to wander off the path of logic and be completely unaware that one has strayed into absurdity. Appendix 7 shows the sort of classic error which can easily be overlooked by an enthusiastic amateur.
Regardless of who had sent in a particular proof, every single one of them had to be scrupulously checked just in case an unknown amateur had stumbled upon the most sought after proof in mathematics. The head of the mathematics department at Göttingen between 1909 and 1934 was Professor Edmund Landau and it was his responsibility to examine the entries for the Wolfskehl Prize. Landau found that his research was being continually interrupted by having to deal with the dozens of confused proofs which arrived on his desk each month. To cope with the situation he invented a neat method of off-loading the work. The professor printed hundreds of cards which read:

Landau would then hand each new entry, along with a printed card, to one of his students and ask them to fill in the blanks.
The entries continued unabated for years, even following the dramatic devaluation of the Wolfskehl Prize – the result of the hyperinflation which followed the First World War. There are rumours which say that anyone winning the competition today would hardly be able to purchase a cup of coffee with the prize money, but these claims are somewhat exaggerated. A letter written by Dr F. Schlichting, who was responsible for dealing with entries during the 1970s, explains that the prize was then still worth over 10,000 Marks. The letter, written to Paulo Ribenboim and published in his book 13 Lectures on Fermat’s Last Theorem, gives a unique insight into the work of the Wolfskehl committee:
Dear Sir,
There is no count of the total number of ‘solutions’ submitted so far. In the first year (1907–1908) 621 solutions were registered in the files of the Akademie, and today they have stored about 3 metres of correspondence concerning the Fermat problem. In recent decades it was handled in the following way: the secretary of the Akademie divides the arriving manuscripts into:
(1) complete nonsense, which is sent back immediately,
(2) material which looks like mathematics.
The second part is given to the mathematical department, and there the work of reading, finding mistakes and answering is delegated to one of the scientific assistants (at German universities these are graduated individuals working for their Ph.D.) – at the moment I am the victim. There are about 3 or 4 letters to answer each month, and this includes a lot of funny and curious material, e.g. like the one sending the first half of his solution and promising the second if we would pay 1,000 DM in advance; or another one, who promised me 1% of his profits from publications, radio and TV interviews after he got famous, if only I would support him now; if not, he threatened to send it to a Russian mathematics department to deprive us of the glory of discovering him. From time to time someone appears in Göttingen and insists on personal discussion.
Nearly all ‘solutions’ are written on a very elementary level (using the notions of high school mathematics and perhaps some undigested papers in number theory), but can nevertheless be very complicated to understand. Socially, the senders are often persons with a technical education but a failed career who try to find success with a proof of the Fermat problem. I gave some of the manuscripts to physicians who diagnosed heavy schizophrenia.
One condition of Wolfskehl’s last will was that the Akademie had to publish the announcement of the prize yearly in the main mathematical periodicals. But already after the first years the periodicals refused to print the announcement, because they were overflowed by letters and crazy manuscripts.
I hope that this information is of interest to you.
Yours sincerely,
F. Schlichting
As Dr Schlichting mentions, competitors did not restrict themselves to sending their ‘solutions’ to the Akademie. Every mathematics department in the world probably has its cupboard of purported proofs from amateurs. While most institutions ignore these amateur proofs, other recipients have dealt with them in more imaginative ways. The mathematical writer Martin Gardner recalls a friend who would send back a note explaining that he was not competent to examine the proof. Instead he would provide them with the name and address of an expert in the field who could help – that is to say, the details of the last amateur to send him a proof. Another of his friends would write: ‘I have a remarkable refutation of your attempted proof, but unfortunately this page is not large enough to contain it.’
Although amateur mathematicians around the world have spent this century trying and failing to prove Fermat’s Last Theorem and win the Wolfskehl Prize, the professionals have continued largely to ignore the problem. Instead of building on the work of Kummer and the other nineteenth-century number theorists, mathematicians began to examine the foundations of their subject in order to address some of the most fundamental questions about numbers. Some of the greatest figures of the twentieth century, including Bertrand Russell, David Hilbert and Kurt Gödel, tried to understand the most profound properties of numbers in order to grasp their true meaning and to discover what questions number theory can and, more importantly, cannot answer. Their work would shake the foundations of mathematics and ultimately have repercussions for Fermat’s Last Theorem.
For hundreds of years mathematicians had been busy using logical proof to build from the known into the unknown. Progress had been phenomenal, with each new generation of mathematicians expanding on their grand structure and creating new concepts of number and geometry. However, towards the end of the nineteenth century, instead of looking forward, mathematical logicians began to look back to the foundations of mathematics upon which everything else was built. They wanted to verify the fundamentals of mathematics and rigorously rebuild everything from first principles, in order to reassure themselves that those first principles were reliable.
Mathematicians are notorious for being sticklers when it comes to requiring absolute proof before accepting any statement. Their reputation is clearly expressed in a story told by Ian Stewart in Concepts of Modern Mathematics:
An astronomer, a physicist, and a mathematician (it is said) were holidaying in Scotland. Glancing from a train window, they observed a black sheep in the middle of a field. ‘How interesting,’ observed the astronomer, ‘all Scottish sheep are black!’ To which the physicist responded, ‘No, no! Some Scottish sheep are black!’ The mathematician gazed heavenward in supplication, and then intoned, ‘In Scotland there exists at least one field, containing at least one sheep, at least one side of which is black.’
Even more rigorous than the ordinary mathematician is the mathematician who specialises in the study of mathematical logic. Mathematical logicians began to question ideas which other mathematicians had taken for granted for centuries. For example, the law of trichotomy states that every number is either negative, positive or zero. This seems to be obvious and mathematicians had tacitly assumed it to be true, but nobody had ever bothered to prove that this really was the case. Logicians realised that, until the law of trichotomy had been proved true, then it might be false, and if that turned out to be the case then an entire edifice of knowledge, everything that relied on the law, would collapse. Fortunately for mathematics, at the end of the last century the law of trichotomy was proved to be true.
Ever since the ancient Greeks, mathematics had been accumulating more and more theorems and truths, and although most of them had been rigorously proved mathematicians were concerned that some of them, such as the law of trichotomy, had crept in without being properly examined. Some ideas had become part of the folklore and yet nobody was quite sure how they had been originally proved, if indeed they ever had been, so logicians decided to prove every theorem from first principles. However, every truth had to be deduced from other truths. Those truths, in turn, first had to be proved from even more fundamental truths, and so on. Eventually the logicians found themselves dealing with a few essential statements which were so fundamental that they themselves could not be proved. These fundamental assumptions are the axioms of mathematics.
One example of the axioms is the commutative law of addition, which simply states that, for any numbers m and n,
m + n = n + m
This and the handful of other axioms are taken to be self-evident, and can easily be tested by applying them to particular numbers. So far the axioms have passed every test and have been accepted as being the bedrock of mathematics. The challenge for the logicians was to rebuild all of mathematics from these axioms. Appendix 8 defines the set of arithmetic axioms and gives an idea of how logicians set about building the rest of mathematics.
A legion of logicians participated in the slow and painful process of rebuilding the immensely complex body of mathematical knowledge using only a minimal number of axioms. The idea was to consolidate what mathematicians thought they already knew by employing only the most rigorous standards of logic. The German mathematician Hermann Weyl summarised the mood of the time: ‘Logic is the hygiene the mathematician practises to keep his ideas healthy and strong.’ In addition to cleansing what was known, the hope was that this fundamentalist approach would also throw light on as yet unsolved problems, including Fermat’s Last Theorem.
The programme was headed by the most eminent figure of the age, David Hilbert. Hilbert believed that everything in mathematics could and should be proved from the basic axioms. The result of this would be to demonstrate conclusively the two most important elements of the mathematical system. First, mathematics should, at least in theory, be able to answer every single question – this is the same ethos of completeness which had in the past demanded the invention of new numbers like the negatives and the imaginaries. Second, mathematics should be free of inconsistencies – that is to say, having shown that a statement is true by one method, it should not be possible to show that the same statement is false via another method. Hilbert was convinced that, by assuming just a few axioms, it would be possible to answer any imaginable mathematical question without fear of contradiction.
On 8 August 1900 Hilbert gave a historic talk at the International Congress of Mathematicians in Paris. Hilbert posed twenty-three unsolved problems in mathematics which he believed were of the most immediate importance. Some of the problems related to more general areas of mathematics, but most of them concentrated on the logical foundations of the subject. These problems were intended to focus the attention of the mathematical world and provide a programme of research. Hilbert wanted to galvanise the community into helping him realise his vision of a mathematical system free of doubt and inconsistency – an ambition he had inscribed on his tombstone:
Wir müssen wissen,
Wir werden wissen.
We must know,
We will know.
Although sometimes a bitter rival of Hilbert, Gottlob Frege was one of the leading lights in the so-called Hilbert programme. For over a decade Frege devoted himself to deriving hundreds of complicated theorems from the simple axioms, and his successes led him to believe that he was well on the way to completing a significant chunk of Hilbert’s dream. One of Frege’s key breakthroughs was to create the very definition of a number. For example, what do we actually mean by the number 3? It turns out that to define 3, Frege first had to define ‘threeness’.
‘Threeness’ is the abstract quality which belongs to collections or sets of objects containing three objects. For instance ‘threeness’ could be used to describe the collection of blind mice in the popular nursery rhyme, or ‘threeness’ is equally appropriate for describing the set of sides of a triangle. Frege noticed that there were numerous sets which exhibited ‘threeness’ and used the idea of sets to define ‘3’ itself. He created a new set and placed inside it all the sets exhibiting ‘threeness’ and called this new set of sets ‘3’. Therefore, a set has three members if and only if it is inside the set ‘3’.
This might appear to be an over-complex definition for a concept we use every day, but Frege’s description of ‘3’ is rigorous and indisputable and wholly necessary for Hilbert’s uncompromising programme.
In 1902 Frege’s ordeal seemed to be coming to an end as he prepared to publish Grundgesetze der Arithmetik (Fundamental Laws of Arithmetic) – a gigantic and authoritative two-volume work intended to establish a new standard of certainty within mathematics. At the same time the English logician Bertrand Russell, who was also contributing to Hilbert’s great project, was making a devastating discovery. Despite following the rigorous protocol of Hilbert, he had come up against an inconsistency. Russell recalled his own reaction to the dreaded realisation that mathematics might be inherently contradictory:
At first I supposed that I should be able to overcome the contradiction quite easily, and that probably there was some trivial error in the reasoning. Gradually, however, it became clear that this was not the case … Throughout the latter half of 1901 I supposed the solution would be easy, but by the end of that time I had concluded that it was a big job … I made a practice of wandering about the common every night from eleven until one, by which time I came to know the three different noises made by nightjars. (Most people only know one.) I was trying hard to solve the contradiction. Every morning I would sit down before a blank sheet of paper. Throughout the day, with a brief interval for lunch, I would stare at the blank sheet. Often when evening came it was still empty.
There was no escaping from the contradiction. Russell’s work would cause immense damage to the dream of a mathematical system free of doubt, inconsistency and paradox. He wrote to Frege, whose manuscript was already at the printers. The letter made Frege’s life’s work effectively worthless, but despite the mortal blow he published his magnum opus regardless and merely added a postscript to the second volume: ‘A scientist can hardly meet with anything more undesirable than to have the foundation give way just as the work is finished. In this position I was put by a letter from Mr Bertrand Russell as the work was nearly through the press.’
Ironically Russell’s contradiction grew out of Frege’s much loved sets, or collections. Many years later, in his book My Philosophical Development, he recalled the thoughts that sparked his questioning of Frege’s work: ‘It seemed to me that a class sometimes is, and sometimes is not, a member of itself. The class of teaspoons, for example, is not another teaspoon, but the class of things that are not teaspoons is one of the things that are not teaspoons.’ It was this curious and apparently innocuous observation that led to the catastrophic paradox.
Russell’s paradox is often explained using the tale of the meticulous librarian. One day, while wandering between the shelves, the librarian discovers a collection of catalogues. There are separate catalogues for novels, reference, poetry, and so on. The librarian notices that some of the catalogues list themselves, while others do not.
In order to simplify the system the librarian makes two more catalogues, one of which lists all the catalogues which do list themselves and, more interestingly, one which lists all the catalogues which do not list themselves. Upon completing the task the librarian has a problem: should the catalogue which lists all the catalogues which do not list themselves, be listed in itself? If it is listed, then by definition it should not be listed. However, if it is not listed, then by definition it should be listed. The librarian is in a no-win situation.
The catalogues are very similar to the sets or classes which Frege used as the fundamental definition of numbers. Therefore the inconsistency which plagues the librarian will also cause problems in the supposedly logical structure of mathematics. Mathematics cannot tolerate inconsistencies, paradoxes or contradictions. For example, the powerful tool of proof by contradiction relies on a mathematics free of paradox. Proof by contradiction states that if an assumption leads to absurdity then the assumption must be false, but according to Russell even the axioms can lead to absurdity. Therefore proof by contradiction could show an axiom to be false, and yet axioms are the foundations of mathematics and acknowledged to be true.
Many intellectuals questioned Russell’s work, claiming that mathematics was an obviously successful and unflawed pursuit. He responded by explaining the significance of his work in the following way:
‘But,’ you might say, ‘none of this shakes my belief that 2 and 2 are 4.’ You are quite right, except in marginal cases – and it is only in marginal cases that you are doubtful whether a certain animal is a dog or a certain length is less than a metre. Two must be two of something, and the proposition ‘2 and 2 are 4’ is useless unless it can be applied. Two dogs and two dogs are certainly four dogs, but cases arise in which you are doubtful whether two of them are dogs. ‘Well, at any rate there are four animals,’ you might say. But there are microorganisms concerning which it is doubtful whether they are animals or plants. ‘Well, then living organisms,’ you say. But there are things of which it is doubtful whether they are living or not. You will be driven into say: ‘Two entities and two entities are four entities.’ When you have told me what you mean by ‘entity’, we will resume the argument.
Russell’s work shook the fundations of mathematics and threw the study of mathematical logic into a state of chaos. The logicians were aware that a paradox lurking in the foundations of mathematics could sooner or later rear its illogical head and cause profound problems. Along with Hilbert and the other logicians, Russell set about trying to remedy the situation and restore sanity to mathematics.
This inconsistency was a direct consequence of working with the axioms of mathematics, which until this point had been assumed to be self-evident and sufficient to define the rest of mathematics. One approach was to create an additional axiom which forbade any class from being a member of itself. This would prevent Russell’s paradox by making redundant the question of whether or not to enter the catalogue of catalogues which do not list themselves in itself.
Russell spent the next decade considering the axioms of mathematics, the very essence of the subject. Then in 1910, in partnership with Alfred North Whitehead, he published the first of three volumes of Principia Mathematica — an apparently successful attempt to partly address the problem created by his own paradox. For the next two decades others used Principia Mathematica as a guide for establishing a flawless mathematical edifice, and by the time Hilbert retired in 1930 he felt confident that mathematics was well on the road to recovery. His dream of a consistent logic, powerful enough to answer every question, was apparently on its way to becoming a reality.
Then in 1931 an unknown twenty-five-year-old mathematician published a paper which would forever destroy Hilbert’s hopes. Kurt Gödel would force mathematicians to accept that mathematics could never be logically perfect, and implicit in his works was the idea that problems like Fermat’s Last Theorem might even be impossible to solve.
Kurt Gödel was born on 28 April 1906 in Moravia, then part of the Austro-Hungarian Empire, now part of the Czech Republic. From an early age he suffered from severe illness, the most serious being a bout of rheumatic fever at the age of six. This early brush with death caused Gödel to develop an obsessive hypochondria which stayed with him throughout his life. At the age of eight, having read a medical textbook, he became convinced that he had a weak heart, even though his doctors could find no evidence of the condition. Later, towards the end of his life, he mistakenly believed that he was being poisoned and refused to eat, almost starving himself to death.
As a child Gödel displayed a talent for science and mathematics, and his inquisitive nature led his family to nickname him der Herr Warum (Mr Why). He went to the University of Vienna unsure of whether to specialise in mathematics or physics, but an inspiring and passionate lecture course on number theory by Professor P. Furtwängler persuaded Gödel to devote his life to numbers. The lectures were all the more extraordinary because Furtwängler was paralysed from the neck down and had to lecture from his wheelchair without notes while his assistant wrote on the blackboard.
By his early twenties Gödel had established himself in the mathematics department, but along with his colleagues he would occasionally wander down the corridor to attend meetings of the Wiener Kreis (Viennese Circle), a group of philosophers who would gather to discuss the day’s great questions of logic. It was during this period that Gödel developed the ideas that would devastate the foundations of mathematics.
In 1931 Gödel published his book Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme (On Formally Undecidable Propositions in Principia Mathematica and Related Systems), which contained his so-called theorems of undecidability. When news of the theorems reached America the great mathematician John von Neumann immediately cancelled a lecture series he was giving on Hilbert’s programme and replaced the remainder of the course with a discussion of Gödel’s revolutionary work.
Gödel had proved that trying to create a complete and consistent mathematical system was an impossible task. His ideas could be encapsulated in two statements.
First theorem of undecidability
If axiomatic set theory is consistent, there exist theorems which can neither be proved or disproved.
Second theorem of undecidability
There is no constructive procedure which will prove axiomatic theory to be consistent.
Essentially Gödel’s first statement said that no matter what set of axioms were being used there would be questions which mathematics could not answer – completeness could never be achieved. Worse still, the second statement said that mathematicians could never even be sure that their choice of axioms would not lead to a contradiction – consistency could never be proved. Gödel had shown that the Hilbert programme was an impossible exercise.
Decades later, in Portraits from Memory, Bertrand Russell reflected on his reaction to Gödel’s discovery:
I wanted certainty in the kind of way in which people want religious faith. I thought that certainty is more likely to be found in mathematics than elsewhere. But I discovered that many mathematical demonstrations, which my teachers expected me to accept, were full of fallacies, and that, if certainty were indeed discoverable in mathematics, it would be in a new field of mathematics, with more solid foundations than those that had hitherto been thought secure. But as the work proceeded, I was continually reminded of the fable about the elephant and the tortoise. Having constructed an elephant upon which the mathematical world could rest, I found the elephant tottering, and proceeded to construct a tortoise to keep the elephant from falling. But the tortoise was no more secure than the elephant, and after some twenty years of arduous toil, I came to the conclusion that there was nothing more that I could do in the way of making mathematical knowledge indubitable.
Although Gödel’s second statement said that it was impossible to prove that the axioms were consistent, this did not necessarily mean that they were inconsistent. In their hearts many mathematicians still believed that their mathematics would remain consistent, but in their minds they could not prove it. Many years later the great number theorist Andre Weil would say: ‘God exists since mathematics is consistent, and the Devil exists since we cannot prove it.’
The proof of Gödel’s theorems of undecidability is immensely complicated, and in fact a more rigorous statement of the First Theorem should be:
To every ω-consistent recursive class k of formulae there correspond recursive class-signs r, such that neither ν Gen r nor Neg(ν Gen r) belongs to Flg(k) (where ν is the free variable of r).
Fortunately, as with Russell’s paradox and the tale of the librarian, Gödel’s first theorem can be illustrated with another logical analogy due to Epimenides and known as the Cretan paradox, or liar’s paradox. Epimenides was a Cretan who exclaimed:
‘I am a liar!’
The paradox arises when we try and determine whether this statement is true or false. First let us see what happens if we assume that the statement is true. A true statement implies that Epimenides is a liar, but we initially assumed that he made a true statement and therefore Epimenides is not a liar – we have an inconsistency. On the other hand let us see what happens if we assume that the statement is false. A false statement implies that Epimenides is not a liar, but we initially assumed that he made a false statement and therefore Epimenides is a liar – we have another inconsistency. Whether we assume that the statement is true or false we end up with an inconsistency, and therefore the statement is neither true nor false.
Gödel reinterpreted the liar’s paradox and introduced the concept of proof. The result was a statement along the following lines:
This statement does not have any proof.
If the statement were false then the statement would be provable, but this would contradict the statement. Therefore the statement must be true in order to avoid the contradiction. However, although the statement is true it cannot be proven, because this statement (which we now know to be true) says so.
Because Gödel could translate the above statement into mathematical notation, he was able to demonstrate that there existed statements in mathematics which are true but which could never be proven to be true, so-called undecidable statements. This was the death-blow for the Hilbert programme.
In many ways Gödel’s work paralleled similar discoveries being made in quantum physics. Just four years before Gödel published his work on undecidability, the German physicist Werner Heisenberg uncovered the uncertainty principle. Just as there was a fundamental limit to what theorems mathematicians could prove, Heisenberg showed that there was a fundamental limit to what properties physicists could measure. For example, if they wanted to measure the exact position of an object, then they could measure the object’s velocity with only relatively poor accuracy. This is because in order to measure the position of the object it would be necessary to illuminate it with photons of light, but to pinpoint its exact locality the photons of light would have to have enormous energy. However, if the object is being bombarded by high-energy photons its own velocity will be affected and becomes inherently uncertain. Hence, by demanding knowledge of an object’s position, physicists would have to give up some knowledge of its velocity.
Heisenberg’s uncertainty principle only reveals itself at atomic scales, when high-precision measurements become critical. Therefore much of physics could carry on regardless while quantum physicists concerned themselves with profound questions about the limits of knowledge. The same was happening in the world of mathematics. While the logicians concerned themselves with a highly esoteric debate about undecidability, the rest of the mathematical community carried on regardless. Although Gödel had proved that there were some statements which could not be proven, there were plenty of statements which could be proven and his discovery did not invalidate anything proven in the past. Furthermore, many mathematicians believed that Gödel’s undecidable statements would only be found in the most obscure and extreme regions of mathematics and might therefore never be encountered. After all Gödel had only said that these statements existed; he could not actually point to one. Then in 1963 Gödel’s theoretical nightmare became a full-blooded reality.
Paul Cohen, a twenty-nine-year-old mathematician at Stanford University, developed a technique for testing whether or not a particular question is undecidable. The technique only works in a few very special cases, but he was nevertheless the first person to discover specific questions which were indeed undecidable. Having made his discovery Cohen immediately flew to Princeton, proof in hand, to have it verified by Gödel himself. Gödel, who by now was entering a paranoid phase of his life, opened the door slightly, snatched the papers and slammed the door shut. Two days later Cohen received an invitation to tea at Gödel’s house, a sign that the master had given the proof his stamp of authority. What was particularly dramatic was that some of these undecidable questions were central to mathematics. Ironically Cohen proved that one of the questions which David Hilbert declared to be among the twenty-three most important problems in mathematics, the continuum hypothesis, was undecidable.
Gödel’s work, compounded by Cohen’s undecidable statements, sent a disturbing message to all those mathematicians, professional and amateur, who were persisting in their attempts to prove Fermat’s Last Theorem – perhaps Fermat’s Last Theorem was undecidable! What if Pierre de Fermat had made a mistake when he claimed to have found a proof? If so, then there was the possibility that the Last Theorem was undecidable. Proving Fermat’s Last Theorem might be more than just difficult, it might be impossible. If Fermat’s Last Theorem were undecidable, then mathematicians had spent centuries in search of a proof that did not exist.
Curiously if Fermat’s Last Theorem turned out to be undecidable, then this would imply that it must be true. The reason is as follows. The Last Theorem says that there are no whole number solutions to the equation
![]()
If the Last Theorem were in fact false, then it would be possible to prove this by identifying a solution (a counter-example). Therefore the Last Theorem would be decidable. Being false would be inconsistent with being undecidable. However, if the Last Theorem were true, there would not necessarily be such an unequivocal way of proving it so, i.e. it could be undecidable. In conclusion, Fermat’s Last Theorem might be true, but there may be no way of proving it.
Pierre de Fermat’s casual jotting in the margin of Diophantus’ Arithmetica had led to the most infuriating riddle in history. Despite three centuries of glorious failure and Gödel’s suggestion that they might be hunting for a non-existent proof, some mathematicians continued to be attracted to the problem. The Last Theorem was a mathematical siren, luring geniuses towards it, only to dash their hopes. Any mathematician who got involved with Fermat’s Last Theorem risked wasting their career, and yet whoever could make the crucial breakthrough would go down in history as having solved the world’s most difficult problem.
Generations of mathematicians were obsessed with Fermat’s Last Theorem for two reasons. First, there was the ruthless sense of one-upmanship. The Last Theorem was the ultimate test and whoever could prove it would succeed where Cauchy, Euler, Kummer, and countless others had failed. Just as Fermat himself took great pleasure in solving problems which baffled his contemporaries, whoever could prove the Last Theorem could enjoy the fact that they had solved a problem which had confounded the entire community of mathematicians for hundreds of years. Second, whoever could meet Fermat’s challenge could enjoy the innocent satisfaction of solving a riddle. The delight derived from solving esoteric questions in number theory is not so different from the simple joy of tackling the trivial riddles of Sam Loyd. A mathematician once said to me that the pleasure he derived from solving mathematical problems is similar to that gained by crossword addicts. Filling in the last clue of a particularly tough crossword is always a satisfying experience, but imagine the sense of achievement after spending years on a puzzle, which nobody else in the world has been able to solve, and then figuring out the solution.
These are the same reasons why Andrew Wiles became fascinated by Fermat: ‘Pure mathematicians just love a challenge. They love unsolved problems. When doing maths there’s this great feeling. You start with a problem that just mystifies you. You can’t understand it, it’s so complicated, you just can’t make head nor tail of it. But then when you finally resolve it, you have this incredible feeling of how beautiful it is, how it all fits together so elegantly. Most deceptive are the problems which look easy, and yet they turn out to be extremely intricate. Fermat is the most beautiful example of this. It just looked as though it had to have a solution and, of course, it’s very special because Fermat said that he had a solution.’
Mathematics has its applications in science and technology, but that is not what drives mathematicians. They are inspired by the joy of discovery. G.H. Hardy tried to explain and justify his own career in a book entitled A Mathematician’s Apology:
I will only say that if a chess problem is, in the crude sense, ‘useless’, then that is equally true of most of the best mathematics … I have never done anything ‘useful’. No discovery of mine has made, or is likely to make, directly or indirectly, for good or ill, the least difference to the amenity of the world. Judged by all practical standards, the value of my mathematical life is nil; and outside mathematics it is trivial anyhow. I have just one chance of escaping a verdict of complete triviality, that I may be judged to have created something worth creating. And that I have created something is undeniable: the question is about its value.
The desire for a solution to any mathematical problem is largely fired by curiosity, and the reward is the simple but enormous satisfaction derived from solving any riddle. The mathematician E.C. Titchmarsh once said: ‘It can be of no practical use to know that π is irrational, but if we can know, it surely would be intolerable not to know.’
In the case of Fermat’s Last Theorem there was no shortage of curiosity. Gödel’s work on undecidability had introduced an element of doubt as to whether the problem was soluble, but this was not enough to discourage the true Fermat fanatic. What was more dispiriting was the fact that by the 1930s mathematicians had exhausted all their techniques and had little else at their disposal. What was needed was a new tool, something that would raise mathematical morale. The Second World War was to provide just what was required – the greatest leap in calculating power since the invention of the slide-rule.
When in 1940 G.H. Hardy declared that the best mathematics is largely useless, he was quick to add that this was not necessarily a bad thing: ‘Real mathematics has no effects on war. No one has yet discovered any warlike purpose to be served by the theory of numbers.’ Hardy was soon to be proved wrong.
In 1944 John von Neumann co-wrote the book The Theory of Games and Economic Behavior, in which he coined the term game theory. Game theory was von Neumann’s attempt to use mathematics to describe the structure of games and how humans play them. He began by studying chess and poker, and then went on to try and model more sophisticated games such as economics. After the Second World War the RAND corporation realised the potential of von Neumann’s ideas and hired him to work on developing Cold War strategies. From that point on, mathematical game theory has become a basic tool for generals to test their military-strategies by treating battles as complex games of chess. A simple illustration of the application of game theory in battles is the story of the truel.
A truel is similar to a duel, except there are three participants rather than two. One morning Mr Black, Mr Grey and Mr White decide to resolve a conflict by truelling with pistols until only one of them survives. Mr Black is the worst shot, hitting his target on average only one time in three. Mr Grey is a better shot hitting his target two times out of three. Mr White is the best shot hitting his target every time. To make the truel fairer Mr Black is allowed to shoot first, followed by Mr Grey (if he is still alive), followed by Mr White (if he is still alive), and round again until only one of them is alive. The question is this: Where should Mr Black aim his first shot? You might like to make a guess based on intuition, or better still based on game theory. The answer is discussed in Appendix 9.
Even more influential in wartime than game theory is the mathematics of code breaking. During the Second World War the Allies realised that in theory mathematical logic could be used to unscramble German messages, if only the calculations could be performed quickly enough. The challenge was to find a way of automating mathematics so that a machine could perform the calculations, and the Englishman who contributed most to this code-cracking effort was Alan Turing.
In 1938 Turing returned to Cambridge having completed a stint at Princeton University. He had witnessed first-hand the turmoil caused by Gödel’s theorems of undecidability and had become involved in trying to pick up the pieces of Hilbert’s dream. In particular he wanted to know if there was a way to define which questions were and were not decidable, and tried to develop a methodical way of answering this question. At the time calculating devices were primitive and effectively useless when it came to serious mathematics, and so instead Turing based his ideas on the concept of an imaginary machine which was capable of infinite computation. This hypothetical machine, which consumed infinite amounts of imaginary ticker-tape and could compute for an eternity, was all that he required to explore his abstract questions of logic. What Turing was unaware of was that his imagined mechanisation of hypothetical questions would eventually lead to a breakthrough in performing real calculations on real machines.
Despite the outbreak of war, Turing continued his research as a fellow of King’s College, until on 4 September 1939 his contented life as a Cambridge don came to an abrupt end. He had been commandeered by the Government Code and Cypher School, whose task it was to unscramble the enemy’s coded messages. Prior to the war the Germans had devoted considerable effort to developing a superior system of encryption, and this was a matter of grave concern to British Intelligence who had in the past been able to decipher their enemy’s communications with relative ease. The HMSO’s official war history British Intelligence in the Second World War describes the state of play in the 1930s:
By 1937 it was established that, unlike their Japanese and Italian counterparts, the German army, the German navy and probably the air force, together with other state organisations like the railways and the SS used, for all except their tactical communications, different versions of the same cypher system – the Enigma machine which had been put on the market in the 1920s but which the Germans had rendered more secure by progressive modifications. In 1937 the Government Code and Cypher School broke into the less modified and less secure model of this machine that was being used by the Germans, the Italians and the Spanish nationalist forces. But apart from this the Enigma still resisted attack, and it seemed likely that it would continue to do so.
The Enigma machine consisted of a keyboard connected to a scrambler unit. The scrambler unit contained three separate rotors and the positions of the rotors determined how each letter on the keyboard would be enciphered. What made the Enigma code so difficult to crack was the enormous number of ways in which the machine could be set up. First, the three rotors in the machine were chosen from a selection of five, and could be changed and swapped around to confuse the code-breakers. Second, each rotor could be positioned in one of twenty-six different ways. This means that the machine could be set up in over a million different ways. In addition to the permutations provided by the rotors, plugboard connections at the back of the machine could be changed by hand to provide a total of over 150 million million million possible setups. To increase security even further, the three rotors were continually changing their orientation, so that every time a letter was transmitted, the set-up for the machine, and therefore the encipherment, would change for the next letter. So typing ‘DODO’ could generate the message ‘FGTB’ – the ‘D’ and the ‘O’ are sent twice, but encoded differently each time.
Enigma machines were given to the German army, navy and air force, and were even operated by the railways and other government departments. As with all code systems used during this period, a weakness of the Enigma was that the receiver had to know the sender’s Enigma setting. To maintain security the Enigma settings had to be changed on a daily basis. One way for senders to change settings regularly and keep receivers informed was to publish the daily settings in a secret code-book. The risk with this approach was that the British might capture a U-boat and obtain the code-book with all the daily settings for the following month. The alternative approach, and the one adopted for the bulk of the war, was to transmit the daily settings in a preamble to the actual message, encoded using the previous day’s settings.
When the war started, the British Cypher School was dominated by classicists and linguists. The Foreign Office soon realised that number theorists had a better chance of finding the key to cracking the German codes and, to begin with, nine of Britain’s most brilliant number theorists were gathered at the Cypher School’s new home at Bletchley Park, a Victorian mansion in Bletchley, Buckinghamshire. Turing had to abandon his hypothetical machines with infinite ticker-tape and endless processing time and come to terms with a practical problem with finite resources and a very real deadline.
Cryptography is an intellectual battle between the code-maker and the code-breaker. The challenge for the code-maker is to shuffle and scramble an outgoing message to the point where it would be indecipherable if intercepted by the enemy. However, there is a limit on the amount of mathematical manipulation possible because of the need to dispatch messages quickly and efficiently. The strength of the German Enigma code was that the coded message underwent several levels of encryption at very high speed. The challenge for the code-breaker was to take an intercepted message and to crack the code while the contents of the message were still relevant. A German message ordering a British ship to be destroyed had to be decoded before the ship was sunk.
Turing led a team of mathematicians who attempted to build mirror-images of the Enigma machine. Turing incorporated his pre-war abstract ideas into these devices, which could in theory methodically check all the possible Enigma machine set-ups until the code was cracked. The British machines, over two metres tall and equally wide, employed electromechanical relays to check all the potential Enigma settings. The constant ticking of the relays led to them being nicknamed bombes. Despite their speed it was impossible for the bombes to check every one of the 150 million million million possible Enigma settings within a reasonable amount of time, and so Turing’s team had to find ways to significantly reduce the number of permutations by gleaning whatever information they could from the sent messages.
One of the greatest breakthroughs made by the British was the realisation that the Enigma machine could never encode a letter into itself, i.e. if the sender tapped ‘R’ then the machine could potentially send out any letter, depending on the settings of the machine, apart from ‘R’. This apparently innocuous fact was all that was needed to drastically reduce the time required to decipher a message. The Germans fought back by limiting the length of the messages they sent. All messages inevitably contain clues for the team of code-breakers, and the longer the message, the more clues it contains. By limiting all messages to a maximum of 250 letters, the Germans hoped to compensate for the Enigma machine’s reluctance to encode a letter as itself.
In order to crack codes Turing would often try to guess keywords in messages. If he was right it would speed up enormously the cracking of the rest of the code. For example, if the code-breakers suspected that a message contained a weather report, a frequent type of coded report, then they would guess that the message contained words such as ‘fog’ or ‘windspeed’. If they were right they could quickly crack that message, and thereby deduce the Enigma settings for that day. For the rest of the day, other, more valuable, messages could be broken with ease.
When they failed to guess weather words, the British would try and put themselves in the position of the German Enigma operators to guess other keywords. A sloppy operator might address the receiver by a first name or he might have developed idiosyncrasies which were known to the code-breakers. When all else failed and German traffic was flowing unchecked, it is said that the British Cypher School even resorted to asking the RAF to mine a particular German harbour. Immediately the German harbour-master would send an encrypted message which would be intercepted by the British. The code-breakers could be confident that the message contained words like ‘mine’, ‘avoid’ and ‘map reference’. Having cracked this message, Turing would have that day’s Enigma settings and any further German traffic was vulnerable to rapid decipherment.
On 1 February 1942 the Germans added a fourth wheel to Enigma machines which were employed for sending particularly sensitive information. This was the greatest escalation in the level of encryption during the war, but eventually Turing’s team fought back by increasing the efficiency of the bombes. Thanks to the Cypher School, the Allies knew more about their enemy than the Germans could ever have suspected. The impact of German U-boats in the Atlantic was greatly reduced and the British had advanced warning of attacks by the Luftwaffe. The code-breakers also intercepted and deciphered the exact position of German supply ships, allowing British destroyers to be sent out to sink them.
At all times the Allied forces had to take care that their evasive actions and uncanny attacks did not betray their ability to decipher German communications. If the Germans suspected that Enigma had been broken then they would increase their level of encryption, and the British might be back to square one. Hence there were occasions when the Cypher School informed the Allies of an imminent attack, and the Allies chose not to take extreme countermeasures. There are even rumours that Churchill knew that Coventry was to be targeted for a devastating raid, yet he chose not to take special precautions in case the Germans became suspicious. Stuart Milner-Barry who worked with Turing denies the rumour, and states that the relevant message concerning Coventry was not cracked until it was too late.
The restrained use of decoded information worked perfectly. Even when the British used intercepted communications to inflict heavy losses, the Germans did not suspect that the Enigma code had been broken. They believed that their level of encryption was so high that it would be absolutely impossible to crack their codes. Instead they blamed any exceptional losses on the British secret service infiltrating their own ranks.
Because of the secrecy surrounding the work carried out at Bletchley by Turing and his team, their immense contribution to the war effort could never be publicly acknowledged, even for many years after the war. It used to be said that the First World War was the chemists’ war and that the Second World War was the physicists’ war. In fact, from the information revealed in recent decades, it is probably true to say that the Second World War was also the mathematicians’ war – and in the case of a third world war their contribution would be even more critical.
Throughout his code-breaking career Turing never lost sight of his mathematical goals. The hypothetical machines had been replaced with real ones, but the esoteric questions remained. By the end of the war Turing had helped build Colossus, a fully electronic machine consisting of 1500 valves, which were much faster than the electromechanical relays employed in the bombes. Colossus was a computer in the modern sense of the word, and with the extra speed and sophistication Turing began to think of it as a primitive brain – it had a memory, it could process information, and states within the computer resembled states of mind. Turing had transformed his imaginary machine into the first real computer.
When the war ended Turing continued to build increasingly complex machines, such as the Automatic Computing Engine (ACE). In 1948 he moved to Manchester University and built the world’s first computer to have an electronically stored program. Turing had provided Britain with the most advanced computers in the world, but he would not live long enough to see their most remarkable calculations.
In the years after the war Turing had been under surveillance from British Intelligence, who were aware that he was a practising homosexual. They were concerned that the man who knew more about Britain’s security codes than anyone else was vulnerable to blackmail and decided to monitor his every move. Turing had largely come to terms with being constantly shadowed, but in 1952 he was arrested for violation of British homosexuality statutes. This humiliation made life intolerable for Turing. Andrew Hodges, Turing’s biographer, describes the events leading up to his death:
Alan Turing’s death came as a shock to those who knew him … That he was an unhappy, tense, person; that he was consulting a psychiatrist and suffered a blow that would have felled many people – all this was clear. But the trial was two years in the past, the hormone treatment had ended a year before, and he seemed to have risen above it all.
The inquest, on 10 June 1954, established that it was suicide. He had been found lying neatly in his bed. There was froth round his mouth, and the pathologist who did the post-mortem easily identified the cause of death as cyanide poisoning … In the house was a jar of potassium cyanide, and also a jar of cyanide solution. By the side of his bed was half an apple, out of which several bites had been taken. They did not analyse the apple, and so it was never properly established that, as seemed perfectly obvious, the apple had been dipped in the cyanide.
Turing’s legacy was a machine which could take an unpractically long calculation, if performed by a human, and complete it in a matter of hours. Today’s computers perform more calculations in a split second than Fermat performed in his entire career. Mathematicians who were still struggling with Fermat’s Last Theorem began to use computers to attack the problem, relying on a computerised version of Kummer’s nineteenth-century approach.
Kummer, having discovered a flaw in the work of Cauchy and Lamé, showed that the outstanding problem in proving Fermat’s Last Theorem was disposing of the cases when n equals an irregular prime – for values of n up to 100 the only irregular primes are 37, 59 and 67. At the same time Kummer showed that in theory all irregular primes could be dealt with on an individual basis, the only problem being that each one would require an enormous amount of calculation. To make his point Kummer and his colleague Dimitri Mirimanoff put in the weeks of calculation required to dispel the three irregular primes less than 100. However, they and other mathematicians were not prepared to begin on the next batch of irregular primes between 100 and 1,000.
A few decades later the problems of immense calculation began to vanish. With the arrival of the computer awkward cases of Fermat’s Last Theorem could be dispatched with speed, and after the Second World War teams of computer scientists and mathematicians proved Fermat’s Last Theorem for all values of n up to 500, then 1,000, and then 10,000. In the 1980s Samuel S. Wagstaff of the University of Illinois raised the limit to 25,000 and more recently mathematicians could claim that Fermat’s Last Theorem was true for all values of n up to 4 million.
Although outsiders felt that modern technology was at last getting the better of the Last Theorem, the mathematical community were aware that their success was purely cosmetic. Even if supercomputers spent decades proving one value of n after another they could never prove every value of n up to infinity, and therefore they could never claim to prove the entire theorem. Even if the theorem was to be proved true for up to a billion, there is no reason why it should be true for a billion and one. If the theorem was to be proved up to a trillion, there is no reason why it should be true for a trillion and one, and so on ad infinitum. Infinity is unobtainable by the mere brute force of computerised number crunching.
David Lodge in his book The Picturegoers gives a beautiful description of eternity which is also relevant to the parallel concept of infinity: ‘Think of a ball of steel as large as the world, and a fly alighting on it once every million years. When the ball of steel is rubbed away by the friction, eternity will not even have begun.’
All that computers could offer was evidence in favour of Fermat’s Last Theorem. To the casual observer the evidence might seem to be overwhelming, but no amount of evidence is enough to satisfy mathematicians, a community of sceptics who will accept nothing other than absolute proof. Extrapolating a theory to cover an infinity of numbers based on evidence from a few numbers is a risky (and unacceptable) gamble.
One particular sequence of primes shows that extrapolation is a dangerous crutch upon which to rely. In the seventeenth century mathematicians showed by detailed examination that the following numbers are all prime:
31; 331; 3,331; 33,331; 333,331; 3,333,331; 33,333,331.
The next numbers in the sequence become increasingly giant, and checking whether or not they are also prime would have taken considerable effort. At the time some mathematicians were tempted to extrapolate from the pattern so far, and assume that all numbers of this form are prime. However, the next number in the pattern, 333,333,331, turned out not to be a prime:
![]()
Another good example which demonstrates why mathematicians refused to be persuaded by the evidence of computers is the case of Euler’s conjecture. Euler claimed that there were no solutions to an equation not dissimilar to Fermat’s equation:
![]()
For two hundred years nobody could prove Euler’s conjecture, but on the other hand nobody could disprove it by finding a counterexample. First manual searches and then years of computer sifting failed to find a solution. Lack of a counter-example was strong evidence in favour of the conjecture. Then in 1988 Naom Elkies of Harvard University discovered the following solution:
![]()
Despite all the evidence Euler’s conjecture turned out to be false. In fact Elkies proved that there were infinitely many solutions to the equation. The moral is that you cannot use evidence from the first million numbers to prove a conjecture about all numbers.
But the deceptive nature of Euler’s conjecture is nothing compared to the overestimated prime conjecture. By scouring through larger and larger regimes of numbers, it becomes clear that the prime numbers become harder and harder to find. For instance, between 0 and 100 there are 25 primes but between 10,000,000 and 10,000,100 there are only 2 prime numbers. In 1791, when he was just fourteen years old, Carl Gauss predicted the approximate manner in which the frequency of prime numbers among all the other numbers would diminish. The formula was reasonably accurate but always seemed slightly to overestimate the true distribution of primes. Testing for primes up to a million, a billion or a trillion would always show that Gauss’s formula was marginally too generous and mathematicians were strongly tempted to believe that this would hold true for all numbers up to infinity, and thus was born the overestimated prime conjecture.
Then, in 1914, J.E. Littlewood, G.H. Hardy’s collaborator at Cambridge, proved that in a sufficiently large regime Gauss’s formula would underestimate the number of primes. In 1955 S. Skewes showed that the underestimate would occur sometime before reaching the number
![]()
This is a number beyond the imagination, and beyond any practical application. Hardy called Skewes’s number ‘the largest number which has ever served any definite purpose in mathematics’. He calculated that if one played chess with all the particles in the universe (1087), where a move meant simply interchanging any two particles, then the number of possible games was roughly Skewes’s number.
There was no reason why Fermat’s Last Theorem should not turn out to be as cruel and deceptive as Euler’s conjecture or the overestimated prime conjecture.
In 1975 Andrew Wiles began his career as a graduate student at Cambridge University. Over the next three years he was to work on his Ph.D. thesis and in that way serve his mathematical apprenticeship. Each student was guided and nurtured by a supervisor and in Wiles’s case that was the Australian John Coates, a professor at Emmanuel College, originally from Possum Brush, New South Wales.
Coates still recalls how he adopted Wiles: ‘I remember a colleague told me that he had a very good student who was just finishing part III of the mathematical tripos, and he urged me to take him as a student. I was very fortunate to have Andrew as a student. Even as a research student he had very deep ideas and it was always clear that he was a mathematician who would do great things. Of course, at that stage there was no question of any research student starting work directly on Fermat’s Last Theorem. It was too difficult even for a thoroughly experienced mathematician.’
For the past decade everything Wiles had done was directed towards preparing himself to meet Fermat’s challenge, but now that he had joined the ranks of the professional mathematicians he had to be more pragmatic. He remembers how he had to temporarily surrender his dream: ‘When I went to Cambridge I really put aside Fermat. It’s not that I forgot about it – it was always there – but I realised that the only techniques we had to tackle it had been around for 130 years. It didn’t seem that these techniques were really getting to the root of the problem. The problem with working on Fermat was that you could spend years getting nowhere. It’s fine to work on any problem, so long as it generates interesting mathematics along the way – even if you don’t solve it at the end of the day. The definition of a good mathematical problem is the mathematics it generates rather than the problem itself.’
It was John Coates’s responsibility to find Andrew a new obsession, something which would occupy his research for at least the next three years. ‘I think all a research supervisor can do for a student is try and push him in a fruitful direction. Of course, it’s impossible to be sure what is a fruitful direction in terms of research but perhaps one thing that an older mathematician can do is use his horse sense, his intuition of what is a good area, and then it’s really up to the student as to how far he can go in that direction.’ In the end Coates decided that Wiles should study an area of mathematics known as elliptic curves. This decision would eventually prove to be a turning point in Wiles’s career and give him the techniques he would require for a new approach to tackling Fermat’s Last Theorem.
The name ‘elliptic curves’ is somewhat misleading for they are neither ellipses nor even curved in the normal sense of the word. Rather they are any equations which have the form
![]()
They got their name because in the past they were used to measure the perimeters of ellipses and the lengths of planetary orbits, but for clarity I will simply refer to them as elliptic equations rather than elliptic curves.
The challenge with elliptic equations, as with Fermat’s Last Theorem, is to figure out if they have whole number solutions, and, if so, how many. For example, the elliptic equation
![]()
has only one set of whole number solutions, namely
![]()
Proving that this elliptic equation has only one set of whole number solutions is an immensely difficult task, and in fact it was Pierre de Fermat who discovered the proof. You might remember that in Chapter 2 it was Fermat who proved that 26 is the only number in the universe sandwiched between a square and a cube number. This is equivalent to showing that the above elliptic equation has only one solution, i.e. 52 and 33 are the only square and cube that differ by 2, and therefore 26 is the only number that can be sandwiched between two such numbers.
What makes elliptic equations particularly fascinating is that they occupy a curious niche between other simpler equations which are almost trivial and other more complicated equations which are impossible to solve. By simply changing the values of a, b and c in the general elliptic equation mathematicians can generate an infinite variety of equations, each one with its own characteristics, but all of them just within the realm of solubility.
Elliptic equations were originally studied by the ancient Greek mathematicians, including Diophantus who devoted large parts of his Arithmetica to exploring their properties. Probably inspired by Diophantus, Fermat also took up the challenge of elliptic equations, and, because they had been studied by his hero, Wiles was happy to explore them further. Even after two thousand years elliptic equations still offered formidable problems for students such as Wiles: ‘They are very far from being completely understood. There are many apparently simple questions I could pose on elliptic equations that are still unresolved. Even questions that Fermat himself considered are still unresolved. In some way all the mathematics that I’ve done can trace its ancestry to Fermat, if not Fermat’s Last Theorem.’
In the equations which Wiles studied as a graduate student, determining the exact number of solutions was so difficult that the only way to make any progress was to simplify the problem. For example, the following elliptic equation is almost impossible to tackle directly:
![]()
The challenge is to figure out how many whole number solutions there are to the equation. One fairly trivial solution is x = 0 and y = 0:
![]()
A slightly more interesting solution is x = 1 and y = 0:
![]()
There may be other solutions but, with an infinite quantity of whole numbers to investigate, giving a complete list of solutions to this particular equation is an impossible task. A simpler task is to look for solutions within a finite number space, so-called clock arithmetic.
Earlier we saw how numbers can be thought of as marks along the number line which extends to infinity, as shown in Figure 13. To make the number space finite, clock arithmetic involves truncating the line and looping it back on itself to form a number ring as opposed to a number line. Figure 14 shows a 5-clock, where the number line has been truncated at 5 and looped back to 0. The number 5 vanishes and becomes equivalent to 0, and therefore the only numbers in 5-clock arithmetic are 0, 1, 2, 3, 4.

Figure 13. Conventional arithmetic can be thought of as movements up and down the number line.
In normal arithmetic we can think of addition as moving along the line a certain number of spaces. For example, 4 + 2 = 6 is the same as saying: begin at 4, and move along the number line 2 spaces, and arrive at 6.
However, in 5-clock arithmetic:
![]()
This is because if we start at 4 and move round 2 spaces then we arrive back at 1. Clock arithmetic might appear unfamiliar but in fact, as the name suggests, it is used every day when people discuss the time. Four hours after 11 o’clock (that is to say, 11 = 4) is generally not called 15 o’clock, but rather 3 o’clock. This is 12-clock arithmetic.
As well as addition we can perform all the other common mathematical operations, such as multiplication. In 12-clock arithmetic 5 × 7 = 11. This multiplication can be thought of as follows: if you start at 0, then move along 5 lots of 7 spaces, you will eventually arrive at 11. Although this is one way of thinking about multiplication in clock arithmetic, there are short cuts which speed up calculations. For example, to calculate 5 × 7 in 12-clock arithmetic, we can begin by just working out the normal result which is 35. We then divide 35 by 12 and work out the remainder, which is the answer to the original question. So 12 goes into 35 only twice, with a remainder of 11, and sure enough 5 × 7 in 12-clock arithmetic is 11. This is equivalent to imagining going around the clock twice and still having 11 spaces to travel.
Because clock arithmetics only deal with a limited number space, it is relatively easy to work out all the possible solutions to an elliptic equation for a given clock arithmetic. For example, working in 5-clock arithmetic it is possible to list all the possible solutions to the elliptic equation
![]()

Figure 14. In 5-clock arithmetic the number line is truncated at 5 and looped back on itself. The number 5 coincides with 0, and therefore is replaced by it.

Although some of these solutions would not be valid in normal arithmetic, in 5-clock arithmetic they are acceptable. For example, the fourth solution (x = 1, y = 4) works as follows:

But remember, 20 is equivalent to 0 in 5-clock arithmetic, because 5 will divide into 20 with a remainder of 0.
Because they could not list all the solutions to an elliptic equation working in infinite space, mathematicians, including Wiles, settled for working out the number of solutions in all the different clock arithmetics. For the elliptic equation given above the number of solutions in 5-clock arithmetic is four, and so mathematicians say E5 = 4. The number of solutions in other clock arithmetics can also be calculated. For example, in 7-clock arithmetic the number of solutions is nine, and so E7 = 9.
To summarise their results, mathematicians list the number of solutions in each clock arithmetic and call this list the L-series for the elliptic equation. What the L stands for has been long forgotten although some have suggested that it is the L of Gustav Lejeune-Dirichlet, who worked on elliptic equations. For clarity I will use the term E-series – the series that is derived from an elliptic equation. For the example given above the E-series is as follows:

Because mathematicians cannot say how many solutions some elliptic equations have in normal number space which extends up to infinity, the E-series appears to be next best thing. In fact the E-series encapsulates a great deal of information about the elliptic equation it describes. In the same way that biological DNA carries all the information required to construct a living organism, the E-series carries the essence of the elliptic equation. The hope was that by studying the E-series, this mathematical DNA, mathematicians would ultimately be able to calculate everything they could ever wish to know about an elliptic equation.
Working alongside John Coates, Wiles rapidly established his reputation as a brilliant number theorist with a profound understanding of elliptic equations and their E-series. As each new result was achieved and each paper published, Wiles did not realise that he was gathering the experience which would many years later bring him to the verge of a proof for Fermat’s Last Theorem.
Although nobody was aware of it at the time, the mathematicians of post-war Japan had already triggered a chain of events which would inextricably link elliptic equations to Fermat’s Last Theorem. By encouraging Wiles to study elliptic equations, Coates had given him the tools which would later enable him to work on his dream.