
The mathematician’s patterns, like the painter’s or the poet’s, must be beautiful; the ideas, like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in the world for ugly mathematics.
G.H. Hardy
In the January of 1954 a talented young mathematician at the University of Tokyo paid a routine visit to his departmental library. Goro Shimura was in search of a copy of Mathematische Annalen, Vol. 24. In particular he was after a paper by Deuring on his algebraic theory of complex multiplication, which he needed in order to help him with a particularly awkward and esoteric calculation.
To his surprise and dismay, the volume was already out. The borrower was Yutaka Taniyama, a vague acquaintance of Shimura who lived on the other side of the campus. Shimura wrote to Taniyama explaining that he urgently needed the journal to complete the nasty calculation, and politely asked when it would be returned.
A few days later, a postcard landed on Shimura’s desk. Taniyama had replied, saying that he too was working on the exact same calculation and was stuck at the same point in the logic. He suggested that they share their ideas and perhaps collaborate on the problem. This chance encounter over a library book ignited a partnership which would change the course of mathematical history.
Taniyama was born on 12 November 1927 in a small town a few miles north of Tokyo. The Japanese character symbolising his first name was intended to read ‘Toyo’, but most people outside his family misinterpreted it as ‘Yutaka’, and as Taniyama grew up he accepted and adopted this title. As a child Taniyama’s education was constantly interrupted. He suffered several bouts of ill health, and during his teenage years he was struck down by tuberculosis and had to miss two years of high school. The onset of war caused even greater disruption to his schooling.
Goro Shimura, one year younger than Taniyama, had his education stopped altogether during the war years. His school was shut down and, instead of attending lessons, Shimura had to help the war effort by working in a factory assembling aircraft parts. Each evening he would attempt to make up for his lost schooling and in particular found himself drawn to mathematics. ‘Of course there are many subjects to learn, but mathematics was the easiest because I could simply read mathematical textbooks. I learnt calculus by reading books. If I’d wanted to pursue chemistry or physics then I would have needed scientific equipment and I had no access to such things. I never thought that I was talented. I was just curious.’
A few years after the war had finished, Shimura and Taniyama found themselves at university. By the time they had exchanged postcards over the library book, life in Tokyo was beginning to return to normal and the two young academics could afford one or two small luxuries. They spent their afternoons in the coffee-shops, in the evenings they dined in a little restaurant specialising in whale meat, and at weekends they would stroll through the botanical gardens or the city park. All ideal locations for discussing their latest mathematical thoughts.
Although Shimura had a whimsical streak – even today he retains his fondness for Zen jokes – he was far more conservative and conventional than his intellectual partner. Shimura would rise at dawn and immediately get down to work, whereas his colleague would often still be awake at this time, having worked through the night. Visitors to his apartment would often find Taniyama fast asleep in the middle of the afternoon.
While Shimura was fastidious, Taniyama was sloppy to the point of laziness. Surprisingly this was a trait that Shimura admired: ‘He was gifted with the special capability of making many mistakes, mostly in the right direction. I envied him for this and tried in vain to imitate him, but found it quite difficult to make good mistakes.’
Taniyama was the epitome of the absent-minded genius and this was reflected in his appearance. He was incapable of tying a decent knot, and so he decided that rather than tie his shoelaces a dozen times a day he would not tie them at all. He would always wear the same peculiar green suit with a strange metallic sheen. It was made from a fabric which was so outrageous that it had been rejected by the other members of his family.
When they met in 1954 Taniyama and Shimura were just beginning their mathematical careers. The tradition was, and still is, for young researchers to be taken under the wing of a professor who would guide the fledgling brain, but Taniyama and Shimura rejected this form of apprenticeship. During the war real research had ground to a halt and even by the 1950s the mathematics faculty had still not recovered. According to Shimura, the professors were ‘tired, jaded and disillusioned’. In comparison the post-war students were passionate and eager to learn, and they soon realised that the only way forward would be for them to teach themselves. The students organised regular seminars, taking it in turn to inform each other of the latest techniques and breakthroughs. Despite his otherwise lackadaisical attitude, when it came to the seminars Taniyama provided a ferocious driving force. He would encourage the more senior students to explore uncharted territory, and for the younger students he acted as a father figure.
Because of their isolation, the seminars would occasionally cover subjects which were generally considered passe in Europe and America. The students’ naïvety meant that they studied equations which had been abandoned in the West. One particularly unfashionable topic which fascinated both Taniyama and Shimura was the study of modular forms.
Modular forms are some of the weirdest and most wonderful objects in mathematics. They are one of the most esoteric entities in mathematics and yet the twentieth-century number theorist Martin Eichler rated them as one of the five fundamental operations: addition, subtraction, multiplication, division and modular forms. Most mathematicians would consider themselves masters of the first four operations, but the fifth one they still find a little confusing.
The key feature of modular forms is their inordinate level of symmetry. Although most people are familiar with the everyday concept of symmetry, it has a very particular meaning in mathematics, which is that an object has symmetry if it can be transformed in a particular way and yet afterwards appear to be unchanged. To appreciate the immense symmetry of a modular form it helps to first examine the symmetry of a more mundane object such as a simple square.

Figure 15. A simple square exhibits both rotational and reflectional symmetry.
In the case of a square, one form of symmetry is rotational. That is to say, if we imagine a pivot at the point where the x-axis and y-axis cross, then the square in Figure 15 can be rotated by one quarter of a turn, and afterwards it will appear to be unchanged. Similarly, rotations by half a turn, three-quarters of a turn and one full turn will also leave the square apparently unchanged.
In addition to rotational symmetry the square also possesses reflectional symmetry. If we imagine a mirror placed along the x-axis then the top half of the square would reflect exactly onto the lower half, and vice versa, so after the transformation the square would appear to remain unchanged. Similarly we can define three other mirrors (along the y-axis and along the two diagonals) for which the reflected square would appear to be identical to the original one.
The simple square is relatively symmetric, possessing both rotational and reflectional symmetries, but it does not possess any translational symmetry. This means that if the square were to be shifted in any direction, an observer would spot the movement immediately because its position relative to the axes would have changed. However, if the whole of the space were tiled with squares, as shown in Figure 16, this infinite collection of squares would then have translational symmetry. If the infinite tiled surface were to be shifted up or down by one or more tile spaces, then the translated tiling would appear to be identical to the original one.

Figure 16. An infinite surface tiled with squares exhibits rotational and reflectional symmetry, and in addition has translational symmetry.
The symmetry of tiled surfaces is a relatively straightforward idea, but as with many seemingly simple concepts there are many subtleties hidden within it. For example, in the 1970s the British physicist and recreational mathematician Roger Penrose began dabbling with different tiles on the same surface. Eventually he identified two particularly interesting shapes, called the kite and the dart, which are shown in Figure 17. On their own, there is only one way these shapes can be used to tile a surface without gaps or overlaps, but together they could be used to create a rich set of tiling patterns. The kites and darts can be fitted together in an infinite number of ways, and although each pattern is apparently similar, in detail they all vary. One pattern made from kites and darts is shown in Figure 17.

Figure 17. By using two different tiles, the kite and the dart, Roger Penrose was able to cover a surface. However, Penrose tiling does not possess translational symmetry.
Another remarkable feature of Penrose tilings (the patterns generated by tiles such as the kite and dart) is that they can exhibit a very restricted level of symmetry. At first sight it would appear that the tiling shown in Figure 17 would have translational symmetry, and yet any attempt to shift the pattern across so that it effectively remains unchanged ends in failure. Penrose tilings are deceptively unsymmetrical, and this is why they fascinate mathematicians and have become the starting point for a whole new area of mathematics.
Curiously Penrose tiling has also had repercussions in material science. Crystallographers always believed that crystals had to be built on the principles behind square tiling, possessing a high level of translational symmetry. In theory building crystals relied on a highly regular and repetitive structure. However, in 1984 scientists discovered a metallic crystal made of aluminium and manganese which was built along Penrose principles. The mosaic of aluminium and manganese behaved like the kites and darts, generating a crystal which was almost regular, but not quite. A French company has recently developed a Penrose crystal into a coating for frying-pans.
While the fascinating thing about Penrose’s tiled surfaces is their restricted symmetry, the interesting property of modular forms is that they exhibit infinite symmetry. The modular forms studied by Taniyama and Shimura can be shifted, switched, swapped, reflected and rotated in an infinite number of ways and still they remain unchanged, making them the most symmetrical of mathematical objects. When the French polymath Henri Poincaré studied modular forms in the nineteenth century, he had great difficulty coming to terms with their immense symmetry. After working on a particular type of modular form, he described to his colleagues how every day for two weeks he would wake up and try and find an error in his calculations. On the fifteenth day he realised and accepted that modular forms were indeed symmetrical in the extreme.
Unfortunately, drawing, or even imagining, a modular form is impossible. In the case of the square tiling we have an object which lives in two dimensions, its space being defined by the x-axis and the y-axis. A modular form is also defined by two axes, but the axes are both complex, i.e. each axis has a real and an imaginary part and effectively becomes two axes. Therefore the first complex axis must be represented by two axes, xr-axis (real) and xi-axis (imaginary), and the second complex axis is represented by two axes, yr-axis (real) and yi-axis (imaginary). To be precise, modular forms live in the upper half-plane of this complex space, but what is most important to appreciate is that this is a four-dimensional space (xr, xi, yr, yi).
This four-dimensional space is called hyperbolic space. The hyperbolic universe is tricky to comprehend for humans, who are constrained to living in a conventional three-dimensional world, but four-dimensional space is a mathematically valid concept, and it is this extra dimension which gives the modular forms such an immensely high level of symmetry. The artist Mauritz Escher was fascinated by mathematical ideas and attempted to convey the concept of hyperbolic space in some of his etchings and paintings. Escher’s Circle Limit IV embeds the hyperbolic world into the two-dimensional page. In true hyperbolic space the devils and angels would be the same size, and the repetition is indicative of the high level of symmetry. Although some of this symmetry can be seen on the two-dimensional page, there is an increasing distortion towards the edge of the picture.
The modular forms which live in hyperbolic space come in various shapes and sizes, but each one is built from the same basic ingredients. What differentiates each modular form is the amount of each ingredient it contains. The ingredients of a modular form are labelled from one to infinity (M1, M2, M3, M4, …) and so a particular modular form might contain one lot of ingredient one (M1 = 1), three lots of ingredient two (M2 = 3), two lots of ingredient three (M3 = 2), etc. This information describing how a modular form is constructed can be summarised in a so-called modular series, or M-series, a list of the ingredients and the quantity of each one required:
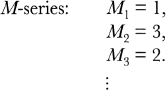
Just as the E-series is the DNA for elliptic equations, the M-series is the DNA for modular forms. The amount of each ingredient listed in the M-series is critical. Depending how you change the amount of, say, the first ingredient you might generate a completely different, but equally symmetrical, modular form, or you might destroy the symmetry altogether and generate a new object which is not a modular form. If the quantity of each ingredient is arbitrarily chosen, then the result will probably be an object with little or no symmetry.
Modular forms stand very much on their own within mathematics. In particular, they would seem to be completely unrelated to the subject that Wiles would study at Cambridge, elliptic equations. The modular form is an enormously complicated beast, studied largely because of its symmetry and only discovered in the nineteenth century. The elliptic equation dates back to the ancient Greeks and has nothing to do with symmetry. Modular forms and elliptic equations live in completely different regions of the mathematical cosmos, and nobody would ever have believed that there was the remotest link between the two subjects. However, Taniyama and Shimura were to shock the mathematical community by suggesting that elliptic equations and modular forms were effectively one and the same thing. According to these two maverick mathematicians, they could unify the modular and elliptic worlds.
In September 1955 an international symposium was held in Tokyo. It was a unique opportunity for the many young Japanese researchers to show off to the rest of the world what they had learned. They handed round a collection of thirty-six problems related to their work, accompanied by a humble introduction – Some unsolved problems in mathematics: no mature preparation has been made, so there may be some trivial or already solved ones among these. The participants are requested to give comments on any of these problems.
Four of the questions were from Taniyama, and these hinted at a curious relationship between modular forms and elliptic equations. These innocent questions would ultimately lead to a revolution in number theory. Taniyama had looked at the first few terms in the M-series of a particular modular form. He recognised the pattern and realised that it was identical to the list of numbers in the E-series of a well-known elliptic equation. He calculated a few more terms in each series, and still the M-series of the modular form and E-series of the elliptic equation matched perfectly.
This was an astonishing discovery because, for no apparent reason, this modular form could be related to an elliptic equation through their respective M-series and E-series – these series were identical. The mathematical DNA which made up these two entities was exactly the same. This was a doubly profound discovery. First, it suggested that deep down there was a fundamental relationship between the modular form and the elliptic equation, objects which come from opposite ends of mathematics. Second, it meant that mathematicians, who already knew the M-series for the modular form, would not have to calculate the E-series for the corresponding elliptic equation because it would be the same as the M-series.
Relationships between apparently different subjects are as creatively important in mathematics as they are in any discipline. The relationship hints at some underlying truth which enriches both subjects. For instance, originally scientists had studied electricity and magnetism as two completely separate phenomena. Then, in the nineteenth century, theorists and experimentalists realised that electricity and magnetism were intimately related. This resulted in a deeper understanding of both of them. Electric currents generate magnetic fields, and magnets can induce electricity in wires passing close to them. This led to the invention of dynamos and electric motors, and ultimately the discovery that light itself is the result of magnetic and electric fields oscillating in harmony.
Taniyama examined a few other modular forms and in each case the M-series seemed to correspond perfectly with the E-series of an elliptic equation. He began to wonder if it could be that every single modular form could be matched with an elliptic equation. Perhaps every modular form has the same DNA as an elliptic equation: perhaps each modular form is an elliptic equation in disguise? The questions he handed out at the symposium were related to this hypothesis.
The idea that every elliptic equation was related to a modular form was so extraordinary that those who glanced at Taniyama’s questions treated them as nothing more than a curious observation. Sure enough Taniyama had demonstrated that a few elliptic equations could be related to particular modular forms, but they claimed that this was nothing more than a coincidence. According to the sceptics Taniyama’s claim of a more general and universal relationship seemed to be largely unsubstantiated. The hypothesis was based on intuition rather than on any real evidence.
Taniyama’s only ally was Shimura, who believed in the power and depth of his friend’s idea. Following the symposium he worked with Taniyama in an attempt to develop the hypothesis to a level where the rest of the world could no longer ignore their work. Shimura wanted to find more evidence to back up the relationship between the modular and elliptic worlds. The collaboration was temporarily halted when in 1957 Shimura was invited to attend the Institute for Advanced Study in Princeton. Following his two years as a visiting professor in America he intended to resume working with Taniyama, but this was never to happen. On 17 November 1958, Yutaka Taniyama committed suicide.
Shimura still keeps the postcard that Taniyama sent him when they first made contact over the library book. He also keeps the last letter Taniyama wrote to him while he was away in Princeton, but it contains not the merest hint as to what would happen just two months later. To this day Shimura has no understanding of what was behind Taniyama’s suicide. ‘I was very much puzzled. Puzzlement may be the best word. Of course I was sad, but it was so sudden. I got his letter in September and he died in early November, and I was unable to make sense out of this. Of course, later I heard various things and I tried to reconcile myself with his death. Some people said that he lost confidence in himself but not mathematically.’
What was particularly confusing for Taniyama’s friends was that he had just fallen in love with Misako Suzuki and planned to marry her later that year. In a personal tribute published in the Bulletin of the London Mathematical Society, Goro Shimura recollects Taniyama’s engagement to Misako and the weeks which led up to his suicide:
When informed of their engagement, I was somewhat surprised, since I had vaguely thought she was not his type, but I felt no misgivings. I was told afterward that they had signed a lease for an apartment, apparently a better one, for their new home, had bought some kitchenware together, and had been preparing for their wedding. Everything looked promising for them and their friends. Then the catastrophe befell them.
On the morning of Monday, November 17, 1958, the superintendent of his apartment found him dead in his room with a note left on a desk. It was written on three pages of a notebook of the type he had been using for his scholastic work; its first paragraph read like this:
‘Until yesterday, I had no definite intention of killing myself. But more than a few must have noticed that lately I have been tired both physically and mentally. As to the cause of my suicide, I don’t quite understand it myself, but it is not the result of a particular incident, nor of a specific matter. Merely may I say, I am in the frame of mind that I lost confidence in my future. There may be someone to whom my suicide will be troubling or a blow to a certain degree. I sincerely hope that this incident will cast no dark shadow over the future of that person. At any rate, I cannot deny that this is a kind of betrayal, but please excuse it as my last act in my own way, as I have been doing my own way all my life.’
He went on to describe, quite methodically, his wish of how his belongings should be disposed of, and which books and records were the ones he had borrowed from the library or from his friends, and so on. Specifically he says: ‘I would like to leave the records and the player to Misako Suzuki provided she will not be upset by me leaving them to her’. Also he explains how far he reached in the undergraduate courses on calculus and linear algebra he was teaching, and concludes the note with an apology to his colleagues for the inconveniences this act could cause.
Thus one of the most brilliant and pioneering minds of the time ended his life by his own will. He had attained the age of thirty-one only five days earlier.
A few weeks after the suicide, tragedy struck a second time. His fiancée, Misako Suzuki, also took her own life. She reportedly left a note which read: ‘We promised each other that no matter where we went, we would never be separated. Now that he is gone, I must go too in order to join him.’
During his short career Taniyama contributed many radical ideas to mathematics. The questions he handed out at the symposium contained his greatest insight, but it was so ahead of its time that he would never live to see its enormous influence on number theory. His intellectual creativity was to be sadly missed, along with his guiding role within the community of young Japanese scientists. Shimura clearly remembers Taniyama’s influence: ‘He was always kind to his colleagues, especially to his juniors, and he genuinely cared about their welfare. He was the moral support of many of those who came into mathematical contact with him, including of course myself. Probably he was never concious of this role he was playing. But I feel his noble generosity in this respect even more strongly now than when he was alive. And yet nobody was able to give him any support when he desperately needed it. Reflecting on this, I am overwhelmed by the bitterest grief.’
Following Taniyama’s death, Shimura concentrated all his efforts on understanding the exact relationship between elliptic equations and modular forms. As the years passed he struggled to gather more evidence and one or two pieces of logic to support the theory. Gradually he became increasingly convinced that every single elliptic equation must be related to a modular form. Other mathematicians were still dubious and Shimura recalls a conversation with an eminent colleague. The professor inquired, ‘I hear that you propose that some elliptic equations can be linked to modular forms.’
‘No, you don’t understand,’ replied Shimura. ‘It’s not just some elliptic equations, it’s every elliptic equation!’
Shimura could not prove that this was the case but every time he tested the hypothesis it seemed to be true, and in any case it all seemed to fit in with his broad mathematical philosophy. ‘I have this philosophy of goodness. Mathematics should contain goodness. So in the case of the elliptic equation, one might call the equation good if it is parametrised by a modular form. I expect all elliptic equations to be good. It’s a rather crude philosophy but one can always take it as a starting point. Then, of course, I had to develop various technical reasons for the conjecture. I might say that the conjecture stemmed from that philosophy of goodness. Most mathematicians do mathematics from an aesthetic point of view and that philosophy of goodness comes from my aesthetic viewpoint.’
Eventually Shimura’s accumulation of evidence meant that his theory about elliptic equations and modular forms became more widely accepted. He could not prove to the rest of the world that it was true, but at least it was now more than mere wishful thinking. There was enough evidence for it to be worthy of the title of conjecture. Initially it was referred to as the Taniyama–Shimura conjecture in recognition of the man who inspired it and his colleague who went on to develop it fully.
In due course André Weil, one of the godfathers of twentieth-century number theory, was to adopt the conjecture and publicise it in the West. Weil investigated the idea of Shimura and Taniyama, and found even more solid evidence in favour of it. As a result, the hypothesis was often referred to as the Taniyama–Shimura–Weil conjecture, sometimes as the Taniyama–Weil conjecture and occasionally as the Weil conjecture. In fact there has been much debate and controversy over the official naming of the conjecture. For those of you interested in combinatorics there are 15 possible permutations given the three names involved, and it is quite probable that every one of those combinations has appeared in print over the years. However, I will refer to the conjecture by its original title, the Taniyama–Shimura conjecture.
Professor John Coates, who guided Andrew Wiles when he was a student, was himself a student when the Taniyama–Shimura conjecture became a talking point in the West. ‘I began research in 1966 when the conjecture of Taniyama and Shimura was sweeping through the world. Everyone was amazed and began to look seriously at the issue of whether all elliptic equations could be modular. This was a tremendously exciting time; the only problem, of course, was that it seemed very hard to make progress. I think it’s fair to say that beautiful though this idea was it seemed very difficult to actually prove, and that’s what we’re primarily interested in as mathematicians.’
During the late sixties hoards of mathematicians repeatedly tested the Taniyama–Shimura conjecture. Starting with an elliptic equation and its E-series they would search for a modular form with an identical M-series. In every single case the elliptic equation did indeed have an associated modular form. Although this was good evidence in favour of the Taniyama–Shimura conjecture, it was by no means a proof. Mathematicians suspected that it was true, but until somebody could find a logical proof it would remain merely a conjecture.
Barry Mazur, a professor at Harvard University, witnessed the rise of the Taniyama–Shimura conjecture. ‘It was a wonderful conjecture – the surmise that every elliptic equation is associated with a modular form – but to begin with it was ignored because it was so ahead of its time. When it was first proposed it was not taken up because it was so astounding. On the one hand you have the elliptic world, and on the other you have the modular world. Both these branches of mathematics had been studied intensively but separately. Mathematicians studying elliptic equations might not be well versed in things modular, and conversely. Then along comes the Taniyama–Shimura conjecture which is the grand surmise that there’s a bridge between these two completely different worlds. Mathematicians love to build bridges.’
The value of mathematical bridges is enormous. They enable communities of mathematicians who have been living on separate islands to exchange ideas and explore each other’s creations. Mathematics consists of islands of knowledge in a sea of ignorance. For example, there is the island occupied by geometers who study shape and form, and then there is the island of probability where mathematicians discuss risk and chance. There are dozens of such islands, each one with its own unique language, incomprehensible to the inhabitants of other islands. The language of geometry is quite different to the language of probability, and the slang of calculus is meaningless to those who speak only statistics.
The great potential of the Taniyama–Shimura conjecture was that it would connect two islands and allow them to speak to each other for the first time. Barry Mazur thinks of the Taniyama–Shimura conjecture as a translating device similar to the Rosetta stone, which contained Egyptian demotic, ancient Greek and hieroglyphics. Because demotic and Greek were already understood, archaeologists could decipher hieroglyphics for the first time. ‘It’s as if you know one language and this Rosetta stone is going to give you an intense understanding of the other language,’ says Mazur. ‘But the Taniyama–Shimura conjecture is a Rosetta stone with a certain magical power. The conjecture has the very pleasant feature that simple intuitions in the modular world translate into deep truths in the elliptic world, and conversely. What’s more, very profound problems in the elliptic world can get solved sometimes by translating them using this Rosetta stone into the modular world, and discovering that we have the insights and tools in the modular world to treat the translated problem. Back in the elliptic world we would have been at a loss.’
If the Taniyama–Shimura conjecture was true it would enable mathematicians to tackle elliptic problems which had remained unsolved for centuries by approaching them through the modular world. The hope was that the fields of elliptic equations and modular forms could be unified. The conjecture also inspired the hope that links might exist between various other mathematical subjects.
During the 1960s Robert Langlands, at the Institute for Advanced Study, Princeton, was struck by the potency of the Taniyama–Shimura conjecture. Even though the conjecture had not been proved, Langlands believed that it was just one element of a much grander scheme of unification. He was confident that there were links between all the main mathematical topics and began to look for these unifications. Within a few years a number of links began to emerge. All these other unification conjectures were much weaker and more speculative than Taniyama–Shimura, but they formed an intricate network of hypothetical connections between many areas of mathematics. Langlands’s dream was to see each of these conjectures proved one by one, leading to a grand unified mathematics.
Langlands discussed his plan for the future and tried to persuade other mathematicians to take part in what became known as the Langlands programme, a concerted effort to prove his myriad of conjectures. There seemed to be no obvious way to prove such speculative links, but if the dream could be made a reality then the reward would be enormous. Any insoluble problem in one area of mathematics could be transformed into an analogous problem in another area, where a whole new arsenal of techniques could be brought to bear on it. If a solution was still elusive, the problem could be transformed and transported to yet another area of mathematics, and so on, until it was solved. One day, according to the Langlands programme, mathematicians would be able to solve their most esoteric and intractable problems by shuffling them around the mathematical landscape.
There were also important implications for the applied sciences and engineering. Whether it is modelling the interactions between colliding quarks or discovering the most efficient way to organise a telecommunications network, often the key to the problem is performing a mathematical calculation. In some areas of science and technology the complexity of the calculations is so immense that progress in the subject has been severely hindered. If only mathematicians could prove the linking conjectures of the Langlands programme, then there would be short cuts to solving real-world problems, as well as abstract ones.
By the 1970s the Langlands programme had become a blueprint for the future of mathematics, but this route to a problem-solver’s paradise was blocked by the simple fact that nobody had any real idea how to prove any of Langlands’s conjectures. The strongest conjecture within the programme was still Taniyama–Shimura, but even this seemed out of reach. A proof of the Taniyama–Shimura conjecture would be the first step in the Langlands programme, and as such it had become one of the biggest prizes in modern number theory
Despite its status as an unproven conjecture, Taniyama–Shimura was still mentioned in hundreds of mathematical research papers speculating about what would happen if it could be proved. The papers would begin by clearly stating the caveat Assuming that the Taniyama–Shimura conjecture is true …’, and then they would continue to outline a solution for some unsolved problem. Of course, these results could themselves only be hypothetical, because they relied on the Taniyama–Shimura conjecture being true. These new hypothetical results were in turn incorporated into other results until there existed a plethora of mathematics which relied on the truth of the Taniyama–Shimura conjecture. This one conjecture was a foundation for a whole new architecture of mathematics, but until it could be proved the whole structure was vulnerable.
At the time, Andrew Wiles was a young researcher at Cambridge University, and he recalls the trepidation that plagued the mathematics community in the 1970s: ‘We built more and more conjectures which stretched further and further into the future, but they would all be ridiculous if the Taniyama–Shimura conjecture was not true. So we had to prove Taniyama–Shimura to show that this whole design we had hopefully mapped out for the future was correct.’
Mathematicians had constructed a fragile house of cards. They dreamed that one day someone would give their architecture the solid foundation it needed. They also had to live with the nightmare that one day someone might prove that Taniyama and Shimura were in fact wrong, causing two decades’ worth of research to crash to the ground.
During the autumn of 1984 a select group of number theorists gathered for a symposium in Oberwolfach, a small town in the heart of Germany’s Black Forest. They had been brought together to discuss various breakthroughs in the study of elliptic equations, and naturally some of the speakers would occasionally report any minor progress that they had made towards proving the Taniyama–Shimura conjecture. One of the speakers, Gerhard Frey, a mathematician from Saarbrücken, could not offer any new ideas as to how to attack the conjecture, but he did make the remarkable claim that if anyone could prove the Taniyama–Shimura conjecture then they would also immediately prove Fermat’s Last Theorem.
When Frey got up to speak he began by writing down Fermat’s equation:
![]()
Fermat’s Last Theorem claims that there are no whole number solutions to this equation, but Frey explored what would happen if the Last Theorem were false, i.e. that there is at least one solution. Frey had no idea what his hypothetical, and heretical, solution might be and so he labelled the unknown numbers with the letters A, B and C:
![]()
Frey then proceeded to ‘rearrange’ the equation. This is a rigorous mathematical procedure which changes the appearance of the equation without altering its integrity. By a deft series of complicated manoeuvres Frey fashioned Fermat’s original equation, with the hypothetical solution, into
![]()
Although this rearrangement seems very different from the original equation, it is a direct consequence of the hypothetical solution. That is to say if, and it is a big ‘if, there is a solution to Fermat’s equation and Fermat’s Last Theorem is false, then this rearranged equation must also exist. Initially Frey’s audience was not particularly impressed by his rearrangement, but then he pointed out that this new equation was in fact an elliptic equation, albeit a rather convoluted and exotic one. Elliptic equations have the form
![]()
but if we let
![]()
then it is easier to appreciate the elliptical nature of Frey’s equation.
By turning Fermat’s equation into an elliptic equation, Frey had linked Fermat’s Last Theorem to the Taniyama–Shimura conjecture. Frey then pointed out to his audience that his elliptic equation, created from the solution to the Fermat equation, is truly bizarre. In fact, Frey claimed that his elliptic equation is so weird that the repercussions of its existence would be devastating for the Taniyama–Shimura conjecture.
Remember that Frey’s elliptic equation is only a phantom equation. Its existence is conditional on that fact that Fermat’s Last Theorem is false. However, if Frey’s elliptic equation does exist, then it is so strange that it would be seemingly impossible for it ever to be related to a modular form. But the Taniyama–Shimura conjecture claims that every elliptic equation must be related to a modular form. Therefore the existence of Frey’s elliptic equation defies the Taniyama–Shimura conjecture.
In other words, Frey’s argument was as follows:
(1) If (and only if) Fermat’s Last Theorem is wrong, then Frey’s elliptic equation exists.
(2) Frey’s elliptic equation is so weird that it can never be modular.
(3) The Taniyama–Shimura conjecture claims that every elliptic equation must be modular.
(4) Therefore the Taniyama–Shimura conjecture must be false!
Alternatively, and more importantly, Frey could run his argument backwards:
(1) If the Taniyama–Shimura conjecture can be proved to be true, then every elliptic equation must be modular.
(2) If every elliptic equation must be modular, then the Frey elliptic equation is forbidden to exist.
(3) If the Frey elliptic equation does not exist, then there can be no solutions to Fermat’s equation.
(4) Therefore Fermat’s Last Theorem is true!
Gerhard Frey had come to the dramatic conclusion that the truth of Fermat’s Last Theorem would be an immediate consequence of the Taniyama–Shimura conjecture being proved. Frey claimed that if mathematicians could prove the Taniyama–Shimura conjecture then they would automatically prove Fermat’s Last Theorem. For the first time in a hundred years the world’s hardest mathematical problem looked vulnerable. According to Frey, proving the Taniyama–Shimura conjecture was the only hurdle to proving Fermat’s Last Theorem.
Although the audience was impressed by Frey’s brilliant insight, they were also struck by an elementary blunder in his logic. Almost everyone in the auditorium, except Frey himself, had spotted it. The mistake did not appear to be serious: nonetheless as it stood Frey’s work was incomplete. Whoever could correct the error first would take the credit for linking Fermat and Taniyama–Shimura.
Frey’s audience dashed out of the lecture theatre and headed for the photocopying room. Often the importance of a talk can be gauged by the length of the queue waiting to run off copies of the lecture. Once they had a complete outline of Frey’s ideas, they returned to their respective institutes and began to try and fill in the gap.
Frey’s argument depended on the fact that his elliptic equation derived from Fermat’s equation was so weird that it was not modular. His work was incomplete because he had not quite demonstrated that his elliptic equation was sufficiently weird. Only when somebody could prove the absolute weirdness of Frey’s elliptic equation would a proof of the Taniyama–Shimura conjecture then imply a proof of Fermat’s Last Theorem.
Initially mathematicians believed that proving the weirdness of Frey’s elliptic equation would be a fairly routine process. At first sight Frey’s mistake seemed to have been elementary and everyone who had been at Oberwolfach assumed that it was going to be a race to see who could shuffle the algebra most quickly. The expectation was that somebody would send out an e-mail within a matter of days describing how they had established the true weirdness of Frey’s elliptic equation.
A week passed and there was no such e-mail. Months passed and what was supposed to be a mathematical mad dash was turning into a marathon. It seemed that Fermat was still teasing and tormenting his descendants. Frey had outlined a tantalising strategy for proving Fermat’s Last Theorem, but even the first elementary step, proving that Frey’s hypothetical elliptic equation was not modular, was baffling mathematicians around the globe.
To prove that an elliptic equation is not modular, mathematicians were looking for invariants similar to those described in Chapter 4. The knot invariant showed that one knot could not be transformed into another, and Loyd’s puzzle invariant showed that his 14–15 puzzle could not be transformed into the correct arrangement. If number theorists could discover an appropriate invariant to describe Frey’s elliptic equation, then they could prove that, no matter what was done to it, it could never be transformed into a modular form.
One of those toiling to prove and complete the connection between the Taniyama–Shimura conjecture and Fermat’s Last Theorem was Ken Ribet, a professor at the University of California at Berkeley. Since the lecture at Oberwolfach, Ribet had become obsessed with trying to prove that Frey’s elliptic equation was too weird to be modular. After eighteen months of effort he, along with everybody else, was getting nowhere. Then, in the summer of 1986, Ribet’s colleague Professor Barry Mazur was visiting Berkeley to attend the International Congress of Mathematicians. The two friends met up for a cappuccino at the Café Strada and began sharing bad luck stories and grumbling about the state of mathematics.
Eventually they started discussing the latest news on the various attempts to prove the weirdness of Frey’s elliptic equation, and Ribet began explaining a tentative strategy which he had been exploring. The approach seemed vaguely promising but he could only prove a very minor part of it. ‘I sat down with Barry and told him what I was working on. I mentioned that I’d proved a very special case, but I didn’t know what to do next to generalise it to get the full strength of the proof.’
Professor Mazur sipped his cappuccino and listened to Ribet’s idea. Then he stopped and stared at Ken in disbelief. ‘But don’t you see? You’ve already done it! All you have to do is add some gamma-zero of (M) structure and just run through your argument and it works. It gives you everything you need.’
Ribet looked at Mazur, looked at his cappuccino, and looked back at Mazur. It was the most important moment of Ribet’s career and he recalls it in loving detail. ‘I said you’re absolutely right – of course – how did I not see this? I was completely astonished because it had never occurred to me to add the extra gamma-zero of (M) structure, simple as it sounds.’
It should be noted that, although adding gamma-zero of (M) structure sounds simple to Ken Ribet, it is an esoteric step of logic which only a handful of the world’s mathematicians could have concocted over a casual cappuccino.
‘It was the crucial ingredient that I had been missing and it had been staring me in the face. I wandered back to my apartment on a cloud, thinking: My God is this really correct? I was completely enthralled and I sat down and started scribbling on a pad of paper. After an hour or two I’d written everything out and verified that I knew the key steps and that it all fitted together. I ran through my argument and I said, yes, this absolutely has to work. And there were of course thousands of mathematicians at the International Congress and I sort of casually mentioned to a few people that I’d proved that the Taniyama–Shimura conjecture implies Fermat’s Last Theorem. It spread like wildfire and soon large groups of people knew; they were running up to me asking, Is it really true you’ve proved that Frey’s elliptic equation is not modular? And I had to think for a minute and all of a sudden I said, Yes, I have.’
Fermat’s Last Theorem was now inextricably linked to the Taniyama–Shimura conjecture. If somebody could prove that every elliptic equation is modular, then this would imply that Fermat’s equation had no solutions, and immediately prove Fermat’s Last Theorem.
For three and half centuries Fermat’s Last Theorem had been an isolated problem, a curious and impossible riddle on the edge of mathematics. Now Ken Ribet, inspired by Gerhard Frey, had brought it centre stage. The most important problem from the seventeenth century was coupled to the most significant problem of the twentieth century. A puzzle of enormous historical and emotional importance was linked to a conjecture that could revolutionise modern mathematics. In effect, mathematicians could now attack Fermat’s Last Theorem by adopting a strategy of proof by contradiction. To prove that the Last Theorem is true, mathematicians would begin by assuming it to be false. The implication of being false would be to make the Taniyama–Shimura conjecture false. However, if Taniyama–Shimura could be proven true, then this would be incompatible with Fermat’s Last Theorem being false, therefore it, too, would have to be true.
Frey had clearly defined the task ahead. Mathematicians would automatically prove Fermat’s Last Theorem if they could first prove the Taniyama–Shimura conjecture.
Initially there was renewed hope but then the reality of the situation dawned. Mathematicians had been trying to prove Taniyama–Shimura for thirty years and they had failed. Why should they make any progress now? The sceptics believed that what little hope there was of proving the Taniyama–Shimura conjecture had now vanished. Their logic was that anything that might lead to a solution of Fermat’s Last Theorem must, by definition, be impossible.
Even Ken Ribet, who had made the crucial breakthrough, was pessimistic: ‘I was one of the vast majority of people who believed that the Taniyama–Shimura conjecture was completely inaccessible. I didn’t bother to try and prove it. I didn’t even think about trying to prove it. Andrew Wiles was probably one of the few people on earth who had the audacity to dream that you can actually go and prove this conjecture.’