The structure of a graph-based and tree-based data model.
How conceptually we can use nesting to represent such a model in Python native data structures.
With JSON and XML as representative format instances of hierarchical models, understand correct syntax and structure to represent data within this model.
The use of paths in JSON and XML to identify individual elements within the tree.
Construct in-memory structures from local files and strings containing JSON and XML formatted data.
Carry out simple extraction of data from JSON or XML format.
In Sect. 5.4, we presented an overview of the hierarchical model, briefly describing its tree-based structure, and providing example formats such as JSON, XML, and XHTML. The current chapter deepens our discussion of the structure of hierarchical data, beginning with a formal treatment of trees, how to represent them in Python, and common terminology we will need for subsequent chapters. We then discuss the syntactic details of the JSON and XML formats.
procedural programming operations for JSON and XML,
declarative data query operation for XML using XPath, and
encoding and enforcing constraints using JSON Schema, Document Type Definition (DTD), and XML Schema.
Operational examples will include access of data from a hierarchical structure, and storing it in appropriate data structures, learning how to modify data in a hierarchical structure, and using constraints to guarantee that a structure we build or receive is a well-formed tree, containing the data we need in the location we expect.
15.1 Motivation
Examples of hierarchical data abound in data science. For instance, we have already seen that file systems are naturally hierarchical. Date/time data is hierarchical. We will see that data obtained from web scraping and from APIs is also often naturally hierarchical. Data from emails has a hierarchical structure. Even linguistic data can be viewed as having a hierarchical structure, as can be seen from sentence diagramming and grammatical rules. Furthermore, many topics in statistics can be viewed more clearly through a hierarchical lens, including time series analysis (with a level for time), clustering (with a level telling which cluster an individual belongs in), multiple linear regression, ANOVA, longitudinal data analysis, multi-level modeling, and statistical methods for filling in missing data in a data set (with one level for modeling the missing data, and another level for modeling the response variable). For the moment, we will limit our discussion to local files with JSON and XML formats, but the reader is encouraged to remember that these files can store data from a wide variety of application areas.
It is worth taking a moment to compare the hierarchical model with the relational and tabular data models. The relational model is the most structured (e.g., constraints are built-in), followed by the tabular model (where constraints are “by convention” to achieve tidy data). We will see that the hierarchical model is the least structured of the three. This will create added complexity when we engage our discussion of hierarchical constraints.
First, as we have already described, the hierarchical model has tremendous expressive power. Furthermore, anything that can be expressed in tabular form can also be expressed in hierarchical form, as we will see below.
Second, hierarchical models are excellent for storing large and complex data sets in such a way as to make the data efficiently searchable. We have already seen this with our example of the file-structure, where it is possible to get from the root directory to each file in a small number of steps, even though there might be a large number of files in total.
Third, the hierarchical model is very flexible. We will see in the next chapter that it is much easier to add data in the hierarchical model (indeed, anywhere in the tree) than it is to add data to the tabular or relational models. This also makes it easier to including missing data in our model. Instead of requiring a special symbol like NA, we can represent missing data simply by the absence of a leaf in the tree.
15.2 Representation of Trees
Hierarchical data refers to data with the underlying structure of a tree, so we must pursue a careful discussion of trees, and begin this discussion with the more general concept of a graph.

Network architecture
Here the nodes represent devices (either routers or hosts), and an edge denotes a medium through which information can flow (e.g., a physical wire, a fiber optic cable, etc.). A path is a sequence of edges v 1v 2…v k from some initial node v 1 (the source) to some node v k (the destination). When we think of edges as bidirectional, we sometimes say the path goes between v 1 and v k. The reader is encouraged to trace out a path (following the edges, one by one) from the “Cloud Server,” a host in the lower right of the figure, to the one of the “Desktop” host nodes on the far left of the figure.
If v k = v 1, the path is called a cycle. The graph above has several cycles, including triangles, quadrilaterals, and one hexagon. We say a graph G is connected if, for any two nodes in G, there exists at least one path between them.
A graph with no cycles is called a forest. A graph that is connected and has no cycles is called a tree. In this way, a forest is made up of one or more disconnected trees. Both trees and forests are common in data mining algorithms. We recall the following picture of a tree, from Sect. 5.4.
In this figure, nodes are labeled by strings of text. The edge between author and "Tolstoy" denotes that the author of “War and Peace” was Tolstoy. The edges beneath book [id="bk102"] denote that author, title, and price are constituent pieces of book bk102. The edge above book bk102 signifies that bk102 is part of the catalog. It is not difficult to show that if a tree has n nodes, then it must have n − 1 edges. With any fewer edges, the tree would not be connected. With any more edges, it would have a cycle. We note that it is possible to extend beyond hierarchical data to graph-structured data, and that the resulting model has even more expressive power and flexibility, but we will not delve into it here.
15.2.1 Terminology
The node at the top is called the root.
For a given node, the nodes directly below it are called its children. For example, the children of the root, catalog, are bk101, bk102, …, bk200.
For a given node, the node directly above it is called its parent. For example, the parent of bk102 is catalog.
For a given node X, the nodes along the path from the root to X are the ancestors of X. Nodes below X, whose paths from the root contain X, are the descendants of X.
If two nodes have the same parent, we call them siblings.
We allow nodes to have a symbolic name, sometimes called a tag or label.
We allow two different nodes to have the same label (e.g., there are 100 nodes labeled author), and we use their location in the tree to distinguish them.
A node with no children is called a leaf node.
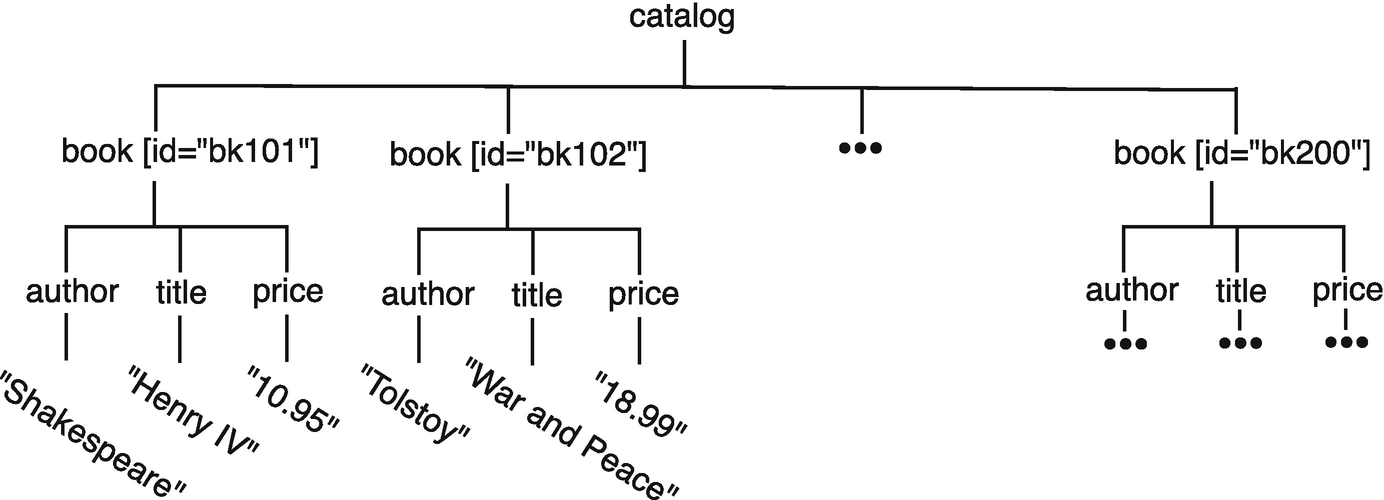
Book catalog tree
We note that there is a unique path between any two nodes in a given tree. The length of this unique path (that is, the number of edges in the path) is called the distance between the two nodes. In Fig. 15.2, all leaves are distance three from the root. In such a case, we say the tree has depth three.
15.2.2 Python Native Data Structures and Nesting
15.2.2.1 Representing Graphs
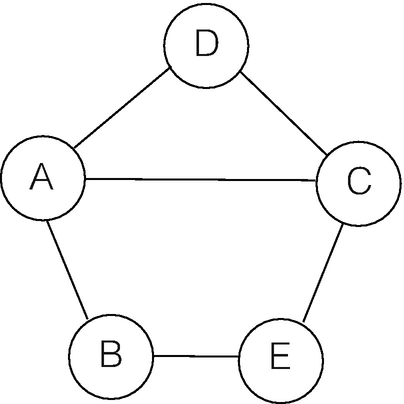
Example graph

This representation makes it easy to find out which nodes a given node is adjacent to, but it duplicates information (representing each edge twice). In the case of a tree, this representation could be modified so that each node (key) is associated with its list of children. However, such a representation suffers from the drawback that it is challenging to determine the parent of a given node.

We read the first row as saying node A has edges to nodes B, C, D (the three middle 1s in the row) and does not have edges to A or E. Like the previous way of representing a graph, this representation duplicates information. Note that if you reflect the matrix over its diagonal (the line from the upper left to the lower right), you do not change the matrix at all, because the information that A has an edge to C is the same as the information that C has an edge to A. Furthermore, this representation contains a great deal of unnecessary information in the form of 0s. Many graphs in the world have a huge number of nodes, but not very many edges. Such graphs are called sparse, and examples include the web, the Internet, and social network graphs. When using an adjacency matrix, the number of bits required to represent a graph only depends on the number of nodes, not on how sparse the graph is.
15.2.2.2 Representing Trees
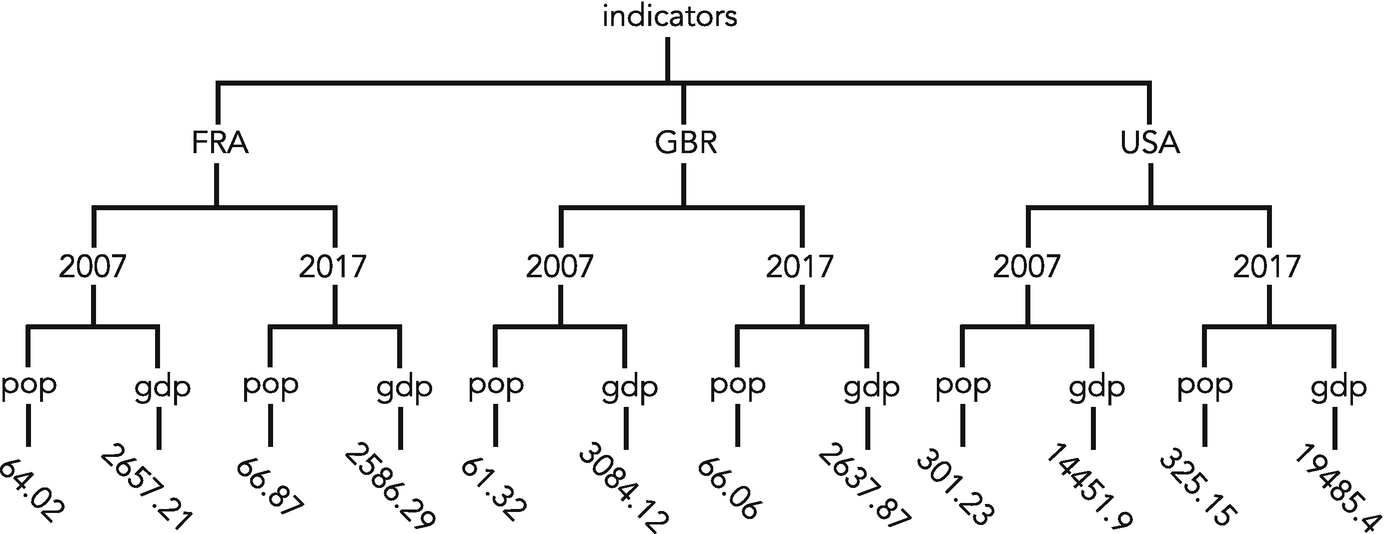
Indicators0 tree
The essential structure here is the information that indicators has children "FRA", "GBR", and "USA", that each country has children for years "2007" and "2017", that each year has children pop and gdp, and that each of these has children consisting of a real-valued number. As we did for graphs, we can represent this as either a dictionary or a list, but now with radically different interpretations. In both cases, we use nesting of data structures to correspond to the levels in the tree, something we could not do for a general graph. Each additional level of nesting corresponds to an additional level as we descend the tree.

Note that we have used horizontal white space (indentation) to make it easier to “see” the tree structure, though of course Python does not care about this white space. For example, we can see that the children of the node “USA” are “2007” and “2017” (the keys of the dictionary associated with “USA”), because these are below “USA” and indented one level farther to the right. Similarly, we can see that the children of “2017” at the bottom are “pop” and “gdp.” In this particular example, leaf nodes have no siblings. If a tree had leaf nodes with siblings, e.g., if there were two children of the final “gdp” instead of one, then we could use a list for the innermost layer of this nested data structure. But in all of our examples, we will have leaf nodes without any siblings, because a leaf will represent a unit of data, and the path from the root to a leaf will represent the meaning of that datum. We will not belabor this point.
When we use dictionaries as the primary structure used in the nesting to achieve a tree, we will call this a Dictionary of Dictionaries (DoD). We use this terminology even when there are more than two levels of nesting, e.g., the previous example is technically a dictionary of dictionaries of dictionaries but we do not call it a DoDoD.
We can also represent a tree as a Python list, again using the root as the name of the list, and children as the elements in the list. Here, each child may itself be a list, representing the tree below it. This means we would represent ind0 as a list indicators = [FRA, GBR, USA] where each of FRA, GBR, USA are themselves lists. For example, FRA could be the list [F07, F17], where F07 is the list [F07P,F07G], and F07P = 64.02, F07G = 2657.21. Similarly, F17 is a list (consisting of the population and gdp in France in 2017), and GBR and USA are defined as nested lists analogously to FRA. This means indicators is a 3D lists, because the tree ind0 has depth three.
When we use lists as the primary structure used in the nesting to achieve a tree, we will use the same List of Lists (LoL) term introduced in Chap. 3. Again, a particular tree can have additional levels that are also lists, but we will still use the LoL designation.


Nested lists as a tree
The root is named L.
The children of the root are labeled 0, 1, 2, …, r, and each represents one of the lists L i.
Each i has c children, where c is the number of columns, i.e., c is len(L 0).
The j th child of node i represents the data stored at L[i][j].
This procedure is essentially what happened with ind0, except we ended up with a third layer, because ind0 has a two-level index. This helps justify our use of the term “level” in Chap. 7. Note that not every tree can be represented as a list of lists, e.g., trees of many levels, or irregular trees (e.g., where not all leaves are the same distance from the root).
Both the dictionary representation and the list representation of trees have the property that compositions allow multiple levels of the tree. That is, to build on the tree to make it one level deeper, we can simply nest our data structures one level deeper, rather than having to build a new representation from scratch.
15.2.3 Traversals and Paths
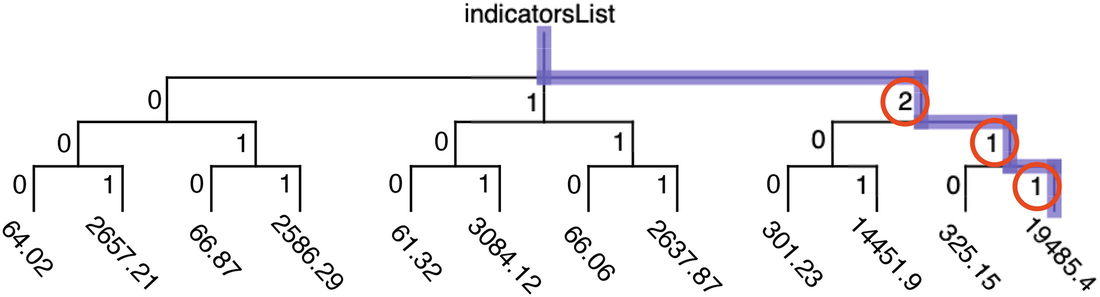
Nested lists path traversal
This way of thinking–that moving through the nested data structures one by one is equivalent to stepping through the tree one level at a time–will come up again in Chap. 16, when we discuss XPath.
15.2.4 Reading Questions
You may have seen trees before, when learning about binary search. A list of numbers can be represented as a tree, with one node for each item. The tree structure determines how quickly we can search for a given item. For example, let
If you represent L as a linear tree, this means the root is 1, and there are edges 1->3, 3->4, 4->6, etc. Searching this tree for item = 17 requires 13 steps, i.e., a path of length 13. We say item 17 is stored at depth 13 in the tree.
Please use the language of trees (root, paths, depth, etc.) to explain what makes binary search faster than linear search. Start by thinking about how to represent L in a way that lines up with binary search, analogously to how we just did it for linear search. Please also give a binary search path in L to the item 17, and include the depth of 17 in your answer. If you are stumped, you could search for “Binary Search Tree” online. Be sure to explain what tree property makes binary search take time O(log(n)) while linear search takes time O(n).
Building on the question above, why is the tree structure on your computer’s file system important? What sorts of things does it make more efficient? Please illustrate with a concrete example, then give another real-world example where a tree structure makes something more efficient.
Please discuss the trade-offs between structuring data into a tree form, to facilitate efficient retrieval, versus leaving data in an unstructured form. It might help to think about the cost involved with sorting a list, to facilitate the use of binary search, versus leaving it unsorted. At what point does it become worthwhile to build the additional structure?
Consider a data set consisting of a university web site, with news, academics, admissions, events, research, etc. Would this be best to represent in relational form or hierarchical form? Justify your answer.
Consider a data set consisting of university records: students, courses, grades, etc. Would this be best to represent in relational form or hierarchical form? Justify your answer.
Please make an analogy between how paths are given when we use a native Python dictionary to represent a tree, and your experience with URLs on the web, and with using the Terminal or Command Prompt on your machine. Please give a concrete example illustrating the analogy.
15.3 JSON
As discussed in Sect. 2.4, the JavaScript Object Notation (JSON) format is a programming language independent, straightforward, way to move between data stored in a text file, and data stored in a data structure. This makes JSON a very convenient format for hierarchical data, as both of the Python native data structures of dictionaries and lists, discussed above, can be easily converted into JSON format [9, 21, 28].
It is important to note that the only scalars allowed for JSON are Booleans, numbers, strings, and a special data type called null. Thus, a JSON file cannot store a tree of file objects, but can store a tree of strings (including file names). Furthermore, strings must be represented by double quotes, instead of single quotes, e.g., “Chris” is an acceptable string, but “Lane” is not.
In JSON, when data is stored inside square brackets, in an ordered list, such as [1,"one",True] or our indicatorsList is example, the data type is known as an array. When data is stored inside curly brackets, with key:value pairs, like {"Noah":2, "Becky":1, "Evan":1}, or our indicatorsDict example, the data type is known as an object. These are the only two container data types allowed by JSON, though nesting is possible (that is, we can have an array of numbers, an array of arrays, or even an array of objects). These data structures are universal, and so connect easily with Python, C++, Java, and many other languages.


The resulting string, mystring, could easily be passed as a parameter to a function. This is one way to avoid concerns about mutability of a Python native data structure.


This code assumes there is a file "ind0Dict.json" in the data directory. We open the file with the intent to read, then load the data from the file into indicatorsDict, then close the file. If the data was given to us as a json-formatted string, s, instead of a file, we would load it using the line indicatorsDict = json.loads( s) .
We will demonstrate programming with JSON in the next chapter, followed by JSON Schema and constraints in Chap. 17. We will also see JSON files in Chaps. 20 and 21, in the context of data obtained from Internet sources and web scraping.
15.3.1 Reading Questions
Explain the difference between JSON, which is textual (i.e., in a text file, or in a string in our programs), and the data structure that we get from performing a load( ) or loads( ) based on the JSON.
What is the name for the JSON equivalent of a Python list? What about a Python dictionary?
Go to https://www.json.org/json-en.html and look up the allowed syntax for a JSON string. Based on that syntax, write down three examples of Python strings that would be illegal as JSON strings.
Look carefully at the syntax diagrams (aka train-track diagrams) for JSON at https://www.json.org/json-en.html. Consider the following nested structure as JSON:
Using the syntax diagrams, trace through the example. Then describe why JSON supports trees of information through nesting.
Suppose you have the following small subsets of data from the subjects and courses tables of the school database. Write a single JSON text string (or file) whose contents, in a single tree, represent the same information.
subject | name | department |
|---|---|---|
CS | Computer Science | MATH |
MATH | Mathematics | MATH |
ENGL | English Literature | ENGL |
subject | coursenum | title |
|---|---|---|
CS | 110 | Computing with Digital Media |
CS | 372 | Operating Systems |
MATH | 210 | Proof Techniques |
ENGL | 213 | Early British Literature |
Please write down a portion of your family tree with depth at least three, and with at least 8 nodes. You will be the root. Please give your tree in the form of a JSON object, following the model in the reading. Please use horizontal whitespace to make the tree structure easy to follow, and represent one node per line.
15.3.2 Exercises
Consider the table of data:
subject | name | department |
|---|---|---|
CS | Computer Science | MATH |
MATH | Mathematics | MATH |
ENGL | English Literature | ENGL |
This could be represented in a Python program as a dictionary mapping from a key, "subjects", to a list of dictionaries, one per subject. These inner dictionaries map from subject, name, and department to the respective value for the row.
Write Python code to construct the above representation as a Python in-memory data structure called ds, and then have your code encode the data structure into a JSON-formatted string, and print the string. Then take ds and encode it as a JSON-formatted string, but include indent=2 as an argument in the conversion, and print it.
As in the last question, create the in-memory data structure, but now create a local file named school.json with the JSON-formatted data. Use the indent=2 argument when encoding as JSON.
This question assumes that you successfully accomplished the previous question, and have a file school.json with the JSON-formatted data structure originally specified in the first exercise.
Write code to read and decode the JSON-formatted school.json file into a data structure, assigning to variable ds2. Once created, manipulate the ds2 data structure by appending a row of data to the subjects list with value:
15.4 XML
More powerful, general, and widespread than the JSON format, the eXtensible Markup Language (XML) is a general structure for modeling hierarchical data, with the power to create a wide variety of new formats [90]. XML was created initially for the Internet, and can be viewed as a super-set of the HyperText Markup Language commonly seen in web design (that is, HTML is a special case of XML). The XML format is a common format widely used for data sharing and data transport, e.g., when data is provided by an API, in web pages, and in local files. XML data is stored as plain text, so an XML file can be opened with any text editor (ideally, one that is “syntax aware”). Like JSON, XML is designed to be programming language agnostic, that is, to work with any application that seeks to use it. Because XML data is simple text data, it is easy to communicate between operating systems, data systems, applications, etc. In web scraping, one often comes across XML pages as well as HTML and XHTML pages [73]. XML files are also commonly used as a format for data hosted by the US Government, e.g., [69].
Despite the word “language” appearing in its name, XML does not represent a programming language. When given an XML file, there is no code to execute. Instead, it is a language for communicating hierarchical data with great power and generality, with certain grammatical rules that we will discuss shortly.
15.4.1 XML Structure
An XML document represents a tree, and we will provide an example shortly displaying the indicators data set in XML format. As a tree, an XML document must have exactly one root. There are several types of nodes in an XML tree, including text nodes, attribute nodes, and internal nodes. Each internal node represents an XML element, which starts with a start tag (e.g., <indicators> for the root) and ends with the corresponding end tag (in this case, </indicators>). All data between the start tag and end tag represents data that is structurally subordinate to the node in question. Since the tree contains internal nodes under the root, there will be more start and end tags under <indicators> and above </indicators>. This is analogous to the use of curly brackets and nested dictionaries in JSON. To validly represent a tree, an XML document must properly nest these start and end tags.
Tagged elements, which may be nested within one another.
Attributes on elements, representing metadata associated with the element.
Text, often representing essential data.
For example, to represent the tree of Fig. 15.2 in XML, we would start with the element catalog as the root, and the entire tree would be nested under this element. We would have 100 elements tagged book, all children of catalog. Each book element has a single attribute, mapping the key id to the value consisting of the id for the book in question. In general, attributes are stored in a dictionary, though in this example each attribute dictionary only has one key:value pair. In this example structure, each book has three elements nested under it: author, title, and price. The first author element has one child, a text node with the value "Shakespeare".
the tree structure, with a specific organization that constrains what tags are legal children of other tags, etc.
the interpretation of those tags, which assigns meaning that, for instance, <h1> is a top level header, etc.
XML, on the other hand, only governs the legal structure–the tags and XML do not, in of themselves, have interpretations
In XML, we use the tags to denote the meaning of data, e.g. <Student>, <Book_Title>, etc. Tags can be any strings (case sensitive), subject to some restrictions on the characters allowed. Tags are chosen by the person creating the data set, and are part of the data, analogous to column headings in the tabular model. The tag structure means an XML document describes its own syntax. The structure of XML makes it both human and machine readable. As in our examples from the previous section, the tree structure is indicated both by start and end tags (which, for JSON, were curly brackets), and via the horizontal white space on each line (to clearly display the nesting structure). This structure can be seen below where we display the indicators0 data set in XML format.
In the example below, the first line is an optional XML prolog, and is not part of the XML tree itself. This prolog is almost always present when the XML is in a file. The second line and last line are the start and end tags for indicators discussed above. We also see the same structure for each of the three children of the root (countries). Each country element starts and ends with a tag. For example, the start tag for France occurs on line 3 and the corresponding end tag on line 12, denoting that all data associated with France is on these lines in the XML file. Similarly, the timedata start and end tags denote portions of the tree for 2007 (under FRA), for 2017 (under FRA), for 2007 (under GBR), etc. Lastly, under each timedata we have the population and gdp, each containing a single number (in text form, as is required by XML), wrapped in start and end tags.
Because of this logical structure, it is easy to write code to identify sections of the tree, by searching for an end tag corresponding to a given start tag. The nested structure also allows us to build more complicated trees using composition, or to quickly identify locations to add new data to the tree. For example, if we receive data from a fourth country, we could find an end tag </country> and then add the data we receive starting on the next line with a new start tag <country> corresponding to the new data. Additionally, the information about how to decode the XML file is present in the top level tag, which also specifies the XML version used.
As we have mentioned, XML attributes allow us to store metadata in the tags. Specifically, every XML element comes with a set of attributes of the form key="value". For example, we see this in tags above like <country code="FRA" name="France"> and <timedata year="2007">. We see that when an element has multiple attributes, they are separated by a space. For a given element, attribute keys must be unique (e.g., one could not have <country code="FRA" name="France" code="fra">). Note that some authors write “name” where we have written “key,” but we chose to avoid confusion with the explicit key name in the indicators example. Attributes are common in HTML, e.g., the href attribute that we will discuss in Chap. 22.
One special attribute is the identifier attribute id, which assigns an identifier to an element, unique across all elements in the XML tree. Including this special attribute is analogous to including an index in the tabular or relational data models.
Lastly, text nodes are encoded in XML as strings of text that appear between a start tag and an end tag, e.g., <pop>301.23</pop> tells us that the internal node pop has one child, "301.23". It is possible for an element to have both element children and text children (e.g., if the text "Home of the Free" was added after the start tag <country code="USA" name="United States"> and before the first timedata child in indicators0 above). Such an element is said to have mixed content. We shall not consider such elements, as they violate our policy that text leaf nodes should not have siblings. As XML allows a great deal of flexibility, defining and communicating such constraints on XML trees is extremely important in practice. This is the topic of Chap. 17.
The person creating the XML data decides whether data appears as an attribute or as an element. For example, in indicators, instead of the element
we could provide the same data in the form
It is always possible to translate an XML that uses attributes into one that does not by making each attribute a child of the element in question.
This decision is made based on whether year is thought of as metadata or not. Of course, to extract XML data into another form (e.g., tabular), one needs to know ahead of time whether the data is encoded via attributes or text nodes. Since attributes cannot contain tree structure or multiple values, there is an argument for avoiding attributes as a way to store anything other than metadata. For instance, choosing to store all the data in a single attribute dictionary undermines all the values of XML data.
XML allows the user to define their own tags, elements, or attributes, and this explains the way in which XML is “extensible” (i.e., it is possible to extend it to meet your needs). Applications built to work for an old version of an XML file will continue to work for a new version, even if some tags are deleted and others added. Applications should be designed to work with the tags that are present at any moment.
XML files are required to satisfy a “grammar” with rules such as “there must be exactly one root element,” “every start-tag must have a corresponding end-tag,” and “elements must nest properly” (e.g., in indicators, we could not close a country element before closing one of its timedata children). Tag names cannot contain whitespace, colons, or the sequence xml, and attribute values cannot use the symbols &, <, or >, to avoid confusion with the symbols reserved for starting and ending tags. XML has reference characters, such as > for > and & for &, that allow us to include these reserved symbols in a way that does not cause confusion.
When an XML file satisfies the grammatical rules, we call it well-formed. When an XML file is well-formed, it can be read in an automated way, the relationships between elements (i.e., the edge structure) can be mapped, and the hierarchical data represented can be drawn as a unique tree. This automated process is known as parsing, and we return to it in Chap. 17. Often, data system providers will create constraints, so that only a certain set of tags can be used, and only in certain ways. Such constraints streamline the process of transmitting XML data between different applications. Examples include XMLNews (for XML data in news media applications), XML for national weather data applications, and, of course, HTML.
For the purposes of this book, we will always include an end tag associated with every start tag. However, the reader should be aware that there are XML files that omit end tags, by using a special syntax for start tags. Specifically, if a start tag ends with the symbol /, this means no end tag will appear. This sometimes happens when a node has no children. For example, if we wanted to add a fourth country, China, for which we had no data on population or gdp in 2007 or 2017, then we could add the China node as a child of the root, and without any children of its own. We could do so with a single self-ending tag <country code="CHN" name="China"/>, e.g., placed in the second-to-last line of the XML file above.
We also feel obliged to mention that XML data can be formatted using CSS (Cascading Style Sheets) or XSL (Extensible Stylesheet Language) to translate XML to HTML. However, we will not have need of this fact. We also mention that XML files can contain comments, and we will return to this point in Chap. 17.
15.4.2 Extracting Data from an XML File
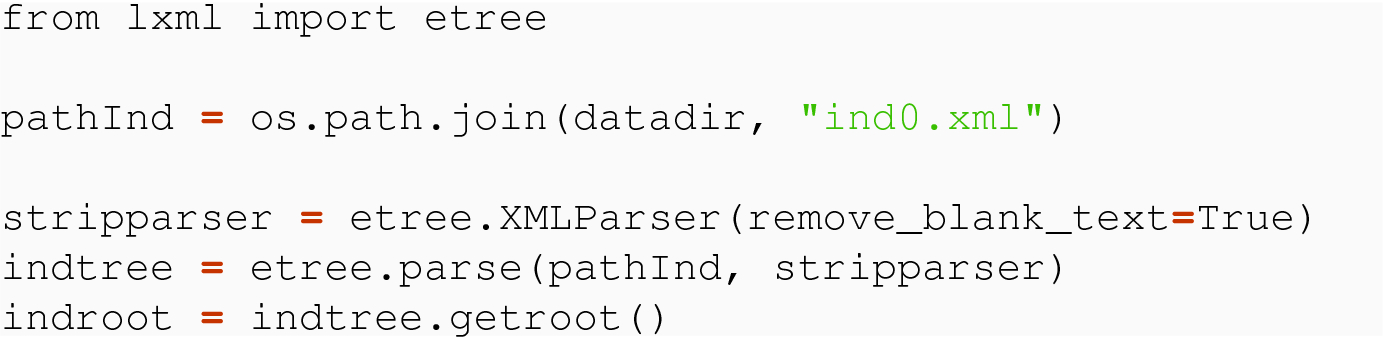

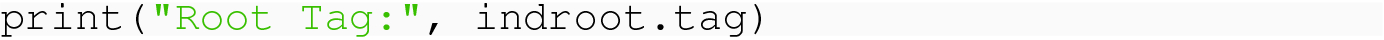





We have already seen in Chap. 2, the importance of being able to provide a path from the root of a file system tree to any individual element. Relative paths, such as from a node representing a folder to a file stored in some sub-folder, are also important. Finding such paths in XML trees is easy, and forms the basis for XPath, which we will discuss in the next chapter.
15.4.3 Reading Questions
Please write down a portion of your family tree with depth at least three, and with at least 8 nodes. You will be the root. Please give your tree in the form of a XML format, with one node per line, and using tags and attributes as illustrated in the reading. Use horizontal whitespace to make the tree structure clear to follow.
Please describe three kinds of attributes you might include in your family tree, and why it would be valuable to store this data.
When we use the lxml library, why is it that doing getroot( ) then printing the result, has the effect of printing the entire tree?
Is it possible to use the find( ) function within the etree module to determine the depth of an element you are interested in?
15.4.4 Exercises
Consider the table of subjects data:
subject | name | department |
|---|---|---|
CS | Computer Science | MATH |
MATH | Mathematics | MATH |
ENGL | English Literature | ENGL |
Using a text editor, edit and create a file named subjects.xml in the current directory that creates a legal XML representation of this data. Once created, write a Python code sequence to read and parse the file, and then, using the technique from this section, print the entire tree.
Building on the last question, using a text editor, edit and create school.xml that contains a single XML tree with both the subjects table from the previous question, and the courses table presented here:
subject | coursenum | title |
|---|---|---|
CS | 110 | Computing with Digital Media |
CS | 372 | Operating Systems |
MATH | 210 | Proof Techniques |
ENGL | 213 | Early British Literature |
Once created, write a Python code sequence to read and parse the file, and then, using the technique from this section, print the entire tree.
Further Exploration
There are many online lessons and tutorials that can be used to delve more deeply into JSON and XML [72, 65, 77, 66].
In addition, there are online resources for formatting and validating JSON and XML [12, 27, 13, 5].