© Springer Nature Switzerland AG 2020

T. Bressoud, D. WhiteIntroduction to Data Systemshttps://doi.org/10.1007/978-3-030-54371-6_7

7. Tabular Model: Access Operations and pandas

Thomas Bressoud¹   and David White¹

(1)

Mathematics and Computer Science, Denison University, Granville, OH, USA

 

Chapter Goals

Upon completion of this chapter, you should understand the following:

• The logical access operations to query data.

• The logical operations to manipulate vectors of data.

Upon completion of this chapter, you should be able to do the following:

• Query data using attributes and methods of DataFrame and Series objects.

• Perform computations on single and multiple Series.

We learned in Sects. 5.​2 and 6.​1 that our fundamental structure of the tabular data model is a two-dimensional structure made up of rows and columns, and that logical operations on that structure include access of one or more columns, selecting rows through filtering, performing column-vector operations between columns and between columns and scalars, and updating and adding columns, among others. We have also been cautioned that we may acquire data that is two-dimensional in rows and columns, but the data may not conform to the constraints of the tabular model, and we may need operations that can manipulate and transform the data to normalize it.

7.1 Tabular Operations Overview

We start with a conceptual summary of the types of operations we want and need. This will allow us to better understand the pandas package in context. Subsequent sections will then show pandas realizations of these operations. Many of the summaries will give high-level examples using the top baby names data set, which has columns year, sex, name, and count.

7.1.1 Access Operations

Access operations are those that read or query data values out of a table. There are many types of operations needed to access data values, and we list the most common here. We should note that there are many variations, even among this list. For instance, it may be possible to identify columns and/or rows both logically or by integer position. Each of these combinations gives operational variations to consider.

• Single-element access At one end of the spectrum, we may wish to access a single data value, which is the intersection of a column and a row. For instance, we may wish to read the value from the name column and the row associated with the year 2018 and the sex of "Female" (recall that we need values of both independent variables to uniquely refer to a row).

• Column access When we seek a subset of a data frame based on one or more columns, we call that a projection of the desired columns.¹ For instance, we may wish to project the vector associated with the count column, including the values for all the rows. We also might want a subtable obtained by projecting the year, sex, and count columns, with all rows included. A projection might also be used to obtain a new table with the columns re-ordered.

• Single row We may wish to select ² a single row, obtaining the values of all columns in that row. So we may want the year, sex, name, and count column values obtained by selecting, say, the first row in the data set.

• Multiple rows In this operation, we want a subset of the data consisting of all the columns, but a limited set of the rows. This, in general, is also called selection, but is often called filtering, when we want the chosen rows to satisfy some condition. For instance, we may want all the rows where the year is between 1920 and 1950.

• Subset rows and columns The most general form of access operation would allow us to both project a subset of the columns and filter for a particular subset of the rows.

For access operations in the tabular model, we need to pay attention to the data type of the result. For example, when we use an operation to obtain a single element, it will make a difference if we expect a scalar (i.e., a non-vector unit of data), like an integer or a string, or expect a data frame consisting of exactly one row and one column. It is important to distinguish between these cases, as downstream functions will break if they expect a string and we pass them a data frame, or vice versa. The pandas operation examples will illustrate some of these data type result differences.

7.1.2 Computational Operations

Given that the access operations allow us to subset the data in various ways, computational operations allow us to compute with these various subsets of the data:

• Column-vector operations Given one/two columns, we may want to perform unary/binary operations between the columns to obtain a new column of data. For instance, if we had the count column and an equal sized column for the total number of applicants in a given year, we could compute the percentage of applicants for the top name for each sex for each year as an equal sized vector or column. Analogously, in our indicators data, we could compute GDP per capita in this way.

• Aggregation operations Given a column, and perhaps a subset of the rows, we may want to compute some aggregate value for the set of values. We may want max, min, sum, or mean, of the count column, for instance.

• Boolean operations We may want to compute a Boolean predicate elementwise on a column vector. For instance, we may want to compute a Boolean vector whose values are True if the count is above 20000, and False otherwise. This is really just a particular type of column-vector operation, but is listed separately as such a Boolean vector could then be used in an access operation where we want to filter rows based on a condition.

7.1.3 Mutation Operations

The mutation operations provide a means to update a data set. Allied with mutation, we may also wish to create a separate in-memory data structure that is a copy of some subset of the rows and columns, but that allows a mutation to be independent of the original data set. We list common mutation operations.

• Add a column We want to be able to create and add a new column to a data set. For instance, after computing a column of GDP per capita, we may wish to add this new column to the indicators data set.

• Update a column In this operation, an update to the values of an existing column would be made in place, overwriting original values in the column. A variation of this operation would update only a subset of the rows, based on some predicate. We commonly need this operation if our data source releases updated data.

• Delete column(s) In this operation, we wish to delete one or more existing columns from the data set. If an analysis were only interested in the count of applications, the name column could be deleted. The deletion of a column is referred to as a drop of the column.

• Add rows Adding to a data set involves augmenting the data set with one or more additional rows. Care needs to be taken on the order in which new rows are placed in the data frame.

• Delete rows We sometimes need an operation to delete one or more rows. The operation must allow us to specify exactly which rows are to be deleted, such as by index, or by satisfying a Boolean condition.

• Change order The most common example of an operation to change the order of the rows in the table would be to sort the rows based on values in one or more columns. For instance, we might want to sort the rows in our baby name data set in decreasing order of the year value, to create a time series.

7.1.4 Advanced Operations

Because the operations of the tabular model are procedural, many of the above operations may be combined as a set of steps in interesting and helpful ways, building more powerful aggregate operations. A few of these more advanced operations are listed here.

• Iteration Built on lower-level access operations, we can define operations (iterators) that allow us to iterate over rows, over fields within rows, and over other subsets of the data in a data frame.

• Generalized Aggregation This operation allows us to aggregate multiple columns at once, possibly using a different aggregation function on different columns, e.g., finding the maximum population and minimum GDP.

• Group By This operation refers to a means of partitioning a data set into multiple disjoint parts and then performing some aggregate operation that summarizes each partition, and then combining these summaries into a new table. For instance, in the baby names data set, we could “GroupBy” year, so each partition would include the two rows for any given year, and then we could sum the count field in the partition. This would give us a table whose independent variable was year and whose dependent variable is the total applications for the top names in the year. In Chap. 8 we will see an example where we group countries by their region, and so obtain a new data frame with summary information on Asia, Europe, etc.

• Table Combination These operations allow us to take data that are in more than one table and combine them into a single table result. For example, if we wanted to combine our indicators data set with another data set containing health-related information on countries, we could join the two data sets together and so obtain more information per country than either data set had by itself.

• Transformations These can be complex operations that allow us to transform columns into rows or rows into columns, or perform a transpose on a table. These operations are used when we have data in a two-dimensional structure, but it does not satisfy the needed structure of the tabular data model (i.e., is not in tidy data form). Or, we might have data in a tidy data form, but want to transform it to create a view of the data that is easier to communicate information, or in preparation for a visualization. Because of their applicability in normalization, these operations will be covered in Chap. 9.

7.1.5 Reading Questions

7.1

Give an example of filtering in the context of the data set of top names.

7.2

Give an example where you might wish to update a column in place.

7.3

Give an example of a real-world situation that would require you to add rows to a data set.

7.4

Give an example of a real-world situation requiring you to delete rows.

7.5

Give an example when you might want to iterate over the rows.

7.6

What does it mean to “aggregate multiple columns at once?” Refer to the earlier discussion of aggregation and give an example.

7.7

We illustrated GroupBy with the example of grouping by the year. Give another example of GroupBy with a different variable in the same data set, and describe the resulting data set.

7.8

Give an example of a time when you have needed to transform a data set.

7.9

In previous data analysis work, have you ever needed to combine two different tables? If so, describe the situation. If not, think up an example where this would be important. If you cannot, refer to the exercises in Chap. 3, where such an example is provided.

7.2 Preliminaries and Example Data Sets

For use in illustrating operations in pandas, we will employ two different data sets (along with some variations thereof). One is the top baby names data set from earlier. The data set consists of 278 rows and 4 columns (year, sex, name, and count) of data, and has functional dependency:

We will use Python variable topnames0 to refer to the DataFrame that has only the default integer index for rows, and topnames to refer to the DataFrame that has the two-level index of year and sex, the independent variables of the data set.

The other data set consists of indicator data for a set of countries. The data set is organized as a single row per country with columns:

• code: the unique international three character code for the country.

• country: the English name of the country, including spaces and capitalization.

• pop: the population of the country, in units of millions of persons.

• gdp: the gross domestic product of the country, measured in units of billions of US dollars.

• life: the life expectancy of the country, in years.

• cell: the number of cell phone subscribers in the country, in millions of subscribers.

For this data set, the functional dependency is:

The pandas DataFrame with default integer index is referred to by the Python variable indicators0, and indicators is used for the DataFrame that uses code as the row label index. The data is obtained from the World Bank Open Data, and is available through the Creative Commons License. As in Chap. 6, we create the indicators DataFrame so that the index is the code column, giving us symbolic names for the rows.

To make it more manageable for the purposes of illustration, the indicators data frame is limited to just five countries (rows), and the data is only from the year 2017. The current entirety of the data set is presented in Table 7.1.

Table 7.1

World indicators 2017

Code	Country	Pop	Gdp	Life	Cell
CHN	China	1386.40	12143.49	76.41	1469.88
IND	India	1338.66	2652.55	68.80	1168.90
RUS	Russian Federation	144.50	1578.62	72.12	227.30
USA	United States	325.15	19485.39	78.54	391.60
VNM	Vietnam	94.60	223.78	76.45	120.02

In variations we will see later, we extend the data set to include information on the indicators for years from 1960 through 2017, and for approximately 120 countries. Because the indicators change over time, each of the indicator values is dependent on both country and year, so the functional dependency of the expanded data set becomes:

Pandas Terminology

We identify some of the terminology, attributes, and class types specific to pandas:

• Index is the class name for a collection of symbols/values used in referencing the set of rows or the set of columns of a data frame.

• index is an attribute that refers to the Index for the rows of a data frame. It can be as simple as a range of integers supplied by default at data frame creation, or can incorporate one or more of the original columns to uniquely identify rows through a hierarchical index (like year and sex in the top baby names example). These are also called the row labels.

• columns is an attribute that refers to the Index for the columns of a data frame. It, like index, can be as simple as a one-dimensional sequence of string column names, or can have additional complexity. These are also called column labels, and column names.

• Series is the class name for a one-dimensional sequence of data. It has a sequence of values, like the values in a column, or the values in a row, and also has an Index. The Index comes from the row labels when the Series is a column, and comes from the column labels when the Series is a row.

• DataFrame is the class name for a two-dimensional collection of data. It has a collection of columns, each a Series, supports an Index each for column labels and for row labels, and supports the tabular model operations.

When a package, like pandas, and its object classes are being designed in an object-oriented language, the designers have multiple tools enabled by the language at their disposal to provide functionality for their classes. These tools and features are used to provide the operations supported by the class. So in the pandas realization of data frames following, we will see the use of:

• methods—functions that operate on a data frame and are invoked by naming an object, naming the method, and passing arguments that govern the behavior of the operation.

• attributes—these appear as variable-like names composed of the name of an object and give access to data associated with an object.

• access operators—drawing from their use in lists and dictionaries, the access operator ([ ]) is used to give access to subsets of the data maintained by the object.

• operators—an object class can overload the meaning of familiar operators like +, − , *, and so forth, to define binary and unary operations that extend to the type of object.

7.2.1 Reading Questions

7.10

Using the topnames DataFrame, constructed in the previous chapter, give an example (listing all data) of a row Series, including the index.

7.11

Give an example (listing all data) of a column Series in indicators, including the index.

7.12

Give an example of a pandas method. We note that several were used in the previous chapter.

7.13

Give an example of a pandas attribute, in the context of the indicators DataFrame.

7.3 Access and Computation Operations

Some of the most common and fundamental operations are those that access and query data and allow computation on that data.

7.3.1 Single Column Projection and Vector Operations

This subsection looks at some pandas paradigms for projecting single columns and performing column-vector operations with those columns.

We can use access operators (square brackets) on a DataFrame object with a string column label as the indexer, just like we would a Python dictionary, yielding the column associated with the column name. When we project a single column in this way, we always obtain a Series as the projected column.

We illustrate with an example. From topnames0 we project and assign to names the name column of the data frame, and use head( ) ³ to get a prefix of the result:

| 0    Mary

| 1    John

| 2    Mary

| 3    John

| 4    Mary

| Name: name, dtype: object

Note how pandas displays a Series, with the index/value pairs first, followed by the metadata of the “Name” of the Series (the column name name, in this case), and the type of the data values in the Series (namely, object, which is the type pandas uses to denote a string). When we project the 'name' column from topnames, as opposed to topnames0, we get:

| year  sex

| 1880  Female    Mary

|       Male      John

| 1881  Female    Mary

|       Male      John

| 1882  Female    Mary

| Name: name, dtype: object

This result is still a Series, but here the index of the Series, coming from the index of the DataFrame, are comprised of year and sex values.

If a column is already defined (i.e., we are not in the process of creating it), and if the name of the column satisfies the requirements of a variable name,⁴ and is not the name of an existing attribute or method, then pandas gives us a shortcut for projecting a single column, by making the column name an attribute of the DataFrame object. So, from the indicators data frame, we can easily project the gdp column:

| code

| CHN    12143.49

| IND     2652.55

| RUS     1578.62

| USA    19485.39

| VNM      223.78

| Name: gdp, dtype: float64

In this example, the row label (code) is part of the Series object. If we had not created the data frame with code as its index, the data frame, and consequently, this Series, would have integers indexing the Series, just like our previous topnames0 example.

If we want to see or verify the type of an entity in Python, we can call the type( ) function with the object as an argument.

| <class 'pandas.core.series.Series'>

So we see that this single-column projection indeed yields a Series.

If we have a Series and wish to reference a single element within it, we can again use the access operator. The row label is used to specify the desired element. In this next example, we project the pop column, and then access and print the 'RUS' and 'USA' elements of the Series:

| 144.5 325.15

Similar to other two-dimensional structures, we can compose access operator use in a single expression. So, for example, accessing the 'USA' row of the 'pop' column could be accomplished by the expression indicators['pop']['USA'], where the indicators['pop'] part of the expression yields the column Series, and the ['USA'] operates on the Series to obtain the 'USA' element.

If the row label/index of a Series are integers, we would use integer indexing to access individual elements:

| Mary John Emma Liam

Series are powerful objects in their own right. We can work with Series as vectors, and perform operations in a vector-oriented way. Say for instance, we wanted to create a Series with 25% greater population based on the population column.

we want the vector

each of whose entries is 25% larger than the corresponding entry in the original vector population. In pandas, this is exactly what we do:

| code

| CHN    1733.0000

| IND    1673.3250

| RUS     180.6250

| USA     406.4375

| VNM     118.2500

| Name: pop, dtype: float64

Similarly, we can perform binary operations on two columns in vector fashion. If we wanted to create a Series vector calculating the number of cell phone subscriptions per person in a country, and given that the units of both are millions, we want:

and in pandas, we write:

| code

| CHN    1.060214

| IND    0.873187

| RUS    1.573010

| USA    1.204367

| VNM    1.268710

| dtype: float64

Contrast the ease of notation and readability of the operations shown above with what would be required of vectors represented as Python lists or dictionaries. These would require a for loop or a list comprehension to achieve the same result.

Vector-style operations on Series vectors are not limited to arithmetic operations. Consider the following example, where, on the right-hand side of the assignment, we specify a one-column projection followed by a relational operator and a scalar:

| code

| CHN    False

| IND     True

| RUS     True

| USA    False

| VNM    False

| Name: life, dtype: bool

The operation, elementwise, computes whether an element in the Series is less than the scalar value 75, and builds a new Series with the Boolean results of each of these condition results. So, in this example, the values at index IND and RUS met the threshold of being less than 75, and the other four did not. Such Boolean Series results are important, and form the basis of row-filtering.

We can also create more complex Boolean Series vectors using Boolean operators. In particular, we can use:

• ~, a unary operator to logically negate the elements of its Series operand,

• &, a binary operator to perform a binary and operation elementwise over the values of its two operands, and

• |, a binary operator to perform a binary or operation elementwise over the values of its two operands.

For instance, to build a Boolean Series for rows where life expectancy is not less than 75, and the GDP is at least 10 trillion, we can compute:

| code

| CHN     True

| IND    False

| RUS    False

| USA     True

| VNM    False

| dtype: bool

Instead of using intermediate variables like long_life and big_gdp, we can build a single more complex expression, using parentheses to achieve the needed functionality:

Another common-vector operation is the application of a unary function on each of the elements of a source vector to obtain a vector of resultant values, as discussed in Chap. 3. If the source vector is a Series, we can use the apply method on the source Series. The argument to apply is a function, and that function should take an element as a parameter and produce a value result. For instance, the len( ) function takes an object, like a string, and computes and returns an integer result. So len would be a function that satisfies the requirements for the type of a function that is needed by apply( ) .

In the following code, we apply the len( ) function to the string names of each of the countries to yield a vector of integers, where each element has the length of that country’s name:

| code

| CHN     5

| IND     5

| RUS    18

| USA    13

| VNM     7

| Name: country, dtype: int64

This is the Series vector equivalent of what we did with Python lists in Sect. 3.​1.​2. This technique can be used in general to obtain a unary operation on a Series. The function applied can be a built-in, like demonstrated here, or could be user-defined, or even be an anonymous function defined by a lambda expression.

7.3.2 Multicolumn Projection of a DataFrame

When we want to project one or more columns and want to yield a DataFrame instead of a Series, we employ a slightly different operation on a tabular data structure. In pandas, we still use the square bracket ([ ]) accessor with an existing DataFrame object, but the expression inside the square brackets is different. Instead of a single value of a column label, we can use a sequence, most often a list, that specifies the collection of columns to project.

To get the columns gdp and country, we create a list ['gdp', 'country'] and use it as the sequence argument of the square bracket accessors:

|            gdp             country

| code

| CHN   12143.49               China

| IND    2652.55               India

| RUS    1578.62  Russian Federation

| USA   19485.39       United States

| VNM     223.78             Vietnam

So the outer brackets are again being used to specify a query of the data frame, but the inner brackets are giving an explicit list of the desired columns by label. When using a list to project one or more columns, the elements in the list must match column labels of the DataFrame.

In this example, we requested the columns in an order different from their order in the DataFrame, and this requested order was respected in the result, so projection can also be used to retrieve columns in a new order.

We can also use a list of length one to obtain a DataFrame consisting of a single column. Consider the following two variations for getting the 'gdp' column from our indicators DataFrame:

The gdp1 assignment line obtains a single column projection in the manner discussed in Sect. 7.3.1, which yields a Series object. The gdp2 assignment line, on the other hand, obtains a single column projection as a one-column data frame in its own right, which means the type of gdp2 is a DataFrame.

| <class 'pandas.core.frame.DataFrame'>

7.3.3 Row Selection by Slice

Another common form of query access to a data frame is when we want a subset of one or more rows. When the order of rows within the data frame allows us to define desired subsets based on that order, pandas provides a syntax for easily expressing the desired rows using a slicing notation. In Python, we use slicing, incorporating one or two : characters along with specification of where to start, where to go to, and how to “step,” to define subset elements of a list. pandas uses this familiar notation to similarly specify a subset of elements in a DataFrame.

Whether or not the index of row labels for a data frame have been defined to be other than their default integers, there always exist integer-based positions for each of the rows and each of the columns in any DataFrame. These start at 0 and go up to the number of rows or number of columns minus one.

The syntax for a slice is:

The math-style square brackets here are distinct from Python bracket syntax; here indicating an optional element in the syntax. In the syntax, start specifies the position or label for the beginning of the set of items to be included, end specifies the position or label determining the end of the set of the items to be included, and stride specifies a step of how to proceed from one item to the next. If the : stride is omitted, the default stride is 1. If start or end is omitted, it indicates the beginning or end of the collection, respectively.

7.3.3.1 Position Slicing for Selecting Rows

In pandas, we can specify an integer-based slice inside the accessor operator brackets applied to a DataFrame, and this defines an operation that selects the specified rows (and all columns) from the DataFrame. This operation always yields a DataFrame result. Slicing using integers operates in the same way as slicing for a Python list, in that the slices defines the position “up to, but not including” the end item. For instance, in the indicators frame, we select the rows starting at position 3 and (using the default stride of 1) up to, but not including, position 5 (i.e., positions 3 and 4):

|             country     pop       gdp   life    cell

| code

| USA   United States  325.15  19485.39  78.54  391.60

| VNM         Vietnam   94.60    223.78  76.45  120.02

We select rows starting at the beginning and proceeding up to, but not including position 2:

|      country      pop       gdp   life     cell

| code

| CHN    China  1386.40  12143.49  76.41  1469.88

| IND    India  1338.66   2652.55  68.80  1168.90

7.3.3.2 Index Slicing for Selecting Rows

One of the advantages of pandas DataFrames over native structures is the facility for the row index, the logical names identifying rows based on a value or combination of values that uniquely identify a row. This uses the Index class of pandas. For instance, in our indicators data set, the code column gave three letter strings uniquely associated with each row. In our topnames data set, when we set the index to ['year', 'sex'], the combination of values of the integer year and string 'Female' or 'Male' identifies the row.

Using the row labels/index attribute, we can define a slice and specify a start and end where the values of these come from the row labels. For instance, we select the rows in indicators from CHN to RUS as follows:

|             country      pop      gdp   life     cell

| code

| CHN            China  1386.40  12143.49  76.41  1469.88

| IND            India  1338.66   2652.55  68.80  1168.90

| RUS  Russian Federation 144.50 1578.62 72.12   227.30

A notable difference from position-based slices for selecting rows: the end is inclusive, not “up to, but not including.” So in the above example, the 'RUS' row is included in the result.

The stride can be specified, and works as one might expect, so we can select rows in a descending position sequence by using a stride of − 1.

|                 country     pop      gdp  life    cell

| code

| RUS  Russian Federation  144.50  1578.62 72.12  227.30

| IND               India 1338.66  2652.55 68.80 1168.90

| CHN               China 1386.40 12143.49 76.41 1469.88

When we have a row Index that consists of multiple levels like in topnames with year and sex making up the two levels of the index, a value of a row label is a tuple with specific values at each of the levels. Then we can select rows using a slice where the start and end values are tuples:

|               name  count

| year sex

| 1950 Male    James  86224

| 1951 Female  Linda  73978

|      Male    James  87261

| 1952 Female  Linda  67082

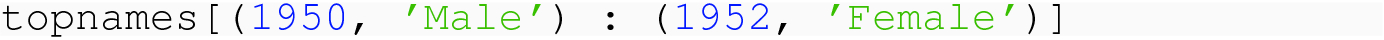
All of these types of row selection using slices depend on the order of the rows in the data set. The operation of setting an index does not change the order of the rows, and so one could imagine a data set where the row ordering did not follow a regular pattern and so did not enable effective slice-based row selection. One solution to this problem would be to perform a sort_index as a means of changing the order, and thus allowing the techniques in these last two subsections.

7.3.4 Row Selection by Condition

The ability to select rows by an order-based slice may not be sufficient when we are trying to use operations to query the data to obtain a subset that helps answer a question. We often want to perform row selection based on finding the rows that match a Boolean condition, a condition defined by values of the row label index and by values of certain column fields within the row. This is more commonly known as filtering, and was previously discussed in Chap. 3.

We know from Sect. 7.3.1 that we can define a column vector (Series) whose values are Boolean True and False based on column values:

| code

| CHN     True

| IND     True

| RUS    False

| USA    False

| VNM    False

| Name: pop, dtype: bool

Given such a Boolean vector, we can use square bracket accessor operators with a Boolean vector inside the brackets, and this serves to select exactly those rows for which the Boolean vector is True.

|      country      pop       gdp   life     cell

| code

| CHN    China  1386.40  12143.49  76.41  1469.88

| IND    India  1338.66   2652.55  68.80  1168.90

Often, if only used once, the Boolean vector is not assigned to an intermediate variable:

|      country      pop       gdp   life     cell

| code

| CHN    China  1386.40  12143.49  76.41  1469.88

| IND    India  1338.66   2652.55  68.80  1168.90

When we need more complex Boolean conditions, say to perform a logical OR operation, like finding the rows where population is greater than 1000 million people or where life expectancy is greater than 77, we need to perform an elementwise OR between two Boolean vectors. If we use intermediate variables for each of the conditions:

We then use the | as an or operator (see Sect. 7.3.1):

| code

| CHN     True

| IND     True

| RUS    False

| USA     True

| VNM    False

| dtype: bool

Then, indicators[combined] would select the desired rows returning the resulting DataFrame. Alternatively, we can specify the conditions directly inside the accessor operator:

|            country     pop      gdp  life    cell

| code

| CHN          China 1386.40 12143.49 76.41 1469.88

| IND          India 1338.66  2652.55 68.80 1168.90

| USA  United States  325.15 19485.39 78.54  391.60

Sometimes we need to add parentheses to force the precedence; to act as a Boolean logical operator on Series, the vertical bar must have operands that are Boolean Series vectors. In many_people | large_area, this is satisfied. If we were to write indicators['pop'] > 1000 | indicators.life > 77, the | would, by Python precedence, try to operate between the integer 1000 and the indicators.life Series, and would result in an error.

A common use of Boolean filtering is to filter out missing data. Whenever a data entry (characterized by its (row, column) pair) is missing, pandas represents that data entry by the special NaN. In pandas, the built-in pd.notna( ) (read “not N.A.”) takes as argument a Series and returns True for every row of the Series that does not represent missing data. The built-in pd.isna( ) has the logically opposite functionality. For example, if we were concerned that some rows of indicators might be missing the life expectancy data, the filter indicators[pd.notna( indicators.life) ] would yield only the rows where life expectancy data is present. We will return to missing data in Chap. 8.

In Sects. 7.3.1 through 7.3.4, we have seen the same operator syntax, the access operator ([]), be used to project a single column, project multiple columns, select rows by slicing, and select rows by condition filtering. To effectively use this operator, it helps to understand that pandas is using the type of the operand between the square brackets to determine the actual operation performed. Table 7.2 summarizes these operations supported by the access operator, when operating directly on a DataFrame.

Table 7.2

Operations supported by the DataFrame access operator

Access operator Arg type	Operation	Result type
String	Project single column by label	Series
List of strings	Project one or more columns by label	DataFrame
Integer slice	Select one or more rows by position	DataFrame
Non-integer slice	Select one or more rows by ordered row label/Index value	DataFrame
Boolean Series	Select zero or more rows by Boolean condition as filter	DataFrame

The pandas DataFrame provides two additional methods that give a specialized form of row selection based on a Boolean condition, and these do not use the access operator. Often we wish to select a set of rows whose values for a particular column are the largest (or smallest) among all of the rows in the data set. For these methods, we provide n, the number of largest (or smallest) rows to select, and the column label to be used in evaluating the value of the row.

In the following example, we select the five rows with the largest count column value in the topnames DataFrame:

|                 name  count

| year sex

| 1947 Female    Linda  99689

| 1948 Female    Linda  96211

| 1947 Male      James  94757

| 1957 Male    Michael  92704

| 1949 Female    Linda  91016

In similar fashion, the following expression selects the three rows in the indicators DataFrame with the smallest value in the life column:

|                country     pop      gdp  life    cell

| code

| IND              India 1338.66  2652.55 68.80 1168.90

| RUS Russian Federation  144.50  1578.62 72.12  227.30

| CHN              China 1386.40 12143.49 76.41 1469.88

7.3.5 Combinations of Projection and Selection

For any pandas DataFrame, .loc[] and .iloc[] are Python attributes of the DataFrame object that use square bracket accessors to flexibly specify rows and/or columns, enabling the combination of projection and selection in a single operation. The difference between loc and iloc is that loc is Index based, so its specification of rows and of columns is relative to the row label and column labels defined for the DataFrame. On the other hand, iloc is integer position based, and so for both rows and columns, the specification of rows and columns is based on the integer position of the rows/columns involved.

We always use square bracket accessors with either the .loc or the .iloc attributes. Inside the square brackets, we specify a first component that determines the desired rows, then a comma, and then a second component that determines the desired columns. This gives a row-comma-column notation familiar from algebra when subscripting two-dimensional variables. Syntactically, we have

This syntax specification can be translated as:

1. 1.

   Name the dataframe object.

    
2. 2.

   Append the loc or iloc attribute with a period.

    
3. 3.

   Follow the attribute with the access operator:

   • inside the access operator, compose a row specifier (rowspec) followed by a comma, followed by a column specifier (colspec).

    

The rowspec and colspec can range from identifying a single row and/or column to identifying all rows or all columns. For each of rowspec and colspec, the syntax variations define specification of either:

1. 1.

   Exactly one row or column of the data frame:

   • these are specified with a single value of an Index or a single positional integer.

    
2. 2.

   Potentially more than one row or column of the data frame:

   • these may be specified with a list, a slice, or a Boolean Series.

    

The next few subsections will cover some of the possibilities among these variations.

7.3.5.1 Access a Single Element

When accessing a single element in a data frame, we use a rowspec and a colspec that both specify exactly one row or column. This means, for loc that we use a value of the Index in each dimension, and for iloc we use a single integer position. In the indicators set, our Index are strings in both dimensions, so accessing the 'gdp' for 'VNM':

| 223.78

The result is a scalar with the data type of the entry. (So not, for instance, a DataFrame of one row and one column.)

In the topnames dataframe, the Index for the row has two levels, year and sex, and a value for a row is then a tuple, so we can access the top 'Male' name from 1961:

| 'Michael'

Using iloc on the indicators data set, if we know that the 'VNM' row is at position 3, and the gdp column is at position 2:

| 223.78

7.3.5.2 Querying a Single Column or Single Row

We can use slicing to specify potentially more than one row or to specify potentially more than one column, when the desired items are based on the order in the data frame. In the limit, a slice with no start nor end (i.e., : by itself) specifies all the positions.

So if we desire a single column, like cell, from the indicators data set, and all rows, we can use a rowspec of : for all rows, and the column label 'cell' to specify exactly one column:

| code

| CHN    1469.88

| IND    1168.90

| RUS     227.30

| USA     391.60

| VNM     120.02

| Name: cell, dtype: float64

The result is a Series, since the row dimension has (potentially) many elements and the column dimension specifies exactly one.

Similarly, if we want one row, like ( 1961, 'Female') and all columns from topnames:

| name      Mary

| count    47680

| Name: (1961, Female), dtype: object

We again get a Series, but since the data types of different columns may be different from one another, the type of the Series, dtype, is a generic object.

In both examples, one of the rowspec or colspec had exactly one in one dimension and potentially more than one in the other dimension, so it makes sense that the result is a one-dimensional Series.

The .iloc can be used in similar fashion, so to project the single column at position 1 and all rows from indicators:

| code

| CHN    1386.40

| IND    1338.66

| RUS     144.50

| USA     325.15

| VNM      94.60

| Name: pop, dtype: float64

obtaining the Series for the population column.

Once we have a Series result, we can obtain elements from within the Series using another access operator, and referring to elements by the appropriate label. So, if in the example above, we obtain a particular row, the top 'Female' baby name in 1961, and assign to a variable, we can then access the individual column elements 'name' and 'count':

| Mary 47680

7.3.5.3 Querying a Subset of a Single Column or Single Row

As opposed to using an unbounded slice (:) to specify all the elements in one dimension, we may wish to query a subset of the rows for a single column, or a subset of the columns for a single row. We have three options for specifying such a subset:

1. 1.

   Use a slice, but bound the start and/or end of the slice.

    
2. 2.

   Use an explicit list and, by Index value or by position, identify the exact items for the subset.

    
3. 3.

   Use a Boolean Series (like we did in Sect. 7.3.4), where the items corresponding to True values are to be included, and the items corresponding to False values are not.

    

Regardless of which of these three methods we use to specify the subset, if we combine, in the other dimension, with an exactly one specification for row or column, we will again obtain a Series result.

There are many permutations of specifying the rowspec and colspec when using .loc and .iloc, so in the following we just show a limited sample of examples. The one restriction is that, for loc, the values used in slices and lists must by values of the appropriate Index, and for iloc, the values used in the slices and lists must be integer positions.

In general, for both readability and for avoiding errors and fragile code that could arise when changes occur in the data frame, we prefer loc over iloc.

Suppose we want the 'count' column for the ordering of rows from ( 1990, 'Female') to ( 1991, 'Male') in topnames. We use a slice to specify the subset of rows, and a single value to specify the column.

| year  sex

| 1990  Female    46475

|       Male      65290

| 1991  Female    43478

|       Male      60785

| Name: count, dtype: int64

Or we might want the 'cell' column for those countries whose 'gdp' is less than 2000 million US dollars. We use a Boolean Series to specify/filter the rows, and use a single value to specify the column.

| code

| RUS    227.30

| VNM    120.02

| Name: cell, dtype: float64

If we want an explicit subset of the columns, say 'country', 'life', and 'pop' for the 'USA' row, we can do the following:

| country    United States

| life               78.54

| pop               325.15

| Name: USA, dtype: object

Lastly, we illustrate how to use .iloc to obtain the same result, by knowing that the 'USA' row is at position 3, and the desired columns are at positions 0, 3, and 1.

| country    United States

| life               78.54

| pop               325.15

| Name: USA, dtype: object

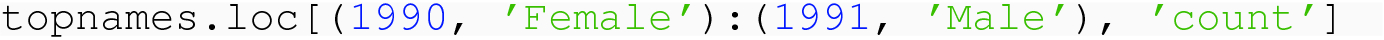
7.3.5.4 Generalized Projection and Selection

In the general case, we want, in a single operation, to project a subset of the columns as well as a subset of the rows. We already have the machinery needed to do this, and simply need to use both a rowspec and a colspec that specify potentially more than one item in the particular dimension. Our choices for these specifications are a combination, one per dimension, of

• a slice to specify the subset based on order,

• a list to explicitly specify the items in the subset, and

• a Boolean Series to allow a condition, obtained in a subordinate operation, to determine the subset.

Again, many permutations are possible, so we present an illustrative set.

Suppose, in the topnames0 data set, whose index is the default integer indices, we want to select rows where the count of applicants is more than 92000, and to select the explicit columns of 'count', 'sex', and 'year':

|      count     sex  year

| 134  99689  Female  1947

| 135  94757    Male  1947

| 136  96211  Female  1948

| 155  92704    Male  1957

We might want to select the explicit rows of 'RUS' and 'VNM', and project all the numeric columns, which are ordered from 'pop' to the end of the columns:

|         pop      gdp   life    cell

| code

| RUS   144.5  1578.62  72.12  227.30

| VNM    94.6   223.78  76.45  120.02

Many more examples are explored in the Reading Questions, and the reader is encouraged to approach them with a “problem-solving” mindset rather than a “guess and check” mindset. Think first about whether your DataFrame has an index, then which rows and columns you want, and then whether you want the result as a DataFrame, Series, or scalar. Once you are ready, carefully write down the access operator and test it.

7.3.6 Iteration over Rows and Columns

There are times when we need to process a data frame by operating row-by-row, or column-by-column over the entire frame. This, in fact, allows us to compose and build more advanced operations, like those for transforming and combining data frames. When operations are procedural, this requires the use of a for or while loop and, at each iteration of the loop, we must be able to obtain the information for the unit of iteration. For a column-by-column iterations, the information would be the label for the column, along with the column Series. For row-by-row iterations, the information would be the row label, along with a row Series.

While the pandas DataFrame class has a number of variations and methods that enable iteration, the most efficient of these provides an iterator that can be used in a for loop, and does so very efficiently, even for large data sets.

In our first example, we iterate over the rows of the indicators DataFrame. The iterrows( ) method gives the iterator to use in the for loop. At each iteration of the loop, the iterator yields the label of the row and the Series for the row, which in our example are associated with variables rowlabel and rowseries, respectively. In the body of the loop, at each iteration, we simply print the label and access the 'gdp' and 'pop' columns of the row.

| CHN: 12143.49 1386.4

| IND: 2652.55 1338.66

| RUS: 1578.62 144.5

| USA: 19485.39 325.15

| VNM: 223.78 94.6

The second value returned in each iteration, rowseries, is a pandas Series object. As we learned previously about a Series object, there is a pandas Index object along with the data itself, giving each element in the Series a logical name. When the Series is a row of the data set, the names of the individual elements are the column labels. This is why we can use the column name as the accessor value inside the square brackets (e.g., rowseries['pop']) to get, in dictionary-like fashion, the value associated with that element of the Series.

Column-by-column iteration is very similar. The iteritems( ) method provides the iterator for the for loop, and at each iteration, provides a tuple of a column label and a column Series. This is analogous to the dictionary items( ) method from Chap. 3. In the provided example, we iterate over the columns of topnames DataFrame. We use the Series to get the column label, and we use the Index to access the data desired. For a two-level index like in topnames, access involves a tuple, as shown below. We retrieve values for two specific rows, and for all columns.

| name: Mary Jennifer

| count: 47680 56783

If we employ the operation of iteration row-by-row, and, inside that loop, include an inner loop that iterates over all the elements of the row Series, we can individually access all table entries of a frame. We could accomplish the same thing with column-by-column iteration. But with the Series type of operations supported by pandas, there is little need for such algorithms.

7.3.7 Reading Questions

7.14

In order to project onto a column using its name, like indicators.gdp, it must be the case that the column name is not the name of an existing attribute or method. Give an example where this could fail.

7.15

When accessing an element in a data frame via double subsetting, what happens if you swap the rows and columns, e.g., indicators['USA']['pop']? Explain.

7.16

When accessing an element in a data frame via double subsetting, what happens if you combine the row and column identifiers, e.g., indicators[' pop','USA']?

7.17

We can multiply a Series by a number (e.g., population ∗ 1.25) and can divide one Series by another (cell∕population). Do you know another data structure with the same functionality?

7.18

What happens if you apply ~ to a Series of strings (instead of Booleans)?

7.19

Give a different example application of apply, using either a built-in function (but not len) or defining your own function.

7.20

Give an example of an application of apply using an anonymous lambda expression.

7.21

To better understand the difference between the Series gdp1 and the DataFrame gdp2, try to use the various Series built-ins on gdp2, including multiplication by a number, filtering by a Boolean condition, and apply. Which of these work?

7.22

Where have you previously seen something like stride?

7.23

It was a design decision to make slicing include its end row when index is used rather than position. Explain on a human level why this is a good design decision.

7.24

In the generic syntax for a slice, it says start:end[:stride], but the example in the text says indicators['RUS','CHN',-1]. Explain.

7.25

How does Python decide which countries should be included in a slice like indicators['CHN':'RUS']? Is it always alphabetical? What if someone wanted a slice by GDP?

7.26

The examples show how to get a subset of rows where a Boolean condition is True, e.g., with indicators[large_country]. How could you get exactly the rows where large_country is False?

7.27

Would it ever make sense to introduce a row of Booleans instead of a column of Booleans?

7.28

How do you think Python extracts the relevant rows when you call nlargest? If you were designing pandas would you have it sort every time? Justify your answer.

7.29

When using loc, what happens if you swap the rows and columns, like indicators.loc['gdp','VNM']?

7.30

Write a use of loc that specifies all columns, for the bottom three rows of indicators.

7.31

When using iloc and slicing, does it include both endpoints?

7.32

Write down three more example uses of loc, including 1. The GDPs and populations for China and the USA 2. All years where the count for male names in topnames was bigger than 60,000. 3. An example using slicing of both rows and columns.

7.33

What type of object do you get from indicators.loc[ ['VNM'], : ]? Explain.

7.34

The ability to iterate over rows and columns is a major upside of pandas data frames. Discuss how this functionality compares to list of lists and dictionary of lists representations of two-dimensional data.

7.35

Write three lines of code that iterate over the rows of topnames and print counts of male births in years like 1950, 1960, etc. Use an if-statement.

7.36

Write three lines of code that iterate over the columns of indicators and print every country name where life > 75 and gdp > 10, 000.

7.3.8 Exercises

7.37

Convert the following into a data frame and name it df:

[[1, 2, 3],[4, 5, 6],[7, 8, 9],

[10, 11, 12],[13, 14, 15],[16, 17, 18]]

Then display the data frame.

7.38

With reference to the above, assign the columns the following labels: “A,” “B,” and “C.”

Assign the rows the following labels: “U,” “V,” “W,” “X,” “Y,” and “Z”

Then, display the data frame.

7.39

In a single line of code, slice off everything besides the first 3 rows and 2 columns of the data frame. Call this new data frame df1. Then display the new data frame.

7.40

Convert the following dictionary to a data frame called df and compute the mean test score for Test1:

{'Name' : ['Owen', 'Rachel', 'Kyle'],

         'Test1' : [82, 85, 95],

         'Test2' : [89, 85, 90],

         'Test3' : [93, 85, 87]}

7.41

Print the following:

1. 1.

   The test scores of Test1

    
2. 2.

   Rachel’s test scores

    
3. 3.

   Kyle’s third test score

    
4. 4.

   Using indexing, the scores of Owen and Rachel

    

7.42

Add a column, “Final,” that equals the average of the three test scores, rounded to 2 decimal places. (You may need to explore the built-in function round( ) in addition to adding a column to a data frame based on a computation.)

7.43

Using the drop method, delete the column you just made.

7.44

Read the following into a data frame:

data = {'animal': ['cat','cat','snake','dog',

    'dog','cat','snake','cat','dog','dog'],

'age': [2.5, 3, 0.5, 7, 5, 2, 4.5, 4, 7, 3],

'visits': [1, 3, 2, 3, 2, 3, 1, 1, 2, 1],

'priority': ['yes','yes','no','yes','no',

             'no','no','yes','no', 'no']}

Using as index:

labels = ['a', 'b', 'c', 'd', 'e',

          'f', 'g', 'h', 'i', 'j']

Then, carry out a selection of rows d through g, inclusive.

7.45

Select the data in rows 2, 3, and 4 and project the columns “animal” and “age.”

7.46

Create and add a column age_visit which, for each row, is the age of the animal divided by the number of visits for the animal.

7.47

Select only the rows where the age is greater than 3.

7.48

Compute the sum of the number of visits of animals in the data set.

7.49

Project the animal and visits columns from those rows where priority is yes.

7.50

On the book web page you will find a data file us_rent_income.csv. Read it into a data frame, then:

1. 1.

   Extract the shape of the data into a variable called sh.

    
2. 2.

   Extract the list of estimate, into a variable called L (hint: be very careful about type).

    
3. 3.

   Define a list of Booleans K where K[i] is True exactly when variable[i] is income.

    
4. 4.

   Define a Boolean N which is True for any rows with missing data. Do this using a pandas built-in function, rather than by using the math module. The documentation will help.

    
5. 5.

   Use a projection or built-in function to define a new dataframe df2 consisting of only the rows of df without missing data.

    
6. 6.

   Create a new data frame df3, via slicing and iloc, corresponding to the rows that are about Ohio and the columns for variable and estimate. Your data frame should have two rows and two columns.

    
7. 7.

   Use a projection to define a new dataframe df4 consisting of only columns without missing data. Use loc.

    
8. 8.

   Create a new data frame df5 with the same rows as before, but with a new column CI defined as a string interval [estimate-moe, estimate+moe]. For example, in the first row, it would be [24476-136,24476+136], i.e., [24340,24612].

    
9. 9.

   Iterate over the rows to find the state with the largest income. Beware that this will involve checking the variable column to see if it says “income” or “rent.”

    

7.51

On the book web page you will find a file education.csv, based on data hosted by www.​census.​gov. Read it into a data frame, then:

1. 1.

   Extract the shape of the data into a variable called sh.

    
2. 2.

   Extract the Series of Geography.

    
3. 3.

   Write lambda functions to split a given entry (of the form shown in Geography) into city and state.

    
4. 4.

   Apply your functions to the Geography Series, obtaining new Series for city and state.

    
5. 5.

   Create a new data frame, via slicing and loc, corresponding to the rows that are about Ohio and the Estimate columns (but not the Margin of Error columns).

    
6. 6.

   Select 2–3 estimates you are interested in, then use a projection to reduce down to a smaller data frame with just the columns you are interested in.

    
7. 7.

   Get rid of the descriptive first row.

    
8. 8.

   Select a geography you are most interested in, then iterate over the columns to find the one with the largest Estimate.

    

7.52

On the book web page you will find a data file world_bank_pop.csv. Read it into a data frame, then:

1. 1.

   Extract the shape of the data into a variable called sh.

    
2. 2.

   Extract the list of years the data set concerns.

    
3. 3.

   Extract the list of countries the data set concerns. Be sure not to include duplicates.

    
4. 4.

   Extract a list of indicators present in the data. Do not include duplicates.

    
5. 5.

   Use row and column projection to reduce the data to just a few countries, a few years, and one indicator. Decide which based on your interests.

    
6. 6.

   Create a Series whose values are the log (base 10) of each of the total population values in the data set. Create such a Series, utilizing the numpy function log10( ) , which can operate on an argument that is either a one-column DataFrame, a Series, or a numpy array. Add this Series as a column.

    
7. 7.

   Iterate over the rows or columns of your resulting data frame to answer an interesting question.

    

References

1. 4.
   Codd, E.F.: A relational model of data for large shared data banks. Communications of the ACM 13(6), 377–387 (1970)Crossref

Footnotes

1

The term projection for access of one or more columns has been employed in the domain of relational algebra for relational databases from the beginnings of that theory [4].

 

2

The select term for access of one or more rows also has its origins in relational algebra.

 

3

In Sect. 6.​3.​2, we saw the use of head( ) to get a prefix of a DataFrame. Here, we see the same method is also defined for a Series, and has similar semantics.

 

4

Python variable names must begin with a letter or underscore, be composed of letters, numbers, and underscores, and have no embedded spaces or special characters.