Upon completion of this chapter, you should understand the following:
Mutation operations to update, add, and delete data.
Operations to group and aggregate data.
The need for operations specific to handling missing data.
Perform aggregations on single and multiple Series.
Aggregate and summarize information on group-based partitions of data frames.
Combine and update data frames.
Detect and mutate data frames to handle missing data.
Carry out these operations in pandas.
8.1 Aggregating and Grouping Data
In many analyses as well as in data exploration, we need to summarize data from a data frame in various ways. We may, for a single column, want to get some individual values that help characterize the data in that column, called aggregating, by finding its mean, median, max, min, and so forth. Sometimes we want a single aggregate for a column, but sometimes we want to compute multiple aggregates for a single column. We can extend this, and if we have a data frame with multiple columns of numeric data, we may want to characterize those multiple columns in a single operation, perhaps finding the mean for one column and the max and min for another column.
When the variables of a data frame allow us to define different row subsets of the data, we often want to compute aggregates for one or more of these subsets. This can allow us to focus on and characterize a single subset, or it can allow us to draw comparisons between the different subsets. An example is grouping countries by their regions of the world and computing aggregates over different regions. This kind of grouping often relies on the independent variables of the data frame, or values of other columns in the data frame, like columns containing categorical variables.
The collection of operations that support such aggregation and grouping are the subject of the current subsection.
8.1.1 Aggregating Single Series
The simplest form of aggregation occurs when we have a single Series, often a single column projection from a DataFrame, and want to compute one or more functions over the values in the Series. The pandas Series class defines methods that operate on a Series, and these methods include many/most that one might need. You will notice in the description that aggregation functions often omit missing values (values with a NaN entry in the DataFrame) from their computation.
Aggregation function/methods
Method | Description |
|---|---|
mean( ) | Arithmetic mean, not including missing values |
median( ) | Value occurring halfway through the population, omitting missing values |
sum( ) | Arithmetic sum of the non-missing values |
min( ) | Smallest value in the set |
max( ) | Largest value in the set |
nunique( ) | Number of unique values in the set |
size( ) | Size of the set |
count( ) | Number of non-missing values in the set |
Many of the methods are overloaded—they have the same name as built-in functions, so some may be invoked by passing the Series as the argument to the function, instead of invoking a method (with no argument) on a Series object. For example, if s is a Series of integers, then max( s) and s.max( ) compute the maximum value in s.
Aggregation to Series methods
Method | Description |
|---|---|
unique( ) | Construct a subset Series consisting of the unique values from the source Series |
value_count( ) | Construct a Series of integers capturing the number of times each unique value is found in a source Series; the Index of the new Series consists of the unique values from the source Series |


8.1.2 Aggregating a Data Frame

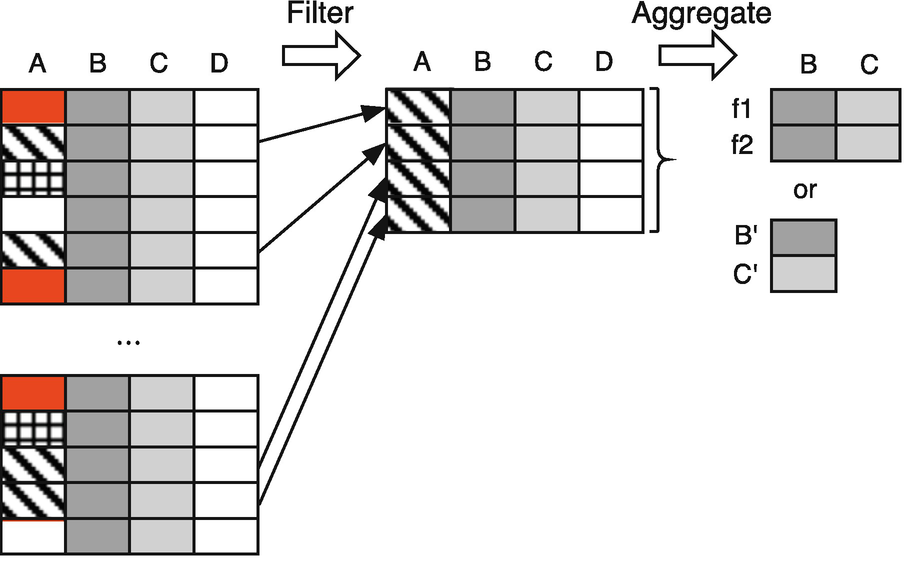
Aggregating a data frame
The left side of the figure depicts an original data frame with four columns, A, B, C, and D. Assuming that column A is a level of an index, or a column with a categorical variable, and, by color and shading, we see three different “categories” of values for A. Let us assume that columns B and C are numerical and are columns that we want to employ aggregation to characterize the data in the frame. Column D might be a string value and, by assumption, is not of interest in our aggregation. For example, suppose the source frame is our indicators data set, column A is the index (code), column B is the life expectancy column, and column C is the cell subscriber column.
The goal then is, starting with a source data frame, to perform an operation on the frame and get a result that is composed of (multiple) aggregations, e.g., the minimum life expectancy and median number of cell subscribers.
On the right side of the figure, column A is gone because we have aggregated over it. We no longer have one row per country, but now instead have one row per aggregation function. Figure 8.1 shows the general case, where, for any given column, we might apply multiple different aggregations. We show the result as a table in its own right, with columns corresponding to the columns from the original (B and C), and rows corresponding to different aggregation functions (f 1 and f 2, in this case). When, for any given column, we only have a single aggregation function, an alternative view of the result is as a vector, where the elements contain the particular aggregation for each of the requested columns. We label these as B′ and C′ to emphasize that they are different, by their aggregation, from the original column.
If f1 were the min aggregation and f2 were the median aggregation, the entries in the result would allow us to lookup, by the original column and aggregation function, each of the individual results. Suppose further that we wanted the min and median for the life column, but only the median for cell column. The figure would still be a valid representation of the result, but at column cell and row min, there would be a missing value (NaN), because we did not request to compute the minimum number of cell phone subscribers.
In pandas, we use the agg( ) method of a DataFrame to perform this general form of the aggregation operation. The argument to agg( ) must convey, for each column of the original DataFrame, what aggregation function or functions to perform. One way of doing is this is with a dictionary, where we map from a column name to a function or string function name, or to a list of specified functions.


The Index of the Series reflects the names of the columns being aggregated, but the information on what aggregation is performed is not part of the result.

This is like the prior example: since there is only a single aggregation function per column, the result is a Series containing the results. Also notice that pandas will, whenever possible, perform the aggregation over all columns. Here, the max( ) aggregation, when applied to the string column of country names, results in the alphabetically last country name of the collection.
8.1.3 Aggregating Selected Rows
Often, we wish to focus on a subset of a data frame and then characterize, through aggregation, the data within that subset. At one level, this is a composition of operations we have already seen:
- 1.
Create a subset by selecting just the rows in the data frame that form the subset, yielding a new data frame.
- 2.
Perform aggregation on the new subset data frame.
This “subset and aggregation” is also a critical piece in understanding the more general group partitioning and aggregation that is to follow, and so we will look at this limited example first.
Filtering and aggregating
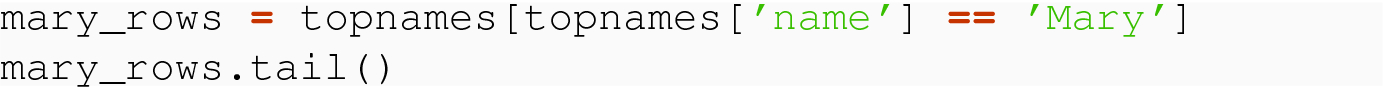
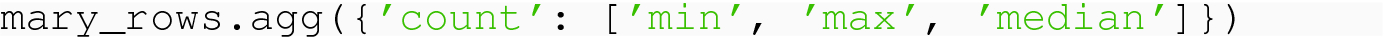
The result is a DataFrame with a single column, and the labels of the rows are the three aggregation functions.
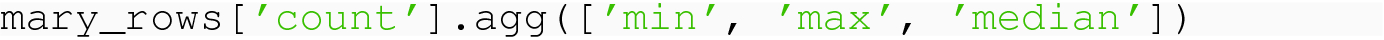
The result is a Series, with the row labels denoting the requested aggregations.
Sometimes when we wish to define a row selection, it is based on part of the row Index, not based on a regular column. This can occur when we have a multi-level index. Consider our topnames DataFrame. We may want a selection of rows that consists of just one of the sex values, like just the Female rows, which would be a subset that includes half the rows of the original DataFrame. Or, we might be interested in a row selection of a single year, say 1961, in which case the subset would consist of exactly two rows.

This allows us, in this case, to compare the application counts for when 'Mary' was the top baby name against the population of 'Female' entries overall.
8.1.4 General Partitioning and GroupBy

Partition/aggregate/combine
We call this partitioning to draw on the mathematical meaning: each and every row from the original is selected into exactly one of the sets. Following the figure, from left to right, we start on the left with a single data frame. The partitioning operation occurs, called a groupby operation (pronounced “group by”), yielding, logically, a set of data frames, each called a partition. Each of these partitions then has an aggregation performed upon it, and so, from each partition, we obtain a single row of values. Finally, the set of individual rows are combined to build a single data frame result. For our gender example, we would end up with three data frames after the groupby operation, one for each of “Male,” “Female,” and “Non-Binary.” The aggregation could then compute, for example, the number in each group, so that the resulting data frame would have one column (“number”) and three rows (“Male,” “Female,” and “Non-Binary”).
In general, for the aggregation, we need to yield a result that is a single row per partition. Each row contains a column corresponding to the column (or columns) that we use for the partitioning, known as the groupby column. By the definition of how the partitioning works, each discrete value in the groupby column yields exactly one partition and then exactly one row after the aggregation. So the values in the groupby column are unique, and in pandas, they form a row label index for the final combined result. In Fig. 8.3, A is the groupby column and so the unique values in A form the row labels in the final combined data frame.
For the rest of the columns in Fig. 8.3 that result from the aggregation, we use subscripts to denote that these are some aggregation function over the elements of some particular column and are not the same as the column itself. In the figure, we depict two different aggregations that are based on the B column, and one aggregation that is based on the C column. This would be like if, in our gender example, we originally had columns B and C for the salary and number of years of education and then in the aggregation computed the median salary and average number of years of education, for each of the three gender groups.

We see that partitioning by name yields 18 partition groups, which is the same as the number of unique names from the data frame. When we group by sex, we, as expected, get 2 partition groups, and when we group by year, we get 139 partition groups, one for each year in the data set.
To perform the aggregation step, we use the agg( ) method, defined for GroupBy objects in a fashion similar to the Series and DataFrame agg( ) methods. This lets us specify which columns and which aggregation methods to apply to each partition group. The result is the data frame obtained after both the aggregation step (to get a single row per partition group) and the combine step that concatenates these aggregation rows together.

The result shows how row and column Index objects are constructed when performing this kind of partition/aggregate/combine operation. The row labels come from the column specified in the groupby( ) , with a unique row per discrete value from the column. The column labels yield a two-level index, with the outer level determined by the column being aggregated, and the inner level determined by the set of aggregation functions applied to the column. This allows fully general aggregation over multiple columns and using multiple, different, aggregation functions.
8.1.5 Indicators Grouping Example
World indicators
Code | Country | Region | Income | Pop | Gdp |
|---|---|---|---|---|---|
AGO | Angola | Sub-Saharan Africa | Lower middle income | 29.82 | 122.12 |
ARE | United Arab Emirates | Middle East & North Africa | High income | 9.49 | 382.58 |
ARG | Argentina | Latin America & Caribbean | Upper middle income | 44.04 | 642.70 |
AUS | Australia | East Asia & Pacific | High income | 24.60 | 1330.80 |
AUT | Austria | Europe & Central Asia | High income | 8.80 | 416.84 |

The regions range from just two countries in the “North America” region to 24 countries in the “Europe & Central Asia” region.

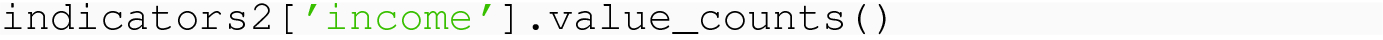


8.1.6 Reading Questions
Thinking back to what you know about data analysis, give an example when you might want multiple aggregates of a single column.
Give an example of an aggregate you might use on a column of string data.
At a high level, how do you think the method unique( ) is implemented?
At a high level, how do you think the method value_count( ) is implemented?
In the example that calls max, median, and nunique, what would happen if you called nunique on topnames0 instead of topnames0['name']?
Give an example of a data set of the sort described in the figures, i.e., with columns A, B, C, and D, where A has three levels (and multiple rows of each level). Then, give an example of two possible aggregation functions f 1 and f 2.
Give an example of a dictionary mapping from column names to lists of functions (rather than function names). Use more than just built-in functions. Hint: you do not need parentheses because you are not calling the functions.
The command indicators.max( ) applies the function max to every column. How would you change this command to perform the max aggregation for all the columns except the country column? Use the agg method.
Why is it that, “when the condition for the row selection is based on a value of an index level, rather than a value of a column, we cannot use a Boolean Series to obtain our subset”?
Write a sentence to explain why len( groupby_name) is 18, and why len( groupby_year) is 139, in the topnames example.
8.1.7 Exercises
Use agg to return a data set with the max and min counts per year in topnames for males born in the 1960s. Is your data set a DataFrame or a Series, and how do you know?
Write code to add a new column popSize to indicators, which takes value “high” if pop > 1000, “low” if pop < 100, and “medium” otherwise.
Building on the question above, use groupby to partition indicators by this new column popSize.
Building on the question above, use agg to report the average population in each of the three groups.
Use one line of code to sort indicators by pop and gdp. Warning: pay attention to your inplace settings.
Modify the indicators2 example to find the maximum and minimum population and GDP in each of the three income categories.
Modify the indicators2 example to project onto the columns country, pop, gdp, region for all lower middle income countries. Then find the number of countries in each region of the resulting data frame.
This is a pencil and paper exercise. Suppose we have the following data set named df, and our goal is, for column C, to add together values for various row subsets of the data, and for column D, to average values from that column for various row subsets of the data.
A | B | C | D |
|---|---|---|---|
foo | one | 0.4 | -1 |
foo | two | -1.5 | 0 |
bar | three | -1.1 | 1 |
bar | two | -0.1 | -1 |
foo | three | -1.0 | 1 |
Show the partitioning (i.e., the sets of rows) that would result if we did a GroupBy the A column.
Give the result of
dropping the A and C columns,
grouping by the B column, and
specifying aggregation by taking the mean( ) of the D column
df[[‘B’, ‘D’]].groupby(‘B’).mean()
On the book web page, you will find a file sat.csv, based on data from www.onlinestatbook.com. This data contains the high school GPA, SAT math score, SAT verbal score, and college GPAs, for a number of students. Read the data into a pandas dataframe dfsat with column headers. Use agg to compute the average of each numeric column in the data set.
On the book web page, you will find a file education.csv, based on data hosted by www.census.gov. Each row is a US metropolitan area, with data on population (row[3]), number unemployed without a high school degree (row[15]), number unemployed with a terminal high school degree (row[29]), number unemployed with some college (row[43]), and number unemployed with a college degree (row[57]). Read the data into a pandas data frame dfedu with column headers. Then use agg to compute the total number of people in each unemployment category and to report the fraction of unemployed people from each category.
The reading showed three ways to group the topnames data but only carried out agg using one of them. Use grouping and aggregation to produce a DataFrame containing the average number of male applications and the average number of female applications.
Similarly to the previous exercise, produce a DataFrame containing the maximum number of applications (regardless of gender) each year.
Similarly to the previous exercise, find the year that had the maximum number of applications (regardless of gender).
To practice with a two-level index, use read_csv to read
8.2 Mutation Operations for a Data Frame
Up to this point, we have learned operations to project columns and select rows from a data frame, as well as partitioning and aggregating data frames, but none of the operations have modified an existing data frame. To achieve our needs for specific domain and analysis goals, and for normalizing data frames, like we do in Chap. 9, we also need to perform such update operations, as summarized previously in Sect. 7.1.
Because pandas is implemented to take advantage of many of the object-oriented facilities in Python, much of the syntax learned in Sect. 7.3 will be used in similar fashion for mutations, often with the specification of data frame rows, columns, and subsets on the left-hand side of an assignment.
In what follows, we will primarily use the indicators data set for each of the examples. Each of the examples will start from the same initial state, with the indicators data frame as shown initially in Table 7.1, with information on five countries from 2017, an index of code, and columns of country, pop, gdp, life, and cell. The first step in each example will be to copy the original data frame, since many mutations will change the data frame directly, and we want to maintain the original.
8.2.1 Operations to Delete Columns and Rows
8.2.1.1 Single Column Deletion
When we wish to delete a single column from a DataFrame, the easiest method is to use the Python del statement, using an argument specifying the single column. This is accomplished with the access operator using a column label.



8.2.1.2 Multiple Column Deletion

The axis=1 argument indicates the “dimension” for what is to be dropped, in this case, 1 indicates the column dimension (and an axis of 0 would indicate the row dimension).

8.2.1.3 Row Deletion

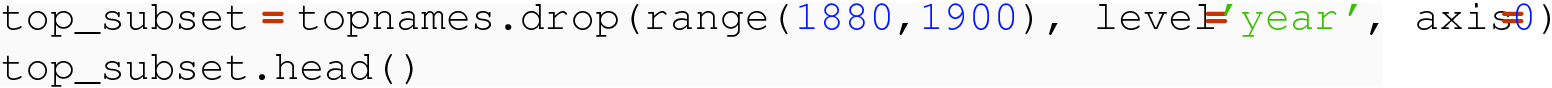
So in this example, we dropped all rows in the range of years from 1880 up to 1900 and did not have to specify the sex level.
8.2.2 Operation to Add a Column
One of the most common mutation operations is the addition of a new column to an existing data frame. The values of a new column is normally a Series (or other list-like set of values of the proper length) that is specified on the right-hand side of an assignment. We can also specify a scalar assignment to a new column, which would create the column as a Series with the scalar value repeated for the length of the vector, e.g., adding a column with value “Male” for every row of a data set of male individuals, perhaps in preparation for combining the data set with a different data set of females.
The left-hand side of these assignments uses the same notation we use for a single column projection we learned previously: the name of the data frame followed by the access operator with a column label between the brackets.
So the right-hand side could use the single column projection of one or more existing columns and perform column-vector computations to realize a new Series. This is then assigned, using the column label on the left-hand side to give a name to the new column. In the following example, we compute a Series based on a scalar multiple of an existing Series to get a 15% growth in GDP. We also carry out a vector division of two Series to compute the number of cell phone subscriptions per person in a country.


When pandas uses a list of column names for projection, the result is actually a view or reference to the columns as they reside in their original data frame. For read-only access to the data, this is much more efficient, particularly for large data sets. However, if, after projecting the columns, the result is then updated, perhaps by adding a new column, then pandas does not know if the programmer’s intent is to add a column to the subset data frame, or to add a column to the original data frame. The reader may be familiar with this phenomenon from a previous study of lists in Python, as an analogous issue motivates the use of the copy( ) function.
For example, when we set country_cell = indicators[['country', 'cell']], the new data frame country_cell is bound to indicators, so that changes in indicators will cause changes in country_cell. This means, if we later add a column to country_cell, pandas will be confused as to whether or not to add the same column to indicators and will produce an error stating "A value is trying to be set on a copy of a slice from a DataFrame."

8.2.3 Updating Columns
Instead of creating an entirely new column in a data frame, we often want to change values in an existing column.
8.2.3.1 Update Entire Column


Like creating new columns, the right-hand side of the assignment for a column update operation can utilize all the column projection and column-vector computation operations we have learned previously.
8.2.3.2 Selective Column Assignment
When we wish to change a subset of the values of an existing column, we need a mechanism to specify which row positions should be updated. In pandas, we use the same mechanism that we use to select row positions in a filter—the Boolean vector, where values in the vector of True mean that the column’s row position should be updated, and values in the vector of False mean that the column’s row position should be left at its current value.


We get the desired result where just 'CHN' and 'USA' rows of the column are updated. From our understanding of .loc and .iloc in Sect. 7.3.5, we can generalize our selective update and use .loc and .iloc and specify rows by explicit list and by slice as well as by Boolean Series.
8.2.4 Reading Questions
Why is it important to maintain a copy of the original data frame? Give an example of a previous time you needed to retain a copy of the original data.
Does the drop( ) method have the same functionality as iterated calls to del?
Give a real-world example where you would use drop( ) with axis = 0.
After popping 'code' from ind2, into a variable code_series, how could we create a new column in the data frame with the same value as code_series? In other words, how could we put 'code' back into the data frame?
Check out the online documentation for the insert( ) command in pandas, and then write down a line of code that would insert a column named 'code', with values code_series, in position index 2, into ind2.
Can you use apply on a whole data frame instead of just a single column? Explain.
The reading highlighted the importance of the copy( ) method, when working with a subset of the columns, as in country_cell = indicators[[ 'country', 'cell']].copy( ) . Give another example of a time in your life that failing to work with a copy could confuse Python about where you meant to change something.
Run the following code, and then explain precisely why Python gets confused.
The reading shows how to update the 'CHN' and 'USA' rows of ind2 to add 5 to the values in the life expectancy column. Show how to do the same thing using iloc.
Read the online documentation about sort_values( ) in pandas and then show how to mutate the ind2 data frame to sort it by the values in the life expectancy column.
8.2.5 Exercises
On the book web page, you will find members.csv, with (fake) information on a number of individuals in Ohio. We will use this for the next several exercises. Read this data set into a pandas DataFrame using read_csv. Name it members0, and do not include an index.
Repeat the above, but now do include an index, by specifying index_col in the constructor. Name your DataFrame members.
Write a projection that will isolate just the 'Phone' column into a variable phone_series. What type are the values in this column?
Write a selection that will isolate just those rows where the phone number starts with a 614 area code. Selection involves picking which rows will be shown.
In order to complete this:
- 1.
Write a lambda function that will, given a string, isolate the first three characters and compare these to '614'.
- 2.
Apply the lambda function to the column you isolated in the last question.
- 3.
Use the result as an index to the pandas DataFrame.
- 1.
Write a lambda function that will, given a string, split on space and select only the first element in the resultant list.
- 2.
Apply the lambda function to the Name column, and save the result.
- 3.
Access the data frame text using a new column name (FName), and assign the result from step 2.
- 4.
Acquire the last name from the Name column and create a new column in the data frame called LName.
- 5.
Acquire the city from the Address column and create a new column in the data frame called City.
- 6.
Acquire the state from the Address column and create a new column in the data frame called State.
- 7.
Drop the original “Name” and “Address” columns.
- 1.
Read the data into a pandas data frame dfsat with column headers.
- 2.
Add a new column 'total_SAT' containing the total SAT score for each student, calling the resulting data frame dfsat2.
- 3.
Add a new column 'GPA_change' with the change in GPA from high school to college, calling the resulting data frame dfsat3.
- 4.
Update the column 'total_SAT' to scale it so that the max score is 2400 instead of 1600 (i.e., multiply each entry by 1.5).
- 5.
Delete the column 'total_SAT', calling the resulting data frame dfsat5.
Building on the exercise above, create a new column that partitions students by their high school GPA, into groups from 2.0 to 2.5, 2.5–3.0, 3.0–3.5, and 3.5–4.0, such that each group includes its upper bound but not its lower bound. Then use grouping and aggregation to compute the average of each numeric column in the data set.
On the book web page, you will find a file education.csv, based on data hosted by www.census.gov. Each row is a U.S. metropolitan area, with data on population (row[3]), number unemployed without a high school degree (row[15]), number unemployed with a terminal high school degree (row[29]), number unemployed with some college (row[43]), and number unemployed with a college degree (row[57]). Read the data into a pandas data frame dfedu with column headers. Create a new column 'total_unemployed' with the total number of unemployed people in each metro area (i.e., the sum of the columns just listed).
Building on the exercise above, use a regular expression to extract the state (e.g., 'TX') from the geography column, and add state as a new column in your data frame. Then use grouping and aggregation to compute the total number of people in each unemployment category, in each state.
Building on the exercises above, enrich your data frame with a column containing the population of each state and then use grouping and aggregation to compute the per capita total unemployment in each state.
8.3 Combining Tables
The operations associated with combining tables will, in pandas, use two source DataFrame objects with a goal of a single resulting DataFrame that has some union or intersection of the rows, columns, and values from the source data frames.
The need for combining tables comes up most often when:
We have one data set with a particular set of columns and need to append by adding additional rows, but with the same set of columns. This could be indicative of a “growing” data set, perhaps along a time dimension, where the variables remain the same, but additional rows mapping the independent variables to the dependent variables are to be appended.
We have two data sets with, logically, the same set of rows, but with different columns, and want to create a data set with those same rows and the columns from both the source data sets. Here, we are adding new variables with their corresponding values to the data set, e.g., to enrich an old data set with more information on each individual.
We have two tables that are related to each other through the values of a particular column or index level that already exist in both tables. Here we want to combine the tables so that the values of columns of the source tables are combined, but constrained to the matching values. We saw an example, in Chap. 6, of combining tables on classes and students to get information about which students are in which class sections.
We will deal with each of these cases in turn, showing a representative example, and limiting ourselves to two-table combinations. There are many variations possible when combining tables that are DataFrame objects. One source of variation comes about depending on whether or not we have a “meaningful” index for row labels or column labels. By this we mean, for instance, that for a row index, the index and its levels capture what makes rows unique vis-a-vis the independent variables of the data set.
In Chap. 12, we will examine more deeply some of the same table combination concepts in the context of the relational model.
8.3.1 Concatenating Data Frames Along the Row Dimension
For the examples and use cases we illustrate here, we make the assumption that, for the tables being combined, the source data frames represent different information. When combining along the row dimension, that implies that there is no intersection of value combination of the independent variables (i.e., the same mapping is not present in both data frames). Because pandas is designed to be general purpose for more than data frames that conform to the tidy data standard, the operations to combine tables have many additional arguments that can perform, for instance, union or intersection of columns when this assumption is not met. But these variations will not be covered here.
When we want to concatenate along the row dimension, we are referring to the situation where we have two source data frames, each with the same set of columns, but, at least logically, rows that are non-intersecting between the two source data frames.
8.3.1.1 Meaningful Row Index
In normalized tidy data, a row index is meaningful if the index is composed of the independent variable(s) of the data set. So if a data set has one independent variable, the value of that variable is unique per row, and the remaining columns give the values of the dependent variables. For instance, the code variable is independent for the indicators data set, and the values of this variable form the row label index. In the topnames data set, the year and sex variables are independent, and the combinations of year and sex give the row labels for the data frame.


How the two source data frames might be obtained or constructed does not matter, but that they have the same columns and different rows, and a meaningful index, where the row labels give the independent variable code does.
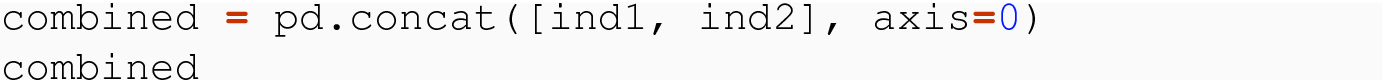
The order of the result is based simply on the order of the data frames in the list, and no sorting occurs.
8.3.1.2 Meaningful Index with Levels


If we want to combine these into a single, tidy data frame, we are, in essence, adding an independent variable of year, so that each row in the result is uniquely identified by the combination of a year and a code.
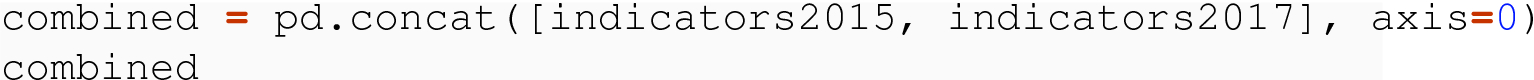


8.3.1.3 No Meaningful Index
As we manipulate data frames, even ones that satisfy the structural constraints of tidy data, we often process through cycles where the index of a data frame has been reset, or, on first construction, has only the default integer index for the row labels. When we combine such tables through concat( ) , we need to understand what happens.


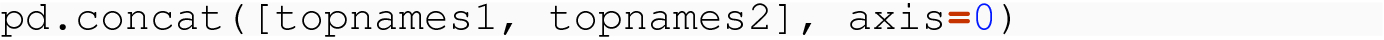
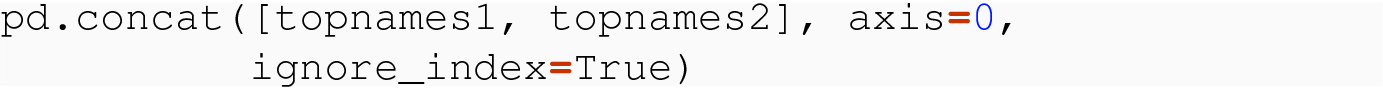
8.3.2 Concatenating Data Frames Along the Column Dimension
For combining data frames along the column dimension, we make assumptions similar to those made in Sect. 8.3.1. When we are using tidy data and we want to combine tables, we assume that the two source data frames have the same rows and an entirely different set of columns. In tidy data, the stipulation of the same rows means that the values of the independent variables are the same, and here we assume that they are incorporated into a meaningful index, and the stipulation of different columns means the data frames have different dependent variables. Since we use the names of variables as the column labels, we rarely have columns whose Index is generated by pandas.
8.3.2.1 Single Level Row Index and New Columns


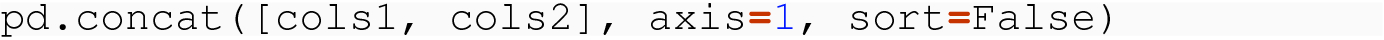
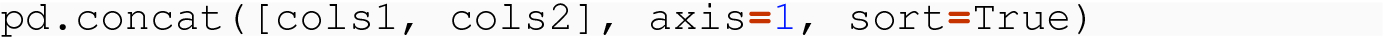
8.3.2.2 Introducing a Column Level
Having discussed data frames with a two-level row index, we now briefly explain the concept of a two-level column index, and how to create one during a concatenation, again using the keys= named parameter. We will also use this as an opportunity to introduce an unfortunate common form of untidy data, where columns represent years. We will see in Chap. 9 how to wrangle such data into tidy form, with a column called year and years represented in the rows where they belong.


While the tables females and males are not tidy, they do satisfy the initial assumptions of this section that the two tables have the same rows (name and count) and the columns have all logically different data, even if some of the column names are the same.

The use of the argument axis=1 tells pandas that both the concatenation and the index setting are occurring in the column direction. The name for the new column level is sex. In Chap. 9, we will see how to extract data out of a column index and reshape the data into tidy form.
8.3.3 Joining/Merging Data Frames
When combining data from two frames becomes more complicated than concatenation along the row or column dimension, as with the example of combining data on students with data on classes (Fig. 5.1), we need a more powerful tool. The pandas package provides two variations, depending on the frames we are combining, and whether or not we match up rows of the two tables based on their row label index, or on values from a regular column.
One variation, the join( ) , is a DataFrame method and uses the row label index for matching rows between the source frames. The other variation, the merge( ) , is a function of the package and can use any column (or index level) for matching rows between the source frames. The combined frame has columns from both the original source frames with values populated based on the matching rows. If the two frames have columns with the same column name, the join/merge will include both, with the column names modified to distinguish the source frame of the overlapping column. If we had three pandas DataFrames representing the three tables of Fig. 5.1, we could join/merge schedule and classes along the column classRegNum to get a single table with the six distinct columns contained in these two tables.
8.3.3.1 Using Index Level
Suppose we have a one-level index, the code, in the indicators data set, and we have one data frame, join1, that has columns for imports and exports, and another data frame, join2, that has columns for the country name, country, and the land area of the country, land. These two data frames might, in fact, come from different sources and might have code row labels that are not identical.




Both have the same independent variable, code, and so we could want to combine the tables so that matching codes yield rows with the union of the dependent variable columns, e.g., GBR would now have data on imports, exports, the country name, and the land mass. It is essential to note that the code values between the tables may not all match up. In this case, join1 has a row for CAN that is not in join2, and join2 has rows for BEL and VNM that are not in join1. There are several choices for what to do with the partial data present for these three rows, and the choice is made based on the analysis one desires to carry out.

So we see the appropriate values for the matched rows, and missing values where the right-hand frame did not have a match to correspond to the left frame. In this situation, we think of the left frame as being dominant, and taking whatever values it can from the right frame, to enrich rows present in the left frame.
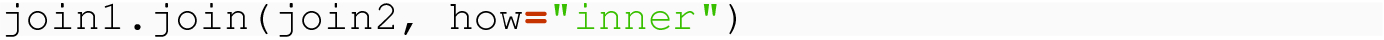
The result includes just the two rows where code is in common between the two frames, namely GBR and USA. In this case, we think of the new table as sitting between the two old tables, and drawing from both sides, whenever the same code is present in both.

Rows BEL and VNM are present in join2 but not in join1, so these are the ones that are augmented with missing values for the join1 columns.
There also exist join types of a right join where the right-hand frame has all its rows included, and we fill in with missing values for unmatched rows from the left-hand frame, and an outer join that includes all rows from both source frames.



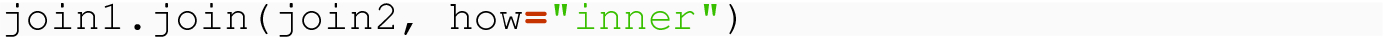
Note how, in the result, we have redundant data in the country and land columns. Care needs to be taken so that redundant data does not cause inconsistency problems if data frames are updated, but the possibility exists that such updates might not be applied to all instances of redundant data. In Chap. 9, we discuss how such redundant data is a sign that two different tables have been combined but, by TidyData3, should be separate.
8.3.3.2 Using Specific Columns
Sometimes, we wish to combine two tables based on common values between the two tables, but the values are in a regular column and not part of an index. This could be because the column is, in fact, not an independent variable and would not be part of an index, or it could be because, for the sake of manipulation and transformation, we have a column that could be an index, or a level of an index, and is not. Both cases come up frequently. For example, with indicators, we could reasonably use either the country code or name as an index and (based on the specifics of the table we combine with) might need to combine using whichever is not the index.
Logically, the operation is like the join( ) we have examined above, but, without the extra knowledge of index levels, we need to call a different method, called merge( ) , and we need to provide additional information to make the table combination possible.
Consider the two data sets we have been working with in this chapter: the topnames has, by year and by sex, the name and count of the top application for the US social security card. In the full indicators data set, we have, among other things, the population for each of the countries, including the population for the USA. We might want to create a new data frame based primarily on the topnames data set, but where we augment each row with the US population for that year. That could be used, in an analysis, to divide the count of applicants by the population for that year to be able to see what percentage of the population is represented. This could give a more fair comparison as we try to compare between years, because an absolute count does not take into consideration the changes in the population over time.

Note that the units of the pop column are in persons, not in millions of persons, like our earlier examples.

The merge( ) function has, as its first two arguments, the two DataFrame objects to be combined, where the first argument is considered the “left” and the second argument is considered the “right.” The on= named argument specifies the name of a column expected to exist in both data frames and to be used for matching values. The how= named parameter allows us to specify the logical equivalent of an inner join, a left join, or a right join.
In the following code, we show both a left join/merge and an inner join/merge. Since topnames0 is the “left,” the first will give us all the rows of topnames0 and will add the pop column from matching rows in us_pop. For those rows and years where us_pop does not have population data (i.e., those years before 1960), the merge1 will have NaN indicating missing data.


The merge( ) function is quite versatile and can be used for almost all the variations of combining taken covered in this section. It can also be used for hybrid situations where the criteria for matching rows between two tables might involve an index or index level from one source frame, and a regular column from the other source frame. See the pandas documentation for all the parameters that make this possible.
8.3.4 Reading Questions
Give a real-world example of two data sets with the same set of rows, but with different columns, that you might want to combine.
Give a real-world example of two tables that are related to each other through the values of a particular column, where you might want to combine the tables based on matching values.
What could go wrong if you try to naively concatenate two data frames along the row dimension, when they do contain rows with the same row index? Give an example.
Consider the code that concatenates indicators1 and indicators2 by row (axis=0). Suppose that, when defining indicators1, we use the code
indicators1 = indicators.loc[['CHN', 'IND', 'USA'], 'life' ] instead of
indicators1 = indicators.loc[['CHN', 'IND', 'USA'], :'life' ] Explain what happens in combined and why.
What happens if we use concat with ignore_index = True on a data frame that does have a meaningful index, like 'code' in indicators?
Consider the example of concatenating data frames along the column dimension. When you do this with a command like pd.concat( [cols1, cols2], axis=1, sort=True) , what field does it sort based on?
Give a real-world example, different from the one in the book, when you might want to combine two data sets with the same rows but different columns, along a column level. Does your example represent tidy data? Why or why not?
Is the inner join symmetric? In other words, does it matter if you do join1.join( join2, how="inner") or join2.join( join1, how="inner") ?
Do you get the same data by doing join1.join( join2, how="left") versus by doing join2.join( join1, how="right") ?
Give a real-world example, different from the one in the book, plus a reason you might want to do an inner join instead of a left or right join.
What happens if you use join when you meant to use merge, i.e., on a column that is not an index?
What happens if you use merge when you meant to use join, i.e., on a column that is an index?
8.3.5 Exercises
On the book web page, you will find two csv files, educationTop.csv and educationBottom.csv, both based on data hosted by www.census.gov. Both have the same columns, and each row is a US metropolitan area, with data on population, education, and unemployment. The first csv file contains metropolitan areas starting with A–K, and the second starting with L–Z. Read both into pandas data frames, using the column GEO.id2 as an index. Concatenate these two data frames along the row dimension (with the top one on top), and call the result educationDF.
On the book web page, you will find two csv files, educationLeft.csv and educationRight.csv, both based on data hosted by www.census.gov. Both have the same rows, and each row is a US metropolitan area, with data on population, education, and unemployment. The first has information on individuals without a college degree, and the second has information on individuals with a college degree. Read both into pandas data frames. Concatenate these two data frames along the column dimension, and call the result educationDF2.
On the book web page, you will find two csv files, educationLeftJ.csv and educationRightJ.csv, both based on data hosted by www.census.gov. In both, rows represent US metropolitan area, with data on population, education, and unemployment. However, they do not have exactly the same set of rows, and the columns are totally different except for the index column Geography. 0. Read both into pandas data frames, with names educationLeftJ and educationRightJ. 1. Make a copy of educationLeftJ called educationLeftOriginal. 2. Starting with educationLeftJ, do a left join to bring in the data from educationRightJ, storing your answer as dfJ. 3. Starting with educationLeftOriginal, do an inner join to bring in the data from educationRightJ, storing your answer as dfJ2. 4. Now read the original csv files in as eduLeft and eduRight with no meaningful index. Then, starting from eduLeft, do an inner merge along the column Geography, storing your answer as dfJ3.
Finish the application from the end of the section. This means, merge together topnames0 and us_pop, using whichever type of join is appropriate for this application, and then normalize the application counts by pop. Use the resulting data frame to find the highest and lowest percentage counts over the years, and think about why a social scientist might be interested in this kind of information.
8.4 Missing Data Handling
We conclude with a brief discussion of the issues that arise with missing data. As we have seen, both join and merge operations can easily produce missing data. So can operations that create a new column, e.g., life∕cell if a row had 0 for cellphones. Lastly, many data sets encountered in the wild are missing data, as the following examples illustrate. Missing data can occur when:
Individuals do not respond to all questions on a survey.
Countries fail to maintain or report all their data to the World Bank.
An organization keeping personnel records does not know where everyone lives.
Laws prevent healthcare providers from disclosing certain types of data.
Different users of social media select different privacy settings, resulting in some individuals having only some of their data publicly visible.
Many other situations analogous to these.
When encountered in the real world, there is no true standard by which data sources denote (or “code”) missing data. For example, a provider of healthcare data may code missing white blood cell counts as 0, knowing that no reader versed in healthcare would ever think that an individual truly had no white blood cells. In this situation, blindly applying an aggregation function (like mean( ) ) could result in a badly wrong result. Even worse, some providers code missing data using a string, like "N/A", "Not Applicable", "Not applic.", "NA", "N.A.", etc. Such a situation can entirely break simple code, e.g., that reads from a CSV file into a native dictionary of lists and then invoking an aggregation function.
Thankfully, information on how missing data is coded is almost always contained in the metadata associated with the data set, sometimes called a codebook. Whenever investigating a new data source, the reader should seek out this metadata and learn how missing data is coded, before attempting to read the data into native data structures or pandas. If there is no associated metadata, then it is usually possible to figure out how missing data is coded by a combination of the following steps:
Careful inspection of the data in its original format.
Visualizations (e.g., histograms and scatterplots), to look for data values that stand out from the rest.
Consultation with an expert, to learn about conventions in the field, and about which data values look unusual or impossible.










If we prefer to fill in nan values with some specific scalar, this can be done with the fillna option, but we will not need that functionality. It would be appropriate, for example, if we had survey data and one column asked if individuals were willing to be contacted for a follow-up survey. If a survey recipient left that question blank, we could probably safely fill in the answer “No.”
Lastly, it is common for a CSV file to have blank cells for missing data, e.g., the line "Michael","Male",,"35" means the third column is missing. The pandas.read_csv( ) method will automatically read such missing cells in as nan in the relevant row–column location, and hence the methods of this section apply.
8.4.1 Reading Questions
Have you ever analyzed a data set with missing data? If so, how were missing values coded?
Have you ever analyzed a data set with an attached codebook? If so, describe the data set and codebook. What kind of information was in the codebook?
The developers of Python made a design decision that adding a number and nan should yield nan. The developers of pandas made a design decision that methods should ignore nan values. What considerations do you think went into those design decisions?
In the reading, we discussed several options for dealing with missing data, including replacing aggregates by nan when nan data is encountered, ignoring nan data, dropping nan data, and filling in a single scalar value for all nan data encountered. Can you think of other ways of dealing with missing data?
Imagine at a scatterplot with a regression line, based on a data set of individuals where you know the age and salary of each. Suppose you want to predict the salary of a 32-year old, but none of the individuals in your data set were 32. What technique could you use to predict the salary of a 32-year old based on the other data that you do have? Could an approach like this be used to fill in missing data? Would it always work?
The book web page has a file, indicators.csv, with our indicators data for many countries, from 1960 forward. It has tons of missing data (e.g., because there were no cell phones in the 1960s). Use pandas to read this data into a DataFrame, then illustrate each of the functions from the reading on that DataFrame. Please use the cell column when you illustrate the fillna( ) function, and remember that there were no cellphones before 1980.