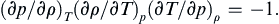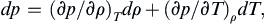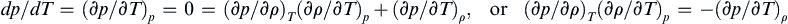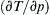1.8. Classical Thermodynamics
Classical thermodynamics is the study of equilibrium states of matter, in which the properties are assumed uniform in space and time. Here, the reader is assumed to be familiar with the basic thermodynamic concepts, so this section merely reviews the main ideas and the most commonly used relations in this book.
A thermodynamic system is a quantity of matter that exchanges heat and work, but no mass with its surroundings. A system in equilibrium is free of fluctuations, such as those generated during heat or work input from, or output to, its surroundings. After any such thermodynamic change, fluctuations die out or relax, a new equilibrium is reached, and once again the system’s properties, such as pressure and temperature, are well defined. Here, the system’s relaxation time is defined as the time taken by the system to adjust to a new thermodynamic state.
This thermodynamic system concept is obviously not directly applicable to a macroscopic volume of a moving fluid in which pressure and temperature may vary considerably. However, experiments show that classical thermodynamics does apply to small fluid volumes commonly called fluid particles. A fluid particle is a small deforming volume carried by the flow that: 1) always contains the same fluid molecules, 2) is large enough so that its thermodynamic properties are well defined when it is at equilibrium, but 3) is small enough so that its relaxation time is short compared to the time scales of fluid-motion-induced thermodynamic changes. Under ordinary conditions (the emphasis here), molecular densities (n), average speeds (v ¯ 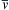 ), and average collisions rates (
), and average collisions rates (v ¯ 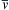 /l) are high enough so that the conditions for the existence of fluid particles are met, and classical thermodynamics can be directly applied to flowing fluids. However, there are circumstances involving rarified gases, shock waves, and high-frequency acoustic waves where one or more of the fluid particle requirements are not met and molecular-kinetic and quantum theories are needed.
/l) are high enough so that the conditions for the existence of fluid particles are met, and classical thermodynamics can be directly applied to flowing fluids. However, there are circumstances involving rarified gases, shock waves, and high-frequency acoustic waves where one or more of the fluid particle requirements are not met and molecular-kinetic and quantum theories are needed.
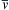 ), and average collisions rates (
), and average collisions rates (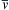 /l) are high enough so that the conditions for the existence of fluid particles are met, and classical thermodynamics can be directly applied to flowing fluids. However, there are circumstances involving rarified gases, shock waves, and high-frequency acoustic waves where one or more of the fluid particle requirements are not met and molecular-kinetic and quantum theories are needed.
/l) are high enough so that the conditions for the existence of fluid particles are met, and classical thermodynamics can be directly applied to flowing fluids. However, there are circumstances involving rarified gases, shock waves, and high-frequency acoustic waves where one or more of the fluid particle requirements are not met and molecular-kinetic and quantum theories are needed.The basic laws of classical thermodynamics are empirical, and cannot be derived from anything more fundamental. These laws essentially establish definitions, upon which the subject is built. The first law of thermodynamics can be regarded as a principle that defines the internal energy of a system, and the second law can be regarded as the principle that defines the entropy of a system.
First Law of Thermodynamics
The first law of thermodynamics states that the energy of a system is conserved;
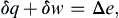 (1.16)
(1.16)
where δq is the heat added to the system, δw is the work done on the system, and Δe is the increase of the system’s internal energy. All thermodynamic quantities in (1.16) are normalized by the mass of the system and have units of J kg–1; thus, these are intensive variables and appear as lower case letters. When (1.16) is written without normalization by the system mass, δQ + δW = ΔE, it portrays the same thermodynamic law but the variables have units of energy (J); these are extensive variables and appear as capital letters. If two identical thermodynamic systems are combined, the combination’s intensive variables are unchanged while its extensive variables are doubled.
The internal energy (aka, thermal energy) e is a manifestation of the random molecular motion of the system’s constituents. In fluid flows, the kinetic energy of the fluid particles’ macroscopic motion has to be included in the e-term in (1.16) in order that the principle of conservation of energy is satisfied. For developing the relations of classical thermodynamics, however, we shall consider e to only represent the thermal energy.
Heat, work, and internal energy are all different. Heat and work are forms of energy in transition, which appear at the boundary of the system and are not contained within the matter. In contrast, the internal energy resides within the matter. If equilibrium states 1 and 2 of a system are known, then Q and W depend on the process or path followed by the system in going from state 1 to state 2. The change Δe = e2 − e1, in contrast, does not depend on the path. In short, e is a thermodynamic property and is a function of the thermodynamic state of the system. Thermodynamic properties are called state functions, in contrast to heat and work, which are path functions.
Frictionless quasi-static processes, carried out at an extremely slow rate so that the system is at all times in equilibrium with the surroundings, are called reversible processes. For a compressible fluid, the most common type of reversible work is by the expansion or contraction of the boundaries of the fluid particle. Let υ = 1/ρ be the specific volume, that is, the volume per unit mass. The work done per unit mass by a fluid particle in an infinitesimal reversible process is −pdυ, where dυ is the increase of υ. The first law (1.16) for a reversible process then becomes
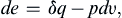 (1.17)
(1.17)
provided that q is also reversible. Note that irreversible forms of work, such as those done against frictional stresses, are excluded from (1.17).
Equations of State
A relation defining one state function in terms of two or more others is called an equation of state. For a simple compressible substance composed of a single component (the applicable model for nearly all pure fluids), the specification of two independent thermodynamic properties completely determines the state of the system. We can write relations such as the thermal and caloric equations of state:
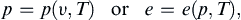 (1.18)
(1.18)
respectively. For more complicated systems composed of more than one component, the specification of additional properties is needed to completely determine the state. For example, seawater contains dissolved salt so its density is a function of temperature, pressure, and salinity.
Specific Heats
Before we define the specific heats of a substance, we define the thermodynamic property enthalpy as
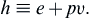 (1.19)
(1.19)
It is the sum of the thermal energy and the pressure-volume potential energy, and arises naturally in the study of compressible fluid flows.
For single-component systems, the specific heat capacities at constant pressure and constant volume are defined as
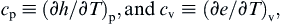 (1.20, 1.21)
(1.20, 1.21)
respectively. Here, (1.20) means that we regard h as a function of p and T, and find the partial derivative of h with respect to T, keeping p constant. Equation (1.21) has an analogous interpretation. The specific heats as defined are thermodynamic properties because they are defined in terms of other properties of the system. That is, cp and cv can be determined when two other system properties (say, p and T) are known.
For certain processes common in fluid flows, the heat exchanged can be related to the specific heats. Consider a reversible process in which the work done is given by pdυ, so that the first law of thermodynamics has the form of (1.17). Dividing by the change of temperature, it follows that the heat transferred per unit mass per unit temperature change in a constant volume process is
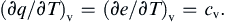
This shows that cvdT represents the heat transfer per unit mass in a reversible constant-volume process, in which the only type of work done is of the pdυ type. It is misleading to define cv = (dq/dT)v without any restrictions imposed, as the temperature of a constant-volume system can increase without heat transfer, such as by vigorous stirring.
Similarly, the heat transferred at constant pressure during a reversible process is given by
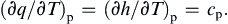
Second Law of Thermodynamics
The second law of thermodynamics restricts the direction in which real processes can proceed as time increases. Its implications are discussed in Chapter 4. Some consequences of this law are the following:
(i) There must exist a thermodynamic property s, known as entropy, whose change between states 1 and 2 is given by
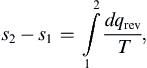 (1.22)
(1.22)
where the integral is taken along any reversible path between the two states.
(ii) For an arbitrary process between states 1 and 2, the entropy change is
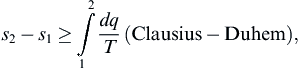
which states that the entropy of an isolated system (dq = 0) can only increase. Such increases may be caused by friction, mixing, and other irreversible phenomena.
(iii) Molecular transport coefficients such as species diffusivity κm, thermal conductivity k, and viscosity μ must be positive. Otherwise, spontaneous unmixing, or thermal or momentum separation would occur and lead to a decrease of entropy of an isolated system.
Property Relations
Two common relations are useful in calculating entropy changes during a process. For a reversible process, the entropy change is given by
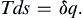 (1.23)
(1.23)
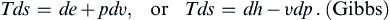 (1.24)
(1.24)
It is interesting that these relations (1.24) are also valid for irreversible (frictional) processes, although the relations (1.17) and (1.23), from which (1.24) are derived, are true for reversible processes only. This is because (1.24) are relations between thermodynamic state functions alone and are therefore true for any process. The association of Tds with heat and −pdυ with work does not hold for irreversible processes. Consider stirring work done at constant volume that raises a fluid element’s temperature; here de = Tds is the increment of stirring work done.
Speed of Sound
In a compressible fluid, infinitesimal isentropic changes in density and pressure propagate through the medium at a finite speed, c. In Chapter 15, it is shown that the square of this speed is given by a the thermodynamic derivative:
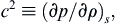 (1.25)
(1.25)
where the subscript s signifies that the derivative is taken at constant entropy. This is the speed of sound. For incompressible fluids, ∂ ρ / ∂ p → 0 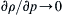 under all conditions so
under all conditions so c → ∞ . 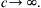
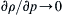 under all conditions so
under all conditions so 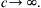
Thermal Expansion Coefficient
When fluid density is a function of temperature, we define the thermal expansion coefficient
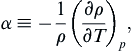 (1.26)
(1.26)
where the subscript p signifies that the partial derivative is taken at constant pressure. This expansion coefficient appears frequently in the study of nonisothermal systems.