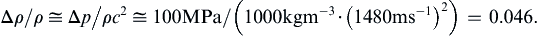Several startling and fascinating phenomena, which defy intuition and expectations developed from incompressible flows, arise in compressible flows and are described in this chapter. Near discontinuities (shock waves) may appear within the flow. An increase (or decrease) in flow area may accelerate (or decelerate) a uniform stream. Friction may increase a flow's speed. And, heat addition may lower a flow's temperature. These phenomena are therefore worthy of our attention because they either have no counterpart or act oppositely in low-speed flows. Except for the treatment of friction in constant-area ducts in
Section 15.6, the material presented here is limited to that of frictionless flows outside boundary layers. In spite of this simplification, the results presented here have a great deal of practical value because boundary layers are especially thin in high-speed flows. Gravitational effects, which are of minor importance in compressible flows, are also neglected.
As discussed in
Section 4.11, the importance of compressibility for moving fluids can be assessed by considering the Mach number
M, defined as:
Here, the subscript
s signifies that the partial derivative is taken at constant entropy. In particular, the dimensionless scaling
(4.109) of the compressible-flow continuity equation for isentropic conditions leads to:
where ρ0 and p0 are appropriately chosen reference values for density and pressure. In (4.110), the pressure is scaled by fluid inertia parameters as is appropriate for primarily frictionless high-speed flow. In engineering practice, the incompressible flow assumption is presumed valid
if M < 0.3
, but not at higher Mach numbers.
Equation (4.110) suggests that
M = 0.3 corresponds to ∼10% departure from perfectly incompressible flow behavior when the remainder of the right side of
(4.110) is of order unity.
Although the significance of the ratio
U/
c was known for a long time, the Swiss aerodynamist Jacob Ackeret introduced the term
Mach number, just as the term Reynolds number was introduced by Sommerfeld many years after Reynolds’ experiments. The name of the Austrian physicist Ernst Mach (1836–1916) was chosen because of his pioneering studies on supersonic motion and his invention of the so-called
Schlieren method for optical visualization of flows involving density changes; see
von Karman (1954, p. 106). (Mach distinguished himself equally well in philosophy. Einstein acknowledged that his own thoughts on relativity were influenced by “Mach’s principle,” which states that properties of space had no independent existence but are determined by the mass distribution within it. Strangely, Mach never accepted either the theory of relativity or the atomic structure of matter.)
Using the Mach number, compressible flows can be nominally classified as follows:
(ii) Subsonic flow: 0 < M < 1. The Mach number does not exceed unity anywhere in the flow field. Shock waves do not appear in the flow. In engineering practice, subsonic flows for which M < 0.3 are often treated as being incompressible.
(iii)
Transonic flow: The Mach number in the flow lies in the range 0.8–1.2. Shock waves may appear. Analysis of transonic flows is difficult because the governing equations are inherently nonlinear, and also because a separation of the inviscid and viscous aspects of the flow is often impossible. (The word “transonic” was invented by von Karman and Hugh Dryden, although the latter argued in favor of spelling it “transsonic.”
von Karman [1954] stated, “I first introduced the term in a report to the U.S. Air Force. I am not sure whether the general who read the word knew what it meant, but his answer contained the word, so it seemed to be officially accepted” [p.
116].)
(iv) Supersonic flow: M > 1. Shock waves are generally present. In many ways analysis of a flow that is supersonic everywhere is easier than analysis of a subsonic or incompressible flow as we shall see. This is because information propagates along certain directions, called characteristics, and a determination of these directions greatly facilitates the computation of the flow field.
Perfect Gas Thermodynamic Relations
Internalenergy:e=cvT,Enthalpy:h=cpT,Thermalequationofstate:p=ρRT,
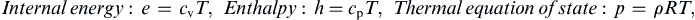 (15.1a– c)
(15.1a– c)
Specificheats:cv=Rγ−1,cp=γRγ−1,cp−cv=R,γ=cp/cv,
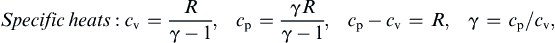 (15.1d– g)
(15.1d– g)
SpeedofSound:c=γRT=γp/ρ,andEntropychange:s2−s1=cpln(T2T1)−Rln(p2p1)=cvln(T2T1)−Rln(ρ2ρ1).
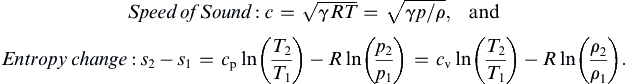 (15.1h, 15.1i)
(15.1h, 15.1i)
Equation (15.1h) implies that
c is larger in monotonic and low-molecular weight gases (where
γ and
R are larger), and that it increases with increasing temperature. An isentropic process involving a perfect gas between states 1 and 2 obeys the following relations:
p2p1=(ρ2ρ1)γ,andT2T1=(ρ2ρ1)γ−1=(p2p1)(γ-1)/γ.
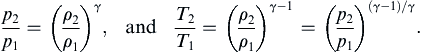 (15.2a, 15.2b)
(15.2a, 15.2b)
Some important properties of air at ordinary temperatures and pressures are:
R=287m2/(s2K),cv=717m2/(s2K),cp=1004m2/(s2K),andγ=1.40;
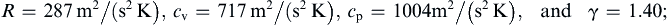 (15.3a– d)
(15.3a– d)
these values are useful for solution of the exercises at the end of this chapter.
Example 15.1
Which of the following are compressible flows? a) A weather balloon rises at 5 m/s from sea level to an altitude of more than 15 km. b) Water flows through the nozzle of a water jet cutter and the gage pressure drops from 100 MPa to zero. c) The piston of an internal combustion engine moves at 15 m/s and compresses air and gaseous fuel from 40 kPa to 1300 kPa. d) Liquid nitrogen at 100 kPa with density 807 kg/m3 evaporates from a stationary dewar in a 1 m/s airflow to become nitrogen gas with density 1.16 kg/m3. e) A 1.0 MPa compression wave travels at 1.0 km/s into air at 15°C and 1.0 atm.
Solution
Δρ/ρ≅Δp/ρc2≅100MPa/(1000kgm−3·(1480ms−1)2)=0.046.
This flow might qualify as compressible depending on the level of accuracy that is sought. For c), the pressure and density of the combustion gases rise by factors of more than 30 and 10, respectively. However, like the weather balloon, such changes primarily depend on piston location and are largely independent of the low-Mach number piston speed, so this is not a compressible flow. For d), the nitrogen accelerates to 1 m/s and its density drops by a factor ∼700, but there are no significant pressure variations, so this flow is not compressible. For e), the wave speed is supersonic and the increase in air pressure (a factor of ∼10) and density (a factor of ∼4) across the wave are significant. This is a compressible flow.
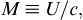 (4.111)
(4.111)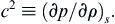 (1.25)
(1.25) (4.110)
(4.110) (15.1a– c)
(15.1a– c) (15.1d– g)
(15.1d– g) (15.1h, 15.1i)
(15.1h, 15.1i)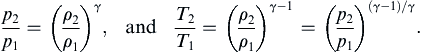 (15.2a, 15.2b)
(15.2a, 15.2b)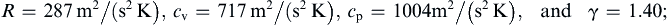 (15.3a– d)
(15.3a– d)