10.11. Secondary Flows
Large Reynolds number flows with curved streamlines tend to generate additional velocity components because of the properties of boundary layers. These additional components are commonly called secondary flows. An example of such a flow is made dramatically visible by randomly dispersing finely crushed tea leaves into a cup of water, and then stirring vigorously in a circular motion. When the motion has ceased, all of the particles have collected in a mound at the center of the bottom of the cup (see Figure 10.33). An explanation of this phenomenon is given in terms of thin boundary layers. The stirring motion imparts a primary velocity, uφ(R) (see Appendix B.6 for coordinates), large enough for the Reynolds number to be large enough for the boundary layers on the cup’s sidewalls and bottom to be thin. The two largest terms in the R-momentum equation are:
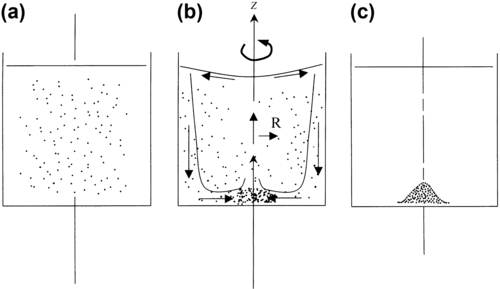
Figure 10.33 Secondary flow in a teacup. Tea leaf fragments are slightly denser than water. (a) Tea leaf fragments randomly dispersed—initial state; (b) stirred vigorously—transient motion; and (c) final state where all the tea leaf fragments are piled near the axis of rotation on the bottom of the cup.
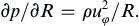
Away from the walls, the flow is inviscid. As the boundary layer on the bottom is thin, boundary-layer theory yields ∂p/∂z = 0 from the axial momentum equation. Thus, the pressure in the bottom boundary layer is the same as for the inviscid flow just outside the boundary layer. However, within the boundary layer, uφ is less than the inviscid value at the edge. Thus p(R) is everywhere larger in the boundary layer than that required for circular streamlines inside the boundary layer, and this pressure difference pushes the streamlines inward toward the center of the cup. That is, the pressure gradient within the boundary layer generates an inwardly directed uR. This motion induces a downwardly directed flow in the sidewall boundary layer and an outwardly directed flow on the top surface. This secondary flow is closed by an upward flow along the cup's centerline. The visualization is accomplished by crushed tea leaves which are slightly denser than water. They descend by gravity or are driven outward by centrifugal acceleration. If they enter the sidewall boundary layer, they are transported downward and thence to the center by the secondary flow. If the tea particles enter the bottom boundary layer from above, they are quickly swept to the center and dropped as the flow turns upward. All the particles collect at the center of the bottom of the teacup. A practical application of this effect, illustrated in Exercise 10.31, relates to sand and silt transport by the Mississippi River.