In pure mathematics a value's representation may take require an arbitrary number of bits. Computers, on the other hand, generally work with some specific number of bits. Common collections are single bits, groups of 4 bits (called nibbles), groups of 8 bits (bytes), groups of 16 bits (words), groups of 32 bits (double words or dwords), groups of 64 bits (quad words or qwords), groups of 128 bits (long words or lwords), and more. The sizes are not arbitrary. There is a good reason for these particular values. This section will describe the bit groups commonly used on the Intel 80x86 chips.
The smallest unit of data on a binary computer is a single bit. With a single bit, you can represent any two distinct items. Examples include 0 or 1, true or false, on or off, male or female, and right or wrong. However, you are not limited to representing binary data types (that is, those objects that have only two distinct values). You could use a single bit to represent the numbers 723 and 1,245 or, perhaps, the values 6,254 and 5. You could also use a single bit to represent the colors red and blue. You could even represent two unrelated objects with a single bit. For example, you could represent the color red and the number 3,256 with a single bit. You can represent any two different values with a single bit. However, you can represent only two different values with a single bit.
To confuse things even more, different bits can represent different things. For example, you could use one bit to represent the values 0 and 1, while a different bit could represent the values true and false. How can you tell by looking at the bits? The answer, of course, is that you can't. But this illustrates the whole idea behind computer data structures: data is what you define it to be. If you use a bit to represent a boolean (true/false) value, then that bit (by your definition) represents true or false. For the bit to have any real meaning, you must be consistent. If you're using a bit to represent true or false at one point in your program, you shouldn't use that value to represent red or blue later.
Because most items you'll be trying to model require more than two different values, single-bit values aren't the most popular data type you'll use. However, because everything else consists of groups of bits, bits will play an important role in your programs. Of course, there are several data types that require two distinct values, so it would seem that bits are important by themselves. However, you will soon see that individual bits are difficult to manipulate, so we'll often use other data types to represent two-state values.
A nibble is a collection of 4 bits. It wouldn't be a particularly interesting data structure except for two facts: binary-coded decimal (BCD) numbers[21] and hexadecimal numbers. It takes 4 bits to represent a single BCD or hexadecimal digit. With a nibble, we can represent up to 16 distinct values because there are 16 unique combinations of a string of 4 bits:
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
In the case of hexadecimal numbers, the values 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F are represented with 4 bits. BCD uses 10 different digits (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) and requires also 4 bits (because we can only represent 8 different values with 3 bits, the additional 6 values we can represent with 4 bits are never used in BCD representation). In fact, any 16 distinct values can be represented with a nibble, though hexadecimal and BCD digits are the primary items we can represent with a single nibble.
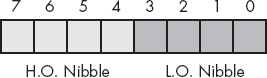
Without question, the most important data structure used by the 80x86 microprocessor is the byte, which consists of 8 bits. Main memory and I/O addresses on the 80x86 are all byte addresses. This means that the smallest item that can be individually accessed by an 80x86 program is an 8-bit value. To access anything smaller requires that we read the byte containing the data and eliminate the unwanted bits. The bits in a byte are normally numbered from 0 to 7, as shown in Figure 2-1.
Bit 0 is the low-order bit or least significant bit, and bit 7 is the high-order bit or most significant bit of the byte. We'll refer to all other bits by their number.
Note that a byte also contains exactly two nibbles (see Figure 2-2).
Bits 0..3 compose the low-order nibble, and bits 4..7 form the high-order nibble. Because a byte contains exactly two nibbles, byte values require two hexadecimal digits.
Because a byte contains 8 bits, it can represent 28 (256) different values. Generally, we'll use a byte to represent numeric values in the range 0..255, signed numbers in the range −128..+127 (see 2.8 Signed and Unsigned Numbers), ASCII/IBM character codes, and other special data types requiring no more than 256 different values. Many data types have fewer than 256 items, so 8 bits is usually sufficient.
Because the 80x86 is a byte-addressable machine, it turns out to be more efficient to manipulate a whole byte than an individual bit or nibble. For this reason, most programmers use a whole byte to represent data types that require no more than 256 items, even if fewer than 8 bits would suffice. For example, we'll often represent the boolean values true and false by 000000012 and 000000002, respectively.
Probably the most important use for a byte is holding a character value. Characters typed at the keyboard, displayed on the screen, and printed on the printer all have numeric values. To communicate with the rest of the world, PCs typically use a variant of the ASCII character set. There are 128 defined codes in the ASCII character set.
Because bytes are the smallest unit of storage in the 80x86 memory space, bytes also happen to be the smallest variable you can create in an HLA program. As you saw in the last chapter, you can declare an 8-bit signed integer variable using the int8 data type. Because int8 objects are signed, you can represent values in the range −128..+127 using an int8 variable. You should only store signed values into int8 variables; if you want to create an arbitrary byte variable, you should use the byte data type, as follows:
static
byteVar: byte;The byte data type is a partially untyped data type. The only type information associated with a byte object is its size (1 byte). You may store any 8-bit value (small signed integers, small unsigned integers, characters, and the like) into a byte variable. It is up to you to keep track of the type of object you've put into a byte variable.
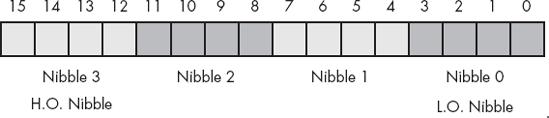
A word is a group of 16 bits. We'll number the bits in a word from 0 to 15, as Figure 2-3 shows. Like the byte, bit 0 is the low-order bit. For words, bit 15 is the high-order bit. When referencing the other bits in a word, we'll use their bit position number.
Notice that a word contains exactly 2 bytes. Bits 0..7 form the low-order byte, and bits 8..15 form the high-order byte (see Figure 2-4).
Of course, a word may be further broken down into four nibbles, as shown in Figure 2-5. Nibble 0 is the low-order nibble in the word, and nibble 3 is the high-order nibble of the word. We'll simply refer to the other two nibbles as nibble 1 or nibble 2.
With 16 bits, you can represent 216 (65,536) different values. These could be the values in the range 0..65,535 or, as is usually the case, the signed values −32,768..+32,767, or any other data type with no more than 65,536 values. The three major uses for words are short signed integer values, short unsigned integer values, and Unicode characters.
Words can represent integer values in the range 0..65,535 or −32,768..32,767. Unsigned numeric values are represented by the binary value corresponding to the bits in the word. Signed numeric values use the two's complement form for numeric values (see 2.8 Signed and Unsigned Numbers). As Unicode characters, words can represent up to 65,536 different characters, allowing the use of non-Roman character sets in a computer program. Unicode is an international standard, like ASCII, that allows computers to process non-Roman characters such as Asian, Greek, and Russian characters.
As with bytes, you can also create word variables in an HLA program. Of course, in the last chapter you saw how to create 16-bit signed integer variables using the int16 data type. To create an arbitrary word variable, just use the word data type, as follows:
static
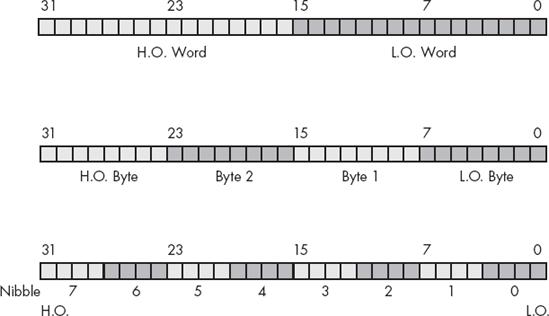
w: word;A double word is exactly what its name implies, a pair of words. Therefore, a double-word quantity is 32 bits long, as shown in Figure 2-6.
Naturally, this double word can be divided into a high-order word and a low-order word, four different bytes, or eight different nibbles (see Figure 2-7).
Double words (dwords) can represent all kinds of different things. A common item you will represent with a double word is a 32-bit integer value (that allows unsigned numbers in the range 0..4,294,967,295 or signed numbers in the range −2,147,483,648..2,147,483,647). 32-bit floating-point values also fit into a double word. Another common use for double-word objects is to store pointer values.
In Chapter 1, you saw how to create 32-bit signed integer variables using the int32 data type. You can also create an arbitrary double-word variable using the dword data type, as the following example demonstrates:
static
d: dword;Obviously, we can keep on defining larger and larger word sizes. However, the 80x86 supports only certain native sizes, so there is little reason to keep on defining terms for larger and larger objects. Although bytes, words, and double words are the most common sizes you'll find in 80x86 programs, quad word (64-bit) values are also important because certain floating-point data types require 64 bits. Likewise, the SSE/MMX instruction set of modern 80x86 processors can manipulate 64-bit values. In a similar vein, long-word (128-bit) values are also important because the SSE instruction set on later 80x86 processors can manipulate 128-bit values. HLA allows the declaration of 64- and 128-bit values using the qword and lword types, as follows:
static
q :qword;
l :lword;Note that you may also define 64-bit and 128-bit integer values using HLA declarations like the following:
static
i64 :int64;
i128 :int128;However, you may not directly manipulate 64-bit and 128-bit integer objects using standard instructions like mov, add, and sub because the standard 80x86 integer registers process only 32 bits at a time. In Chapter 8, you will see how to manipulate these extended-precision values.
[21] Binary-coded decimal is a numeric scheme used to represent decimal numbers using 4 bits for each decimal digit.