 1 =
1 =  2 =
2 =  3 in Figure 35.1 There is also a point P’ different from P such that
3 in Figure 35.1 There is also a point P’ different from P such that  P’ AC =
P’ AC =  P’ CB =
P’ CB =  P’ BA.
P’ BA.The doctrines of pure geometry often, and in many questions, give a simple and natural way to penetrate to the origin of truths, to lay bare the mysterious chain which unites them, and to make them known individually, luminously and completely.
MICHEL CHASLES
For over one hundred years after the introduction of analytic geometry by Descartes and Fermat, algebraic and analytic methods dominated geometry almost to the exclusion of synthetic methods. During this period some men, for example the English mathematicians who persisted in trying to found the calculus rigorously on geometry, produced new results synthetically. Geometric methods, elegant and intuitively clear, always captivated some minds. Maclaurin, especially, preferred synthetic geometry to analysis. Pure geometry, then, retained some life even if it was not at the heart of the most vital developments of the seventeenth and eighteenth centuries. In the early nineteenth century several great mathematicians decided that synthetic geometry had been unfairly and unwisely neglected and made a positive effort to revive and extend that approach.
One of the new champions of synthetic methods, Jean-Victor Poncelet, did concede the limitations of the older pure geometry. He says, “While analytic geometry offers by its characteristic method general and uniform means of proceeding to the solution of questions which present themselves … while it arrives at results whose generality is without bound, the other [synthetic geometry] proceeds by chance; its way depends completely on the sagacity of those who employ it and its results are almost always limited to the particular figure which one considers.” But Poncelet did not believe that synthetic methods were necessarily so limited and he proposed to create new ones which would rival the power of analytic geometry.
Michel Chasles (1793-1880) was another great proponent of geometrical methods. In his Aperçu historique sur I’origine et le developpement des méthodes en géométric (1837), a historical study in which Chasles admitted that he ignored the German writers because he did not know the language, he states that the mathematicians of his time and earlier had declared geometry a dead language which in the future would be of no use and influence. Not only does Chasles deny this but he cites Lagrange, who was entirely an analyst, as saying in his sixtieth year,1 when he had encountered a very difficult problem of celestial mechanics, “Even though analysis may have advantages over the old geometric methods, which one usually, but improperly, calls synthesis, there are nevertheless problems in which the latter appear more advantageous, partly because of their intrinsic clarity and partly because of the elegance and ease of their solutions. There are even some problems for which the algebraic analysis in some measure does not suffice and which, it appears, the synthetic methods alone can master.” Lagrange cites as an example the very difficult problem of the attraction of an ellipsoid of revolution exerted on a point (unit mass) on its surface or inside. This problem had been solved purely synthetically by Maclaurin.
Chasles also gives an extract from a letter he received from Lambert Adolphe Quetelet (1796-1874), the Belgian astronomer and statistician. Quetelet says, “It is not proper that most of our young mathematicians value pure geometry so lightly.” The young men complain of lack of generality of method, continues Quetelet, but is this the fault of geometry or of those who cultivate geometry, he asks. To counter this lack of generality, Chasles gives two rules to prospective geometers. They should generalize special theorems to obtain the most general result, which should at the same time be simple and natural. Second, they should not be satisfied with the proof of a result if it is not part of a general method or doctrine on which it is naturally dependent. To know when one really has the true basis for a theorem, he says, there is always a principal truth which one will recognize because other theorems will result from a simple transformation or as a ready consequence. The great truths, which are the foundations of knowledge, always have the characteristics of simplicity and intuitiveness.
Other mathematicians attacked analytic methods in harsher language. Carnot wished “to free geometry from the hieroglyphics of analysis.” Later in the century Eduard Study (1862-1922) referred to the machine-like process of coordinate geometry as the “clatter of the coordinate mill.”
The objections to analytic methods in geometry were based on more than a personal preference or taste. There was, first of all, a genuine question of whether analytic geometry was really geometry since algebra was the essence of the method and results, and the geometric significance of both were hidden. Moreover, as Chasles pointed out, analysis through its formal processes neglects all the small steps which geometry continually makes. The quick and perhaps penetrating steps of analysis do not reveal the sense of what is accomplished. The connection between the starting point and the final result is not clear. Chasles asks, “Is it then sufficient in a philosophic and basic study of a science to know that something is true if one does not know why it is so and what place it should take in the series of truths to which it belongs?” The geometric method, on the other hand, permits simple and intuitively evident proofs and conclusions.
There was another argument which, first voiced by Descartes, still appealed in the nineteenth century. Geometry was regarded as the truth about space and the real world. Algebra and analysis were not in themselves significant truths even about numbers and functions. They were merely methods of arriving at truths, and artificial at that. This view of algebra and analysis was gradually disappearing. Nevertheless the criticism was still vigorous in the early nineteenth century because the methods of analysis were incomplete and even logically unsound. The geometers rightly questioned the validity of the analytic proofs and credited them with merely suggesting results. The analysts could retort only that the geometric proofs were clumsy and inelegant.
The upshot of the controversy is that the pure geometers reasserted their role in mathematics. As if to revenge themselves on Descartes because his creation of analytic geometry had caused the abandonment of pure geometry, the early nineteenth-century geometers made it their objective to beat Descartes at the game of geometry. The rivalry between analysts and geometers grew so bitter that Steiner, who was a pure geometer, threatened to quit writing for Crelle’s Journal für Mathematik if Grelle continued to publish the analytical papers of Plücker.
The stimulus to revive synthetic geometry came primarily from one man, Gaspard Monge. We have already discussed his valuable contributions to analytic and differential geometry and his inspiring lectures at the Ecole Poly technique during the years 1795 to 1809. Monge himself did not intend to do more than bring geometry back into the fold of mathematics as a suggestive approach to and an interpretation of analytic results. He sought only to stress both modes of thought. However, his own work in geometry and his enthusiasm for it inspired in his pupils, Charles Dupin, François-Joseph Servois, Charles-Julien Brianchon, Jean-Baptiste Biot (1774-1862), Lazare-Nicholas-Marguerite Carnot, and Jean-Victor Poncelet, the urge to revitalize pure geometry.
Monge’s contribution to pure geometry was his Traité de géométrie descriptive (1799). This subject shows how to project orthogonally a three-dimensional object on two planes (a horizontal and a vertical one) so that from this representation one can deduce mathematical properties of the object. The scheme is useful in architecture, the design of fortifications, perspective, carpentry, and stonecutting and was the first to treat the projection of a three-dimensional figure into two two-dimensional ones. The ideas and method of descriptive geometry did not prove to be the avenue to subsequent developments in geometry or, for that matter, to any other part of mathematics.
Though the geometers who reacted to Monge’s inspiration turned to projective geometry, we shall pause to note some new results in synthetic Euclidean geometry. These results, perhaps minor in significance, nevertheless exhibit new themes arid the almost inexhaustible richness of this old subject. Actually hundreds of new theorems were produced, of which we can give just a few examples.
Associated with every triangle ABC are nine particular points, the midpoints of the sides, the feet of the three altitudes, and the midpoints of the segments which join the vertices to the point of intersection of the altitudes. All nine points lie on one circle, called the nine-point circle. This theorem was first published by Gergonne and Poncelct.2 It is often credited to Karl Wilhelm Feuerbach (1800-34), a high-school teacher, who published his proof in Eigensckaften einiger merkwürdigen Punkte des geradlinigen Dreiecks (Properties of Some Distinctive Points of the Rectilinear Triangle, 1822). In this book Feuerbach added another fact about the nine-point circle. An excircle (escribed circle) is one which is tangent to one of the sides and to the extensions of the other two sides. (The center of an escribed circle lies on the bisectors of two exterior angles and the remote interior angle.) Feuerbach’s theorem states that the nine-point circle is tangent to the inscribed circle and the three excircles.
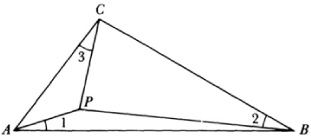
In a small book published in 1816, Über einige Eigenschaften des ebenen geradlinigen Dreiecks (On Some Properties of Plane Rectilinear Triangles), Crelle showed how to determine a point P inside a triangle such that the lines joining P to the vertices of the triangle and the sides of the triangle make equal angles. That is,  1 =
1 =  2 =
2 =  3 in Figure 35.1 There is also a point P’ different from P such that
3 in Figure 35.1 There is also a point P’ different from P such that  P’ AC =
P’ AC =  P’ CB =
P’ CB =  P’ BA.
P’ BA.
The conic sections, we know, were treated definitively by Apollonius as sections of a cone and then introduced as plane loci in the seventeenth century. In 1822 Germinal Dandelin (1794-1847) proved a very interesting theorem about the conic sections in relation to the cone.3 His theorem states that if two spheres are inscribed in a circular cone so that they are tangent to a given plane cutting the cone in a conic section, the points of contact of the spheres with the plane are the foci of the conic section, and the intersections of the plane with the planes of the circles along which the spheres touch the cone are the directrices of the conic.
Another interesting theme pursued in the nineteenth century was the solution of maximum and minimum problems by purely geometric methods, that is, without relying upon the calculus of variations. Of the several theorems Jacob Steiner proved by using synthetic methods, the most famous result is the isoperimetric theorem: Of all plane figures with a given perimeter the circle bounds the greatest area. Steiner gave various proofs.4 Unfortunately, Steiner assumed that there exists a curve that does have maximum area. Dirichlet tried several times to persuade him that his proofs were incomplete on that account but Steiner insisted that this was self-evident. Once, however, he did write (in the first of the 1842 papers):5 “and the proof is readily made if one assumes that there is a largest figure.”
The proof of the existence of a maximizing curve baffled mathematicians for a number of years until Weierstrass in his lectures of the 1870s at Berlin resorted to the calculus of variations.6 Later Constantin Caratheodory (1873-1950) and Study7 in a joint paper rigorized Steiner’s proofs without employing that calculus. Their proofs (there were two) were direct rather than indirect as in Steiner’s method. Hermann Amandus Schwarz, who did great work in partial differential equations and analysis and who served as a professor at several universities including Göttingen and Berlin, gave a rigorous proof for the isoperimetric problem in three dimensions.8
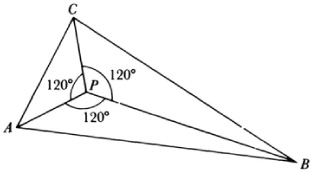
Steiner also proved (in the first of the 1842 papers) that of all triangles with a given perimeter, the equilateral has the greatest area. Another of his results9 states that if A, B, and C are three given points (Fig. 35.2) and if each of the angles of triangle ABC is less than 120°, then the point P for which PA + PB + PC is a minimum is such that each of the angles at P is 120°. If, however, one angle of the triangle, say angle A, is equal to or larger than 120°, then P coincides with A. This result had been proven much earlier by Cavalieri (Exercitationes Geometricae Sex, 1647) but it was undoubtedly unknown to Steiner. Steiner also extended the result to n points.
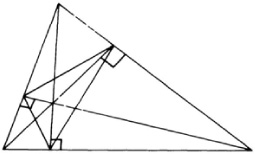
Schwarz solved the following problem: Given an acute-angled triangle, consider all triangles such that each has its vertices on the three sides of the original triangle; the problem is to find the triangle that has least perimeter. Schwarz proved synthetically10 that the vertices of this triangle of minimum perimeter are the feet of the altitudes of the given triangle (Fig. 35.3).11
A theorem novel for Euclidean geometry was discovered in 1899 by Frank Morley, professor of mathematics at Johns Hopkins University, and proofs were subsequently published by many men.12 The theorem states that if the angle trisectors are drawn at each vertex of a triangle, adjacent trisectors meet at the vertices of an equilateral triangle (Fig. 35.4). The novelty lies in the involvement of angle trisectors. Up to the middle of the nineteenth century no mathematician would have considered such lines because only those elements and figures that are constructible were regarded as having legitimacy in Euclidean geometry. Constructibility guaranteed existence. However, the conception of what established existence changed as we shall see more clearly when we examine the work on the foundations of Euclidean geometry.
A number of efforts were directed toward reducing the use of straight-edge and compass along the lines initiated by Mohr and Mascheroni (Chap. 12, sec. 2). In his Traité of 1822 Poncelet showed that all constructions possible with straightedge and compass (except the construction of circular arcs) are possible with straightedge alone provided that we are given a fixed circle and its center. Steiner re-proved the same result more elegantly in a small book, Die geometrischen Constructionen ausgeführt mittelst der geraden Linie und eines festen Kreises (The Geometrical Constructions Executed by Means of the Straight Line and a Fixed Circle).13 Though Steiner intended the book for pedagogical purposes, he does claim in the preface that he will establish the conjecture which a French mathematician had expressed.
The brief sampling above of Euclidean theorems established by synthetic methods should not leave the reader with the impression that analytic geometric methods were not also used. In fact, Gergonne gave analytic proofs of many geometric theorems which he published in the journal he founded, the Annales de Mathématiques.
The major area to which Monge and his pupils turned was projective geometry. This subject had had a somewhat vigorous but short-lived burst of activity in the seventeenth century (Chap. 14) but was submerged by the rise of analytic geometry, the calculus, and analysis. As we have already noted, Desargues’s major work of 1639 was lost sight of until 1845 and Pascal’s major essay on conies (1639) was never recovered. Only La Hire’s books, which used some of Desargues’s results, were available. What the nineteenth-century men learned from La Hire’s books they often incorrectly credited to him. On the whole, however, these geometers were ignorant of Desargues’s and Pascal’s work and had to re-create it.
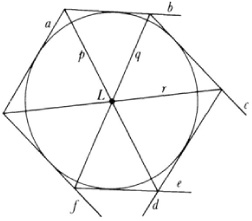
The revival of projcctive geometry was initiated by Lazare N. M. Carnot (1753-1823), a pupil of Monge and father of the distinguished physicist Sadi Carnot. His major work was Géométric deposition (1803) and he also contributed the Essai sur la theorie des transversales (1806). Monge had espoused the joint use of analysis and pure geometry, but Carnot refused to use analytic methods and started the championship of pure geometry. Many of the ideas we shall shortly discuss more fully are at least suggested in Carnot’s work. Thus the principle that Monge called contingent relations and which became known also as the principle of correlativity and more commonly as the principle of continuity is to be found there. To avoid separate figures for various sizes of angles and directions of lines Carnot did not use negative numbers, which he regarded as contradictory, but introduced a complicated scheme called “correspondence of signs.”
Among the early nineteenth-century workers in projective geometry we shall just mention François-Joseph Servois and Charles-Julien Brianchon (1785-1864), both of whom made applications of their work to military problems. Though they aided in reconstructing, systematizing, and extending old results, the only new theorem of consequence is Brianchon’s famous result,14 which he proved while still a student at the Ecole. The theorem states that if there are six tangents to a conic (Fig. 35.5), thus forming a circumscribed hexagon, the three lines, each of which joins two opposite vertices, pass through one point. Brianchon derived this theorem by using the pole-polar relationship.
The revival of projective geometry received its main impetus from Poncelet (1788-1867). Poncelet was a pupil of Monge and he also learned much from Carnot. While serving as an officer in Napoleon’s campaign against Russia, he was captured and spent the year 1813-14 in a Russian prison at Saratoff. There Poncelet reconstructed without the aid of any books what he had learned from Monge and Carnot and then proceeded to create new results. He later expanded and revised this work and published it as the Traité des propriétés projectives des figures (1822). This work was his chief contribution to projective geometry and to the erection of a new discipline. In his later life he was obliged to devote a great deal of time to government service, though he did hold professorships for limited periods.
Poncelet became the most ardent champion of synthetic geometry and even attacked the analysts. He had been friendly with the analyst Joseph-Diez Gergonne (1771-1859) and had published papers in Gergonne’s Annales de Mathématiques, but his attacks were soon directed to Gergonne also. Poncelet was convinced of the autonomy and importance of pure geometry. Though he admitted the power of analysis he believed that one could give the same power to synthetic geometry. In a paper of 1818, published in Gergonne’s Annales,15 he said that the power of analytic methods lay not in the use of algebra but in its generality and this advantage resulted from the fact that the metric properties discovered for a typical figure remain applicable, other than for a possible change of sign, to all related figures which spring from the typical or basic one. This generality could be secured in synthetic geometry by the principle of continuity (which we shall examine shortly).
Poncelet was the first mathematician to appreciate fully that projective geometry was a new branch of mathematics with methods and goals of its own. Whereas the seventeenth-century projective geometers had dealt with specific problems, Poncelet entertained the general problem of seeking all properties of geometrical figures that were common to all sections of any projection of a figure, that is, remain unaltered by projection and section. This is the theme that he and his successors took up. Because distances and angles are altered by projection and section Poncelet selected and developed the theory of involution and of harmonic sets of points but not the concept of cross ratio. Monge had used parallel projection in his work; like Desargues, Pascal, Newton, and Lambert, Poncelet used central projection, that is, projection from a point. This concept Poncelet elevated into a method of approach to geometric problems. Poncelet also considered projective transformation from one space figure to another, of course in purely geometric form. Here he seemed to have lost interest in projective properties and was more concerned with the use of the method in bas-relief and stage design.
His work centers about three ideas. The first is that of homologous figures. Two figures are homologous if one can be derived from the other by one projection and a section, which is called a perspectivity, or by a sequence of projections and sections, that is, a projectivity. In working with homologous figures his plan was to find for a given figure a simpler homologous figure and by studying it find properties which are invariant under projection and section, and so obtain properties of the more complicated figure. The essence of this method was used by Desargues and Pascal, and Poncelet in his Traité praised Desargues’s originality in this and other respects.
Poncelet’s second leading theme is the principle of continuity. In his Traité he phrases it thus: “If one figure is derived from another by a continuous change and the latter is as general as the former, then any property of the first figure can be asserted at once for the second figure.” The determination of when both figures are general is not explained. Poncelet’s principle also asserts that if a figure should degenerate, as a hexagon does into a pentagon when one side is made to approach zero, any property of the original figure will carry over into an appropriately worded statement for the degenerate figure.
The principle was really not new with Poncelet. In a broad philosophical sense it goes back to Leibniz, who stated in 1687 that when the differences between two cases can be made smaller than any datum in the given, the differences can be made smaller than any given quantity in the result. Since Leibniz’s time the principle was recognized and used constantly. Monge began the use of the principle of continuity to establish theorems. He wanted to prove a general theorem but used a special position of the figure to prove it and then maintained that the theorem was true generally, even when some elements in the figures became imaginary. Thus to prove a theorem about a line and a surface he would prove it when the line cuts the surface and then maintain that the result holds even when the line no longer cuts the surface and the points of intersection are imaginary. Neither Monge nor Carnot, who also used the principle, gave any justification of it.
Poncelet, who coined the term “principle of continuity,” advanced the principle as an absolute truth and applied it boldly in his Traité. To “demonstrate” its soundness he takes the theorem on the equality of the products of the segments of intersecting chords of a circle and notes that when the point of intersection moves outside the circle one obtains the equality of the products of the secants and their external segments. Further, when one secant becomes a tangent, the tangent and its external segment become equal and their product continues to equal the product of the other secant and its external segment. All of this was reasonable enough, but Poncelet applied the principle to prove many theorems and, like Monge, extended the principle to make assertions about imaginary figures. (We shall note some examples later.)
The other members of the Paris Academy of Sciences criticized the principle of continuity and regarded it as having only heuristic value. Cauchy, in particular, criticized the principle but unfortunately his criticism was directed at applications made by Poncelet wherein the principle did work. The critics also charged that the confidence which Poncelet and others had in the principle really came from the fact that it could be justified on an algebraic basis. As a matter of fact, the notes Poncelet made in prison show that he did use analysis to test the soundness of the principle. These notes, incidentally, were written up by Poncelet and published by him in two volumes entitled Applications d’analyse et de géométrie (1862-64) which is really a revision of his Traité of 1822, and in the later work he does use analytic methods. Poncelet admitted that a proof could be based on algebra but he insisted that the principle did not depend on such a proof. However, it is quite certain that Poncelet relied on the algebraic method to see what should be the case and then affirmed the geometric results using the principle as a justification.
Chasles in his Aperçu defended Poncelet. Chasles’s position was that the algebra is an a posteriori proof of the principle. However, he hedged by pointing out that one must be careful not to carry over from one figure to another any property which depends essentially on the elements being real or imaginary. Thus one section of a cone may be a hyperbola, and this has asymptotes. When the section is an ellipse the asymptotes become imaginary. Hence one should not prove a result about the asymptotes alone because these depend upon the particular nature of the section. Also one should not carry the results for a parabola over to the hyperbola because the cutting plane does not have a general position in the case of the parabola. Then he discusses the case of two intersecting circles which have a common chord. When the circles no longer intersect, the common chord is imaginary. The fact that the real common chord passes through two real points is, he says, an incidental or a contingent property. One must define the chord in some way which does not depend on the fact that it passes through real points when the circles intersect but so that it is a permanent property of the two circles in any position. Thus one can define it as the (real) radical axis, which means that it is a line such that from any point on it the tangents to the two circles are equal, or one can define it by means of the property that any circle drawn about any point of the line as a center cuts the two circles orthogonally.
Chasles, too, insisted that the principle of continuity is suited to treat imaginary elements in geometry. He first explains what one means by the imaginary in geometry. The imaginary elements pertain to a condition or state of a figure in which certain parts are nonexistent, provided these parts are real in another state of the figure. For, he adds, one cannot have any idea of imaginary quantities except by thinking of the related states in which the quantities are real. These latter states are the ones which he called “accidental” and which furnish the key to the imaginary in geometry. To prove results about imaginary elements one has only to take the general condition of the figure in which the elements are real, and then, according to the principle of accidental relations or the principle of continuity, one may conclude that the result holds when the elements are imaginary. “So one sees that the use and the consideration of the imaginary are completely justified.” The principle of continuity was accepted during the nineteenth century as intuitively clear and therefore having the status of an axiom. The geometers used it freely and never deemed that it required proof.
Though Poncelet used the principle of continuity to assert results about imaginary points and lines he never gave any general definition of such elements. To introduce some imaginary points he gave a geometrical definition which is complicated and hardly perspicuous. We shall understand these imaginary elements more readily when we discuss them from an algebraic point of view. Despite the lack of clarity in Poncelet’s approach he must be credited with introducing the notion of the circular points at infinity, that is, two imaginary points situated on the line at infinity and common to any two circles.16 He also introduced the imaginary spherical circle which any two spheres have in common. He then proved that two real conies which do not intersect have two imaginary common chords, and two conies intersect in four points, real or imaginary.
The third leading idea in Poncelet’s work is the notion of pole and polar with respect to a conic. The concept goes back to Apollonius and was used by Desargues (Chap. 14, sec. 3) and others in the seventeenth-century work on projective geometry. Also Euler, Legendre, Monge, Servois, and Brianchon had already used it. But Poncelet gave a general formulation of the transformation from pole to polar and conversely and used it in his Traité of 1822 and in his “Mémoire sur la théorie générale des polaires réciproques” presented to the Paris Academy in 182417 as a method of establishing many theorems.
One of Poncelet’s objectives in studying polar reciprocation with respect to a conic was to establish the principle of duality. The workers in projective geometry had observed that theorems dealing with figures lying in one plane when rephrased by replacing the word “point” by “line” and “line” by “point” not only made sense but proved to be true. The reason for the validity of theorems resulting from such a rephrasing was not clear, and in fact Brianchon questioned the principle. Poncelet thought that the pole and polar relationship was the reason.
However, this relation required the mediation of a conic. Gergonne18 insisted that the principle was a general one and applied to all statements and theorems except those involving metric properties. Pole and polar were not needed as an intermediary supporting device. He introduced the term “duality” to denote the relationship between the original and new theorem. He also observed that in three-dimensional situations point and plane are dual elements and the line is dual to itself.
To illustrate Gergonne’s understanding of the principle of duality let us examine his dualization of Desargues’s triangle theorem. We should note first what the dual of a triangle is. A triangle consists of three points not all on the same line, and the lines joining them. The dual figure consists of three lines not all on the same point, and the points joining them (the points of intersection). The dual figure is again a triangle and so the triangle is called self-dual. Gergonne invented the scheme of writing dual theorems in double columns with the dual alongside the original proposition.
Now let us consider Desargues’s theorem, where this time the two triangles and the point 0 lie in one plane, and let us see what results when we interchange point and line. Gergonne in the 1825-26 paper already referred to wrote this theorem and its dual as follows:

Here the dual theorem is the converse of the original theorem.
Gergonne’s formulation of the general principle of duality was somewhat vague and had deficiencies. Though he was convinced it was a universal principle, he could not justify it and Poncelet rightly objected to the deficiencies. Also he disputed with Gergonne over priority of discovery of the principle (which really belongs to Poncelet) and even accused Gergonne of plagiarism. However, Poncelet did rely upon pole and polar and would not grant that Gergonne had taken a step forward in recognizing the wider application of the principle. Later discussions among Poncelet, Gergonne, Möbius, Chasles, and Plücker clarified the principle for all, and Möbius in his Der barycentrische Calcul and Plücker, later, gave a good statement of the relationship of the principle of duality to pole and polar: The notion of duality is independent of conies and quadric forms but agrees with pole and polar when the latter can be used. The logical justification of the general principle of duality was not supplied at this time.
The synthetic development of projective geometry was furthered by Jacob Steiner (1796-1863). He is the first of a German school of geometers who took over French ideas, notably Poncelet’s, and favored synthetic methods to the extent of even hating analysis. The son of a Swiss farmer, he himself worked on the farm until he was nineteen years old. Though he was largely self-educated he ultimately became a professor at Berlin. In his younger years he was a teacher in Pestalozzi’s school and was impressed by the importance of building up the geometric intuition. It was Pestalozzi’s principle to get the student to create the mathematics with the lead of the teacher and the use of the Socratic method. Steiner went to extremes. He taught geometry but used no figures, and in training doctoral candidates he darkened the room. In his own later work Steiner took over theorems and proofs published in English and other journals and gave no indication in his own publications that his results had already been established. He had done good original work when younger and sought to maintain his reputation for productivity.
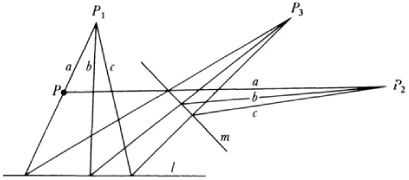
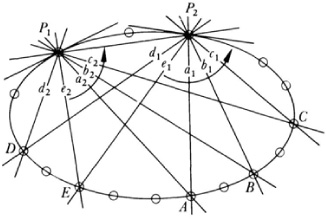
His major work was Systematische Entwicklung der Abhängigkeit geometrischen Gestalten von einander (Systematic Development of the Dependence of Geometric Forms on One Another, 1832) and his chief principle was to use projective concepts to build up more complicated structures from simple ones such as points, lines, pencils of lines, planes, and pencils of planes. His results were not especially new but his method was.
To illustrate his principle we shall examine his now standard projective method of defining the conic sections. One starts (Fig. 35.6) with two pencils of lines (families of concurrent lines), say p1, and p3, that are perspectively related through a pencil of points on a line l, and the pencils p3 and p2 that are perspectively related by means of a pencil of points on another line m. Then the pencils p1 and p2 are said to be projectively related. The lines marked a in the pencil with center at P1 and the pencil with center at P2 are examples of corresponding lines of the projectivity between the two pencils p1 and p2. A conic is now defined as the set of points of intersection of all pairs of corresponding lines of the two projective pencils. Thus P is a point on the conic. Moreover, the conic passes through P1 and P2 (Fig. 35.7). In this manner Steiner built up the conies or second degree curves by means of the simpler forms, pencils of lines. However, he did not identify his conies with sections of a cone.
He also built up the ruled quadrics, the hyperboloid of one sheet and the hyperbolic paraboloid, in a similar manner, making projective correspondence the basis of his definitions. Actually his method is not sufficiently general for all of projective geometry.
In his proofs he used cross ratio as a fundamental tool. However, he ignored imaginary elements and referred to them as “the ghosts” or the “shadows of geometry.” He also did not use signed quantities though Möbius, whose work we shall soon examine, had already introduced them.
Steiner used the principle of duality from the very outset of his work. Thus he dualized the definition of a conic to obtain a new structure called a line curve. If one starts with two projectively (but not perspectively) related pencils of points then the family of lines (Fig. 35.8) joining the corresponding points of the two pencils is called a line conic. To distinguish such families of lines, which also describe a curve, the usual curve as a locus of points is called a point curve. The tangent lines of a point curve are a line curve and in the case of a conic do constitute the dual curve. Conversely every line conic envelopes a point conic or is the collection of tangents of a point conic.
With Steiner’s notion of a dual to a point conic, one can dualize many theorems. Let us take Pascal’s theorem and form the dual statement. We shall write the theorem on the left and the new statement on the right.

Figure 14.12 of Chapter 14 illustrates Pascal’s theorem. The dual theorem is the one that Brianchon had discovered by means of the pole and polar relationship (Fig. 35.5 above). Steiner, like Gergonne, did nothing to establish the logical basis for the principle of duality. However, he developed projective geometry systematically by classifying figures and by noting the dual statements as he proceeded. He also studied thoroughly curves and surfaces of the second degree.
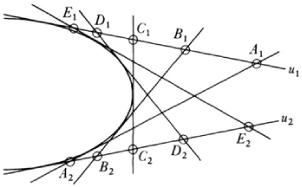
Michel Chasles, who devoted his entire life to geometry, followed up on the work of Poncelet and Steiner, though he did not personally know Steiner’s work because, as we have noted, Chasles could not read German. Chasles presented his own ideas in his Traité de géométrie supérieure (1852) and Traité des sections coniques (1865). Since much of Chasles’s work either unintentionally duplicated Steiner’s or was superseded by more general concepts, we shall note just a few major results that are due to him.
Chasles got the idea of cross ratio from his attempts to understand the lost work of Euclid, Porisms (though Steiner and Möbius had already reintroduced it). Desargues, too, had used the concept, but Chasles knew only what La Hire had written about it. Chasles did learn at some time that the idea is also in Pappus because in Note IX of his Aperçu (p. 302) he refers to Pappus’s use of the idea. One of Chasles’s results in this area19 is that four fixed points of a conic and any fifth point of the conic determine four lines with the same cross ratio.
In 1828 Chasles20 gave the theorem: Given two sets of collinear points in one-to-one correspondence and such that the cross ratio of any four points on one line equals that of the corresponding points on the other, then the lines joining corresponding points are tangent to a conic that touches the two given lines. This result is the equivalent of Steiner’s definition of a line conic, because the cross ratio condition here ensures that the two sets of collinear points are projectively related and the lines joining corresponding points are the lines of Steiner’s line conic.
Chasles pointed out that by virtue of the principle of duality lines can be as fundamental as points in the development of plane projective geometry and credits Poncelet and Gergonne with being clear on this point. Chasles also introduced new terminology. The cross ratio he called anharmonic ratio. He introduced the term homography to describe a transformation of a plane into itself or another plane, which carries points into points and lines into lines. This term covers homologous or projectively related figures. He added the condition that the transformation must preserve cross ratio but this latter fact can be proved. The transformation that carries points into lines and lines into points he called a correlation.
Though he defended pure geometry Chasles thought analytically but presented his proofs and results geometrically. This approach is called the “mixed method” and was used later by others.
By 1850 the general concepts and goals of projective geometry as distinguished from Euclidean geometry were clear; nevertheless the logical relationship of the two geometries was not clarified. The concept of length was used in projective geometry from Desargues to Chasles. In fact the concept of cross ratio was defined in terms of length. Yet length is not a projective concept because it is not invariant under projective transformation. Karl Georg Christian von Staudt (1798-1867), a professor at Erlangen who was interested in foundations, decided to free projective geometry from dependence on length and congruence. The essence of his plan, presented in his Geometrie der Lage (Geometry of Position, 1847), was to introduce an analogue of length on a projective basis. His scheme is called “the algebra of throws.” One chooses three arbitrary points on a line and assigns to them the symbols 0, 1, ∞. Then by means of a geometric construction (which in itself comes from Möbius)—a “throw”—a symbol is attached to any arbitrary point P.
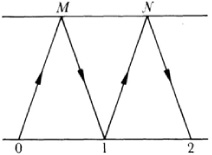
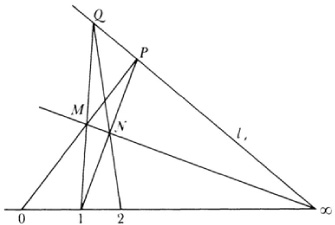
To see what the construction amounts to in Euclidean geometry suppose we start with the points labelled 0 and 1 on a line (Fig. 35.9). Through the point M on a parallel line draw 0M and then draw 1 N parallel to 0M. Now draw 1M and draw N2 parallel to 1M. It is immediate that 01 = 12 because opposite sides of a parallelogram are equal. Thus one carries over the length 01 to 12 by a geometric construction.
Now to treat the projective case we start with three points 0, 1, ∞ (Fig. 35.10). The point ∞ lies on l∞, the line at infinity, but this is just an ordinary line in projective geometry. Now pick a point M and draw a “parallel” to the line 01 through M. This means that the line through M must meet the line 01 at ∞ and so we draw M∞. Now draw 0M and prolong it to l∞. Next we draw through 1 a “parallel” to 0M. This means the “parallel” through I must meet 0M on l∞. We thereby get the line IP and this determines N. Now draw 1M and prolong it until it meets l∞ at Q. The line through N parallel to 1M is QN and where it meets 01 we get a point which is labeled 2.
By this type of construction we can attach “rational coordinates” to points on the line 0l∞. To assign irrational numbers to points on the line one must introduce an axiom of continuity (Chap. 41). This notion was not well understood at that time and as a consequence von Staudt’s work lacked rigor.
Von Staudt’s assignment of coordinates to the points of a line did not involve length. His coordinates, though they were the usual number symbols, served as systematic identification symbols for the points. To add or subtract such “numbers” von Staudt could not then use the laws of arithmetic. Instead he gave geometric constructions that defined the operations with these symbols so that, for example, the sum of the numbers 2 and 3 is the number 5. These operations obeyed all the usual laws of numbers. Thus his symbols or coordinates could be treated as ordinary numbers even though they were built up geometrically.
With these labels attached to his points von Staudt could define the cross ratio of four points. If the coordinates of these points are x1 x2, x3, and x4, then the cross ratio is defined to be
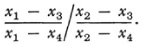
Thus von Staudt had the fundamental tools to build up projective geometry without depending on the notions of length and congruence.
A harmonic set of four points is one for which the cross ratio is – 1. On the basis of harmonic sets von Staudt gave the fundamental definition that two pencils of points are projectively related when under a one-to-one correspondence of their members a harmonic set corresponds to a harmonic set. Four concurrent lines form a harmonic set if the points in which they meet an arbitrary transversal constitute a harmonic set of points. Thus the pro-jectivity of two pencils of lines can also be defined. With these notions von Staudt defined a collineation of the plane into itself as a one-to-one transformation of point to point and line to line and showed that it carries a set of harmonic elements into a set of harmonic elements.
The principal contribution of von Staudt in his Geometrie der Lage was to show that projective geometry is indeed more fundamental than Euclidean. Its concepts are logically antecedent. This book and his Beiträge zur Geometrie der Lage (Contributions to the Geometry of Position, 1856, 1857, 1860) revealed projective geometry as a subject independent of distance. However, he did use the parallel axiom of Euclidean geometry, which from a logical standpoint was a blemish because parallelism is not a projective invariant. This blemish was removed by Felix Klein.21
While the synthetic geometers were developing projective geometry, the algebraic geometers pursued their methods of treating the same subject. The first of the new algebraic ideas was what are now called homogeneous coordinates. One such scheme was created by Augustus Ferdinand Möbius (1790-1868), who like Gauss and Hamilton made his living as an astronomer but devoted considerable time to mathematics. Though Möbius did not take sides in the controversy on synthetic versus algebraic methods his contributions were on the algebraic side.
His scheme for representing the points of a plane by coordinates introduced in his major work, Der barycentrische Calcul,22 was to start with a fixed triangle and to take as the coordinates of any point P in the plane the amount of mass which must be placed at each of the three vertices of the triangle so that P would be the center of gravity of the three masses. When P lies outside the triangle then one or two of the coordinates can be negative. If the three masses are all multiplied by the same constant the point P remains the center of gravity. Hence in Möbius’s scheme the coordinates of a point are not unique; only the ratios of the three are determined. The same scheme applied to points in space requires four coordinates. By writing the equations of curves and surfaces in this coordinate system the equations become homogeneous; that is, all terms have the same degree. We shall see examples of the use of homogeneous coordinates shortly.
Möbius distinguished the types of transformations from one plane or space to another. If corresponding figures are equal, the transformation is a congruence and if they are similar, the transformation is a similarity. Next in generality is the transformation that preserves parallelism though not length or shape and this type is called affine (a notion introduced by Euler). The most general transformation that carries lines into lines he called a collineation. Möbius proved in Der bary centrische Calcul that every collineation is a projective transformation; that is, it results from a sequence of perspectivities. His proof assumed that the transformation is one-to-one and continuous, but the continuity condition can be replaced by a weaker one. He also gave an analytical representation of the transformation. As Möbius pointed out, one could consider invariant properties of figures under each of the above types of transformations.
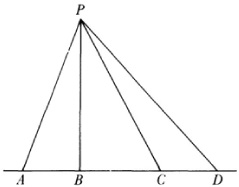
Möbius introduced signed elements in geometry not only for the line segments but for areas and volumes. Consequently he was able to give a complete treatment of the notion of the signed cross ratio of four points on a line. He also showed that the cross ratio of four lines of a pencil can be expressed in terms of the sines of the angles at the vertex P (Fig. 35.11) by
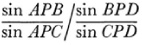
and this ratio is the same as the cross ratio of the four points A, B, C, and D cut out on any transversal to the lines of the pencil. Hence cross ratio is unaltered by projection and section. Möbius had many other ideas which he developed slowly and did not push very far.
The man who gave the algebraic approach to projective geometry its efficacy and vitality is Julius Plücker (1801-68). After serving as a professor of mathematics at several institutions until 1836, he became a professor of mathematics and physics at Bonn, a position he held for the rest of his life. Plücker was primarily a physicist and in fact an experimental physicist in which activity he made many notable discoveries. From 1863 on he again devoted himself to mathematics.
Plücker, too, introduced homogeneous coordinates but in a manner different from Möbius’s. His first notion, trilinear coordinates,23 was also presented in the second volume of his Analytisch-geometrische Entwickelungen (1828 and 1831). He starts with a fixed triangle and takes the coordinates of any point P to be the signed perpendicular distances from P to the sides of the triangle; each distance can be multiplied by the same arbitrary constant. Later in the second volume he introduced a special case which amounts to regarding one line of the triangle as the line at infinity. This is equivalent to replacing the usual rectangular Cartesian coordinates x and y by x = x1/x3 and y = x2/x3 so that the equations of curves become homogeneous in x1, x2, and x3. The latter notion is the one which became more widely used.
By using homogeneous coordinates and Euler’s theorem on homogeneous functions, which states that if f(tx1, tx2, tx3) = tnf(x1, x2, x3) then
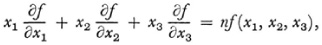
Plücker was able to give elegant algebraic representations of geometric ideas. Thus if f(x1, x2, x3) = 0 is the equation of a conic with (x1, x2, x3) as the coordinates of a point on the conic then
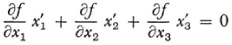
can be interpreted, when x′1, x′2, x′3 are the running coordinates, as the equation of the tangent at the point (x1, x2 x3) or, when x1, x2, x3 are the running coordinates, as the equation of the polar line of the arbitrary point x′1, x′2, x′3) with respect to the conic.
Using homogeneous coordinates Plücker gave the algebraic formulation of the infinitely distant line, the circular points at infinity, and other notions. In the homogeneous coordinate system (x1, x2, x3) the equation of the infinitely distant line is x3 = 0. This line is not exceptional in projective geometry, but in our visualization of the geometric elements each normal point of the Euclidean plane is at a finite position given by x = x1/x3 and y = x2/x3 and so we are obliged to think of points on x3 = 0 as infinitely distant.
The equation of a circle
(x – a)2 + (y – b)2 = r2
becomes on the introduction of homogeneous Cartesian coordinates x1 x2, and x3 through x = x1/x3 and y = x2/x3
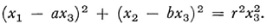
Since the equation of the infinitely distant line is x3 = 0, the intersection of this line with the circle is given by
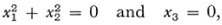
and this is the equation of the circular points at ∞. These circular points have the coordinates (1, i, 0) and (1, –i, 0) or triples proportional to them. Likewise the equation of the spherical circle (Kugelkreis) at infinity is
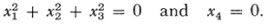
If we write the equation of a straight line in the homogeneous form (we shall use x, y, and z in place of x1, x2, and x3)
Ax + By + Cz = 0
and now require that the line pass through the points (x1, y1, z1) and (1, i, 0) then the resulting nonhomogeneous equation of the line is
x – x0 + i(y – y0) = 0
wherein x0 = x1\z1, and y0 = y1\z1. Likewise the equation of the line through (x1, y1, z1) and (1, –i, 0) is
x – x0 – i(y – y0) = 0.
Each of these lines is perpendicular to itself because the slope equals its negative reciprocal. Sophus Lie called them crazy lines; they are now called isotropic lines.
Plucker’s efforts to treat duality algebraically led him to a beautiful idea, line coordinates.24 If the equation of a line in homogeneous coordinates is
ux + vy + wz = 0,
and if x, y, and z are fixed quantities, u, v, and w or any three numbers proportional to them are the coordinates of a line in the plane. Then just as an equation f(x1, x2 x3) = 0 represents a collection of points, so f(u, v, w) = 0 represents a collection of lines or a line curve.
With this notion of line coordinates Plücker was able to give an algebraic formulation and proof of the principle of duality. Given any equation f(r, s, t) = 0 if we interpret r, s, and t as the homogeneous coordinates x1, x2, and x3 of a point then we have the equation of a point curve, whereas if we interpret them as u, v, and w we have the dual line curve. Any property proved by algebraic processes for the point curve will, because the algebra is the same under either interpretation of the variables, give rise to the dual property of the line curve.
In this second 1830 paper and in Volume 2 of his Entwickelungen Plücker also pointed out that the very same curve regarded as a collection of points can also be regarded as the collection of lines tangent to the curve because the tangents determine the shape as much as the points do. The family of tangents is a line curve and has an equation in line coordinates. The degree of this equation is called the class of the curve, whereas the degree of the equation in point coordinates is called the order.
The eighteenth-century men had done some work on curves of degree higher than the second (Chap. 23, sec. 3) but the subject was dormant from 1750 to 1825. Plücker took up third and fourth degree curves and used projective concepts freely in this work.
In his System der analytischen Geometrie (1834) he used a principle, which though helpful was hardly well grounded, to establish canonical forms of curves. To show that the general curve of order (degree) 4, say, could be put into a particular canonical form he argued that if the number of constants were the same in the two forms then one could be converted into the other. Thus he argued that a ternary (three-variable) form of fourth order could always be put in the form
C4 = pqrs + μΩ2,
where p, q, r, and s are linear and Ω is a quadratic form, because both sides contained 14 constants. In his equations μ was real as were the coefficients.
Plücker also took up the number of intersection points of curves, a topic which had also been pursued in the eighteenth century. He used a scheme for representing the family of all curves which go through the intersections of two nth degree curves C′n and C″n which had been introduced by Lamé in a book of 1818. Any curve Cn passing through these intersections can be expressed as
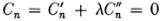
where λ is a parameter.
Using this scheme Plücker gave a clear explanation of Cramer’s paradox (Chap. 23, sec. 3). A general curve Cn is determined by n(n + 3)/2 points because this is the number of essential coefficients in its equation. On the other hand, since two Cn’s intersect in n2 points, through the n(n + 3)/2 points in which two Cn’s intersect an infinite number of other Cn’s pass. The apparent contradiction was explained by Plücker.25 Any two nth degree curves do indeed meet in n2 points. However, only (n/2) (n + 3) – 1 points are independent. That is, if we take two nth degree curves through the (n/2) (n + 3) – 1 points any other nth degree curve through these points will pass through the remaining (n – 1)(n – 2)/2 of the n2 points. Thus when = 4, 13 points are independent. Any two curves through the 13 points determine 16 points but any other curve through the 13 will pass through the remaining three.
Plücker then took up26 the theory of intersections of an mth degree curve and an nth degree curve. He regarded the latter as fixed and the curves intersecting it as variable. Using the abridged notation Cn for the expression for the nth degree curve and similar notation for the others he wrote
Cm = C′m + Am-n Cn = 0
for the case where m > n so that Am-n is a polynomial of degree m – n. From this equation Plücker got the correct method of determining the intersections of a Cn with all curves of degree m. Since according to this equation m – n + 1 linearly independent curves (the number of coefficients in Am-n) pass through the intersections of C′m and Cn, Plücker’s conclusion was, given mn – (n – 1)(n – 2)/2 arbitrary points on Cn, the remaining (n – 1)(n – 2)/2 of the mn intersection points with a Cm are determined. The same result was obtained at about the same time by Jacobi.27
In his System of 1834 and more explicitly in his Theorie der algebraischen Curven (1839) Plücker gave what are now called the Plücker formulas which relate the order n and the class k of a curve and the simple singularities. Let d be the number of double points (singular points at which the two tangents are distinct) and r the number of cusps. To the double points there correspond in the line curve double tangents (a double tangent is actually tangent at two distinct points) the number of which is, say, t. To the cusps there correspond osculating tangents (tangents which cross the curve at inflection points) the number of which is, say, w. Then Plücker was able to establish the following dual formulas:
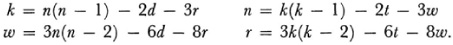
The number of any one element includes real and imaginary cases.
In the case when n = 3, d = 0, and r = 0, then w, the number of inflection points, is 9. Up to Plücker’s time, De Gua and Maclaurin had proved that a line through two inflection points of the general curve of third order goes through a third one, and the fact that a general C3 had three real inflection points had been assumed from Clairaut’s time on. In his System of 1834 Plücker proved that a C3 has either one or three real inflection points, and in the latter case they lie on one line. He also arrived at the more general result which takes complex elements into account. A general C3 has nine inflection points of which six are imaginary. To derive this result he used his principle of counting constants to show that
C3 = fgh – l3,
where f, g, h, and l are linear forms, and derived the result of De Gua and Maclaurin. He then showed (with incomplete arguments) that the nine inflection points of C3 lie three on a line so that there are twelve such lines. Ludwig Otto Hesse (1811-74), who served as a professor at several universities, completed Plücker’s proof28 and showed that the twelve lines can be grouped into four triangles.
As an additional example of the discovery of general properties of curves we shall consider the problem of the inflection points of an nth degree curve f(x, y) = 0. Plücker had expressed the usual calculus condition for an inflection point when y = f(x), namely, d2y/dx2 = 0, in the form appropriate to f(x, y) = 0 and obtained an equation of degree 3n – 4. Since the original curve and the new curve must have n(3n – 4) intersections, it appeared that the original curve has n(3n – 4) points of inflection. Because this number was too large Plücker suggested that the curve of the equation of degree 3n – 4 has a tangential contact with each of the n infinite branches of the original curve f = 0, so that 2n of the common points are not inflection points, and so obtained the correct number, 3n(n – 2). Hesse clarified this point29 by using homogeneous coordinates; that is, he replaced x by x/x3, and y by x2/x3, and by using Euler’s theorem on homogeneous functions he showed that Plücker’s equation for the inflection points can be written as
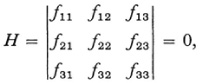
where the subscripts denote partial derivatives. This equation is of degree 3(n – 2) and so meets the curve f(x1, x2, x3 = 0 of the nth degree in the correct number of inflection points. The determinant itself is called the Hessian of f, a notion introduced by Hesse.30
Plücker among others took up the investigation of quartic curves. He was the first to discover (Theorie der algebraischen Curven, 1839) that such curves contain 28 double tangents of which eight at most were real. Jacobi then proved31 that a curve of nth order has in general n(n – 2)(n2 – 9)/2 double tangents.
The work in algebraic geometry also covered figures in space. Though the representation of straight lines in space had already been introduced by Euler and Cauchy, Plücker in his System der Geometrie des Raumes (System of Geometry of Space, 1846) introduced a modified representation
x = rz + ρ, y = sz + σ
in which the four parameters r, p, s, and ρ fix the line. Now lines can be used to build up all of space, since, for example, planes are no more than collections of lines, and points are intersections of lines. Plücker then said that if lines are regarded as the fundamental element of space, space is four-dimensional because four parameters are needed to cover all of space with lines. The notion of a four-dimensional space of points he rejected as too metaphysical. That the dimension depends on the space-element is the new thought.
The study of figures in space included surfaces of the third and fourth degrees. A ruled surface is generated by a line moving according to some law. The hyperbolic paraboloid (saddle-surface) and hyperboloid of one sheet are examples, as is the helicoid. If a surface of the second degree contains one line it contains an infinity of lines and it is ruled. (It must then be a cone, cylinder, the hyperbolic paraboloid, or the hyperboloid of one sheet.) However, this is not true of cubic surfaces.
As an example of a remarkable property of cubic surfaces there was Cayley’s discovery in 184932 of the existence of exactly 27 lines on every surface of the third degree. Not all need be real but there are surfaces for which they are all real. Clebsch gave an example in 1871.33 These lines have special properties. For example, each is cut by ten others. Much further work was devoted to the study of these lines on cubic surfaces.
Among many discoveries concerning surfaces of fourth order one of Kummer’s results deserves mention. He had worked with families of lines that represent rays of light, and by considering the associated focal surfaces34 he was led to introduce a fourth degree surface (and of class four) with 16 double points and 16 double planes as the focal surface of a system of rays of second order. This surface, known as the Kummer surface, embraces as a special case the Fresnel wave surface, which represents the wave front of light propagating in anisotropic media.
The work on synthetic and algebraic projective geometry of the first half of the nineteenth century opened up a brilliant period for geometrical researches of all kinds. The synthetic geometers dominated the period. They attacked each new result to discover some general principle, often not demonstrable geometrically, but from which they nevertheless derived a spate of consequences tied one to the other and to the general principle. Fortunately, algebraic methods were also introduced and, as we shall see, ultimately dominated the field. However, we shall interrupt the history of projective geometry to consider some revolutionary new creations that affected all subsequent work in geometry and, in fact, altered radically the face of mathematics.
Berzolari, Luigi: “Allgemeine Theorie der höheren ebenen algebraischen Kurven,” Encyk. der Math. Wiss., B. G. Teubner, 1903-15, III C4, 313-455.
Boyer, Carl B.: History of Analytic Geometry, Scripta Mathematica, 1956, Chaps. 8–9.
Brill, A., and M. Noether: “Die Entwicklung der Theorie der algebraischen Functionen in älterer und neuerer Zeit,” Jahres, der Deut. Math.-Verein., 3, 1892/3, 109-566, 287-312 in particular.
Cajori, Florian: A History of Mathematics, 2nd ed., Macmillan, 1919, pp. 286-302, 309-14.
Coolidge, Julian L.: A Treatise on the Circle and the Sphere, Oxford University Press, 1916.
——: A History of Geometrical Methods, Dover (reprint), 1963, Book I, Chap. 5 and Book II, Chap. 2.
——: A History of the Conic Sections and Quadric Surfaces, Dover (reprint), 1968.
——: “The Rise and Fall of Projective Geometry,” American Mathematical Monthly, 41, 1934, 217-28.
Fano, G.: “Gegensatz von synthetischer und analytischer Geometrie in seiner historischen Entwicklung im XIX. Jahrhundert,” Encyk. der Math. Wiss., B. G. Teubner 1907-10, III AB4a, 221-88.
Klein, Felix: Elementary Mathematics from an Advanced Standpoint, Macmillan, 1939; Dover (reprint), 1945, Geometry, Part 2.
Kötter, Ernst: “Die Entwickelung der synthetischen Geometrie von Monge bis auf Staudt,” 1847, Jahres, der Deut. Math.-Verein., Vol. 5, Part II, 1896 (pub. 1901), 1-486.
Möbius, August F.: Der bary centrische Calcul (1827), Georg Olms (reprint), 1968. Also in Vol. 1 of Gesammelte Werke, pp. 1-388.
——: Gesammelte Werke, 4 vols., S. Hirzel, 1885-87; Springer-Verlag (reprint), 1967.
Plücker, Julius: Gesammelle wissenschaftliche Abhandlungen, 2 vols., B. G. Teubner, 1895-96.
Schoenflics, A.: “Projektive Geometrie,” Encyk. der Math. Wiss., B. G. Teubner, 1907-10, III AB5, 389-480.
Smith, David Eugene: A Source Book in Mathematics, Dover (reprint), 1959, Vol. 2, pp. 315-23, 331-45, 670-76.
Steiner, Jacob: Geometrical Constructions With a Ruler (a translation of his 1833 book), Scripta Mathematica, 1950.
——: Gesammelte Werke, 2 vols., G. Reimer, 1881-82; Chelsea (reprint), 1971.
Zacharias, M.: “Elementargeometrie and elementare nicht-euklidische Geometrie in synthetischer Behandlung,” Encyk. der Math. Wiss., B. G. Teubner, 1907-10, III, AB9, 859-1172.