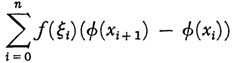
If Newton and Leibniz had thought that continuous functions do not necessarily have a derivative—and this is the general case—the differential calculus would never have been created.
EMILE PICARD
The theory of functions of one or more real variables grew out of the attempt to understand and clarify a number of strange discoveries that had been made in the nineteenth century. Continuous but non-differentiable functions, series of continuous functions whose sum is discontinuous, continuous functions that are not piecewise monotonic, functions possessing bounded derivatives that are not Riemann integrable, curves that are rectifiable but not according to the calculus definition of arc length, and nonintegrable functions that are limits of sequences of integrable functions—all seemed to contradict the expected behavior of functions, derivatives, and integrals. Another motivation for the further study of the behavior of functions came from the research on Fourier series. This theory, as built up by Dirichlet, Riemann, Cantor, Ulisse Dini (1845-1918), Jordan, and other mathematicians of the nineteenth century, was a quite satisfactory instrument for applied mathematics. But the properties of the series, as thus far developed, failed to give a theory that could satisfy the pure mathematicians. Unity, symmetry, and completeness of relation between function and series were still wanting.
The research in the theory of functions emphasized the theory of the integral because it seemed that most of the incongruities could be resolved by broadening that notion. Hence to a large extent this work may be regarded as a direct continuation of the work of Riemann, Darboux, Du Bois-Reymond, Cantor, and others (Chap. 40, sec. 4).
Actually the first extension of the notion of integral came from a totally different class of problems than those just described. In 1894 Thomas Jan Stieltjes (1856-94) published his “Recherches sur les fractions continues,”1 a most original paper in which he started from a very particular question and solved it with rare elegance. This work suggested problems of a completely novel nature in the theory of analytic functions and in the theory of functions of a real variable. In particular, in order to represent the limit of a sequence of analytic functions Stieltjes was obliged to introduce a new integral that generalized the Riemann-Darboux concept.
Stieltjes considers a positive distribution of mass along a line, a generalization of the point concept of density which, of course, had already been used. He remarks that such a distribution of mass is given by an increasing function φ(x) which specifies the total mass in the interval [0, x] for x > 0, the discontinuities of φ corresponding to masses concentrated at a point. For such a distribution of mass in an interval [a, b] he formulates the Riemann sums
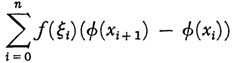
wherein the x0, x1, … xn are a partition of [a, b] and ξi is within [xi, xi+1]. He then showed that when f is continuous in [a, b] and the maximum sub-interval of the partitions approaches 0, the sums approach a limit which he denoted by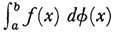 
. Though he used this integral in his own work, Stieltjes did not push further the integral notion itself, except that for the interval (0, ∞) he defined
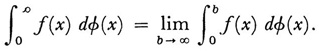
His integral concept was not taken up by mathematicians until much later, when it did find many applications (see Chap. 47, sec. 4).
Quite another line of thought led to a different generalization of the notion of integral, the Lebesgue integral. The study of the sets of discontinuities of functions suggested the question of how to measure the extent or “length” of the set of discontinuities, because the extent of these discontinuities determines the integrability of the function. The theory of content and later the theory of measure were introduced to extend the notion of length to sets of points that are not full intervals of the usual straight line.
The notion of content is based on the following idea: Consider a set E of points distributed in some manner over an interval [a, b]. To be loose for the moment, suppose that it is possible to enclose or cover these points by small subintervals of [a, b] so that the points of E arc either interior to one of the subintervals or at worst an endpoint. We reduce the lengths of these subintervals more and more and add others if necessary to continue to enclose the points of E, while reducing the sum of the lengths of the sub-intervals. The greatest lower bound of the sum of those subintervals that cover points of E is called the (outer) content of E. This loose formulation is not the definitive notion that was finally adopted, but it may serve to indicate what the men were trying to do.
A notion of (outer) content was given by Du Bois-Reymond in his Die allgemeine Funktionentheorie (1882), Axel Harnack (1851-88) in his Die Elemente der Differential-und Integralrechnung (1881), Otto Stolz,2 and Cantor.3Stolz and Cantor also extended the notion of content to two and higher-dimensional sets using rectangles, cubes, and so forth in place of intervals.
The use of this notion of content, which was unfortunately not satisfactory in all respects, nevertheless revealed that there were nowhere dense sets (that is, the set lies in an interval but is not dense in any subinterval of that interval) of positive content and that functions with discontinuities on such sets were not integrable in Riemann’s sense. Also there were functions with bounded nonintegrable derivatives. But mathematicians of this time, the 1880s, thought that Riemann’s notion of the integral could not be extended.
To overcome limitations in the above theory of content and to rigorize the notion of area of a region, Peano (Applicazioni geometriche del calcolo infinitesimale, 1887) introduced a fuller and much improved notion of content. He introduced an inner and outer content for regions. Let us consider two dimensions. The inner content is the least upper bound of all polygonal regions contained within the region R and the outer content is the greatest lower bound of all polygonal regions containing the region R. If the inner and outer content are equal, this common value is the area. For a one-dimensional set the idea is similar but uses intervals instead of polygons. Peano pointed out that if f(x) is non-negative in [a, b] then
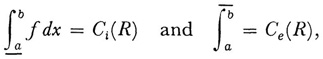
where the first integral is the least upper bound of the lower Riemann sums of ƒ on [a, b] and the second is the greatest lower bound of the upper Riemann sums and C1(R) and Ce(R) are the inner and outer content of the region R bounded above by the graph of f. Thus f is integrable if and only if R has content in the sense that C1(R) = Ce(R).
Jordan made the most advanced step in the nineteenth-century theory of content (étendue). He too introduced an inner and outer content,4 but formulated the concept somewhat more effectively. His definition for a set of points E contained in [a, b] starts with the outer content. One covers E by a finite set of subintervals of [a, b] such that each point of E is interior to or an endpoint of one of these subintervals. The greatest lower bound of the sum of all such sets of subintervals that contain at least one point of E is the outer content of E. The inner content of E is defined to be the least upper bound of the sum of the subintervals that enclose only points of E in [a, b]. If the inner and outer content of E are equal, then E has content. The same notion was applied by Jordan to sets in ?-dimensional space except that rectangles and the higher-dimensional analogues replace the subintervals. Jordan could now prove what is called the additivity property: The content of the sum of a finite number of disjoined sets with content is the sum of the contents of the separate sets. This was not true for the earlier theories of content, except Peano’s.
Jordan’s interest′ in content derived from the attempt to clarify the theory of double integrals taken over some plane region E. The definition usually adopted was to divide the plane into squares Rij by lines parallel to the coordinate axes. This partition of the plane induces a partition of E into Eij’s. Then, by definition,
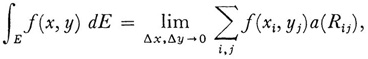
where a(Rij) denotes the area of Rij and the sum is over all Rij interior to E and all Rij that contain any points of E but may also contain points outside of E. For the integral to exist it is necessary to show that the Rij that are not entirely interior to E can be neglected or that the sum of the areas of the Rij that contain boundary points of E approaches 0 with the dimensions of the Rij. It had been generally assumed that this was the case and Jordan himself did so in the first edition of his Cows d'analyse (Vol. 2, 1883). However the discovery of such peculiar curves as Peano’s square-filling curve made the mathematicians more cautious. If E has two-dimensional Jordan content, then one can neglect the Rij that contain the boundary points of E. Jordan was also able to obtain results on the evaluation of double integrals by repeated integration.
The second edition of Jordan’s Cours d’analyse (Vol. 1, 1893) contains Jordan’s treatment of content and its application to integration. Though superior to that of his predecessors, Jordan’s definition of content was not quite satisfactory. According to it an open bounded set does not necessarily have content and the set of rational points contained in a bounded interval does not have content.
The next step in the theory of content was made by Borei. Borei was led to study the theory, which he called measure, while working on the sets of points on which series representing complex functions converge. His Leçons sur la théorie des fonctions (1898) contains his first major work on the subject. Borei discerned the defects in the earlier theories of content and remedied them.
Cantor had shown that every open set U on the line is the union of a denumerable family of open intervals, no two having a point in common. In place of approaching U by enclosing it in a finite set of intervals Borei, using Cantor’s result, proposed as the measure of a bounded open set U the sum of the lengths of the component intervals. He then defined the measure of the sum of a countable number of disjoined measurable sets as the sum of the individual measures and the measure of the set A — B, if A and B are measurable and B is contained in A, as the difference of the measures. With these definitions he could attach a measure to sets formed by adding any countable number of disjoined measurable sets and to the difference of any two measurable sets A and B if A contains B. He then considered sets of measure 0 and showed that a set of measure greater than 0 is non-denumerable.
Borel’s theory of measure was an improvement over Peano’s and Jordan’s notions of content, but it was not the final word, nor did he consider its application to integration.
The generalization of measure and the integral that is now considered definitive was made by Henri Lebesgue (1875-1941), a pupil of Borei and a professor at the Collège de France. Guided by Borel’s ideas and also by those of Jordan and Peano, he first presented his ideas on measure and the integral in his thesis, “Intégrale, longueur, aire.”5 His work superseded the nineteenth-century creations and, in particular, improved on Borel’s theory of measure.
Lebesgue’s theory of integration is based on his notion of measure of sets of points and both ideas apply to sets in n-dimensional space. For illustrative purposes we shall consider the one-dimensional case. Let E be a set of points in a ≤ x ≤ b. The points of E can be enclosed as interior points in a finite or counlably infinite set of intervals d1, d2, … lying in [a, b]. (The endpoints of [a, b] can be endpoints of a d1.) It can be shown that the set of intervals {di} can be replaced by a set of non-overlapping intervals δ1, δ2, … such that every point of E is an interior point of one of the intervals or the common endpoint of two adjacent intervals. Let ∑ δn denote the sum of the lengths δi. The lower bound of ∑δn for all possible sets {δi} is called the exterior measure of £ and denoted by me (E). The interior measure mi(E) of E is defined to be the exterior measure of the set C(E), that is, the complement of E in [a, b] or the points of a ≤ x ≤ b not in E.
Now one can prove a number of subsidiary results, including the fact that mi(E) ≤ me (E). The set E is defined to be measurable if mi(E) = me(E) and the measure m(E) is taken to be this common value. Lebesgue showed that a union of a countable number of measurable sets that are pairwise disjoined has as its measure the sum of the measures of the component sets. Also all Jordan measurable sets are Lebesgue measurable and the measure is the same. Lebesgue’s notion of measure differs from Borel’s by the adjunction of a part of a set of measure 0 in the sense of Borei. Lebesgue also called attention to the existence of nonmeasurable sets.
His next significant notion is that of a measurable function. Let E be a bounded measurable set on the x-axis. The function f(x), defined on all points of E, is said to be measurable in E if the set of points of E for which f(x) > A is measurable for every constant A.
Finally we arrive at Lebesgue’s notion of an integral. Let f(x) be a bounded and measurable function on the measurable set E contained in [a, b]. Let A and B be the greatest lower and least upper bounds of f(x) on E. Divide the interval [A, B] (on the y-axis) into n partial intervals
[A, l1], [l1, l2], … [ln–1, B],
with A = l0 and B = ln. Let er be the set of points of E for which lr-1 ≤ f(x) ≤ lr, r = 1, 2, …,n. Then e1, e2, …, en are measurable sets. Form the sums S and s where
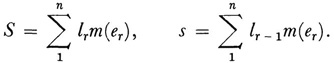
The sums S and s have a greatest lower bound J and a least upper bound I, respectively. Lebesgue showed that for bounded measurable functions I = J, and this common value is the Lebesgue integral of f(x) on E. The notation is
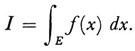
If E consists of the entire interval a ≤ x ≤ b, then we use the notation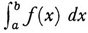 
, but the integral is understood in the Lebesgue sense. If f(x) is Lebesgue integrable and the value of the integral is finite, then f(x) is said to be summable, a term introduced by Lebesgue. An f{x) that is Riemann integrable on [a, b] is Lebesgue integrable but not necessarily conversely. If f(x) is integrable in both senses, the values of the two integrals are the same.
The generality of the Lebesgue integral derives from the fact that a Lebesgue integrable function need not be continuous almost everywhere (that is, except on a set of measure 0). Thus the Dirichlet function, which is 1 for rational values of x and 0 for irrational values of x in [a, b], is totally discontinuous and though not Riemann integrable is Lebesgue integrable. In this case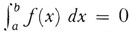 
The notion of the Lebesgue integral can be extended to more general functions, for example unbounded functions. If f(x) is Lebesgue integrable but not bounded in the interval of integration, the integral converges absolutely. Unbounded functions may be Lebesgue integrable but not Riemann integrable and conversely.
For practical purposes the Riemann integral suffices. In fact Lebesgue showed (Leçons sur l’ intégration et la recherche des fonctions primitives, 1904) that a bounded function is Riemann integrable if and only if the points of discontinuity form a set of measure 0. But for theoretical work the Lebesgue integral affords simplifications. The new theorems rest on the countable additivity of Lebesgue measure as contrasted with the finite additivity of Jordan content.
To illustrate the simplicity of theorems using Lebesgue integration, we have the result given by Lebesgue himself in his thesis. Suppose u1 (x), u2 (x), … are summablc functions on a measurable set E and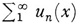 
converges to f(x). Then f(x) is measurable. If in addition sn(x) = 
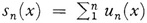is uniformly bounded (|sn (x) | ≤ B for all x in E and all n), then it is a theorem that f (x) is Lebesgue integrable on [a, b] and
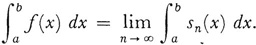
If we were working with Riemann integrals we would need the additional hypothesis that the sum of the series is integrable; this case for the Riemann integral is a theorem due to Cesare Arzelà (1847-1912).6 Lebesgue made his theorem the cornerstone in the exposition of his theory in his Leçons sur V intégration.
The Lebesgue integral is especially useful in the theory of Fourier series and most important contributions were made in this connection by Lebesgue himself.7 According to Riemann, the Fourier coefficients an and bn of a bounded and integrable function tend to 0 as n becomes infinite. Lebesgue’s generalization states that
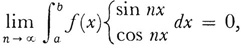
where f(x) is any function, bounded or not, that is Lebesgue integrable. This fact is now referred to as the Riemann-Lebesgue lemma.
In this same paper of 1903 Lebesgue showed that if ƒ is a bounded function represented by a trigonometric series, that is,
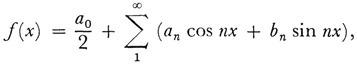
then the an and bn are Fourier coefficients. In 19058 Lebesgue gave a new sufficient condition for the convergence of the Fourier series to a function f(x) that included all previously known conditions.
Lebesgue also showed (Leçons sur les séries trigonométriques, 1906, p. 102) that term-by-term integration of a Fourier series does not depend on the uniform convergence of the series to f(x) itself. What does hold is that
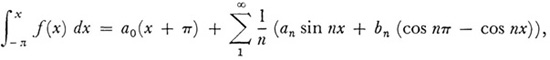
where x is any point in [–π, π], for any f(x) that is Lebesgue integrable, whether or not the original series for f(x) converges. And the new series converges uniformly to the left side of the equation in the interval [–π, π].
Further, Parseval’s theorem that
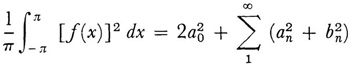
holds for any f(x) whose square is Lebesgue integrable in [–π, π] (Leçons, 1906, p. 100). Then Pierre Fatou (1878-1929) proved9 that
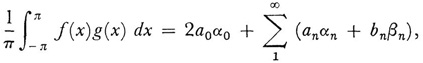
where an and bn, and αn and βn are the Fourier coefficients for f(x) and g(x) whose squares are Lebesgue integrable in [– π, π]. Despite these advances in the theory of Fourier series, there is no known property of an f(x) Lebesgue integrable in [– π, π] that is necessary and sufficient for the convergence of its Fourier series.
Lebesgue devoted most of his efforts to the connection between the notions of integral and of primitive functions (indefinite integrals). When Riemann introduced his generalization of the integral, the question was posed whether the correspondence between definite integral and primitive function, valid for continuous functions, held in the more general case. But it is possible to give examples of functions f integrable in Riemann’s sense and such that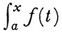 
does not have a derivative (not even a right or left derivative) at certain points. Conversely Volterra showed in 188110 that a function F(x) can have a bounded derivative in an interval I that is not integrable in Riemann’s sense over the interval. By a subtle analysis Lebesgue showed that if f is integrable in his sense in [a, b], then 
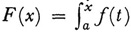dt has a derivative equal to f(x) almost everywhere, that is, except on a set of measure zero (Leçons sur l’intégration). Conversely, if a function g is differentiable in [a, b] and if its derivative g’ = f is bounded, then f is Lebesgue integrable and the formula g(x) — g(a) = 
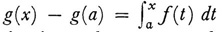dt holds. However, as Lebesgue established, the situation is much more complex if g’ is not bounded. In this case g’ is not necessarily integrable, and the first problem is to characterize the functions g for which g’ exists almost everywhere and is integrable. Limiting himself to the case where one of the derived numbers11 of g is finite everywhere, Lebesgue showed that g is necessarily a function of bounded variation (Chap. 40, sec. 6). Finally Lebesgue established (in the 1904 book) the reciprocal result. A function g of bounded variation admits a derivative almost everywhere and g’ is integrable. But one does not necessarily have
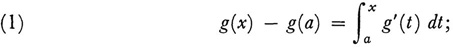
the difference between the two members of this equation is a nonconstant function of bounded variation with derivative zero almost everywhere. As for the functions of bounded variation g for which (1) does hold, these have the following property: The total variation of g in an open set U (that is, the sum of the total variations of g in each of the connected components of U) tends to 0 with the measure of U. These functions were called absolutely continuous by Giuseppe Vitali (1875-1932), who studied them in detail.
Lebesgue’s work also advanced the theory of multiple integrals. Under his definition of the double integral, the domain of functions for which the double integral can be evaluated by repeated integration is extended. Lebesgue gave a result in his thesis of 1902, but the better result was given by Guido Fubini (1879-1943):12 If f(x, y) is summable over the measurable set G, then
(a) f(x, y) as a function of x and as a function of y is summable for almost all y and x, respectively;
(b) the set of points (x0, y0) for which either f(x, y0) or f(x0, y) is not summable has measure 0;
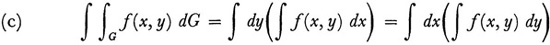
where the outer integrals are taken over the set of points y (respectively x) for which f(x, y) as a function of x (as a function of y, respectively) are summable.
Finally, in 191013 Lebesgue arrived at results for multiple integrals that extended those for the derivatives of single integrals. He associated with a function f integrable in every compact region of Rn, the set function (as opposed to functions of numerical variables) F(E) = ∫E f(x) dx (x represents n coordinates) defined for each integrable domain E of Rn. This concept generalizes the indefinite integral. He observed that the function F possesses two properties:
(1) It is completely additive; that is,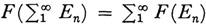 
where the En are pairwise disjoined measurable sets.
(2) It is absolutely continuous in the sense that F(E) tends to 0 with the measure of E.
The essential part of this paper of Lebesgue was to show the converse of this proposition, that is, to define a derivative of F (E) at a point P of n-dimensional space. Lebesgue arrived at the following theorem: If F(E) is absolutely continuous and additive, then it possesses a finite derivative almost everywhere, and F is the indefinite integral ofthat summable function which is the derivative of F where it exists and is finite but is otherwise arbitrary at the remaining points.
The principal tool in the proof is a covering theorem due to Vitali,14 which remains fundamental in this area of integration. But Lebesgue did not stop there. He indicated the possibility of generalizing the notion of functions of bounded variation by considering functions F(E) where E is a measurable set, the functions being completely additive and such that ∑n |F(En)| remains bounded for every denumerable partition of E into measurable subsets En. It would be possible to cite many other theorems of the calculus that have been generalized by Lebesgue’s notion of the integral.
Lebesgue’s work, one of the great contributions of this century, did win approval but, as usual, not without some resistance. We have already noted (Chap. 40, sec. 7) Hermite’s objections to functions without derivatives. He tried to prevent Lebesgue from publishing a “Note on Non-Ruled Surfaces Applicable to the Plane,”15 in which Lebesgue treated non-differentiable surfaces. Lebesgue said many years later in his Notice (p. 13, see bibliography),
To many mathematicians I became the man of the functions without derivatives, although I never at any time gave myself completely to the study or consideration of such functions. And since the fear and horror which Hermite showed was felt by almost everybody, whenever I tried to take part in a mathematical discussion there would always be an analyst who would say, “This won’t interest you; we are discussing functions having derivatives.” Or a geometer would say it in his language: “We’re discussing surfaces that have tangent planes.”
Lebesgue also said (Notice, p. 14),
Darboux had devoted his Mémoire of 1875 to integration and to functions without derivatives; he therefore did not experience the same horror as Hermite. Nevertheless I doubt whether he ever entirely forgave my “Note on Applicable Surfaces.” He must have thought that those who make themselves dull in this study are wasting their time instead of devoting it to useful research.
We have already indicated the advantages of Lebesgue integration in generalizing older results and in formulating neat theorems on series. In subsequent chapters we shall meet additional applications of Lebesgue’s ideas. The immediate developments in the theory of functions were many extensions of the notion of integral. Of these we shall merely mention one by Johann Radon (1887-1956), which embraces both Stieltjes’s and Lebesgue’s integral and is in fact known as the Lebesgue-Stieltjes integral.16 The generalizations cover not only broader or different notions of integrals on point sets of n- dimensional Euclidean space but on domains of more general spaces such as spaces of functions. The applications of these more general concepts are now found in the theory of probability, spectral theory, ergodic theory, and harmonic analysis (generalized Fourier analysis).
Borei, Emile: Notice sur les travaux scientifiques de Al. Emile Borei, 2nd ed., Gauthier-Villars, 1921.
Bourbaki, Nicolas: Eléments d’histoire de mathématiques, Hermann, 1960, pp. 246-59.
Collingwood, E. F.: “Emile Borei,” Jour. Lon. Math. Soc, 34, 1959, 488-512.
Fréchet, M.: “La Vie et l’œuvre d’Emile Borei,” L’Enseignement Mathématique, (2), 11, 1965, 1-94.
Hawkins, T. W., Jr.: Lebesgue’s Theory of Integration: Its Origins and Development, University of Wisconsin Press, 1970, Chaps. 4-6.
Hildebrandt, T. H.: “On Integrals Related to and Extensions of the Lebesgue Integral,” Amer. Math. Soc. Bull., 24, 1918, 113-77.
Jordan, Camille: Œuvres, 4 vols., Gauthier-Villars, 1961-64.
Lebesgue, Henri: Measure and the Integral, Holden-Day, 1966, pp. 176-94. Translation of the French La Mesure des grandeurs.
_______ : Notice sur les travaux scientifiques de M. Henri Lebesgue, Edouard Privat, 1922.
_______ : Leçons sur l’intégration et la recherche des fonctions primitives, Gauthier-Villars, 1904, 2nd ed., 1928.
McShane, E. J.: “Integrals Devised for Special Purposes,” Amer. Math. Soc. Bull., 69, 1963, 597-627.
Pesin, Ivan M.: Classical and Modern Integration Theories, Academic Press, 1970.
Plancherel, Michel: “Le Développement de la théorie des séries trigonométriques dans le dernier quart de siècle,” L’Enseignement Mathématique, 24, 1924/25, 19-58.
Riesz, F.: “L’Evolution de la notion d’intégrale depuis Lebesgue,” Annales de l’Institut Fourier, 1, 1949, 29-42.