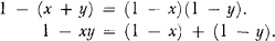
Logic is invincible because in order to combat logic it is necessary to use logic.
PIERRE BOUTROUX
We know that mathematicians care no more for logic than logicians for mathematics. The two eyes of exact science are mathematics and logic: the mathematical sect puts out the logical eye, the logical sect puts out the mathematical eye, each believing that it can see better with one eye than with two.
AUGUSTUS DE MORGAN
By far the most profound activity of twentieth-century mathematics has been the research on the foundations. The problems thrust upon the mathematicians, and others that they voluntarily assumed, concern not only the nature of mathematics but the validity of deductive mathematics.
Several activities converged to bring foundational problems to a head in the first part of the century. The first was the discovery of contradictions, euphemistically called paradoxes, notably in set theory. One such contradiction, the Burali-Forti paradox, has already been noted (Chap. 41, sec. 9). A number of others were discovered in the first few years of this century. Clearly the discovery of contradictions disturbed the mathematicians deeply. Another problem that had gradually been recognized and that emerged into the open early in this century was the consistency of mathematics (Chap. 43, sec. 6). In view of the paradoxes of set theory consistency had to be established especially in this area.
During the latter part of the nineteenth century a number of men had begun to reconsider the foundations of mathematics and, in particular, the relationship of mathematics to logic. Research in this area (about which we shall say more later) suggested to some mathematicians that mathematics could be founded on logic. Others questioned the universal application of logical principles, the meaningfulncss of some existence proofs, and even the reliance upon logical proof as the substantiation of mathematical results. Controversies that had been smoldering before 1900 broke out into open fire when the paradoxes and the consistency problem added fuel. Thereupon the question of the proper foundation for all mathematics became vital and of widespread concern.
Following hard upon the discovery by Cantor and Burali-Forti of the paradox involving ordinal numbers came a number of other paradoxes or antinomies. Actually the word paradox is ambiguous, for it can refer to a seeming contradiction. But what the mathematicians actually encountered were unquestionably contradictions. Let us see first what they were.
One paradox was put in popular form by Bertrand Russell (1872-1970) in 1918, as the “barber” paradox. A village barber, boasting that he has no competition, advertises that of course he does not shave those people who shave themselves, but does shave all those who do not shave themselves. One day it occurs to him to ask whether he should shave himself. If he should shave himself, then by the first half of his assertion, he should not shave himself; but if he does not shave himself, then in accordance with his boast, he must shave himself. The barber is in a logical predicament.
Still another paradox was formulated by Jules Richard (1862—1956).1 A simplified version of it was given by G. G. Berry and Russell and published by the latter.2 The simplified paradox, also known as Richard’s, reads as follows: Every integer can be described in words requiring a certain number of letters. For example, the number 36 can be described as thirty-six or as four times nine. The first description uses nine letters and the second thirteen. There is no one way to describe any given number, but this is not essential. Now let us divide all the positive whole numbers into two groups, the first to include all those that can be described (in at least one way) in 100 letters or fewer and the second group to include all those numbers that require a minimum of 101 letters, no matter how described. Only a finite number of numbers can have a description in 100 or fewer letters, for there are at most 27100 expressions with 100 or fewer letters (and some of these are meaningless). There is then a smallest integer in the second group. It can be described by the phrase, “the least integer not describable in one hundred or fewer letters.” But this phrase requires fewer than 100 letters. Hence, the least integer not describable in 100 or fewer letters can be described in fewer than 100 letters.
Let us consider another form of this paradox, first stated by Kurt Greiling (1886-1941) and Leonard Nelson (1882-1927) in 1908 and published in an obscure journal.3 Some words are descriptive of themselves. For example, the word “polysyllabic” is polysyllabic. On the other hand, the word “monosyllabic” is not monosyllabic. We shall call those words that are not descriptive of themselves heterological. In other words the word X is heterological if X is not itself X. Now let us replace X by the word “heterological.” Then the word “heterological” is heterological if heterological is not heterological.
Cantor pointed out, in a letter to Dedekind of 1899, that one could not speak of the set of all sets without ending in a contradiction (Chap. 41, sec. 9). This is essentially what is involved in Russell’s paradox (The Principles of Mathematics, 1903, p. 101). The class of all men is not a man. But the class of all ideas is an idea; the class of all libraries is a library; and the class of all sets with cardinal number greater than 1 is such a set. Hence, some classes are not members of themselves and some are. This description of classes includes all and the two types are mutually exclusive. Let us now denote by M the class of all classes that are members of themselves and by N the class of all classes that are not members of themselves. Now N is itself a class and we ask whether it belongs to M or to N. If N belongs to N then N is a member of itself and so must belong to M. On the other hand, if N is a member of M, since M and N are mutually exclusive classes, N does not belong to N. Hence N is not a member of itself and should, by virtue of the definition of N, belong to N.
The cause of all these paradoxes, as Russell and Whitehead point out, is that an object is defined in terms of a class of objects that contains the object being defined. Such definitions are also called impredicative and occur particularly in set theory. This type of definition is also used, as Zermelo noted in 1908, to define the lower bound of a set of numbers and to define other concepts of analysis. Hence classical analysis contains paradoxes.
Cantor’s proof of the nondenumerability of the set of real numbers (Chap. 41, sec. 7) also uses such an impredicative set. A one-to-one correspondence is assumed to hold between the set of all positive integers and the set M of all real numbers. Then to each integer k, there corresponds the set f{k). Now f(k) does or does not contain k. Let N be the set of all k such that k does not belong to f(k). This set N (taken in some order) is a real number. Hence there should be, by the initial one-to-one correspondence, an integer n such that n corresponds to N. Now if n belongs to N, it should not by the definition of N. If n does not belong to N, then by the definition of N it should belong to N. The definition of the set N is impredicative because k belongs to N if and only if there exists a set K in M such that K = f(k) and k does not belong to K. Thus in defining N we make use of the totality M of sets which contains N as a member. That is, to define N, N must already be in the set M.
It is rather easy to fall unwittingly into the trap of introducing impredicative definitions. Thus if one defines the class of all classes that contain more than five members, he has defined a class that contains itself. Likewise the statement, the set S of all sets definable in twenty-five or fewer words, defines S impredicatively.
These paradoxes jolted the mathematicians, while they compromised not only set theory but large portions of classical analysis. Mathematics as a logical structure was in a sad state, and mathematicians looked back longingly to the happier days before the paradoxes were recognized.
It is perhaps not surprising that the mathematicians’ first recourse was to axiomatize Cantor’s rather freely formulated and, as some are wont to say today, naive set theory. The axiomatization of geometry and the number system had resolved logical problems in those areas, and it seemed likely that axiomatization would clarify the difficulties in set theory. The task was first undertaken by the German mathematician Ernst Zermelo who believed that the paradoxes arose because Cantor had not restricted the concept of a set. Cantor in 18954 had defined a set as a collection of distinct objects of our intuition or thought. This was rather vague, and Zermelo therefore hoped that clear and explicit axioms would clarify what is meant by a set and what properties sets should have. Cantor himself was not unaware that his concept of a set was troublesome. In a letter to Dedekind of 18995 he had distinguished between consistent and inconsistent sets. Zermelo thought he could restrict his sets to Cantor’s consistent ones and these would suffice for mathematics. His axiom system6 contained fundamental concepts and relations that are defined only by the statements in the axioms themselves. Among such concepts was the notion of a set itself and the relation of belonging to a set. No properties of sets were to be used unless granted by the axioms. The existence of an infinite set and such operations as the union of sets and the formation of subsets were also provided for in the axioms. Notably Zermelo included the axiom of choice (Chap. 41, sec. 8).
Zermelo’s plan was to admit into set theory only those classes that seemed least likely to generate contradictions. Thus the null class, any finite class, and the class of natural numbers seemed safe. Given a safe class, certain classes formed from it, such as any subclass, the union of safe classes, and the class of all subsets of a safe class, should be safe classes. However, he avoided complementation for, while x might be a safe class, the complement of x, that is, all non-x, in some large universe of objects might not be safe.
Zermelo’s development of set theory was improved by Abraham A. Fraenkel (1891-1965).7 Additional changes were made by von Neumann.8 The hope of avoiding the paradoxes rests in the case of the Zermelo-Fraenkel system on restricting the types of sets that are admitted while admitting enough to serve the foundations of analysis. Von Neumann’s idea was a little more daring. He makes the distinction between classes and sets. Classes are sets so large that they are not contained in other sets or classes, whereas sets are more restricted classes and may be members of a class. Thus sets are the safe classes. As von Neumann pointed out, it was not the admission of the classes that led to contradictions but their being treated as members of other classes.
Zermelo’s formal set theory, as modified by Fraenkel, von Neumann, and others, is adequate for developing the set theory required for practically all of classical analysis and avoids the paradoxes to the extent that, as yet, no one has discovered any within the theory. However, the consistency of the axiomatized set theory has not been demonstrated. Apropos of the open question of consistency Poincaré remarked, “We have put a fence around the herd to protect it from the wolves but we do not know whether some wolves were not already within the fence.”
Beyond the problem of consistency, the axiomatization of set theory used the axiom of choice, which is needed to establish parts of standard analysis, topology, and abstract algebra. This axiom was considered objectionable by a number of mathematicians, among them Hadamard, Lebesgue. Borei, and Baire, and in 1904, when Zermelo used it to prove the well-ordering theorem (Chap. 41, sec. 8), a host of objections flooded the journals.9 The questions of whether this axiom was essential and whether it was independent of the others were raised and remained unanswered for some time (see sec. 8).
The axiomatization of set theory, despite the fact that it left open such questions as consistency and the role of the axiom of choice, might have put mathematicians at ease with respect to the paradoxes and have led to a decline in the interest in foundations. But by this time several schools of thought on the foundations of mathematics, no doubt stirred into life by the paradoxes and the problem of consistency, had become active and contentious. To the proponents of these philosophies the axiomatic method as practiced by Zermelo and others was not satisfactory. To some it was objectionable because it presupposed the logic it used, whereas by this time logic itself and its relation to mathematics was under investigation. Others, more radical, objected to the reliance upon any kind of logic, particularly as it was applied to infinite sets. To understand the arguments that various schools of thought propounded, we must go back in time somewhat.
One development that caused new controversies as well as dissatisfaction with the axiomatization of set theory concerns the role of logic in mathematics; it arose from the nineteenth-century mathematization of logic. This development has its own history.
The power of algebra to symbolize and even mechanize geometrical arguments had impressed both Descartes and Leibniz, among others (Chap. 13, sec. 8), and both envisioned a broader science than the algebra of numbers. They contemplated a general or abstract science of reasoning that would operate somewhat like ordinary algebra but be applicable to reasoning in all fields. As Leibniz put it in one of his papers, “The universal mathematics is, so to speak, the logic of the imagination,” and ought to treat “all that which in the domain of the imagination is susceptible of exact determination.” With such a logic one might build any edifice of thought from its simple elements to more and more complicated structures. The universal algebra would be part of logic but an algcbraicized logic. Descartes began modestly by attempting to construct an algebra of logic; an incomplete sketch of this work is extant.
In pursuit of the same broad goal as Descartes’s, Leibniz launched a more ambitious program. He had paid attention to logic throughout his life and rather early became entranced with the scheme of the scientist and theologian Raymond Lull (1235—1315) whose book Ars Magna et Ultima offered a naive mechanical method for producing new ideas by combining existing ones but who did have the concept of a universal science of logic that would be applicable to all reasoning. Leibniz broke from scholastic logic and from Lull but became impressed with the possibility of a broad calculus that would enable man to reason in all fields mechanically and effortlessly. Leibniz says of his plan for a universal symbolic logic that such a science, of which ordinary algebra is but a small part, would be limited only by the necessity of obeying the laws of formal logic. One could name it, he said, “algebraico-logical synthesis.”
This general science was to provide, first of all, a rational, universal language that would be adapted to thinking. The concepts, having been resolved into primitive distinct and nonoverlapping ones, could be combined in an almost mechanical way. He also thought that symbolism would be necessary in order to keep the mind from getting lost. Here the influence of algebraic symbolism on his thinking is clear. He wanted a symbolic language capable of expressing human thoughts unambiguously and aiding deduction. This symbolic language was his “universal characteristic.”
In 1666 Leibniz wrote his De Arte Combinatoria,10 which contains among other matters his early plans for his universal system of reasoning. He then wrote numerous fragments, which were never published but which are available in the edition of his philosophical writings (see note 10). In his first attempt he associated with each primitive concept a prime number; any concept composed of several primitive ones was represented by the product of the corresponding primes. Thus if 3 represents “man” and 7 “rational,” 21 would represent “rational man.” He then sought to translate the usual rules of the syllogism into this scheme but was not successful. He also tried, at another time, to use special symbols in place of prime numbers, where again complex ideas would be represented by combinations of symbols. Actually Leibniz thought that the number of primitive ideas would be few, but this proved to be erroneous. Also one basic operation, conjunction, for compounding primitive ideas did not suffice.
He also commenced work on an algebra of logic proper. Directly and indirectly Leibniz had in his algebra concepts we now describe as logical addition, multiplication, identity, negation, and the null class. He also called attention to the desirability of studying abstract relations such as inclusion, one-to-one correspondence, many-to-one correspondences, and equivalence relations. Some of these, he recognized, have the properties of symmetry and transitivity. Leibniz did not complete this work; he did not get beyond the syllogistic rules, which he himself recognized do not encompass all the logic mathematics uses. Leibniz described his ideas to l'Hospital and others, but they paid no attention. His logical works remained unedited until the beginning of the twentieth century and so had little direct influence. During the eighteenth and early nineteenth centuries a number of men sketched attempts similar to Leibniz’s but got no further than he had.
A more effective if less ambitious step was taken by Augustus De Morgan. De Morgan published Formal Logic (1847) and many papers, some of which appeared in the Transactions of the Cambridge Philosophical Society. He sought to correct defects of and improve on Aristotelian logic. In his Formal Logic he added a new principle to Aristotelian logic. In the latter the premises “Some M’s are A’s” and “Some M’s are B’s” permit no conclusion; and, in fact, this logic says that the middle term M must be used universally, that is, “All M’s” must occur. But De Morgan pointed out that from “Most M’s are A’s” and “Most M’s arc B’s,” it follows of necessity that “Some A’s are B’s.” De Morgan put this fact in quantitative form. If there are m of the M’s, and a of the M’s are in A and b of the M’s are in B, then there are at least (a + b – m) A’s that are B’s. The point of De Morgan’s observation is that the terms may be quantified. He was able as a consequence to introduce many more valid forms of the syllogism. Quantification also eliminated a defect in Aristotelian logic. The conclusion “Some A’s are B’s” which in Aristotelian logic can be drawn from “All A’s are B’s” implies the existence of A’s but they need not exist.
De Morgan also initiated the study of the logic of relations. Aristotelian logic is devoted primarily to the relationship “to be” and either asserts or denies this relationship. As De Morgan pointed out, this logic could not prove that if a horse is an animal, then a horse’s tail is an animal’s tail. It certainly could not handle a relation such as x loves y. De Morgan introduced symbolism to handle relations but did not carry this subject very far.
In the area of symbolic logic Dc Morgan is widely known for what are now called De Morgan’s laws. As he stated them,11 the contrary of an aggregate is the compound of the contraries of the aggregates; the contrary of a compound is the aggregate of the contraries of the components. In logical notation these laws read
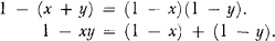
The contribution of symbolism to an algebra of logic was the major step made by George Boole (1815-1864), who was largely self-taught and became professor of mathematics at Queens College in Cork. Boole was convinced that the symbolization of language would rigorize logic. His Mathematical Analysis of Logic, which appeared on the same day as De Morgan’s Formal Logic, and his An Investigation of the Laws of Thought (1854) contain his major ideas.
Boole’s approach was to emphasize extensional logic, that is, a logic of classes, wherein sets or classes were denoted by x, y, z,… whereas the symbols X, Y, Z,… represented individual members. The universal class was denoted by 1 and the empty or null class by 0. He used xy to denote the intersection of two sets (he called the operation election), that is, the set of elements common to both x and y, and x + y to denote the set consisting of all the elements in x and in y. (Strictly for Boole addition or union applied only to disjoint sets; W. S. Jevons [1835-82] generalized the concept.) The complement of x is denoted by 1 — x. More generally x – y is the class of x’s that are not y’s. The relation of inclusion, that is, x is contained in y, he wrote as xy = x. The equal sign denoted the identity of the two classes.
Boole believed that the mind grants to us at once certain elementary processes of reasoning that are the axioms of logic. For example, the law of contradiction, that A cannot be both B and not B, is axiomatic. This is expressed by
x(l - x) = 0.
It is also obvious to the mind that
xy = yx
and so this commutative property of intersection is another axiom. Equally obvious is the property
xx = x.
This axiom is a departure from ordinary algebra. Boole also accepted as axiomatic that
x + y = y + X
and
x(u + v) = xu + xv.
With these axioms the law of excluded middle could be stated in the form
x + (1 - x) = 1;
that is, everything is x or not x. Every X is Y becomes x(l – y) = 0. No X is Y reads as xy = 0. Some X are Y is denoted by xy ≠ 0 and some X are not Y by x(1 - y) ≠ 0.
From the axioms Boole planned to deduce the laws of reasoning by applying the processes permitted by the axioms. As trivial conclusions he had that 1·x = x and 0·x = 0. A slightly more involved argument is illustrated by the following. From
x + (1 – x) = 1
it follows that
z[x + (1 - x)] = z·1
and then that
zx + z(l — x) = z.
Thus the class of objects z consists of those that are in x and those that are in 1 – x.
Boole observed that the calculus of classes could be interpreted as a calculus of propositions. Thus if x and y arc propositions instead of classes, then xy is the joint assertion of x and y and x + y is the assertion of x or y or both. The statement x = 1 would mean that the proposition x is true and x = 0 that x is false. 1 – x would mean the denial of x. However Boole did not get very far with his calculus of propositions.
Both De Morgan and Boole can be regarded as the reformers of Aristotelian logic and the initiators of an algebra of logic. The effect of their work was to build a science of logic which thenceforth was detached from philosophy and attached to mathematics.
The calculus of propositions was advanced by Charles S. Peirce. Peirce distinguished between a proposition and a propositional function. A proposition, John is a man, contains only constants. A propositional function, x is a man, contains variables. Whereas a proposition is true or false, a propositional function is true for some values of the variable and false for others. Peirce also introduced propositional functions of two variables, for example, x knows y.
The men who had built symbolic logic thus far were interested in logic and in mathematizing that subject. With the work of Gottlob Frege (1848-1925), professor of mathematics at Jena, mathematical logic takes a new direction, the one that is pertinent to our account of the foundations of mathematics. Frege wrote several major works, Begriffsschrift (Calculus of Concepts, 1879), Die Grundlagen der Arithmetik (The Foundation of Arithmetic, 1884), and Grundgesetze der Arithmetik (The Fundamental Laws of Arithmetic; Vol. 1, 1893; Vol. 2, 1903). His works are characterized by precision and thoroughness of detail.
In the area of logic proper, Frege expanded on the use of variables, quantifiers, and propositional functions; most of this work was done independently of his predecessors, including Peirce. In his Begriffsschrift Frege gave an axiomatic foundation to logic. He introduced many distinctions that acquired great importance later, for example the distinction between the statement of a proposition and the assertion that it is true. The assertion is denoted by placing the symbol ├ in front of the proposition. He also distinguished between an object x and the set {x} containing just x, and between an object belonging to a set and the inclusion of one set in another. Like Peirce, he used variables and propositional functions, and he indicated the quantification of his propositional functions, that is, the domain of the variable or variables for which they are true. He also introduced (1879) the concept of material implication: A implies B means either that A is true and B is true or A is false and B is true or A is false and B is false. This interpretation of implication is more convenient for mathematical logic. The logic of relations was also taken up by Frege; thus the relation of order involved in stating, for example, that a is greater than b was important in his work.
Having built up logic on explicit axioms, he proceeded in his Grundlagen to his real goal, to build mathematics as an extension of logic. He expressed the concepts of arithmetic in terms of the logical concepts. Thus the definitions and laws of number were derived from logical premises. We shall examine this construction in connection with the work of Russell and Whitehead. Unfortunately Frege’s symbolism was quite complex and strange to mathematicians. His work was in fact not well known until it was discovered by Russell. Rather ironic too is the fact that, just as the second volume of Grundgesetze was about to go to press, he received a letter from Russell, who informed him of the paradoxes of set theory. At the close of Volume 2 (p. 253), Frege remarks, “A scientist can hardly meet with anything more undesirable than to have the foundation give way just as the work is finished. I was put in this position by a letter from Mr. Bertrand Russell when the work was nearly through the press.”
We left the account of the work on the foundations of mathematics at the point where the axiomatization of set theory had provided a foundation that avoided the known paradoxes and yet served as a logical basis for the existing mathematics. We did point out that this approach was not satisfactory to many mathematicians. That the consistency of the real number system and the theory of sets remained to be proved was acknowledged by all; consistency was no longer a minor matter. The use of the axiom of choice was controversial. But beyond these problems was the overall question of what the proper foundation for mathematics was. The axiomatic movement of the late nineteenth century and the axiomatization of set theory had proceeded on the basis that the logic employed by mathematics could be taken for granted. But by the early nineteen-hundreds there were several schools of thought that were no longer content with this presupposition. The school led by Frege sought to rebuild logic and to build mathematics on logic. This plan, as we have already noted, was set back by the appearance of the paradoxes, but it was not abandoned. It was in fact independently conceived and pursued by Bertrand Russell and Alfred North Whitehead. Hilbert, already impressed by the need to establish consistency, began to formulate his own systematic foundation for mathematics. Still another group of mathematicians, known as intuitionists, was dissatisfied with the concepts and proofs introduced in late nineteenth-century analysis. These men were adherents of a philosophical position that not only could not be reconciled with some of the methodology of analysis but also challenged the role of logic. The development of these several philosophies was the major undertaking in the foundations of mathematics; its outcome was to open up the entire question of the nature of mathematics. We shall examine each of these three major schools of thought.
The first of these is known as the logistic school and its philosophy is called logicism. The founders are Russell and Whitehead. Independently of Frege, they had the idea that mathematics is derivable from logic and therefore is an extension of logic. The basic ideas were sketched by Russell in his Principles of Mathematics (1903); they were developed in the detailed work by Whitehead and Russell, the Principia Mathematica (3 vols., 1910-13). Since the Principia is the definitive version, we shall base our account on it.
This school starts with the development of logic itself, from which mathematics follows without any axioms of mathematics proper. The development of logic consists in stating some axioms of logic, from which theorems are deduced that may be used in subsequent reasoning. Thus the laws of logic receive a formal derivation from axioms. The Principia also has undefined ideas, as any axiomatic theory must have since it is not possible to define all the terms without involving an infinite regress of definitions. Some of these undefined ideas are the notion of an elementary proposition, the notion of a propositional function, the assertion of the truth of an elementary proposition, the negation of a proposition, and the disjunction of two propositions.
Russell and Whitehead explain these notions, though, as they point out, this explanation is not part of the logical development. By a proposition they mean simply any sentence stating a fact or a relationship: for example, John is a man; apples are red; and so forth. A propositional function contains a variable, so that substitution of a value for that variable gives a proposition. Thus “X is an integer” is a propositional function. The negation of a proposition is intended to mean, “It is not true that the proposition holds,” so that if p is the proposition that John is a man, the negation of p, denoted by ~p, means, “It is not true that John is a man,” or “John is not a man.” The disjunction of two propositions p and q, denoted by p ν q, means p or q. The meaning of “or” here is that intended in the sentence, “Men or women may apply.” That is, men may apply; women may apply; and both may apply. In the sentence, “That person is a man or a woman,” “or” has the more common meaning of either one or the other but not both. Mathematics uses “or” in the first sense, though sometimes the second sense is the only one possible. For example, “the triangle is isosceles or the quadrilateral is a parallelogram” illustrates the first sense. We also say that every number is positive or negative. Here additional facts about positive and negative numbers say that both cannot be true. Thus the assertion p ν q means p and q, ~p and q, or p and ν q.
A most important relationship between propositions is implication, that is, the truth of one proposition compelling the truth of another. In the Principia implication, p  q, is defined by ~p ν q, which in turn means ~p and q, p and q, or and ~ q. As an illustration consider the implication, If X is a man, then X is mortal. Here the state of affairs could be
q, is defined by ~p ν q, which in turn means ~p and q, p and q, or and ~ q. As an illustration consider the implication, If X is a man, then X is mortal. Here the state of affairs could be
X is not a man and X is mortal;
X is a man and X is mortal;
X is not a man and X is not mortal.
Any one of these possibilities is allowable. What the implication forbids is
X is a man and X is not mortal.
Some of the postulates of the Principia are:
(a) Anything implied by a true elementary proposition is true.
(b) (p ν p)  p.
p.
(c) q  (p ν q).
(p ν q).
(d) (p ν q)  (q ν p).
(q ν p).
(e) [p ν (q ν r)]  [q ν (p ν r)].
[q ν (p ν r)].
(f) The assertion of p and the assertion p  q permits the assertion of q.
q permits the assertion of q.
The independence of these postulates and their consistency cannot be proved because the usual methods do not apply. From these postulates the authors proceed to deduce theorems of logic and ultimately arithmetic and analysis. The usual syllogistic rules of Aristotle occur as theorems.
To illustrate how even logic itself has been formalized and made deductive, let us note a few theorems of the early part of Principia Mathematica:

This is the principle of reductio ad absurdum. In words, if the assumption of p implies that p is false, then p is false.
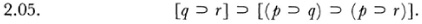
This is one form of the syllogism. In words, if q implies r, then if p implies q, p implies r.

This is the principle of excluded middle: p is true or p is false.

In words, p implies that not-p is false.

If p implies q, then not-q implies not-p.
Propositions are a step to propositional functions that treat sets by means of properties rather than by naming the objects in a set. Thus the propositional function “x is red” denotes the set of all red objects.
If the members of a set are individual objects, then the propositional functions applying to such members are said to be of type 0. If the members of a set are themselves propositional functions, any propositional function applying to such members is said to be of type 1. And generally propositional functions whose variables are of types less than and equal to n are of type n + 1.
The theory of types seeks to avoid the paradoxes, which arise because a collection of objects contains a member that itself can be defined only in terms of the collection. The resolution by Russell and Whitehead of this difficulty was to require that “whatever involves all members of a collection must not itself be a member of the collection.” To carry out this restriction in the Principia, xthey specify that a (logical) function cannot have as one of its arguments anything defined in terms of the function itself. They then discuss the paradoxes and show that the theory of types avoids them.
However, the theory of types leads to classes of statements that must be carefully distinguished by type. If one attempts to build mathematics in accordance with the theory of types, the development becomes exceedingly complex. For example, in the Principia two objects a and b are equal if for every property P(x), P(a) and P(b) are equivalent propositions (each implies the other). According to the theory of types, P may be of different types because it may contain variables of various orders as well as the individual objects a or b, and so the definition of equality must apply for all types of P; in other words, there is an infinity of relations of equality, one for each type of property. Likewise, an irrational number defined by the Dedekind cut proves to be of higher type than a rational number, which in turn is of higher type than a natural number, and so the continuum consists of numbers of different types. To escape this complexity, Russell and Whitehead introduced the axiom of reducibility, which affirms the existence, for each propositional function of whatever type, of an equivalent propositional function of type zero.
Having treated propositional functions, the authors take up the theory of classes. A class, loosely stated, is the set of objects satisfying some propositional function. Relations are then expressed as classes of couples satisfying propositional functions of two variables. Thus “x judges y” expresses a relation. On this basis the authors are prepared to introduce the notion of cardinal number.
The definition of a cardinal number is of considerable interest. It depends upon the previously introduced relation of one-to-one correspondence between classes. If two classes are in one-to-one correspondence, they are called similar. The relationship of similarity is proven to be reflexive, symmetric, and transitive. All similar classes possess a common property, and this is their number. However, similar classes may have more than one common property. Russell and Whitehead get around this, as had Frege, by defining the number of a class as the class of all classes that are similar to the given class. Thus the number 3 is the class of all three-membered classes and the denotation of all thrce-membered classes is {x, y, z} with x ≠ y ≠ z. Since the definition of number presupposes the concept of one-to-one correspondence, it would seem as though the definition is circular. The authors point out, however, that a relation is one-to-one if, when x and x' have the relation to y, then x and x' are identical, and when x has the relation to y and y', then y and y' are identical. Hence the concept of one-to-one correspondence does not involve the number 1.
Given the cardinal or natural numbers, it is possible to build up the real and complex number systems, functions, and in fact all of analysis. Geometry can be introduced through numbers. Though the details in the Principia differ somewhat, our own examination of the foundations of the number system and of geometry (Chaps. 41 and 42) shows that such constructions are logically possible without additional axioms.
This, then, is the grand program of the logistic school. What it does with logic itself is quite a story, which we are skimming over here briefly. What it does for mathematics, and this we must emphasize, is to found mathematics on logic. No axioms of mathematics are needed; mathematics becomes no more than a natural extension of the laws and subject matter of logic. But the postulates of logic and all their consequences are arbitrary and, moreover, formal. That is, they have no content; they have merely form. As a consequence, mathematics too has no content, but merely form. The physical meanings we attach to numbers or to geometric concepts are not part of mathematics. It was with this in mind that Russell said that mathematics is the subject in which we never know what we are talking about nor whether what we are saying is true. Actually, when Russell started this program in the early part of the century, he (and Frege) thought the axioms of logic were truths. But he abandoned this view in the 1937 edition of the Principles of Mathematics.
The logistic approach has received much criticism. The axiom of reducibility aroused opposition, for it is quite arbitrary. It has been called a happy accident and not a logical necessity; it has been said that the axiom has no place in mathematics, and that what cannot be proved without it cannot be regarded as proved at all. Others called the axiom a sacrifice of the intellect. Moreover, the system of Russell and W'hitehead was never completed and is obscure in numerous details. Many efforts were made later to simplify and clarify it.
Another serious philosophical criticism of the entire logistic position is that if the logistic view is correct, then all of mathematics is a purely formal, logico-deductive science whose theorems follow from the laws of thought. Just how such a deductive elaboration of the laws of thought can represent wide varieties of natural phenomena such as acoustics, electromagnetics, and mechanics seems unexplained. Further, in the creation of mathematics perceptual or imaginative intuition must supply new concepts, whether or not derived from experience. Otherwise, how could new knowledge arise? But in the Principia all concepts reduce to logical ones.
The formalization of the logistic program apparently does not represent mathematics in any real sense. It presents us with the husk, not the kernel. Poincaré said, snidely (Foundations of Science, p. 483), “The logistic theory is not sterile; it engenders contradictions.” This is not true if one accepts the theory of types, but this theory, as noted, is artificial. Weyl also attacked logicism; he said that this complex structure “taxes the strength of our faith hardly less than the doctrines of the early Fathers of the Church or of the Scholastic philosophers of the Middle Ages.”
Despite the criticisms, the logistic philosophy is accepted by many mathematicians. The Russell-Whitehead construction also made a contribution in another direction. It carried out a thorough axiomatization of logic in entirely symbolic form and so advanced enormously the subject of mathematical logic.
A radically different approach to mathematics has been undertaken by a group of mathematicians called intuitionists. As in the case of logicism, the intuitionist philosophy was inaugurated during the late nineteenth century when the rigorization of the number system and geometry was a major activity. The discovery of the paradoxes stimulated its further development.
The first intuitionist was Kronecker, who expressed his views in the 1870s and 80s. To Kronecker, Weierstrass’s rigor involved unacceptable concepts, and Cantor’s work on transfinite numbers and set theory was not mathematics but mysticism. Kronecker was willing to accept the whole numbers because these are clear to the intuition. These “were the work of God.” All else was the work of man and suspect. In his essay of 1887, “Über den Zahlbegriff” (On the Number Concept),12 he showed how some types of numbers, fractions for example, could be defined in terms of the whole numbers. Fractional numbers as such were acceptable as a convenience of notation. The theory of irrational numbers and of continuous functions he wished to strip away. His ideal was that every theorem of analysis should be interpretable as giving relations among the integers only.
Another objection Kronecker made to many parts of mathematics was that they did not give constructive methods or criteria for determining in a finite number of steps the objects with which they dealt. Definitions should contain the means of calculating the object defined in a finite number of steps, and existence proofs should permit the calculation to any required degree of accuracy of the quantity whose existence is being established. Algebraists were content to say that a polynomial f(x) may have a rational factor, in which case f(x) is reducible. In the contrary case it is irreducible. In his Festschrift “Grundzüge einer arithmetischen Theorie der algebraischen Grössen” (Elements of an Arithmetic Theory of Algebraic Quantities)13 Kronecker said, “The definition of reducibility is devoid of a sure foundation until a method is given by means of which it can be decided whether a given function is irreducible or not.”
Again, though the several theories of the irrational numbers give definitions as to when two real numbers a and b are equal or when a > b or b > a, they do not give criteria to determine which alternative holds in a given case. Hence Kronecker objected to such definitions. They are definitions only in appearance. The entire theory of irrationals was unsatisfactory to him and one day he said to Lindemann, who had proved that π is a transcendental irrational, “Of what use is your beautiful investigation regarding π Why study such problems, since irrational numbers are non-existent?”
Kronecker himself did little to develop the intuitionist philosophy except to criticize the absence of constructive procedures for determining quantities whose existence was merely established. He tried to rebuild algebra but made no efforts to reconstruct analysis. Kronecker produced fine work in arithmetic and algebra which did not conform to his own requirements because, as Poincaré remarked,14 he temporarily forgot his own philosophy.
Kronecker had no supporters of his philosophy in his day and for almost twenty-five years no one pursued his ideas. However, after the paradoxes were discovered, intuitionism was revived and became a widespread and serious movement. The next strong advocate was Poincaré. His opposition to set theory because it gave rise to paradoxes has already been noted. Nor would he accept the logistic program for rescuing mathematics. He ridiculed attempts to base mathematics on logic on the ground that mathematics would reduce to an immense tautology. He also mocked the (to him) highly artificial derivation of number. Thus in the Principia I is defined as 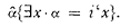 . Poincaré said sarcastically that this was an admirable definition to give to people who never heard of the number 1.
. Poincaré said sarcastically that this was an admirable definition to give to people who never heard of the number 1.
In Science and Alethod (Foundations of Science, p. 480) he stated,
Logistic has to be made over, and one is none too sure of what can be saved. It is unnecessary to add that only Cantorism and Logistic are meant; true mathematics, that which serves some useful purpose, may continue to develop according to its own principles without paying any attention to the tempests raging without, and it will pursue step by step its accustomed conquests which arc definitive and which it will never need to abandon.
Poincaré objected to concepts that cannot be defined in a finite number of words. Thus a set chosen in accordance with the axiom of choice is not really defined when a choice has to be made from each of a transfinite number of sets. He also contended that arithmetic cannot be justified by an axiomatic foundation. Our intuition precedes such a structure. In particular, mathematical induction is a fundamental intuition and not just an axiom that happens to be useful in some system of axioms. Like Kronecker, he insisted that all definitions and proof should be constructive.
He agreed with Russell that the source of the paradoxes was the definition of collections or sets that included the object defined. Thus the set A of all sets contains A. But A cannot be defined until each member of A is defined, and if A is one member the definition is circular. Another example of an impredicative definition is the definition of the maximum value of a continuous function defined over a closed interval as the largest value that the function takes on in this interval. Such definitions were common in analysis and especially in the theory of sets.
Further criticisms of the current logical state of mathematics were developed and discussed in an exchange of letters among Borei, Baire, Hadamard, and Lebesgue.15 Borei supported Poincaré’s assertion that the integers cannot be founded axiomatically. He too criticized the axiom of choice because it calls for a nondenumerable infinity of choices, which is inconceivable to the intuition. Hadamard and Lebesgue went further and said that even a denumerable infinity of arbitrary successive choices is not more intuitive because it calls for an infinity of operations, which it is impossible to conceive as being effectively realized. For Lebesgue the difficulties all reduced to knowing what one means when one says that a mathematical object exists. In the case of the axiom of choice he argued that if one merely “thinks” of a way of choosing, may one then not change his choices in the course of his reasoning? Even the choice of a single object in one set, Lebesgue maintained, raises the same difficulties. One must know the object “exists” which means that one must name the choice explicitly. Thus Lebesgue rejected Cantor’s proof of the existence of transcendental numbers. Hadamard pointed out that Lebesgue’s objections led to a denial of the existence of the set of all real numbers, and Borei drew exactly the same conclusion.
All of the above objections by intuitionists were sporadic and fragmented. The systematic founder of modern intuitionism is Brouwer. Like Kronecker, much of his mathematical work, notably in topology, was not in accord with his philosophy, but there is no question as to the seriousness of his position. Commencing with his doctoral dissertation, On the Foundations of Mathematics (1907), Brouwer began to build up the intuitionist philosophy. From 1918 on he expanded and expounded his views in papers in various journals, including the Mathematische Annalen of 1925 and 1926.
Brouwer’s intuitionist position stems from a broader philosophy. The fundamental intuition, according to Brouwer, is the occurrence of perceptions in a time sequence. “Mathematics arises when the subject of twoness, which results from the passage of time, is abstracted from all special occurrences. The remaining empty form [the relation of n to n + 1] of the common content of all these twonesses becomes the original intuition of mathematics and repeated unlimitedly creates new mathematical subjects.” Thus by unlimited repetition the mind forms the concept of the successive natural numbers. This idea that the whole numbers derive from the intuition of time had been maintained by Kant, William R. Hamilton in his “Algebra as a Science of Time,” and the philosopher Arthur Schopenhauer.
Brouwer conceives of mathematical thinking as a process of construction that builds its own universe, independent of the universe of our experience and somewhat as a free design, restricted only in so far as it is based upon the fundamental mathematical intuition. This fundamental intuitive concept must not be thought of as an undefined idea, such as occurs in postulational theories, but rather as something in terms of which all undefined ideas that occur in the various mathematical systems are to be intuitively conceived, if they are indeed to serve in mathematical thinking.
Brouwer holds that “in this constructive process, bound by the obligation to notice with care which theses are acceptable to the intuition and which are not, lies the only possible foundation for mathematics.” Mathematical ideas are imbedded in the human mind prior to language, logic, and experience. The intuition, not experience or logic, determines the soundness and acceptability of ideas. It must of course be remembered that these statements concerning the role of experience are to be taken in the philosophical sense, not the historical sense.
The mathematical objects are for Brouwer acquired by intellectual construction, wherein the basic numbers 1,2,3,… furnish the prototype of such a construction. The possibility of the unlimited repetition of the empty form, the step from n to n + 1, leads to infinite sets. However, Brouwer’s infinite is the potential infinity of Aristotle, whereas modern mathematics, as founded for example by Cantor, makes extensive use of actually infinite sets whose elements are all present “at once.”
In connection with the intuitionist notion of infinite sets, Weyl, who belonged to the intuitionist school, says that
… the sequence of numbers which grows beyond any stage already reached … is a manifold of possibilities opening to infinity; it remains forever in the status of creation, but is not a closed realm of things existing in themselves. That we blindly converted one into the other is the true source of our difficulties, including the antinomies—a source of more fundamental nature than Russell’s vicious circle principle indicated. Brouwer opened our eyes and made us see how far classical mathematics, nourished by a belief in the absolute that transcends all human possibilities of realization, goes beyond such statements as can claim real meaning and truth founded on evidence.
The world of mathematical intuition is opposed to the world of causal perceptions. In this causal world, not in mathematics, belongs language, which serves there for the understanding of common dealings. Words or verbal connections are used to communicate truths. Language serves to evoke copies of ideas in men’s minds by symbols and sounds. But thoughts can never be completely symbolized. These remarks apply also to mathematical language, including symbolic language. Mathematical ideas are independent of the dress of language and in fact far richer.
Logic belongs to language. It offers a system of rules that permit the deduction of further verbal connections and also are intended to communicate truths. However, these latter truths are not such before they are experienced, nor is it guaranteed that they can be experienced. Logic is not a reliable instrument to uncover truths and can deduce no truths that are not obtainable just as well in some other way. Logical principles are the regularity observed a posteriori in the language. They are a device for manipulating language, or they are the theory of representation of language. The most important advances in mathematics are not obtained by perfecting the logical form but by modifying the basic theory itself. Logic rests on mathematics, not mathematics on logic.
Since Brouwer does not recognize any a priori obligatory logical principles, he does not recognize the mathematical task of deducing conclusions from axioms. Mathematics is not bound to respect the rules of logic, and for this reason the paradoxes are unimportant even if we were to accept the mathematical concepts and constructions the paradoxes involve. Of course, as we shall see, the intuitionists do not accept all these concepts and proofs.
Weylx16 expands on the role of logic:
According to his [Brouwer’s] view and reading of history, classical logic was abstracted from the mathematics of finite sets and their subsets… . Forgetful of this limited origin, one afterwards mistook that logic for something above and prior to all mathematics, and finally applied it, without justification, to the mathematics of infinite sets. This is the Fall and original sin of set theory, for which it is justly punished by the antinomies. It is not that such contradictions showed up that is surprising, but that they showed up at such a late stage of the game.
In the realm of logic there are some clear, intuitivelyacceptable logical principles or procedures that can be used to assert new theorems from old ones. These principles are part of the fundamental mathematical intuition. However, not all logical principles are acceptable to the basic intuition and one must be critical of what has been sanctioned since the days of Aristotle. Because mathematicians have applied freely these Aristotelian laws, they have produced antinomies. The intuitionists therefore proceed to analyze which logical principles are allowable in order that the usual logic conform to and properly express the correct intuitions.
As a specific example of a logical principle that is applied too freely, Brouwer cites the law of excluded middle. This principle, which asserts that every meaningful statement is true or false, is basic to the indirect method of proof. It arose historically in the application of reasoning to subsets of finite sets and was abstracted therefrom. It was then accepted as an independent a priori principle and was unjustifiably applied to infinite sets. Whereas for finite sets one can decide whether all elements possess a certain property ?by testing each one, this procedure is no longer possible for infinite sets. One may happen to know that an element of the infinite set does not possess the property or it may be that by the very construction of the set we know or can prove that every element has the property. In any case, one cannot use the law of excluded middle to prove the property holds.
Hence if one proves that not all elements of an infinite set possess a property, then the conclusion that there exists at least one element which does not have the property is rejected by Brouwer. Thus from the denial that ab = baholds for all numbers the intuitionists do not conclude that there exists an aand bfor which ab ≠ ba.Consequently many existence proofs are not accepted by the intuitionists. The law of excluded middle can be used in cases where the conclusion can be reached in a finite number of steps, for example, to decide the question of whether a book contains misprints. In other cases the intuitionists deny the possibility of a decision.
The denial of the law of excluded middle gives rise to a new possibility, undecidable propositions. The intuitionists maintain, with respect to infinite sets, that there is a third state of affairs, namely, there may be propositions which are neither provable nor unprovable. As an example of such a proposition, let us define the kth position in the decimal expansion of π to be the position of the first zero which is followed by the integers 1 … 9. Aristotelian logic says that K either exists or does not exist and mathematicians following Aristotle may then proceed to argue on the basis of these two possibilities. Brouwer would reject all such arguments, for we do not know whether we shall ever be able to prove that it does or does not exist. Hence all reasoning about the number K is rejected by the intuitionists. Thus there are sensible mathematical questions which may never be settled on the basis of the statements contained in the axioms of mathematics. The questions seem to us to be decidable but actually our basis for expecting that they must be decidable is really nothing more than that they involve mathematical concepts.
With respect to the concepts they will accept as legitimate for mathematical discussion, the intuitionists insist on constructive definitions. For Brouwer, as for all intuitionists, the infinite exists in the sense that one can always find a finite set larger than the given one. To discuss any other type of infinite, the intuitionists demand that one give a method of constructing or defining this infinite in a finite number of steps. Thus Brouwer rejects the aggregates of set theory.
The requirement of constructibility is another ground for excluding any concept whose existence is established by indirect reasoning, that is, by the argument that the nonexistence leads to a contradiction. Aside from the fact that the existence proof may use the objectionable law of excluded middle, to the intuitionists this proof is not satisfactory because they want a constructive definition of the object whose existence is being established. The constructive definition must permit determination to any desired accuracy in a finite number of steps. Euclid’s proof of the existence of an infinite number of primes (Chap. 4, sec. 7) is nonconstructive; it does not afford the determination of the nth prime. Hence it is not acceptable. Further, if one proved merely the existence of integers x, y, z, and n satisfying xn + yn = zn, the intuitionist would not accept the proof. On the other hand, the definition of a prime number is constructive, for it can be applied to determine in a finite number of steps whether a number is prime. The insistence on a constructive definition applies especially to infinite sets. A set constructed by the axiom of choice applied to infinitely many sets would not be acceptable.
Weyl said of nonconstructive existence proofs (Philosophy of Mathematics and Natural Science, p. 51) that they inform the world that a treasure exists without disclosing its location. Proof through postulation cannot replace construction without loss of significance and value. He also pointed out that adherence to the intuitionist philosophy means the abandonment of the existence theorems of classical analysis—for example, the Weierstrass-Bolzano theorem. A bounded monotonie set of real numbers does not necessarily have a limit. For the intuitionists, if a function of a real variable exists in their sense then it is ipso facto continuous. Transfinite induction and its applications to analysis and most of the theory of Cantor arc condemned outright. Analysis, Weyl says, is built on sand.
Brouwer and his school have not limited themselves to criticism but have sought to build up a new mathematics on the basis of constructions they accept. They have succeeded in saving the calculus with its limit processes, but their construction is very complicated. They also reconstructed elementary portions of algebra and geometry. Unlike Kronecker, Weyl and Brouwer do allow some kinds of irrational numbers. Clearly the mathematics of the intuitionists differs radically from what mathematicians had almost universally accepted before 1900.
The third of the principal philosophies of mathematics is known as the formalist school and its leader was Hilbert. He began work on this philosophy in 1904. His motives at that time were to provide a basis for the number system without using the theory of sets and to establish the consistency of arithmetic. Since his own proof of the consistency of geometry reduced to the consistency of arithmetic, the consistency of the latter was a vital open question. He also sought to combat Kronccker’s contention that the irrationals must be thrown out. Hilbert accepted the actual infinite and praised Cantor’s work (Chap. 41, sec. 9). He wished to keep the infinite, the pure existence proofs, and concepts such as the least upper bound whose definition appeared to be circular.
Hilbert presented one paper on his views at the International Congress of 1904.17 He did no more on this subject for fifteen years; then, moved by the desire to answer the intuitionists’ criticisms of classical analysis, he took up problems of the foundations and continued to work on them for the rest of his scientific career. He published several key papers during the nincteen-twenties. Gradually a number of men took up his views.
Their mature philosophy contains many doctrines. In keeping with the new trend that any foundation for mathematics must take cognizance of the role of logic, the formalists maintain that logic must be treated simultaneously with mathematics. Mathematics consists of several branches and each branch is to have its own axiomatic foundation. This must consist of logical and mathematical concepts and principles. Logic is a sign language that puts mathematical statements into formulas and expresses reasoning by formal processes. The axioms merely express the rules by which formulas follow from one another. All signs and symbols of operation arc freed from their significance with respect to content. Thus all meaning is eliminated from the mathematical symbols. In his 1926 paper18 Hilbert says the objects of mathematical thought are the symbols themselves. The symbols arc the essence; they no longer stand for idealized physical objects. The formulas may imply intuitively meaningful statements, but these implications are not part of mathematics.
Hilbert retained the law of excluded middle because analysis depends upon it. He said,19 “Forbidding a mathematician to make use of the principle of excluded middle is like forbidding an astronomer his telescope or a boxer the use of his fists.” Because mathematics deals only with symbolic expressions, all the rules of Aristotelian logic can be applied to these formal expressions. In this new sense the mathematics of infinite sets is possible. Also, by avoiding the explicit use of the word “all,” Hilbert hoped to avoid the paradoxes.
To formulate the logical axioms Hilbert introduced symbolism for concepts and relations such as “and,” “or,” “negation,” “there exists,” and the like. Luckily the logical calculus (symbolic logic) had already been developed (for other purposes) and so, Hilbert says, he has at hand what he needs. All the above symbols are the building blocks for the ideal expressions —the formulas.
To handle the infinite, Hilbert uses, aside from ordinary noncontrover-sial axioms, the transfinite axiom
A(τA) → A(A).
This, he says, means: If a predicate A applies to the fiducial object τ A, it applies to all objects a. Thus suppose A stands for being corruptible. If Aristides the Just is fiducial and corruptible, then everybody is corruptible.
Mathematical proof will consist of this process: the assertion of some formula; the assertion that this formula implies another; the assertion of the second formula. A sequence of such steps in which the asserted formulas or the implications are preceding axioms or conclusions will constitute the proof of a theorem. Also, substitution of one symbol for another or a group of symbols is a permissible operation. Thus formulas are derived by applying the rules for manipulating the symbols of previously established formulas.
A proposition is true if and only if it can be obtained as the last of a sequence of propositions such that every proposition of the sequence is either an axiom in the formal system or is itself derived by one of the rules of deduction. Everyone can check as to whether a given proposition has been obtained by a proper sequence of propositions. Thus under the formalist view proof and rigor arc well defined and objective.
To the formalist, then, mathematics proper is a collection of formal systems, each building its own logic along with its mathematics, each having its own concepts, its own axioms, its own rules for deducing theorems such as rules about equality or substitution, and its own theorems. The development of each of these deductive systems is the task of mathematics. Mathematics becomes not a subject about something, but a collection of formal systems, in each of which formal expressions are obtained from others by formal transformations. So much for the part of Hubert’s program that deals with mathematics proper.
However, we must now ask whether the deductions are free of contradictions. This cannot necessarily be observed intuitively. But to show noncontradiction, all we need to show is that one can never arrive at the formal statement 1 = 2. (Since by a theorem of logic any other false proposition implies this proposition, we may confine ourselves to this one.)
Hilbert and his students Wilhelm Ackermann (1896-1962), Paul Bernays (1888-), and von Neumann gradually evolved, during the years 1920 to 1930, what is known as Hubert’s Beweistheorie [proof theory] or metamathematics, a method of establishing the consistency of any formal system. In metamathematics Hilbert proposed to use a special logic that was to be basic and free of all objections. It employs concrete and finite reasoning of a kind universally admitted and very close to the intuitionist principles. Controversial principles such as proof of existence by contradiction, trans-finite induction, and the axiom of choice are not used. Existence proofs must be constructive. Since a formal system can be unending, metamathematics must entertain concepts and questions involving at least potentially infinite systems. However, only finitary methods of proof should be used. There should be no reference either to an infinite number of structural properties of formulas or to an infinite number of manipulations of formulas.
Now the consistency of a major part of classical mathematics can be reduced to that of the arithmetic of the natural numbers (number theory) much as this theory is embodied in the Peano axioms, or to a theory of sets sufficiently rich to yield Peano’s axioms. Hence the consistency of the arithmetic of the natural numbers became the center of attention.
Hilbert and his school did demonstrate the consistency of simple formal systems and they believed they were about to realize the goal of proving the consistency of arithmetic and of the theory of sets. In his article “Über das Unendliche"20 he says,
In geometry and physical theory the proof of consistency is accomplished by reducing it to the consistency of arithmetic. This method obviously fails in the proof for arithmetic itself. Since our proof theory … makes this last step possible, it constitutes the necessary keystone in the structure of mathematics. And in particular what we have twice experienced, first in the paradoxes of the calculus and then in the paradoxe: of set theory, cannot happen again in the domain of mathematics.
But then Kurt Godei (1906-78) entered the picture. Gödel’s first major paper was “Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I.”21 Here Godei showed that the consistency of a system embracing the usual logic and number theory cannot be established if one limits himself to such concepts and methods as can formally be represented in the system of number theory. What this means in effect is that the consistency of number theory cannot be established by the narrow logic permissible in metamathematics. Apropos of this result, Weyl said that God exists since mathematics is consistent and the devil exists since we cannot prove the consistency.
The above result of Gödel’s is a corollary of his more startling result.
The major result (Gödel’s incompleteness theorem) states that if any formal theory ? adequate to embrace number theory is consistent and if the axioms of the formal system of arithmetic are axioms or theorems of T, then ? is incomplete. That is, there is a statement S of number theory such that neither S nor not-S is a theorem of the theory. Now either 5 or not-5 is true; there is, then, a true statement of number theory which is not provable. This result applies to the Russell-YVhitehead system, the Zermelo-Fraenkel system, and Hilbert’s axiomatization of number theory. It is somewhat ironic that Hilbert in his address at the International Congress in Bologna of 1928 (see note 22) had criticized the older proofs of completeness through categoricalness (Chap. 42, sec. 3) but was very confident that his own system was complete. Actually the older proofs involving systems containing the natural numbers were accepted as valid only because set theory had not been axiomatized but was used on a naive basis.
Incompleteness is a blemish in that the formal system is not adequate to prove all the assertions frameable in the system. To add insult to injury, there are assertions that are undecidable but are intuitively true in the system. Incompleteness cannot be remedied by adjoining S or ~S as an axiom, for Godei proved that any system embracing number theory must contain an undecidable proposition. Thus while Brouwer made clear that what is intuitively certain falls short of what is mathematically proved, Godei showed that the intuitively certain goes beyond mathematical proof.
One of the implications of Gödel’s theorem is that no system of axioms is adequate to encompass, not only all of mathematics, but even any one significant branch of mathematics, because any such axiom system is incomplete. There exist statements whose concepts belong to the system, which cannot be proved within the system but can nevertheless be shown to be true by nonformal arguments, in fact by the logic of metamathematics. This implication, that there are limitations on what can be achieved by axiomatization, contrasts sharply with the late nineteenth-century view that mathematics is coextensive with the collection of axiomatized branches. Gödel’s result dealt a death blow to comprehensive axiomatization. This inadequacy of the axiomatic method is not in itself a contradiction, but it was surprising, because mathematicians had expected that any true statement could certainly be established within the framework of some axiomatic system. Of course the above arguments do not exclude the possibility of new methods of proof that would go beyond what Hubert’s metamathematics permits.
Hilbert was not convinced that these blows destroyed his program. He argued that even though one might have to use concepts outside a formal system, they might still be finite and intuitively concrete and so acceptable. Hilbert was an optimist. He had unbounded confidence in the power of man’s reasoning and understanding. At the talk he gave at the 1928 International Congress22 he had asserted, “… to the mathematical understanding there are no bounds … in mathematics there is no Ignorabimus [we shall not know] ; rather we can always answer meaningful questions … our reason does not possess any secret art but proceeds by quite definite and statable rules which are the guarantee of the absolute objectivity of its judgment.” Every mathematician, he said, shares the conviction that each definite mathematical problem must be capable of being solved. This optimism gave him courage and strength, but it barred him from understanding that there could be undccidable mathematical problems.
The formalist program, successful or not, was unacceptable to the intuitionists. In 1925 Brouwer blasted away at the formalists.23 Of course, he said, axiomatic, formalistic treatments will avoid contradictions, but nothing of mathematical value will be obtained in this way. A false theory is none the less false even if not halted by a contradiction, just as a criminal act is criminal whether or not forbidden by a court. Sarcastically he also remarked, “To the question, where shall mathematical rigor be found, the two parties give different answers. The intuitionist says, in the human intellect; the formalist says, on paper.” VVeyl too attacked Hubert’s program. “Hubert’s mathematics may be a pretty game with formulas, more amusing even than chess; but what bearing does it have on cognition, since its formulas admittedly have no material meaning by virtue of which they could express intuitive truths.” In defense of the formalist philosophy, one must point out that it is only for the purposes of proving consistency, completeness, and other properties that mathematics is reduced to meaningless formulas. As for mathematics as a whole, even the formalists reject the idea that it is simply a game; they regard it as an objective science.
Hilbert in turn charged Brouwer and Weyl with trying to throw overboard everything that did not suit them and dictatorially promulgating an embargo.24 He called intuitionism a treason to science. (Yet in his metamathematics he limited himself to intuitively clear logical principles.)
None of the proposed solutions of the basic problems of the foundations—the axiomatization of set theory, logicism, intuitionism, or formalism—achieved the objective of providing a universally acceptable approach to mathematics. Developments since Gödel’s work of 1931 have not essentially altered the picture. However, a few movements and results are worth noting. A number of men have erected compromise approaches to mathematics that utilize features of two basic schools. Others, notably Gerhard Gentzen (1909-45), a member of Hubert’s school, have loosened the restrictions on the methods of proof allowed in Hubert’s metamathematics and, for example, by using transfinite induction (induction over the transfinite numbers), have thereby managed to establish the consistency of number theory and restricted portions of analysis.25
Among other significant results, two are especially worth noting. In The Consistency of the Axiom of Choice and of the Generalized Continuum Hypothesis with the Axioms of Set Theory (1940, rev. ed., 1951), Godei proved that if the Zermelo-Fraenkel system of axioms without the axiom of choice is consistent, then the system obtained by adjoining this axiom is consistent; that is, the axiom cannot be disproved. Likewise the continuum hypothesis that there is no cardinal number between X0 and 2N0, is consistent with the Zermelo-Fraenkel system (without the axiom of choice). In 1963 Paul J. Cohen (1934-), a professor of mathematics at Stanford University, proved26 that the latter two axioms are independent of the Zermelo-Fraenkel system; that is, they cannot be proved on the basis of that system. Moreover, even if one retained the axiom of choice in the Zermelo-Fraenkel system, the continuum hypothesis could not be proved. These results imply that we are free to construct new systems of mathematics in which either or both of the two controversial axioms are denied.
All of the developments since 1930 leave open two major problems: to prove the consistency of unrestricted classical analysis and set theory, and to build mathematics on a strictly intuitionistic basis or to determine the limits of this approach. The source of the difficulties in both of these problems is infinity as used in infinite sets and infinite processes. This concept, which created problems even for the Greeks in connection with irrational numbers and which they evaded in the method of exhaustion, has been a subject of contention ever since and prompted Weyl to remark that mathematics is the science of infinity.
The question as to the proper logical basis for mathematics and the rise particularly of intuitionism suggest that, in a larger sense, mathematics has come full circle. The subject started on an intuitive and empirical basis. Rigor became a goal with the Greeks, and though more honored in the breach until the nineteenth century, it seemed for a moment to be achieved. But the efforts to pursue rigor to the utmost have led to an impasse in which there is no longer any agreement on what it really means. Mathematics remains alive and vital, but only on a pragmatic basis.
There are some who see hope for resolution of the present impasse. The French group of mathematicians who write under the pseudonym of Nicolas Bourbaki, offer this encouragement: 27 “There are now twenty-five centuries during which the mathematicians have had the practice of correcting their errors and thereby seeing their science enriched, not impoverished; this gives them the right to view the future with serenity.”
Whether or not the optimism is warranted, the present state of mathematics has been aptly described by Weyl:28 “The question of the ultimate foundations and the ultimate meaning of mathematics remains open; we do not know in what direction it will find its final solution or even whether a final objective answer can be expected at all. ’ Mathematizing’ may well be a creative activity of man, like language or music, of primary originality, whose historical decisions defy complete objective rationalization.”
Becker, Oskar: Grundlagen der Mathematik in geschichtlicher Entwicklung, Verlag Karl Alber, 1956, 317-401.
Beth, E. W.: Mathematical Thought: An Introduction to the Philosophy of Mathematics, Gordon and Breach, 1965.
Bochenski, I. M.: A History of Formal Logic, University of Notre Dame Press, 1962; Chelsea (reprint), 1970.
Boole, George: An Investigation of the Laws of Thought (1854), Dover (reprint), 1951.
__________: The Mathematical Analysis of Logic (1847), Basil Blackwell (reprint), 1948.
__________: Collected Logical Works, Open Court, 1952.
Bourbaki, N.: Eléments d’histoire des mathématiques, 2nd ed., Hermann, 1969, 1 1-64.
Brouwer, L. E. J.: “Intuitionism and Formalism,” Amer. Math. Soc. Bull., 20, 1913/14, 81-96. An English translation of Brouwer’s inaugural address as professor of mathematics at Amsterdam.
Church, Alonzo: “The Richard Paradox,” Amer. Math. Monthly, 41, 1934, 356-61.
Cohen, Paul J., and Reuben Hcrsh: “ Non-Cantorian Set Theory,” Scientific American, Dec. 1967, 104-16.
Couturat, L.: La Logique de Leibniz d'après des documents inédits, Alean, 1901.
De Morgan, Augustus: On the Syllogism and Other Logical Writings, Yale University Press, 1966. A collection of his papers edited by Peter Heath.
Dresden, Arnold: “Brouwer’s Contribution to the Foundations of Mathematics,” Amer. Math. Soc. Bull., 30, 1924, 31-40.
Enriques, Federigo: The Historic Development of Logic, Henry Holt, 1929.
Fraenkel, A. A.: “The Recent Controversies About the Foundations of Mathematics,” Scripta Mathematica, 13, 1947, 17-36.
Fraenkel, A. A., and Y. Bar-Hillel: Foundations of Set Theory, North-Holland, 1958.
Frege, Gottlob: The Foundations of Arithmetic, Blackwell, 1953, English and German; also English translation only, Harper and Bros., 1960.
________: The Basic Laws of Arithmetic, University of California Press, 1965.
Gerhardt, C. I., ed.: Die philosophischen Schriften von G. W. Leibniz, 1875-80, Vol. 7.
Godei, Kurt: On Formally Undecidable Propositions of Principia Mathematica and Related Systems, Basic Books, 1965.
________: “What Is Cantor’s Continuum Problem?,” Amer. Math. Monthly, 54, 1947, 515-25.
________: The Consistency of the Axiom of Choice and of the Generalized Continuum Hypothesis with the Axioms of Set Theory, Princeton University Press, 1940; rev. ed., 1951.
Kneale, William and Martha: The Development of Logic, Oxford University Press, 1962.
Kneebone, G. T.: Mathematical Logic and the Foundations of Mathematics, D. Van Nostrand, 1963. See the Appendix especially on developments since 1939.
Leibniz, G. W.: Logical Papers, edited and translated by G. A. R. Parkinson, Oxford University Press, 1966.
Lewis, C. I.: A Survey of Symbolic Logic, Dover (reprint), 1960, pp. 1-117.
Meschkowski, Herbert: Probleme des Unendlichen, Werk und Leben Georg Cantors, F. Vieweg und Sohn, 1967.
Mostowski, Andrzcj: Thirty Years of Foundational Studies, Barnes and Noble, 1966.
Nagel, E., and J. R. Newman: GödeVs Proof, New York University Press, 1958.
Poincaré, Henri: The Foundations of Science, Science Press, ¡946, 448-85. This is a reprint in one volume of Science and Hypothesis, The Value of Science, and Science and Method.
Rosser, J. Barkley: “An Informal Exposition of Proofs of Gödel’s Theorems and Church’s Theorem,” Journal of Symbolic Logic, 4, 1939, 53-60.
Russell, Bertrand: The Principles of Mathematics, George Allen and Unwin, 1903; 2nd ed., 1937.
Scholz, Heinrich: Concise History of Logic, Philosophical Library, 1961.
Styazhkin, N. I.: History of Mathematical Logic from Leibniz to Peano, Massachusetts Institute of Technology Press, 1969.
Van Heijcnoort, Jean: From Frege to Godei, Harvard University Press, 1967. Translations of key papers on logic and the foundations of mathematics.
Weyl, Hermann: “Mathematics and Logic,” Amer. Math. Monthly, 53, 1946, 2-13 = Ges. Abh., 4, 268-79.
________: Philosophy of Mathematics and Natural Science, Princeton University Press, 1949.
Wilder, R. L.: “The Role of the Axiomatic Method,” Amer. Math. Monthly, 74, 1967, 115-27.