Geometry is nothing if it be not rigorous. … The methodsof Euclid are, by almost universal consent, unexceptional inpoint of rigor.
H. J. S. SMITH (1873)
It has been customary when Euclid, considered as a textbook, is attacked for his verbosity or his obscurity or his pedantry, to defend him on the ground that his logical excellence is transcendent, and affords an invaluable training to the youthful powers of reasoning. This claim, however, vanishes on a close inspection. His definitions do not always define, his axioms are not always indemonstrable, his demonstrations require many axioms of which he is quite unconscious. A valid proof retains its demonstrative force when no figure is drawn, but very many of Euclid’s earlier proofs fail before this test. … The value of his work as a masterpiece of logic has been very grossly exaggerated.
BERTRAND RUSSELL (1902)
Criticism of Euclid’s definitions and axioms (Chap. 4, sec. 10) dates back to the earliest known commentators, Pappus and Proclus. When the Europeans were first introduced to Euclid during the Renaissance, they too noted flaws. Jacques Peletier (1517-82), in his In Euclidis Elementa Geometrica Demonstrationum (1557), criticized Euclid’s use of superposition to prove theorems on congruence. Even the philosopher Arthur Schopenhauer said in 1844 that he was surprised that mathematicians attacked Euclid’s parallel postulate rather than the axiom that figures which coincide are equal. He argued that coincident figures are automatically identical or equal and hence no axiom is needed, or coincidence is something entirely empirical, which belongs not to pure intuition (Anschauung) but to external sensuous experience. Moreover, the axiom presupposes the mobility of figures; but that which is movable in space is matter, and hence outside geometry. In the nineteenth century it was generally recognized that the method of superposition either rested on unstated axioms or should be replaced by another approach to congruence.
Some critics did not like as an axiom the statement that all right angles are equal and sought to prove it, of course on the basis of the other axioms. Christophorus Clavius (1537-1612), an editor of Euclid’s work, noted the absence of an axiom guaranteeing the existence of a fourth proportional to three given magnitudes (Chap. 4, sec. 5). Rightly Leibniz commented that Euclid relied upon intuition when he asserted (Book 1, Proposition 1) that two circles, each of which passes through the center of the other, have a point in common. Euclid assumed, in other words, that a circle is some kind of continuous structure and so must have a point where it is cut by another circle.
The shortcomings in Euclid’s presentation of geometry were also noted by Gauss. In a letter to Wolfgang Bolyai of March 6, 1832,1 Gauss pointed out that to speak of a part of a plane inside a triangle calls for the proper foundation. He also says, “In a complete development such words as ’between’ must be founded on clear concepts, which can be done, but which I have not found anywhere.” Gauss made additional criticisms of the definition of the straight line2 and of the definition of the plane as a surface in which a line joining any two points of the plane must lie.3
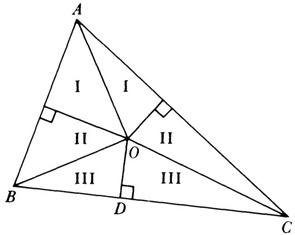
It is well known that many “proofs” of false results can be made because Euclid’s axioms do not dictate where certain points must lie in relation to others. There is, for example, the “proof” that every triangle is isocèles. One constructs the angle bisector at A of triangle ABC and the perpendicular bisector of side BC (Fig. 42.1). If these two lines are parallel, the angle bisector is perpendicular to BC and the triangle is isosceles. We suppose, then, that the lines meet at 0, say, and we shall still “show” that the triangle is isosceles. We now draw the perpendiculars OF to AB and OE to AC.
Then the triangles marked I are congruent, and OF = OE. The triangles marked III are also congruent, and OB = OC. Consequently the triangles marked II are congruent, and FB = EC. From the triangles marked I we have AF = AE. Then AB = AC and the triangle is isosceles.
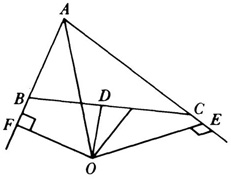
One might question the position of the point 0, and indeed one can show that it must lie outside the triangle on the circumscribed circle. If, however, one draws Figure 42.2, it can again be “proved” that triangle ABC is isosceles. The flaw is that of the two points E and F one must lie inside and the other outside of the respective sides of the triangle. But this means that we must be able to determine the correct position of F with respect to A and B and E with respect to A and C before starting the proof. Of course one should not rely upon drawing a correct figure to determine the locations of E and F, but this was precisely what Euclid and the mathematicians up to 1800 did. Euclidean geometry was supposed to have offered accurate proofs of theorems suggested intuitively by figures, but actually it offered intuitive proofs of accurately drawn figures.
Though criticisms of the logical structure of Euclid’s Elements were launched almost from the time it was written, they were not widely known or the defects were regarded as minor. The Elements was generally taken to be the model of rigor. However, the work on non-Euclidean geometry made mathematicians aware of the full extent of the deficiencies in Euclid’s structure, for in carrying out proofs they had to be especially critical of what they were accepting. The recognition of the many deficiencies finally obliged the mathematicians to undertake the reconstruction of the foundations of Euclidean geometry and of other geometries that contained the same weaknesses. This activity became extensive in the last third of the nineteenth century.
In the 1870s the work on projective geometry in relation to the metric geometries revealed that projective geometry is the fundamental one (Chap. 38). Perhaps for this reason, the foundational work began with projective geometry. However, nearly all of the writers were equally concerned to build up the metric geometries, either on the basis of projective geometry or independently. Hence the books and papers of the late nineteenth and early twentieth centuries dealing with the foundations of geometry cannot be segregated under distinct topics.
The work on non-Euclidean geometry had brought the realization that geometries are man-made constructions bearing upon physical space but not necessarily exact idealizations of it. This fact implied that several major changes had to be incorporated in any axiomatic approach to geometry. These were recognized and stressed by Moritz Pasch (1843-1930), who was the first to make major contributions to the foundations of geometry. His Vorlesungen über neuere Geometrie (1st ed., 1882; 2nd ed., revised by Max Dehn, 1926) is a groundbreaking work.
Pasch noted that Euclid’s common notions, such as point and line, were really not defined. Defining a point as that which has no parts means little, for what is the meaning of parts? In fact, Pasch pointed out, as had Aristotle and a few later mathematicians such as Peacock and Boole, that some concepts must be undefined or else either the process of definition would be unending or mathematics would rest on physical concepts. Once some undefined concepts are selected, others can be defined in terms of these. Thus in geometry point, line, plane (Pasch also used, in his first edition, congruence of line segments) might be chosen as the undefined terms. The choice is not unique. Since there are undefined terms, the question arises as to what properties of these concepts can be used to make proofs about them. The answer given by Pasch is that the axioms make assertions about the undefined terms and these are the only assertions about them that we may use. As Gergonne put it as far back as 1818,4 the undefined concepts are defined implicitly by the axioms.
As for the axioms, Pasch continues, though some may be suggested by experience, once the set is selected it must be possible to execute all proofs without further reference to experience or to the physical meaning of the concepts. Moreover, the axioms are by no means self-evident truths but just assumptions designed to yield the theorems of any particular geometry. He says in his Vorlesungen (2nd ed., p. 90),
… if geometry is to become a genuine deductive science, it is essential that the way in which inferences are made should be altogether independent of the meaning of the geometrical concepts, and also of the diagrams; all that need be considered are the relationships between the geometrical concepts asserted by the propositions and definitions. In the course of deduction it is both advisable and useful to bear in mind the meaning of the geometrical concepts used, but this is in no way essential; in fact it is precisely when this becomes necessary that a gap occurs in the deduction and (when it is not possible to supply the deficiency by modifying the reasoning) we are forced to admit the inadequacy of the propositions invoked as the means of proof.
Pasch did believe that the concepts and axioms should bear on experience, but logically this was irrelevant.
In his Vorlesungen Pasch gave axioms for projective geometry, but many of the axioms or their analogues were equally important for the axiomatization of Euclidean and the non-Euclidean geometries When built up as independent subjects. Thus he was first to give a set of axioms for the order of points on a line (or the concept of betweenness). Such axioms must also be incorporated in a complete set for any one of the metric geometries. We shall see below what the order axioms amount to.
His method of building projective geometry was to add the point, line, and plane at infinity to the proper points, lines, and planes. Then he introduced coordinates (on a geometric basis), using the throw construction of von Staudt and Klein (Chap. 35, sec. 3), and finally the algebraic representation of projective transformations. The non-Euclidean and Euclidean geometries were introduced as special cases on a geometric basis by distinguishing the proper and improper lines and points à la Felix Klein.
A more satisfactory approach to projective geometry was given by Peano.5 This was followed by the work of Mario Pieri (1860-1904), “I Principii della geometria di posizione";6 Federigo Enriques (1871-1946, Lezioni di geometria proiettiva, 1898); Eliakim Hastings Moore (1862-1932);7 Friedrich H. Schur (1856-1932);8 Alfred North Whitehead (1861-1947, The Axioms of Projective Geometry);9 and Oswald Veblen (1880-1960) and John W. Young (1879-1932).10 The last two men gave a completely independent set. The classic text, Veblen and Young’s Projective Geometry (2 vols., 1910 and 1918), carries out Klein’s organization of geometry by starting with projective geometry on a strict axiomatic basis and then specializing this geometry by choosing different absolute quadrics (Chap. 38, sec. 3) to obtain Euclidean and the several non-Euclidean geometries. Their axioms are general enough to include geometries with a finite number of points, geometries with only rational points, and geometries with complex points.
One more point about many of the axiomatic systems for projective geometry and those we shall look at in a moment for Euclidean geometry is worth noting. Some of Euclid’s axioms are existence axioms (Chap. 4, sec. 3). To guarantee the logical existence of figures, the Greeks used construction with line and circle. The nineteenth-century foundational work revised the notion of existence, partly to supply deficiencies in Euclid’s handling of this topic, and partly to broaden the notion of existence so that Euclidean geometry could include points, lines, and angles not necessarily constructible with line and circle. We shall see what the new kind of existence axioms amount to in the systems we are about to examine.
In his Sui fondamenti della geometria (1894), Giuseppe Peano gave a set of axioms for Euclidean geometry. He, too, stressed that the basic elements are undefined. He laid down the principle that there should be as few undefined concepts as possible and he used point, segment, and motion. The inclusion of motion seems somewhat surprising in view of the criticism of Euclid’s use of superposition; however, the basic objection is not to the concept of motion but to the lack of a proper axiomatic basis if it is to be used. A similar set was given by Peano’s pupil Pieri11 who adopted point and motion as undefined concepts. Another set, using line, segment, and congruence of segments as undefined elements, was given by Giuseppe Veronese (18541917) in his Fondamenti di geometria (1891).
The system of axioms for Euclidean geometry that seems simplest in its concepts and statements, hews closest to Euclid’s, and has gained most favor is due to Hilbert, who did not know the work of the Italians. He gave the first version in his Grundlagen der Geometrie (1899) but revised the set many times. The following account is taken from the seventh (1930) edition of this book. In his use of undefined concepts and the fact that their properties are specified solely by the axioms, Hilbert follows Pasch. No explicit meaning need be assigned to the undefined concepts. These elements, point, line, plane, and others, could be replaced, as Hilbert put it, by tables, chairs, beer mugs, or other objects. Of course, if geometry deals with “things,” the axioms are certainly not self-evident truths but must be regarded as arbitrary even though, in fact, they are suggested by experience.
Hilbert first lists his undefined concepts. They are point, line, plane, lie on (a relation between point and line), lie on (a relation between point and plane), betweenness, congruence of pairs of points, and congruence of angles. The axiom system treats plane and solid Euclidean geometry in one set and the axioms are broken up into groups. The first group contains axioms on existence:
II1. To each two points A and B there is one line a which lies on A and B.
I2. To each two points A and B there is not more than one line which lies on A and B.
I3. On each line there are at least two points. There exist at least three points which do not lie on one line.
I4. To any three points A, B, and C which do not lie on one line there is a plane α which lies on [contains] these three points. On each plane there is [at least] one point.
I5. To any three points A, B, and C not on one line there is not more than one plane containing these three points.
I6. If two points of a line lie on a plane α then every point of the line lies on α.
I7. If two planes α and β have a point A in common, then they have at least one more point B in common.
I8. There are at least four points not lying on the same plane.
The second group of axioms supplies the most serious omission in Euclid’s set, namely, axioms about the relative order of points and lines:
II. Axioms of Betweenness
II1. If a point B lies between points A and C then A, B, and C are three different points on one line and B also lies between C and A.
II2. To any two points A and C there is at least one point B on the line AC such that C lies between A and B.
II3. Among any three points on a line there is not more than one which lies between the other two.
Axioms II2 and II3 amount to making the line infinite.
Definition. Let A and B be two points of a line a. The pair of points A, B or B, A is called the segment AB. The points between A and B are called points of the segment or points interior to the segment. A and B are called endpoints of the segment. All other points of line a arc said to be outside the segment.
II4. (Pasch’s Axiom) Let A, B, and C be the three points not on one line and let a be any line in the plane of A, B, and C but which docs not go through (lie on) A, B, or C. If a goes through a point of the segment AB then it must also go through a point of the segment AC or one of the segment BC.
III. Axioms of Congruence
III1. If A, B are two points of a line a and A′ is a point of a or another line a′, then on a given side (previously defined) of A′ on the line a′ one can find a point B′ such that the segment AB is congruent to A′B′. In symbols AB ≡ A′B′.
III2. If A′B′ and A″B″ are congruent to AB then A′B′ ≡ A″B″
This axiom limits Euclid’s “Things equal to the same thing are equal to each other” to line segments.
III3. Let AB and BC be segments without common interior points on a line a and let A′B′ and B′C′ be segments without common interior points on a line a′. If AB ≡ A′B′ and BC ≡ B′C,′ then AC ≡ A′C′.
This amounts to Euclid’s “Equals added to equals gives equals” applied to line segments.
III4. Let 
(h, k) lie in a plane α and let a line a′ lie in a plane α′ and a definite side of a’ in α’ be given. Let h′ be a ray of a′ which emanates from the point O′. Then in α′ there is one and only one ray k′ such that (h, k) is congruent to (h′, k′) and all inner points of (h′, k′) lie on the given side of a′. Each angle is congruent to itself.
III5. If for two triangles ABC and A′B′C′ we have AB ≡ A′B′, AC ≡ A′C′, and BAC ≡ B′A′C’ then ABC ≡ A′B′C′.
This last axiom can be used to prove that ACB = A′C′B′. One considers the same two triangles and the same hypotheses. However, by taking first AC ≡ A′C′ and then AB ≡ A′B′, we are entitled to conclude that ACB ≡ A′C′B′ because the wording of the axiom applied to the new order of the hypotheses yields this new conclusion.
IV. The Axiom on Parallels
Let a be a line and A a point not on a. Then in the plane of a and A there exists at most one line through A which docs not meet a.
The existence of at least one line through A which docs not meet a can be proved and hence is not needed in this axiom.
V. Axioms of Continuity
V1. (Axiom of Archimedes) If AB and CD are any two segments, then there exists on the line AB a number of points A1, A2, …, An such that the segments AA1, A1A2, A2A3, …, An -1 An are congruent to CD and such that B lies between A and An.
V2. (Axiom of Linear Completeness) The points of a line form a collection of points which, satisfying axioms I1 I2, II, III, and V1 cannot be extended to a larger collection which continues to satisfy these axioms.
This axiom amounts to requiring enough points on the line so that the points can be put into one-to-one correspondence with the real numbers. Though this fact had been used consciously and unconsciously since the days of coordinate geometry, the logical basis for it had not previously been stated.
With these axioms Hilbert proved some of the basic theorems of Euclidean geometry. Others completed the task of showing that all of Euclidean geometry does follow from the axioms.
The arbitrary character of the axioms of Euclidean geometry, that is, their independence of physical reality, brought to the fore another problem, the consistency of this geometry. As long as Euclidean geometry was regarded as the truth about physical space, any doubt about its consistency seemed pointless. But the new understanding of the undefined concepts and axioms required that the consistency be established. The problem was all the more vital because the consistency of the non-Euclidean geometries had been reduced to that of Euclidean geometry (Chap. 38, sec. 4). Poincaré brought this matter up in 189812 and said that we could believe in the consistency of an axiomatically grounded structure if we could give it an arithmetic interpretation. Hilbert proceeded to show that Euclidean geometry is consistent by supplying such an interpretation.
He identifies (in the case of plane geometry) point with the ordered pair of real numbers13 (a, b) and line with the ratio (u:v:w) in which u and v are not both 0. A point lies on a line if
ua + vb + w = 0.
Congruence is interpreted algebraically by means of the expressions for translation and rotation of analytic geometry; that is, two figures are congruent if one can be transformed into the other by translation, reflection in the x-axis, and rotation.
After every concept has been interpreted arithmetically and it is clear that the axioms are satisfied by the interpretation, Hubert’s argument is that the theorems must also apply to the interpretation because they are logical consequences of the axioms. If there were a contradiction in Euclidean geometry, then the same would hold of the algebraic formulation of geometry, which is an extension of arithmetic. Hence if arithmetic is consistent, so is Euclidean geometry. The consistency of arithmetic remained open at this time (sec Chap. 51).
It is desirable to show that no one of the axioms can be deduced from some or all of the others of a given set, for if it can be deduced there is no need to include it as an axiom. This notion of independence was brought up and discussed by Peano in the 1894 paper already referred to, and even earlier in his Arithmetices Principia (1889). Hilbert considered the independence of his axioms. However, it is not possible in his system to show that each axiom is independent of all the others because the meaning of some of them depends upon preceding ones. What Hilbert did succeed in showing was that all the axioms of any one group cannot be deduced from the axioms of the other four groups. His method was to give consistent interpretations or models that satisfy the axioms of four groups but do not satisfy all the axioms of the fifth group.
The proofs of independence have a special bearing on non-Euclidean geometry. To establish the independence of the parallel axiom, Hilbert gave a model that satisfies the other four groups of axioms but does not satisfy the Euclidean parallel axiom. His model uses the points interior to a Euclidean sphere and special transformations which take the boundary of the sphere into itself. Hence the parallel axiom cannot be a consequence of the other four groups because if it were, the model as a part of Euclidean geometry would possess contradictory properties on parallelism. This same proof shows that non-Euclidean geometry is possible because if the Euclidean parallel axiom is independent of the other axioms, a denial of this axiom must also be independent; for if it were a consequence, the full set of Euclidean axioms would contain a contradiction.
Hubert’s system of axioms for Euclidean geometry, which first appeared in 1899, attracted a great deal of attention to the foundations of Euclidean geometry and many men gave alternative versions using different sets of undefined elements or variations in the axioms. Hilbert himself, as we have already noted, kept changing his system until he gave the 1930 version. Among the numerous alternative systems we shall mention just one. Veblen 14 gave a set of axioms based on the undefined concepts of point and order. He showed that each of his axioms is independent of the others, and he also established another property, namely, categoricalness. This notion was first clearly stated and used by Edward V. Huntington (1874-1952) in a paper devoted to the real number system.15 (He called the notion sufficiency.) A set of axioms P1, P2, …, Pn connecting a set of undefined symbols S1, S2, …, Sm is said to be categorical if between the elements of any two assemblages, each of which contains undefined symbols and satisfies the axioms, it is possible to set up a one-to-one correspondence of the undefined concepts which is preserved by the relationships asserted by the axioms; that is, the two systems are isomorphic. In effect categoricalness means that all interpretations of the axiom system differ only in language. This property would not hold if, for example, the parallel axiom were omitted, because then Euclidean and hyperbolic non-Euclidean geometry would be noniso-morphic interpretations of the reduced set of axioms.
Categoricalness implies another property which Veblen called disjunctive and which is now called completeness. A set of axioms is called complete if it is impossible to add another axiom that is independent of the given set and consistent with the given set (without introducing new primitive concepts). Categoricalness implies completeness, for if a set A of axioms were categorical but not complete it would be possible to introduce an axiom S such that S and not-S are consistent with the set A. Then, since the original set A is categorical, there would be isomorphic interpretations of A together with S and A together with not-S. But this would be impossible because the corresponding propositions in the two interpretations must hold, whereas S would apply to one interpretation and not-S to the other.
The clear delineation of the axioms for Euclidean geometry suggested the corresponding investigations for the several non-Euclidean geometries. One of the nice features of Hubert’s axioms is that the axioms for hyperbolic non-Euclidean geometry are obtained at once by replacing the Euclidean parallel axiom by the Lobatchevsky-Bolyai axiom. All the other axioms in Hilbert’s system remain the same.
To obtain axioms for either single or double elliptic geometry, one must not only abandon the Euclidean parallel axiom in favor of an axiom to the effect that any two lines have one point in common (single elliptic) or at least one in common (double elliptic), but one must also change other axioms. The straight line of these geometries is not infinite but has the properties of a circle. Hence one must replace the order axioms of Euclidean geometry by order axioms that describe the order relations of points on a circle. Several such axiom systems have been given. George B. Halsted (1853-1922), in his Rational Geometry,16 and John R. Kline (1891-1955)17 have given axiomatic bases for double elliptic geometry; and Gerhard Hessenberg (1874-1925)18 gave a system of axioms for single elliptic geometry.
Another class of investigations in the foundations of geometry is to consider the consequences of denying or just omitting one or more of a set of axioms. Hilbert in his independence proofs had done this himself, for the essence of such a proof is to construct a model or interpretation that satisfies all of the axioms except the one whose independence is to be established. The most significant example of an axiom that was denied is, of course, the parallel axiom. Interesting results have come from dropping the axiom of Archimedes, which can be stated as in Hubert’s V1. The resulting geometry is called non-Archimedean; in it there are segments such that the multiple of one by any whole number, however large, need not exceed another. In Fondamenti di geometria, Giuseppe Veronese constructed such a geometry. He also showed that the theorems of this geometry approximate as closely as one wishes those of Euclidean geometry.
Max Dehn (1878-1952) also obtained19 many interesting theorems by omitting the Archimedean axiom. For example, there is a geometry in which the angle sum is two right angles, similar but noncongruent triangles exist, and an infinity of straight lines that are parallel to a given line may be drawn through a given point.
Hilbert pointed out that the axiom of continuity, axiom V2, need not be used in constructing the theory of areas in the plane. But for space Max Dehn proved20 the existence of polyhedra having the same volume though not decomposable into mutually congruent parts (even after the addition of congruent polyhedra). Hence in three dimensions the axiom of continuity is needed.
The foundation of Euclidean geometry was approached in an entirely different manner by some mathematicians. Geometry, as we know, had fallen into disfavor because mathematicians found that they had unconsciously accepted facts on an intuitive basis, and their supposed proofs were consequently incomplete. The danger that this would continually recur made them believe that the only sound basis for geometry would be arithmetic. The way to erect such a basis was clear. In fact, Hilbert had given an arithmetic interpretation of Euclidean geometry. What had to be done now, for plane geometry say, was not to interpret point as the pair of numbers (x, y) but to define point to be the pair of numbers, to define a line as a ratio of three numbers (u:v:w), to define the point (x, y) as being on the line (u, v, w) if and only if ux + vy + w = 0, to define circle as the set of all (x, y) satisfying the equation (x – a)2 + (y – b)2 = r2, and so on. In other words, one would use the analytic geometry equivalents of purely geometric notions as the definitions of the geometrical concepts and algebraic methods to prove theorems. Since analytic geometry contains in algebraic form the complete counterpart of all that exists in Euclidean geometry, there was no question that the arithmetic foundations could be obtained. Actually the technical work involved had really been done, even for «-dimensional Euclidean geometry, for example by Grassmann in his Calculus of Extension; and Grassmann himself proposed that this work serve as the foundation for Euclidean geometry.
The critical investigation of geometry extended beyond the reconstruction of the foundations. Curves had of course been used freely. The simpler ones, such as the ellipse, had secure geometrical and analytical definitions. But many curves were introduced only through equations and functions. The rigorization of analysis had included not only a broadening of the concept of function but the construction of very peculiar functions, such as continuous functions without derivatives. That the unusual functions were troublesome from the geometric standpoint is readily seen. Thus the curve representing Weierstrass’s example of a function which is continuous everywhere but is differentiable nowhere certainly did not fit the usual concept, because the lack of a derivative means that such a curve cannot have a tangent anywhere. The question that arose was, Are the geometrical representations of such functions curves? More generally, what is a curve?
Jordan gave a definition of a curve.21 It is the set of points represented by the continuous functions x = f(t), y = g(t), for t0 
t . Such a curve is now called a Jordan curve. For some purposes Jordan wished to restrict his curves so that they did not possess multiple points. He therefore required that f(t) ≠ and f(t′) and g(t) ≠, for t and t′ in (t0, t1,) or that to each (x, y) there is one t.
It was in this work that he added the notion of closed curve,22 which requires merely that f(t0)) = f(t0) and g(t0) = g(t1), and stated the theorem that a closed curve divides the plane into two parts, an inside and an outside. Two points of the same region can always be joined by a polygonal path that does not cut the curve. Two points not in the same region cannot be joined by any polygonal line or continuous curve that does not cut the simple closed curve. The theorem is more powerful than it seems at first sight because a simple closed curve can be quite crinkly in shape. In fact, since the functions f(t) and g(t) need be only continuous, the full variety of complicated continuous functions is involved. Jordan himself and many distinguished mathematicians gave incorrect proofs of the theorem. The first rigorous proof is due to Veblen.23
However, Jordan’s definition of a curve, though satisfactory for many applications, was too broad. In 1890 Peano24 discovered that a curve meeting Jordan’s definition can run through all the points of a square at least once. Peano gave a detailed arithmetic description of the correspondence between the points of the interval [0, 1] and the points of the square which, in effect, specifies two functions x = f(t), y = g(t) that are single-valued and continuous for 0 ≤ t ≤ 1 and such that x and y take on values belonging to each point of the unit square. However, the correspondence of (x, y) to t is not single-valued, nor is it continuous. A one-to-one continuous correspondence from the ¿-valúes to the (x, y)-valucs is impossible; that is, both f(t) and g(t) cannot be continuous. This was proved by Eugen E. Netto (1846-1919).25
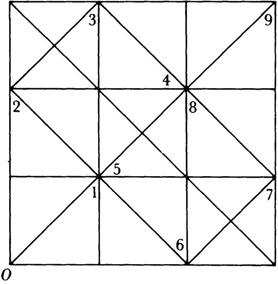
The geometrical interpretation of Peano’s curve was given by Arthur M. Schoenflies (185 3-1928)26 and E. H. Moore.27 One maps the line segment [0, 1] into the nine segments shown in Figure 42.3, and then within each subsquare breaks up the segment contained there into the same pattern but making the transition from one subsquare to the next one a continuous one. The process is repeated ad infinitum, and the limiting point set covers the original square. Ernesto Gesàro (1859-1906)28 gave the analytical form of Peano’s f and g.
Hilbert29 gave another example of the continuous mapping of a unit segment onto the square. Divide the unit segment (Fig. 42.4) and the square into four equal parts, thus:
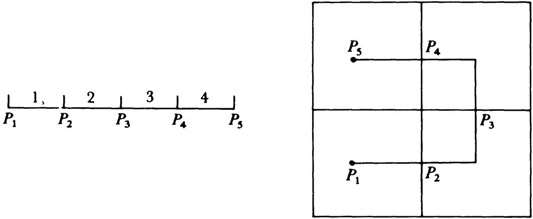
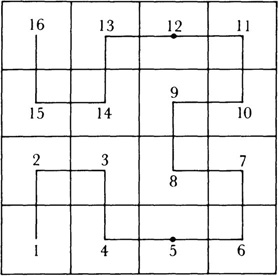
Travel through each subsquare so that the path shown corresponds to the unit segment. Now divide the unit square into 16 subsquares numbered as shown in Figure 42.5 and join the centers of the 16 subsquares as shown.
We continue the process of dividing each subsquare into four parts, numbering them so that we can traverse the entire set by a continuous path. The desired curve is the limit of the successive polygonal curves formed at each stage. Since the subsquares and the parts of the unit segment both contract to a point as the subdivision continues, we can see intuitively that each point on the unit segment maps into one point on the square. In fact, if we fix on one point in the unit segment, say t = 2/3, then the image of this point is the limit of the successive images of t = 2/3 which appear in the successive polygons.
These examples show that the definition of a curve Jordan suggested is not satisfactory because a curve, according to this definition, can fill out a square. The question of what is meant by a curve remained open. Felix Klein remarked in 189830 that nothing was more obscure than the notion of a curve. This question was taken up by the topologists (Chap. 50, sec. 2).
Beyond the problem of what is meant by a curve, the extension of analysis to functions without derivatives also raised the question of what is meant by the length of a curve. The usual calculus formula
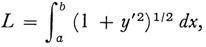
where y = f(x), calls, at the very least, for the existence of the derivative. Hence, the concept no longer applies to the non-differentiable functions. Various efforts to generalize the concept of length of curve were made by Du Bois-Reymond, Peano, Ludwig Scheeffer (1859-85), and Jordan, using either generalized integral definitions or geometric concepts. The most general definition was formulated in terms of the notion of measure, which we shall examine in Chapter 44.
A similar difficulty was noted for the concept of area of a surface. The concept favored in the texts of the nineteenth century was to inscribe in the surface a polyhedron with triangular faces. The limit of the sum of the areas of these triangles when the sides approach 0 was taken to be the area of the surface. Analytically, if the surface is represented by
x = ø(u, v), y = ψ(u, v), z = X(u, v)
then the formula for surface area becomes
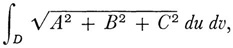
where A, B, and C are the Jacobians of y and z, x and z, and x and y, respectively. Again the question arose of what the definition should be if x, y, and z do not possess derivatives. To complicate the situation, in a letter to Hcrmite, H. A. Schwarz gave an example31 in which the choice of the triangles leads to an infinite surface area even for any ordinary cylinder.32 The theory of surface area was also reconsidered in terms of the notion of measure.
By 1900 no one had proved that every closed plane curve, as defined by Jordan and Peano, encloses an area. Helge von Koch (1870-1924)33 complicated the area problem by giving an example of a continuous but non-differentiable curve with infinite perimeter which bounds a finite area. One starts with the equilateral triangle ABC (Fig. 42.6) of side 3s. On the middle third of each side construct an equilateral triangle of side s and delete the base of each triangle. There will be three such triangles. Then on each outside segment of length s of the new figure construct on each middle
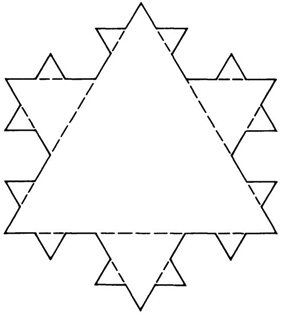
third an equilateral triangle of side s/3 and delete the base of each triangle. There will be twelve such triangles. Then on the outside segments of the resulting figure, construct a new equilateral triangle of side s/9. There will be 48 of these triangles. The perimeters of the successive figures are 9s, 12s, 6s,… and these perimeters become infinite. However, the area of the limiting figure is finite. For, by the well-known formula for the area of an equilateral triangle in terms of its side, namely, if the side is b, the area is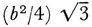 
, then the area of the oris; inai triangle is 
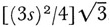. The area of the first three triangles added is 
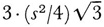. Since the side of the next triangles added is s/3 and there are 12, these areas are 
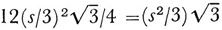. The sum of the areas is
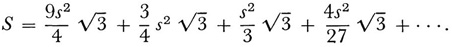
This is an infinite geometric progression (aside from the first term) with common ratio 4/9. Then
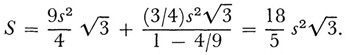
The Peano and Hilbert curves also raised the question of what we mean by dimension. The square is two-dimensional in itself, but, as the continuous image of a curve, should be one-dimensional. Moreover, Cantor had shown that the points of a line segment can be put into one-to-one correspondence with the points of a square (Chap. 41, sec. 7). Though this correspondence is not continuous from the line segment to the square or the other way, it did show that dimension is not a matter of multiplicity of points. Nor is it a matter of the number of coordinates needed to fix the position of a point, as Riemann and Helmholtz had thought, because the Peano curve assigns a unique (x, y) to each value of t.
In the light of these difficulties we sec that the rigorization of geometry certainly did not answer all the questions that were raised. Many were settled by the topologists and analysts of the next century. The very fact that questions about fundamental concepts continued to arise illustrates once more that mathematics docs not grow as a logical structure. Advances into new fields and even the perfection of old ones reveal new and unsuspected defects. Beyond the resolution of the problems involving curves and surfaces we have yet to sec whether the ultimate stage in rigor was reached by the foundational work in analysis, the real number system, and basic geometry.
Becker, Oskar: Grundlagen der Mathematik in gescliichtlicher Entwicklung, Karl Alber, 1954, 199-212.
Enriques, Federigo: “Prinzipien der Geometrie,” Encyk. der Math. Wiss.,?. G.
Teubner, 1907-10, III ABl, 1-129. Hilbert, David: Grundlagen der Geometrie, 7th ed., B. G. Teubner, 1930. Pasch, M. and M. Dehn: Vorlesungen über neuere Geometrie, 2nd ed., Julius Springer, 1926, 185-271.
Peano, Giuseppe: Opere scelle. 3 vols.. Edizioni Cremonese, 1957-59. Rcichardt, Hans: C. E. Gauss, Leben und Werke. Haude und Spenersche, 1960, 111-50.
Schmidt, Arnold: “Zu Hilberts Grundlegung der Geometrie,” in Hubert’s Gesammelte Abhandlungen, 2, 404 -14.
Singh, A. N.: “The Theory and Construction of Xon-Differentiable Functions,” in E. W. Hobson: Squaring the Circle and Other Monographs, Chelsea (reprint), 1953.