Chapter 4
The tide in shelf seas
The great ocean basins are bordered by shallow seas lying on the continental shelves: extensions of the continents which flooded at the end of the last ice age. Shelf seas are generally less than 200 metres deep and vary in width from almost nothing to hundreds of kilometres. It is in these shallow seas and the rivers that flow into them that the most spectacular tides are found.
Progressive waves
As the tide rises and falls in the ocean it sends waves, with tidal period, travelling across the continental shelves towards the shore. The tidal forcing of the shelf seas by the ocean tide is more important than the direct action of the tide-generating force. If, for example, the tide in the ocean rises by half a metre at the edge of a continental shelf 100 kilometres wide, the pressure gradient force created by the tilted water surface is 0.5/100,000 or 5 × 10-6 times that of Earth’s gravity, fifty times larger than the Moon’s tidal force.
Water waves which travel, called progressive waves, consist of a series of moving crests (or high waters) interspersed with troughs (or low waters—see Figure 19). The speed at which the crest of a tide wave travels across the ground is equal to √(gd) where g is the acceleration due to gravity and d the water depth (this formula works so long as the waves are in shallow water compared to their wavelength; this is always true for tide waves). Tide waves travel on the shelf more slowly than they do in the deep ocean but they still move quickly. In water of depth 100 metres, for example, the wave speed is 113 kilometres per hour. Progressive tide waves in shelf seas move at the speed of a fast car on a good road.
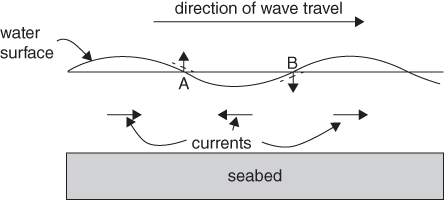
19. A progressive wave in shallow water showing how the currents move beneath the wave.
The waves are also long. The wavelength—the distance between crests—is equal to the wave speed times the period. For an M2 tide wave with period 12.42 hours travelling in water 100 metres deep, the length of the wave is 1,400 kilometres. Only a fraction of the wave will fit into most of the world’s shelf seas.
Beneath the sloping water surface, the pressure gradient force creates accelerations. Between a low water and the following high, the acceleration is in the direction of wave travel and it accumulates such that maximum velocity in this direction occurs beneath the crest of the wave. Maximum velocity in the opposite direction occurs beneath the wave trough. As the wave travels past a fixed point, the current oscillates, flowing first with and then against the direction of wave travel. You can see this by throwing a small stick onto waves passing the end of a pier: the stick moves backwards and forwards as the waves pass through.
When the tide is behaving as a progressive wave, as it does for example in Chesapeake Bay on the east coast of the United States, the high tide travels along the coast at a speed governed by the depth of water. Maximum current occurs at times of high and low water, with slack water halfway between.
Water waves progress, or move forward, in the following way. In the column of water at point A in Figure 19 the currents are converging from both sides. This causes the water surface to rise at A and this has the effect of making the sloping face of the wave move forward to the position shown by the dashed line. At point B on the opposite face of the wave, the currents are diverging. As water flows away from B, the surface falls and moves forward to the dashed line. The effect is that the shape of the wave moves along while the water (as we have just seen) oscillates about a fixed point.
The speed of the currents in a progressive wave depends on the height of the wave, the water depth, and the acceleration due to gravity. Typically, tidal currents in shallow water are of order 1 metre per second. They can be faster in extreme cases but will rarely exceed 10 metres per second. Generally, the speed of the current in a progressive tide wave is much less than the speed at which the wave travels, but this can change as the wave enters very shallow water—in a river, for example.
Standing waves
When a progressive wave hits a coast it bounces back (coastlines appear to be very good at reflecting long tide waves). The tide near the coast behaves as the sum of the incoming and reflected waves, creating a pattern called a standing wave (see Chapter 2). The water surface oscillates between the positions shown by the solid and dashed lines in Figure 20.

20. A standing wave produced by a perfect reflection of a progressive wave at a coastline. A and C are antinodes and B and D are nodes. Double-headed arrows represent the size of the currents oscillating back and forth beneath the wave.
Standing waves can often be seen when sea waves reflect off a harbour wall: the water goes up and down without the wave going anywhere. The pattern is created by the interference of two equal waves travelling in opposite directions. There are places, called antinodes (A and C in Figure 20), where the waves always add constructively and the surface goes up and down the most. Between these there are nodes (B and D) where there is no vertical motion of the water surface. At the nodes, the elevation of the incoming wave cancels that of the reflected wave at all times. For this to work, the reflected wave must always be half a wavelength out of phase with the incoming wave. There is a node one quarter of a wavelength from the reflecting coast, another at three-quarters of a wavelength, then five-quarters, and so on.
The sloping water surface in the standing waves drives accelerations in the water beneath. When it is high water at the coast A, the slope accelerates water offshore, towards B, and the flow (the ebb tide) reaches its maximum three lunar hours later when the water surface is flat. The water surface then starts to slope down from B towards A and the offshore flow is decelerated, becoming slack when it is low water at A. The currents and elevations in a standing wave are therefore out of phase. Places where the tide behaves as a standing wave (e.g. the northern Irish Sea in Europe) experience slack water at high and low tide with maximum current halfway between.
It is a characteristic of a standing wave that the extent of the up-and-down movement of the surface (the tidal range) varies from place to place, from zero at the node up to a maximum at the antinodes. High water occurs everywhere between two adjacent nodes at the same time, and when it is high tide on one side of a node it is low tide on the other side. The fastest currents occur at the nodes.
Resonance
Figure 20 allows us to anticipate the reason why we can get large tides in shelf seas. If the progressive tide wave travelling from the shelf edge to the coast is reflected and bounces back without any loss of energy, a standing wave tide will be created on the continental shelf. The movement of the standing wave at the edge of the shelf must match that of the ocean tide. If the edge of the shelf is close to a node in the standing wave, a small tide in the ocean will produce much larger tides at the antinodes. In particular, there will be a large tide at the coast, which is always located at an antinode of the standing wave. The shelf sea is said to be in resonance with the tidal forcing and there is amplification of the tide from the ocean to the coast.
The condition for resonance is that the width of the shelf should be an odd number of quarter wavelengths of the tide. For a shelf sea of depth 100 metres, the required width to be in quarter-wavelength resonance with the M2 tide is 350 kilometres (a shelf twice as wide would be in resonance with the diurnal tide). Several of the world’s shelf sea areas, particularly in South America, north-west Europe, north-eastern America, and the Arctic are close to resonance with the semi-diurnal tide. These places have large tides and dissipate a disproportionately large quantity (compared to their size) of the world’s tidal energy through friction.
What happens, exactly, when a shelf sea is in resonance? How can a small tide at the edge of the ocean produce a much larger tide hundreds of kilometres away? The rise and fall of the ocean at the edge of the shelf can be thought of as a paddle, pushing water onto the shelf when the ocean tide is high, and pulling water off the shelf when the ocean tide is low. In a resonant shelf sea, this motion is matched by the natural period at which water flows on and off the shelf. The ocean tide continually feeds energy into the shelf sea, and the tide on the shelf grows until its height is limited by friction.
Localized resonance can also occur in part of a shelf, for example a large bay or gulf. If the length of the bay from the head to the mouth is close to the resonant length, a relatively small tide at the mouth will produce a much larger tide at the head of the bay. A celebrated example of this kind of resonance occurs in the Bay of Fundy in Canada. In this bay, a mean tidal range of 5 metres at the mouth is amplified to nearly 12 metres at the head. The amplification factor is not so great—about 2.4—but, acting on what is already a big tide at the mouth, resonance produces exceptional tides in the upper reaches of the Bay of Fundy.
An example of a resonant shelf sea
The capital of South Australia, Adelaide, lies on the eastern shore of a shallow gulf, Gulf St Vincent, which is connected to the open sea by Investigator Strait and the smaller Backstairs Passage (Figure 21). The mean depth of water is about 30 metres and the speed of a progressive tide wave is 62 kilometres per hour. The wavelength of the M2 component of the tide is 767 kilometres and one quarter of a wavelength is 192 kilometres. The distance from the head of the gulf to Stenhouse Bay at the western entrance of Investigator Strait is about 180 kilometres. The system is therefore close to quarter-wavelength resonance with the semi-diurnal tide and we would expect to see the tide amplified within the gulf.
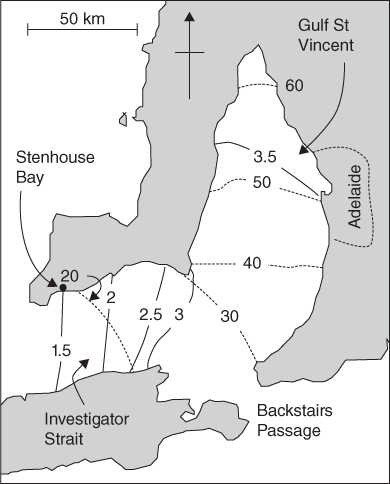
21. Co-tidal (continuous) and co-range (dashed, in centimetres) lines for the M2 tide in the approaches to Adelaide, South Australia (based on Bowers and Lennon, 1990).
Figure 21 shows co-tidal and co-range lines for the M2 tide in the region. The amplitude increases from 17 centimetres at the western end of Investigator Strait to 62 centimetres at the head of Gulf St Vincent, an amplification factor of 3.6. Within Investigator Strait the tide has the appearance of a progressive wave: the high water moves from west to east, taking 1.5 hours to travel the length of the strait. In Gulf St Vincent, the tide is a standing wave: high water occurs at the same time (within half an hour or so) over the whole area of the gulf, and the tidal range increases towards the head of the gulf. The tidal streams act in unison throughout the area, turning at the times of high and low tide at the head of the gulf.
The transition from a progressive wave at the entrance to a standing wave at the head of the bay is observed in many semi-enclosed seas. In between these regimes the tide is in transition from one kind of wave to another: it is part standing and part progressive. The behaviour can be understood by allowing for the effect of friction. A progressive wave loses energy through friction, first as it travels towards the shore, and then again after it is reflected and is travelling in the opposite direction. The energy in a water wave is proportional to the square of its height (the vertical distance from crest to trough), so a loss of energy means that the wave height becomes smaller as the wave travels along. The easiest way to allow for this is to let the wave lose a constant proportion of its height for every kilometre it travels across the ground.
The shape of the water surface in the bay at any time can be found by adding the incoming and reflected waves. We can start at any time and draw the shape of the wave approaching the coast. The wave will decrease in height with distance towards the shore because of the effect of friction. We can then draw the shape of the reflected wave (which will decrease in height with distance offshore) and add the two waves to get the shape of the water surface. We then step forward in time by an hour. The incoming wave will move one hour’s worth, or 62 kilometres, towards the shore, and the reflected wave 62 kilometres in the opposite direction. We again add these two waves to get the shape of the surface at this time. The procedure is repeated every hour through a tidal cycle.
Figure 22 shows the result. To match the shape to observations, we have let the wave height decrease by 0.05 per cent per kilometre (the procedure teaches us something about the magnitude of tidal friction). The pattern shown in Figure 22 explains many of the features of the observed tide. There is an amplification of the tidal range from Stenhouse Bay to the head of the gulf. Within a distance of about 90 kilometres from the head of the gulf, high water occurs simultaneously—the tide is behaving as a standing wave. Further away from the head—in Investigator Strait—the time of high tide changes with distance, becoming earlier with increasing distance from the gulf head. Here, the tide is behaving as a partly progressive wave travelling inwards. High water at Stenhouse Bay occurs two hours before that at the head of the bay.
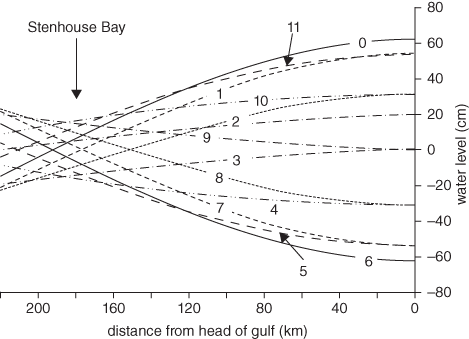
22. The shape of the water surface in Investigator Strait and Gulf St Vincent at hourly intervals (indicated by labels).
Near the head of the gulf, the incoming and reflected waves are of similar size and add together to produce a standing wave. Further offshore, the reflected wave is reduced to the point where it is considerably smaller than the incoming wave. Here, the incoming wave is dominant and this explains the progressive nature of the tide wave. Because the incoming and reflected waves are no longer of equal size at the node, they no longer cancel, and the node is replaced by a region of reduced tidal range, the extent of the reduction depending on the relative size of the two waves.
Most of the time, the water surface shown in Figure 22 is sloping. The slope creates a pressure gradient force which either drives accelerations or balances the effect of bed friction. At hour 0 the slope in Gulf St Vincent is creating an offshore acceleration which turns the flood into ebb (and vice-versa at hour 6). Hours 3 and 9 are the times of maximum ebb and flood current, and at these times the pressure gradient force created by the surface slope balances the effect of bed friction. The water surface slopes down towards the head of the gulf during the flood and in the opposite direction during the ebb.
Effect of Earth rotation
A detail of Figure 21 that is not explained by the account above is the fact that the 20 centimetres co-range line crosses Investigator Strait diagonally. The tidal range on the northern side of the strait is greater than that at a point opposite on the southern shore. This is a result of the Earth’s rotation.
The effect of Earth rotation on a progressive tide wave is to create slopes in the water surface at right angles to the direction the wave is travelling. Imagine a progressive wave travelling down a channel in the southern hemisphere. At the crest of the wave, the current is flowing with the wave and the Coriolis effect pushes water towards the left hand shore of the channel, looking in the direction of wave travel. At the wave trough, the current is flowing against the direction of wave travel and the Coriolis effect pushes water towards the right hand shore. The result is a wave which has higher crests and lower troughs (and so a greater tidal range) on the left hand shore of the channel. In the northern hemisphere, the larger tidal range is found on the right hand shore looking down the direction of wave travel. This kind of wave is called a Kelvin wave, after William Thomson, Lord Kelvin, born in Belfast in 1824 (the same Kelvin that we came across at the end of Chapter 3). It is this effect and the progressive nature of the wave in Investigator Strait that creates the larger tides on the northern shore.
When a Kelvin wave reflects off the head of a bay or gulf, the tide will behave as the sum of two Kelvin waves travelling in opposite directions. If the gulf is wide enough for Earth rotation effects to matter (that is, it takes a significant part of a tidal cycle for a wave to cross from one side to the other) an amphidromic system will form, with the crest of the wave (the high tide) sweeping around the gulf in an anti-clockwise direction in the northern hemisphere and clockwise in the south.
In the absence of friction, the amphidromic point will form at a point B one quarter wavelength from the head and in the middle of the bay, equidistant from the shores at C and D in Figure 23.
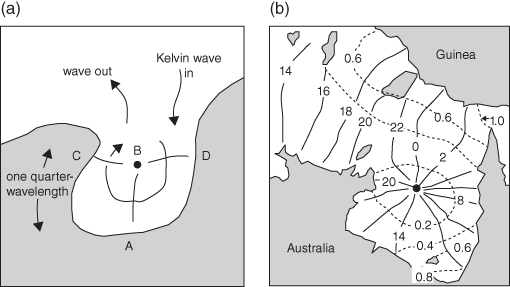
23. (a) A sketch of an amphidromic system, created by a Kelvin wave reflected off the head of a bay in the southern hemisphere (the amphidromic point is labelled B). (b) Co-tidal lines (continuous) for the diurnal tide in the Gulf of Carpentaria, marked with the time of high water in lunar hours and co-range lines (dashed) with tidal amplitude in metres (based on Webb, 2012).
The Gulf of Carpentaria, in northern Australia, is an example of a shallow sea which is close to quarter-wavelength resonance with the diurnal tide. The bay is about 500 kilometres wide and measures between 500 and 600 kilometres from its southern shore to where it joins the Arafura Sea and Torres Strait in the north. The mean depth of the bay is 60 metres and the speed of a progressive tide wave is 87 kilometres per hour. The length of the diurnal tide wave (with period twenty-four lunar hours) is 2,183 kilometres. One quarter of a wavelength is 546 kilometres and the amphidromic point of the diurnal tide is close to the mouth of the gulf. In contrast, the semi-diurnal tide (which has a wavelength half that of the diurnal tide) has an amphidrome located about 250 kilometres from the shore; there is no amplification of the semi-diurnal tide from the mouth to the head of the gulf.
A co-tidal chart of the diurnal tide in the Gulf of Carpentaria is shown in Figure 23(b). The high water travels around the bay in a clockwise direction about an amphidromic point located close to the mouth of the gulf. The tidal range is largest at the shore (particularly at the south-east corner) at points furthest from the amphidrome, and decreases to nothing at the amphidromic point. In the top left of this picture, the tide is behaving as a Kelvin wave. The high tide travels from west to east, and the tidal range is greatest on the northern shore (that is the left hand shore looking down the direction of wave travel).
Not all bays or gulfs exhibit an amphidromic system. First, the gulf needs to stretch, from the mouth to the head, a distance of at least one quarter of a tidal wavelength and, as we have seen, that can be a distance of several hundred kilometres. Only large bays will be big enough to contain an amphidrome. Second, the bay must be wide enough for Earth rotation to matter. In practice that means that the time taken for a tide wave to cross from one side of the bay to another must be a significant fraction of a tidal cycle. On a rotating Earth, a progressive wave will always be converted into a Kelvin wave, but the difference in water level from one side to the other will be small in a narrow channel.
The effect of friction and a poor reflection of the wave at the head of the bay will make the reflected wave smaller than the incoming wave. The two waves will no longer cancel along the centre line of the bay, and the amphidromic point moves to a place where the reflected wave is large enough to cancel the incoming wave. It moves to the left (in the northern hemisphere) and to the right (in the southern hemisphere) looking into the bay. In extreme cases, where the friction is very high, the reflected wave becomes too weak to cancel the incoming wave anywhere. The amphidromic point appears to move right out of the sea altogether, on to the adjacent land, and it is called a degenerate amphidrome.
Tides in shallow water
When a progressive wave enters water shallow compared to the wave height, the crest, being in deeper water, travels noticeably faster than the trough. As the wave travels up a shallow estuary (for example), the crest catches up with the preceding trough and the front face of the wave is steepened. As British physicist Lord Rayleigh put it:
When waves advance over shallow water … the crests tend to gain upon the hollows, so that the anterior slopes become steeper and steeper and the posterior slopes more gradually sloping.
The same effect is seen in estuaries where the tide is a standing wave, but here the process is different. The tide floods into the estuary when it is high tide in the open sea, and the greater depth of water reduces the effect of bottom friction. The flood current is faster than the ebb and, since equal volumes of water (equal to the tidal prism) must enter and leave the estuary over a tidal cycle, the duration of the flood is shortened relative to the ebb. An example of the quick rise and slow fall of the tide in an estuary can be seen in Figure 12.
The distortion of the tidal curve in shallow water presents a problem for the accurate prediction of the times of high and low waters. There is no longer a fixed time interval between a high tide and the following low tide. This effect cannot be simulated using just the harmonics that are part of the tide-generating force. Harmonics with periods equal to a fraction of the semi-diurnal tidal period are needed to produce the shape of the tidal curve. Tidal analysts have a toolbox of such higher harmonics that they can fit to the observed tidal curve to create the required shape and produce accurate predictions of both high and low tides in shallow water.
A rare feature of the tide in shallow water, seen at just a few locations worldwide, is a double high water or its close relative, a double low water. In a double high water, the tide rises to a first high, falls for a short while, and then rises again to a second high before finally falling to a single low tide. The most famous example is found at Southampton on the south coast of England where the extended period of deep water around high tide was important to the development of the port. Figure 24 shows an example of a small Scottish port which has a double high water.
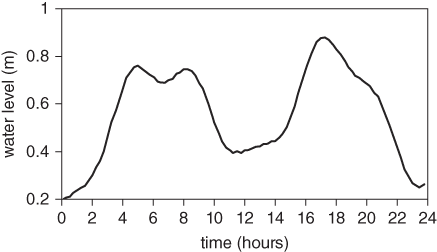
24. The double high water at Port Ellen in Scotland on the morning of 19th February 2010.
Double high waters can be made by adding higher harmonics to the semi-diurnal tidal curve. If the higher harmonic has a trough or low water at the time of the high in the M2 tide, a double high water can be made if the harmonic has a large enough amplitude. The reason that double tides are so rare is that the higher harmonics are not usually big enough for the job and they don’t have the right phase relative to the principal tidal constituent. Port Ellen lies near an amphidrome of the semi-diurnal tide and the shallow-water harmonics (particularly one with a period of four lunar hours) are large enough to create a double high water at neap tides. It is often the case that, on the other side of the semi-diurnal amphidrome from the double high tide, there is a double low tide to be found. For example, on the eastern coast of the United States, a double high tide is observed at Woods Hole in Massachusetts and a double low tide at Providence, Rhode Island.