IV
GOLDEN ARCHITECTURE & DESIGN
“Some say they see poetry in my paintings; I see only science.” 1
—Georges Seurat
Everything that you see or hear can be described mathematically and geometrically. There is mathematics in the orthogonal lines of a cityscape converging on a vanishing point on the horizon. It is seen in the 256 values of red, green, and blue of each pixel on your screen monitor that produce the 16,777,216 unique color combinations 2 that define every image. Every beautiful moment of every song can be expressed as a mathematically defined combination of frequencies and amplitudes.
As we’ve seen, fascination with the many unique aspects of the golden ratio by artists and philosophers has inspired its use in the arts. When and where that first happened, we do not know, but there is evidence that the ancient Egyptians recognized that there was something special about this proportion.

The five thousand-year-old Great Pyramids tower over the desert on the outskirts of Giza, Egypt’s third-largest city.
PHI, PI, AND THE PYRAMIDS OF GIZA
The pyramid complex at Giza, about 10 miles (16 km) south of modern-day Cairo and 5 miles (8 km) west of the Nile River, has had a towering presence in the collective human psyche for more than four thousand years. Three massive, pyramidal, mortuary temples dominate the landscape and commemorate three pharaohs of Egypt’s prosperous fourth dynasty: Khufu; his son, Khafre; and his grandson, Menkaure. The famous Great Sphinx, which bears Khafre’s visage, reclines some 546 yards (500 m) east of Khafre’s pyramid. Even in our advanced technological age, archaeologists marvel at the incredible technology and manpower that must have been required to haul thousands of 2-ton (1.8 mt) limestone blocks into such precise and immense formations.
THE GREAT PYRAMID
The Great Pyramid of Giza—also known as the Pyramid of Khufu or the Pyramid of Cheops—is the oldest of the Seven Wonders of the Ancient World. It is also the only one that remains largely intact. There is ongoing debate as to the geometric principles used in the design of the Great Pyramid. Thought to be built around 2560 BCE, its once planar, smooth, outer shell is gone, and all that remains is the craggy inner core, so it is difficult to know the original dimensions with absolute certainty. Luckily, however, the outer shell remains at the apex, helping archeologists establish a close estimate.
There’s little to dispute as to whether the dimensions of the Great Pyramid reflect pi and the golden ratio with a high degree of accuracy. The only dispute concerns whether the ancient Egyptians actually knew of these constants and intentionally applied them in the design. So how might the Great Pyramid have embodied either or both of these concepts? There are several possibilities based on various measurements and observations that we will explore.

This illustration shows nomadic Bedouins resting near the Great Pyramid of Giza during the late nineteenth century.
1. A pyramid based on Ф varies by only 0.07 percent from the Great Pyramid’s estimated dimensions.
As mentioned shown here, phi is the only number with the mathematical property of its square being one more than itself, allowing Johannes Kepler to derive his eponymous triangle by connecting this property with the Pythagorean theorem. Using the Kepler right triangle with sides √Φ, 1, and Φ to describe the relationship between a pyramid’s height and the length of its four sides allows us to create a pyramid with a base width of 2 and a height of √Φ, which is approximately 1.272 in decimal notation. The ratio of the height to the base width of this pyramid, then, is approximately 0.636.
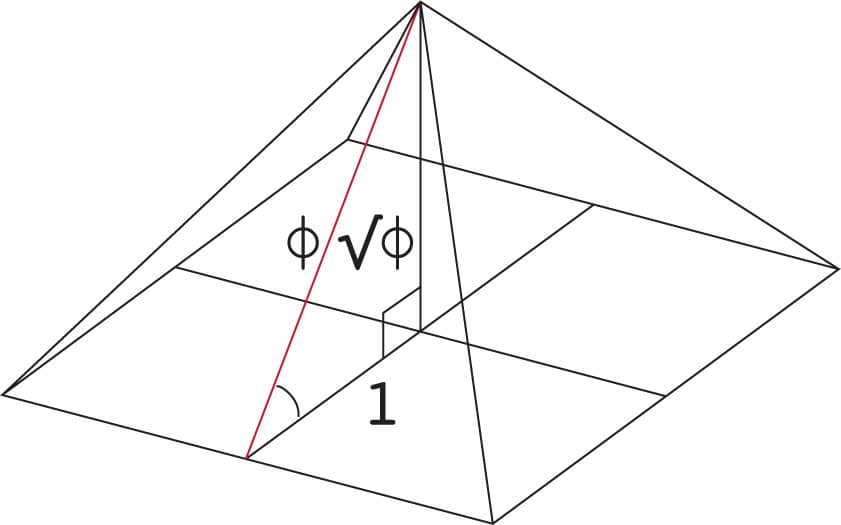
The Great Pyramid of Giza has an estimated original height of 480.94 feet (146.59 m) and a base width of 755.68 feet (230.33 m), 3 which also creates a height to base width ratio of 0.636! This result indicates that the Great Pyramid does indeed represent an example of a Kepler triangle, at least to within three significant decimal places of accuracy. If the base is exactly 755.68 feet (230.33 m), then a perfect golden ratio would yield a height of 480.62 feet (146.49 m), which varies from the estimated actual dimensions of the Great Pyramid by a mere 3.85 inches (0.10 m), or 0.067 percent. This would be an incredible coincidence if the design had nothing at all to do with the golden ratio.
A pyramid based on a Kepler triangle would have other interesting properties. For example, the surface area of the four sides would be a golden ratio of the surface area of the base:
• The area of the triangular sides on each face is equal to half of the base length (2) multiplied by their height (Φ), which yields Φ.
• The surface area of the base is 2 × 2, which equals 4.
• Thus, the ratio of the surface area of the four sides (4Φ) to the surface area of the base (4) is Φ.
2. A pyramid based on π varies by only 0.03 percent from the Great Pyramid’s estimated dimensions.
In 1838 H. C. Agnew proposed another interesting hypothesis in A letter from Alexandria on the evidence of the practical application of the quadrature of the circle, in the configuration of the great pyramids of Gizeh: 4 What if the Egyptians calculated the height of the pyramid based on the radius of a circle with the same circumference and area as the pyramid’s base? Imagine a circle with a circumference of 8, which matches the length of the perimeter of this pyramid with its base width of 2. If you calculate the radius of this circle by dividing the circumference by 2π, you obtain the value of 4/π, or approximately 1.273—less than one-tenth of a percent different than the value of 1.272 computed above using Kepler’s triangle. Multiplying the 755.68-foot (230.33-m) base width of the pyramid by half this value yields a height of 481.08 feet (146.63 m)—a difference in height between the two methods of only 5.5 inches (0.14 m), and a difference of only 1.7 inches (0.04 m) from the pyramid’s estimated height.
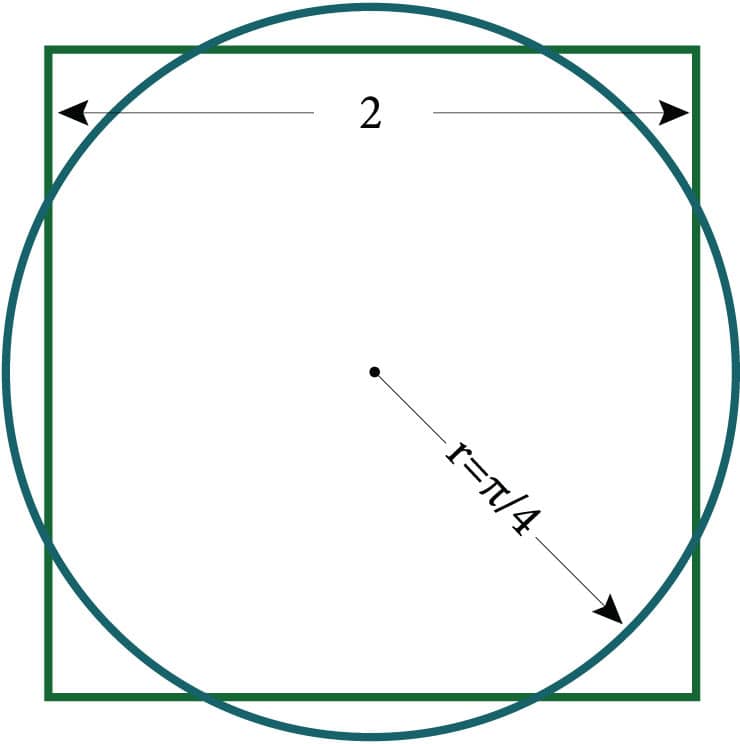
This diagram shows the relationship between a pyramid with a base length of 2 and the radius of a circular base with the same perimeter of length 8.
3. A pyramid based on areas is identical in geometry to one based on Ф. 5
In addition to the relationships of the Great Pyramid’s dimensions to Ф and π, it’s also possible that the pyramid was constructed using a completely different approach that coincidentally produced the phi relationship. The writings of the Greek historian Herodotus make a vague and often-debated reference to a relationship between the height of a pyramid and the area of one of its faces, expressed as follows:
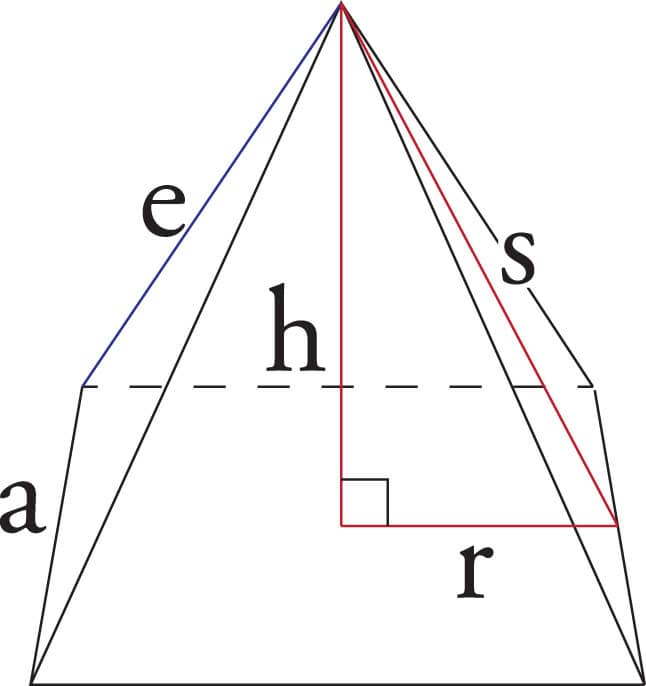
Area of the Face = Area of the Square formed by the Height (h)
(2r × s) / 2 = h2
Also, from the Pythagorean Theorem we know that r2 + h2 = s2, which means h2 = s2 – r2
Therefore, r × s = s2 – r2
When r = 1, we find that s = s2 – 1. Recall from here that Ф is the only number whose square is one more than itself, and Ф is therefore the only positive solution to this equation when we solve for s. In conclusion, we find that if the height area to side area were the basis for the dimensions of the Great Pyramid, it would be in a perfect phi relationship, whether or not that relationship was intended by its designers.
4. A pyramid based on the ancient Egyptian seked varies by 0.01 percent from the Great Pyramid’s estimated dimensions.
There’s a good possibility that the Great Pyramid was built using the seked, a measurement technique that describes the inclination of a pyramid in terms of ancient Egyptian royal cubits, as a ratio of the run (i.e., half of the base width) to the rise (i.e., height). The seked concept appears in excavated Egyptian papyri, including the famous Rhind Mathematical Papyrus dating to around 1550 BCE, but the royal cubit unit of measure dates as far back as the third millennium BCE 6, prior to the Great Pyramid’s construction. The royal cubit is equivalent in measure to 20.7 inches (52.5 cm) or 7 palms, each of which is made up of four digits. Modern surveys of the Great Pyramid suggest a seked slope of 5.5—that is, a run of 5 1/2 palms (i.e., 5 palms, 2 digits) over a rise of 1 cubit (i.e., 7 palms). 7 Since the run is only half of the base length, the height to base ratio based on this measurement technique is 7/11, or .63636. If we multiply the most accurate and up-to-date base width of 755.68 feet (230.33 m) by this ratio, we produce an estimated height of 480.87 feet (146.57 m)—an incredible 0.6 inches (0.016 m) less than the actual estimated height of the Great Pyramid.
This portion of the Palermo Stone recounts the Nile flood levels during the reign of King Nynetjer (d. 2845 BCE), measured in cubits, palms, and digits.
We really don’t know with certainty how the pyramid was designed, and knowledge of the specific geometric relationships and concepts could have existed and then been lost. We do know the Egyptians built the pyramids with amazing precision and left little to chance, as evidenced by their alignment to within 1/20th of a degree from true north. The builders may have chosen approaches that produced almost identical geometric relationships to those of pyramids based on phi and pi.
If the ancient Egyptians’ knowledge and application of the golden ratio were limited to this one exceptionally accurate appearance in the Great Pyramid, it could still be argued that it was due to chance. However, we now have additional evidence that suggests that the golden ratio also appears in the positions and relative sizes of the pyramids at the Giza site. These recent findings make for a much more compelling case.

An aerial view of the Giza necropolis.
COMPARING KHUFU, KHAFRE, AND MENKAURE
Consider the pyramid complex as a whole. Using satellite mapping images, if you create a rectangle with a perimeter that outlines the bases of the two largest pyramids at the site, Khufu and Khafre, you’ll discover that the eastern edge of Khafre’s base is closely aligned with the golden cut, moving westward from the eastern edge of the perimeter rectangle to the western edge. You’ll also find a similar ratio comparing the distance between Khufu’s northern edge and Khafre’s northern edge to the distance between the northern and southern edges of Khafre’s base.
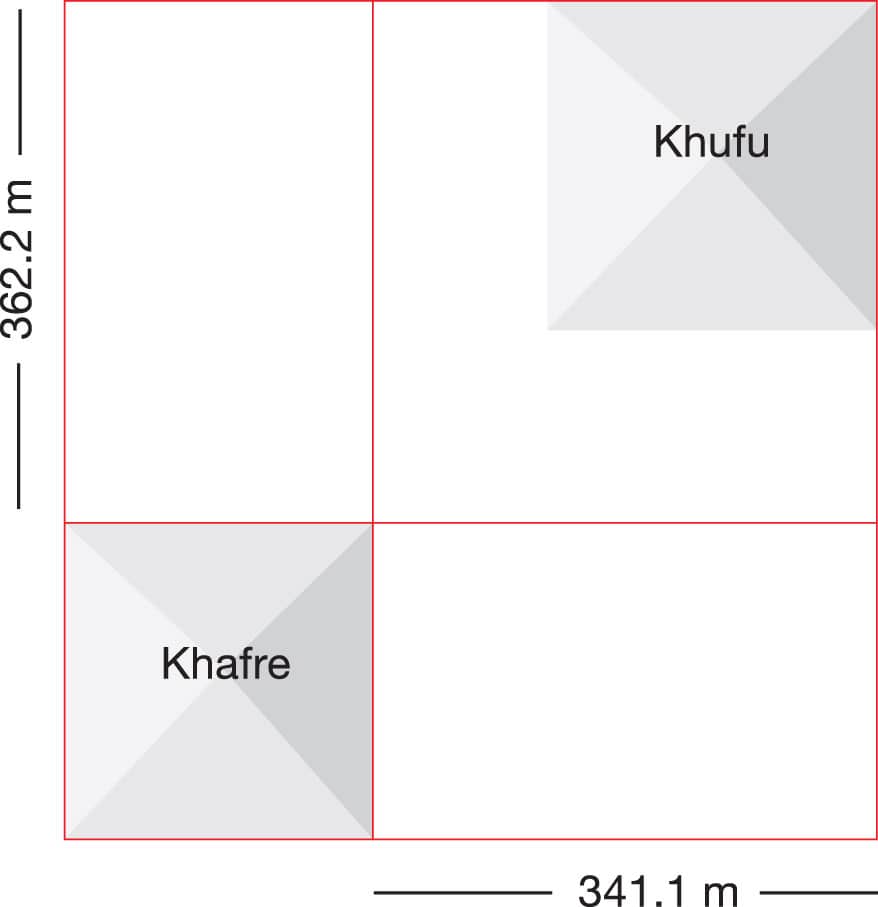
These relationships are confirmed by the distances at the Giza complex, as calculated by archeologist Glen Dash. 8 For example, the width of the perimeter rectangle that encloses the two larger pyramids is approximately 1,825.5 feet (556.4 m), whereas the height of this same rectangle is 1,894.4 feet (577.4 m). Meanwhile, the base width of Khafre is 707 feet (215.3 m). 9 If we subtract this number from both rectangle lengths, we discover a distance of 1,119.1 feet (341.1 m) between the eastern edges of Khufu and Khafre’s bases, and a distance of 1,188.3 feet (362.2 m) between the northern edges of Khufu and Khafre’s bases. Dividing the perimeter lengths by these distances gives ratios of 1.631 and 1.594. The average of these ratios is 1.613, which is mighty close to 1.618.
Another analysis of the Giza complex site by Chris Tedder 10 provides an even simpler and more elegant relationship between the locations of the apexes of Khufu, Khafre, and Menkaure. The relationship involves two golden rectangles (one in portrait orientation, one in landscape orientation) whose corners align with the apex of each pyramid, as shown on the following page.
Again, relying on Dash’s very precise measurements at the Giza site, the east-to-west distance between Khufu and Khafre’s apexes is 1,095.5 feet (333.9 m), and the east-to-west distance between Khafre and Menkaure’s apexes is 785.76 feet (239.5 m). From north to south, the distances between apexes are 1,162.4 feet (354.3 m) and 1,265.4 feet (385.7 m), respectively. This allows us to construct two rectangles with dimensions of 1,881.2 × 1,162.4 feet (573.4 × 354.3 m, shown in blue) and 1,265.4 × 785.76 feet (385.7 × 239.5 m, shown in red). The larger rectangle has perfect golden proportions, whereas the second has proportions within 0.08 of phi.

The Tedder grid shows the two golden rectangles formed in the distances between the apexes of Menkaure (left) and Khafre (center), and Khufu (right). Note: The top of the diagram faces west.
In sum, here is what the geometric relationships between the most up-to-date Giza site measurements show us about the three main pyramids:
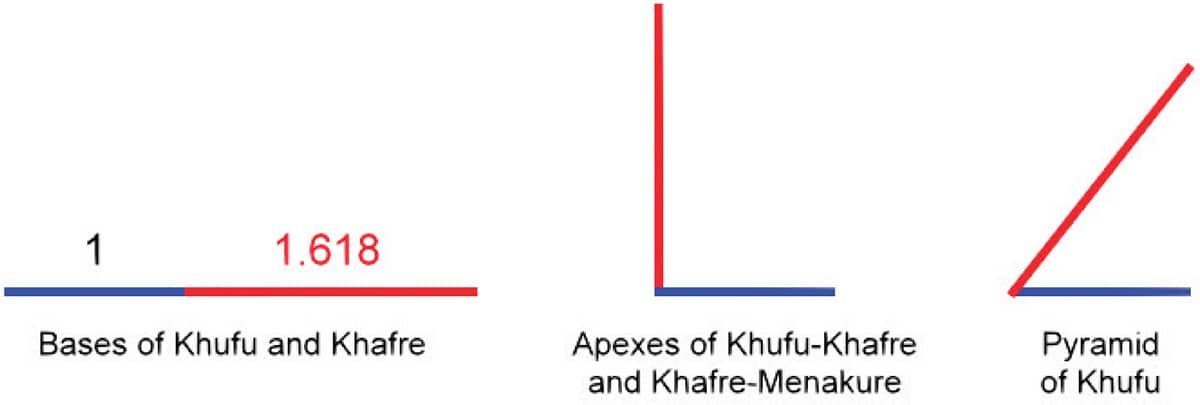
• The average ratio of the distance between the eastern and northern edges of Khufu and Khafre’s bases to the width of Khafre’s base is approximately 1.618.
• The ratio of the east-west distance between Khufu and Menkaure’s apexes to the north-south distance between Khufu and Khafre’s apexes is 1.618.
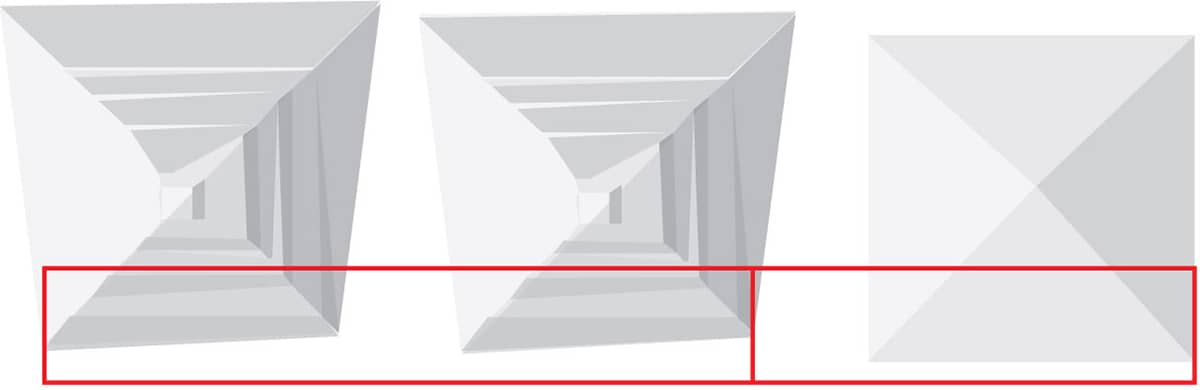
• The right triangle formed by Khufu’s height, the length of its four slanted faces (hypotenuse), and horizontal distance between its apex and the perimeter of its base (width) produces a hypotenuse to width ratio of 1.618—identical to that of the Kepler triangle.
THE PYRAMIDS OF QUEENS
In the site’s East Field, next to the Khufu Pyramid, are three smaller pyramids, thought to contain the tombs of Khufu’s mother, Queen Hetepheres I, his wife, Queen Meritites I, and his other wife (or possibly his daughter), Henutsen. 11 As shown below, the length of the rectangle around all three pyramids to the length of the rectangle around the base of Meritites’s and Henutsen’s pyramids can be represented by Ф.
Just south of the Menakaure Pyramid are the three Pyramids of Queens. Although irregularly shaped, the distance between the corners of their bases on the south-facing sides reveal the very same golden ratio relationship that appeared in the three pyramids next to Khufu.

When seen from satellite, the positions of the three pyramids adjacent to the Khufu Pyramid appear to reflect the golden ratio in their relative positions.
The southern edges of the satellite positions of the Pyramids of Queens also appear to reflect the golden ratio.
THE GREAT SPHINX
There’s one more major monument at the Giza site that I’d be remiss to exclude from this analysis: The Great Sphinx. Again, using satellite topological images and examining the relationship between the full length of the monument on each side and the length from the front paws and back paws on each side, we discover yet another example of golden proportions!
There is still much to understand about the history, mathematics, design, and purpose of the building of the pyramids, but one thing is pretty clear: Many key features of the Giza site appear to closely embody the geometry of the golden ratio. I hope these discoveries and analyses provide others with an incentive for more research. For now, the question persists: Why did the ancient builders choose this particular configuration for the great pyramids? Because it appeared more beautiful and more aligned with nature? If not, why does the golden ratio appear to be so prevalent in the most notable surviving monuments of the ancient world?

This 1904 painting by Russian artist V. F. Ulyanov (1878–1940) portrays the majestic Sphinx during twilight.
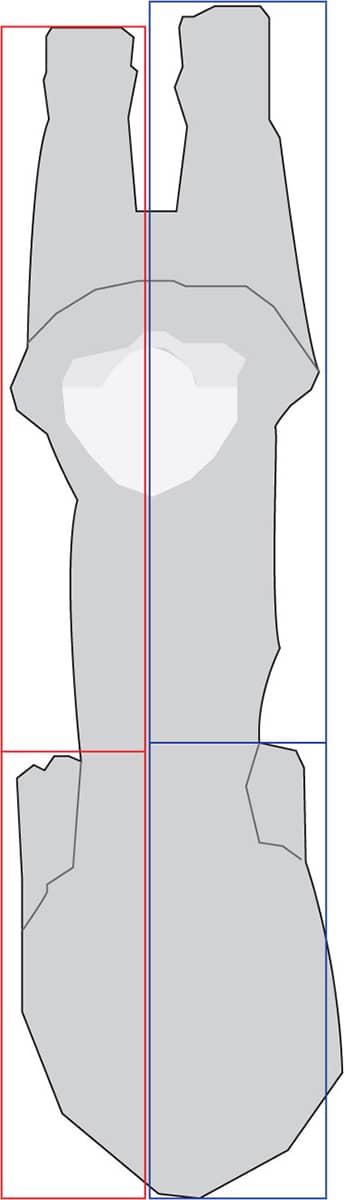
When viewed from satellite, both sides of the Great Sphinx appear to reflect golden proportions.
PHIDIAS AND THE PARTHENON
The ancient Greek sculptor, painter, and architect Phidias, who lived from about 480 to 430 BCE, deserves special recognition in our story, as he inspired the use of the Greek letter Ф to designate the number 1.618. Although none of his original works remain, numerous copies exist. Among his great achievements was the statue of Zeus in the Temple of Zeus at Olympia, one of the Seven Wonders of the Ancient World. He also created the statues of the Parthenon, including that of the goddess Athena, and there’s evidence that he applied the golden ratio in these designs. While his statues of Zeus and Athena did not survive, his legacy lives on in ancient Greek canon and the enduring structures on the Athenian Acropolis, perched above the city as a monument to classical Greece.
The Parthenon in Athens, built by the ancient Greeks between 447 and 438 BCE, is regarded by many as a prime example of architecture that makes use of the golden ratio. Of course there are those who disagree, pointing out that more than a century elapsed between the completion of the Parthenon and the first documentation of the golden ratio in Euclid’s Elements.

This nineteenth-century drawing portrays Phidias’s massive gold and ivory sculpture of Zeus in Olympia. One of the world’s original Seven Wonders, it stood 39 feet (12 m) high 13 and was adorned with paintings and precious stones.

This 1887 statue by Parisian sculptor Aimé Millet shows Phidias and a miniature replicant of his famous sculpture Athena Parthenos, which once stood within the Parthenon.

The ruins of the Parthenon are perched on the rocky Acropolis, high above the modern Athenian cityscape.
There are several challenges in determining definitively whether the Parthenon’s architects intentionally incorporated 1.618 into its construction:
• The Parthenon embodies a variety of numbers and proportions with its forty-six perimeter columns and thirty-nine interior columns spaced at varying distances from one another.
• The Parthenon is now partially collapsed, making its original features and height dimension subject to some conjecture.
Two of the most familiar appearances of the golden ratio are present in the dimensions of the shorter side of the structure. The image below shows the Parthenon with a superimposed golden rectangle and embedded golden spiral. However, this assumption requires the alignment of the golden rectangle with the bottom of the second step of the structure and with the estimated position of the triangular pediment’s original apex. With this alignment, the top of the columns and base of the roof line are in a close golden ratio proportion to the height of the Parthenon. This, however, is not the most compelling evidence that the ancient Greeks used the golden ratio intentionally in the design of this iconic temple.

View into the Heyday of Greece (1836) by German painter August Ahlborn depicts the construction of the Parthenon.

Phidias (center) shows off the frieze of the Parthenon to his friends in this 1868 painting by Dutch-British artist Sir Lawrence Alma-Tadema.
Applying the grid lines to the building’s entablature reveals other interesting proportions. Zooming in on the entablature frieze and embedded metope-triglyph pattern, we discover that the horizontal dividing line of the entablature is at a precise golden ratio of its height. We also find beautiful golden rectangles enclosing the metopes, with yet another golden relationship between the width of the triglyphs and that of the metopes.

Golden proportions are apparent in the remaining structure of the nearly 2,500-year-old Parthenon.
Finally, let’s examine the floorplan of the Parthenon, which shows eight columns supporting the shorter side and seventeen columns supporting the longer side. Just inside the perimeter on each of the shorter sides are six columns, followed by entrances to two interior chambers. My analysis reveals the following:
• The wall that separates the east and west interior chambers is closely aligned to the golden cut of the rectangle aligned with the centers of the east and west perimeter columns.
• The centers of the four columns in the western interior chamber and the base of the Statue of Athena are positioned at the two golden cuts of the distance between the centers of the north and south perimeter columns.
• The entrances to both interior chambers are positioned at the golden cuts of the distance between the north and south walls of each interior chapter.
More than four hundred years following the Parthenon’s construction, Roman military engineer Vitruvius (see here) proposed what he considered the perfect Roman house floorplan in his famous book De Architectura (c. 20 BCE). Considering the quantity of golden proportions throughout, it seems likely that he was aware of the use of the golden ratio by the ancient Greeks in their art and architecture.

A closeup of artist Godfried Semper’s colored reproduction of the Parthenon’s frieze shows the golden relationship between the metope and triglyph more clearly.

The floorplan of the Parthenon displays golden dimensions.

This illustration of an ideal Greek home floorplan from Vitruvius’s De Architectura is full of golden rectangles and other phi-based dimensions.
GOLDEN CATHEDRALS
The construction of awe-inspiring cathedrals as Christianity spread throughout Europe was an outward expression of an inner reverence for God’s glory and a focal point for community life for centuries to follow. It was also an outlet for the creative energy of medieval European society. The massive financial, technical, artistic, and physical resources required made each a community effort that was approached with great ambition and enthusiasm. Construction often took over a century, inspiring generations to be a part of something larger than oneself.

The north rose window of Notre-Dame cathedral in Paris, France, beautifully exhibits the Divine proportion.

Many phi-based proportions are found in the western façade of Notre Dame.
One of the finest cathedrals in existence was begun in Paris in 1163 under the direction of Bishop Maurice de Sully. He died in 1196, and finally, in 1225, construction of the western façade was complete. Another century passed before the entire cathedral had been built, and nearly eight hundred years later, it is one of Paris’s top tourist attractions: the Notre-Dame Cathedral. Interestingly, the western façade, as well as the north-facing Gothic stained-glass rose window, reflect the golden ratio in their dimensions.
Not long after construction was underway on Notre-Dame in Paris, another cathedral was commissioned in Chartres, about 50 miles (80 km) southwest of Paris. This one was complete by 1220, and like Notre-Dame, golden proportions are found throughout the structure. In fact, the golden ratio seems to reappear in various cathedrals throughout Europe.

Above and Below: The windows of the western façade of Notre-Dame de Chartres Cathedral also exhibit the golden ratio, as shown in these details from a detailed 1867 architectural drawing of the cathedral.
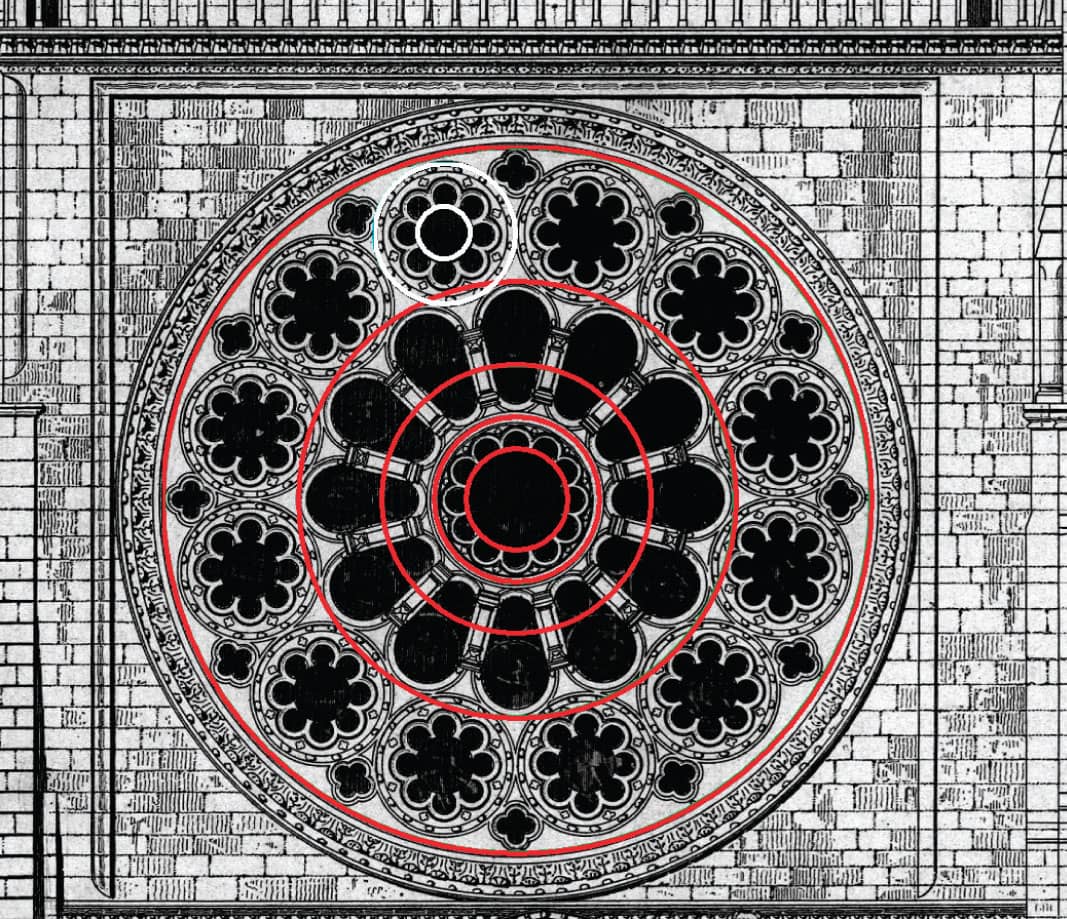

The stunning north-facing transept rose window of Chatres Cathedral, constructed c. 1235.

A view of the cathedral’s southern façade towering over the Chartres cityscape.

This colored monograph of a portion of a south transept window leaves little doubt as to whether phi was worked into the Chartres Cathedral’s design.
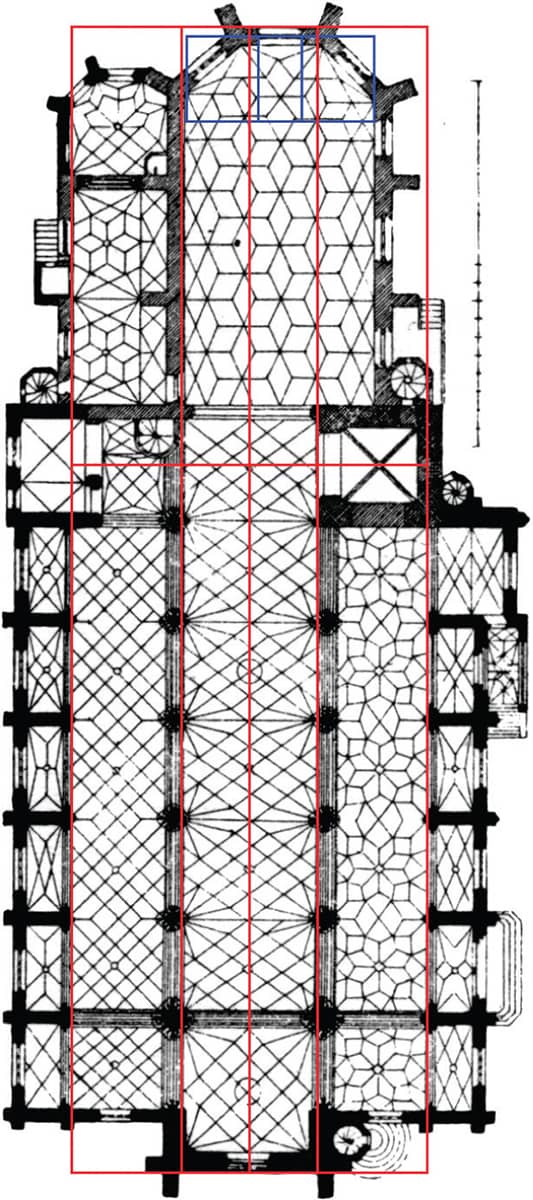
The floorplan of the Stiftskirche (“Collegiate Church”), constructed mostly over a three-hundred-year span between 1240 and 1547 in Stuttgart, Germany, appears to have some phi-based dimensions based on this late-nineteenth-century drawing.

The western façade of the Gothic-Romanesque Limburg Cathedral in Hesse, Germany.
In 1296 construction began on another of the world’s most famous and identifiable architectural wonders: Florence, Italy’s Cattedrale di Santa Maria del Fiore (Cathedral of Saint Mary of the Flower). Tuscan architect Arnolfo di Cambio came up with the winning design, which included three wide naves and an octagonal dome. After his death, work resumed under a series of architects, including Francesco Talenti, who expanded the length of the naves to make the cathedral Europe’s largest in the 1350s. He also completed the almost 300-foot-(91 m)-tall campanile near the basilica’s main entrance in 1359. 14
The famous dome was one of the last structures to be built. In 1418 the powerful Medici family announced a contest for the dome’s design, and master goldsmith Filippo Brunelleschi received the commission. In 1436 the dome was finally complete. A technological marvel, it began 171 feet (52 m) above the floor of the building, spanning 144 feet (44 m) and rising to 375 feet (114.5 m) in total, with the crowning lantern included. 15 The span of the dome was too large and too high for wooden supports, so Brunelleschi had to devise ingenious construction techniques—not to mention more than four million bricks—to accomplish his task, but all the effort paid off in what is still the largest brick dome in the world. If that isn’t enough, this magnificent structure also embodies golden proportions!

Aside from being a masterpiece of engineering, Bruneschelli’s famous octagonal dome appears to reflect golden proportions.

The golden ratio can be seen in many elements of the cathedral’s final floorplan.

Many architectural elements of Florence’s gigantic Cathedral of Saint Mary of the Flower have phi-based dimensions.
THE TAJ MAHAL
Almost 4,000 miles (6,437 km) from Greece and almost two millennia into the future, we encounter the Taj Mahal. The Mughal emperor Shah Jahan commissioned the monument to house the tomb of his favorite wife, Mumtaz Mahal, following her death during childbirth in 1631. Within twelve years the beautiful mausoleum was mostly complete, with other phases of the project continuing for another ten years.

Mumtaz Mahal (born Arjumand Banu Begum, 1593–1631) and her husband, Shah Jahan (1592–1666), are shown in these miniature portraits from Udaipu, India, which are painted on camel bone with inlaid semiprecious stones.
Located in Agra in northern India, the Taj Mahal is considered one of the finest examples of architecture that exists today. Persian architect Ustad Ahmad Lahori directed its construction, employing around twenty thousand artisans in the effort. Evidence of the golden ratio as a foundational aspect of its design is observed in the width of the center arch in relation to the width of the building.
The golden ratio can also be seen in the width and position of the arched windows at the center of the rectangular frame around the central arch. Other golden proportions appear throughout, including the relationship between the height and width of the central structure and those of the towers on either side.

The monumental ivory and marble Taj Mahal mausoleum has obvious phi-based proportions.
LE CORBUSIER’S MODULOR DESIGNS
The architecture icon known as Le Corbusier was born Charles-Édouard Jeanneret in Switzerland in 1887. He was the son of an artisan who decorated watches and took frequent hikes in the Jura Mountains where they lived. Jeanneret developed a love of nature as well as the decorative arts, teaching himself the basics of architecture and philosophy by reading through the books of his local library. In his early twenties, following the trend of other artists of the era, he adopted the pseudonym Le Corbusier. Years later, in his fifties, he developed a system of design based on the golden ratio and the human body called the Modulor. This system, which sought to unite the metric and imperial systems of measurement, was intended as a universal standard of measure that engineers, architects, and designers could use to produce forms that were both practical and beautiful. He represented this “range of harmonious measurements” with the abstract form of a 6-foot-tall (1.83-m) man with a raised arm that was bent in alignment with the top of his head, which was conveniently positioned at the golden ratio cut between his navel and the top of his raised arm. Australian architecture professor Michael J. Ostwald describes it as:
“For Le Corbusier, what industry needed was a system of proportional measurement that would reconcile the needs of the human body with the beauty inherent in the Golden Section. If such a system could be devised, which could simultaneously render the Golden Section proportional to the height of a human, then this would form an ideal basis for universal standardization.” 17
In Le Corbusier’s attempt to use the mathematical proportions of the human body to improve both the appearance and function of architecture, he followed in the footsteps of Vitruvius, Da Vinci, Pacioli, and the Renaissance masters who used the study of mathematics and nature to imbue their artistic masterpieces with a divine quality.
After its formulation in the mid-1940s, Corbusier applied the new system to several buildings, including:
• the world headquarters of the United Nations in New York, NY (completed in 1952).
• several modernist housing developments throughout Europe, beginning with the Cité radieuse (Radiant City) in Marseille, France (completed in 1953).
• Convent Sainte Marie de la Tourette near Lyon, France (completed in 1961).

An engraving of Le Corbusier’s Modulor appears on the exterior of the Corbusierhaus.

Various architectural features in Le Corbusier’s 1958 Unité d’Habitation of Berlin (now known as Corbusierhaus) residential project reflect the golden ratio, including the windows, floor heights, and balcony widths.

Le Corbusier’s Modulor system forms the basis of the UN Secretariat building’s design, as shown.
Let us take a look at one prominent example of Le Corbusier’s Modulor design approach and his utilization of golden ratios. In 1947 the Brazilian architect Oscar Niemeyer and Le Corbusier joined forces to design the UN headquarters in New York City, a 505-foot (154-m) tower called the Secretariat building. 18 At the time, Le Corbusier was in the process of developing his Modulor design system, and Niemeyer, another giant in the world of modern architecture, was highly influenced by this Swiss-born artist, designer, and urban planner. As architect Richard Padovan described in his book Proportion: Science, Philosophy, Architecture:
“Le Corbusier placed systems of harmony and proportion at the center of his design philosophy, and his faith in the mathematical order of the universe was closely bound to the golden section and the Fibonacci series, which he described as ‘rhythms apparent to the eye and clear in their relations with one another. And these rhythms are at the very root of human activities. They resound in Man by an organic inevitability, the same fine inevitability which causes the tracing out of the Golden Section by children, old men, savages, and the learned.’” 19
For the UN project, Le Corbusier conceived a tall, central building that would house all of the Secretariat offices. Known as project 23A, the main building dimensions consisted of three stacked golden rectangles. Niemeyer’s project 32, on the other hand, featured a tall, slightly wider central building with the dimensions of the golden rectangle. The final design combined elements from both Niemeyer’s and Le Corbusier’s schemes but used three stacked golden rectangles as the basis of the design.
At first glance, the four noticeable bands on the façade of the building make it seem like most of the thirty-nine floors are divided equally into three rectangles, but closer inspection reveals that their dimensions differ slightly. The first rectangle is only nine floors tall, whereas the second and third rectangles are eleven and ten floors tall, respectively. Also, while the building width is stable at 287 feet (87 m), the building height ranges from 505 to 550 feet (154 to 168 m), 20 depending on the elevation as one moves from street level at the building’s front to the shore at its rear.

Le Corbusier’s UN Secretariat building overlooks New York City’s East River.
If the building were a perfect golden rectangle, as Niemeyer had proposed, the building would rise to only 464 feet (141 m), which is within 0.5 percent of its occupied height. However, a building precisely composed of three stacked golden rectangles with a length of 287 feet (87 m) would result in a building that is 532 (162 m) feet tall. The average height of the building is, in fact, 527.5 feet (160.7 m)–0.9 percent less than a perfect stack of three golden rectangles. That’s a small discrepancy, but in addition to the uneven elevation of the land between the street and the river, where the UN building stands, there are a few explanations for this:
1. The golden ratio is an irrational number that cannot be expressed in integers, whereas architects are faced with a number of real world constraints that are based on integers, such as the number of floors and windows.
2. The standard dimensions of construction materials, such as drywall and building framing components, are subject to various building standards.
3. There are the engineering constraints required to construct a 500-foot (152-m)-tall skyscraper that take precedent over its pure artistic design elements.
Regardless, if you apply grid lines to the building based on Le Corbusier’s Modulor system, which involves multiplying the height of each dimension by 1.618, a very revealing pattern emerges, as shown opposite. Also, if you apply golden grid lines, you’ll find that several key elevations in the building have a phi relationship. Both approaches demonstrate the presence of the golden ratio in the overall design.
This attention to detail in the consistent application of design principles welcomes visitors as they enter the UN building, too. The front entrance displays golden proportions in the following ways:
• Columns on either side of the front entrance are placed at the golden cut of the distance from the midpoint of the entrance to the edge of the entrance.
• The transparent entrances to the left and right of the center entrance area are golden rectangles.
• The doors on the left and right side of the center entrance are golden rectangles.
• The rectangles formed by the central floor-to-ceiling windows and the entrances on either side have golden proportions.
The windows within the horizontal bands on the face of the building are also a collection of golden rectangles, and the bands are divided at two golden cuts to frame the windows at their centers!
As illustrated by the intricate nesting of golden ratios in his Modulor design template, Le Corbusier’s passion and vision for the golden ratio was far more sophisticated than simply designing a building in the shape of a golden rectangle. No detail was overlooked in the building’s design, and the intricate beauty of his creation only gets easier and easier to appreciate as these golden proportions are revealed. As exemplified in the works of Leonardo, Michelangelo, Raphael, and others that followed, this is the “very delicate, subtle and admirable teaching” and “very secret science” of which Pacioli wrote. The application of the golden ratio to great masterpieces of art and design in order to create visual harmony persists in our modern world.

Color gridlines define the various phi-based relationships in the dimensions of the UN Secretariat building.
LOGO AND PRODUCT DESIGN
In addition to its use in painting, architecture, and graphic design, the golden ratio also appears in numerous product designs. In some cases, it enhances performance of the product. For example, many string instruments display golden ratio proportions. As an illustration, the world-famous Stradivarius violins—developed in the seventeenth and eighteenth centuries by the Italian Stradivari family—seem to exhibit golden proportions. Known for their superior materials, construction, and sound quality, today these sought-after violins can fetch millions of dollars at auction.
In other cases, the golden ratio adds style and aesthetic appeal. Corporations invest millions of dollars on branding and logo design, knowing that they must capture the hearts and minds of as many potential customers as possible in an instant. They are so protective of their powerful, iconic symbols that I cannot visually present in these pages all the examples of golden proportions which appear in logo design. However, I can tell you where to look.
Google captured the attention of the design world in 2015 with their announcement of a major redesign of their logo, fonts, and other branding symbols and icons, but one thing they smartly retained and enhanced was the use of phi in determining the dimensions and spacing of the letters. For example, on close inspection it’s clear that the ratio of the height of the uppercase G and lowercase L to the height of the other lowercase letters (excepting the little tail of the G) equals Ф. The ratio of the width of the capital G to that of the lowercase G is also golden, as is the position of the search field in relation to the top of the logo and the bottom of the search buttons on the Google search home page, which also happens to be the most visited website in the world. Even the little microphone icon at the right of the search bar reflects golden proportions, and yet more golden relationships abound. It appears as if the golden ratio was used for just about every decision on position and proportion for this multinational tech giant. If you didn’t know better, you might wonder if Luca Pacioli and Leonardo da Vinci themselves had been leading the design project!

Golden proportions abound in the Lady Blunt Stradivarius violin, constructed in 1721 by Antonio Stradivari. In 2011 it fetched a record-setting $15.9 million at auction.

These diagrams show the various ways in which the logos of some of the world’s biggest corporations reflect the golden ratio.
Google is certainly not the first to use the golden ratio in their branding. Measure the three ovals that constitute the Toyota logo, and you’ll find that the width of the small, narrow oval in the center is defined by two golden cuts of the width of the largest oval. The inner edge of the middle oval on top is positioned at the golden cut of the logo’s overall height. Even the crossbar of the A and the fork in Y are positioned at golden cuts.
Other examples abound in logos of some of the richest and most highly regarded companies worldwide. The position of the horizontal bar in the Nissan logo is defined by the two golden ratio cuts of the logo’s height. The concentric circles that make up the yellow and green BP “flower mandala” logo are in golden proportion to one another. The National Geographic logo is simply a golden rectangle.
Among cartoon and video animators, use of the golden ratio in character and scene design may be more than just an occasional tip of the hat. One former Disney animator shared with me that although the golden ratio is never discussed among designers—most are very secretive about their process—he has been systematically applying it in his artistic creations. The Disney logo itself is a stylized version of Walt Disney’s signature, which appears to venerate the golden ratio. The design of the D uses the golden ratio at least three times in the proportions and positions of its scrolled arc and vertical stroke, but even more obviously, the “dot” above the I strongly resembles the symbol representing phi. Also, the Y is not like any Y you’ve ever seen before, but it does resemble a script lowercase phi symbol.
One of the world’s premier luxury car brands, Aston Martin, has applied the same concept to the design of its cars. Describing the Rapide S, DB9, and V8 Vantage models, Aston Martin made sure to emphasize the centrality of the golden ratio in many aspects of their design in their advertising campaign, touting the cars’ balance, perfection, elegance, harmony, purity, and simplicity. 21
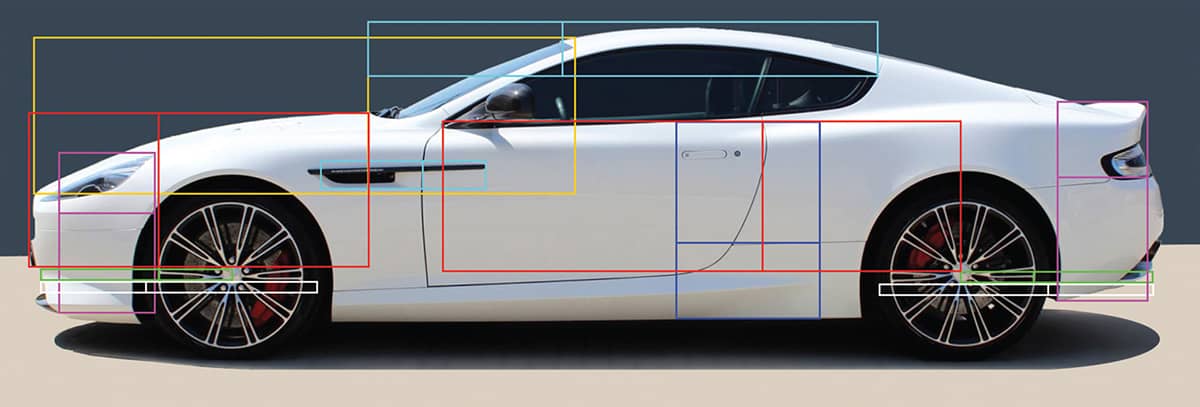
Color gridlines define the various golden proportions in the design of Aston Martin’s DB9 coupe.
Given the elegance of its design, it’s not too surprising that golden proportions are incorporated into the design of the Star Treks USS Enterprise. In the 1960s, series creator Gene Roddenberry turned to Matt Jefferies, an aviation and mechanical artist, with his request to “design a space ship unlike any other, with no fins, rocket exhaust trails, powerful and capable of exceeding the speed of light with a crew of several hundred on a five-year mission to explore unknown galaxies in outer space.” 22 Jefferies started with a blank page, a marker, and a very pragmatic design ethic, producing a ship with very distinct phi-based proportions.
His design documents revealed that he specified the dimensions on his designs to the 1/10,000th of an inch. This was clearly beyond the accuracy required for the construction of the small-scale models used on the Star Trek TV set and indicates that he was working with a mathematical precision based on geometric formulas and proportions. Many other golden ratios can be found in Jefferies’ design of the Enterprise, in the front and side views as well as in the fine detail. Jefferies clearly understood the concept of applying the golden ratio to just about every design decision on proportion and position.
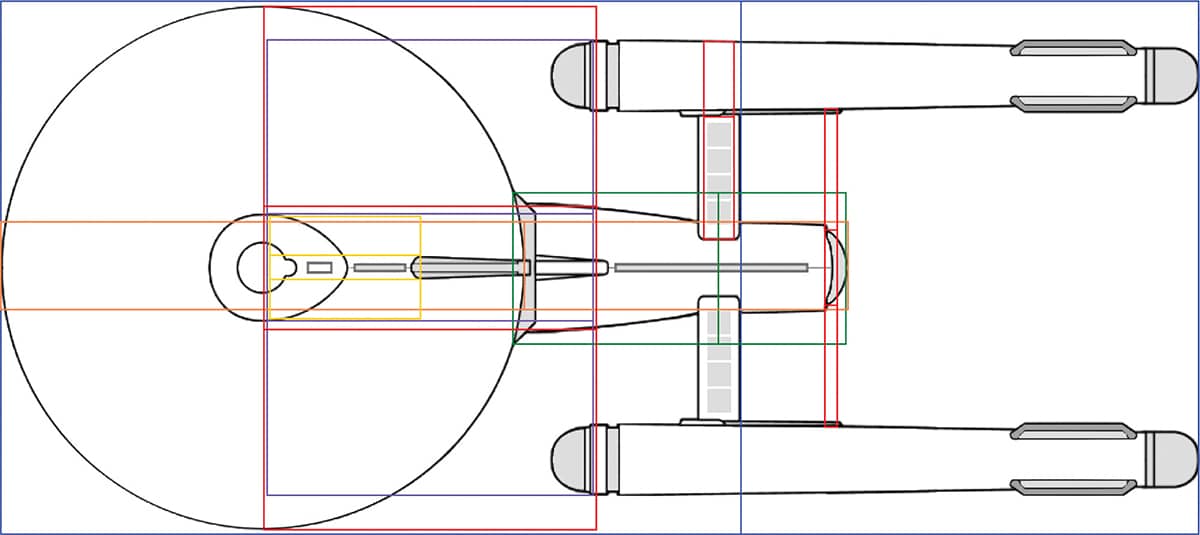
Golden dimensions also abound in Matt Jeffries’s design of Star Trek’s USS Enterprise.
You may be amazed to find that the golden ratio has been right there in front of you all the time, gently nudging you to buy a product or use a service. According to Darrin Crescenzi, former Design Director of Innovation at Interbrand New York, and one of Fast Company Magazine’s “Most Creative People in Business,”
“The visually-inclined—artists, architects, and designers, historically keen observers and documentarians of both nature and the human condition and who we can thank for much of what we know about the world—have for ages incorporated this ratio into their work due to its intrinsically alluring balance between symmetry and asymmetry.” 23
As suggested by Crescenzi, the golden ratio offers much more than just a more natural alternative to the rule of thirds. In fact, it is a mathematically unique system of ratios within ratios that can keep an entire composition in visual harmony, and even though it’s just one of many tools that good designers use to achieve great composition, no designer should be without knowledge of its concepts and application. “The golden ratio is intended to be invisible, a compositional organizing principle that is felt rather than understood,” says Crescenzi. Furthermore, he added:
“It is the unique visual tension between comforting symmetry and compelling asymmetry, and its thoughtful application can bring beauty and harmony and intrigue to all manner of designed things.” 24
The possible variations in applications of the golden ratio to any design are limited only by our creativity, which only means there is no limit at all.
You’ve now developed a solid foundation in the geometry and mathematics of the golden ratio, as well as its appearance in monumental works of art and architecture during more than two thousand years of civilization. As such, you’re well on your way to earning your very unofficial—but very valuable—Doctorate in “Phi”losophy (it’s worth its weight in golden ratios!). The final leg of our journey involves the fascinating study of golden forms in nature and the universe beyond.