VI
A GOLDEN UNIVERSE?
“Where there is matter, there is geometry.” 1
—Johannes Kepler
The frequent appearances of the golden ratio in living organisms is intriguing, but there are still other instances that are far more unexpected, even astounding. As discussed in chapter 1, the eminent mathematician Johannes Kepler represented the cosmos as a series of nested Platonic solids, with the phi-based dodecahedron and icosahedron occupying the spaces between Earth’s orbit and that of Venus and Mars. Although an elegant attempt at capturing the “harmony of the spheres,” his model did not align with observed planetary motions. However, in the end, he did successfully discover and describe the motion of the planets around the Sun, completely transforming our understanding of the cosmos in the process. He also held fast to his reverence for the golden ratio. Could this genius, who sparked the Scientific Revolution, have revealed more secrets about the universe had he lived to a ripe old age?

This illustration of the (fictitious) relationship between the orbits of the first six planets of our solar system and the five Platonic solids appears in Johannes Kepler’s 1619 book Harmonices Mundi.
THE GOLDEN COSMOS
Nearly 2,500 years ago, Plato postulated within Timeaus that the physical universe was made of earth, water, air, and fire, and that each of these elements could be linked to a particular polyhedron. The fifth solid, the dodecahedron, was thought to represent the shape of the universe. Modern science shows that these associations are fictitious, but Plato’s extensive inquiry into the nature of reality revealed other important truths and questions that would eventually lead to new discoveries. For example, a 2003 analysis of the WMAP cosmic background radiation data by Jean-Pierre Luminet and his team showed that the dodecahedron shape could explain some of the observed data better than other models. 2 The jury is still out on this hypothesis, but there are other compelling findings about the structure of our universe. One that amazes me the most involves the relative sizes of the Earth and Moon.

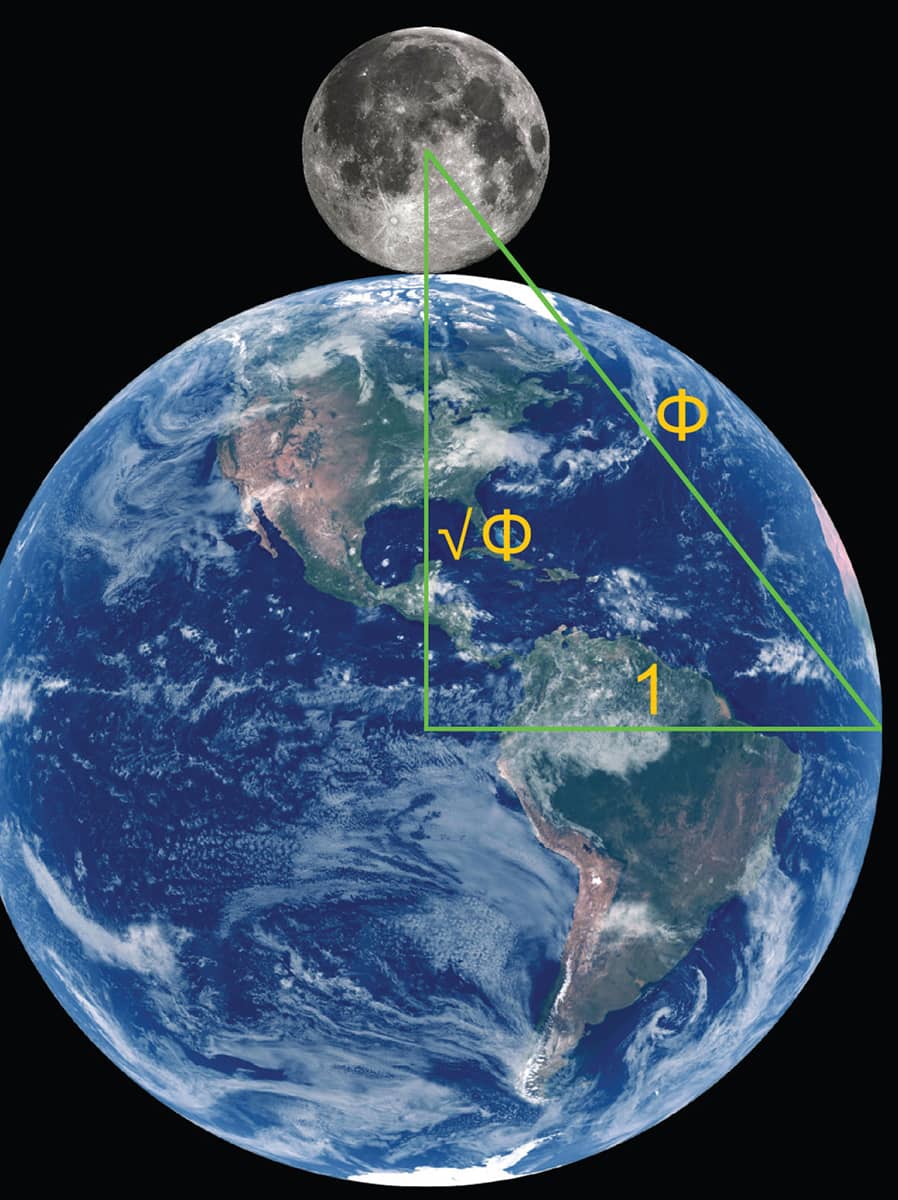
As we observed in chapter 4, the Kepler triangle represents the proportions of the Great Pyramid with a variance of less than 0.2 percent. This same triangle defines a rather amazing relationship between the radii of the Earth and Moon. Consider the following measurements provided by the National Aeronautical Space Agency (NASA) 3:
Earth radius (km): 6,371.00
Moon radius (km): 1,737.40
To visualize their relative sizes, imagine the Moon sitting directly on top of the Earth, with a line connecting the Earth’s center to the Moon’s center. Now imagine a line extended horizontally to Earth’s easternmost point at its perimeter, and then connect that point with the center point of the Moon to form a triangle.
If this triangle reflected the golden ratio as the Kepler triangle does, the height of the triangle (the distance between the centers of the Earth and Moon, equal to their combined radius) to length of the base (Earth’s radius) would equal √Ф, approximately 1.27202. But does it?
There’s an easy way to find out, simply add the radii of the Earth and Moon, then divide this number by the Earth’s radius:
6,371.00 + 1,737.40 = 8,108.40
8,108.40 / 6,371.00 = 1.27270
The variance between this number and √Ф is a mere .0538 percent.
PLANETARY ORBITS
Earth has another unusual relationship with Venus, its next closest neighbor in the Solar System. Earth and Venus have an orbital resonance that brings them to the same positions in space five times during eight Earth orbits and thirteen Venus orbits. Fibonacci strikes again! Now, imagine a line drawn from the orbital positions of Venus to Earth at regular intervals of time. As shown below, the resulting pattern is a beautiful set of nested pentagonal flowers.
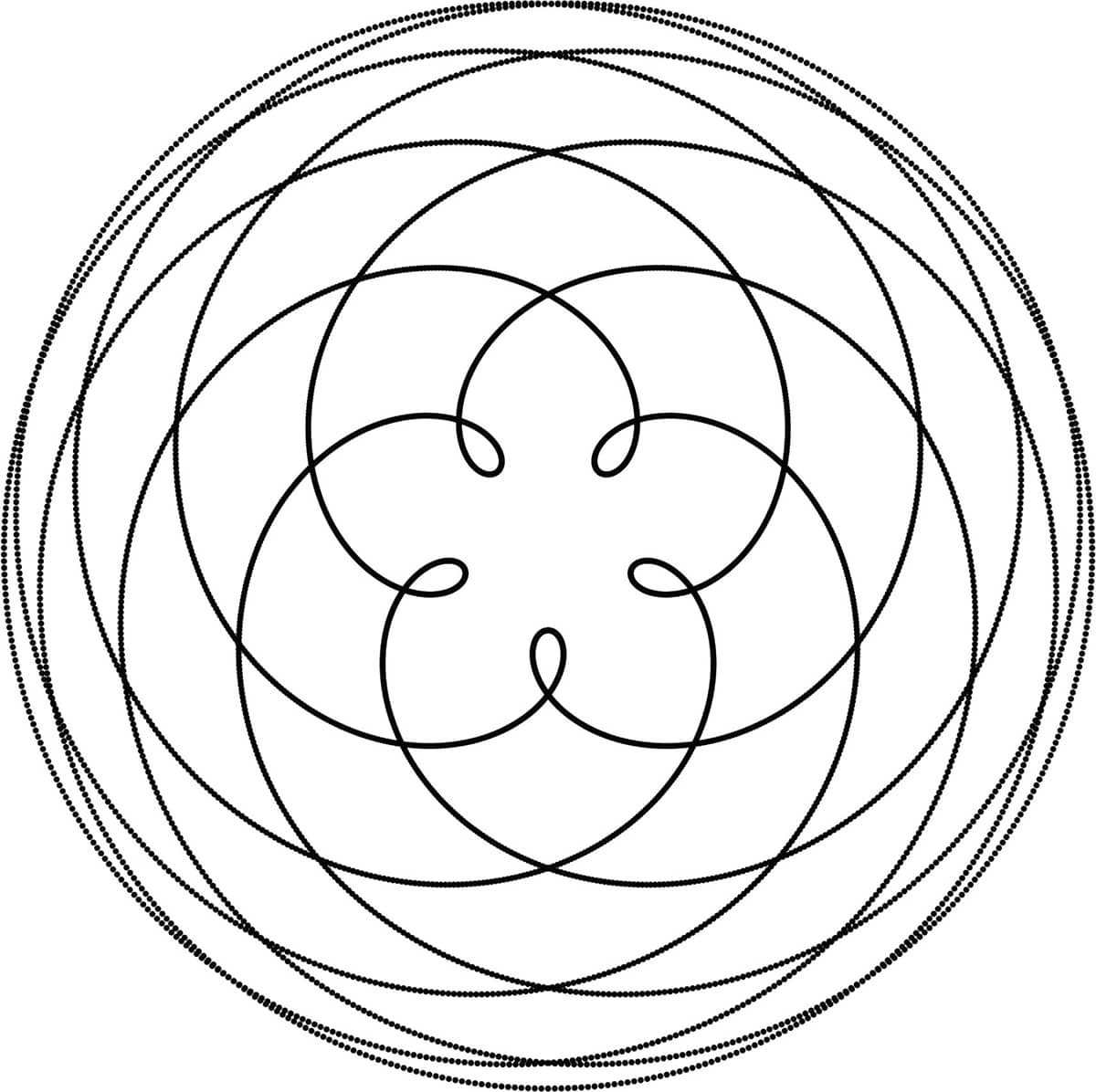
A very similar nested pentagonal pattern emerges from a geocentric viewpoint looking at the relative positions of Venus and the Sun. Additionally, the orbital period of Venus is 224.7 days, about 0.6152 of one Earth year (365.256 days). 4, 5 This number varies only 0.5 percent from 1/Φ.
GOLDEN STARS
Back at the other end of the cosmological scale, a 2015 research article 6 by John Lindner of the University of Hawaii and team reported the discovery of a class of white-blue variable stars that pulsate in a fractal pattern at frequencies close to the golden ratio. The stars are of the RR Lyrae variable class, a unique star class which are at least 10 billion years old and whose brightness can vary by 200 percent in as little as twelve hours. One star was observed at thirty-minute intervals over a four-year period with the Kepler telescope, and was found to have characteristic frequencies in a 4.05-hour and a 6.41-hour cycle, which have a ratio of 1.583, within 2.2 percent of the golden ratio. These stars are referred to as “golden” because the ratio of two of their frequency components is near the golden ratio, and the apparent irrational quality of the relative frequencies is a clue that the pulsing is fractal in time.
To confirm this, the Lindner team performed a fractal analysis of their plots at different magnifications. This was done by converting their plots to frequency spectra. They then counted the number of spikes in the converted plots whose heights surpassed a certain threshold, with a power law dependence on the threshold that was a sign of fractal behavior. The pulsating frequencies conformed to fractal patterns, and when the oscillations were separated into parts, additional weaker frequencies were identified. Researchers described the weaker frequencies as following a pattern similar to shorelines that appear jagged at any distance from which they are viewed. The authors believe that this fractal pulsation may carry information about characteristics of the star’s surface, such as changes in opacity.
It is still not clear whether or not the star’s fractal pattern behavior happens for a reason. If it does, then there are other clues regarding the physics of stars awaiting discovery.
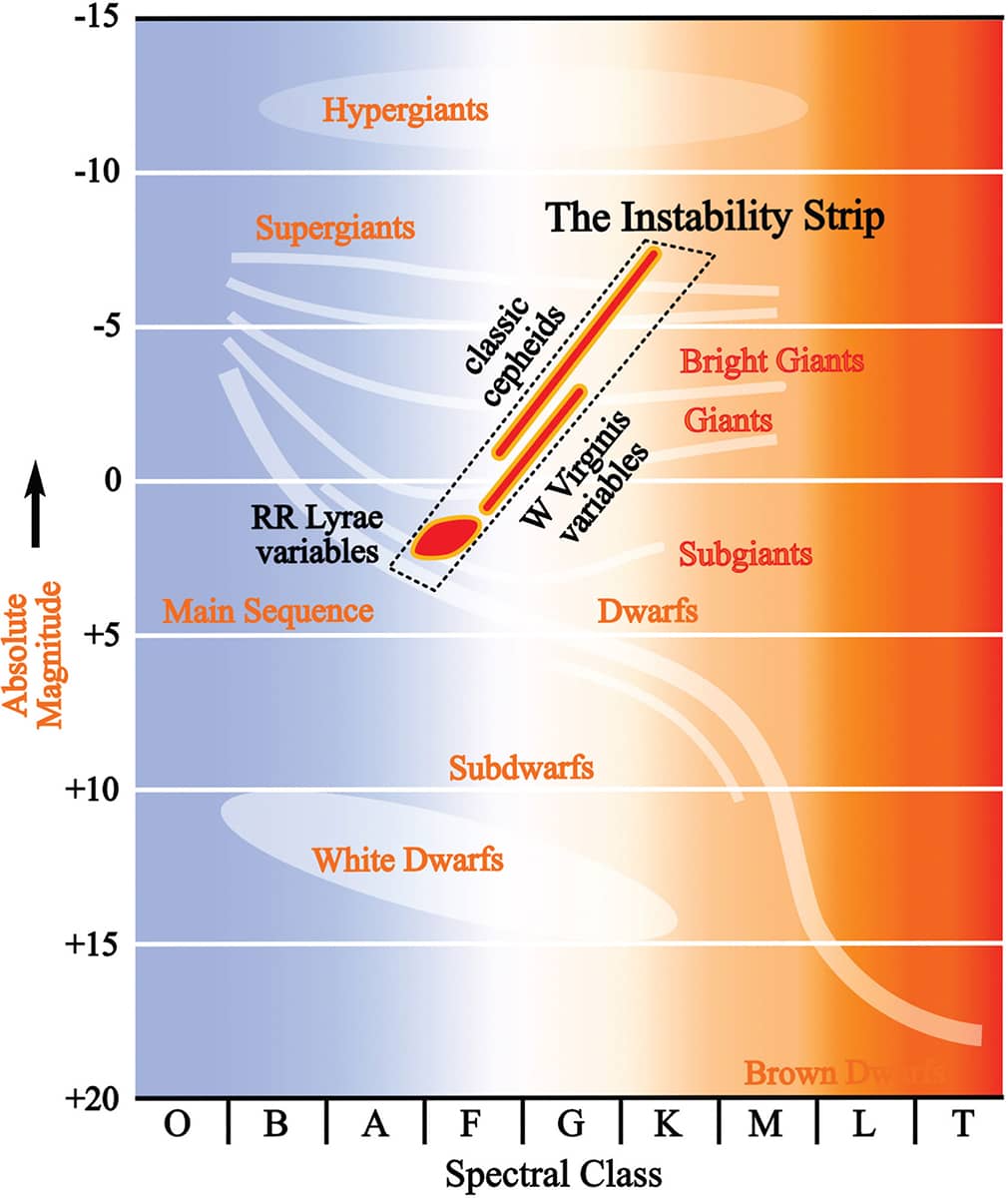
This graphic shows the location of the RR Lyrae variable stars on the Hertzsprung–Russell diagram that compares the color and brightness of different classes of stars.
BLACK HOLES
In 1958, American physicist David Finklestein described black holes as regions in space where the gravitational pull is so strong that nothing—not even light—can escape it. They are believed to occur when massive stars collapse, and after swallowing other stars and merging with other black holes, they become supermassive. Many physicists believe these monstrous, supersized black holes exist at the centers of most galaxies, including our own Milky Way, and over the years they have attempted to describe the unique and powerful physical properties of black holes, including their mass and angular momentum (i.e., speed of rotation), using mathematics.
In a 1989 paper published in Classical and Quantum Gravity, 7 English astrophysicist Paul Davies suggested that a phi-based relationship exists at the transition point of a spinning black hole from one state to another, such as when it changes from a state heating up as it loses energy to a state of cooling down. Specifically, he claimed that the transition occurs when the square of its mass is equal to 1/Ф times the square of its angular momentum, although other physicists have challenged his finding.
Other researchers of black holes have come up with numerous equations involving phi as a constant. Among them are Norman Cruz, Marco Olivares, and J. R. Villanueva of the University of Santiago in Chile. In their 2017 paper “The Golden Ratio in Schwarzschild-Kottler Black Holes,” 8 they presented evidence that phi appears in the movement of particles within a black hole—specifically the ratio between the farthest distance and nearest distance between two photons orbiting at maximal radial acceleration.
A 2011 research paper 9 by J. A. Nieto at the Autonomous University of Sinaloa in Mexico revealed a surprising link between black holes and the golden ratio when he attempted to describe their properties in higher dimensions. Specifically, when describing black holes in four dimensions, he uncovered this formula:

Nieto instantly recognized the famous formula, and in addition to formally establishing a connection between the golden ratio and black holes, he helped to clarify the characteristics of a black hole’s event horizon, which is the point of no return at which the gravitational pull of a massive object becomes so great as to make escape impossible.

An artist rendering of a supermassive black hole at the center of a galaxy.
PHI-BASED MATTER?
Journeying from the expansive scale of outer space to the microscopic world of molecular structures, we encounter quasicrystals, buckyballs, and other forms of matter that appear to reflect the golden ratio in their arrangement of atoms and molecules.

This digital illustration depicts a collection of tiny graphene “buckyballs” (see here).
QUASICRYSTALS
In 1982, scientist Dan Shechtman captured an image with a scanning electron microscope that seemed to contradict basic assumptions in the field of crystallography, a branch of chemistry that studies crystalline solids. Ten bright dots appeared in each circle, revealing a diffraction pattern of ten-fold symmetry. The prevailing wisdom at the time held that crystals could only possess two-fold, three-fold, four-fold, and six-fold rotational symmetry, but Shechtman’s discovery changed all that. In fact, it was so unbelievable that he was asked to leave his research group in the course of trying to defend his findings. The battle raged on, and eventually other scientists were forced to re-examine their understanding of the nature of matter. With the help of Penrose’s tiling mosaics, the scientific world gradually began to accept Shechtman’s findings.

Shechtman (far left) discusses the atomic structure of the quasicrystal at a National Institute of Standards and Technology (NIST) meeting in 1985.
Most crystals in nature, including sugar, salt, and diamonds, are perfectly symmetrical and periodic, with structures arranged in the same orientation throughout the entire crystal. Quasicrystals, however, are asymmetrical and aperiodic. Their discovery presents a new state of matter that was completely unexpected, combining the properties of crystals and with properties of noncrystalline matter, such as glass. While Shechtman first observed quasicrystals in an aluminum-manganese alloy (Al6Mn), hundreds of quasicrystals have since been observed in other substances, many of which are aluminum-based alloys. The first naturally occurring quasicrystal, icosahedrite, was discovered in 2009 in Russia. 10
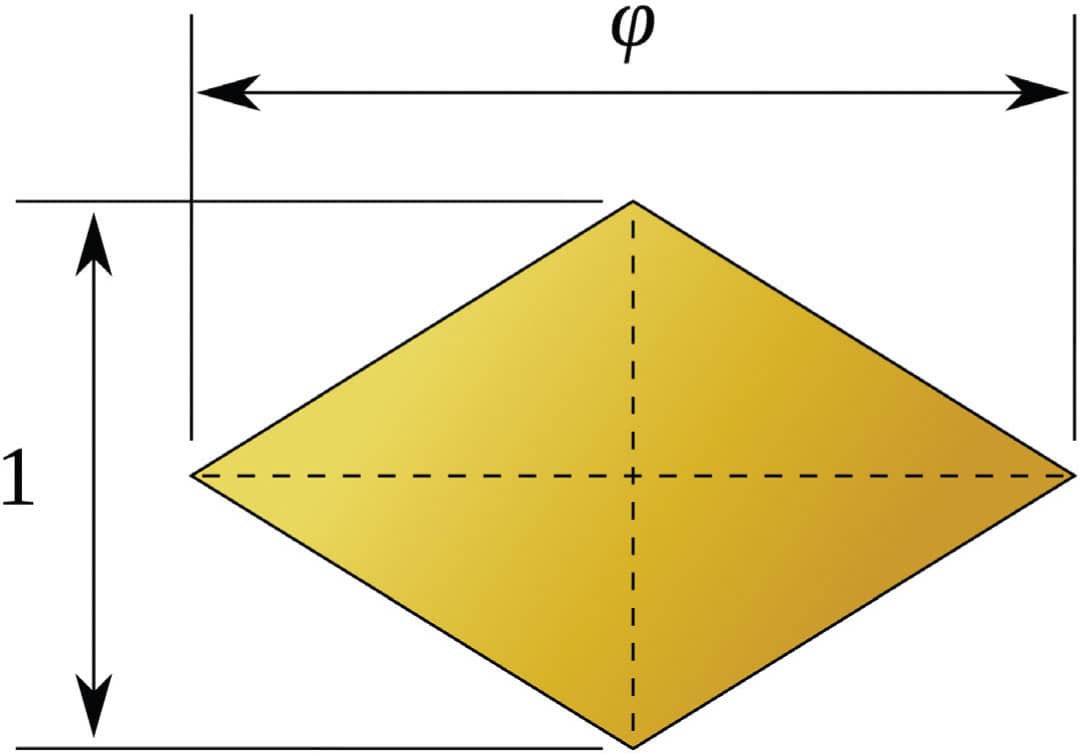
A three-dimensional golden rhombus forms the structural basis of some quasicrystals.

This photograph compares the size of a Ho-Mg-Zn quasicrystal to that of a penny. According to the US Department of Energy, this new material has high potential for use as a low-friction coating for automotive mechanical parts.
The Penrose tiling solution to five-fold symmetry in two dimensions requires two shapes: the dart and the kite. In three dimensions, this can be accomplished with just one shape: a six-sided, three-dimensional diamond with golden proportions.
Other quasicrystals take different forms. In the image below, a Ho-Mg-Zn quasicrystal has formed into the related pentagonal dodecahedron, with true regular pentagons as its faces.
Almost three decades after their discovery, the Nobel Prize in Chemistry was finally awarded to Shechtman in recognition of his quasicrystal discovery. Science has since turned to the medieval Islamic Alhambra palace in Spain and the funerary of shrine Darb-i Imam in Iran, which display magnificent aperiodic phi-based mosaics. With Schechtman’s discovery of quasiperiodicity, an entire new class of solids is possible, and symmetry in any number of dimensions becomes attainable!

The electron diffraction pattern of the Ho-Mg-Zn quasicrystal reveals its five-fold symmetry. Notice the proliferation of pentagrams, pentagons, and other phi-based shapes in the overlaying diagram.

These five girih tiles have been used to create aperiodic geometric patterns in Islamic architecture for almost a thousand years. Note the inclusion of the five-sided pentagon and the golden rhombus.

This girih pattern appears on the walls of the Tuman Aka mausoleum within the Shah-i-Zinda necropolis in Samarkand, Uzbekistan.

Quasiperiodicity 5-fold symmetry.

Quasiperiodicity 7-fold symmetry.

Quasiperiodicity 11-fold symmetry.

Quasiperiodicity 17-fold symmetry.
BUCKYBALLS
As we saw in chapter 3, Luca Pacioli’s seminal publication on the “divine proportion” featured da Vinci-drawn illustrations of three-dimensional skeletonic solids, including the phi-based dodecahedron and icosahedron. These skeletonic solids also included the thirteen Archimedean solids, one of which resembles the modern soccer ball (see here). This three-dimensional solid is formally called a truncated icosahedron, and it consists of twelve pentagons and twenty hexagons.
In 1985, chemists Robert Curl, Harry Kroto, and Richard Smalley announced their discovery of a carbon molecule (C60) with the exact structure of Archimedes’ truncated icosahedron, naming it after American architect and futurist Buckminster Fuller, who popularized the geodesic dome. Like the dodecahedron and icosahedron, the buckminsterfullerene (aka “buckyball”) reflects the golden ratio in its dimensions. For example, when you map the molecule’s sixty points centered at the origin of a three-dimensional Cartesian coordinate system, all sixty coordinates are based on multiples of Φ, as follows 11:
X (0, ±1, ±3Φ)
Y (±1, ±[2 +Φ], ±2Φ)
Z (±2, ±[1 +2Φ], ±Φ)

The structure of buckminsterfullerene carbon molecule mirrors that of the phi-based truncated icosahedron Archimedean solid.
QUANTUM PHI
In January of 2010, Dr. Radu Coldea of Oxford University published a paper discussing the appearance of a golden ratio symmetry in solid state matter. 12 The paper explained that particles on the atomic scale do not behave as those in the macro-atomic world, displaying new properties that emerge as a result of Heisenberg’s Uncertainty Principle. By artificially introducing more quantum uncertainty in their experiments with cobalt niobate, a chain of atoms acting like a nanoscale guitar string created a series or scale of resonant notes, the first two of which had a frequency relationship of 1.618. Coldea is convinced that this was no coincidence, and that it reflected a beautiful property of hidden symmetry of this quantum system, known as E8. The E8, an exceptional simple Lie group, has a beautiful relationship to the golden ratio, as illustrated by the golden ratio concentric half circles overlaying the upper half of the structure in blue, red, gold, and white, revealing a pattern much like the beautiful rose window of Notre-Dame Cathedral.
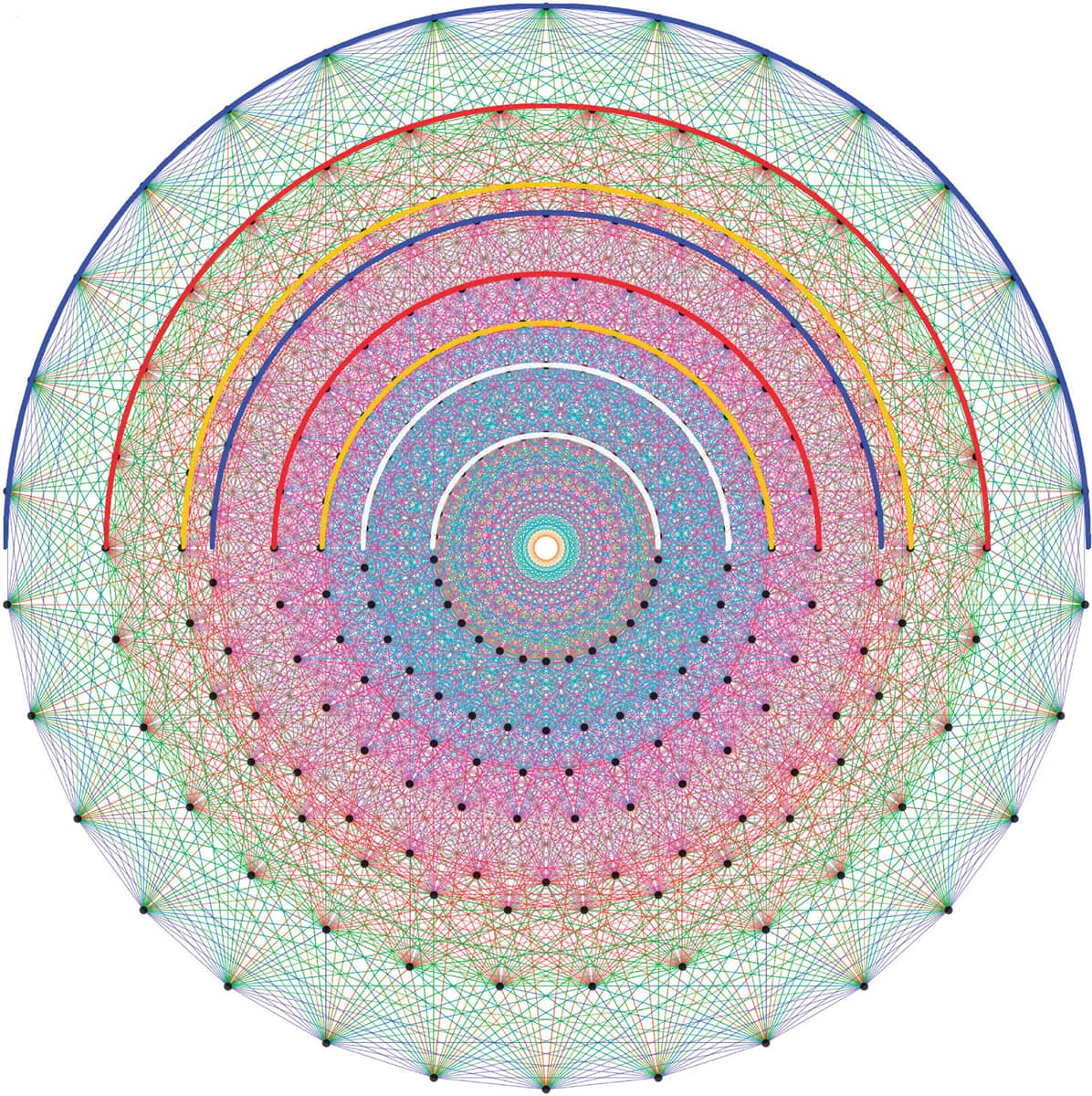
An illustration of the E8 Coxeter plane projection of the 421 semiregular polytope, discovered in 1900 by English mathematician Thorold Gosset, which displays thirty-fold symmetry and golden proportions.

The Coxeter plane projection of the 421 polytope reminds one of the phi-based dimensions of the gorgeous north rose window of Notre-Dame Cathedral.
THE GOLDEN QUESTION
As we look back at mankind’s many discoveries through the millennia, it becomes clear that we live in a universe governed by mathematical laws, golden or not. Whether in Kepler’s laws of planetary orbits, Einstein’s theory of relativity, or the mathematics of the optics in your eye that allow you to read this page, everything we experience in the physical universe can be measured and described by mathematics.
As for the golden ratio, we’ve seen how it has captured the imagination of countless mathematicians, artists, designers, polymaths, biologists, chemists, and even economists with its singular beauty. It is reflected in some of the greatest works of art and architecture ever created in mankind’s history. Not everything is based on the golden ratio, but the number of places in which it seems to appear is truly amazing, and we are sure to uncover it more and more as technology advances and our knowledge of the physical universe expands.
If you explore this topic in more depth, you’ll find some people who will tell you that the golden ratio is a universal constant that defines everything. You’ll find others saying the even the evidence that I’ve presented in this book does not exist at all. This is your golden opportunity to carefully consider what you’ve seen and learned, come to your own thoughtful conclusions, and then ponder the implications.
One question you might ask is why the controversy exists. How and why could this single number found in a simple geometric construction in the writings of an ancient Greek mathematician cause such widespread, passionate discussion and disagreement? The answer may be found in the simple fact that in its own unique way, phi touches upon some of the most fundamental questions of philosophy and the meaning of life. When we discover common threads in the mathematical design of things in our world, especially where it seems unexpected or unexplained, it can beg the question of whether there could be something more than chance at work—a grander plan of design with some guiding purpose, or even a designer. Others may seek to explain these same observations as coincidences arising from natural processes in adaptions and optimizations. Everyone has an underlying belief system that influences their interpretation of everything they see and hear, no matter how much evidence is presented to the contrary. These fundamental questions of where we came from, why we are here, and where we are going, are mysteries that we all must ponder with an open mind and an open heart.
There is another important aspect to the golden ratio, however, that brings a much more universally common response, and that is to touch upon our perceptions of beauty. For some, that beauty is centered on its unique properties in mathematics and geometry, or its ability to create a perfectly formed fractal pattern. For some, it is perceived, whether consciously or not, in the beauty of nature and in the human face and form. For others, intentionally or not, it is expressed in their creative works of art and design.
At whatever level this beauty is perceived, a more important question needs to be asked: How and why do we perceive beauty at all? Why do we have an innate ability to see beauty, and why do we also have a need to express it? From an evolutionary perspective, one could argue that beauty is an indicator of health, and that being drawn to things that are healthy results in better decisions for survival, whether it be which fruit to eat or which mate to select for propagation of the species. That’s logical enough, but what evolutionary advantage is there to the appreciating beauty in a sunset, a starry night, an inspiring work of art, or a song that touches something deep inside you? I think if we’re honest, most people will recognize that there is another aspect to the human experience that goes beyond the facts found solely in scientific, naturalistic explanations of our physical existence. For me, and for many others throughout history, the golden ratio has been a light in the darkness that draws us to a different perspective and a deeper understanding of all that we find around us—and within us.
In this book I’ve only touched on a few of the places where the golden ratio can be found, and a few ways in which it can be applied. More appearances and applications are being discovered all the time, in a surprising number of places. The best way to know for yourself where the golden ratio appears and where it is only imagined is to explore with an open mind, learn all you can, and come to understandings that are truly your own.
As you undertake this journey of discovery, consider the lives and contributions of those who have made this journey before you. Euclid discovered the principles of geometry that taught and inspired people for thousands of years. Leonardo da Vinci and other artists of the Renaissance created a union of mathematics and art that still inspires us today. Johannes Kepler discovered fundamental truths about the solar system that had eluded others for generations before him. Le Corbusier used the inherent harmony of the golden ratio to design the UN Secretariat building that serves as the home of the leading organization to confront common global challenges and bring harmony to the world’s nations. Dan Shechtman discovered a new state of matter that was previously thought impossible. The golden ratio continues to find applications in everything from logo design to quantum mechanics.

Chartres Cathedral illuminated at night.

A closeup of the sunflower’s five-petaled rosettes shows just how ubiquitous the number 5 is in natural life forms.
Luca Pacioli’s appellation of the golden ratio as the “divine proportion” is, indeed, fitting: It is seen and experienced by many as a door to a deeper understanding of beauty and meaning in life, unveiling a hidden harmony or connectedness in so much of what we see. That’s an incredible role for a single number to play, but then again, this one number has played an incredible role in human history, and perhaps in the foundations of life itself.

The spiral in this fractal illustration grows horizontally by a factor of phi.